Closed-Form Sum-Rate Analysis of Interference Alignment with Limited Feedback Based on Scalar Quantization and Random Vector Quantization

Abstract

Interference alignment (IA) is a promising interference management technique to achieve the theoretical optimal degree of freedom (DoF) performance in multi-user cooperation scenarios. However, the effective achievable sum-rate performance of IA is largely affected by the feedback overhead and accuracy of channel state information (CSI) and decoding information (DI). Therefore, it is critical to establish the exact relationship between feedback overhead and the achievable sum-rate of IA to obtain the optimal effective performance. Most existing IA performance analysis approaches focus on the vector quantization (VQ)-based feedback strategy, but the implementation complexity of VQ will be excessive when more quantization bits are required to achieve the expected quantization accuracy for larger-sized matrices or higher signal-to-noise ratio (SNR) regimes. Moreover, the obtained achievable sum-rate formulas are too complicated for quick performance evaluation. In this paper, a new sum-rate performance analysis method for IA under different quantization and feedback strategies is proposed to achieve a trade-off between accuracy and complexity, and the closed-form achievable sum-rate expressions are derived. First, in the IA case with random vector quantization (RVQ)-based CSI feedback, the quantization error of RVQ is transformed into the equivalent VQ error of the Gaussian channel error, based on which the achievable sum-rate formula is obtained. Second, in the IA case with scalar quantization (SQ)-based CSI feedback, the relationship between the effective sum-rate and SQ bits is established. Third, in the IA case with SQ-based CSI feedback and RVQ-based DI feedback, the achievable sum-rate formula is derived by combining these two kinds of quantization errors. Finally, the simulation results confirm that the theoretical results are accurate enough, which can help to determine the optimal CSI feedback overhead in practical channel conditions. Moreover, the theoretical and simulation results demonstrate that RVQ may be more applicable to IA scenarios with fewer receiving antennas and low SNR regimes.

1. Introduction

In the last decade, interference alignment (IA) has received considerable attention due to the advantage that IA can achieve the theoretical optimal degree of freedom (DoF) performance in different kinds of multi-input multi-output (MIMO) interference channels (ICs), interfering multiple-access channels (IMACs) and interfering broadcast channels (IBCs) [1]. A complete cooperative IA transmission process includes several procedures, such as forward channel training and estimation, channel state information (CSI) quantization, quantized CSI feedback, IA solution calculation, decoding information (DI) distribution, and actual payload transmission [2]. Global CSI should be acquired by transmitters to calculate IA precoders and decoders, and the obtained decoders should be known by the receivers to recover their desired signal. Since the channel training sequences, feedback CSI and DI, and actual payload are all transmitted via wireless channels, the effective achievable sum-rate of IA is determined by the time fraction allocation for these procedures [3,4]. When the channel coherence time is given, the more overhead allocated to CSI and DI feedback, the less time is left for actual payload transmission. Conversely, if the quantization accuracy of CSI and DI is reduced, the feedback overhead certainly shrinks, but the effective performance of IA may still be unsatisfactory since the precoders and decoders calculated according to low-accuracy CSI would result in considerable interference leakage and rate loss. Additionally, even though the precoders and decoders can be calculated from accurate CSI, the accuracy of the decoders’ quantization and feedback is another bottleneck for the IA achievable rate. Therefore, a delicate trade-off should be obtained between the quantization accuracy and feedback overhead to optimize the parameter configuration of IA in different cooperative scenarios, and the key is to figure out the relationship between CSI/DI accuracy and effective performance of IA.

In most works, it is a popular method to quantize CSI/DI and feed them back, which is called quantized feedback or limited feedback (LFB). Two common quantization strategies are usually adopted in LFB, i.e., scalar quantization (SQ) and vector quantization (VQ) [5]. In SQ, the real and imaginary parts of each entry in the complex channel matrix/vector are separately quantized. In VQ, a channel matrix or vector is mapped to a codeword from a known codebook, and thus the codeword index is sent instead of the matrix/vector itself. Generally, VQ results in fewer quantization bits and higher complexity than SQ when achieving the same quantization accuracy level. Thus, due to the low feedback overhead advantage, VQ-based LFB has been discussed theoretically in different wireless transmission scenarios, including single-user MIMO, multi-user MIMO and coordinated multiple points [6,7,8]. In practical applications, taking the 3rd Generation Partnerships Project (3GPP) standards for example, the VQ/SQ-based feedback strategies are also called the explicit feedback and implicit feedback, respectively, and the implicit feedback is actually adopted and applied in different closed-loop transmission modes of 4G Long-Term Evolution (LTE) and 5G New Radio (NR) [9,10].

In VQ-based theoretical performance analysis works, the random vector quantization (RVQ) codebook [11] and the Grassmannian codebook [12,13] are two of the most pervasive codebooks. The codewords in RVQ are independent isotropic vectors on a unit complex spherical surface. Due to its simplicity in codebook design, RVQ is usually adopted as the lower bound in performance analysis. The Grassmannian codebook is designed according to the Grassmannian line-packing problem solution, where the minimum value of chordal distances between any two codewords should be maximized [9]. The Grassmannian codebook achieves the upper-bound performance, but its off-line computation complexity for codebook design is high.

Existing performance analysis works of LFB-based IA can be mainly classified into two types: the DoF analysis and the sum-rate analysis. DoF is defined as the ratio of the achievable sum-rate to the logarithm of normalized transmit power $\rho$, and can act as an effective measure of the sum-rate growth in high signal-to-noise ratio (SNR) regimes. Many DoF analysis works established the relationship between the rate loss lower/upper bounds and the quantization bit number, and have concluded that to guarantee the DoF performance in IA, the number of feedback bits should scale with $\rho$ [12,13,14,15]. In DoF-based performance analysis, the RVQ and Grassmannian codebooks obtains identical results. Thukral and Bolcskei were the first to analyze IA performance with LFB, and they found that in K-user frequency-selective single-input single-output (SISO) ICs, the feedback bit number from each receiver should be proportional to $K{log}_2\rho$ [12]. Their analysis method and conclusions were then extended to multi-antenna IA cases, whereby in frequency-selective MIMO ICs, the feedback bit number should scale with the product of transmit and receiver antenna numbers to maintain the DoF slope [13]. When only multi-antenna-domain IA is considered instead of the time or the frequency domain, Xie et al. analyzed the effective DoF in K-user $M\times M$ ICs, where the fed channel quantization bits from each receiver should be $(M^2-1){log}_2\rho$ to maintain the effective DoF [14].

Most works on the DoF performance analyses of LFB-based IA have only focused on the quantization and feedback of CSI and ignored the influence of precoders’ and decoders’ feedback. Wang et al. considered a general centralized feedback model in which the feedback procedures for CSI, precoders and decoders are all involved [16]. In this model, a central unit (CU) is deployed to collect the quantized CSI, design the precoders and decoders, and then separately send the quantized precoders and decoders to transmitters and receivers. By analyzing the influence of quantization bits on rate loss, they also derived the scaling laws of three kinds of feedback bits, i.e., to achieve the same DoF as perfect IA, the feedback bits for each precoder, decoder and channel matrix should be at least $(M-1){log}_2\rho$, $(N-1){log}_2\rho$, and $(MN-1){log}_2\rho$, respectively. The results in [16] are backward compatible with the DoF analyses in [14,15]. Except for the IC case, the IMACs and IBCs are also common IA deployment scenarios in cellular networks, their DoF performance with LFB was investigated in [17,18,19,20], and similar results were also obtained. In addition to the quantitative analysis of DoF performance with quantization bit numbers, some researchers dealt with the imperfect CSI by the Gaussian channel error model to analyze the corresponding rate loss and DoF performance [21,22,23]. However, they did not further connect CSI mismatch to quantization bit numbers.

Since DoF is less effective in measuring the performance at low-moderate SNR regimes, closed-form sum-rate analyses can provide a more direct and accurate rate expression with a given quantization bit number, which is more convenient for performance evaluation during the whole SNR regime. However, different from the diversity of DoF analysis works, sum-rate analysis is rarely involved in IA performance analysis. Chen and Yuen discussed the relationship between the average achievable rate and feedback bit number, derived the closed-form rate formulas, and then also obtained the DoF scaling law, i.e., the DoF performance of LFB-based IA will be identical to perfect CSI cases, as each receiver’s quantization bits increase with $(MN-1){log}_2\rho$ [15]. Similarly, Su et al. comprehensively analyzed the average sum-rate, outage probability, and symbol error rate performances of IA with CSI quantization error, and derived the corresponding closed-form expressions [24]. Though the authors in [15,24] have performed an admirable job in terms of accurate sum-rate analysis, their analysis procedures and the obtained sum-rate formulas are quite complicated and tedious. Therefore, how to evaluate the achievable sum-rate among the whole SNR regime with low complexity and acceptable accuracy is still well worth exploring. Moreover, all those IA performance analyses are based on VQ, whose codebook size grows exponentially with the quantized bits. For large channel matrices or high SNR regime, the increased quantized bit number results in unaffordable complexity when comparing the chordal distances between the target vector and all the codewords. Some researchers tried to reduce the VQ bits from different aspects, including optimizing the codebook design, quantizing the differential CSI, or designing new IA protocols to feedback precoders instead channel matrices [25,26,27,28]. However, their efforts did not change the nature of the exponential complexity problem. Moreover, though SQ is simpler in principle [29], so far few works have investigated the theoretical performance analysis of IA with SQ-based feedback in depth.

To cope with those challenges, in this paper, we focus on establishing a quantitative relationship between feedback bit numbers and the achievable rates of IA based on RVQ and SQ, and derive the concise closed-form sum-rate expressions for convenient performance evaluation. The achievable sum-rate of IA with three feedback types is analyzed, i.e., the RVQ-based CSI feedback case, the SQ-based CSI feedback case, and the mixed case with SQ-based CSI feedback and RVQ-based DI feedback. The closed-form sum-rate formulas of all three cases are derived, and the theoretical analyses are validated by simulation results.

The rest of this paper is organized as follows. In Section 2, we introduce the system model including the CSI and DI feedback procedures. The proposed sum-rate analysis approaches with RVQ-based CSI feedback, SQ-based CSI feedback, and mixed CSI and DI feedback are introduced in Section 3, Section 4 and Section 5, respectively. The simulation results are shown in Section 6, and Section 7 concludes the paper.

Notice that in the following notations, normal letters denote scalar values, boldface lowercase letters and boldface uppercase letters represent vectors and matrices, respectively. ${\mathbf{A}}^H$ denotes the conjugate transpose operator for matrix A.

2. System Model

Consider a K user MIMO IC model, where transmitters and receivers are equipped with M and N antennas, respectively. The transmitters and receivers are denoted as $T_1,T_2,...,T_K$ and $R_1,R_2,...,R_K$, respectively. A complete IA transmission process consists of the following six steps.

• Forward link training and estimation: All K transmitters take turns to broadcast the training symbols. The training matrix for transmitter $T_i$ is denoted by ${\mathsf{\Phi }}_i^{}\in {\mathbb{C}}^{M\times \tau }$, where $\tau \ge M$ is the number of training symbols. Thus, the received signal at receiver $R_k$ can be represented by

  $${\mathbf{y}}_k=\sqrt{\frac{P}{M}}{\mathbf{H}}_{ki}^{}{\mathsf{\Phi }}_i^{}+{\mathbf{n}}_k,$$

  (1)

  where P is the transmit power, ${\mathbf{H}}_{ki}\in {\mathbb{C}}^{N\times M}$ denotes the channel matrix between $T_i$ and $R_k$, and ${\mathbf{n}}_k$ is the Gaussian noise vector. It is assumed that ${\mathbf{H}}_{ki}$ represents the uncorrelated Rayleigh small-scale fading channel, i.e., the elements of ${\mathbf{H}}_{ki}$ are independently and identically distributed (i.i.d.) according to $\mathcal{C}\mathcal{N}(0,1)$. The simplest training matrix is the identity matrix ${\mathsf{\Phi }}_i^{}={\mathbf{I}}_M$. It is assumed that $R_k$ can perfectly estimate ${\mathbf{H}}_{ki,1\le i\le K}^{}$;
• Channel quantization: $R_k$ quantizes the estimated channel matrix ${\mathbf{H}}_{ki,1\le i\le K}^{}$ as ${\widehat{\mathbf{H}}}_{ki,1\le i\le K}^{}$;
• Quantized channel index feedback: $R_k$ feeds back the quantized information of $K-1$ interference channels via the reverse channel. All the K receivers take turns to feed back, and then each transmitter can receive $K(K-1)$ quantized channel matrices;
• IA solution computation: It is assumed that each transmitter computes its own IA precoder and decoder. $T_k$ computes precoding matrix ${\mathbf{V}}_k=[{\mathbf{v}}_k^1,{\mathbf{v}}_k^2,...,{\mathbf{v}}_k^{d_k}]\in {\mathbb{C}}^{M\times d_k}$ and decoding matrix ${\mathbf{U}}_k=[{\mathbf{u}}_k^1,{\mathbf{u}}_k^2,...,{\mathbf{u}}_k^{d_k}]\in {\mathbb{C}}^{N\times d_k}$,where $d_k$ is the transmitted data stream number for transceiver pair $T_i$ and $R_i$. For simplicity, the symmetric IC scenario is considered in this paper, and thus $d_k=d$ holds for all transceiver pairs. Except for some special cases, the IA precoding and decoding matrices are determined via iterative methods [30];
• Quantization and feedback of decoders: To inform $R_k$ of its decoding filter, $T_k$ quantizes ${\mathbf{U}}_k$ as ${\widehat{\mathbf{U}}}_k$ and broadcasts it;
• Concurrent data transmission: All transmitters send their desired signals simultaneously. Then, the received signal at $R_k$ can be represented by

  $${\mathbf{y}}_k=\sum _{i=1}^K{\mathbf{H}}_{ki}{\mathbf{V}}_i{\mathbf{x}}_i+{\mathbf{n}}_k,$$

  (2)

  where ${\mathbf{x}}_i\in {\mathbb{C}}^d$ is the desired signal from $T_i$ to $R_i$.

A typical cellular downlink IA scenario with three user pairs and its transmission process is shown in Figure 1. Via decoding filter ${\widehat{\mathbf{U}}}_k$, the recovered signal for $R_k$ can be written as

$${\widehat{\mathbf{x}}}_k={\widehat{\mathbf{U}}}_k^H\sum _{i=1}^K{\mathbf{H}}_{ki}{\mathbf{V}}_i{\mathbf{x}}_i+{\widehat{\mathbf{U}}}_k^H{\mathbf{n}}_k.$$

(3)

Therefore, the average achievable rate of IA with LFB can be approximated by [4]

$$R_{IA}\approx E\left(\sum _{m,k}{log}_2\left(1+\frac{\frac{P}{d}{\left|{\widehat{\mathbf{u}}}_k^{mH}{\mathbf{H}}_{kk}{\mathbf{v}}_k^m\right|}^2}{{\displaystyle \sum _{(k,m)\ne (i,l)}}\frac{P}{d}{\left|{\widehat{\mathbf{u}}}_k^{mH}{\mathbf{H}}_{ki}{\mathbf{v}}_i^l\right|}^2+{\sigma }^2}\right)\right).$$

(4)

In (4), $\frac{P}{d}{\left|{\widehat{\mathbf{u}}}_k^{mH}{\mathbf{H}}_{ki}{\mathbf{v}}_i^l\right|}^2$ is the interference between different users or different streams belonging to the same user. If CSI and DI could be perfectly fed back, this interference term would be zero. With the inherent quantization error, the interference term decreases the achievable rate. In the following sections, we will discuss the relationship among the achievable rate, quantization bits and quantization error under different quantization strategies.

3. Sum-Rate Performance with RVQ-Based CSI Feedback

3.1. Vector Quantization of Channel Matrix

With VQ-based CSI feedback, channel matrices $\mathbf{H}\in {\mathbb{C}}^{N\times M}$ are vectorized first and then quantized. The normalized $M_h$-dimensional unit complex vector from $\mathbf{H}$ with $M_h=N\times M$ is denoted by

$$\mathbf{h}=\frac{vec\left(\mathbf{H}\right)}{∥vec\left(\mathbf{H}\right)∥}.$$

(5)

Before VQ, the codebook is already known to transmitters and receivers. With B bits to quantize $\mathbf{h}$, the codebook has $N_B=2^B$ codewords, and each codeword is an $M_h$-dimensional unit complex vector. The codebook can be denoted as $C=\left\{{\mathbf{w}}_1,{\mathbf{w}}_2,...,{\mathbf{w}}_{N_B}\right\}$. The quantization of $\mathbf{h}$ is to find the codeword nearest to $\mathbf{h}$ in codebook C, i.e., to search for the index of the vector achieving the minimum inner product with $\mathbf{h}$, which can be denoted by [9]

$$\begin{array}{c}\hfill I_h=arg\underset{j=1,2,...,2^B}{min}{sin}^2\angle \left(\mathbf{h},{\mathbf{w}}_j\right).\end{array}$$

(6)

Here $\angle \left(\mathbf{h},{\mathbf{w}}_j\right)$ is the angle of two unit complex vectors. Index $I_h$ is fed back to the corresponding transmitter, and the transmitter recovers the quantized channel according to vector $\widehat{\mathbf{h}}$, which is exactly the $I_h$-th codeword. $z={sin}^2\angle \left(\mathbf{h},\widehat{\mathbf{h}}\right)$ is defined as the quantization error in VQ, whose distribution depends on the codebook design criterion.

For simplicity, the RVQ codebook is used for performance analysis in this paper. Though the quantization error of the RVQ codebook is higher than that of the Grassmannian codebook, the sum-rate derivation framework is applicable to different codebooks. It has been proved that with the increase in B, the quantization errors of the RVQ and Grassmannian codebooks converge [9].

In RVQ, define $y=1-z={cos}^2\angle \left(\mathbf{h},\widehat{\mathbf{h}}\right)$ as the complementary quantization error. Then, the distribution properties of quantization error z can be obtained by analyzing the distribution of y. In $M_h$-dimensional complex space, the cumulative distribution function (CDF) of the cosine square value of the angle between two random independent isotropic unit complex vectors is [11]

$$F_{cos}\left(x\right)=1-{(1-x)}^{M_h-1}.$$

(7)

Then, the CDF of $y={cos}^2\angle \left(\mathbf{h},\widehat{\mathbf{h}}\right)$ is

$$\begin{array}{c}\hfill F_Y\left(y\right)=\sum _{i=0}^{2^B}{C}_{2^B}^i{(-1)}^i{(1-y)}^{i(M_h-1)}.\end{array}$$

(8)

Its expectation is

$$E\left(y\right)={\int }_0^{1}yf\left(y\right)dy=1-2^{B}Beta\left(2^B,\frac{M_h}{M_h-1}\right),$$

(9)

where $Beta\left(x,y\right)=\frac{\mathsf{\Gamma }\left(x\right)\mathsf{\Gamma }\left(y\right)}{\mathsf{\Gamma }(x+y)}$ is the Beta function, and $\mathsf{\Gamma }\left(x\right)={\int }_0^{\infty }{t}^{x-1}{e}^{-t}dt$ is the Gamma function [9].

Therefore, the CDF of the quantization error in RVQ is

$$F_z\left(z\right)=1-F_X\left(x\right){|}_{x=1-z}=1-{\left(1-z^{M_h-1}\right)}^{2^B},$$

(10)

and its expectation is $E\left(z\right)=2^{B}Beta\left(2^B,\frac{M_h}{M_h-1}\right)$, with upper bound $E\left(z\right)\le 2^{-\frac{B}{M_h-1}}$.

3.2. Similarity between RVQ Error and Gaussian Channel Error

It is complicated to derive the achievable rate by directly using the RVQ error. However, we can approximate the RVQ error as the equivalent Gaussian channel error on the basis of the similarity between the expressions of these two kinds of errors and then cross-verify the validness of this approximation operation by simulation. Notice that the relationship between original vector $\mathbf{h}$ and quantized vector $\widehat{\mathbf{h}}$ in VQ can be rewritten as

$$\mathbf{h}=cos\theta \widehat{\mathbf{h}}+sin\theta \tilde{\mathbf{h}},$$

(11)

where $\theta$ is the angle between $\mathbf{h}$ and $\widehat{\mathbf{h}}$, $\tilde{\mathbf{h}}$ is independent of $\theta$, and $\tilde{\mathbf{h}}$ is isotropically distributed in the $M_h-1$-dimensional subspace orthogonal to $\widehat{\mathbf{h}}$ [11]. As for the Gaussian channel error model, the CSI imperfection can be described by the Gauss-Markov model [4] as

$$\mathbf{H}=\sqrt{1-{\beta }^2}\widehat{\mathbf{H}}+\beta \mathbf{E},$$

(12)

where the entries of $\mathbf{H}$, $\widehat{\mathbf{H}}$ and $\mathbf{E}$ are all independent identically distributed (i.i.d.) according to $\mathcal{CN}(0,1)$. $\mathbf{H}$ is the actual channel matrix, $\widehat{\mathbf{H}}$ is the imperfect observation of $\mathbf{H}$ due to the additive noise term $\mathbf{E}$, and $\beta$ represents the variance of the Gaussian channel error. If $\beta =0$, no Gaussian channel error exists.

According to the similarity between (11) and (12), we made two hypotheses whereby we can adopt the Gaussian channel error model to approximate the RVQ error when the following two conditions are both satisfied: (1) the value of $\beta$ is small enough; (2) two kinds of errors, i.e., the equivalent VQ error of the Gaussian channel error and the original RVQ error, have similar probability distribution functions (PDFs). The equivalent VQ error of the Gaussian channel error is defined as the sin square value of the angle between vectorized and normalized $\mathbf{H}$ and $\widehat{\mathbf{H}}$, denoted by

$$\tilde{z}={sin}^2\angle (vec\left(\mathbf{H}\right),vec(\widehat{\mathbf{H}})).$$

(13)

If the two conditions are satisfied simultaneously, the RVQ error could be transformed into the equivalent Gaussian channel error, and therefore the existing closed-form sum-rate expression based on the Gaussian channel error model in [4] can be used. The validness of this hypothesis can be confirmed by numerical results.

In Figure 2, we transformed Gaussian channel error models with different $\beta$ values into the equivalent VQ error models and compared the expectations of equivalent VQ errors $\tilde{z}$ and ${\beta }^2$. In Figure 2, the expectation of $\tilde{z}={sin}^2\theta$ and ${\beta }^2$ are almost identical for $\beta \le 0.4$. Next, we set $E\left(z\right)={\beta }^2$ and compared the PDFs of RVQ error $z={sin}^2\theta$ and equivalent VQ error $\tilde{z}={sin}^2\angle (vec\left(\mathbf{H}\right),vec(\widehat{\mathbf{H}}))$ separately from the RVQ error model (11) and the Gaussian channel error model (12). In quantizing a $2\times 2$ complex matrix, if $B=20$, the mean of the RVQ error is $E\left(z\right)=0.0088$ and corresponds to $\beta =0.0938$ in (12). The PDFs of RVQ error z and equivalent VQ error $\tilde{z}$ with $\beta =0.0938$ are illustrated in Figure 3, where they are quite similar, with limited drift.

As shown in Figure 2 and Figure 3, we can conclude that the hypothetical conditions are feasible, and then the sum-rate based on RVQ can be transformed into the sum-rate analysis based on Gaussian channel errors. In RVQ, the quantization error mean is $E\left(z\right)=2^{B}Beta(2^B,\frac{NM}{NM-1})$ using B bits to quantize an $N\times M$ complex matrix. Then, $E\left(z\right)$ can be treated as the Gaussian error variance ${\beta }^2$, i.e., $\beta =\sqrt{E\left(z\right)}$. Therefore, the Gaussian channel error model equivalent to the original RVQ model can be denoted by

$$\mathbf{H}=\sqrt{1-E\left(z\right)}\widehat{\mathbf{H}}+\sqrt{E\left(z\right)}\mathbf{E}.$$

(14)

According to Lemma 1 in [4], effective direct channels ${\mathbf{u}}_k^{mH}{\mathbf{H}}_{kk}{\mathbf{v}}_k^m$ are independent and Gaussian-distributed complex variables with unit variance. Thus, the effective direct channel in each IA data stream is equivalent to a Rayleigh fading channel, and the achievable sum-rate of IA with perfect CSI can be represented by

$$R_{IA}\approx E\left(\sum _k\sum _m{r}_k^m\right)\approx Kd{log}_2\left(e\right)e^{1/\rho }{E}_1(\frac{1}{\rho }),$$

(15)

where $\rho =\frac{P}{d{\sigma }^2}$ is the effective SNR in each stream, and $E_1\left(\eta \right)={\int }_1^{\infty }{t}^{-1}{e}^{-\eta t}dt$ is the exponential integral function [4].

In the Gaussian channel error model, the channel matrices obtained by the receivers are $\sqrt{1-{\beta }^2}{\widehat{\mathbf{H}}}_{ki}$; then, the precoding and decoding vectors ${\mathbf{u}}_k^m$ and ${\mathbf{v}}_k^m$ are solved based on imperfect ${\widehat{\mathbf{H}}}_{ki}$. Thus, for $(k,m)\ne (i,l)$, ${\mathbf{u}}_k^{mH}{\widehat{\mathbf{H}}}_{ki}{\mathbf{v}}_i^l=0$ holds, and the intra-stream interference can be written as

$${\mathbf{u}}_k^{mH}{\mathbf{H}}_{ki}{\mathbf{v}}_i^l={\mathbf{u}}_k^{mH}\left(\sqrt{1-{\beta }^2}\widehat{\mathbf{H}}+\beta \mathbf{E}\right){\mathbf{v}}_i^l=\beta {\mathbf{u}}_k^{mH}{\mathbf{Ev}}_i^l,$$

(16)

where ${\mathbf{u}}_k^{mH}{\mathbf{Ev}}_i^l$ are also independent and Gaussian-distributed complex variables with unit variance. Finally, the achievable sum-rate of IA with RVQ-based CSI feedback can be approximated by

$$R_{RVQ}\approx E\left(\sum _{m,k}{log}_2\left(1+\frac{\frac{P}{d}{\left|{\mathbf{u}}_k^{mH}{\mathbf{H}}_{kk}{\mathbf{v}}_k^m\right|}^2}{{\displaystyle \sum _{(k,m)\ne (i,l)}}\frac{P}{d}{\left|\beta {\mathbf{u}}_k^{mH}{\mathbf{Ev}}_i^l\right|}^2+{\sigma }^2}\right)\right)\approx Kd{log}_2\left(e\right)e^{1/{\rho }_{eff}}{E}_1(\frac{1}{{\rho }_{eff}}),$$

(17)

where

$${\rho }_{eff}=\frac{\rho }{\rho (Kd-1){\beta }^2+1}=\frac{\rho }{\rho (Kd-1)2^{B}Beta(2^B,\frac{NM}{NM-1})+1}$$

(18)

denotes the effective SNR with the introduced quantization error from RVQ. The accuracy of (17) is demonstrated in Section 6.

4. Sum-Rate Performance with SQ-Based CSI Feedback

In RVQ, if the channel matrix size is large or the required quantization error is quite small, increased quantization bit number B results in an unaffordable codebook size. The exponentially increasing codebook size increases both the memory size and the codeword searching complexity. Under the circumstances, the traditional SQ method shows up as an alternative. For complex matrix $\mathbf{H}\in {\mathbb{C}}^{N\times M}$, each entry is quantized with $2B$ bits, and the real and imaginary parts of each entry are separately quantized with B bits.

4.1. Achievable Sum-Rate with SQ-Based CSI Feedback

It is assumed that the entries in $\mathbf{H}$ are all i.i.d. according to $\mathcal{CN}(0,1)$; therefore, the real and imaginary parts of entries in $\mathbf{H}$ are all i.i.d. real Gaussian variables with zero mean and 1/2 variance.

For a real Gaussian variable obeying $\mathcal{N}(0,{\sigma }^2)$, since the probability that its value falls out of interval $[-3\sigma ,3\sigma ]$ is less than $0.3\%$, we quantize this real Gaussian variable within $[-3\sigma ,3\sigma ]$. For simplicity, the uniform quantization method is adopted; accordingly, interval $\left(-3\sigma ,3\sigma \right)$ is divided into $M_q=2^B$ equal quantized intervals with B quantization bits, where the length of each quantized interval is $\Delta =\frac{6\sigma }{M_q}=\frac{3\sigma }{2^{B-1}}$. The first quantized interval is from $m_0=-3\sigma$, and the right-end point of the i-th quantized interval is $m_i=m_{i-1}+\Delta ,1\le i\le M_q$. The codeword for the i-th quantized interval is defined by

$$q_i=\frac{m_{i-1}+m_i}{2},1\le i\le M_q.$$

(19)

Therefore, the codebook for uniform scalar quantization in interval $[-3\sigma ,3\sigma ]$ with B quantization bits is $C=\{q_i=(i-0.5)3\sigma /2^{B-1},1\le i\le 2^B\}$. By applying uniform quantization with B bits, the sample of Gaussian random variable x obeying $\mathcal{N}(0,1/2)$ is quantized as a new random variable, $\widehat{x}$, and the variance of the quantization error is defined and approximated as [5]

$$E{(x-\widehat{x})}^2\approx \frac{{\Delta }^2}{12}={\left(\frac{3\sigma }{2^{B-1}}\right)}^2/12=\frac{3}{2^{2B+1}}.$$

(20)

Therefore, if the entries in $\mathbf{H}\in {\mathbb{C}}^{N\times M}$ are all i.i.d. according to $\mathcal{CN}(0,1)$, $\mathbf{H}$ is quantized as $\widehat{\mathbf{H}}$ with $2B$ quantization bits for each entry, and we have $\mathbf{H}=\widehat{\mathbf{H}}+\tilde{\mathbf{H}}$, where $\tilde{\mathbf{H}}$ is the error matrix with each entry i.i.d. with zero mean and variance of ${\sigma }_{\tilde{H}}^2=\frac{3}{2^{2B}}$.

With SQ, the transmitters compute precoders ${\mathbf{v}}_k^m$ and decoders ${\mathbf{u}}_k^m$ according to ${\widehat{\mathbf{H}}}_{ki}$, where ${\mathbf{u}}_k^{mH}{\widehat{\mathbf{H}}}_{ki}{\mathbf{v}}_i^l=0$ holds for $(k,m)\ne (i,l)$. Thus, the interference term can be represented by

$${\mathbf{u}}_k^{mH}{\mathbf{H}}_{ki}{\mathbf{v}}_i^l={\mathbf{u}}_k^{mH}\left({\widehat{\mathbf{H}}}_{ki}+{\tilde{\mathbf{H}}}_{ki}\right){\mathbf{v}}_i^l={\mathbf{u}}_k^{mH}{\tilde{\mathbf{H}}}_{ki}{\mathbf{v}}_i^l.$$

(21)

Since ${\mathbf{v}}_k^m$ and ${\mathbf{u}}_k^m$ are unit vectors, and the entries of ${\tilde{\mathbf{H}}}_{ki}$ all are all i.i.d. with zero mean and variance of $\frac{3}{2^{2B}}$, the entries of ${\mathbf{u}}_k^{mH}{\tilde{\mathbf{H}}}_{ki}{\mathbf{v}}_i^l$ are also i.i.d. with the same distribution as the entries of ${\tilde{\mathbf{H}}}_{ki}$. Therefore, the achievable sum-rate of IA with uniform SQ-based CSI feedback can be approximated by

$$R_{SQ}\approx E\left(\sum _{k,m}{log}_2\left(1+\frac{\frac{P}{d}{\left|{\mathbf{u}}_k^{mH}{\mathbf{H}}_{kk}{\mathbf{v}}_k^m\right|}^2}{(Kd-1)\frac{P{\sigma }_{\tilde{H}}^2}{d}+{\sigma }^2}\right)\right)\approx Kd{log}_2\left(e\right)e^{1/{\rho }_{eff}}{E}_1(\frac{1}{{\rho }_{eff}}),$$

(22)

where

$${\rho }_{eff}=\frac{\rho }{\rho (Kd-1){\sigma }_{\tilde{H}}^2+1}=\frac{\rho }{\rho (Kd-1)\frac{3}{2^{2B}}+1}$$

(23)

denotes the effective SNR with the introduced quantization error from uniform SQ. The accuracy of (22) is also demonstrated in Section 6.

4.2. Complexity Comparison of RVQ and SQ

To compare the implementation complexity quantificationally, we adopt the number of floating-point operations (FLOPs) as the computational complexity measure in SQ and RVQ. A FLOP is either a complex multiplication or a complex summation, and the FlOP numbers for matrix-scaling operation $a\mathbf{A}$ and inner product operation ${\mathbf{a}}^H\mathbf{b}$ are $MN$ and $2N-1$, respectively [31], where $\mathbf{a},\mathbf{b}\in {\mathbb{C}}^N$ and $\mathbf{A}\in {\mathbb{C}}^{N\times M}$.

For complex matrix $\mathbf{H}$, its SQ operation is equivalent to a matrix-scaling operation, and therefore the computational complexity of one SQ operation is $\mathcal{O}\left(MN\right)$. With B bits to quantize complex matrix $\mathbf{H}$, one RVQ operation mainly includes three steps, i.e., vectorizing $\mathbf{H}$ in (5), calculating the inner products of $\mathbf{h}$ and all codewords in (6) and searching for the codeword with the largest inner product value. The vectorization of $\mathbf{H}$ requires $3MN-1$ flops; the inner product of $\mathbf{h}$ and $2^B$ codewords requires $2^B(2MN-1)$ flops; the computational complexity of codeword searching is $\mathcal{O}\left(2^B\right)$. Therefore, the computational complexity of one SQ operation is $\mathcal{O}\left(2^{B}MN\right)$.

5. Sum-Rate Performance with SQ-Based CSI Feedback and RVQ-Based DI Feedback

In Section 3 and Section 5, the analyses are based on the fact that DI is perfectly known to the receivers. In this section, the quantization error resulting from the decoders’ feedback is taken into consideration. Since the decoder’s size is much lower than its channel matrix, we quantize the CSI and DI via SQ and RVQ, respectively, to achieve a trade-off between complexity and feedback overhead.

After the receivers quantize and feed back the channel matrices via SQ, the transmitters determine precoders ${\mathbf{V}}_k$ and decoders ${\mathbf{U}}_k$ according to quantized channel matrices ${\widehat{\mathbf{H}}}_{ki}$. According to the IA principle, ${\mathbf{u}}_k^{mH}{\widehat{\mathbf{H}}}_{ki}{\mathbf{v}}_i^l=0$ holds for $(k,m)\ne (i,l)$. Then, transmitter $T_k$ continues quantizing decoding vectors ${\mathbf{u}}_k^m,1\le m\le d$ and feeds them back to receiver $R_k$. In this section, we continue to adopt RVQ to quantize each decoding vector with $B_u$ bits; thus, ${\mathbf{u}}_k^m$ is quantized to be ${\widehat{\mathbf{u}}}_k^m$.

According to the distribution of the RVQ error, when an $N\times 1$ complex unit vector ${\mathbf{u}}_k^m$ is quantized with $B_u$ bits, the mean quantization error is $E\left(z\right)=2^{B_u}Beta\left(2^{B_u},\frac{N}{N-1}\right)$. Based on the RVQ principle, ${\widehat{\mathbf{u}}}_k^m$ can be rewritten as

$${\widehat{\mathbf{u}}}_k^m=cos\theta {\mathbf{u}}_k^m+sin\theta {\tilde{\mathbf{u}}}_k^m,$$

(24)

where $\theta$ is the angle, ${\tilde{\mathbf{u}}}_k^m$ is independent of $\theta$, and ${\tilde{\mathbf{u}}}_k^m$ is isotropically distributed in the $N-1$-dimensional subspace which is orthogonal to ${\mathbf{u}}_k^m$.

Therefore, for receiver $R_k$, its inter-stream or inter-user interference can be denoted by

$${\widehat{\mathbf{u}}}_k^{mH}{\mathbf{H}}_{ki}{\mathbf{v}}_i^l=sin\theta {\tilde{\mathbf{u}}}_k^{mH}{\mathbf{H}}_{ki}{\mathbf{v}}_i^l+cos\theta {\mathbf{u}}_k^{mH}{\tilde{\mathbf{H}}}_{ki}{\mathbf{v}}_i^l,\forall (k,m)\ne (i,l).$$

(25)

The derivation of (25) is shown as (A1) in Appendix A.

Notice that ${\tilde{\mathbf{u}}}_k^{mH}{\mathbf{H}}_{ki}{\mathbf{v}}_i^l$ is a complex Gaussian random variable with zero mean and unit variance, and ${\mathbf{u}}_k^{mH}{\tilde{\mathbf{H}}}_{ki}{\mathbf{v}}_i^l$ can be approximated as a complex Gaussian random variable with zero mean and ${\sigma }_{\tilde{H}}^2=\frac{3}{2^{2B}}$ variance. Thus, we have

$$E\left({\left|{\widehat{\mathbf{u}}}_k^{mH}{\mathbf{H}}_{ki}{\mathbf{v}}_i^l\right|}^2\right)\approx 2^{B_u}Beta\left(2^{B_u},\frac{N}{N-1}\right)+\left(1-2^{B_u}Beta\left(2^{B_u},\frac{N}{N-1}\right)\right)\frac{3}{2^{2B}}.$$

(26)

The derivation of (26) is shown as (A2) in Appendix A.

Therefore, the average achievable sum-rate for IA with SQ-based CSI feedback and RVQ-based DI feedback can be approximated by

$$\begin{array}{cc}\hfill R_{IA}& \approx E\left(\sum _k\sum _m{log}_2\left(1+\frac{\frac{P}{d}{\left|{\widehat{\mathbf{u}}}_k^{mH}{\mathbf{H}}_{kk}{\mathbf{v}}_k^m\right|}^2}{{\displaystyle \sum _{(k,m)\ne (i,l)}}\frac{P}{d}{\left|{\widehat{\mathbf{u}}}_k^{mH}{\mathbf{H}}_{ki}{\mathbf{v}}_i^l\right|}^2+{\sigma }^2}\right)\right)\hfill \\ \hfill & \approx E\left(\sum _k\sum _m{log}_2\left(1+\frac{\frac{P}{d}{\left|{\widehat{\mathbf{u}}}_k^{mH}{\mathbf{H}}_{kk}{\mathbf{v}}_k^m\right|}^2}{(Kd-1)\frac{P}{d}{\sigma }_{FB}^2+{\sigma }^2}\right)\right)=Kd{log}_2\left(e\right)e^{1/{\rho }_{eff}}{E}_1(\frac{1}{{\rho }_{eff}}),\hfill \end{array}$$

(27)

where

$${\rho }_{eff}=\frac{\rho }{\rho (Kd-1){\sigma }_{FB}^2+1},$$

(28)

and

$${\sigma }_{FB}^2=2^{B_u}Beta\left(2^{B_u},\frac{N}{N-1}\right)+\left(1-2^{B_u}Beta\left(2^{B_u},\frac{N}{N-1}\right)\right)\frac{3}{2^{2B}}.$$

(29)

${\rho }_{eff}$ can be treated as the equivalent SNR after the quantization errors of SQ and RVQ are both introduced.

6. Simulation Results

In this section, the results of a Monte Carlo simulation performed to demonstrate the effectiveness of the proposed sum-rate expressions are shown. The theoretical and simulated sum-rate performances with different cooperative user numbers, quantization bits and feedback strategies were compared. During each snapshot, the channel matrices were randomly generated; then, the instantaneous achievable rate was determined according to the quantized CSI and DI. The final average achievable rate is the mean of all instantaneous rates from all snapshots. The simulation IA scenarios are simply symmetric K-user ICs with the small-scale Rayleigh fading channel model, denoted by $(M\times N,d)K$, where M, N, d, and K separately represent the numbers of transmitter antennas, receiver antennas, data streams, and cooperative users.

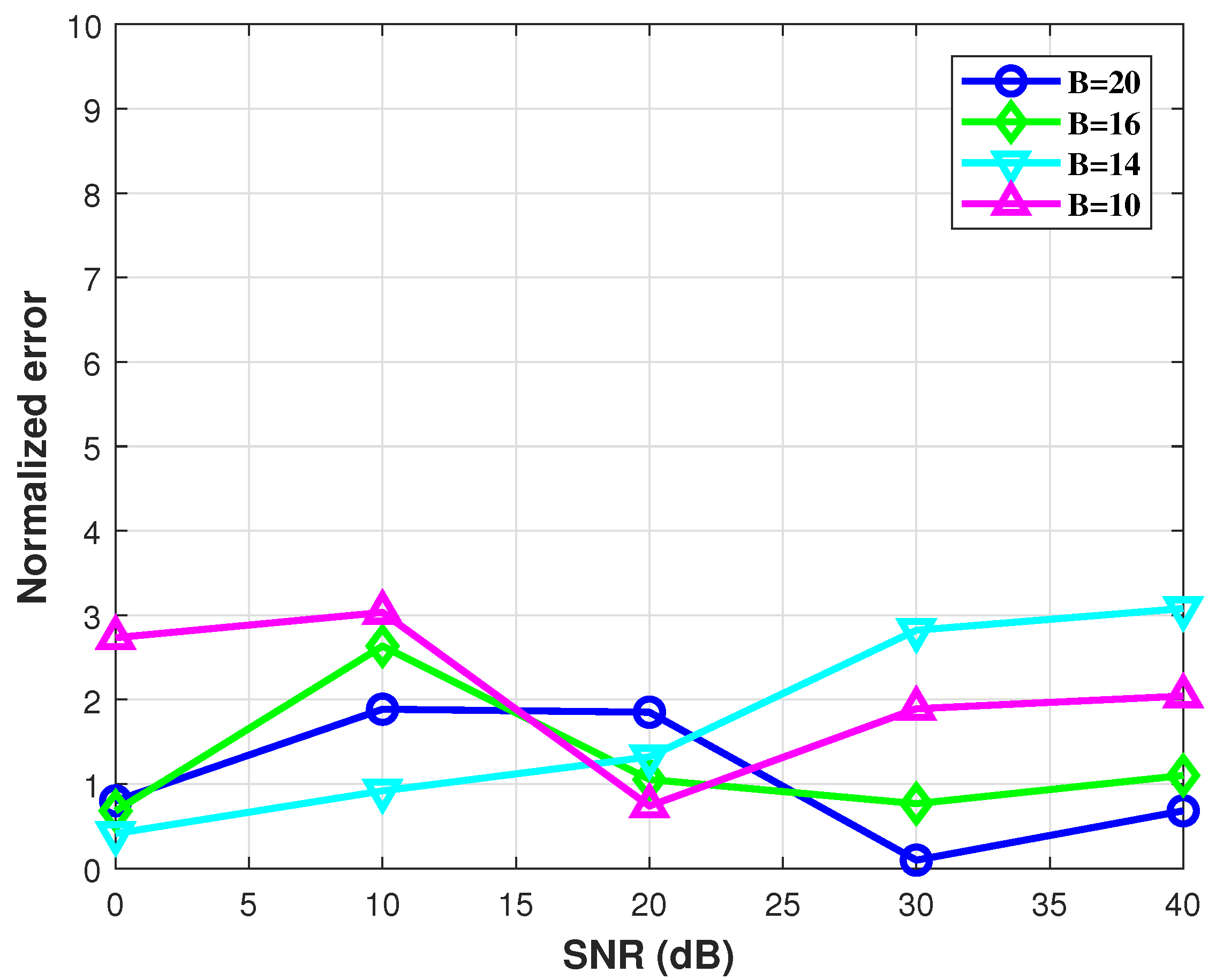
6.1. RVQ-Based CSI Feedback

The sum-rate curves of IA with perfect CSI and RVQ-based CSI feedback with different quantization bits in three $2\times 2$ transceiver pairs are compared in Figure 4, and the corresponding approximation errors are calculated in Figure 5. The theoretical sum-rate curves are based on (17), and the other curves, including the perfect IA and RVQ-based feedback, are all from simulation. In each snapshot, the channel matrices were quantized using RVQ, the precoders and decoders were computed from the quantized CSI, and the decoders were perfectly known to the receivers. From Figure 4 and Figure 5, we can see that the approximation accuracy of (17) is acceptable when quantizing the $2\times 2$ complex matrices with more than 10 bits, and the normalized sum-rate error between the theoretical and simulation results is generally less than $5\%$.

When the SNR is higher than 20 dB in Figure 4, the sum-rate with quantized CSI gradually saturates, and the performance difference between perfect CSI and quantized CSI is significant. To guarantee the DoF performance, the quantization bits should increase with the SNR. However, since the codebook size increases exponentially with the number of quantization bits, the storage space for the codebook and the complexity for codeword searching become obstacles in practical applications. For example, the quantization of a $2\times 2$ complex matrix with 20 bits results in a codebook with more than 60 KB memory space, and $2^{20}$ chordal distances need to be calculated and compared for the optimal codeword in each quantization. Since the $(2\times 2,1)3$ case is the simplest scenario for IA, the codebook oversizing and complexity issues are worse for larger channel matrices. Therefore, a more practical approach to CSI quantization should be adopted in general IA cases.

In Figure 6, the theoretical results of three sum-rate analysis methods with RVQ-based CSI feedback are compared in case $(2\times 2,1)3$, including our proposed method and two other methods separately from [2,16]. The latter two methods derived the rate loss upper bound in LFB-based IA and further discussed the DoF performance. It can be seen from Figure 6 that the proposed sum-rate approximation method achieves much higher accuracy than the rate loss-based analysis methods. Moreover, our closed-form sum-rate formula is much more concise than the accurate but tedious expressions in [15,24], which are in the form of a sum of complicated series.

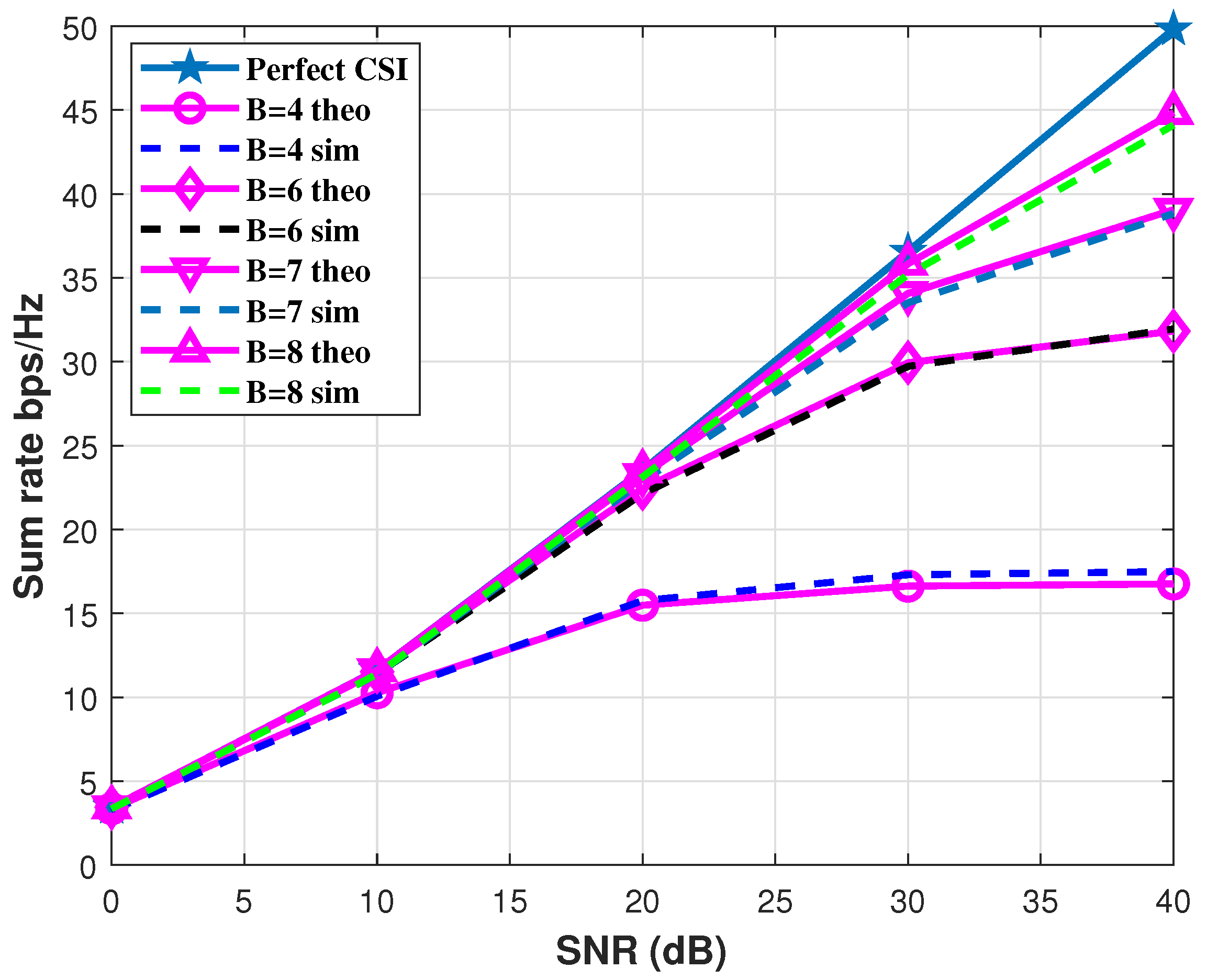
6.2. SQ-Based CSI Feedback

The sum-rate curves of IA with perfect CSI and SQ-based CSI feedback with different quantization bits in $(2\times 2,1)3$, $(3\times 2,1)4$ and $(3\times 3,1)5$ are separately compared in Figure 7, Figure 8 and Figure 9, and the corresponding approximation errors are calculated in Figure 10. The theoretical sum-rate curves are based on (22), and the other curves also result from simulation. In each snapshot, the channel matrices were quantized using SQ, and the decoders were also perfectly known to the receivers, similar to what is described in the previous subsection.

With the increase in quantization bits, the theoretical sum-rates gradually transition from being below the simulation results to being above them, especially when the SNR is higher than 20 dB, but the normalized approximation errors are still less than $5\%$. To guarantee the DoF performance, increasing the quantization bits is feasible in SQ since the implementation complexity of SQ is much lower than that of RVQ. Meanwhile, the total feedback bits of SQ are much more than these of RVQ to maintain the same quantization accuracy level. Therefore, SQ is more applicable to high SNR regimes, larger-sized matrices and real-time implementations of IA.

6.3. SQ-Based CSI Feedback and RVQ-Based DI Feedback

The sum-rate curves of IA with perfect CSI and mixed CSI/DI feedback in $(2\times 2,1)3$, $(3\times 2,1)4$ and $(3\times 3,1)5$ are compared in Figure 11, Figure 12 and Figure 13, respectively, and the corresponding approximation errors are calculated in Figure 14. The theoretical sum-rate curves are based on (27). In each snapshot, the channel matrices and decoders were separately quantized using SQ and RVQ. The quantization bit number for CSI was fixed at $B=8$, and the quantization bits for DI increased from 10 to 16 in $(2\times 2,1)3$ and $(3\times 2,1)3$ and increased from 16 to 21 in $(3\times 3,1)5$. In all the SNR regimes and different quantization bit configurations, the normalized approximation errors are all less than $5\%$, which makes the theoretical sum-rate expressions applicable to general IA scenarios.

As shown in Figure 11 and Figure 12, the rate loss resulting from decoder quantization with $B_u=16$ is minor even for an SNR of 40 dB. Meanwhile, in Figure 13, considerable rate loss results from using RVQ with 21 quantization bits when the SNR is higher than 20 dB. However, since a 21-bit RVQ codebook hardly seems practical, the dominant area for the VQ-based quantization strategy may be limited to scenarios with fewer receiving antennas and low SNR regimes.

7. Conclusions

In this paper, the relationships between the achievable sum-rate of IA and quantization bits under different quantization strategies are analyzed, and the theoretical closed-form formulas of the average IA sum-rates with RVQ-based CSI feedback, SQ-based CSI feedback, and mixed CSI/DI feedback are separately derived. The simulation results have confirmed the validness of the approximated sum-rate results, whose normalized approximation errors are less than 5% in general IA scenarios. The proposed sum-rate analysis method is more accurate than those rate loss-based performance analyses and obtains concise enough sum-rate expressions, achieving a trade-off between accuracy and complexity. The theoretical and simulation results demonstrate that the popular VQ-based feedback may be more applicable to IA scenarios with fewer receiving antennas and low SNR regimes, while the mixed SQ-based CSI and VQ-based DI feedback strategy can have a wider application range. The proposed IA performance analysis method can act as a guidance to determine the optimal feedback overhead in practical channel conditions. In the future, we may extend the analysis results by combining neutrosophic statistics in several directions, such as considering a more complicated neutrosophic Rayleigh model in the wireless channel [32], and reducing the approximation error by analyzing the distribution characteristics of different kinds of quantization errors [33,34,35].