Improved Analytic Expansions in Hybrid A-Star Path Planning for Non-Holonomic Robots

Abstract

In this study, we concisely investigate two phases in the hybrid A-star algorithm for non-holonomic robots: the forward search phase and analytic expansion phase. The forward search phase considers the kinematics of the robot model in order to plan continuous motion of the robot in discrete grid maps. Reeds-Shepp (RS) curve in the analytic expansion phase augments the accuracy and the speed of the algorithm. However, RS curves are often produced close to obstacles, especially at corners. Consequently, the robot may collide with obstacles through the process of movement at these corners because of the measurement errors or errors of motor controllers. Therefore, we propose an improved RS method to eventually improve the hybrid A-star algorithm’s performance in terms of safety for robots to move in indoor environments. The advantage of the proposed method is that the non-holonomic robot has multiple options of curvature or turning radius to move safer on pathways. To select a safer route among multiple routes to a goal configuration, we introduce a cost function to evaluate the cost of risk of robot collision, and the cost of movement of the robot along the route. In addition, generated paths by the forward search phase always consist of unnecessary turning points. To overcome this issue, we present a fine-tuning of motion primitive in the forward search phase to make the route smoother without using complex path smoothing techniques. In the end, the effectiveness of the improved method is verified via its performance in simulations using benchmark maps where cost of risk of collision and number of turning points are reduced by up to around 20%.

1. Introduction

Since the emergence of artificial intelligence, path planning has become an attractive topic investigated in many studies. Popular path planning methods such as probabilistic road map (PRM), rapidly-exploring random tree (RRT), and space skeletonization have their advantages because of the countless number of scenarios in occupancy grid maps [1]. Moreover, diverse path planning algorithms [2,3] have emerged to tackle constraints of motions of robots or autonomous vehicles. Path planning algorithms include Dijkstra algorithm [4,5], A-star algorithm [6,7], Genetic algorithm [8,9], Artificial Neural Network (ANN) [10] and a combination of several algorithms [11,12] to name a few. Resulted waypoints of a path planner are connected to form a trajectory from a start configuration to a goal configuration. The trajectory mainly contains many sharp or angular turns that make a mobile robot move awkwardly. Many experts and scholars have studied path smoothing techniques that produce a smooth path and guarantee a kinematically feasible obstacle-free path to deal with this problem [13]. Velocity, acceleration, and jerk have also been optimized to acquire smoothing trajectories for autonomous vehicles [14,15,16]. While the robot moves on a smooth trajectory, obstacle avoidance has also been considered [17,18]. However, path smoothing methods can not make informed decisions regarding other paths during the search algorithm.

Stanford University researchers have developed a variant of the A-star algorithm, named hybrid A-star, for application to a real car robot in an outdoor racing competition [19]. The hybrid A-star algorithm is a hybrid of discrete state and continuous state. This algorithm consists of two phases: the forward search phase, which takes into account the kinematics of the robot model in order to plan continuous motions of the robot in discrete grid maps, and the analytic expansion phase, which uses the RS curve to augment the accuracy and the speed of the algorithm.

Planning a continuous state in the discrete domain of the hybrid A-star search algorithm has been an inspiration for numerous researchers to investigate and strive to apply it to real applications. Authors in [20] extended the search algorithm to accomplish several challenges, such as planning to a waypoint lying outside the vehicle’s local map in outdoor applications. In [21], the authors proposed a method that is a combination of a visibility diagram and the hybrid A-star algorithm for valet parking applications. Firstly, the visibility diagram algorithm was used to find the shortest visible waypoints from a start position to a goal position. Then, the hybrid A-star was implemented to follow these waypoints with non-holonomic constraints of vehicles. The method proved faster than the standard hybrid A-star. However, RS curves’ drawbacks when the robot approaches the destination were ignored in these two works. In another work [22], the authors strove to optimize paths generated by the hybrid A-star search. A concept of the artificial potential field was applied to reduce unnecessary steering actions and smooth the paths. However, the proposed method was applied in the hybrid A-star path as a post-smoothing technique. Since the RS curves were re-used from the open motion planning library, the problem in implementing the RS curves has remained.

In this study, we investigate the hybrid A-star algorithm for non-holonomic robots in indoor environments. Through this investigation, issues that occurred in each phase of the algorithm are discovered. First, RS curves in the analytic expansion are often generated closely to obstacles, especially at corners. To overcome this issue, we generate multiple RS curves with different curvature values and propose a cost function to evaluate each curve to select the best one on which the robot moves safely in the presence of obstacles. Second, routes developed by the forward search consist of multiple unnecessary turns. To deal with this issue, without using complex smoothing techniques, we suggest effective fine-tuning to reduce unnecessary turns. By resolving these issues, we eventually improve the algorithm’s performance in terms of safety for use in indoor robot applications. Experimental demonstrations are conducted using a non-holonomic robot to highlight the effectiveness of the proposed method in simulations.

The rest of this study is organized as follows. Section 2 briefly describes the hybrid A-star path planning algorithm. Moreover, a problem in the planned path is presented as we implement the bare-bone algorithm in indoor environments. Section 3 presents our proposed solutions to overcome the problem, including a cost function for selecting a safer way to achieve a goal configuration. The proposed solution is verified through intensive tests using benchmark maps in simulations in Section 4. Section 5 presents conclusions and our future work.

2. Statement of the Problem

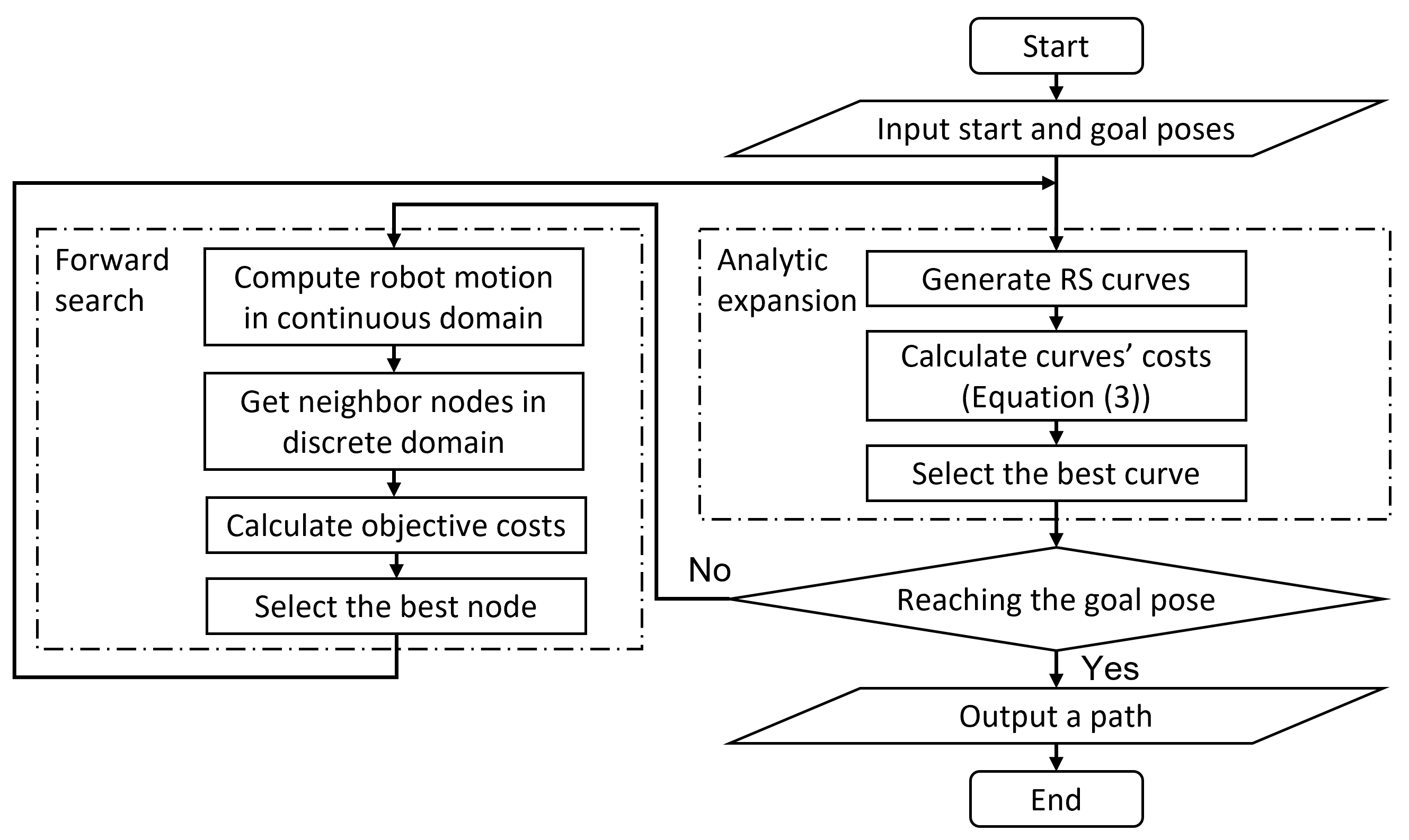
2.1. Hybrid-State A-Star Algorithm

The hybrid-state A-star (or hybrid A-star in short) is known as one of the most efficient path planners for non-holonomic autonomous vehicles. This planner was first implemented in outdoor environments by the Stanford Racing Teams robot, Junior, in the 2007 DARPA urban challenge [19].

The hybrid A-star algorithm includes two phases (the forward search and analytic expansions) to produce an effective path [23,24]. In the forward search, as the conventional A-star algorithm, the hybrid A-star algorithm is guided by a cost-to-go $g\left(n\right)$ which is a cost from the start node to the current node (n), and a heuristic function $h_1\left(n\right)$. The heuristic function $h_1\left(n\right)$ uses the obstacle map to compute the cost of the distance from the current node to the goal in the discrete state. Moreover, like an advanced version of the normal A-star, the hybrid A-star algorithm is also guided by another heuristic function $h_2\left(n\right)$ that ignores obstacles but considers the kinematics of a non-holonomic robot (e.g., autonomous vehicles). Further details can be found in [24,25,26]. The kinematics of the robot model is used to predict motions that depend on the speed, direction, and steering angle of the robot in the continuous state. This way helps the algorithm select the right successor in continuous coordinate, which a non-holonomic robot is able to follow, as shown in Figure 1a.

These continuous coordinate successors have converted approximately to discrete coordinate nodes to compute the total cost of a movement. Equation (1) represents an objective function of the planner at each node n. The successor with the lowest objective value will be chosen until it reaches the goal node.

$$F\left(n\right)=g\left(n\right)+h_1\left(n\right)+h_2\left(n\right)$$

(1)

However, reaching the exact continuous coordinate goal node is hard due to the dependence of the resolution of the grid map and the smallest motion that the robot can take.

Analytic expansions are the second phase of the hybrid A-star algorithm. This phase plays a role in guaranteeing that the algorithm reaches the exact continuous coordinate of the goal state. In this phase, the RS curves have been utilized since the RS curves algorithm was a well-known algorithm that applies to non-holonomic vehicles that can move forward and backward. An RS curve is calculated to produce the shortest path from a start point to a goal point. Figure 1b depicts a combination of Left, Straight, and Right curves (or LSR curve in short) between two configurations: $[0,0,0],[15,2,-\pi /2]$, where the first two values are position, the third value is an orientation of the robot. The red arrow represents the robot’s direction. The curvature value (0.5 in this case) allows the robot to make the most turning angle, or minimum turning radius. The inventors of the hybrid A-star have claimed that the analytic expansion method leads to significant benefits in terms of accuracy and search speed.

Additionally, Voronoi field was proposed to help the vehicle move in narrow opening by adding a path-cost function v as shown in Equation (2) below:

$$v(x,y)=\frac{\alpha }{\alpha +d_0(x,y)}\frac{d_v(x,y)}{d_0(x,y)+d_v(x,y)}{\left(\frac{d_0-d_0^{max}}{d_0^{max}}\right)}^2$$

(2)

where, $\alpha$ is a constant falloff rate ($\alpha >0$), $d_0^{max}$ is a constant maximum effective range of the field ($d_0^{max}>0$), $d_0$ is a distance to the nearest obstacle ($d_0<d_0^{max}$), and $d_v$ is a distance to the nearest edge of the generalized Voronoi diagram. The effectiveness of this function is that the cost is higher in the area near obstacles, and decreases to zero at points that are equidistant to obstacles. As a result, the hybrid A-star path will tend to be in the center of the road.

2.2. Our Path Planning Problem

By implementing the bare-bone algorithm on simulations, we have run into a problem that we should deal with as below.

Figure 2 illustrates two simulations of the hybrid A-star in self-created indoor environments of size $50\times 30$ m, and a resolution of 1 m. The non-holonomic robot is annotated as a red rectangle. The robot’s state is captured along the resultant path, where the blue line represents the results of the forward search, and the green line represents the results of the RS path.

The blue lines lie in the middle of the corridor. However, these blue lines contain non-smooth segments, such as segments indicated by black ellipses. Most importantly, the green lines are often close to walls, especially at corners indicated by black circles. The robot may collide with obstacles through the process of movement at these corners because of the measurement errors or errors of motor controllers. To overcome this problem, in the next section, we will improve the analytic expansions of the algorithm by using an interesting property of RS curves.

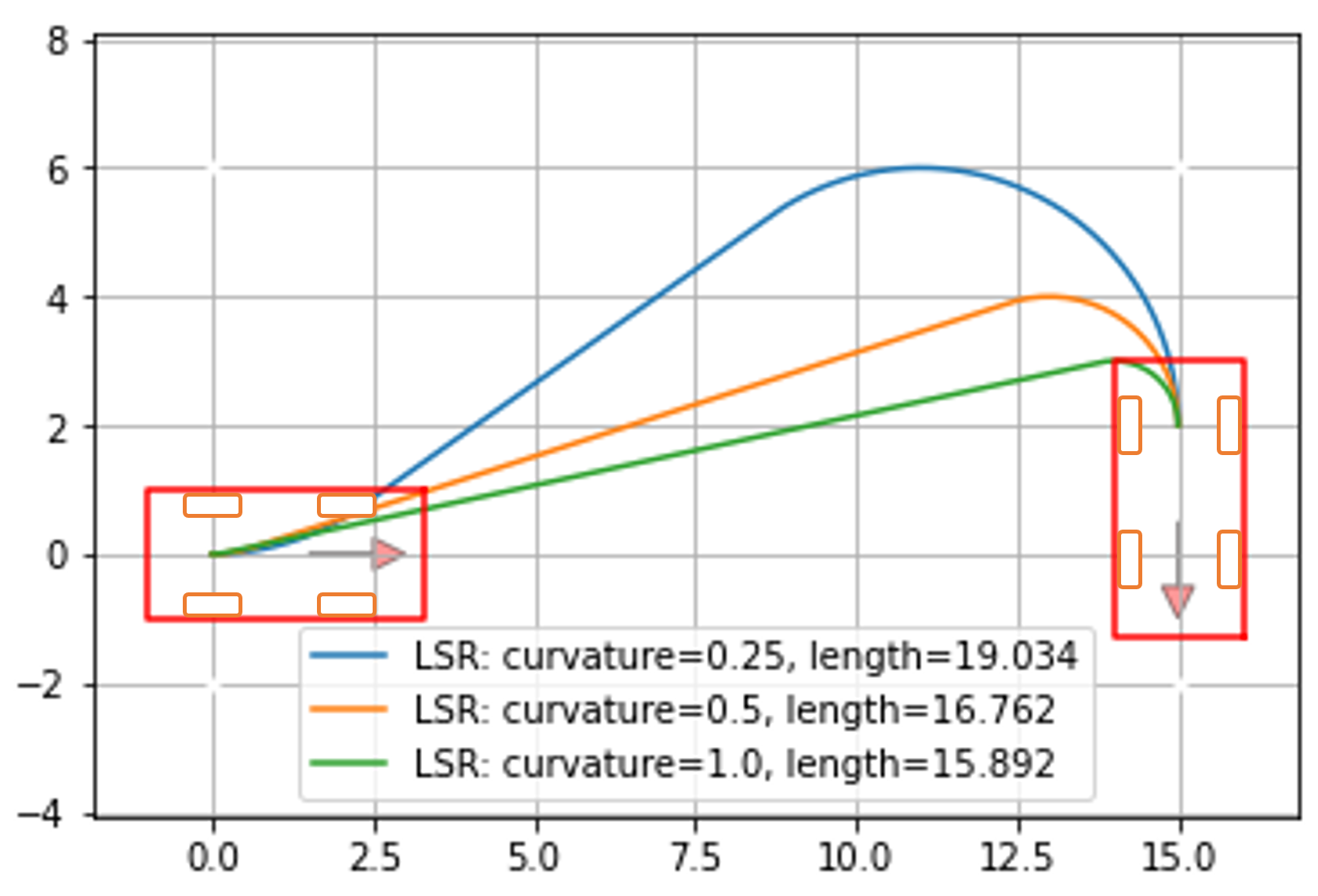
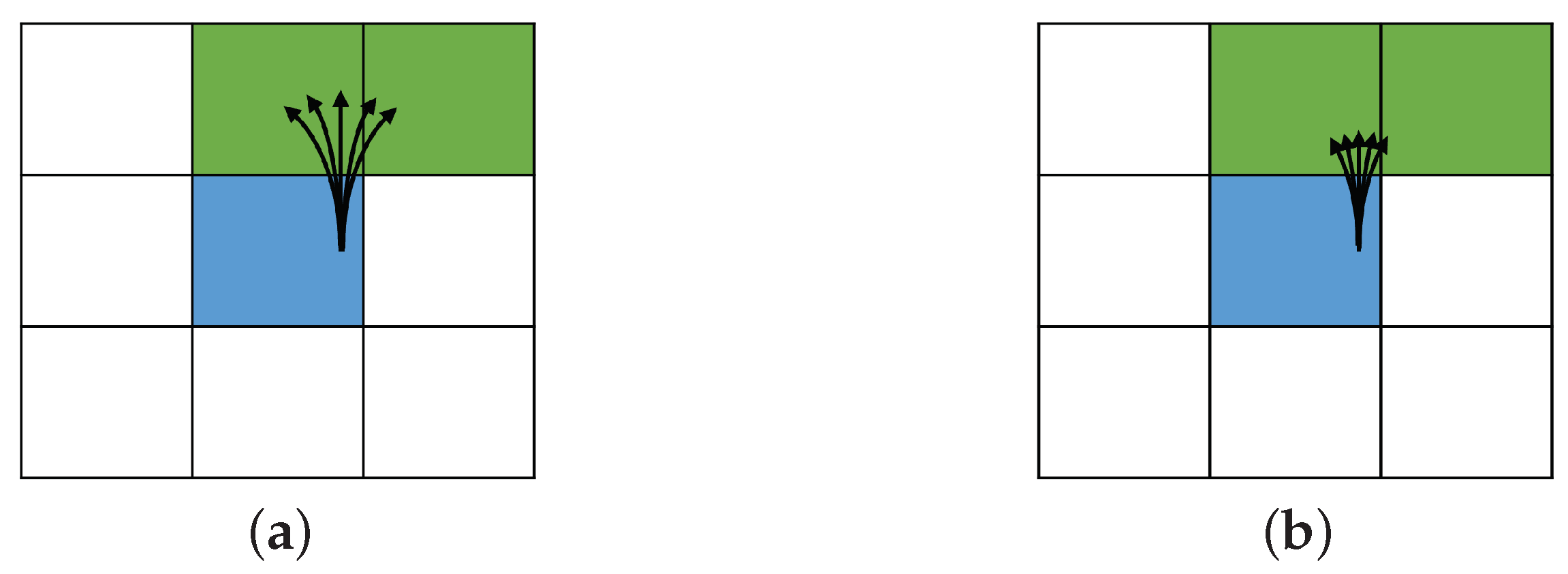
3. An Improved Method

The primary purpose of using the RS method in the analytic expansions is to increase the accuracy and speed up the search because the RS method is a well-known method for a non-holonomic vehicle to move from a configuration $[x_0,y_0,{\theta }_0]$ to another configuration $[x_g,y_g,{\theta }_g]$ in the shortest path. More details about RS curves can be found in [27].

Figure 3 depicts three different LSR routes using the RS method from an initial state $[x_0,y_0,{\theta }_0]=[0,0,0]$ to a goal state $[x_g,y_g,{\theta }_g]=[-3,5,\pi /2]$ according to three different values of curvature. The green route has the biggest curvature, but its length is the shortest of the three. Whereas the blue route corresponds to the smallest curvature, its length is the longest of the three. The turning radius is reversely proportional to curvature. The turning radius in the blue route is much larger than the radius in the orange and green routes. Therefore, it is possible to achieve a safer route for a car-like robot by adjusting curvature value.

Among different paths generated from different curvatures, a better path is selected in terms of safety from a start state to a goal state. In order to evaluate each path, we propose the following objective function:

$$G={\sigma }_1·v+{\sigma }_2·m$$

(3)

where, ${\sigma }_1$ and ${\sigma }_2$ are two coefficients normalizing the two related cost functions. The function v represents the cost of the Voronoi field, which is used in the post-processing Equation (2). The farther the robot is from obstacles, the smaller the value of the cost function. Utilizing this cost function, we see the robot prefers relatively equidistant moves to surrounding obstacles.

Meanwhile, the function m is the cost of movement along the RS path which includes straight lines and curves as mentioned above. For a candidate RS path (p), costs of each straight line or curve are computed including its length ($l_i$), steering angle ($s_i$), and steer switching ($c_i$) in functions of ($l_p$), ($s_p$), and ($c_p$) respectively. With three constant weights $w_1,w_2,w_3$, the cost function m has the following form:

$$\begin{array}{cc}\hfill m& =l_p+s_p+c_p\hfill \\ \hfill l_p& =w_1·\sum l_i\hfill \\ \hfill s_p& =w_2·\sum s_i\hfill \\ \hfill c_p& =w_3·\sum c_i\hfill \end{array}$$

(4)

Because of the safety criteria, a car-like robot or a car does not always make the sharpest turn, or a maximum curvature, but it might choose a less sharp curvature to complete a turn. By combining these two sub-functions ($v,m$), with appropriate weights ${\sigma }_1$, ${\sigma }_2$, we trade off between selecting safer or faster path. If the coefficient ${\sigma }_1$ is larger than ${\sigma }_2$, then the robot prefers the safe path to the short one.

The improved method in the analytic expansion is mainly divided into three steps:

• First, RS curves are generated based on different curvature values from the input state to the goal state. Collision to obstacles is checked along the curves. Hence the curve which does not collide with obstacles is chosen.
• Second, the cost of each curve is calculated according to the Equation (3).
• Third, the curve which has the lowest cost is selected as the best curve. The robot is expected to travel more safely along this curve.

If such an RS curve exists, the method will assign it as the path to the goal and the search ends. If such a curve does not exist, the algorithm will continue with the forward search as in the original method:

• Computes robot continuous coordinates based on a non-holonomic model,
• Converts these coordinates to corresponding discrete coordinates in the grid map,
• Calculates objective costs according to the Equation (1),
• Selects the best successor for the next search loop.

The flowchart of the overall method is shown in Figure 4. To verify the effectiveness of the proposed solution, we conduct simulations in the next section.

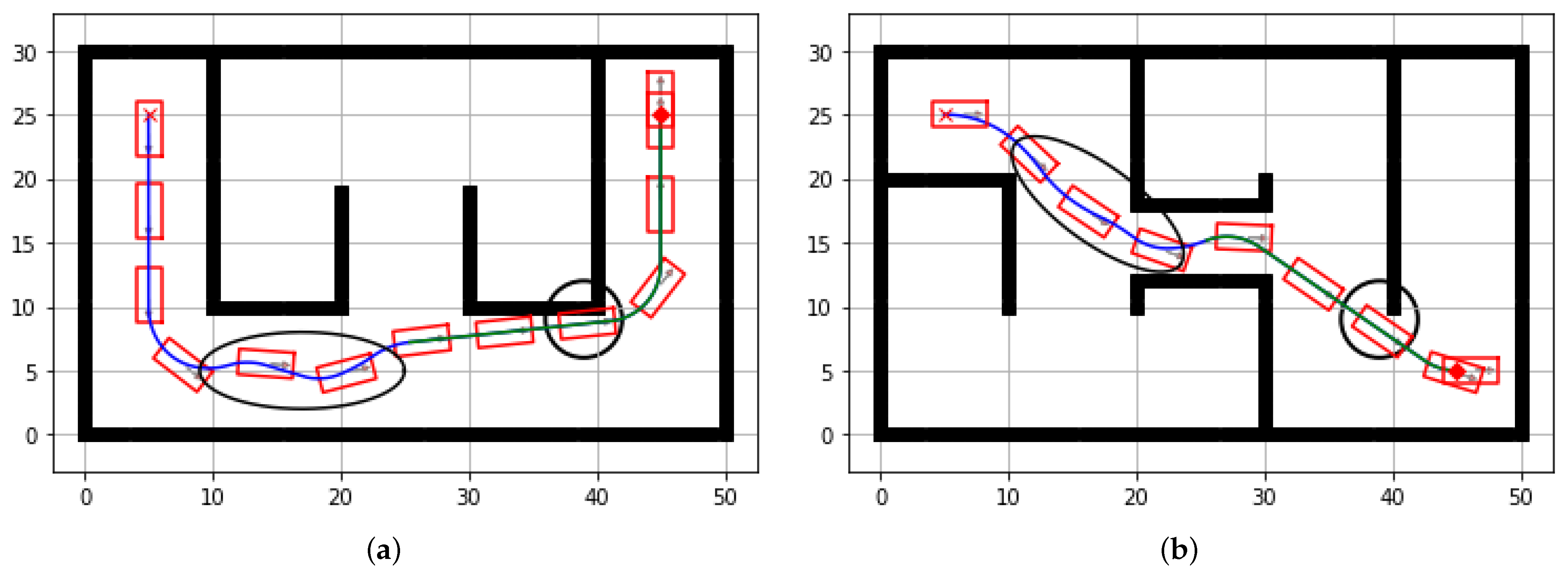
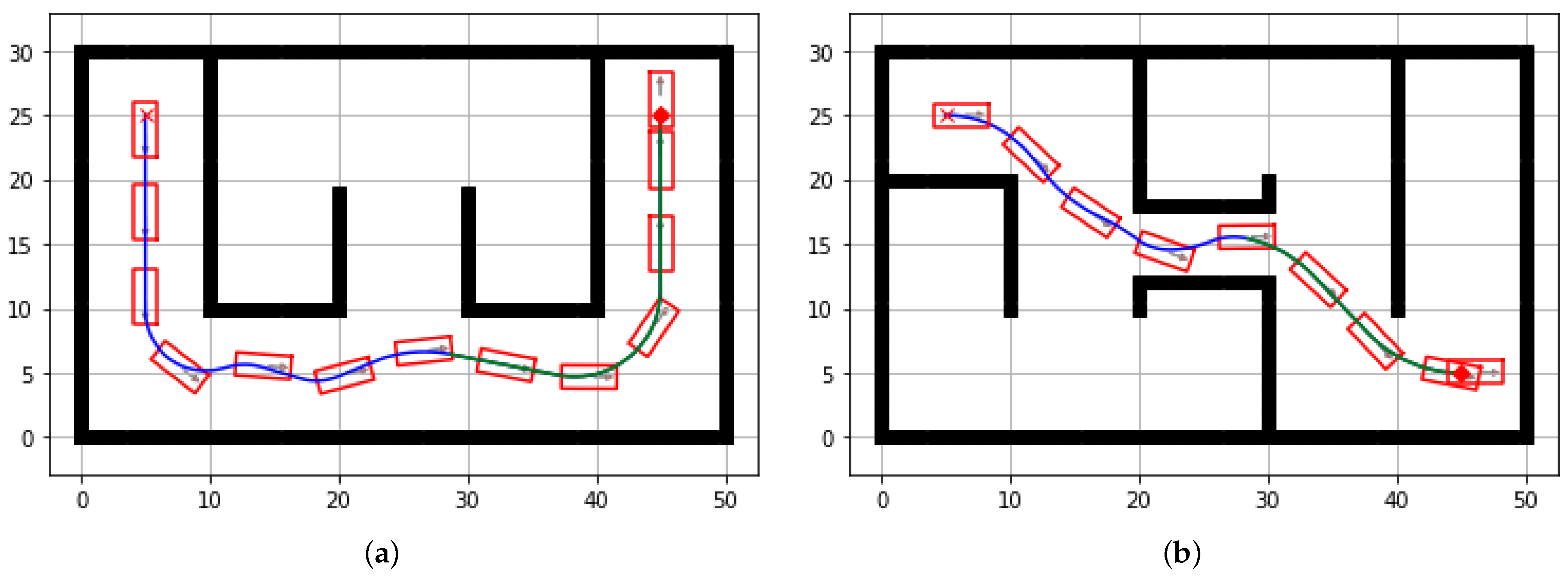
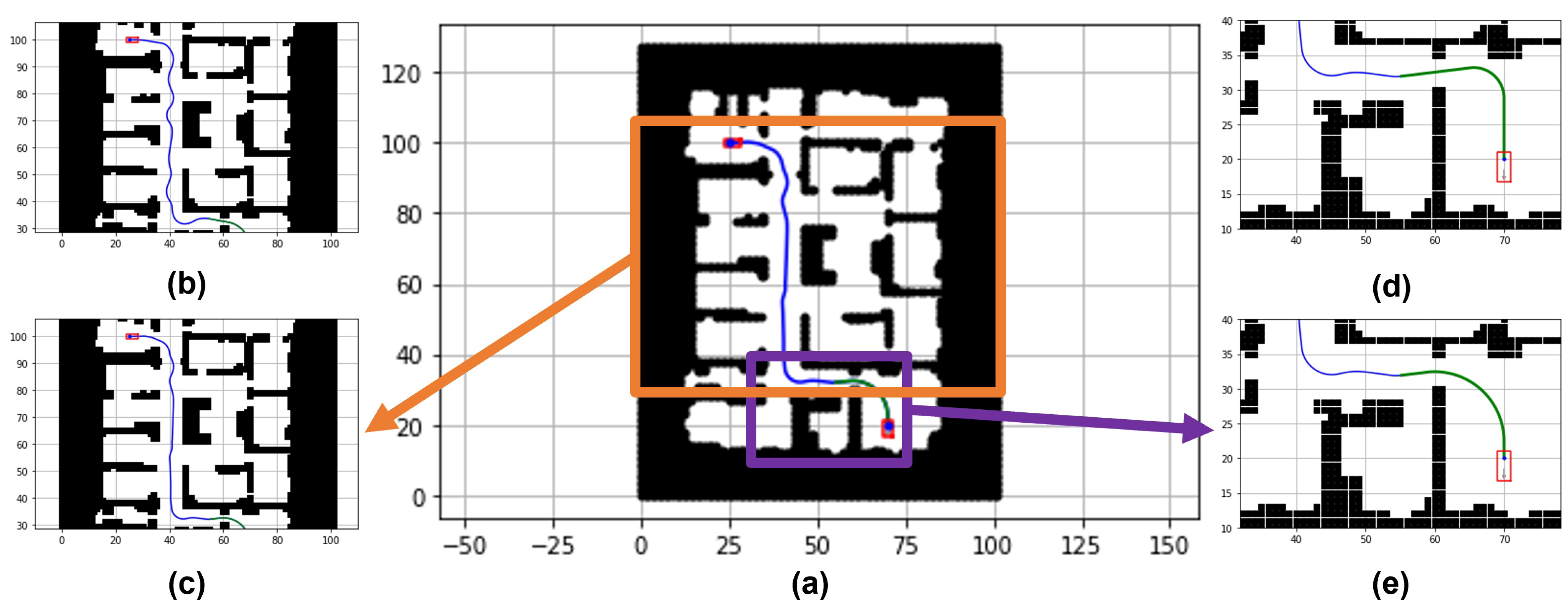
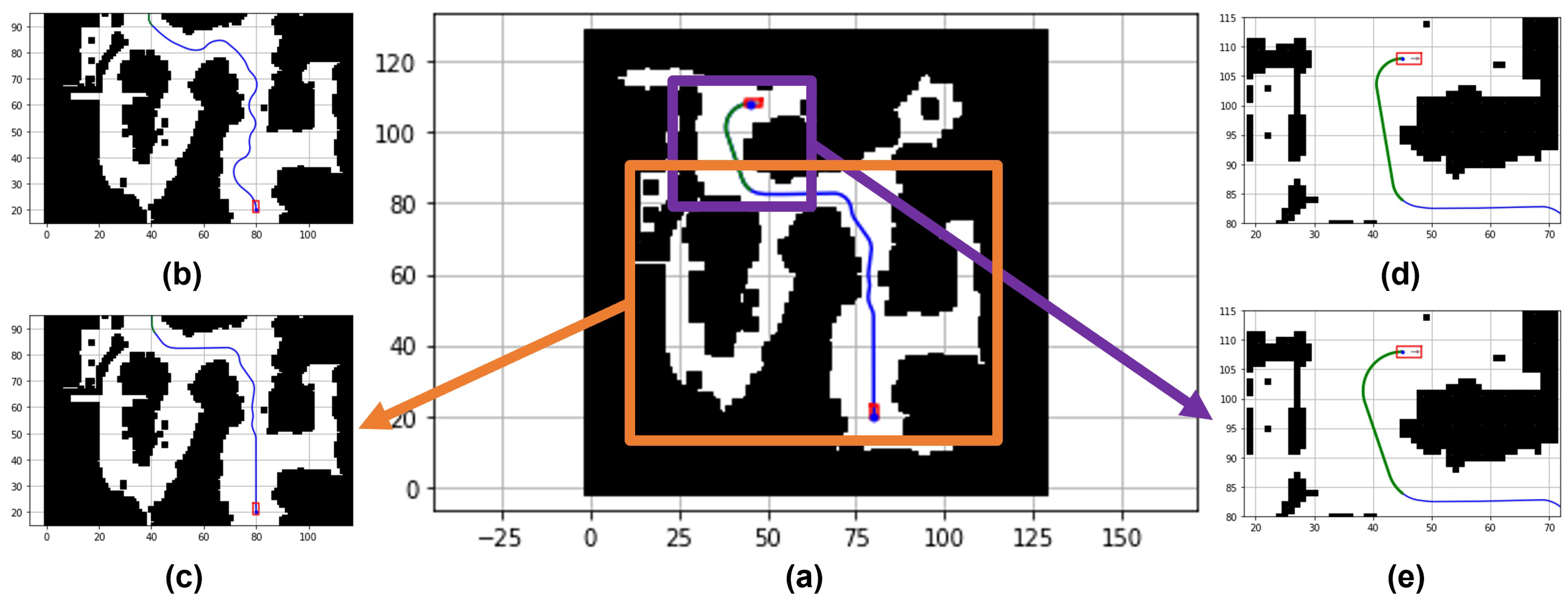
4. Experimental Simulation

4.1. Simulations

We verify the effectiveness of the proposed solution by simulation on the Spyder IDE platform. The algorithm is implemented in Python 3 programming language. The paths generated by the algorithm are visualized by the matplotlib library. The input map is a binary occupancy grid. The robot model is configured with the size of $4.3\times 2.0$ m, wheel base of $3.0$ m, and maximum steer of $0.6$ rad. We vary the robot’s curvature in the range of the maximum steering angle with a resolution of $0.05$. Figure 5 shows two paths generated by the improved algorithm using the same initial and goal state configurations as in the previous simulations.

The comparison of the two simulated results depicted in Figure 2 and Figure 5 reveals no change in the results of the forward search, represented by the blue line, but a significant improvement in the results of the analytic expansions, represented by the green line. In the original method, the RS paths are close to walls when the robot is trying to make a turn at sharp corners. In contrast, the improved method chooses RS paths that are more in the middle of the road to avoid sharp-angled corners thanks to the cost function.

Table 1. Comparison of original and improved methods.

Maps	Original RS Path				Improved RS Path
	Curvature	Cost	Length (m)	Time (s)	Curvature	Cost	Length	Time
Map A	0.23	15.27	34.07	0.022	0.15	8.18	34.05	0.1
Map B	0.23	5.85	19.83	0.015	0.1	5.52	20.25	0.139

summarizes the comparison of the original and improved RS paths in terms of curvature, risk of collision (cost), path length (length) and execution time (time). Higher values indicate higher risks of collision, longer paths and slower finding the goal. Generated by smaller curvatures, the proposed method improves the original method in terms of the risk of colliding with obstacles (8.18 versus 15.27, and 5.52 versus 5.85). Besides, the length of the improved path is shorter in the grid map A, but longer in the grid map B, although the difference is not significant (34.05 versus 34.07 and 20.25 versus 19.83, respectively). In both cases, the proposed method requires more execution time in the analytic expansion phase because more candidate RS paths with corresponding curvatures must be computed. The difference in execution time increases as curvature resolution increases.

4.2. Fine Tunings

Observing Figure 5, the improved hybrid A-star paths in the forward search phase are still unrealistic since they deviate substantially from the true shortest paths, or have many turning points. In Figure 6, we illustrate the smallest continuous motions in discrete domain with two different motion primitives, or arcs, defined as the smallest entities of the path [20]. Each arrow from its tail to head depicts the robot’s movement from a current pose to a possible successor’s pose. Due to different steering angles, the headings of the successors are different in the same motion primitive. Moreover, the headings of the successors also differ by the influence of motion primitives. Compared to Figure 6a with the same steering angle, the headings of successors in Figure 6b are smaller.

After tuning the motion primitives without any exhaustive, we found a value of $1.5$ for motion primitive to give good results. The resulted routes for grid map A and map B are shown in Figure 7a,b. The number of turning points in these figures is dropped from 5 to 2 points and from 6 to 5 points compared to those in Figure 5a,b, respectively.

4.3. Experiments in Benchmark Maps

In this section, the workspace is standard 2-D grid benchmark maps in common sources [28,29]. We use three different benchmark maps, map12, den520d and ost003d, with the size of $433\times 541$ pixel, $1000\times 1000$ pixel, and $1000\times 1000$ pixel, respectively. These three benchmark maps are re-scaled to maximum 128 pixels per dimension with a resolution of 1 m per pixel. Figure 8a, Figure 9a and Figure 10a show full routes obtained by the improved method in the three benchmark maps. To see clearly the improved paths, we zoom in parts of the forward search phase (blue lines) before tunings and parts of the improved RS paths (green lines) as shown in Figure 8c,e, Figure 9c,e and Figure 10c,e. The corresponding sections of the forward search phase after tunings and the original RS paths are arranged in Figure 8b,d, Figure 9b,d and Figure 10b,d to compare between them.

As it can be seen from the data in

Table 2. Comparison of original and improved methods in benchmark maps.

Maps	Turning Points (before)	Original RS Path				Improved RS Path				Turning Points (after)
		Curvature	Cost	Length (m)	Time (s)	Curvature	Cost	Length (m)	Time (s)
map12	13	0.23	6.17	26.29	0.014	0.15	4.69	23.10	0.096	10
den520d	14	0.23	5.03	27.40	0.020	0.15	4.03	29.43	0.140	9
ost003d	8	0.23	3.89	24.51	0.018	0.10	3.27	25.26	0.166	6

, a smaller curvature value is chosen in both cases in the improved RS path. Consequently, the cost of risk of the improved RS path is reduced by 24% in map12 and 10% in map den520d compared to the original RS path in the hybrid A-star algorithm. The RS paths generated by bigger curvatures in Figure 8d, Figure 9d and Figure 10d are closer to obstacles than those generated by smaller curvatures in Figure 8e, Figure 9e and Figure 10e. On the other hand, the lengths of the RS paths in the improved method are not always shorter than those in the original method when safety is preferentially considered (there are no significant differences in lengths). This result is consistent with the properties of RS curves, as presented in Section 3. However, the computation time is a drawback of this method, and more time is required to compute RS paths as curvature resolution increases. The reason is that the original method produces only RS curves using extreme curvature values. Whereas the proposed method needs to generate multiple RS curves in curvature range with some step size. Therefore, the computation time increases at most linearly proportional to the step size of the curvature. And by the fine-tuning, we reduce the motion primitives, which means the discretization of x and y axes increases, respectively, so that the computation time increases proportionally. Another noticeable point is the number of turning points reduced from 12 to 10, 12 to 9, and 6 to 5 after tunings in the three maps (see Figure 8b,c, Figure 9b,c and Figure 10b,c). These paths nearly do not have unnecessary turning points and keep a comfortable distance from obstacles. In summary, in terms of safety criteria, the results indicate that the improved method can reduce the risk of collision and select a safer path to the destination.

5. Conclusions

In this paper, we presented an improved path-planning method for autonomous car-like robots. The method was implemented in the analytic expansion phase of a hybrid A-star path planner to improve its performance in terms of safety. Based on the properties of the RS method, different shortest RS paths were generated based on curvature values. Then, an objective function was formulated to evaluate each candidate path and select the best one that minimizes the cost risk of collision. In addition, an effective tuning in the forward search phase was described to reduce unnecessary turning points without using complicated methods. As proved through intensive tests in simulations, the path planner produced the routes that are smoother and have at least equal to or lower risks of collisions (around 20%) with surrounding obstacles compared to the routes that are produced by the conventional hybrid A-star method. Besides, the number of turning points in the improved route is also reduced by up to around 20%. A drawback is that the computation time of the proposed analytic expansion increases less than about ten times.

Having a smoother route with a lower risk of collision helps the mobile robot vehicle to move more safely while working with humans. The results of this work indicate the potential applications of hybrid A-star methods in the indoor environment that require autonomous driving tasks. However, the proposed method needs to be verified in real environments, which we will investigate in our future work.