Torque-Enhanced Phase Current Detection Schemes for Multiphase Switched Reluctance Motors with Reduced Sensors
Abstract
:1. Introduction
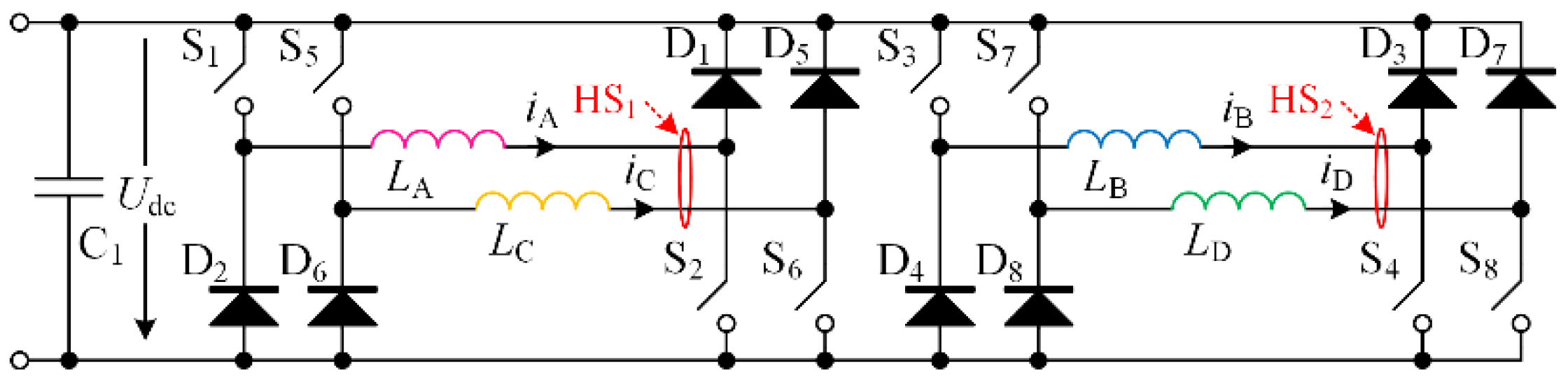
2. Conventional Current Detection Scheme with Np Hall Effect Sensors
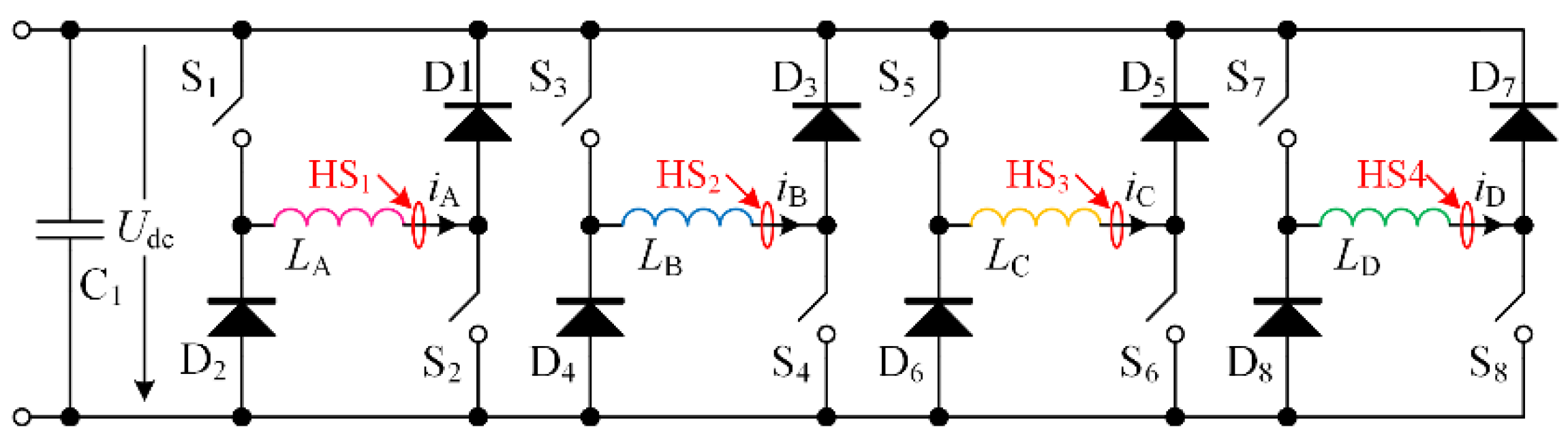
3. Proposed Current Detection Schemes with Reduced Sensors
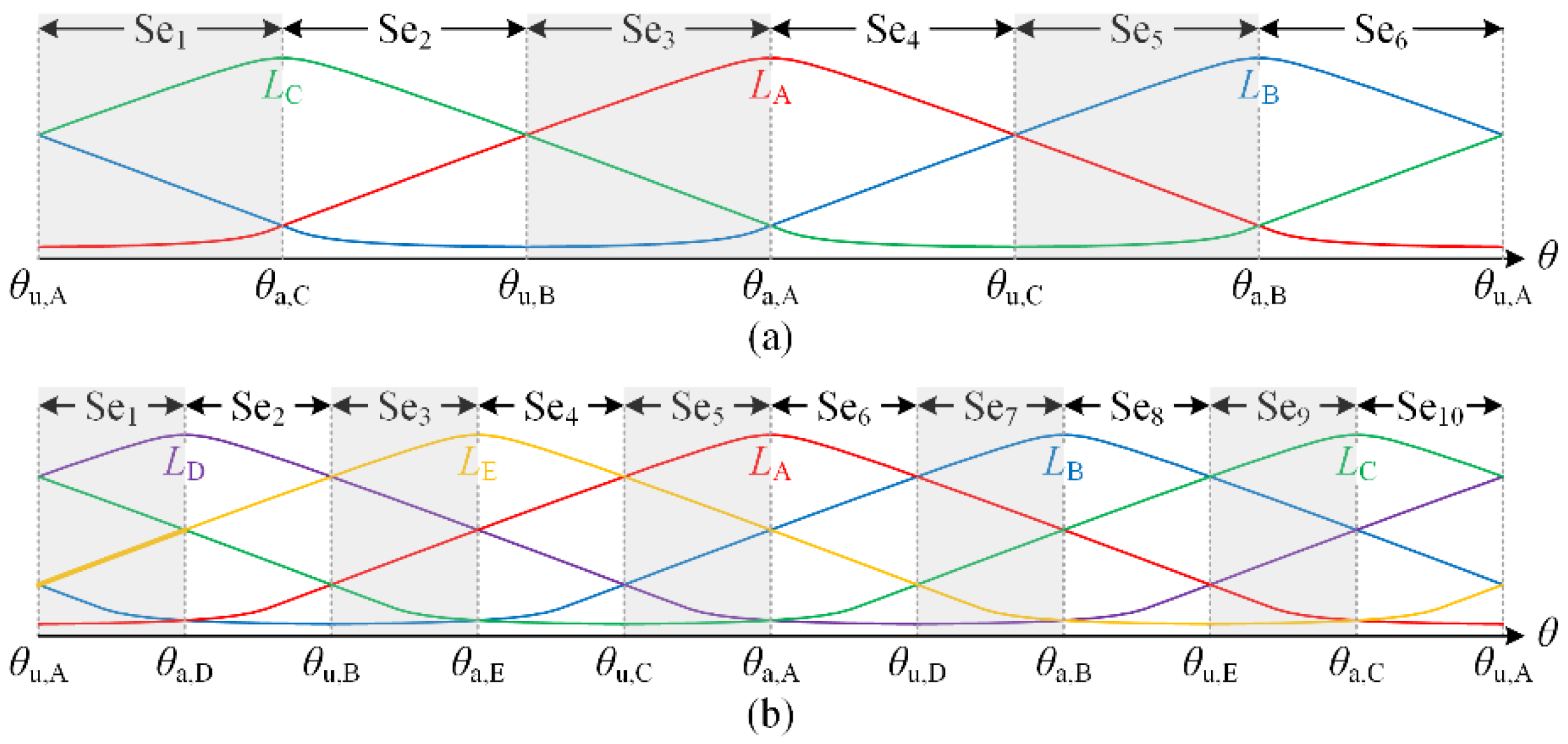
3.1. Phase Grouping in EMSRMs
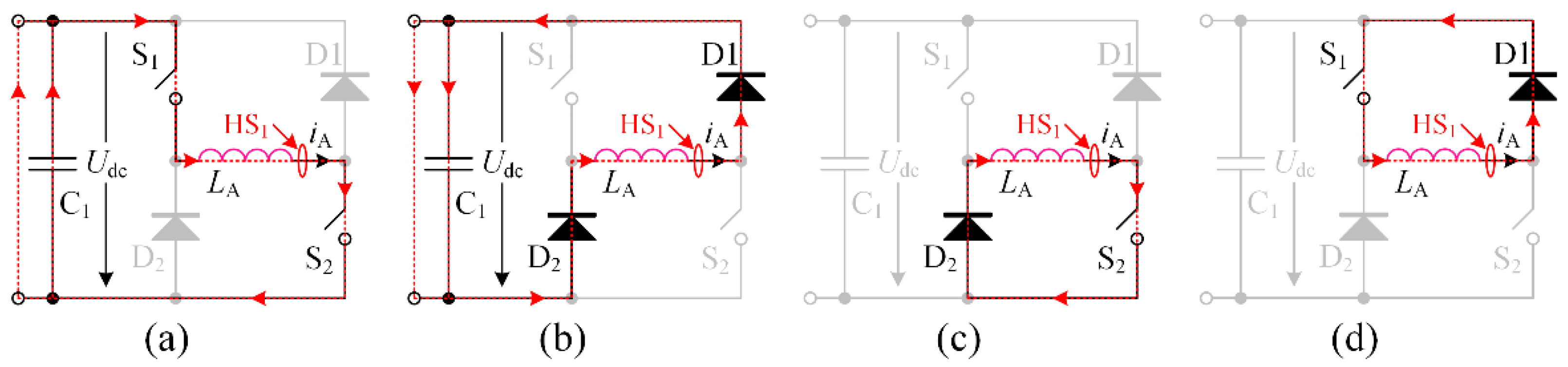
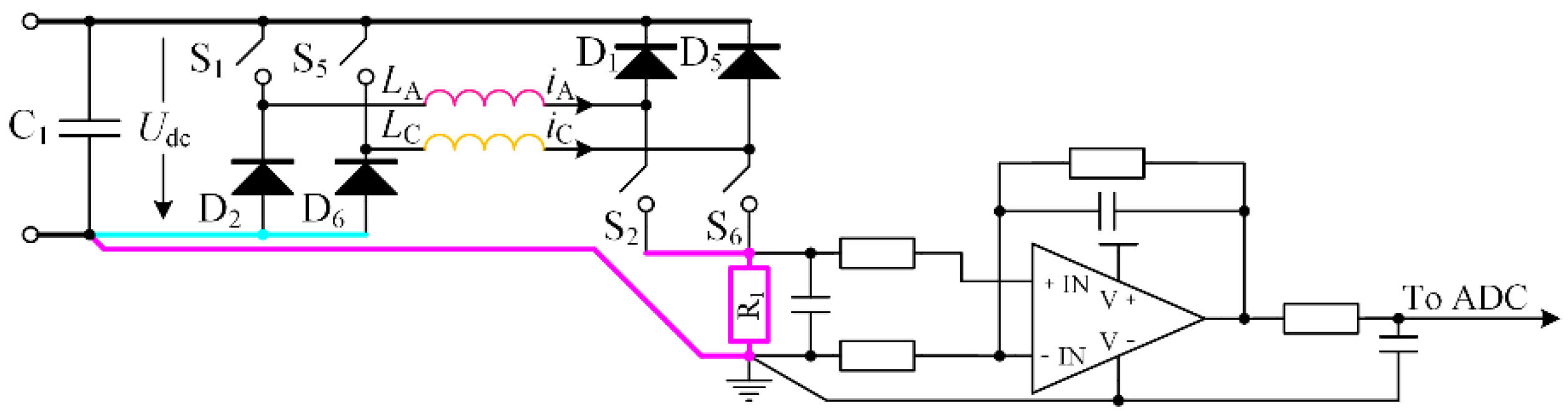
3.2. Sensors-Based Current Detection Scheme for EMSRM
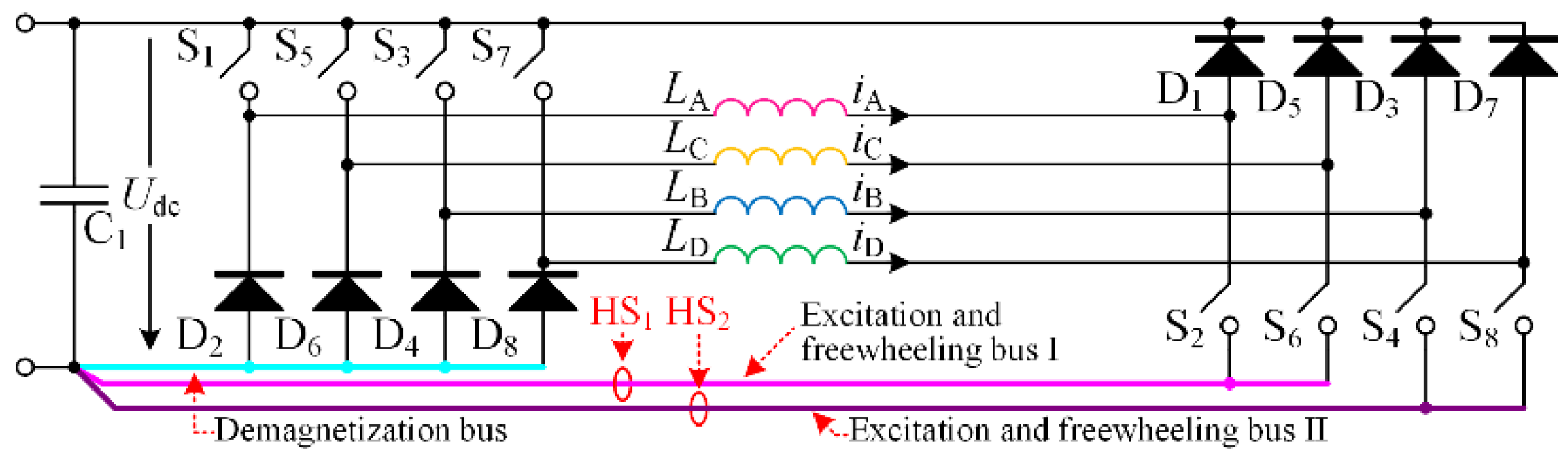
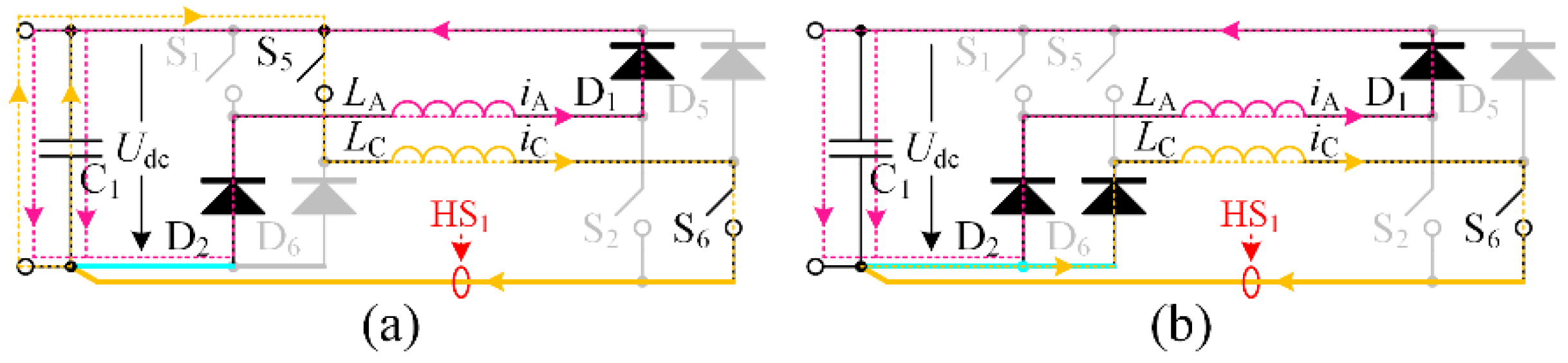
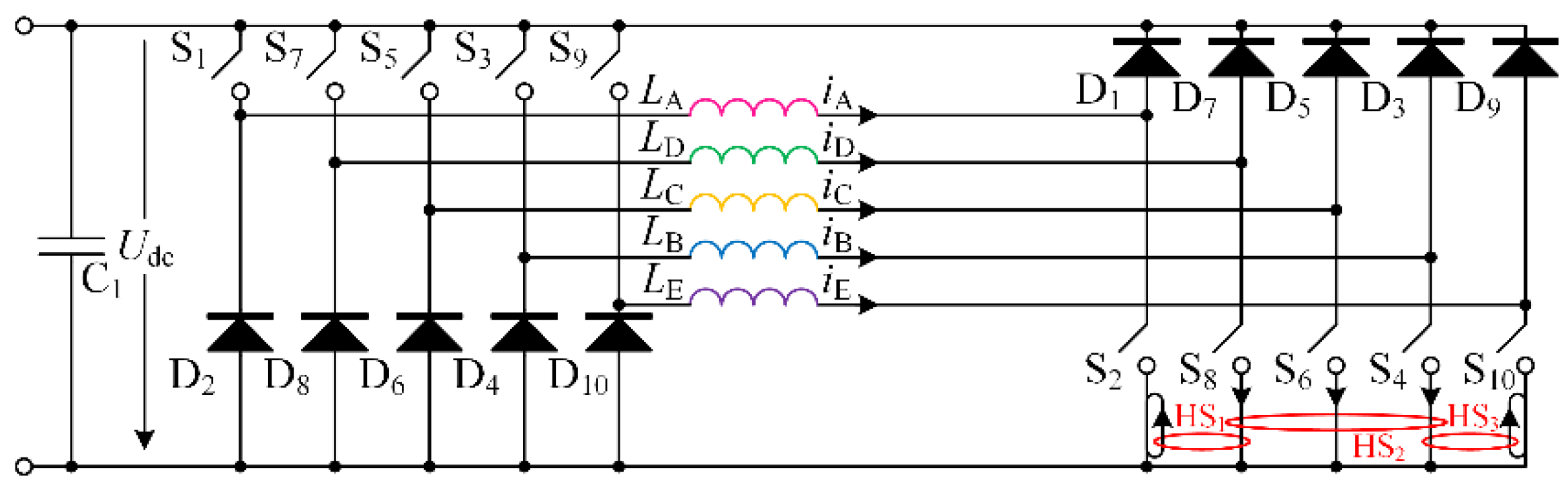
3.3. (Np + 1)/2 Hall Effect Sensors-Based Current Detection Scheme for OMSRM
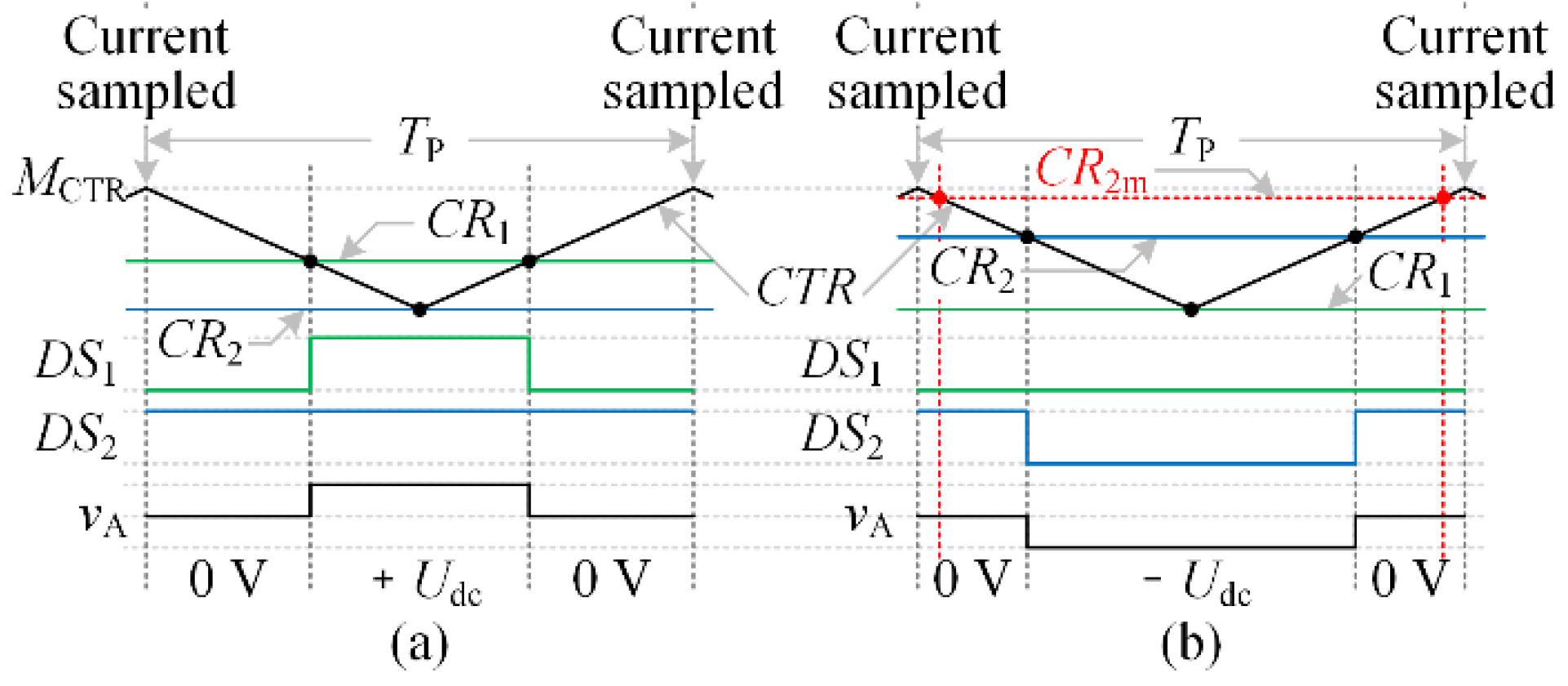
3.4. Current Control without Sampling Demagnetization Current
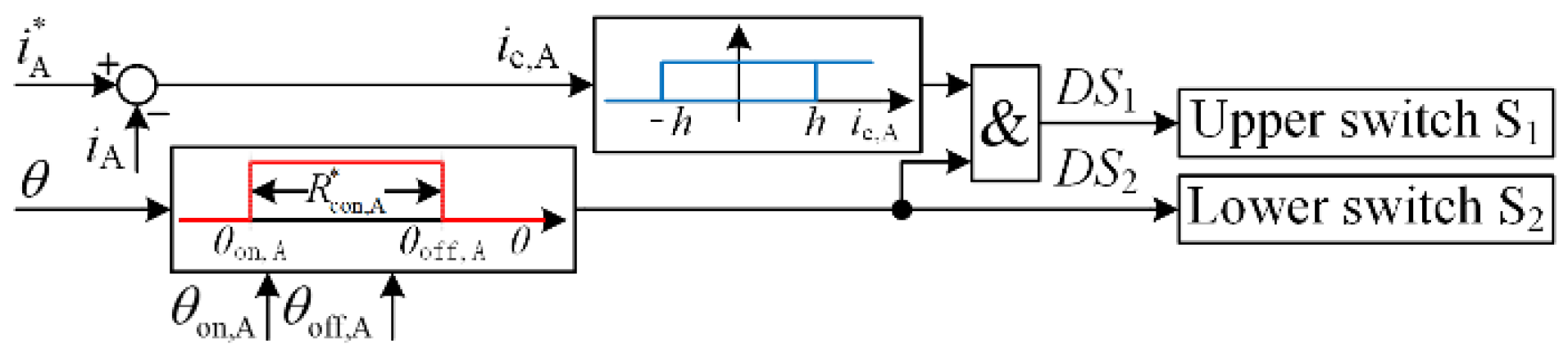
3.4.1. Soft Current Chopping Control (SCCC)
3.4.2. Voltage Pulse-Width Modulation Control (VPC)
4. Simulation Verification
4.1. Simulation Verification of the Np/2 Sensors-Based Schemes
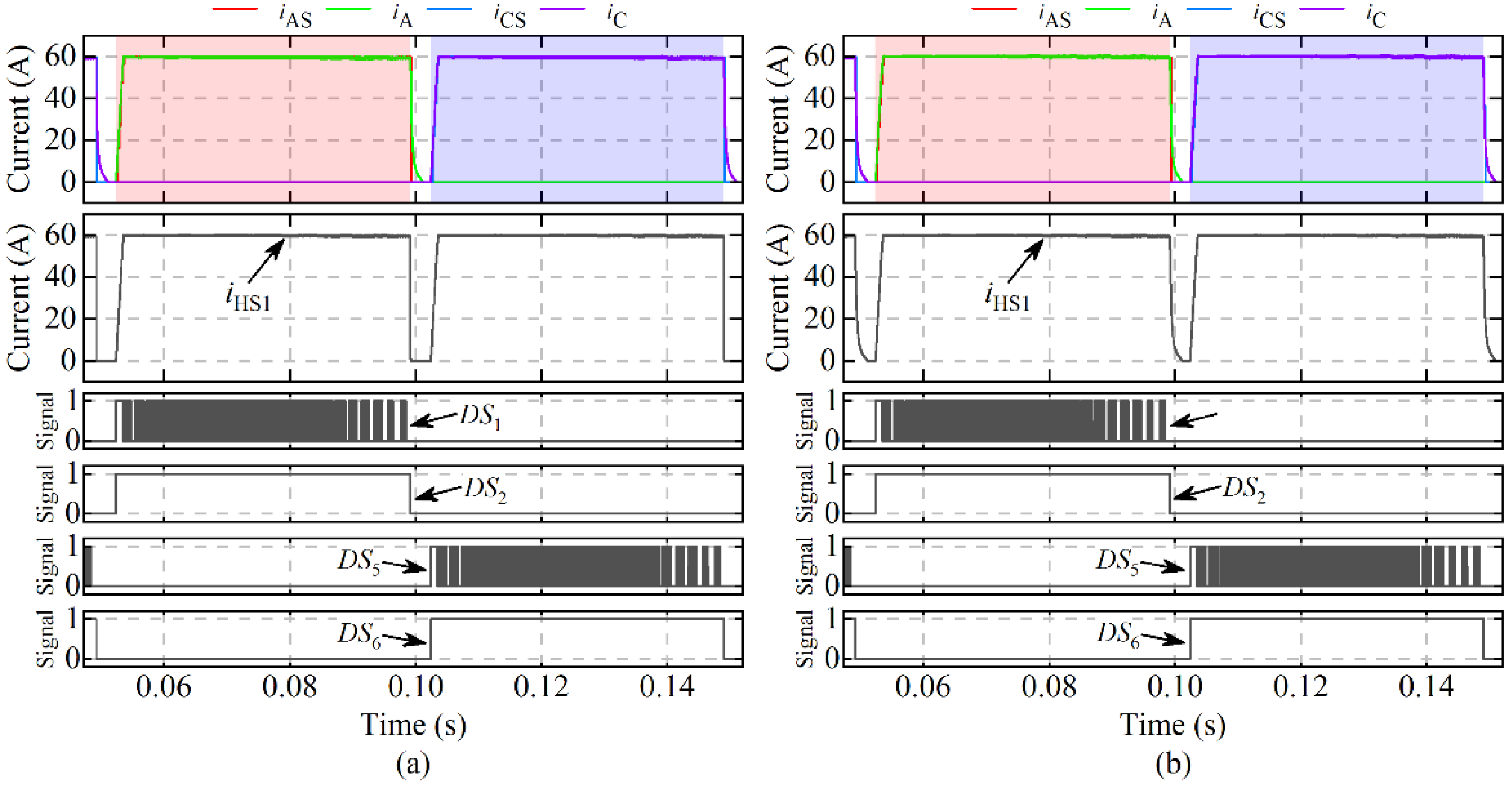
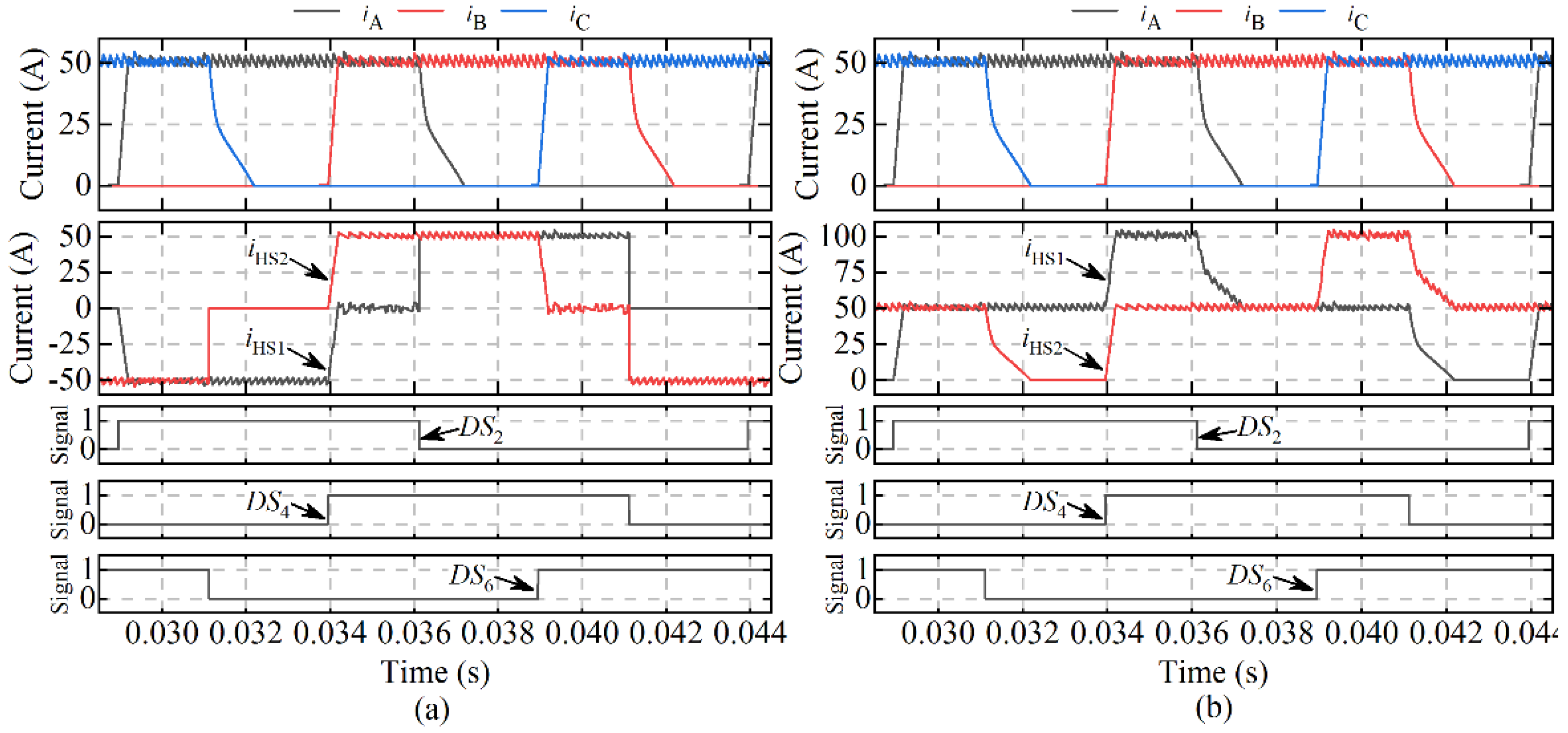
4.1.1. Simulation Results at 100 rpm (i* = 60 A)
4.1.2. Simulation Results at 2000 rpm (i* = 20 A)
4.1.3. Simulation Results at −1500 rpm (i* = 30 A)
4.1.4. Maximum Torque-Speed Characteristics
4.2. Simulation Verification of the (Np + 1)/2 Sensors-Based Schemes
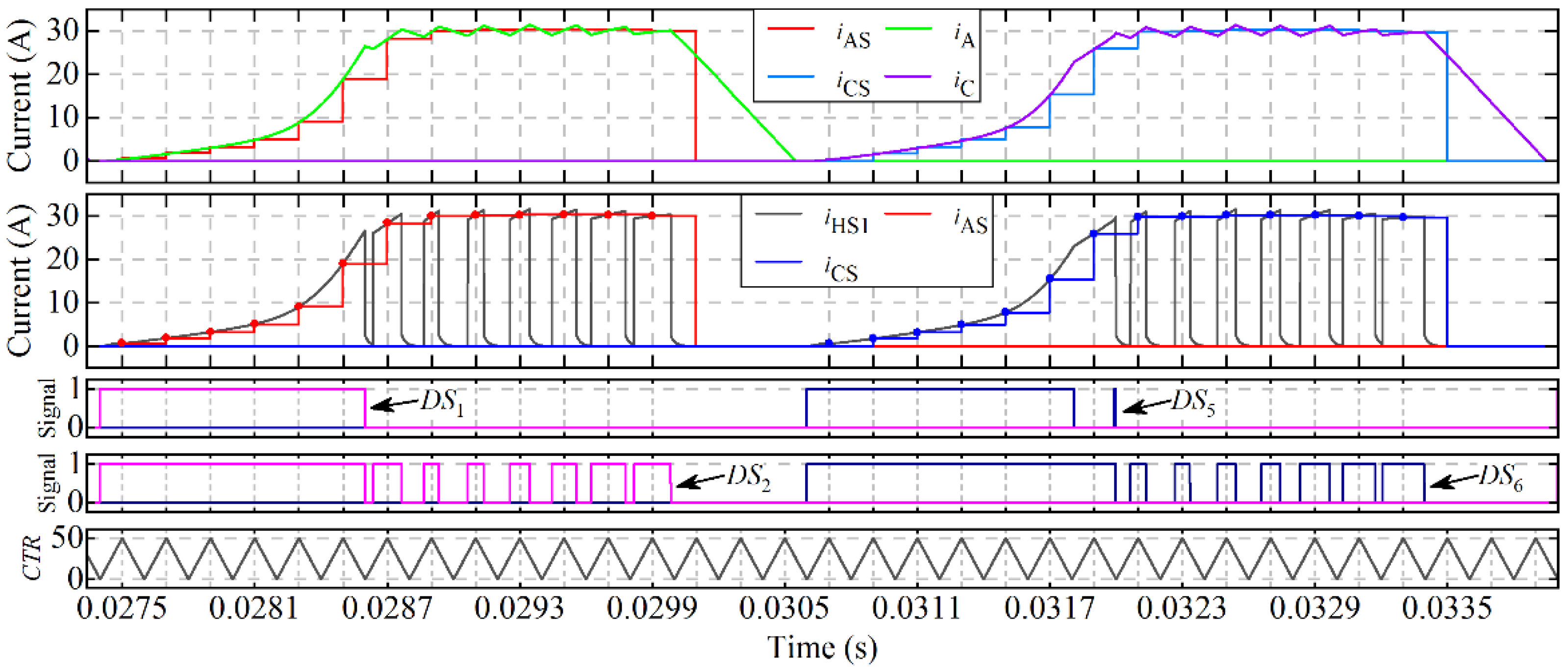
4.2.1. Simulation Results at 500 rpm (i* = 50 A)
4.2.2. Maximum Torque-Speed Characteristics
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gan, C.; Wu, J.; Sun, Q.; Kong, W.; Li, H.; Hu, Y. A Review on Machine Topologies and Control Techniques for Low-Noise Switched Reluctance Motors in Electric Vehicle Applications. IEEE Access 2018, 6, 31430–31443. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Habetler, T.G.; Harley, R.G. Modeling, Design Optimization, and Applications of Switched Reluctance Machines—A Review. IEEE Trans. Ind. Appl. 2019, 55, 2660–2681. [Google Scholar] [CrossRef]
- Goli, C.S.; Manjrekar, M.; Essakiappan, S.; Sahu, P.; Shah, N. Landscaping and Review of Traction Motors for Electric Vehicle Applications. In Proceedings of the 2021 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 21–25 June 2021; pp. 162–168. [Google Scholar]
- Pratapgiri, S. Comparative analysis of Hysteresis Current Control and Direct Instantaneous Torque Control of Switched Reluctance Motor. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 2856–2860. [Google Scholar]
- Ahmad, S.S.; Narayanan, G. Linearized Modeling of Switched Reluctance Motor for Closed-Loop Current Control. IEEE Trans. Ind. Appl. 2016, 52, 3146–3158. [Google Scholar] [CrossRef]
- Mikail, R.; Husain, I.; Sozer, Y.; Islam, M.S.; Sebastian, T. A Fixed Switching Frequency Predictive Current Control Method for Switched Reluctance Machines. IEEE Trans. Ind. Appl. 2014, 50, 3717–3726. [Google Scholar] [CrossRef]
- Shen, S.; Wang, H.; Feng, Y.; Li, M.; Zhong, Y. Predictive Current Control for Switched Reluctance Motor Based on Local Linear Phase Voltage Model. Appl. Sci. 2022, 12, 1688. [Google Scholar] [CrossRef]
- Marques, J.F.; Estima, J.O.; Gameiro, N.S.; Cardoso, A.J.M. A New Diagnostic Technique for Real-Time Diagnosis of Power Converter Faults in Switched Reluctance Motor Drives. IEEE Trans. Ind. Appl. 2014, 50, 1854–1860. [Google Scholar] [CrossRef]
- Fang, C.; Chen, H.; Torkaman, H.; Anuchin, A.; Li, X. Fault Diagnosis for Power Transistors in a Converter of Switched Reluctance Motors Based on Current Features. IEEE Sens. J. 2022, 22, 1414–1423. [Google Scholar] [CrossRef]
- Xiao, D.; Filho, S.R.; Fang, G.; Ye, J.; Emadi, A. Position-Sensorless Control of Switched Reluctance Motor Drives: A Review. IEEE Trans. Transp. Electrif. 2022, 8, 1209–1227. [Google Scholar] [CrossRef]
- Kjaer, P.C.; Gallegos-Lopez, G. Single-sensor current regulation in switched reluctance motor drives. IEEE Trans. Ind. Appl. 1998, 34, 444–451. [Google Scholar] [CrossRef]
- Gan, C.; Wu, J.; Yang, S.; Hu, Y. Phase Current Reconstruction of Switched Reluctance Motors From DC-Link Current Under Double High-Frequency Pulses Injection. IEEE Trans. Ind. Electron. 2015, 62, 3265–3276. [Google Scholar] [CrossRef]
- Gan, C.; Wu, J.; Yang, S.; Hu, Y.; Cao, W. Wavelet Packet Decomposition-Based Fault Diagnosis Scheme for SRM Drives With a Single Current Sensor. IEEE Trans. Energy Convers. 2016, 31, 303–313. [Google Scholar] [CrossRef]
- Gan, C.; Wu, J.; Hu, Y.; Yang, S.; Cao, W.; Kirtley, J.L. Online Sensorless Position Estimation for Switched Reluctance Motors Using One Current Sensor. IEEE Trans. Power Electron. 2016, 31, 7248–7263. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, J.; Gan, C.; Hu, Y.; Jin, N.; Guo, J. A New Phase Current Reconstruction Scheme for Four-Phase SRM Drives Using Improved Converter Topology Without Voltage Penalty. IEEE Trans. Ind. Electron. 2018, 65, 133–144. [Google Scholar] [CrossRef]
- Song, S.; Xia, Z.; Fang, G.; Ma, R.; Liu, W. Phase Current Reconstruction and Control of Three-Phase Switched Reluctance Machine With Modular Power Converter Using Single DC-Link Current Sensor. IEEE Trans. Power Electron. 2018, 33, 8637–8649. [Google Scholar] [CrossRef]
- Han, G.; Chen, H.; Shi, X.; Wang, Y. Phase current reconstruction strategy for switched reluctance machines with fault-tolerant capability. IET Electr. Power Appl. 2017, 11, 399–411. [Google Scholar] [CrossRef]
- Han, G.; Chen, H.; Guan, G. Low-cost SRM drive system with reduced current sensors and position sensors. IET Electr. Power Appl. 2019, 13, 853–862. [Google Scholar] [CrossRef]
- Gan, C.; Sun, Q.; Wu, J.; Shi, C.; Hu, Y. A Universal Two-Sensor Current Detection Scheme for Current Control of Multiphase Switched Reluctance Motors With Multiphase Excitation. IEEE Trans. Power Electron. 2019, 34, 1526–1539. [Google Scholar] [CrossRef]
- Gan, C.; Sun, Q.; Jin, N.; Tolbert, L.M.; Ling, Z.; Hu, Y.; Wu, J. Cost-Effective Current Measurement Technique for Four-Phase SRM Control by Split Dual Bus Line Without Pulse Injection and Voltage Penalty. IEEE Trans. Ind. Electron. 2018, 65, 4553–4564. [Google Scholar] [CrossRef]
- Peng, W.; Gyselinck, J.J.C.; Ahn, J.W.; Lee, D.H. Minimal Current Sensing Strategy for Switched Reluctance Machine Control With Enhanced Fault-Detection Capability. IEEE Trans. Ind. Appl. 2019, 55, 3725–3735. [Google Scholar] [CrossRef]
- Xu, S.; Chen, H.; Yang, J.; Dong, F. Comparative evaluation on switched reluctance motor drive with different phase current sensing methods. IET Electr. Power Appl. 2019, 13, 1964–1975. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, J.; Gan, C.; Guo, J. A Multiplexed Current Sensors-Based Phase Current Detection Scheme for Multiphase SRMs. IEEE Trans. Ind. Electron. 2019, 66, 6824–6835. [Google Scholar] [CrossRef]
- Nasirian, V.; Davoudi, A.; Kaboli, S.; Edrington, C.S. Excitation Shifting: A General Low-Cost Solution for Eliminating Ultra-Low-Frequency Torque Ripple in Switched Reluctance Machines. IEEE Trans. Magn. 2013, 49, 5135–5149. [Google Scholar] [CrossRef]




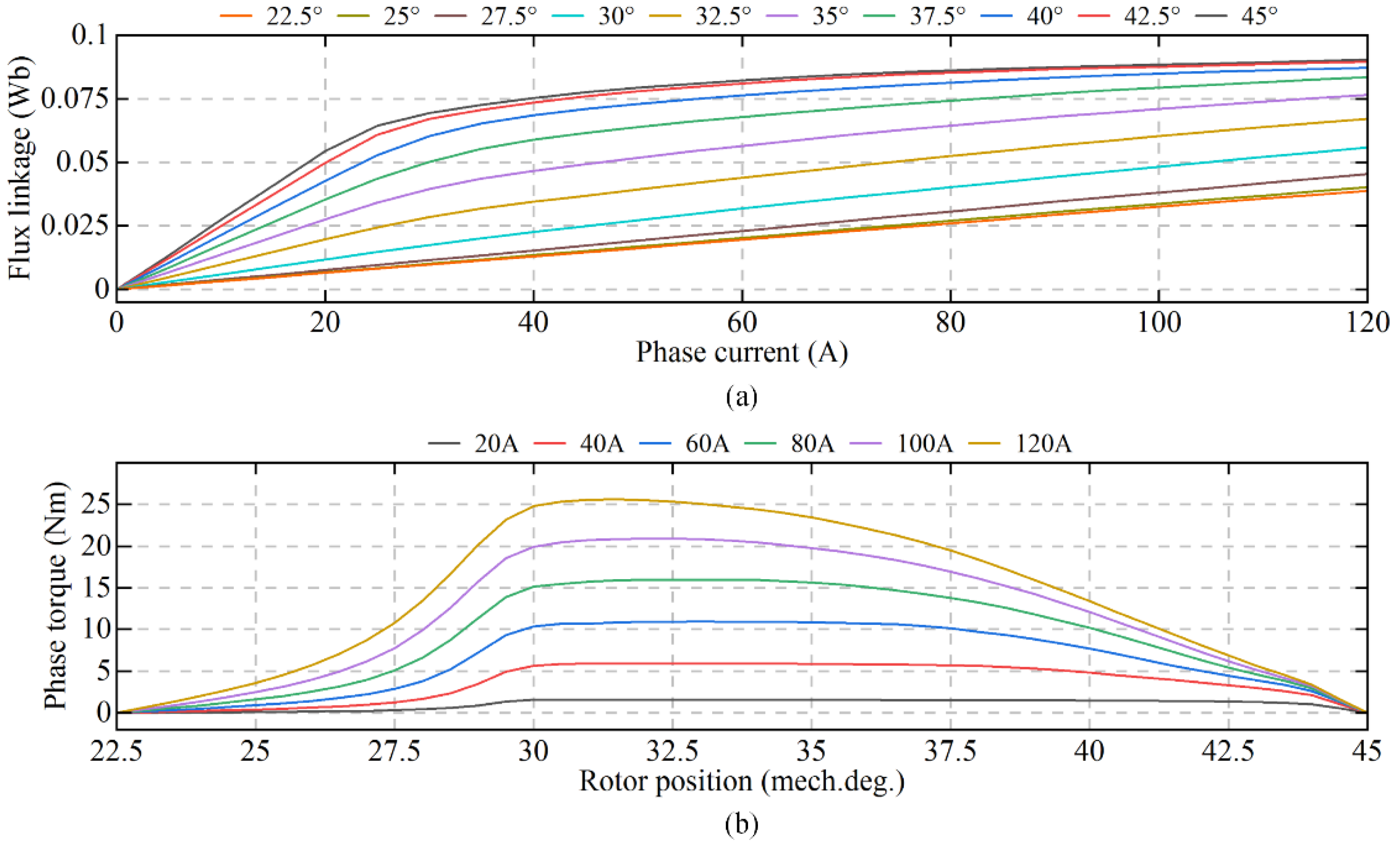




| Parameter Name | Value | Parameter Name | Value |
|---|---|---|---|
| Rated power | 1.5 kW | Number of phases | 3 |
| Rated voltage | 72 V | Number of stator poles | 12 |
| Rated speed | 4300 rpm | Number of rotor poles | 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, S.; Wang, H.; Li, M.; Feng, Y.; Zhong, Y. Torque-Enhanced Phase Current Detection Schemes for Multiphase Switched Reluctance Motors with Reduced Sensors. Appl. Sci. 2022, 12, 5956. https://doi.org/10.3390/app12125956
Shen S, Wang H, Li M, Feng Y, Zhong Y. Torque-Enhanced Phase Current Detection Schemes for Multiphase Switched Reluctance Motors with Reduced Sensors. Applied Sciences. 2022; 12(12):5956. https://doi.org/10.3390/app12125956
Chicago/Turabian StyleShen, Shiqi, Hui Wang, Mengqiu Li, Yaojing Feng, and Yichang Zhong. 2022. "Torque-Enhanced Phase Current Detection Schemes for Multiphase Switched Reluctance Motors with Reduced Sensors" Applied Sciences 12, no. 12: 5956. https://doi.org/10.3390/app12125956
APA StyleShen, S., Wang, H., Li, M., Feng, Y., & Zhong, Y. (2022). Torque-Enhanced Phase Current Detection Schemes for Multiphase Switched Reluctance Motors with Reduced Sensors. Applied Sciences, 12(12), 5956. https://doi.org/10.3390/app12125956






