Reliability Analysis of the Main Pier during the Construction Period of HLCR Bridges
Abstract
:1. Introduction
2. Theoretical Foundation
2.1. Checkpoint Method (JC Method)
- (1)
- Assume that the design checkpoint is initially assigned (generally taken as the mean value point);
- (2)
- Carry out equivalent normalization of the non-normal variable . The statistical parameters and of its equivalent normal distribution are calculated and used in place of and . This is recorded as ,;
- (3)
- From Equation (7), calculate the value of , including and ;
- (4)
- Using Equation (8), calculate the value of ;
- (5)
- Using Equation (10), calculate the new value of ;
- (6)
- Repeat (2)–(5) with this until the difference between the first and second or the absolute value of is less than the allowable error .
2.2. Analysis of Indeterminate Factors Affecting the Resistance of the Main Pier in Cradle Construction
2.3. Resistance Probability Modeling
2.4. Load Probability Modeling
2.4.1. Structural Constant Load
- (1)
- Effect of the action of the cast beam section at the top (bottom) of the pier [1]:Here, is the axial force effect in the axial direction at the bridge pier under the action of cast blocks (kN); is the along-bridge bending moment effect at the bridge pier under the action of cast blocks (kN· m); is the statistical parameter of constant load indeterminacy (according to the literature [30] it obeys a normal distribution, and is taken as , ); is the weight of the i-th block (kN); is the relative deviation coefficient of the self-weight of the beam caused by the construction error on both sides of the cantilever (according to the literature [6], it is taken as , ); is the distance of the center of gravity of block i from the center of the top of the pier (m).
- (2)
- The effect of deviations caused by different overhanging speeds at both ends of the pier top (bottom) [1] is:where is the axial force effect at piers due to beam section deviation (kN); is the parallel moment effect at piers due to beam section deviation (kN·m); is the beam section weight (kN); is the distance from the center of the beam section to the center of the top of the pier (m); is the coefficient of imbalance of the pouring speed at both ends, that is, the ratio of the weight of the beam sections being poured on both sides (according to the literature [1], we assume , ); is the beam section number being poured.
- (3)
- The effect of the self-weight of the bridge pier at the bottom of the pier [1] is:where is the pier bottom axial force effect caused by the self-weight of the bridge pier (kN); is the pier bottom bending moment effect caused by the self-weight of the bridge pier (kN·m); is the bridge pier height (m); is the average self-weight set of bridge piers ().
2.4.2. Construction Live Load
- (1)
- The load effect generated by the construction division live load at the top (bottom) of the bridge pier is [1]:where is the axial force effect at the bottom of the pier caused by the live load of the construction division (kN); is the exclusion of the axial force effect at the bottom of the pier caused by the live load action of the last three remaining girder sections (kN); is the axial force effect at the bottom of the pier caused by the live load action in the construction division of the latter three sections of the beam (kN); is the bending moment effect at the bottom of the pier caused by the live load of the construction division (kN·m); is the exclusion of the moment effect at the bottom of the pier caused by the live load action of the remaining beam sections of the last three segments (kN·m); is the bending moment effect at the bottom of the pier caused by the live load action of the construction division of the rear three sections of the beam (kN·m); is the length of the i-th beam section; is the length of block 0; is the ratio of the actual acting construction load to the theoretically calculated load value (taken as , [33]); is the width of the beam section (m); is the average value of the live load during the construction period for the i-th girder section, excluding the last three sections (); is the average value of the live load during the construction period of block 0 (); is the average value of the live load during the construction period of the i-th beam part of the last three sections (); is the distance from the center of the i-th beam part to the center of the top of the pier (m); is the deviation factor of the construction distribution live load (taken as , [34]).
- (2)
- The effect of the gravity of the hanging cradle at the top (bottom) of the pier is [1]:where is the axial force effect at the bridge pier under the action of the hanging basket (kN); is the bending moment effect at the pier under the action of the hanging basket (and the cantilever construction process on both sides of the selected hanging basket design is the same, so take 0 kN·m); is the weight of the hanging basket (kN).
2.4.3. Wind Load
2.4.4. Combination of Effects
- (1)
- Combination IThe last girder section is being poured for the cantilever without unusually high winds. In this case, the effects of wind loads are not considered due to their small size.
- The combination of load effects at the top of the pier is:
- The combination of load effects at the bottom of the pier is:
- (2)
- Combination IIWhen high winds occur, the last girder section has been cast, the side spans have not yet been closed, and the structure is in the maximum cantilever state.
- The combination of load effects at the top of the pier is:
- The combination of load effects at the top of the pier is:
3. Reliability Analysis of the Main Pier of an HLCR Bridge with a Cradle Construction
3.1. Establishment of Functions
3.2. Target Reliability Indicators
3.3. Project Examples
3.3.1. Load Analysis
- Structural constant load
- (1)
- Self-weight of beam section
- (2)
- Deviation caused by unsynchronized overhanging of beam sections
- (3)
- Self-weight of bridge pier
- 2.
- Live load effect
- (1)
- Construction step-by-step live load
- (2)
- The effect of the self-weight of the hanging basket on the main pier body
- 3.
- Wind Load
3.3.2. Resistance Probability Model
3.3.3. Reliability Calculation
- Combination 1: The last beam section is being poured
- (1)
- The solution for the function of the stability and reliability of the main pier body is:
- (2)
- The solution for the function of the strength of the main pier is:
- Combination II: The last piece is poured and completed to reach the maximum cantilever
- (1)
- The solution for the function of the stability and reliability of the main pier body is:
- (2)
- The solution for the function of the strength of the main pier is:
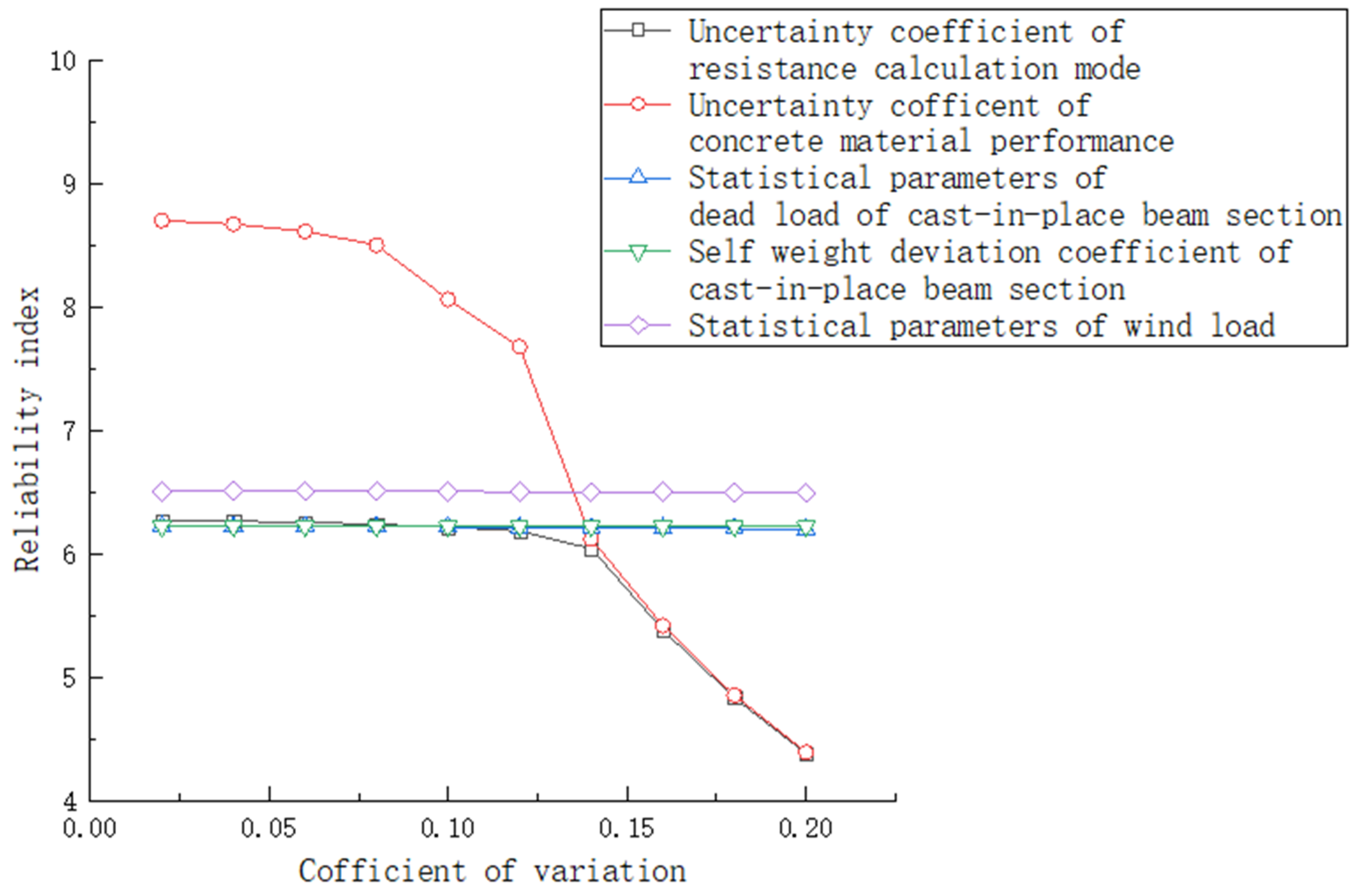
3.3.4. Reliability Parameter Impact Analysis
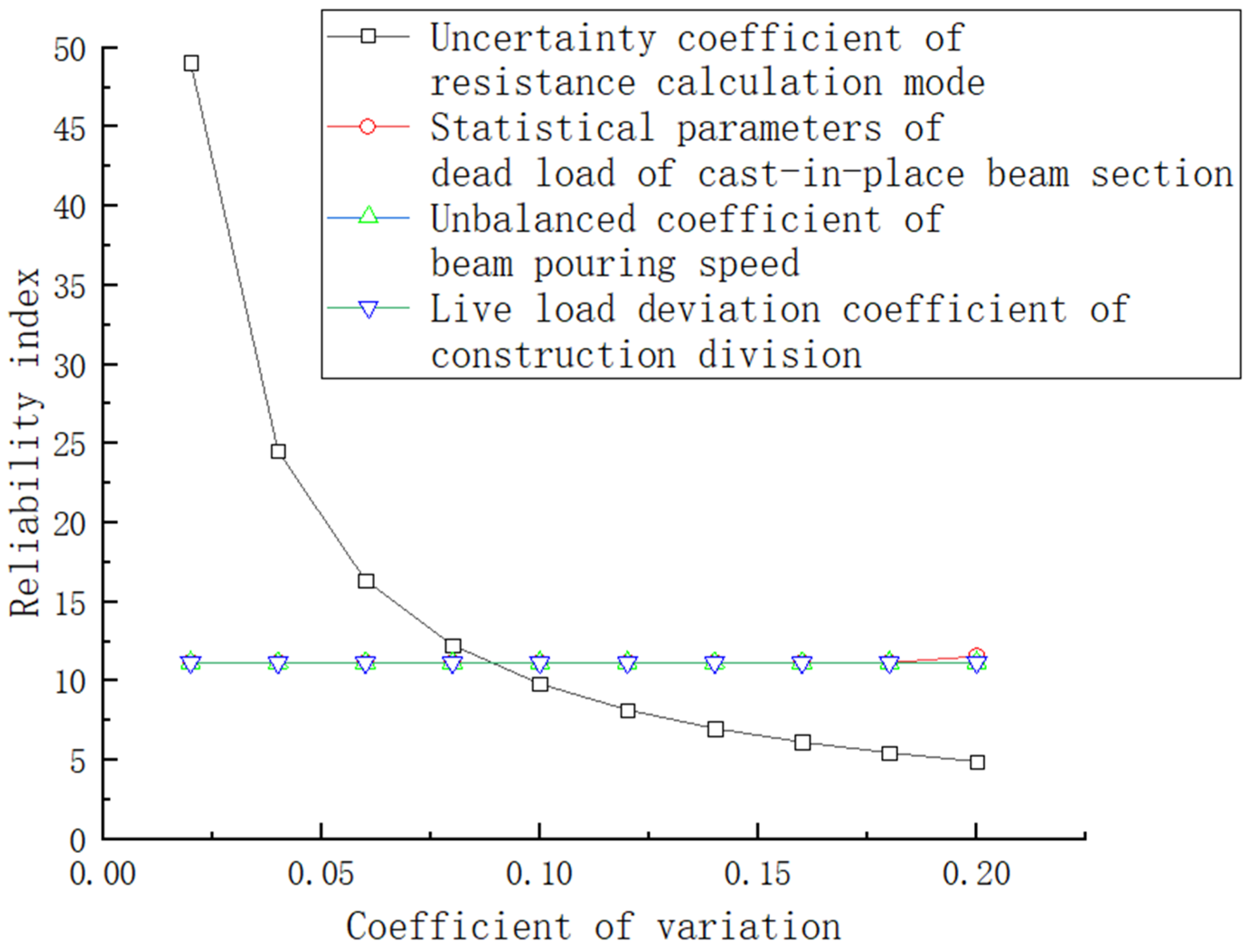
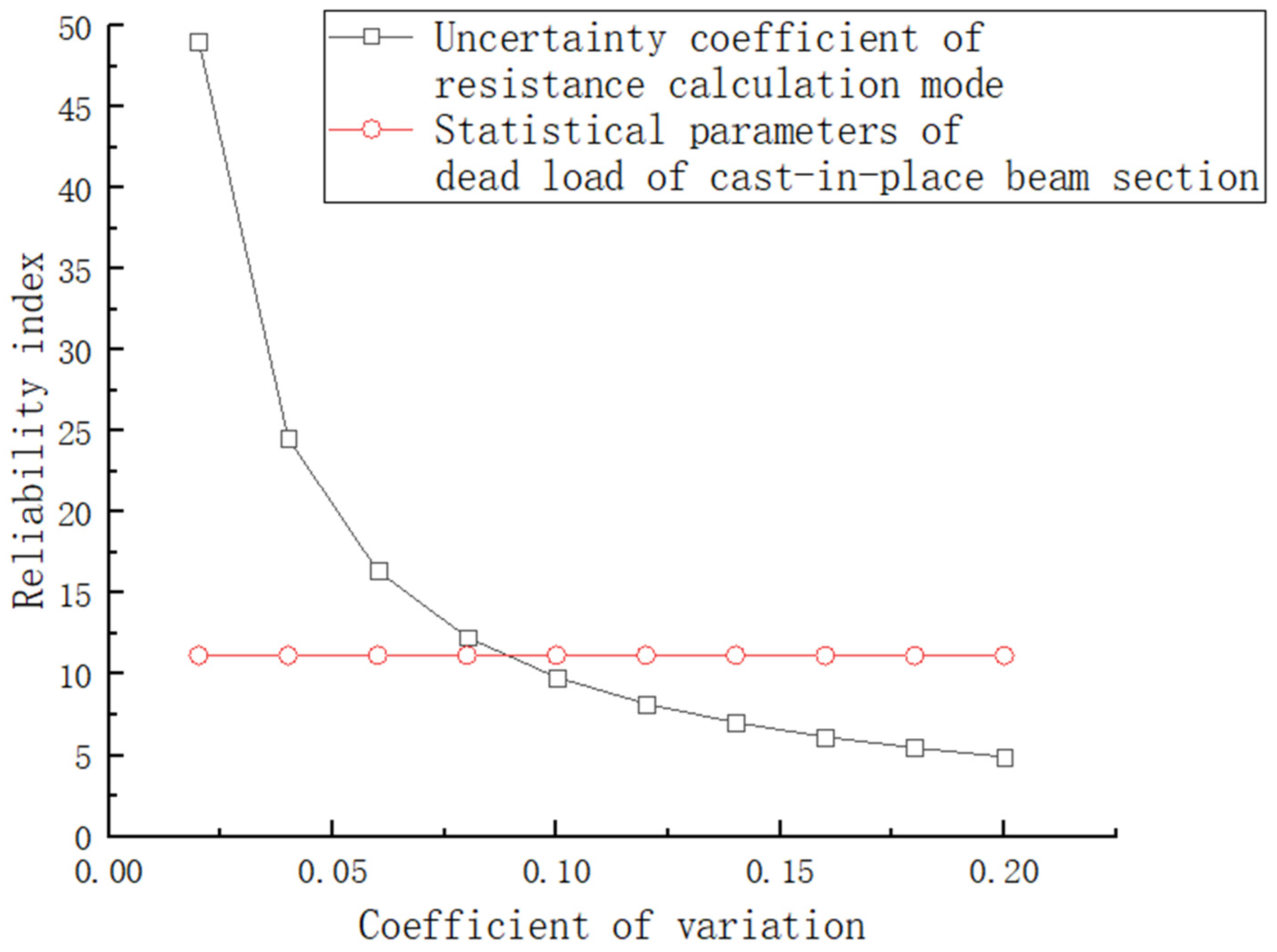
- Analysis of the influence of the stability and reliability parameters of the main pier under combination I
- 2.
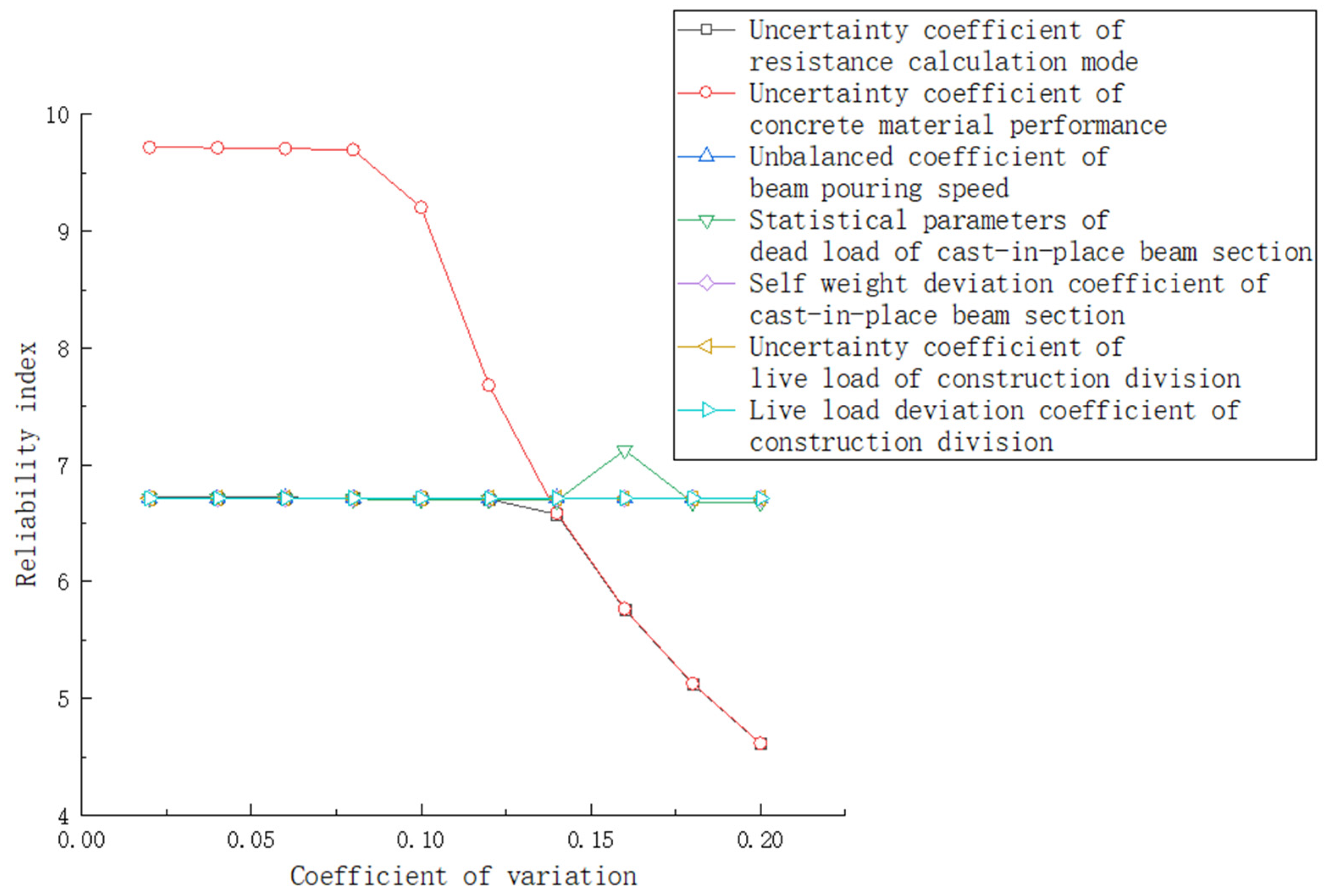
- Analysis of the influence of reliability parameters on the strength of the main pier under combination II
- 3.
- Analysis of the influence of stability reliability parameters of the main pier under combination II
- 4.
- Analysis of the influence of the strength reliability parameters of the main pier under combination II
4. Conclusions
- (1)
- Combined with the design of the HLCR bridge hanging cradle construction and the characteristics of the cantilever construction, the influencing factors of the bearing capacity were determined. The main influencing factors are the uncertainty of the resistance calculation mode, material parameters, the dead load and the live load.
- (2)
- According to the design scheme of the main beam of the HLCR bridge and the technological process of cantilever cradle construction, the structural stress characteristics and failure forms were analyzed in detail. The resistance and action effect models of the main pier under the two most unfavorable conditions were established: (1) There is no abnormal strong wind during the pouring of the last beam section; (2) The last block is poured and reaches the maximum cantilever. At this time, abnormal wind action occurs. Based on these two combinations, a reliability analysis was carried out, which laid the foundation for reliability analysis of the bridge pier during the construction period.
- (3)
- Based on a river-crossing bridge, the reliability function of a cantilever hanging basket during the construction period was established. We utilized MATLAB software to calculate the reliability index for the main pier during the cantilever construction of the bridge girder by using the JC method. The accuracy of the above analysis was proven, and we verified that the construction process for this project has a sufficient safety margin.
- (4)
- Closely combined with the reliability theory, changes in the statistical parameters of various influencing factors were analyzed for their degree of influence as structural reliability indicators, and it was found that the construction distributed live load has a relatively small influence on the reliability of bridge piers during the construction period. The actual construction can be controlled as little as possible to avoid delaying the construction period. Yet, a change in wind load parameters has a relatively large impact on the reliability of piers at the maximum cantilever, so it is necessary to avoid windy weather during construction. A fall of hanging cradles during construction, increase in resistance, change in the statistical parameters of the structural constant load and the performance of concrete materials all largely affect the reliability of piers and need to be controlled during construction, which provides a reference for the construction of subsequent such projects.
- (1)
- The large-scale use of finite element analysis software is very beneficial to the study of engineering cases. This paper mainly relied on reviewing the literature when investigating the factors affecting structural reliability during the construction period. Follow-up research could involve finite element software and time-dependent random theory to facilitate a more comprehensive and accurate analysis of the reliability of the bridge structure during construction.
- (2)
- A bridge structure is a whole system composed of many components. The research on bridge structures in this paper was limited to the analysis of structural components, and did not analyze the stability and reliability of a whole bridge system, which should be covered by future research.
- (3)
- The ultimate goal of academic research is to guide production. In this paper, the relative proportions of the factors affecting the reliability during the construction period were determined through analysis. The relative quantitative weight of each factor could be established in future research; such information will be valuable as it can be directly used in the construction of bridges that are yet to be built.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kang, H. Reliability Analysis of a Rigid Frame Bridge with High Pier Large Span during Constructin Period. Master’s Thesis, Beijing University of Technology, Beijing, China, 2006. [Google Scholar]
- Wang, H. Analysis on the development of continuous rigid frame bridges in the world. Commun. Sci. Technol. Heilongjiang 2006, 64–65. [Google Scholar] [CrossRef]
- Xie, W.; Chen, R.; Mu, J. Design and construction of main tower foundation of cable-stayed bridge in Luoxi Bridge Widening Project. Urban Roads Bridges Flood Control. 2019. [Google Scholar] [CrossRef]
- Zhang, A. Reviews for the research of performance reliability-based design theory for the whole service life of structures. J. Beijing Univ. Technol. 2000, 26, 55–58. [Google Scholar]
- Casas, J.R. Reliability-based partial safety factors in cantilever construction of concrete bridges. J. Struct. Eng. 1997, 123, 305–312. [Google Scholar] [CrossRef]
- Sexsmith, R.G. Reliability during temporary erection phases. Eng. Struct. 1998, 20, 999–1003. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, F. Reliability analysis of the global stability in cantilever construction of continuous bridges. J. Transport. Sci. Eng. 2002, 18, 26–29. [Google Scholar]
- Zhang, J.; Hao, H. Reliability analysis of prestressed concrete continuous beam bridge during Cantilever Construction. Cent. South. Highw. Eng. 2003, 28, 15–18. [Google Scholar]
- Hedjazi, S.; Rahai, A.; Sennah, K. Long-term behavior of segmentally-erected prestressed concrete box-girder bridges. Struct. Eng. Mech. 2005, 20, 673–693. [Google Scholar] [CrossRef]
- Catbas, F.N.; Susoy, M.; Frangopol, D.M. Structural health monitoring and reliability estimation: Long span truss bridge application with environmental monitoring data. Eng. Struct. 2008, 30, 2347–2359. [Google Scholar] [CrossRef]
- Sun, C.; Li, A.; Miao, C.; Qiao, Y. Parameter identification and dynamic reliability evaluation of elevation control for long-span concrete rigid frame bridge. J. Southeast. Univ. 2012, 42, 104–108. [Google Scholar]
- Luo, Z.; Dong, F. Reliability analysis of cantilever construction state of continuous beam bridge. Highw. Eng. 2013, 38, 162–164. [Google Scholar]
- Vican, J.; Repa, J.; Kotes, P.; Andreev, V. Existing bridge evaluation using deficiency point method. In Proceedings of the 5th International Scientific Conference on Integration, Partnership and Innovation in Construction Science and Education (IPICSE), Moscow, Russia, 16–17 October 2016. [Google Scholar] [CrossRef]
- Cheng, Z.; Liu, Y.; Lu, N. Stability reliability analysis of long-span continuous rigid frame bridge during construction period. J. Transport. Sci. Eng. 2018, 34, 58–63. [Google Scholar]
- Lu, N.; Liu, Y. Method and Application of Bridge Reliability Analysis; Southeast University Press: Nanjing, China, 2017. [Google Scholar]
- Cornell, C.A. A probability-based structural code. ACI 1969, 66, 74–985. [Google Scholar]
- Wang, R. Dynamic Reliability Analysis of Retaining Wall with Random Parameter Subjected to Seismic Activity. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, May 2010. [Google Scholar]
- Box, G.E.P.; Wilson, K.B. On the experimental attainment of optimal conditions. J. R. Stat. Soc. 1951, 13, 1–45. [Google Scholar]
- Xie, L. Bridge Seismic Fragility Analysis Based on Improved Kriging Response Surface Method. Master’s Thesis, South China University of Technology, Guangzhou, China, April 2020. [Google Scholar]
- Li, D.Q.; Zheng, D.; Cao, Z.J.; Tang, X.S.; Phoon, K.K. Response surface methods for slope reliability analysis: Review and comparison. Eng. Geol. 2016, 203, 3–14. [Google Scholar] [CrossRef]
- Bucher, G.C.; Bouraund, U. A fast and efficient response surface approach for structural reliability problems. Struct. Saf. 1990, 7, 57–66. [Google Scholar] [CrossRef]
- Hasofer, A.M.; Lind, N.C. Exact and invariant second moment code format. J. Eng. Mech. 1974, 100, 111–121. [Google Scholar] [CrossRef]
- Jing, L. Reliability of the Long-Span Continuous Rigid Frame Bridge with High-Piers in Construction Stage. Master’s Thesis, Zhengzhou University, Zhengzhou, China, April 2020. [Google Scholar]
- He, S.; Wang, S. Structural Reliability Analysis and Design; National Defense Industry Press: Beijing, China, 1993; pp. 14–49. [Google Scholar]
- Song, X.; Tan, Z. Application of improved importance sampling method in power system reliability evaluation. Power Syst. Technol. 2005, 29, 56–59. [Google Scholar]
- Søren, T.; Daniel, M.; Tartakovsky. Estimation of distributions via multilevel Monte Carlo with stratified sampling. J. Comput. Phys. 2020, 419, 109572. [Google Scholar]
- Chen, R.; Low, Y.M. Reducing uncertainty in time domain fatigue analysis of offshore structures using control variates. Mech. Syst. Signal. Process. 2021, 149, 107192. [Google Scholar] [CrossRef]
- Sullivan, R.S.; Hayya, J.C.; Schaul, R. Efficiency of the antithetic variate method for simulating stochastic networks. Manag. Sci. 1982, 28, 563–572. [Google Scholar] [CrossRef]
- Wang, F. Investigation and Seismic Stability Analysis of Highway Slope in Southwestern Yunnan. Master’s Thesis, Chang’an University, Xi’an, China, April 2015. [Google Scholar]
- JTG 2120-2020; Unified Standard for Reliability Design of Highway Engineering Structures. Industry Standard of the People’s Republic of China: Beijing, China, 2020.
- JTG 3362-2018; Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts. Industry Standard of the People’s Republic of China: Beijing, China, 2018.
- Zhang, J.; Guan, G.; Yang, W. Statistical analysis of live load on continuous beam bridge of cantilever casting during construction. J. Transport. Sci. Eng. 2003, 19, 1–5. [Google Scholar]
- Wang, Q. Analysis of wind resistance of piers of Huatupo super large bridge during construction. Railw. Constr. Technol. 2002, 4–7. [Google Scholar]
- Ge, Y. Analysis and Control of Segmental Construction Bridges; People’s Communications Press: Beijing, China, June 2003. [Google Scholar]
- JTG D60-2015; General Specification for Design of Highway Bridges and Culverts. Industry Standard of the People’s Republic of China: Beijing, China, 2015.
- JTG/T 3360-01-2018; Specification for Wind-Resistant Design of Highways and Bridges. Industry Standard of the People’s Republic of China: Beijing, China, 2018.


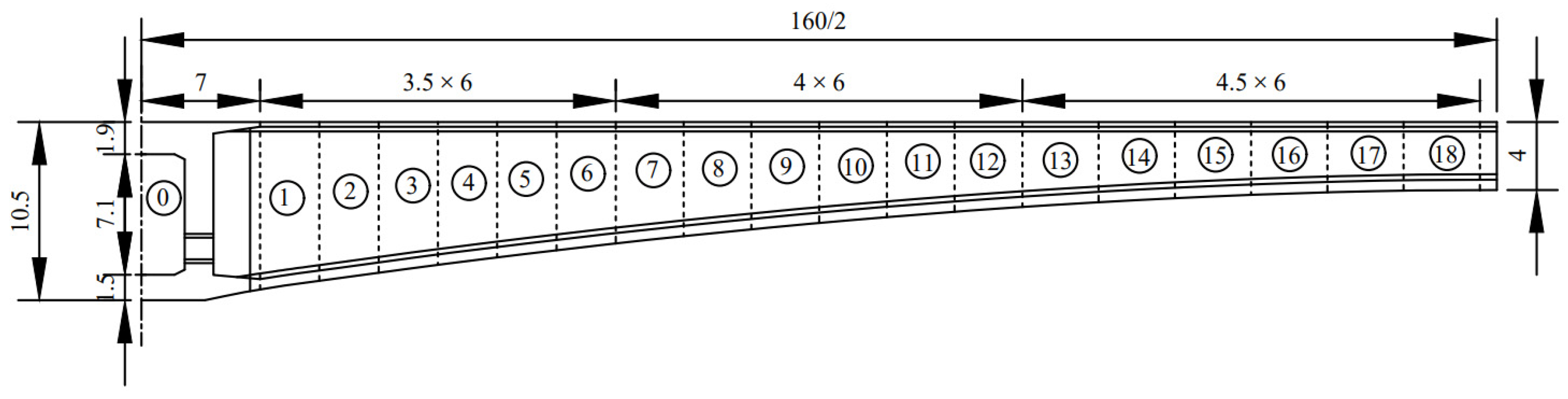
| Beam Section Number | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 16,143.4 | 2345.2 | 2241.2 | 2142.2 | 2046.2 | 1955.2 | 1869.4 | |
| 14 | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 | |
| Beam section number | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 2035.8 | 1934.4 | 1840.8 | 1755 | 1617.2 | 1432.6 | 1484.6 | |
| 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.5 | |
| Beam section number | 14 | 15 | 16 | 17 | 18 | ||
| 1427.4 | 1380.6 | 1341.6 | 1315.6 | 1300 | |||
| 4.5 | 4.5 | 4.5 | 4.5 | 4.5 |
| No. | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Q (kPa) | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| No. | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Q (kPa) | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| No. | 14 | 15 | 16 | 17 | 18 | ||
| Q (kPa) | 0.1 | 0.385925 | 0.622675 | 0.859425 | 0 |
| Name | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Distribution Type | Normal | Normal | Normal | Normal | Normal | Normal | Normal | Normal | Generalized Pareto |
| 1.07 | 1.065 | 1.0212 | 1 | 0.025 | 0.5 | 0.03 | 1.3877 | 8.27 | |
| 0.095 | 0.088 | 0.0462 | 0.144 | 0.15 | 0.15 | 0.15 | 0.1374 | 5.5 |
| Average | Reliability Indicators | Average | Reliability Indicators | Average | Reliability Indicators | Average | Reliability Indicators |
|---|---|---|---|---|---|---|---|
| 1.00 | 11.1451 | 0.90 | 11.1822 | 0.25 | 11.1593 | 0.0 | 11.1594 |
| 1.05 | 11.1555 | 0.95 | 11.1724 | 0.30 | 11.1592 | 0.5 | 11.1589 |
| 1.10 | 11.1650 | 1.00 | 11.1626 | 0.35 | 11.1590 | 1.0 | 11.1585 |
| 1.15 | 11.1731 | 1.05 | 11.1528 | 0.40 | 11.1588 | 1.5 | 11.1580 |
| 1.20 | 11.1816 | 1.10 | 11.1430 | 0.45 | 11.1586 | 2.0 | 11.1575 |
| 1.25 | 11.1889 | 1.15 | 11.1332 | 0.50 | 11.1585 | 2.5 | 11.1571 |
| 1.30 | 11.1956 | 1.20 | 11.233 | 0.55 | 11.1583 | 3.0 | 11.1566 |
| 1.35 | 11.2019 | 1.25 | 11.1135 | 0.60 | 11.1581 | 3.5 | 11.1561 |
| 1.40 | 11.2077 | 1.30 | 11.1036 | 0.65 | 11.1580 | 4.0 | 11.1557 |
| 1.45 | 11.2130 | 1.35 | 11.0937 | 0.70 | 11.1578 | 4.5 | 11.1552 |
| 1.50 | 11.2181 | 1.40 | 11.0838 | 0.75 | 11.1576 | 5.0 | 11.1547 |
| Average | Reliability Indicators | Average | Reliability Indicators | Average | Reliability Indicators | Average | Reliability Indicators |
|---|---|---|---|---|---|---|---|
| 0.90 | 6.6044 | 1.00 | 6.4882 | 0.25 | 6.6611 | 0.90 | 6.7815 |
| 0.95 | 6.6407 | 1.05 | 6.5269 | 0.30 | 6.6717 | 0.95 | 6.7536 |
| 1.00 | 6.734 | 1.10 | 6.5620 | 0.35 | 6.6823 | 1.00 | 6.7257 |
| 1.05 | 6.7028 | 1.15 | 6.5940 | 0.40 | 6.6928 | 1.05 | 6.6977 |
| 1.10 | 6.7296 | 1.20 | 6.6232 | 0.45 | 6.7033 | 1.10 | 6.6697 |
| 1.15 | 6.7539 | 1.25 | 6.6501 | 0.50 | 6.7138 | 1.15 | 6.6416 |
| 1.20 | 6.7763 | 1.30 | 6.6748 | 0.55 | 6.7243 | 1.20 | 6.6135 |
| 1.25 | 6.7968 | 1.35 | 6.6977 | 0.60 | 6.7348 | 1.25 | 6.5853 |
| 1.30 | 6.8156 | 1.40 | 6.7189 | 0.65 | 6.7452 | 1.30 | 6.5570 |
| 1.35 | 6.8330 | 1.45 | 6.7386 | 0.70 | 6.7556 | 1.35 | 6.5287 |
| 1.40 | 6.8492 | 1.50 | 6.7571 | 0.75 | 6.7659 | 1.40 | 6.5003 |
| Average | Reliability Indicators | Average | Reliability Indicators | Average | Reliability Indicators | ||
| 0.000 | 6.7723 | 0.0 | 6.7152 | 0.00 | 6.7145 | ||
| 0.005 | 6.7607 | 0.5 | 6.7145 | 0.01 | 6.7142 | ||
| 0.010 | 6.7490 | 1.0 | 6.7138 | 0.02 | 6.7140 | ||
| 0.015 | 6.7373 | 1.5 | 6.7132 | 0.03 | 6.7138 | ||
| 0.020 | 6.7256 | 2.0 | 6.7126 | 0.04 | 6.7136 | ||
| 0.025 | 6.7138 | 2.5 | 6.7120 | 0.05 | 6.7133 | ||
| 0.030 | 6.7021 | 3.0 | 6.7114 | 0.06 | 6.7131 | ||
| 0.035 | 6.6903 | 3.5 | 6.7106 | 0.07 | 6.7130 | ||
| 0.040 | 6.6784 | 4.0 | 6.7100 | 0.08 | 6.7128 | ||
| 0.045 | 6.6666 | 4.5 | 6.7093 | 0.09 | 6.7126 | ||
| 0.050 | 6.6547 | 5.0 | 6.7087 | 0.10 | 6.7124 | ||
| Average | Reliability Indicators | Average | Reliability Indicators |
|---|---|---|---|
| 1.00 | 11.1479 | 0.90 | 11.1846 |
| 1.01 | 11.1500 | 0.95 | 11.1749 |
| 1.02 | 11.1521 | 1.00 | 11.1652 |
| 1.03 | 11.1542 | 1.05 | 11.1554 |
| 1.04 | 11.1562 | 1.10 | 11.1457 |
| 1.05 | 11.1582 | 1.15 | 11.1360 |
| 1.06 | 11.1601 | 1.20 | 11.1262 |
| 1.07 | 11.1620 | 1.25 | 11.1164 |
| 1.08 | 11.1639 | 1.30 | 11.1066 |
| 1.09 | 11.1657 | 1.35 | 11.0968 |
| 1.10 | 11.1675 | 1.40 | 11.0870 |
| Average | Reliability Indicators | Average | Reliability Indicators | Average | Reliability Indicators |
|---|---|---|---|---|---|
| 0.90 | 5.9672 | 1.00 | 5.6882 | 0.90 | 6.2774 |
| 0.95 | 6.0531 | 1.05 | 5.7817 | 0.95 | 6.2548 |
| 1.00 | 6.1294 | 1.10 | 5.8661 | 1.00 | 6.2323 |
| 1.05 | 6.1975 | 1.15 | 5.9425 | 1.05 | 6.2097 |
| 1.10 | 6.2585 | 1.20 | 6.0119 | 1.10 | 6.1871 |
| 1.15 | 6.3135 | 1.25 | 6.0751 | 1.15 | 6.1644 |
| 1.20 | 6.3632 | 1.30 | 6.1328 | 1.20 | 6.1418 |
| 1.25 | 6.4084 | 1.35 | 6.1857 | 1.25 | 6.1191 |
| 1.30 | 6.4495 | 1.40 | 6.2343 | 1.30 | 6.0963 |
| 1.35 | 6.4871 | 1.45 | 6.2790 | 1.35 | 6.0736 |
| 1.40 | 6.5216 | 1.50 | 6.3204 | 1.40 | 6.0509 |
| Average | Reliability Indicators | Average | Reliability Indicators | ||
| 0.000 | 6.2859 | 11 | 6.4095 | ||
| 0.005 | 6.2734 | 12 | 6.3563 | ||
| 0.010 | 6.2607 | 13 | 6.3007 | ||
| 0.015 | 6.2481 | 14 | 6.2430 | ||
| 0.020 | 6.2354 | 15 | 6.1832 | ||
| 0.025 | 6.2227 | 16 | 6.1214 | ||
| 0.030 | 6.2100 | 17 | 6.0579 | ||
| 0.035 | 6.1972 | 18 | 5.9928 | ||
| 0.040 | 6.1844 | 19 | 5.9262 | ||
| 0.045 | 6.1716 | 20 | 5.8583 | ||
| 0.050 | 6.1587 | 21 | 5.7984 | ||
| Variables | Hanging Cradles Work Properly | Hanging Cradle Falls |
|---|---|---|
| 11.1585 | 11.1585 | |
| 6.7138 | 6.3056 | |
| 11.1611 | 11.1611 | |
| 6.2227 | 5.8423 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, N.; Xu, B.; Zhang, T.; Li, Q. Reliability Analysis of the Main Pier during the Construction Period of HLCR Bridges. Appl. Sci. 2022, 12, 5936. https://doi.org/10.3390/app12125936
Qi N, Xu B, Zhang T, Li Q. Reliability Analysis of the Main Pier during the Construction Period of HLCR Bridges. Applied Sciences. 2022; 12(12):5936. https://doi.org/10.3390/app12125936
Chicago/Turabian StyleQi, Ningning, Baosheng Xu, Tianjing Zhang, and Qingfu Li. 2022. "Reliability Analysis of the Main Pier during the Construction Period of HLCR Bridges" Applied Sciences 12, no. 12: 5936. https://doi.org/10.3390/app12125936
APA StyleQi, N., Xu, B., Zhang, T., & Li, Q. (2022). Reliability Analysis of the Main Pier during the Construction Period of HLCR Bridges. Applied Sciences, 12(12), 5936. https://doi.org/10.3390/app12125936






