Predicting Algorithm of Tissue Cell Ratio Based on Deep Learning Using Single-Cell RNA Sequencing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset Collection
2.2. Structure of Autoptcr Model
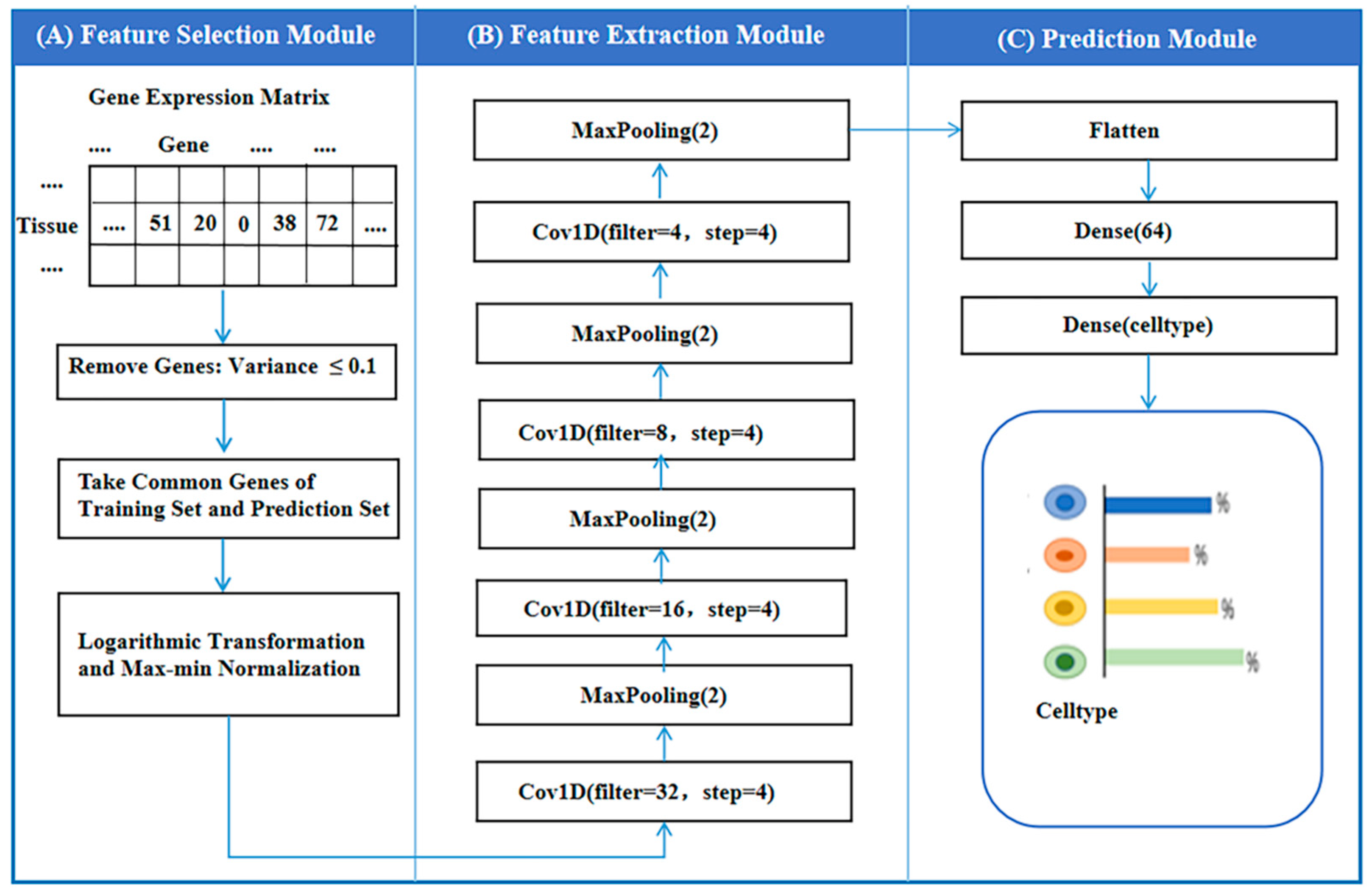
2.2.1. Feature Selection Module
2.2.2. Feature Extraction Module
2.2.3. Feature Prediction Module
2.3. Evaluation Indicators
2.4. Algorithm of Autoptcr Model
| Algorithm 1 Autoptcr | |
| Begin | |
| 1. | Input: is the gene set of the trained ScRNA tissues; Z is the proportion of cells corresponding to ; T is the gene set of the tested tissues; |
| 2. | Set the hyperparameters of the Autoptcr model, LR = 0.001, OA = Adam, LF = MSE, D = 1, V = 32, S = 2000, BS = 128, ; |
| 3. | for c = 1 to q do |
| 4. | if feature variance of |
| 5. | ; |
| 6. | else |
| 7. | ; |
| 8. | end for |
| 9. | ; //Look for the same genes |
| 10. | Perform a data conversion on X to get X’, X<--X’; |
| 11. | fors = 1 to S do |
| 12. | Sample BS data from X; |
| 13. | For j = 1 to 4 do |
| 14. | for v = 1 to V do //Determine the number of convolution filters V |
| 15. | ; //Convolution layer processing |
| 16. | ; //Maxpooling layer processing |
| 17. | end for |
| 18. | ; |
| 19. | V←V/2; |
| 20. | end for |
| 21. | , get one-dimensional data; |
| 22. | Input into two dense layers, get predicted cell ratio of tissue ; |
| 23. | Calculate loss function, ; |
| 24. | Update the training parameters by OA and LR; |
| 25. | end for |
| 26. | Output: Final predicted cell ratio of tissue Z”; |
| End | |
3. Results and Discussion
3.1. Training of Autoptcr
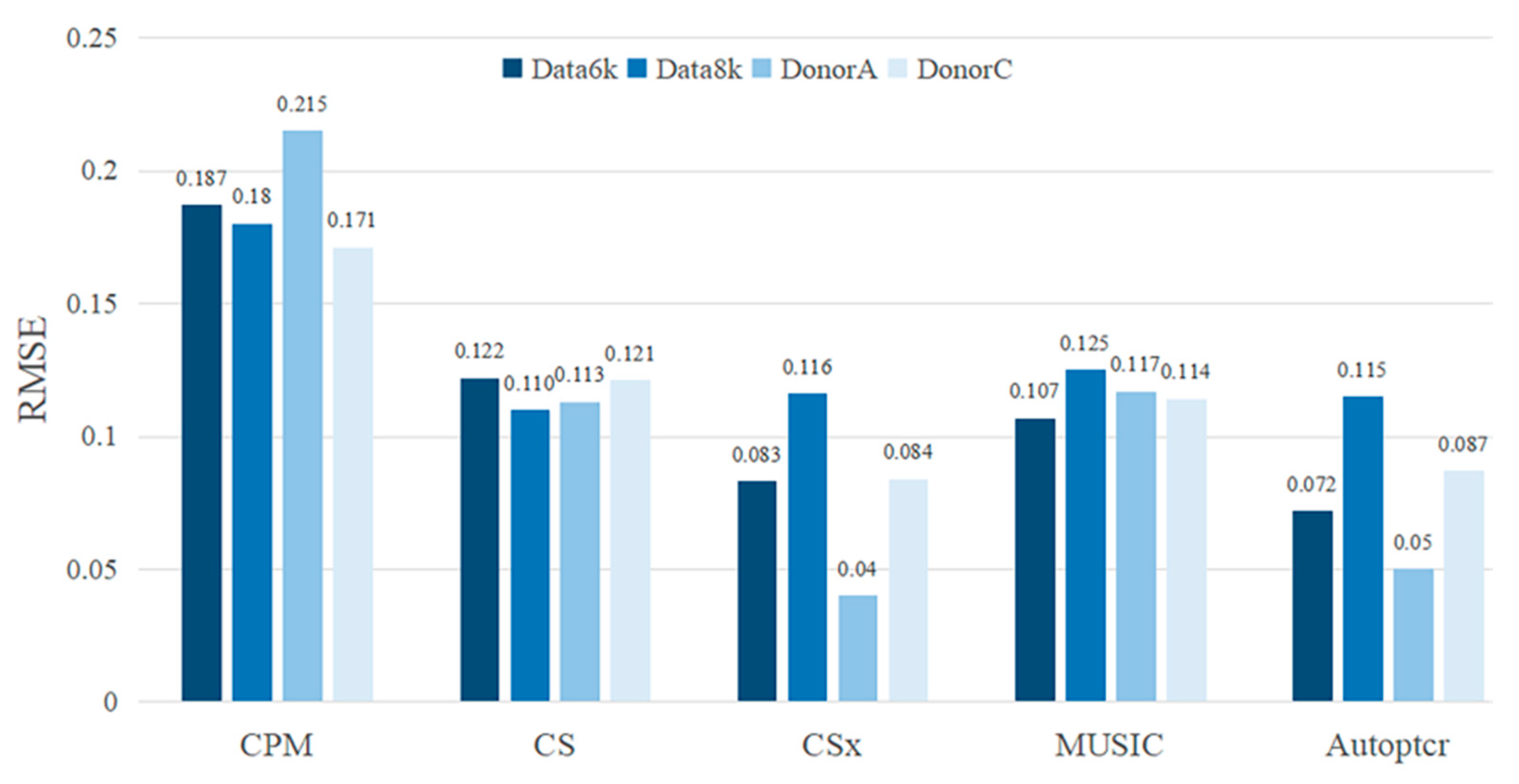
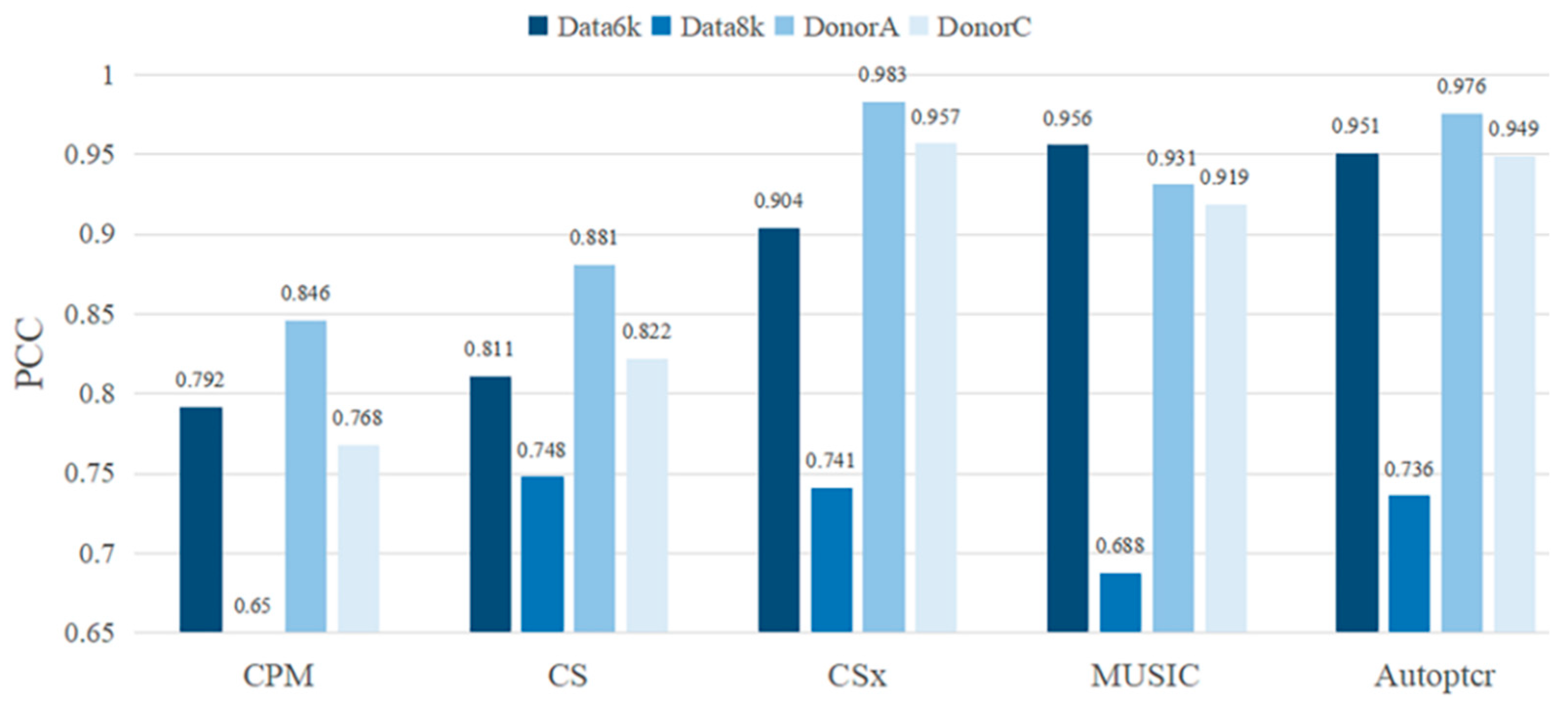
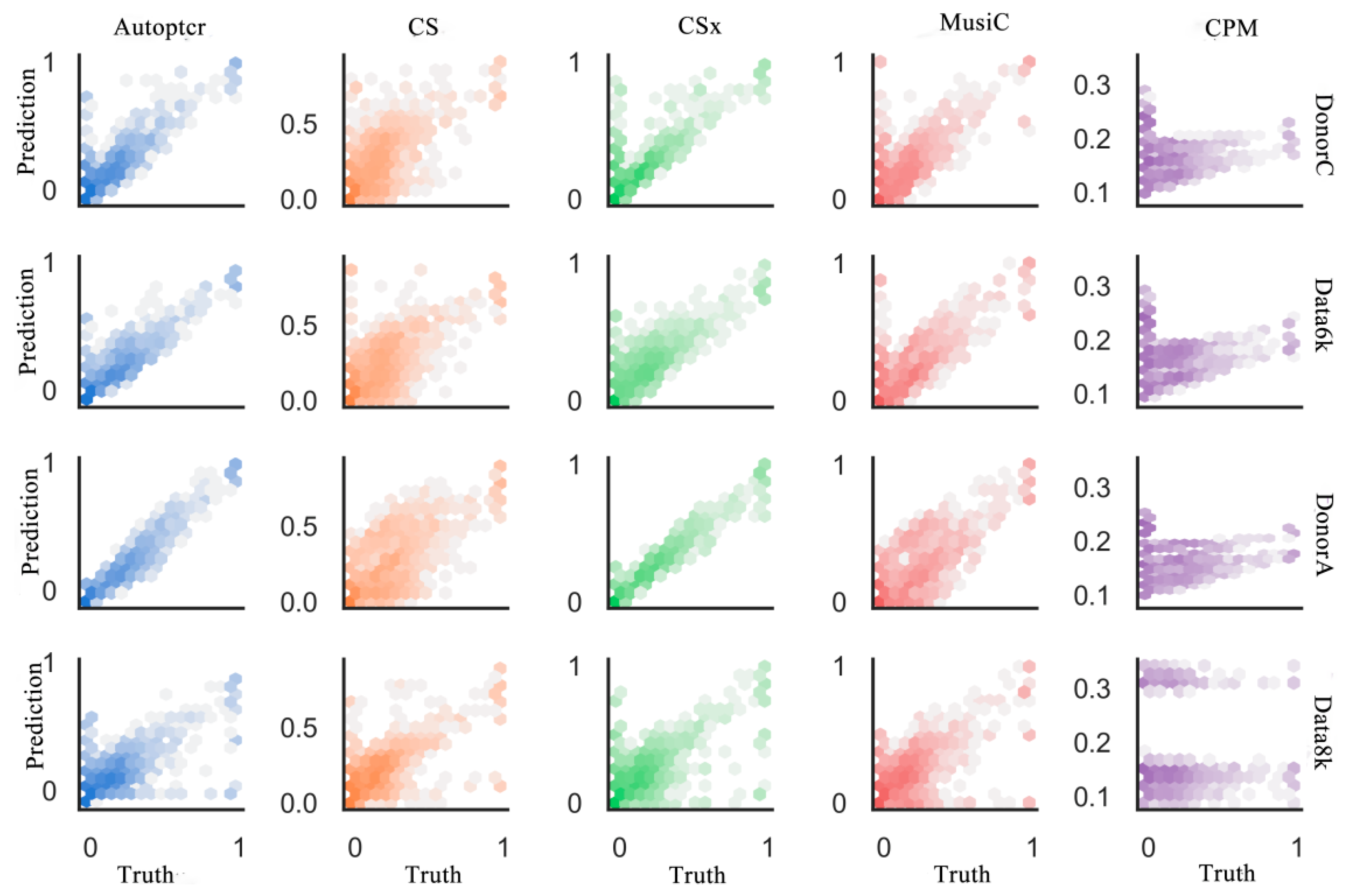
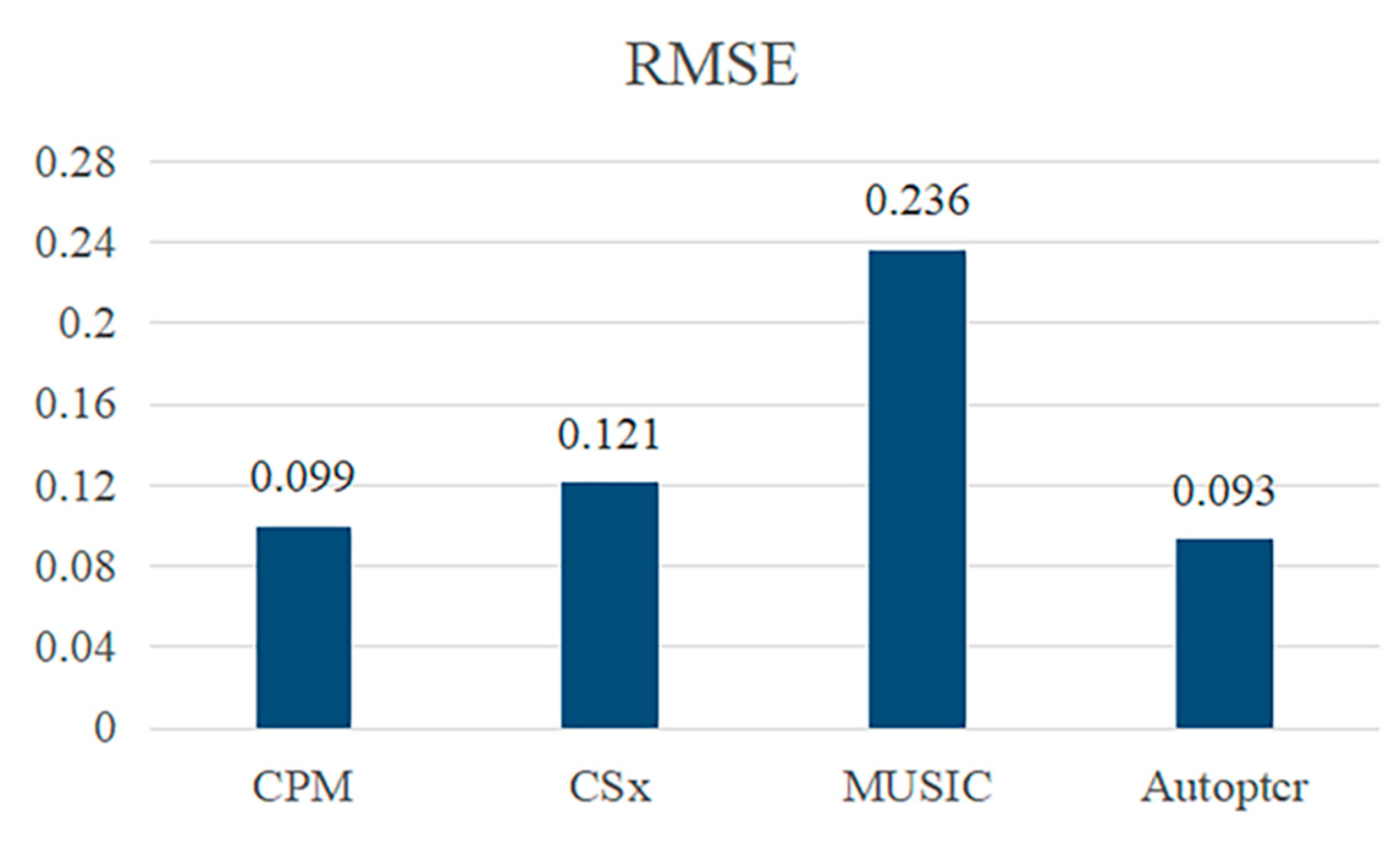
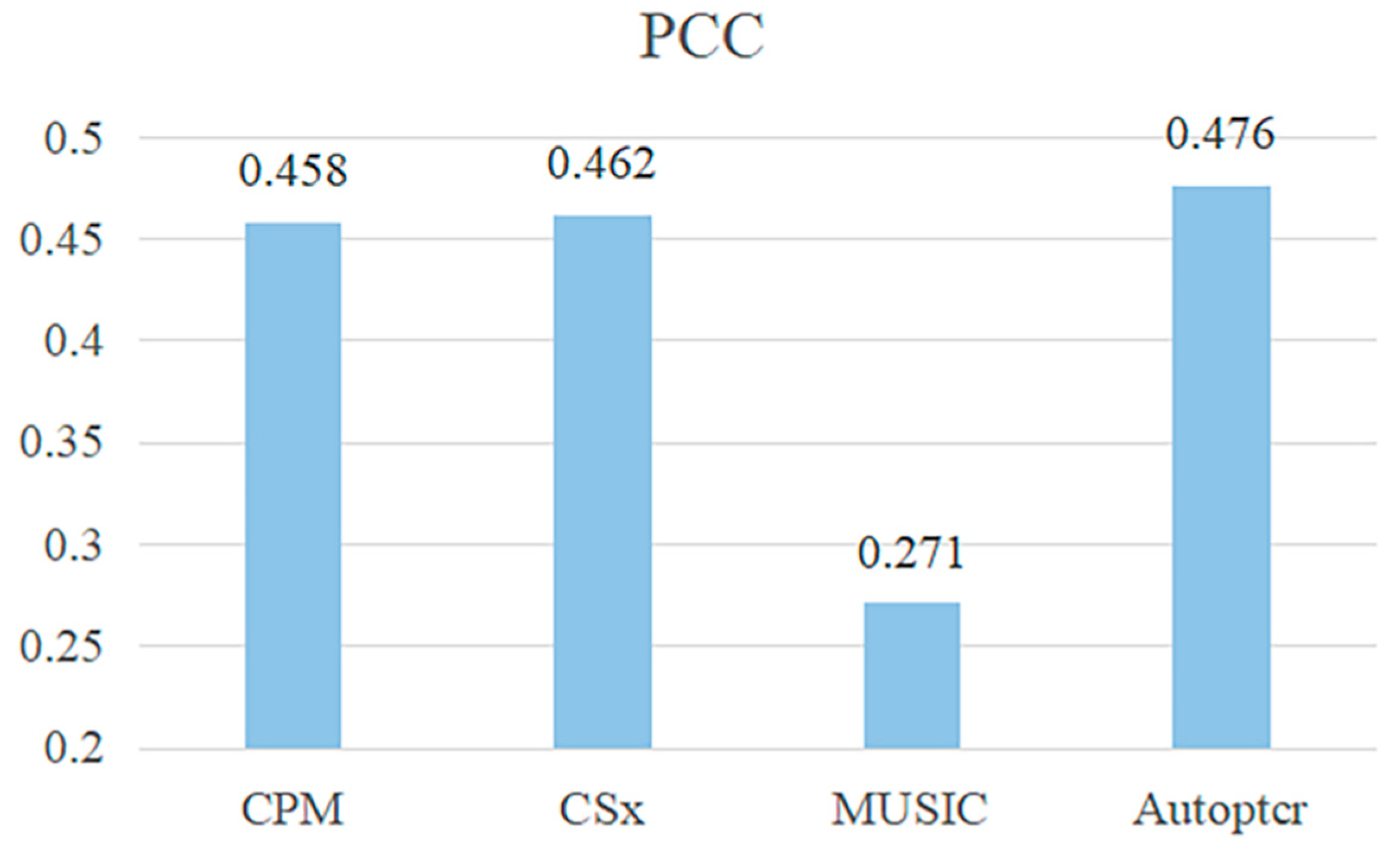
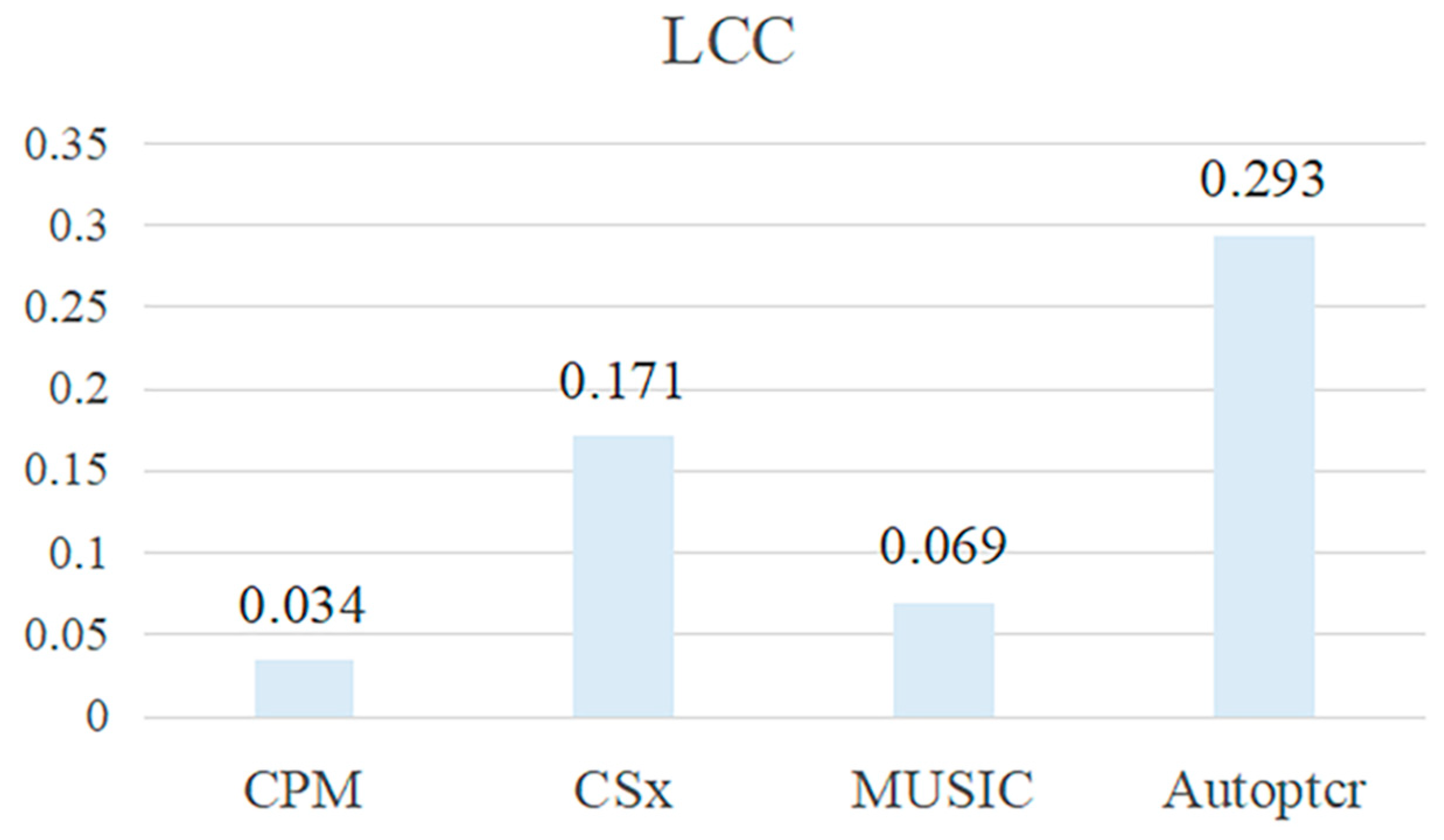
3.2. Test on a Manual Batch Samples
3.3. Test on a Real Dataset PBMC2
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jew, B.; Alvarez, M.; Rahmani, E.; Miao, Z.; Ko, A.; Garske, K.M.; Sul, J.H.; Pietiläinen, K.H.; Halperin, E. Accurate estimation of cell composition in bulk expression through robust integration of single-cell information. Nat. Commun. 2020, 11, 1971. [Google Scholar] [CrossRef] [Green Version]
- Suvà, M.L.; Tirosh, I. Single-cell RNA sequencing in cancer: Lessons learned and emerging challenges. Mol. Cell 2019, 75, 7–12. [Google Scholar] [CrossRef] [PubMed]
- Chakravarthy, A.; Furness, A.; Joshi, K.; Ghorani, E.; Ford, K.; Ward, M.J.; King, E.V.; Lechner, M.; Marafioti, T.; Quezada, S.A.; et al. Pan-cancer deconvolution of tumour composition using DNA methylation. Nat. Commun. 2018, 9, 3220. [Google Scholar] [CrossRef] [Green Version]
- Andersson, A.; Larsson, L.; Stenbeck, L.; Salmén, F.; Ehinger, A.; Wu, S.Z.; Al-Eryani, G.; Roden, D.; Swarbrick, A.; Borg, A.; et al. Spatial deconvolution of HER2-positive breast cancer delineates tumor-associated cell type interactions. Nat. Commun. 2021, 12, 6012. [Google Scholar] [CrossRef]
- Li, B.; Severson, E.; Pignon, J.C.; Zhao, H.; Li, T.; Novak, J.; Jiang, P.; Shen, H.; Aster, J.C.; Rodig, S.; et al. Comprehensive analyses of tumor immunity: Implications for cancer immunotherapy. Genome Biol. 2016, 17, 174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salas, L.A.; Zhang, Z.; Koestler, D.C.; Butler, R.A.; Hansen, H.M.; Molinaro, A.M.; Wiencke, J.K.; Kelsey, K.T.; Christensen, B.C. Enhanced cell deconvolution of peripheral blood using DNA methylation for high-resolution immune profiling. Nat. Commun. 2022, 13, 761. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, J.A.; Gil-Martinez, A.L.; Cisterna, A.; García-Ruíz, S.; Gómez-Pascual, A.; Reynolds, R.H.; Nalls, M.; Hardy, J.; Ryten, M.; Botía, J.A. Modeling multifunctionality of genes with secondary gene co-expression networks in human brain provides novel disease insights. Bioinformatics 2021, 37, 2905–2911. [Google Scholar] [CrossRef]
- Johnson, T.S.; Xiang, S.; Dong, T.; Huang, Z.; Cheng, M.; Wang, T.; Yang, K.; Ni, D.; Huang, K.; Zhang, J. Combinatorial analyses reveal cellular composition changes have different impacts on transcriptomic changes of cell type specific genes in Alzheimer’s Disease. Sci. Rep. 2021, 11, 353. [Google Scholar] [CrossRef] [PubMed]
- You, C.; Wu, S.; Zheng, S.C.; Zhu, T.; Jing, H.; Flagg, K.; Wang, G.; Jin, L.; Wang, S.; Teschendorff, A.E. A cell-type deconvolution meta-analysis of whole blood EWAS reveals lineage-specific smoking-associated DNA methylation changes. Nat. Commun. 2020, 11, 4779. [Google Scholar] [CrossRef]
- Arlehamn, C.S.L.; Dhanwani, R.; Pham, J.; Kuan, R.; Frazier, A.; Dutra, J.R.; Phillips, E.; Mallal, S.; Roederer, M.; Marder, K.S.; et al. α-Synuclein-specific T cell reactivity is associated with preclinical and early Parkinson’s disease. Nat. Commun. 2020, 11, 1875. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asp, M.; Giacomello, S.; Larsson, L.; Wu, C.; Fürth, D.; Qian, X.; Wärdell, E.; Custodio, J.; Reimegård, J.; Salmén, F.; et al. A spatiotemporal organ-wide gene expression and cell atlas of the developing human heart. Cell 2019, 179, 1647–1660. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Kilik, U.; Holloway, E.M.; Tsai, Y.H.; Harmel, C.; Wu, A.; Wu, J.H.; Czerwinski, M.; Childs, C.J.; He, Z.; et al. Charting human development using a multi-endodermal organ atlas and organoid models. Cell 2021, 184, 3281–3298. [Google Scholar] [CrossRef] [PubMed]
- Yadav, V.K.; De, S. An assessment of computational methods for estimating purity and clonality using genomic data derived from heterogeneous tumor tissue samples. Brief. Bioinform. 2015, 16, 232–241. [Google Scholar] [CrossRef] [Green Version]
- Cobos, F.A.; Vandesompele, J.; Mestdagh, P.; Preter, K.D. Computational deconvolution of transcriptomics data from mixed cell populations. Bioinformatics 2018, 34, 1969–1979. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Ji, C.; Shen, Q.; Liu, W.; Qin, F.X.; Wu, A. Tissue-specific deconvolution of immune cell composition by integrating bulk and single-cell transcriptomes. Bioinformatics 2020, 36, 819–827. [Google Scholar] [CrossRef]
- Zhang, J.D.; Hatje, K.; Sturm, G.; Broger, C.; Ebeling, M.; Burtin, M.; Terzi, F.; Pomposiello, S.I.; Badi, L. Detect tissue heterogeneity in gene expression data with BioQC. BMC Genom. 2017, 18, 277. [Google Scholar] [CrossRef]
- Cabili, M.N.; Trapnell, C.; Goff, L.; Koziol, M.; Tazon-Vega, B.; Regev, A.; Rinn, J.L. Integrative annotation of human large intergenic noncoding RNAs reveals global properties and specific subclasses. Genes Dev. 2011, 25, 1915–1927. [Google Scholar] [CrossRef] [Green Version]
- Becht, E.; Giraldo, N.A.; Lacroix, L.; Buttard, B.; Elarouci, N.; Petitprez, F.; Selves, J.; Laurent-Puig, P.; Sautès-Fridman, C.; Fridman, W.H.; et al. Estimating the population abundance of tissue-infiltrating immune and stromal cell populations using gene expression. Genome Biol. 2016, 17, 218. [Google Scholar] [CrossRef]
- Wang, N.; Hoffman, E.P.; Chen, L.; Chen, L.; Zhang, Z.; Liu, C.; Yu, G.; Herrington, D.M.; Clarke, R.; Wang, Y. Mathematical modelling of transcriptional heterogeneity identifies novel markers and subpopulations in complex tissues. Sci. Rep. 2016, 6, 18909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nelms, B.D.; Waldron, L.; Barrera, L.A.; Weflen, A.W.; Goettel, J.A.; Guo, G.; Montgomery, R.K.; Neutra, M.R.; Breault, D.T.; Snapper, S.B.; et al. CellMapper: Rapid and accurate inference of gene expression in difficult-to-isolate cell types. Genome Biol. 2016, 17, 201. [Google Scholar] [CrossRef] [Green Version]
- Newman, A.M.; Liu, C.L.; Green, M.R.; Gentles, A.J.; Feng, W.; Xu, Y.; Hoang, C.D.; Diehn, M.; Alizadeh, A.A. Robust enumeration of cell subsets from tissue expression profiles. Nat. Methods 2015, 12, 453–457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newman, A.M.; Steen, C.B.; Liu, C.L.; Gentles, A.; Chaudhuri, A.A.; Scherer, F.; Khodadoust, M.S.; Esfahani, M.S.; Luca, B.A.; Steiner, D.; et al. Determining cell type abundance and expression from bulk tissues with digital cytometry. Nat. Biotechnol. 2019, 37, 773–782. [Google Scholar] [CrossRef]
- Ziegenhain, C.; Vieth, B.; Parekh, S.; Reinius, B.; Guillaumet-Adkins, A.; Smets, M.; Leonhardt, H.; Heyn, H.; Hellmann, I.; Enard, W. Comparative Analysis of Single-Cell RNA Sequencing Methods. Mol. Cell 2017, 65, 631–643.e4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Svensson, V.; Natarajan, K.N.; Ly, L.H.; Miragaia, R.J.; Labalette, C.; Macaulay, I.C.; Cvejic, A.; Teichmann, S.A. Power analysis of single-cell RNA-sequencing experiments. Nat. Methods 2017, 14, 381–387. [Google Scholar] [CrossRef] [Green Version]
- Vallania, F.; Tam, A.; Lofgren, S.; Schaffert, S.; Azad, T.D.; Bongen, E.; Haynes, W.; Alsup, M.; Alonso, M.; Davis, M.; et al. Leveraging heterogeneity across multiple datasets increases cell-mixture deconvolution accuracy and reduces biological and technical biases. Nat. Commun. 2018, 9, 4735. [Google Scholar] [CrossRef] [Green Version]
- Frishberg, A.; Peshes-Yaloz, N.; Cohn, O.; Rosentul, D.; Steuerman, Y.; Valadarsky, L.; Yankovitz, G.; Mandelboim, M.; Iraqi, F.A.; Amit, I.; et al. Cell composition analysis of bulk genomics using single-cell data. Nat. Methods 2019, 16, 327–332. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.; Susztak, K.; Zhang, N.R.; Li, M. Bulk tissue cell type deconvolution with multi-subject single-cell expression reference. Nat. Commun. 2019, 10, 380. [Google Scholar] [CrossRef] [Green Version]
- Tsoucas, D.; Dong, R.; Chen, H.; Zhu, Q.; Guo, G.; Yuan, G.C. Accurate estimation of cell-type composition from gene expression data. Nat. Commun. 2019, 10, 2975. [Google Scholar] [CrossRef] [PubMed]
- Dong, R.; Yuan, G.C. SpatialDWLS: Accurate deconvolution of spatial transcriptomic data. Genome Biol. 2021, 22, 145. [Google Scholar] [CrossRef]
- Stein-O’Brien, G.L.; Clark, B.S.; Sherman, T.; Zibetti, C.; Hu, Q.; Sealfon, R.; Liu, S.; Qian, J.; Colantuoni, C.; Blackshaw, S.; et al. Decomposing Cell Identity for Transfer Learning across Cellular Measurements, Platforms, Tissues, and Species. Cell Syst. 2021, 12, 203. [Google Scholar] [CrossRef] [PubMed]
- Tang, D.; Park, S.; Zhao, H. NITUMID: Nonnegative matrix factorization-based Immune-TUmor MIcroenvironment Deconvolution. Bioinformatics 2020, 36, 1344–1350. [Google Scholar] [CrossRef]
- Kriebel, A.R.; Welch, J.D. UINMF performs mosaic integration of single-cell multi-omic datasets using nonnegative matrix factorization. Nat. Commun. 2022, 13, 780. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Park, C.Y.; Theesfeld, C.L.; Troyanskaya, O.G. An automated framework for efficiently designing deep convolutional neural networks in genomics. Nat. Mach. Intell. 2021, 3, 392–400. [Google Scholar] [CrossRef]
- Kharchenko, P.V. The triumphs and limitations of computational methods for scRNA-seq. Nat. Methods 2021, 18, 723–732. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Zhang, C.; Le, A. The limitless applications of single-cell metabolomics. Curr. Opin. Biotechnol. 2021, 71, 115–122. [Google Scholar] [CrossRef]
- Doerr, A. Single-cell proteomics. Nat. Methods 2019, 16, 20. [Google Scholar] [CrossRef]
- Choudhary, S.; Satija, R. Comparison and evaluation of statistical error models for scRNA-seq. Genome Biol. 2022, 23, 27. [Google Scholar] [CrossRef] [PubMed]
- Vallejos, C.A.; Risso, D.; Scialdone, A.; Dudoit, S.; Marioni, J.C. Normalizing single-cell RNA sequencing data: Challenges and opportunities. Nat. Methods 2017, 14, 565–571. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Y.; Li, D.; Lv, X.; Chen, X.; Dai, Q. Prediction of the RNA Tertiary Structure Based on a Random Sampling Strategy and Parallel Mechanism. Front. Genet. 2022, 12, 813604. [Google Scholar] [CrossRef] [PubMed]

| Parameters | Value |
|---|---|
| Batch Size | 128 |
| Steps | 2000 |
| Learning Rate | 0.001 |
| Optimized Algorithm | Adam |
| Loss Function | MSE |
| Method Comparison | Value | ||
|---|---|---|---|
| RMSE | PCC | LCC | |
| CPM | 0.188 | 0.599 | 0.073 |
| CS | 0.116 | 0.815 | 0.702 |
| CSx | 0.081 | 0.896 | 0.846 |
| MusiC | 0.115 | 0.873 | 0.799 |
| Autoptcr | 0.081 | 0.903 | 0.851 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Lv, X.; Chen, X.; Li, D.; Qin, M.; Bai, K.; Yang, Y.; Li, X.; Zhang, P. Predicting Algorithm of Tissue Cell Ratio Based on Deep Learning Using Single-Cell RNA Sequencing. Appl. Sci. 2022, 12, 5790. https://doi.org/10.3390/app12125790
Liu Z, Lv X, Chen X, Li D, Qin M, Bai K, Yang Y, Li X, Zhang P. Predicting Algorithm of Tissue Cell Ratio Based on Deep Learning Using Single-Cell RNA Sequencing. Applied Sciences. 2022; 12(12):5790. https://doi.org/10.3390/app12125790
Chicago/Turabian StyleLiu, Zhendong, Xinrong Lv, Xi Chen, Dongyan Li, Mengying Qin, Ke Bai, Yurong Yang, Xiaofeng Li, and Peng Zhang. 2022. "Predicting Algorithm of Tissue Cell Ratio Based on Deep Learning Using Single-Cell RNA Sequencing" Applied Sciences 12, no. 12: 5790. https://doi.org/10.3390/app12125790
APA StyleLiu, Z., Lv, X., Chen, X., Li, D., Qin, M., Bai, K., Yang, Y., Li, X., & Zhang, P. (2022). Predicting Algorithm of Tissue Cell Ratio Based on Deep Learning Using Single-Cell RNA Sequencing. Applied Sciences, 12(12), 5790. https://doi.org/10.3390/app12125790






