Development of the Dynamic Stiffness Method for the Out-of-Plane Natural Vibration of an Orthotropic Plate
Abstract
:1. Introduction
2. Contributions and Relevant Scope of Present Work
- The DSM was formulated to investigate the natural vibration response of thin orthotropic plates.
- The W–W algorithm was applied to compute the natural frequency of the orthotropic plate.
- The DSM results were compared with the published literature and the finite element method.
- A new set of DSM results is reported for different aspect ratios, thickness ratios, and modulus ratios, which may be used as benchmark solutions for comparison.
3. Mathematical Formulation
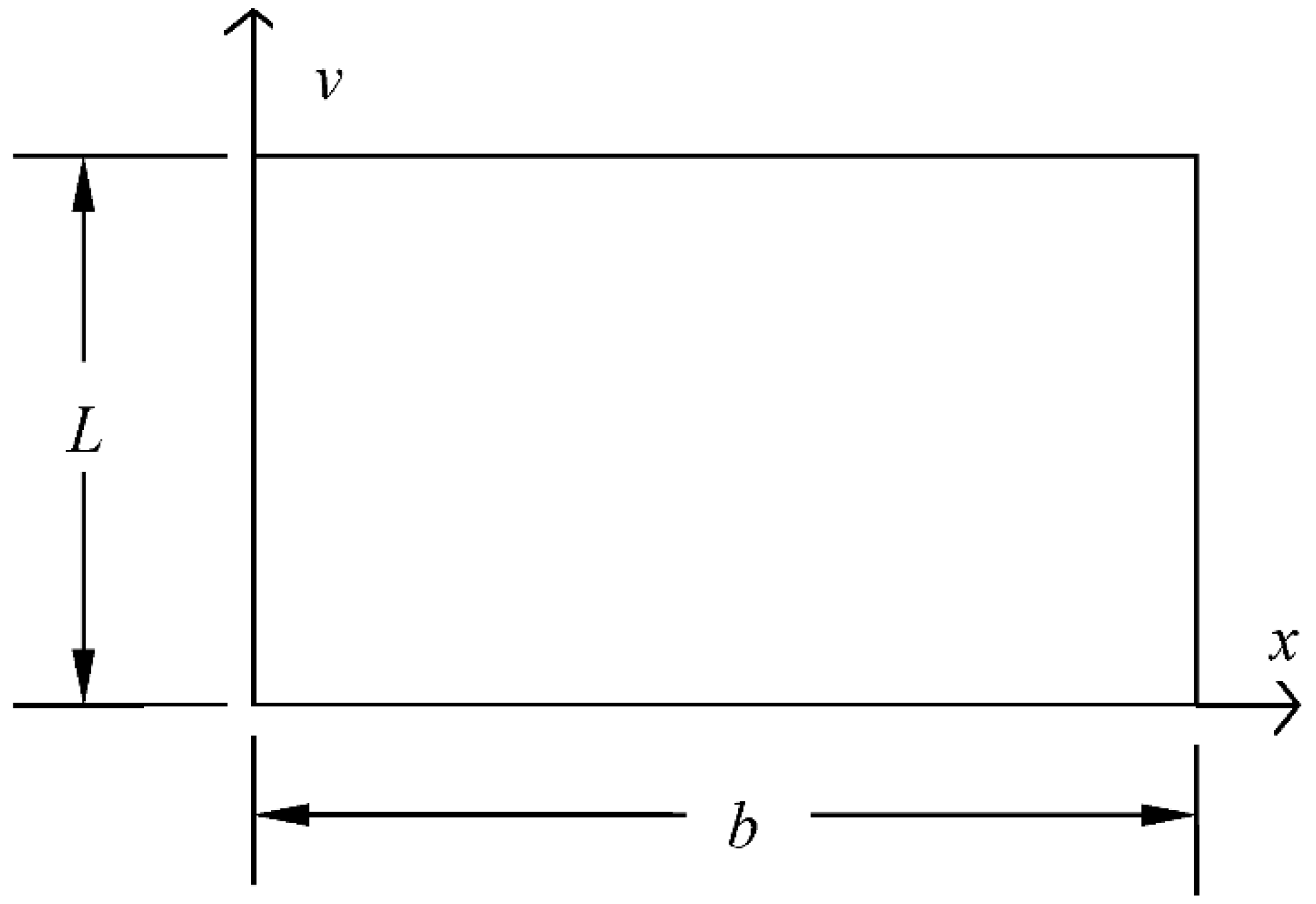
3.1. Description of Geometrical Property
3.2. Equations of Motion
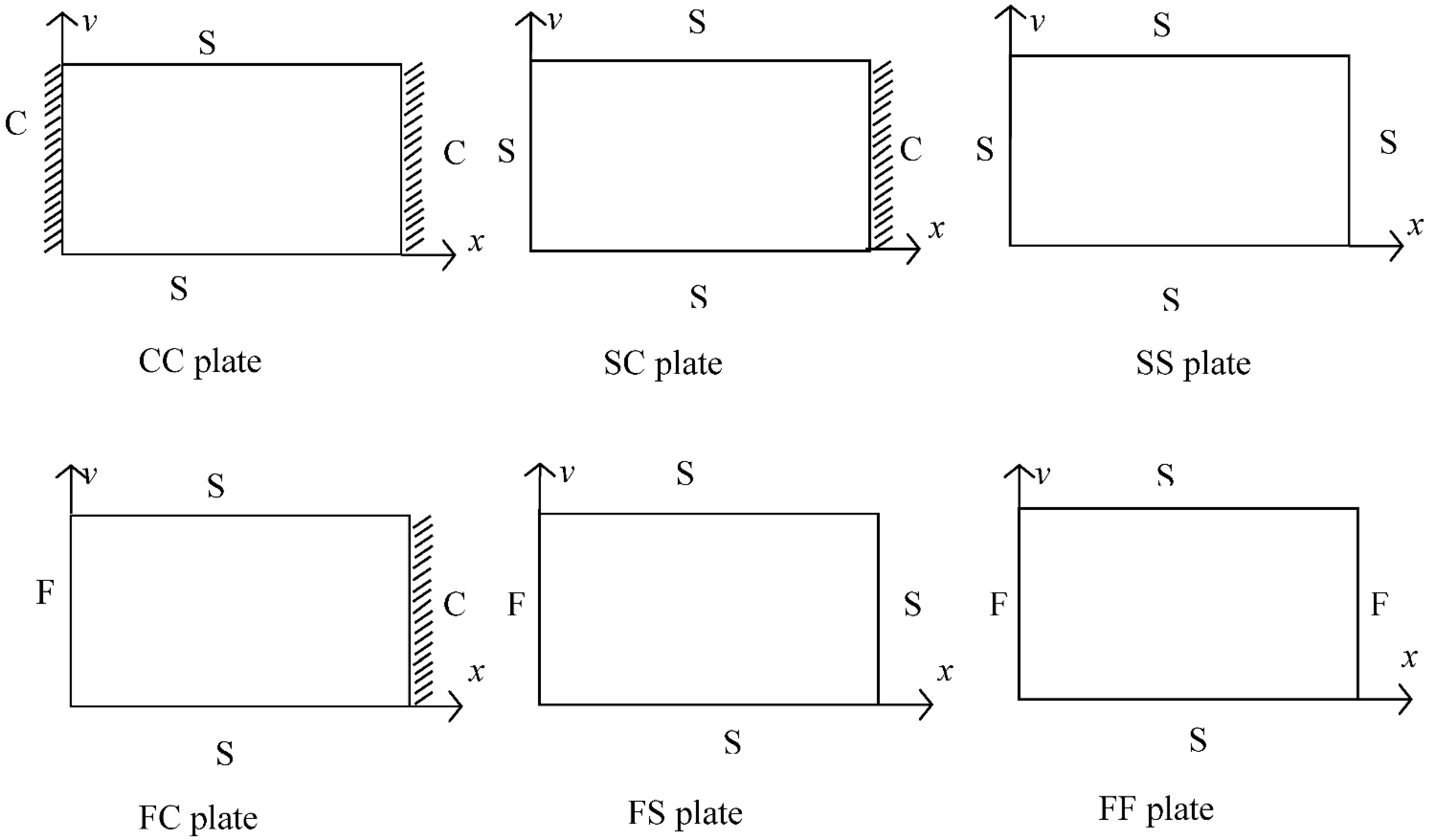
3.3. Boundary Conditions
4. Formulation of Dynamic Stiffness (DS) Matrix with Levy Solution
4.1. Dynamic Stiffness (DS) Matrix Assembly Procedure with Boundary Conditions
- Displacement is penalized for simply supported (S) boundary conditions.
- Displacement ( and rotation ( are penalized for clamped (C) boundary conditions.
- No penalty is implemented for the free (F) boundary condition.

4.2. Application of the Wittrick and Williams (W–W) Algorithm
5. Results and Discussions
5.1. Comparative Study
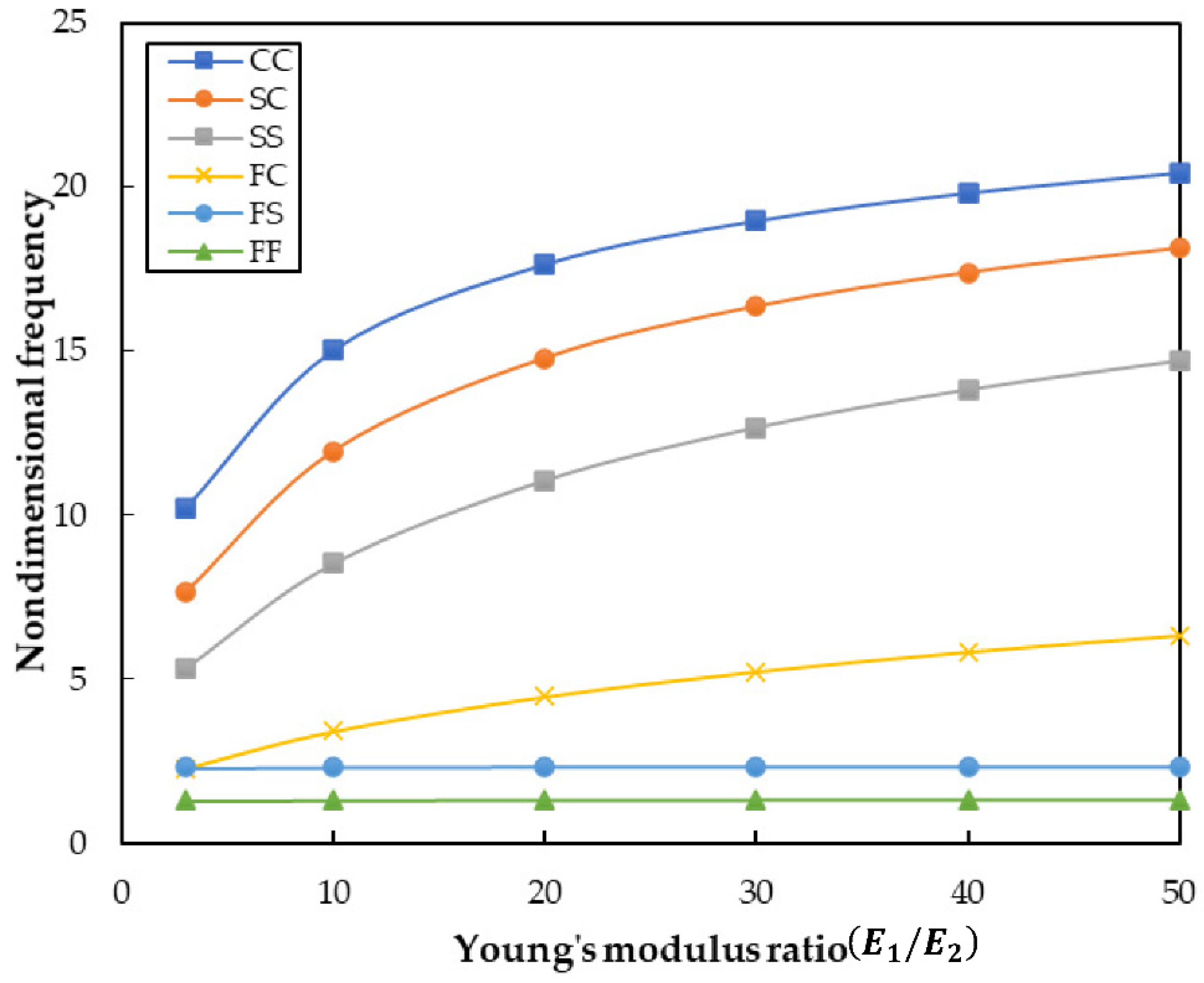
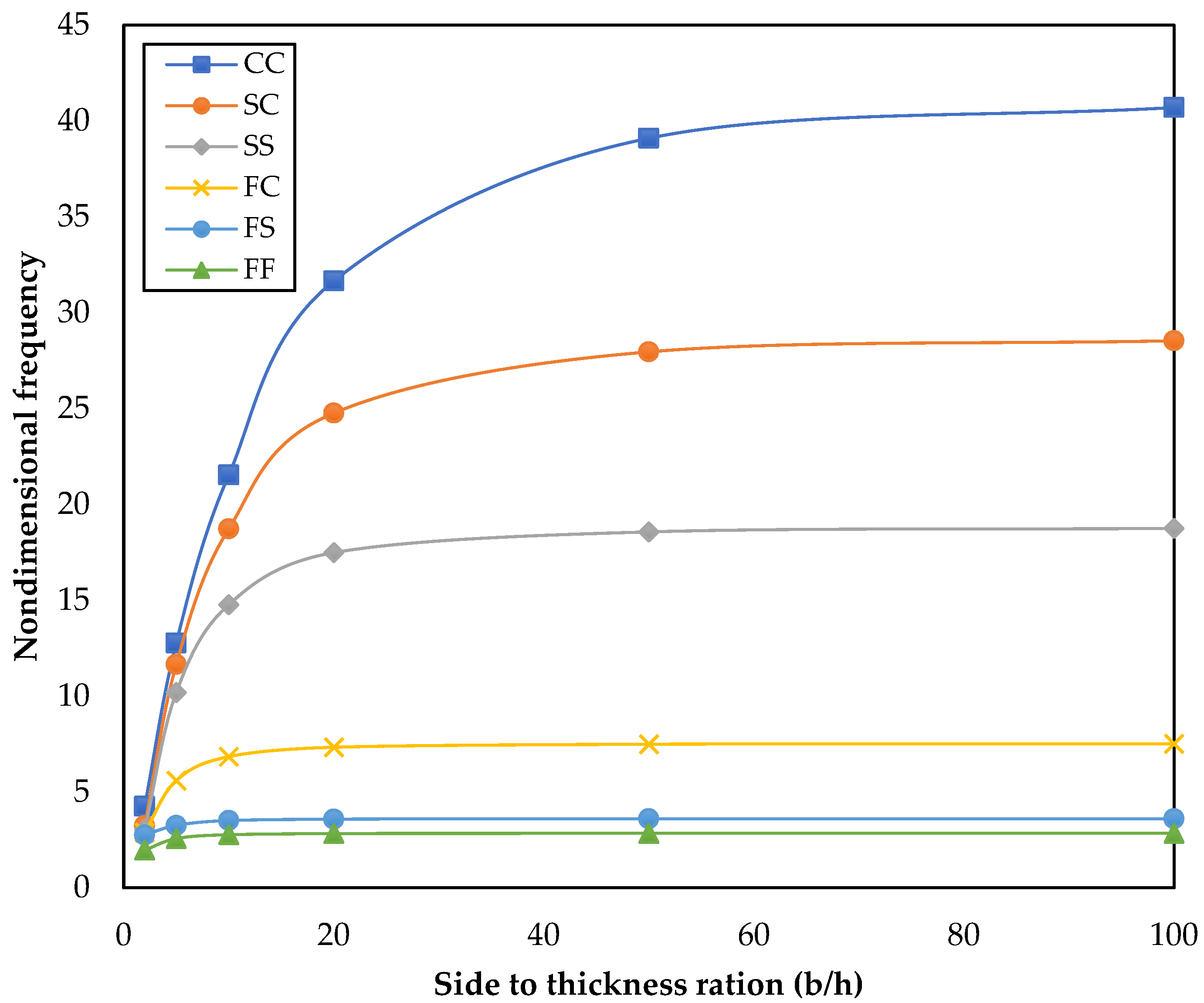
5.2. Parameter Studies
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Rayleigh, L. The Theory of Sound; Macmillan: Dover, NY, USA, 1945; Volume I, pp. 35–42. [Google Scholar]
- Ritz, W. On a new method for solving certain variational problems in mathematical physics. Crelle’s J. 1909, 1–61. [Google Scholar] [CrossRef]
- Bhat, R.B. Natural frequencies of rectangular plates using characteristic orthogonal polynomials in the Rayleigh-Ritz method. J. Sound Vib. 1985, 102, 493–499. [Google Scholar] [CrossRef]
- Gorman, D.J. Accurate free vibration analysis of the completely free orthotropic rectangular plate by the superposition method. J. Sound Vib. 1993, 165, 409–420. [Google Scholar] [CrossRef]
- Kshirsagar, S.; Bhaskar, K. Accurate and elegant free vibration and buckling studies of orthotropic rectangular plates using untruncated infinite series. J. Sound Vib. 2008, 314, 837–850. [Google Scholar] [CrossRef]
- Dalaei, M.; Kerr, A.D. Natural vibration analysis of clamped rectangular orthotropic plates. J. Sound Vib. 1996, 189, 399–406. [Google Scholar] [CrossRef]
- Bercin, A.N. Free vibration solution for clamped orthotropic plates using the Kantorovich method. J. Sound Vib. 1996, 196, 243–247. [Google Scholar] [CrossRef]
- Sakata, T.; Takahashi, K.; Bhat, R.B. Natural frequencies of orthotropic rectangular plates obtained by iterative reduction of the partial differential equation. J. Sound Vib. 1996, 189, 89–101. [Google Scholar] [CrossRef]
- Yu, S.D.; Cleghorn, W.L. Generic free vibration of orthotropic rectangular plates with clamped and simply supported edges. J. Sound Vib. 1993, 163, 439–450. [Google Scholar] [CrossRef]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Leissa, A.W. Free vibration of rectangular plates. J. Sound Vib. 1973, 31, 257–293. [Google Scholar] [CrossRef]
- Gorman, D.J. Free Vibration Analysis of Rectangular Plates; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Gorman, D.J. Accurate free vibration analysis of clamped orthotropic plates by the method of superposition. J. Sound Vib. 1990, 140, 391–411. [Google Scholar] [CrossRef]
- Biancolini, M.E.; Brutti, C.; Reccia, L. Approximate solution for free vibrations of thin orthotropic rectangular plates. J. Sound Vib. 2005, 288, 321–344. [Google Scholar] [CrossRef]
- Thai, H.; Kim, S.E. Levy-type solution for free vibration analysis of orthotropic plates based on two variable refined plate theory. Appl. Math. Model. 2012, 36, 3870–3882. [Google Scholar] [CrossRef]
- Xing, Y.F.; Liu, B. New exact solutions for free vibrations of thin orthotropic rectangular plates. Compos. Struct. 2009, 89, 567–574. [Google Scholar] [CrossRef]
- Hearmon, R. The frequency of flexural vibration of rectangular orthotropic plates with clamped or supported edges. J. Appl. Mech. 1959, 26, 537–540. [Google Scholar] [CrossRef]
- Tret’yak, V. Natural vibrations of orthotropic plates. Int. Appl. Mech. 1966, 2, 27–31. [Google Scholar] [CrossRef]
- Sakata, T.; Hosokawa, K. Vibrations of clamped orthotropic rectangular plates. J. Sound Vib. 1988, 125, 429–439. [Google Scholar] [CrossRef]
- Jayaraman, G.; Chen, P.; Snyder, V.W. Free vibrations of rectangular orthotropic plates with a pair of parallel edges simply supported. Comput.Struct. 1990, 34, 203–214. [Google Scholar] [CrossRef]
- Bardell, N.S.; Dunsdon, J.M.; Langley, R.S. Free vibration analysis of thin coplanar rectangular plate assemblies—Part I: Theory and initial results for specially orthotropic plates. Compos. Struct. 1996, 34, 129–143. [Google Scholar] [CrossRef]
- Bardell, N.S.; Dunsdon, J.M.; Langley, R.S. Free vibration analysis of thin coplanar rectangular plate assemblies—Part II: Theory and initial results for specially orthotropic plates. Compos. Struct. 1996, 34, 145–162. [Google Scholar] [CrossRef]
- Tsay, C.S.; Reddy, J.N. Bending, Stability and free vibrations of thin orthotropic plates by simplified mixed finite elements. J. Sound Vib. 1978, 59, 307–311. [Google Scholar] [CrossRef]
- Banerjee, J.R. Dynamic stiffness formulation and free vibration analysis of Timoshenko beams. J. Sound Vib. 2001, 247, 97–115. [Google Scholar] [CrossRef]
- Banerjee, J.R.; Su, H.; Jackson, D.R. Free vibration of rotating tapered beams using the dynamic stiffness method. J. Sound Vib. 2006, 298, 1034–1054. [Google Scholar] [CrossRef]
- Banerjee, J.R. Free vibration of centrifugally stiffened uniform and tapered beams using the dynamic stiffness method. J. Sound Vib. 2000, 233, 857–875. [Google Scholar] [CrossRef]
- Banerjee, J.R. Free vibration of sandwich beams using the dynamic stiffness method. Comput. Struct. 2003, 81, 1915–1922. [Google Scholar] [CrossRef]
- Banerjee, J.R. Free vibration of axially loaded composite Timoshenko beams using the dynamic stiffness matrix method. Comput. Struct 1998, 69, 197–208. [Google Scholar] [CrossRef]
- Tounsi, D.; Casimir, J.B.; Haddar, M. Dynamic stiffness formulation for circular rings. Comput. Struct. 2012, 112–113, 258–265. [Google Scholar] [CrossRef]
- Tounsi, D.; Casimir, J.B.; Abid, S.; Tawfiq, I.; Haddar, M. Dynamic stiffness formulation and response analysis of stiffened shells. Comput. Struct. 2014, 132, 75–83. [Google Scholar] [CrossRef]
- Fazzolari, F. A refined dynamic stiffness element for free vibration analysis of cross-ply laminated composite cylindrical and spherical shallow shells. Compos. Part B Eng. 2014, 62, 143–158. [Google Scholar] [CrossRef]
- Wittrick, W.H.; Williams, F.W. Buckling and vibration of anisotropic or isotropic plate assemblies under combined loadings. Int. J. Mech. Sci. 1974, 16, 209–239. [Google Scholar] [CrossRef]
- Boscolo, M.; Banerjee, J.R. Dynamic stiffness elements and their applications for plates using first order shear deformation theory. Comput. Struct. 2011, 89, 395–410. [Google Scholar] [CrossRef]
- Boscolo, M.; Banerjee, J.R. Dynamic stiffness formulation for composite Mindlin plates for exact modal analysis of structures- PartI: Theory. Comput. Struct. 2012, 96, 61–73. [Google Scholar] [CrossRef]
- Boscolo, M.; Banerjee, J.R. Dynamic stiffness formulation for composite Mindlin plates for exact modal analysis of structures- Part II: Results and applications. Comput. Struct. 2012, 96, 73–84. [Google Scholar] [CrossRef] [Green Version]
- Fazzolari, F.; Boscolo, M.; Banerjee, J.R. An exact dynamic stiffness element using a higher order shear deformation theory for free vibration analysis of composite plate assemblies. Compos. Struct. 2013, 96, 262–278. [Google Scholar] [CrossRef] [Green Version]
- Boscolo, M.; Banerjee, J.R. Layer-wise dynamic stiffness solution for free vibration analysis of laminated composite plates. J. Sound Vib. 2014, 333, 200–227. [Google Scholar] [CrossRef]
- Banerjee, J.R.; Papkov, S.O.; Liu, X.; Kennedy, D. Dynamic stiffness matrix of a rectangular plate for the general case. J. Sound Vib. 2015, 342, 177–199. [Google Scholar] [CrossRef]
- Thinh, T.I.; Nuguen, M.C.; Ninh, D.G. Dynamic stiffness formulation for vibration analysis of thick composite plates resting on non-homogenous foundations. Compos. Struct. 2014, 108, 684–695. [Google Scholar] [CrossRef]
- Nefovska-Danilovic, M.; Petronijevic, M. In-plane free vibration and response analysis of isotropic rectangular plates using dynamic stiffness method. Comput. Struct. 2015, 152, 82–95. [Google Scholar] [CrossRef]
- Kolarevic, N.; Nefovska-Danilovic, M.; Petronijevic, M. Free vibration analysis of rectangular Mindlin plates using dynamic stiffness method. J. Sound Vib. 2015, 359, 84–106. [Google Scholar] [CrossRef]
- Kolarevic, N.; Marjanovic, M.; Nefovska-Danilovic, M.; Petronijevic, M. Free vibration analysis of plate assemblies using the dynamic stiffness method based on the higher order shear deformation theory. J. Sound Vib. 2016, 364, 110–132. [Google Scholar] [CrossRef]
- Ghorbel, O.; Casimir, J.B.; Hammami, L.; Tawfiq, I.; Haddar, M. Dynamic stiffness formulation for free orthotropic plates. J. Sound Vib. 2015, 346, 361–375. [Google Scholar] [CrossRef]
- Ghorbel, O.; Casimir, J.B.; Hammami, L.; Tawfiq, I.; Haddar, M. In-plane dynamic stiffness matrix for a free orthotropic plate. J. Sound Vib. 2016, 364, 234–246. [Google Scholar] [CrossRef]
- Kumar, S.; Ranjan, V.; Jana, P. Free vibration analysis of thin functionally graded rectangular plates using the dynamic stiffness method. Compos. Struct. 2018, 197, 39–53. [Google Scholar] [CrossRef]
- Chauhan, M.; Ranjan, V.; Sathujhoda, P. Dynamic stiffness method for free vibration analysis of thin functionally graded rectangular plates. Vibroengineering Procedia 2019, 29, 76–81. [Google Scholar] [CrossRef]
- Liu, X.; Banerjee, J.R. An exact spectral-dynamic stiffness method for free flexural vibration analysis of orthotropic composite plate assemblies—Part I: Theory. Compos. Struct. 2015, 132, 1274–1287. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Banerjee, J.R. An exact spectral-dynamic stiffness method for free flexural vibration analysis of orthotropic composite plate assemblies—Part II: Applications. Compos. Struct. 2015, 132, 1288–1302. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Banerjee, J.R. Free vibration analysis for plates with arbitrary boundary conditions using a novel spectral-dynamic stiffness method. Comput. Struct. 2016, 164, 108–126. [Google Scholar] [CrossRef] [Green Version]
- Wittrick, W.H.; Williams, F.W. A general algorithm for computing natural frequencies of elastic structures. Q. J. Mech. Appl. Math. 1970, 24, 263–284. [Google Scholar] [CrossRef]
- Reddy, J. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Reddy, J.N.; Phan, N.D. Stability and vibration of isotropic, orthotropic and laminated plates according to a higher-order shear deformation theory. J. Sound Vib. 1985, 98, 157–170. [Google Scholar] [CrossRef]
- Mukhtar Faisal, M. Free vibration analysis of orthotropic plates by differential transform and Taylor collocation methods based on a refined plate theory. Arch. Appl. Mech. 2017, 87, 15–40. [Google Scholar] [CrossRef]


| b/L | E1/E2 | Method | Boundary Conditions | |||||
|---|---|---|---|---|---|---|---|---|
| CC | SC | SS | FC | FS | FF | |||
| 0.5 | 10 | Ref [52] | 20.6543 | 14.3450 | 9.3421 | 3.5614 | 1.3190 | 0.7124 |
| Ref [15] | 20.5603 | 14.3137 | 9.3331 | 3.5600 | 1.3190 | 0.7123 | ||
| DSM | 20.5857 | 14.3116 | 9.3209 | 3.5154 | 1.3188 | 0.7123 | ||
| FEM | 20.6766 | 14.3565 | 9.3455 | 3.5558 | 1.3186 | 0.7141 | ||
| Error (%) | (−0.1234) | (0.0144) | (0.1309) | (1.2677) | (0.0152) | (0.0011) | ||
| 25 | Ref [52] | 32.4390 | 22.4259 | 14.4578 | 5.3051 | 1.3193 | 0.7123 | |
| Ref [15] | 32.0795 | 22.3069 | 14.4245 | 5.3003 | 1.3192 | 0.7122 | ||
| DSM | 32.4229 | 22.4148 | 14.4507 | 5.3042 | 1.3191 | 0.7122 | ||
| FEM | 32.2347 | 22.3539 | 14.4430 | 5.2925 | 1.3189 | 0.7141 | ||
| Error (%) | (−1.0590) | (−0.4813) | (−0.1815) | (−0.0735) | (0.0076) | (0.0000) | ||
| 40 | Ref [52] | 40.9633 | 28.2855 | 18.1876 | 6.6030 | 1.3194 | 0.7123 | |
| Ref [15] | 40.2478 | 28.0480 | 18.1215 | 6.5937 | 1.3193 | 0.7122 | ||
| DSM | 40.9620 | 28.2846 | 18.1870 | 6.6010 | 1.3190 | 0.7122 | ||
| FEM | 40.4100 | 28.0814 | 18.1426 | 6.5826 | 1.3189 | 0.7141 | ||
| Error (%) | (−1.7436) | (−0.8366) | (−0.3603) | (−0.1106) | (0.0227) | (0.0000) | ||
| 1 | 10 | Ref [52] | 21.2889 | 15.2042 | 10.4963 | 5.0586 | 3.6114 | 2.8503 |
| Ref [15] | 21.2078 | 15.1747 | 10.4863 | 5.0564 | 3.6105 | 2.8496 | ||
| DSM | 21.2405 | 15.1709 | 10.4750 | 5.0144 | 3.6112 | 2.8501 | ||
| FEM | 21.3090 | 15.2098 | 10.4949 | 5.0538 | 3.6125 | 2.8569 | ||
| Error (%) | (−0.1539) | (0.0248) | (0.1080) | (0.8376) | (−0.0194) | (−0.0175) | ||
| 25 | Ref [52] | 32.8464 | 22.9847 | 15.2278 | 6.4146 | 3.6118 | 2.8493 | |
| Ref [15] | 32.5515 | 22.8835 | 15.1972 | 6.4100 | 3.6110 | 2.8486 | ||
| DSM | 32.8303 | 22.9736 | 15.2207 | 6.4014 | 3.6115 | 2.8490 | ||
| FEM | 32.6351 | 22.9073 | 15.2089 | 6.4025 | 3.6128 | 2.8558 | ||
| Error (%) | (−0.8491) | (−0.3921) | (−0.1544) | (0.1343) | (−0.0138) | (−0.0140) | ||
| 40 | Ref [52] | 41.2866 | 28.7305 | 18.8052 | 7.5253 | 3.6121 | 2.8492 | |
| Ref [15] | 40.7062 | 28.5337 | 18.7477 | 7.5178 | 3.6112 | 2.8485 | ||
| DSM | 41.2853 | 28.7296 | 18.8046 | 7.5045 | 3.6120 | 2.8491 | ||
| FEM | 40.7277 | 28.5213 | 18.7566 | 7.5051 | 3.6130 | 2.8557 | ||
| Error (%) | (−1.4027) | (−0.6818) | (−0.3028) | (0.1772) | (−0.0221) | (−0.0211) | ||
| 2 | 10 | Ref [52] | 25.5184 | 20.5941 | 17.1364 | 12.9377 | 12.2379 | 11.4094 |
| Ref [15] | 25.4427 | 20.5543 | 17.1129 | 12.9238 | 12.2259 | 11.3981 | ||
| DSM | 25.4651 | 20.5536 | 17.1046 | 12.9145 | 12.2298 | 11.3998 | ||
| FEM | 25.4958 | 20.5658 | 17.1086 | 12.9324 | 12.2395 | 11.4254 | ||
| Error (%) | (−0.0879) | (0.0032) | (0.0483) | (0.0720) | (−0.0319) | (−0.0149) | ||
| 25 | Ref [52] | 35.7303 | 26.8537 | 20.3682 | 13.5562 | 12.2305 | 11.3993 | |
| Ref [15] | 35.5237 | 26.7659 | 20.3288 | 13.5404 | 12.2186 | 11.3880 | ||
| DSM | 35.7135 | 26.8417 | 20.3596 | 13.5504 | 12.2301 | 11.3895 | ||
| FEM | 35.4925 | 26.7502 | 20.3265 | 13.5433 | 12.2319 | 11.4155 | ||
| Error (%) | (−0.5316) | (−0.2822) | (−0.1514) | (−0.0738) | (−0.0940) | (−0.0132) | ||
| 40 | Ref [52] | 43.6154 | 31.9099 | 23.1622 | 14.1271 | 12.2301 | 11.3977 | |
| Ref [15] | 43.2415 | 31.7630 | 23.1043 | 14.1093 | 12.2182 | 11.3864 | ||
| DSM | 43.6141 | 31.9090 | 23.1616 | 14.1270 | 12.2298 | 11.3944 | ||
| FEM | 43.0347 | 31.6809 | 23.0942 | 14.1072 | 12.2312 | 11.4140 | ||
| Error (%) | (−0.8543) | (−0.4576) | (−0.2473) | (−0.1253) | (−0.0949) | (−0.0702) | ||
| E1/E2 | ||||||
|---|---|---|---|---|---|---|
| 3 | 10 | 20 | 30 | 40 | 50 | |
| DSM | 7.1504 | 10.2475 | 13.4417 | 15.7097 | 17.4294 | 19.0676 |
| 20 × 20 FEM | 7.0938 | 10.1434 | 13.1326 | 15.3657 | 17.1616 | 18.6632 |
| 40 × 40 FEM | 7.0610 | 10.1132 | 13.1070 | 15.3336 | 17.1285 | 18.6298 |
| 80 × 80 FEM | 7.0507 | 10.1040 | 13.0932 | 15.3250 | 17.1192 | 18.6203 |
| 100 × 100 FEM | 7.0494 | 10.1030 | 13.0918 | 15.3239 | 17.1179 | 18.6188 |
| b/L | b/h | Method | E1/E2 | |||||
|---|---|---|---|---|---|---|---|---|
| 3 | 10 | 20 | 30 | 40 | 50 | |||
| 0.5 | 20 | RPT [15] | 8.0410 | 13.6063 | 18.2286 | 21.3634 | 23.7191 | 25.5851 |
| DTM [53] | 8.0500 | - | 18.2250 | 21.3750 | 23.7500 | 25.7900 | ||
| TCM [53] | 8.0418 | - | 18.2310 | 21.3647 | 23.7211 | 25.5865 | ||
| DSM | 8.0368 | 13.5844 | 18.1881 | 21.3584 | 23.7235 | 25.2657 | ||
| FEM | 8.0196 | 13.4668 | 17.8312 | 20.6852 | 21.7298 | 21.7850 | ||
| Error (%) | 0.0523 | 0.1609 | 0.2227 | 0.0234 | −0.0184 | 1.2642 | ||
| 50 | RPT 15] | 8.1690 | 14.2179 | 19.7562 | 23.9265 | 27.3668 | 30.3311 | |
| DTM [53] | 8.1750 | - | 19.9270 | 23.9440 | 27.4445 | 30.4350 | ||
| TCM [53] | 8.1692 | - | 19.7581 | 23.9296 | 27.3706 | 30.3356 | ||
| DSM | 8.1648 | 14.2078 | 19.7124 | 23.9210 | 27.3718 | 30.3117 | ||
| FEM | 8.1883 | 14.2348 | 19.7344 | 23.8543 | 27.2119 | 30.0908 | ||
| Error (%) | 0.0514 | 0.0711 | 0.2222 | 0.0232 | −0.0184 | 0.0639 | ||
| 1 | 20 | RPT [15] | 9.4219 | 14.2277 | 19.0510 | 22.2738 | 24.7632 | 26.7775 |
| DTM [53] | 9.3740 | - | 19.1240 | 22.3250 | 24.8120 | 26.9144 | ||
| TCM [53] | 9.4227 | - | 18.3073 | 22.2747 | 24.7638 | 26.7789 | ||
| DSM | 9.4305 | 14.2204 | 19.3911 | 22.2704 | 24.7508 | 26.6002 | ||
| FEM | 9.3187 | 15.0824 | 18.3699 | 21.0717 | 23.2367 | 25.3476 | ||
| Error (%) | −0.0912 | 0.0513 | −1.7539 | 0.0153 | 0.0501 | 0.6665 | ||
| 50 | RPT [15] | 9.5898 | 14.4921 | 20.4197 | 24.5288 | 27.9597 | 30.9416 | |
| DTM [53] | 9.4265 | - | 20.5705 | 24.5450 | 27.9880 | 30.8850 | ||
| TCM [53] | 9.5900 | - | 20.4210 | 24.5305 | 27.9616 | 30.9441 | ||
| DSM | 9.5986 | 14.5044 | 20.4134 | 24.5251 | 27.9457 | 30.7368 | ||
| FEM | 9.5888 | 15.0722 | 20.3359 | 24.3373 | 27.6373 | 30.4720 | ||
| Error (%) | −0.0919 | −0.0848 | 0.0310 | 0.0149 | 0.0500 | 0.6664 | ||
| 2 | 20 | RPT [15] | 16.3187 | 19.5797 | 23.2516 | 26.1972 | 28.6627 | 30.7812 |
| DTM [53] | 16.3940 | - | 23.3000 | 26.2455 | 28.7151 | 30.8502 | ||
| TCM [53] | 16.3198 | - | 23.2521 | 26.1978 | 28.6630 | 30.7814 | ||
| DSM | 16.3173 | 19.5944 | 23.2510 | 26.1632 | 28.6581 | 30.7657 | ||
| FEM | 16.2784 | 19.5250 | 23.1165 | 26.7783 | 28.1530 | 30.4003 | ||
| 50 | Error (%) | 0.0086 | −0.0750 | 0.0026 | 0.1300 | 0.0161 | 0.0504 | |
| RPT [15] | 16.8218 | 20.4196 | 24.6437 | 28.1975 | 31.3099 | 34.1026 | ||
| DTM [53] | 16.8825 | - | 24.6202 | 28.2062 | 31.3150 | 34.1000 | ||
| TCM [53] | 16.8221 | - | 24.6442 | 28.1982 | 31.3105 | 34.1033 | ||
| DSM | 16.8204 | 20.4214 | 24.6431 | 28.1609 | 31.3050 | 34.0855 | ||
| FEM | 16.7497 | 20.339 | 24.462 | 27.8501 | 30.7535 | 33.3047 | ||
| Error (%) | 0.0084 | −0.0088 | 0.0024 | 0.1298 | 0.0158 | 0.0502 |
| b/L | b/h | Method | E1/E2 | |||||
|---|---|---|---|---|---|---|---|---|
| 3 | 10 | 20 | 30 | 40 | 50 | |||
| 0.5 | 20 | RPT [15] | 5.4685 | 9.1141 | 12.4009 | 14.7974 | 16.7105 | 18.3073 |
| DTM [53] | 5.4774 | - | 12.4005 | 14.7975 | 16.7100 | 18.3070 | ||
| TCM [53] | 5.4685 | - | 12.4009 | 14.7974 | 16.7105 | 18.3073 | ||
| DSM | 5.4996 | 9.1045 | 12.4112 | 14.9467 | 16.6942 | 18.3017 | ||
| FEM | 5.4419 | 9.0998 | 12.3710 | 14.7391 | 16.6188 | 18.1777 | ||
| Error (%) | −0.5655 | 0.1054 | −0.0830 | −0.9989 | 0.0976 | 0.0306 | ||
| 50 | RPT [15] | 5.5126 | 9.3044 | 12.8804 | 15.6246 | 17.9239 | 19.9333 | |
| DTM [53] | 5.5000 | - | 12.9060 | 15.6250 | 17.9240 | 19.9300 | ||
| TCM [53] | 5.5126 | - | 12.8804 | 15.6247 | 17.9239 | 19.9333 | ||
| DSM | 5.4609 | 9.3130 | 12.9564 | 15.7823 | 17.9064 | 19.9273 | ||
| FEM | 5.5125 | 9.3014 | 12.8910 | 15.5475 | 17.9278 | 19.9310 | ||
| Error (%) | 0.9476 | −0.0923 | −0.5867 | −0.9992 | 0.0975 | 0.0301 | ||
| 1 | 20 | RPT [15] | 7.2194 | 10.2349 | 13.2676 | 15.5845 | 17.4839 | 19.1002 |
| DTM [53] | 7.2200 | - | 13.2500 | 15.5840 | 17.4835 | 19.1000 | ||
| TCM [53] | 7.2194 | - | 13.2676 | 15.5846 | 17.4839 | 19.1002 | ||
| DSM | 7.1504 | 10.2475 | 13.4417 | 15.7097 | 17.4294 | 19.0676 | ||
| FEM | 7.0938 | 10.1434 | 13.1326 | 15.3657 | 17.1616 | 18.6632 | ||
| Error (%) | 0.9650 | −0.1230 | −1.2952 | −0.7970 | 0.3127 | 0.1710 | ||
| 50 | RPT [15] | 7.3012 | 10.4530 | 13.7360 | 16.3474 | 18.5726 | 20.5377 | |
| DTM [53] | 7.3000 | - | 13.7600 | 16.3772 | 18.6072 | 20.5765 | ||
| TCM [53] | 7.3012 | - | 13.7360 | 16.3474 | 18.5726 | 20.5377 | ||
| DSM | 7.2312 | 10.4555 | 13.7963 | 16.4788 | 18.5149 | 20.5027 | ||
| FEM | 7.2778 | 10.4426 | 13.7230 | 16.3228 | 18.5285 | 20.4713 | ||
| Error (%) | 0.9686 | −0.0239 | −0.4370 | −0.7972 | 0.3119 | 0.1705 | ||
| 2 | 20 | RPT [15] | 14.9772 | 16.5030 | 18.4742 | 20.2036 | 21.7468 | 23.1427 |
| DTM [53] | 14.9795 | - | 18.4740 | 20.2036 | 21.7469 | 23.1428 | ||
| TCM [53] | 14.9773 | - | 18.4742 | 20.2036 | 21.7468 | 23.1427 | ||
| DSM | 14.7602 | 16.5247 | 18.5482 | 20.3326 | 21.6428 | 23.0351 | ||
| FEM | 14.6185 | 16.2143 | 18.1645 | 19.7863 | 21.1685 | 22.3638 | ||
| Error (%) | 1.4702 | −0.1313 | −0.3990 | −0.6344 | 0.4805 | 0.4671 | ||
| 50 | RPT [15] | 15.3796 | 17.0294 | 19.1992 | 21.1436 | 22.9151 | 24.5504 | |
| DTM [53] | 15.3502 | - | 19.2156 | 21.1663 | 22.9120 | 24.5480 | ||
| TCM [53] | 15.3796 | - | 19.1992 | 21.1436 | 22.9151 | 24.5504 | ||
| DSM | 15.2813 | 17.0145 | 19.2761 | 21.2786 | 22.8056 | 24.4363 | ||
| FEM | 15.2894 | 16.9572 | 19.1294 | 21.0565 | 22.7983 | 24.3920 | ||
| Error (%) | 0.6430 | 0.0876 | −0.3989 | −0.6347 | 0.4803 | 0.4670 |
| b/L | b/h | Method | E1/E2 | |||||
|---|---|---|---|---|---|---|---|---|
| 3 | 10 | 20 | 30 | 40 | 50 | |||
| 0.5 | 20 | RPT [15] | 1.3160 | 1.3163 | 1.3165 | 1.3166 | 1.3166 | 1.3167 |
| DTM [53] | 1.3164 | - | 1.3165 | 1.3166 | 1.3168 | 1.3169 | ||
| TCM [53] | 1.3161 | - | 1.3165 | 1.3166 | 1.3167 | 1.3167 | ||
| DSM | 1.3162 | 1.3162 | 1.3162 | 1.3164 | 1.3164 | 1.3165 | ||
| FEM | 1.2903 | 1.2903 | 1.2906 | 1.2906 | 1.2906 | 1.2906 | ||
| Error (%) | −0.0152 | 0.0076 | 0.0228 | 0.0152 | 0.0152 | 0.0152 | ||
| 50 | RPT [15] | 1.3183 | 1.3186 | 1.3188 | 1.3189 | 1.3189 | 1.3189 | |
| DTM [53] | 1.3189 | - | 1.3189 | 1.3190 | 1.3190 | 1.3190 | ||
| TCM [53] | 1.3183 | - | 1.3188 | 1.3189 | 1.3189 | 1.3190 | ||
| DSM | 1.3118 | 1.3154 | 1.3187 | 1.3187 | 1.3870 | 1.3880 | ||
| FEM | 1.3133 | 1.3135 | 1.3137 | 1.3138 | 1.3137 | 1.3138 | ||
| Error (%) | 0.4946 | 0.2433 | 0.0076 | 0.0152 | 0.0152 | 0.0076 | ||
| 1 | 20 | RPT [15] | 3.5900 | 3.5851 | 3.5854 | 3.5857 | 3.5858 | 3.5859 |
| DTM [53] | 3.5949 | - | 3.5875 | 3.5874 | 3.5876 | 3.5877 | ||
| TCM [53] | 3.5900 | - | 3.5855 | 3.5857 | 3.5859 | 3.5860 | ||
| DSM | 3.5949 | 3.5901 | 3.5853 | 3.5856 | 3.5857 | 3.5885 | ||
| FEM | 3.5358 | 3.5303 | 3.5300 | 3.5301 | 3.5301 | 3.5302 | ||
| Error (%) | −0.1363 | −0.1393 | 0.0028 | 0.0028 | 0.0028 | −0.0725 | ||
| 50 | RPT [15] | 3.6121 | 3.6072 | 3.6074 | 3.6077 | 3.6079 | 3.6080 | |
| DTM [53] | 3.6309 | - | 3.6080 | 3.6082 | 3.6084 | 3.6085 | ||
| TCM [53] | 3.6122 | - | 3.6075 | 3.6078 | 3.6080 | 3.6081 | ||
| DSM | 3.6108 | 3.6001 | 3.6001 | 3.6066 | 3.6078 | 3.6079 | ||
| FEM | 3.6039 | 3.5986 | 3.5984 | 3.5991 | 3.5991 | 3.5991 | ||
| Error (%) | 0.0371 | 0.1972 | 0.2028 | 0.0305 | 0.0028 | 0.0028 | ||
| 2 | 20 | RPT [15] | 11.9528 | 11.9012 | 11.8952 | 11.8945 | 11.8944 | 11.8946 |
| DTM [53] | 12.0400 | - | 11.9100 | 11.9000 | 11.9000 | 11.9050 | ||
| TCM [53] | 11.9551 | - | 11.8960 | 11.8949 | 11.8947 | 11.8947 | ||
| DSM | 11.9520 | 11.8951 | 11.8950 | 11.8948 | 11.8946 | 11.8946 | ||
| FEM | 11.8526 | 11.8090 | 11.7943 | 11.7919 | 11.7910 | 11.7906 | ||
| Error (%) | 0.0067 | 0.0513 | 0.0017 | −0.0025 | −0.0017 | 0.0000 | ||
| 50 | RPT [15] | 12.2370 | 12.1817 | 12.1752 | 12.1743 | 12.1742 | 12.1742 | |
| DTM [53] | 12.3926 | - | 12.1802 | 12.1792 | 12.1790 | 12.1791 | ||
| TCM [53] | 12.2375 | - | 12.1755 | 12.1745 | 12.1744 | 12.1745 | ||
| DSM | 12.2370 | 12.1785 | 12.1751 | 12.1744 | 12.1742 | 12.1742 | ||
| FEM | 12.2274 | 12.1720 | 12.1655 | 12.1655 | 12.1632 | 12.1631 | ||
| Error (%) | 0.0000 | 0.0263 | 0.0008 | −0.0008 | 0.0000 | 0.0000 |
| b/L | b/h | Method | E1/E2 | |||||
|---|---|---|---|---|---|---|---|---|
| 3 | 10 | 20 | 30 | 40 | 50 | |||
| 0.5 | 20 | RPT [15] | 11.1940 | 18.6410 | 24.1770 | 27.5890 | 29.9780 | 31.7720 |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 11.0440 | 18.5440 | 24.0010 | 27.4220 | 29.8140 | 31.6450 | ||
| FEM | 11.2241 | 18.5395 | 23.7936 | 26.9128 | 29.0241 | 30.5589 | ||
| Error (%) | 1.3582 | 0.5231 | 0.7333 | 0.6090 | 0.5501 | 0.4013 | ||
| 50 | RPT [15] | 11.5350 | 20.2830 | 28.0500 | 33.7400 | 38.3200 | 42.1780 | |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 11.4450 | 20.0450 | 28.0010 | 33.4520 | 38.0150 | 42.0040 | ||
| FEM | 11.5988 | 20.3688 | 28.1096 | 33.7420 | 38.2453 | 42.0120 | ||
| Error (%) | 0.7864 | 1.1873 | 0.1750 | 0.8609 | 0.8023 | 0.4142 | ||
| 1 | 20 | RPT [15] | 12.2680 | 19.4910 | 25.2600 | 28.9750 | 31.6500 | 33.6990 |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 12.0540 | 19.3540 | 25.2600 | 28.8990 | 31.6498 | 33.6880 | ||
| FEM | 12.2199 | 19.0866 | 24.1686 | 27.2132 | 29.2816 | 30.7884 | ||
| Error (%) | 1.7720 | 0.7079 | 0.0000 | 0.2630 | 0.0006 | 0.0327 | ||
| 50 | RPT [15] | 12.6300 | 20.9640 | 28.6650 | 34.4150 | 39.1030 | 43.0940 | |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 12.6300 | 20.9620 | 28.6420 | 34.3440 | 39.0050 | 43.0920 | ||
| FEM | 12.6752 | 20.9800 | 28.5476 | 34.0931 | 38.5449 | 42.2785 | ||
| Error (%) | 0.0000 | 0.0095 | 0.0803 | 0.2067 | 0.2512 | 0.0046 | ||
| 2 | 20 | RPT [15] | 18.1620 | 23.7190 | 29.2240 | 33.2480 | 36.3950 | 38.9550 |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 18.0450 | 23.7180 | 29.2140 | 33.1450 | 36.3470 | 38.5450 | ||
| FEM | 17.9076 | 22.9240 | 27.1301 | 29.7723 | 31.6051 | 32.9569 | ||
| Error (%) | 0.6484 | 0.0042 | 0.0342 | 0.3108 | 0.1321 | 1.0637 | ||
| 50 | RPT [15] | 18.8420 | 25.1990 | 32.0380 | 37.5070 | 42.1470 | 46.2150 | |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 18.7540 | 24.9880 | 31.8970 | 37.1240 | 41.8740 | 46.0240 | ||
| FEM | 18.8150 | 25.1027 | 31.6413 | 36.6844 | 40.8220 | 44.3360 | ||
| Error (%) | 0.4692 | 0.8444 | 0.4420 | 1.0317 | 0.6520 | 0.4150 |
| b/L | b/h | Method | E1/E2 | |||||
|---|---|---|---|---|---|---|---|---|
| 3 | 10 | 20 | 30 | 40 | 50 | |||
| 0.5 | 20 | RPT [15] | 2.3220 | 3.5230 | 4.7060 | 5.6190 | 6.3810 | 7.0410 |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 2.3210 | 3.5220 | 4.6990 | 5.6180 | 6.3740 | 7.0010 | ||
| FEM | 2.3013 | 3.4995 | 4.6668 | 4.5382 | 6.2941 | 6.9261 | ||
| Error (%) | 0.0431 | 0.0284 | 0.1490 | 0.0178 | 0.1098 | 0.5713 | ||
| 50 | RPT [15] | 2.3320 | 3.5550 | 4.7800 | 5.7450 | 6.5660 | 7.2910 | |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 2.3310 | 3.5350 | 4.7010 | 5.7440 | 6.5540 | 7.2870 | ||
| FEM | 2.3266 | 3.5479 | 4.7691 | 4.6778 | 6.5441 | 7.2632 | ||
| Error (%) | 0.0429 | 0.5658 | 1.6805 | 0.0174 | 0.1831 | 0.0549 | ||
| 1 | 20 | RPT [15] | 4.2160 | 4.9950 | 5.8970 | 6.6620 | 7.3360 | 7.9420 |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 4.2160 | 4.9920 | 5.8240 | 6.5770 | 7.2540 | 7.8450 | ||
| FEM | 4.1595 | 4.9287 | 5.8066 | 6.5343 | 7.1612 | 7.7141 | ||
| Error (%) | 0.0000 | 0.0601 | 1.2534 | 1.2924 | 1.1304 | 1.2365 | ||
| 50 | RPT [15] | 4.2500 | 5.0480 | 5.9820 | 6.7820 | 7.4940 | 8.1420 | |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 4.2450 | 5.0120 | 5.8440 | 6.4510 | 7.4240 | 8.0140 | ||
| FEM | 4.2402 | 5.0346 | 5.9620 | 6.7541 | 7.4569 | 8.0942 | ||
| Error (%) | 0.1178 | 0.7183 | 2.3614 | 5.1310 | 0.9429 | 1.5972 | ||
| 2 | 20 | RPT [15] | 12.2640 | 12.5540 | 12.9420 | 13.3020 | 13.6470 | 13.9780 |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 12.1240 | 12.4510 | 12.8450 | 13.2040 | 13.6140 | 13.8540 | ||
| FEM | 11.8526 | 12.4252 | 12.7885 | 13.1213 | 13.4293 | 13.7178 | ||
| Error (%) | 1.1547 | 0.8272 | 0.7552 | 0.7422 | 0.2424 | 0.8950 | ||
| 50 | RPT [15] | 12.5670 | 12.8740 | 13.2880 | 13.6750 | 14.0460 | 14.4050 | |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 12.4570 | 12.7450 | 13.1440 | 13.2470 | 14.0440 | 14.4020 | ||
| FEM | 12.2274 | 12.5838 | 13.2596 | 13.6953 | 14.0022 | 14.3510 | ||
| Error (%) | 0.8830 | 1.0122 | 1.0956 | 3.2309 | 0.0142 | 0.0208 |
| b/L | b/h | Method | E1/E2 | |||||
|---|---|---|---|---|---|---|---|---|
| 3 | 10 | 20 | 30 | 40 | 50 | |||
| 0.5 | 20 | RPT [15] | 2.3250 | 2.3260 | 2.3260 | 2.3260 | 2.3260 | 2.3260 |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 2.3240 | 2.3250 | 2.3258 | 2.3258 | 2.3258 | 2.3258 | ||
| FEM | 2.3252 | 2.3245 | 2.3260 | 2.3266 | 2.3260 | 2.3260 | ||
| Error (%) | 0.0430 | 0.0430 | 0.0086 | 0.0086 | 0.0086 | 0.0086 | ||
| 50 | RPT [15] | 2.3310 | 2.3310 | 2.3320 | 2.3320 | 2.3320 | 2.3320 | |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 2.3312 | 2.335 | 2.3322 | 2.3325 | 2.3328 | 2.3320 | ||
| FEM | 2.3315 | 2.3315 | 2.3325 | 2.3325 | 2.3325 | 2.3325 | ||
| Error (%) | −0.0086 | −0.1716 | −0.0086 | −0.0214 | −0.0343 | 0.0000 | ||
| 1 | 20 | RPT [15] | 2.8380 | 2.8300 | 2.8290 | 2.8290 | 2.8290 | 2.8290 |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 2.8140 | 2.8244 | 2.8344 | 2.8344 | 2.8344 | 2.8344 | ||
| FEM | 2.8440 | 2.8371 | 2.8364 | 2.8466 | 2.8466 | 2.8466 | ||
| Error (%) | 0.8529 | 0.1983 | −0.1905 | −0.1905 | −0.1905 | −0.1905 | ||
| 50 | RPT [15] | 2.8560 | 2.8470 | 2.8460 | 2.8460 | 2.8460 | 2.8460 | |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 2.8488 | 2.8444 | 2.8442 | 2.8442 | 2.8442 | 2.8442 | ||
| FEM | 2.8626 | 2.8543 | 2.8534 | 2.8549 | 2.8549 | 2.8549 | ||
| Error (%) | 0.2527 | 0.0914 | 0.0633 | 0.0633 | 0.0633 | 0.0633 | ||
| 2 | 20 | RPT [15] | 11.1510 | 11.0960 | 11.0880 | 11.0860 | 11.0850 | 11.0850 |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 11.1500 | 11.0900 | 11.0820 | 11.0810 | 11.0810 | 11.0810 | ||
| FEM | 11.3046 | 11.1211 | 11.2471 | 11.2455 | 11.2455 | 11.2455 | ||
| Error (%) | 0.0090 | 0.0541 | 0.0541 | 0.0451 | 0.0361 | 0.0361 | ||
| 50 | RPT [15] | 11.4160 | 11.3570 | 11.3490 | 11.3460 | 11.3460 | 11.3450 | |
| DTM [53] | - | - | - | - | - | - | ||
| TCM [53] | - | - | - | - | - | - | ||
| DSM | 11.3967 | 11.3450 | 11.3460 | 11.3460 | 11.3450 | 11.3450 | ||
| FEM | 11.4429 | 11.3850 | 11.3778 | 11.3759 | 11.3759 | 11.3759 | ||
| Error (%) | 0.1695 | 0.1058 | 0.0264 | 0.0000 | 0.0088 | 0.0000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chauhan, M.; Mishra, P.; Dwivedi, S.; Ragulskis, M.; Burdzik, R.; Ranjan, V. Development of the Dynamic Stiffness Method for the Out-of-Plane Natural Vibration of an Orthotropic Plate. Appl. Sci. 2022, 12, 5733. https://doi.org/10.3390/app12115733
Chauhan M, Mishra P, Dwivedi S, Ragulskis M, Burdzik R, Ranjan V. Development of the Dynamic Stiffness Method for the Out-of-Plane Natural Vibration of an Orthotropic Plate. Applied Sciences. 2022; 12(11):5733. https://doi.org/10.3390/app12115733
Chicago/Turabian StyleChauhan, Manish, Pawan Mishra, Sarvagya Dwivedi, Minvydas Ragulskis, Rafał Burdzik, and Vinayak Ranjan. 2022. "Development of the Dynamic Stiffness Method for the Out-of-Plane Natural Vibration of an Orthotropic Plate" Applied Sciences 12, no. 11: 5733. https://doi.org/10.3390/app12115733
APA StyleChauhan, M., Mishra, P., Dwivedi, S., Ragulskis, M., Burdzik, R., & Ranjan, V. (2022). Development of the Dynamic Stiffness Method for the Out-of-Plane Natural Vibration of an Orthotropic Plate. Applied Sciences, 12(11), 5733. https://doi.org/10.3390/app12115733








