An Asymmetric Bargaining Model for Natural-Gas Distribution
Abstract
:1. Introduction
2. The Natural-Gas Scenario in Pakistan
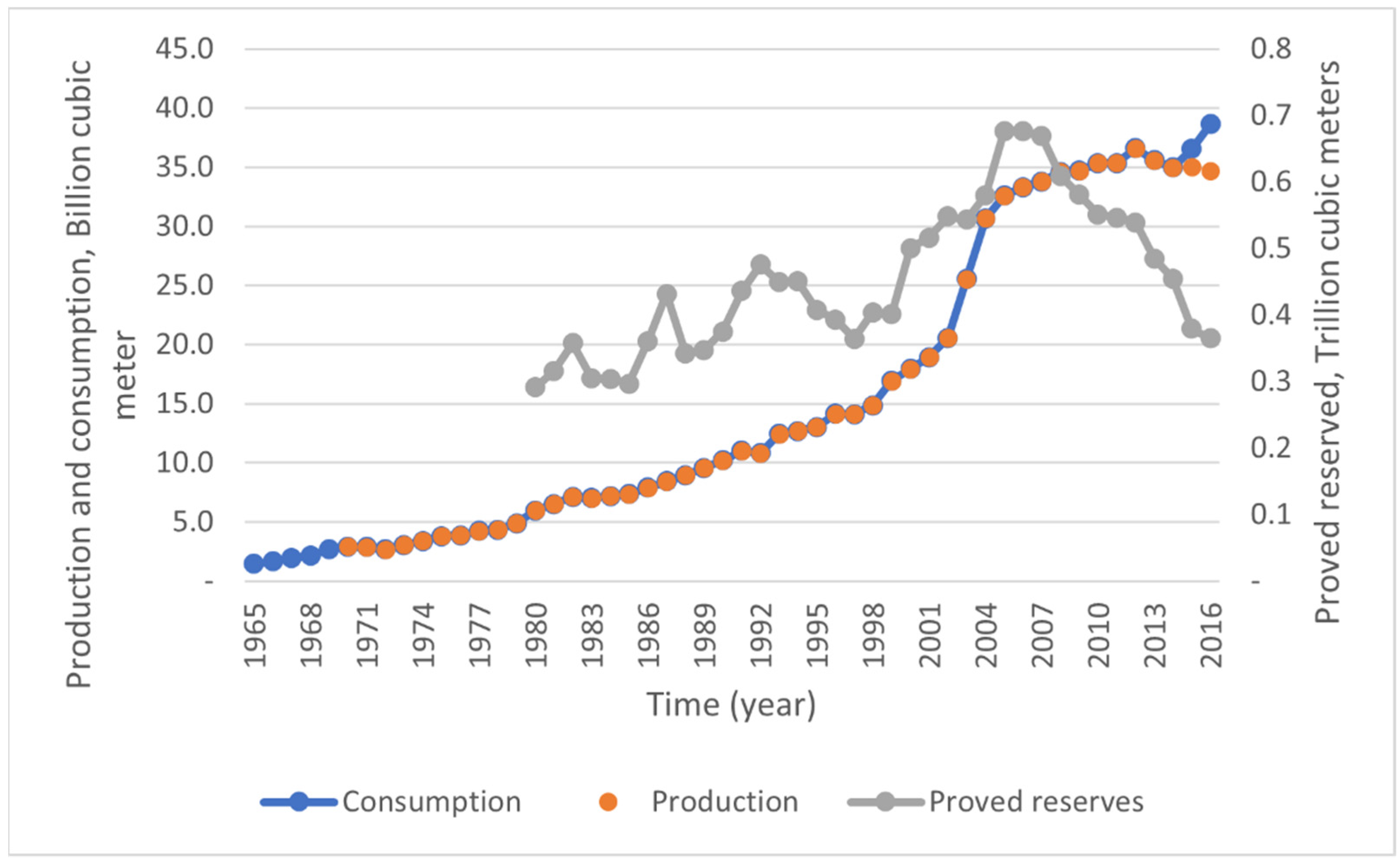
3. Pakistan’s Natural-Gas Production, Consumption, and Supply–Demand Gap
| Country | Total Gas Production (Bcm) | Per cent of World Production |
|---|---|---|
| Pakistan | 41.5 | 1.2 |
| China | 138.4 | 3.9 |
| Russia | 579.4 | 16.3 |
| Canada | 152.0 | 4.3 |
| United States | 749.2 | 21.1 |
| Qatar | 181.2 | 5.1 |
| Iran | 202.4 | 5.7 |
| Norway | 116.6 | 3.3 |
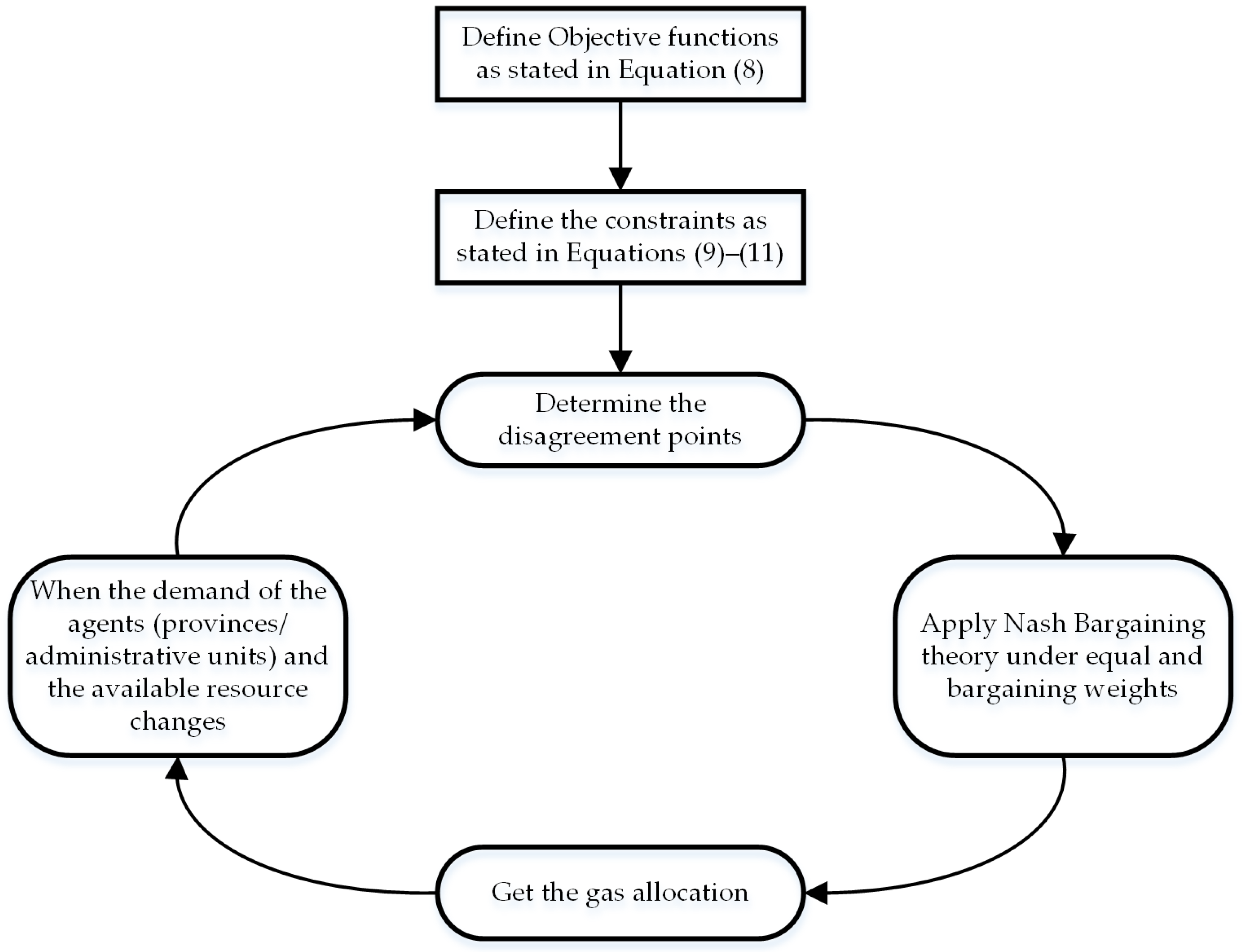
4. An Asymmetric Hybrid Bankruptcy and Nash Bargaining Model for Gas Distribution
- The gas allocation of each province must be equal to or more than its lower threshold value.
- 2.
- The gas allocation of each province must be equal to or less than its upper threshold value (claim) but more than or equal to its lower threshold value.
- 3.
- The total gas allocation must be equal to or less than the total available gas.
| Year 2020 | Year 2021 | Year 2022 |
|---|---|---|
| x(Pun) + x (Sin) + x(Bal) + x(Kpk) + x(Ot) = 1658 631 ≤ x(P) ≤ 922 376 ≤ x(S) ≤ 667 92≤ x(B) ≤ 184 48 ≤ x(K) ≤ 95 41 ≤ x(Ot) ≤ 81 | x(Pun) + x (Sin) + x(Bal) + x(Kpk) + x(Ot) = 1801 721 ≤ x(P) ≤ 968 452 ≤ x(S) ≤ 699 97 ≤ x(B) ≤ 194 50 ≤ x(K) ≤ 99 44 ≤ x(Ot) ≤ 88 | x(Pun) + x (Sin) + x(Bal) + x(Kpk) + x(Ot) = 1701 568 ≤ x(P) ≤ 1013 367 ≤ x(S) ≤ 734 103 ≤ x(B) ≤ 205 51 ≤ x(K) ≤ 102 46 ≤ x(Ot) ≤ 92 |
| Year 2023 | Year 2024 | Year 2025 |
| x(Pun) + x (Sin)+ x(Bal) + x(Kpk) + x(Ot) = 1603 533 ≤ x(P) ≤ 1066 385 ≤ x(S) ≤ 770 108 ≤ x(B) ≤ 215 55 ≤ x(K) ≤ 109 48 ≤ x(Ot) ≤ 95 | x(Pun) + x (Sin) + x(Bal)+ x(Kpk) + x(Ot)= 1870 619 ≤ x(P) ≤ 1119 405 ≤ x(S) ≤ 809 113 ≤ x(B) ≤ 226 59 ≤ x(K) ≤ 117 50 ≤ x(Ot) ≤ 99 | x(Pun) + x (Sin) + x(Bal) + x(Kpk) + x(Ot) = 1987 673 ≤ x(P) ≤ 1176 426 ≤ x(S) ≤ 851 119 ≤ x(B) ≤ 237 60 ≤ x(K) ≤ 120 53 ≤ x(Ot) ≤ 106 |
| Year 2026 | Year 2027 | Year 2028 |
| x(Pun) + x (Sin) + x(Bal) + x(Kpk) + x(Ot) = 2107 731 ≤ x(P) ≤ 1236 447 ≤ x(S) ≤ 893 124 ≤ x(B) ≤ 247 64 ≤ x(K) ≤ 127 55 ≤ x(Ot) ≤ 109 | x(Pun) + x (Sin) + x(Bal) + x(Kpk) + x(Ot) = 2063 650 ≤ x(P) ≤ 1299 470 ≤ x(S) ≤ 939 131 ≤ x(B) ≤ 261 67 ≤ x(K) ≤ 134 59 ≤ x(Ot) ≤ 117 | x(Pun) + x (Sin) + x(Bal) + x(Kpk) + x(Ot) = 2026 682 ≤ x(P) ≤ 1363 492 ≤ x(S) ≤ 985 136 ≤ x(B) ≤ 272 71 ≤ x(K) ≤ 141 62 ≤ x(Ot) ≤ 124 |
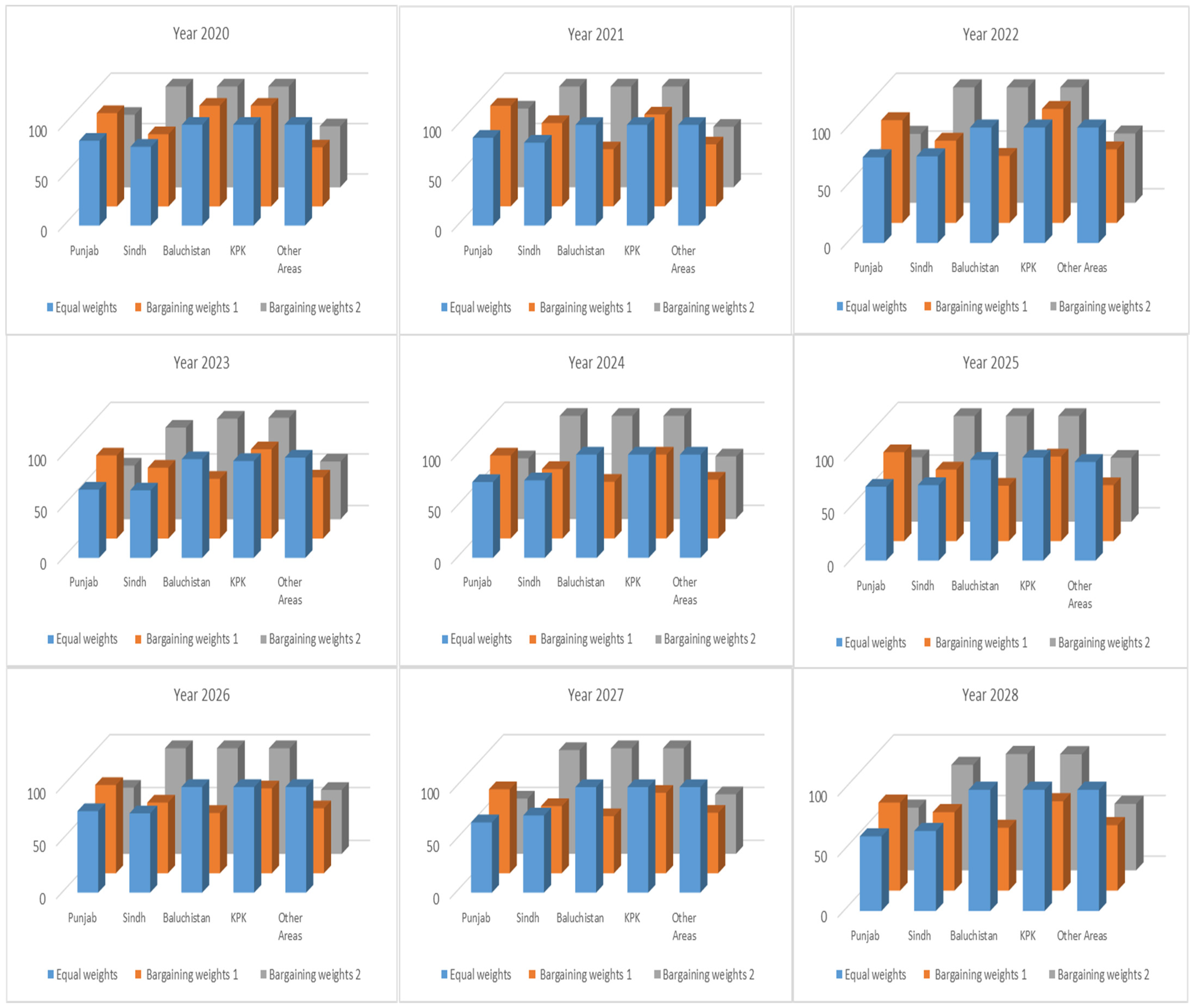
Bargaining Weights Determination
5. Results and Discussion
6. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ravnik, J.; Hriberšek, M. A method for natural gas forecasting and preliminary allocation based on unique standard natural gas consumption profiles. Energy 2019, 180, 149–162. [Google Scholar] [CrossRef]
- Ahmad, H.; Hayat, N. Markov chain based modelling and prediction of natural gas allocation structure in Pakistan. Int. J. Energy Sect. Manag. 2020, 14, 911–933. [Google Scholar] [CrossRef]
- Khan, M.A. Modelling and forecasting the demand for natural gas in Pakistan. Renew. Sustain. Energy Rev. 2015, 49, 1145–1159. [Google Scholar] [CrossRef]
- Dudley, B. BP Statistical Review of World Energy; BP Statistical Review: London, UK, 2018. [Google Scholar]
- Janjua, S.; Hassan, I.; Zarghami, M.; Islam, S. Addressing the supply-demand gap in shared rivers using water diplomacy framework: Utility of game theory in the Indus River within Pakistan. Water Policy 2020, 22, 789–810. [Google Scholar] [CrossRef]
- De Stefano, L.; Edwards, P.; de Silva, L.; Wolf, A.T. Tracking cooperation and conflict in international basins: Historic and recent trends. Water Policy 2010, 12, 871–884. [Google Scholar] [CrossRef] [Green Version]
- De Amorim, W.S.; Valduga, I.B.; Ribeiro, J.M.P.; Williamson, V.G.; Krauser, G.E.; Magtoto, M.K.; Baltazar, J.; de Andrade Guerra, A.O. The nexus between water, energy, and food in the context of the global risks: An analysis of the interactions between food, water, and energy security. Environ. Impact Assess. Rev. 2019, 72, 1–11. [Google Scholar] [CrossRef]
- Thomson, W. Axiomatic and game-theoretic analysis of bankruptcy and taxation problems: An update. Math. Soc. Sci. 2015, 74, 41–59. [Google Scholar] [CrossRef] [Green Version]
- Thomson, W. Axiomatic and game-theoretic analysis of bankruptcy and taxation problems: A survey. Math. Soc. Sci. 2003, 45, 249–297. [Google Scholar] [CrossRef]
- Herrero, C.; Villar, A. The three musketeers: Four classical solutions to bankruptcy problems. Math. Soc. Sci. 2001, 42, 307–328. [Google Scholar] [CrossRef]
- Ansink, E. Game-Theoretic Models of Water Allocation in Transboundary River Basins. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 2009. [Google Scholar]
- Madani, K.; Zarezadeh, M. Bankruptcy methods for resolving water resources conflicts. In World Environmental and Water Resources Congress 2012: Crossing Boundaries; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 2247–2252. [Google Scholar]
- Zarezadeh, M.; Mirchi, A.; Read, L.; Madani, K. Ten bankruptcy methods for resolving natural resource allocation conflicts. In Water Diplomacy in Action. Contingent Approaches to Managing Complex Water Problems; Islam, S., Madani, K., Eds.; Anthem Press: London, UK, 2012; pp. 37–50. [Google Scholar]
- Madani, K.; Zarezadeh, M. Game theory and water resources. J. Hydrol. 2010, 381, 225–238. [Google Scholar] [CrossRef]
- Madani, K.; Zarezadeh, M.; Morid, S. A new framework for resolving conflicts over transboundary rivers using bankruptcy methods. Hydrol. Earth Syst. Sci. 2014, 18, 3055–3068. [Google Scholar] [CrossRef] [Green Version]
- Mianabadi, H.; Mostert, E.; Zarghami, M. A new bankruptcy method for conflict resolution in water resources allocation. J. Environ. Manag. 2014, 144, 152–159. [Google Scholar] [CrossRef] [PubMed]
- Janjua, S.; Hassan, I. Transboundary water allocation in critical scarcity conditions: A stochastic bankruptcy approach. J. Water Supply Res. Technol. AQUA 2020, 69, 224–237. [Google Scholar] [CrossRef] [Green Version]
- Janjua, S.; Hassan, I. Use of bankruptcy methods for resolving interprovincial water conflicts over transboundary river: Case study of Indus River in Pakistan. River Res. Appl. 2020, 36, 1334–1344. [Google Scholar] [CrossRef]
- Ansink, E.; Weikard, H.-P. Sequential sharing rules for river sharing problems. Soc. Choice Welfare 2012, 38, 187–210. [Google Scholar] [CrossRef] [Green Version]
- Ansink, E.; Marchiori, C. Reallocating Water: An Application of Sequential Sharing Rules to Cyprus. SSRN Electron. J. 2015, 1, 1550018. [Google Scholar] [CrossRef] [Green Version]
- Giménez-Gómez, J.M. A Way to Play Claims Problems. Group Decis. Negot. 2014, 23, 617–627. [Google Scholar] [CrossRef]
- Dagan, N.; Volij, O. The bankruptcy problem: A cooperative bargaining approach. Math. Soc. Sci. 1993, 26, 287–297. [Google Scholar] [CrossRef] [Green Version]
- Casas-Méndez, B.; Fragnelli, V.; García-Jurado, I. Weighted bankruptcy rules and the museum pass problem. Eur. J. Oper. Res. 2011, 215, 161–168. [Google Scholar] [CrossRef]
- Janjua, S.; Ali, M.U.; Kallu, K.D.; Ibrahim, M.M.; Zafar, A.; Kim, S. A Game-Theoretic Approach for Electric Power Distribution during Power Shortage: A Case Study in Pakistan. Appl. Sci. 2021, 11, 5084. [Google Scholar] [CrossRef]
- Degefu, D.M.; He, W. Power allocation among socio-economic sectors with overlapping demands during power shortage: A bankruptcy approach. In Proceedings of the 2016 4th IEEE International Conference Smart Energy Grid Engineering SEGE 2016, Oshawa, ON, Canada, 21–24 August 2016; pp. 6–10. [Google Scholar] [CrossRef]
- Gallastegui, C.; Inarra, E.; Prellezo, R. Bankruptcy of Fishing Resources: The Northern European Anglerfish Fishery. Mar. Resour. Econ. 2002, 17, 291–307. [Google Scholar] [CrossRef]
- Tian, J.; Yu, Y.; Li, T.; Zhou, Y.; Li, J.; Wang, X.; Han, Y. A cooperative game model with bankruptcy theory for water allocation: A case study in China Tarim River Basin. Environ. Sci. Pollut. Res. Int. 2022, 29, 2353–2364. [Google Scholar] [CrossRef] [PubMed]
- Safari, N.; Zarghami, M.; Szidarovszky, F. Nash bargaining and leader-follower models in water allocation: Application to the Zarrinehrud River basin, Iran. Appl. Math. Model. 2014, 38, 1959–1968. [Google Scholar] [CrossRef]
- Fu, J.; Zhong, P.A.; Zhu, F.; Chen, J.; Wu, Y.N.; Xu, B. Water resources allocation in transboundary river based on asymmetric Nash-Harsanyi Leader-Follower game model. Water 2018, 10, 270. [Google Scholar] [CrossRef] [Green Version]
- Nash, Z. The bargaining problem. Econometrica 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Nash, J. Two-person cooperative games. Econometrica 1953, 21, 128–140. [Google Scholar] [CrossRef]
- Houba, H. Asymmetric Nash Solutions in the River Sharing Problem; Tinbergen Institute: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Sgobbi, A. A Stochastic Multiple Players Multi-Issues Bargaining Model for the Piave River Basin. Strateg. Behav. Environ. 2011, 1, 119–150. [Google Scholar] [CrossRef] [Green Version]
- Degefu, D.M.; He, W. Allocating Water under Bankruptcy Scenario. Water Resour. Manag. 2016, 30, 3949–3964. [Google Scholar] [CrossRef]
- Qin, J.; Fu, X.; Peng, S.; Xu, Y.; Huang, J.; Huang, S. Asymmetric Bargaining Model for Water Resource Allocation over Transboundary Rivers. Int. J. Environ. Res. Public Health 2019, 16, 1733. [Google Scholar] [CrossRef] [Green Version]
- Karmakar, S.; Seikh, M.R.; Castillo, O. Type-2 intuitionistic fuzzy matrix games based on a new distance measure: Application to biogas-plant implementation problem. Appl. Soft Comput. 2021, 106, 107357. [Google Scholar] [CrossRef]
- Seikh, M.R.; Dutta, S.; Li, D.F. Solution of matrix games with rough interval pay-offs and its application in the telecom market share problem. Int. J. Intell. Syst. 2021, 36, 6066–6100. [Google Scholar] [CrossRef]
- Seikh, M.R.; Karmakar, S.; Castillo, O. A novel defuzzification approach of type-2 fuzzy variable to solving matrix games: An application to plastic ban problem. Iran. J. Fuzzy Syst. 2021, 18, 155–172. [Google Scholar] [CrossRef]
- Aized, T.; Shahid, M.; Bhatti, A.A.; Saleem, M.; Anandarajah, G. Energy security and renewable energy policy analysis of Pakistan. Renew. Sustain. Energy Rev. 2018, 84, 155–169. [Google Scholar] [CrossRef]
- Hussain, S.; Hussain, F. Natural Gas Allocation and Management in Pakistan: Issues and Actors; Natural Gas Allocation and Management in Pakistan: Islamabd, Pakistan, 2014. [Google Scholar]
- Jan, H.A.; Jan, S.; Bussmann, R.W.; Wali, S.; Sisto, F.; Ahmad, L. Complementary and alternative medicine research, prospects and limitations in Pakistan: A literature review. Shengtai Xuebao Acta Ecol. Sin. 2020, 40, 451–463. [Google Scholar] [CrossRef]
- Khalil, H.B.; Abas, N. Smart grids: An approach to integrate the renewable energies and efficiently manage the energy system of Pakistan. In Proceedings of the 5th International Conference on Computing Communication and Networking Technologies, ICCCNT 2014, Hefei, China, 11–13 July 2014. [Google Scholar] [CrossRef]
- Janjua, S.; Hassan, I. Fuzzy AHP-TOPSIS multi-criteria decision analysis applied to the Indus Reservoir system in Pakistan. Water Sci. Technol. Water Supply 2020, 20, 1933–1949. [Google Scholar] [CrossRef]
- Malik, S.R.; Maqbool, M.A. Energy potential of Pakistan. NFC IEFR J. Eng. Sci. Res. 2017, 1, 78–86. [Google Scholar]
- Goss, R.M. BP. 2017. BP Statistical Review of World Energy; Pure Print Group Limited: London, UK, 2017. [Google Scholar]
- Ministry of Energy of Pakistan. Development Plan for Pakistan Oil and Gas Industry; Ministry of Energy of Pakistan: Islamabad, Pakistan, 2020. [Google Scholar]
- Chen, Y.W.; Halford, J.T.; Hsu, H.C.S.; Bin Lin, C. Personal bankruptcy laws and corporate policies. J. Financ. Quant. Anal. 2020, 55, 2397–2428. [Google Scholar] [CrossRef]
- Moridi, A. A bankruptcy method for pollution load reallocation in river systems. J. Hydroinformatics 2019, 21, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Harsanyi, J.C. A simplified bargaining model for the n-person cooperative game. Pap. Game Theory 1982, 4, 44–70. [Google Scholar]
| 2020 | 2021 | 2022 | 2023 | 2024 | 2025 | 2026 | 2027 | 2028 | |
|---|---|---|---|---|---|---|---|---|---|
| Committed and anticipated Supply/domestic supply (BCF) | 1220 | 1144 | 1044 | 946 | 859 | 783 | 692 | 649 | 612 |
| LNG supply (BCF) | 438 | 657 | 657 | 657 | 657 | 657 | 657 | 657 | 657 |
| Iran–Pakistan (BCF) | 0 | 0 | 0 | 0 | 0 | 96 | 274 | 274 | 274 |
| TAPI (BCF) | 0 | 0 | 0 | 0 | 354 | 451 | 484 | 484 | 484 |
| Total supply (BCF) | 1658 | 1801 | 1701 | 1957 | 1967 | 2026 | 2113 | 2069 | 2033 |
| Punjab’s demand (BCF) | 922 | 968 | 1013 | 1066 | 1119 | 1176 | 1236 | 1299 | 1363 |
| Sindh’s demand (BCF) | 667 | 699 | 734 | 770 | 809 | 851 | 893 | 939 | 985 |
| Baluchistan’s demand (BCF) | 184 | 194 | 205 | 215 | 226 | 237 | 247 | 261 | 272 |
| KPK’s demand (BCF) | 95 | 99 | 102 | 109 | 117 | 120 | 127 | 134 | 141 |
| Other’s demand (BCF) | 81 | 88 | 92 | 95 | 99 | 106 | 109 | 117 | 124 |
| Total demand (BCF) | 1949 | 2048 | 2146 | 2255 | 2370 | 2490 | 2612 | 2750 | 2885 |
| Gap/shortfall (BCF) | 291 | 247 | 445 | 298 | 403 | 464 | 499 | 681 | 852 |
| Provinces | ||||||
|---|---|---|---|---|---|---|
| Punjab | Sindh | Baluchistan | KPK | Other Areas | Total | |
| Percentage share in total production | 4 | 62.6 | 21.4 | 11 | 1 | 100 |
| Bargaining weight | 0.04 | 0.626 | 0.214 | 0.11 | 0.01 | 1.00 |
| Number of consumers (domestic, commercial and industrial), in millions | 5.80 | 2.70 | 0.28 | 0.87 | 0.2 | 9.85 |
| Bargaining weight | 0.588 | 0.274 | 0.028 | 0.088 | 0.022 | 1.00 |
| (a) | ||||
|---|---|---|---|---|
| Punjab | Sindh | Baluchistan | KPK | Others |
| Year 2020 | ||||
| 777 | 522 | 184 | 95 | 81 |
| Year 2021 | ||||
| 845 | 576 | 194 | 99 | 88 |
| Year 2022 | ||||
| 751 | 551 | 205 | 102 | 92 |
| Year 2023 | ||||
| 702 | 502 | 205 | 102 | 92 |
| Year 2024 | ||||
| 821 | 607 | 226 | 117 | 99 |
| Year 2025 | ||||
| 886 | 639 | 237 | 120 | 106 |
| Year 2026 | ||||
| 954 | 670 | 247 | 127 | 109 |
| Year 2027 | ||||
| 865 | 686 | 261 | 134 | 117 |
| Year 2028 | ||||
| 839 | 650 | 272 | 141 | 124 |
| (b) | ||||
| Punjab | Sindh | Baluchistan | KPK | Others |
| Year 2020 | ||||
| 663 | 667 | 184 | 95 | 47 |
| Year 2021 | ||||
| 756 | 699 | 194 | 99 | 88 |
| Year 2022 | ||||
| 605 | 734 | 205 | 102 | 55 |
| Year 2023 | ||||
| 552 | 682 | 209 | 107 | 53 |
| Year 2024 | ||||
| 658 | 809 | 226 | 117 | 60 |
| Year 2025 | ||||
| 715 | 851 | 237 | 120 | 64 |
| Year 2026 | ||||
| 774 | 893 | 247 | 127 | 66 |
| Year 2027 | ||||
| 679 | 923 | 261 | 134 | 66 |
| Year 2028 | ||||
| 705 | 857 | 261 | 135 | 68 |
| (c) | ||||
| Punjab | Sindh | Baluchistan | KPK | Others |
| Year 2020 | ||||
| 854 | 478 | 184 | 95 | 47 |
| Year 2021 | ||||
| 986 | 578 | 110 | 90 | 54 |
| Year 2022 | ||||
| 901 | 522 | 119 | 101 | 59 |
| Year 2023 | ||||
| 812 | 515 | 121 | 97 | 59 |
| Year 2024 | ||||
| 986 | 576 | 130 | 114 | 64 |
| Year 2025 | ||||
| 1059 | 606 | 137 | 118 | 67 |
| Year 2026 | ||||
| 1134 | 635 | 143 | 124 | 70 |
| Year 2027 | ||||
| 1053 | 658 | 150 | 127 | 74 |
| Year 2028 | ||||
| 1025 | 652 | 152 | 122 | 75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janjua, S.; Ali, M.U.; Kallu, K.D.; Zafar, A.; Hussain, S.J.; Gardezi, H.; Lee, S.W. An Asymmetric Bargaining Model for Natural-Gas Distribution. Appl. Sci. 2022, 12, 5677. https://doi.org/10.3390/app12115677
Janjua S, Ali MU, Kallu KD, Zafar A, Hussain SJ, Gardezi H, Lee SW. An Asymmetric Bargaining Model for Natural-Gas Distribution. Applied Sciences. 2022; 12(11):5677. https://doi.org/10.3390/app12115677
Chicago/Turabian StyleJanjua, Shahmir, Muhammad Umair Ali, Karam Dad Kallu, Amad Zafar, Shaik Javeed Hussain, Hasnain Gardezi, and Seung Won Lee. 2022. "An Asymmetric Bargaining Model for Natural-Gas Distribution" Applied Sciences 12, no. 11: 5677. https://doi.org/10.3390/app12115677
APA StyleJanjua, S., Ali, M. U., Kallu, K. D., Zafar, A., Hussain, S. J., Gardezi, H., & Lee, S. W. (2022). An Asymmetric Bargaining Model for Natural-Gas Distribution. Applied Sciences, 12(11), 5677. https://doi.org/10.3390/app12115677








