Semi-Analytical Solution for Elastoplastic Deflection of Non-Prismatic Cantilever Beams with Circular Cross-Section
Featured Application
Abstract
1. Introduction
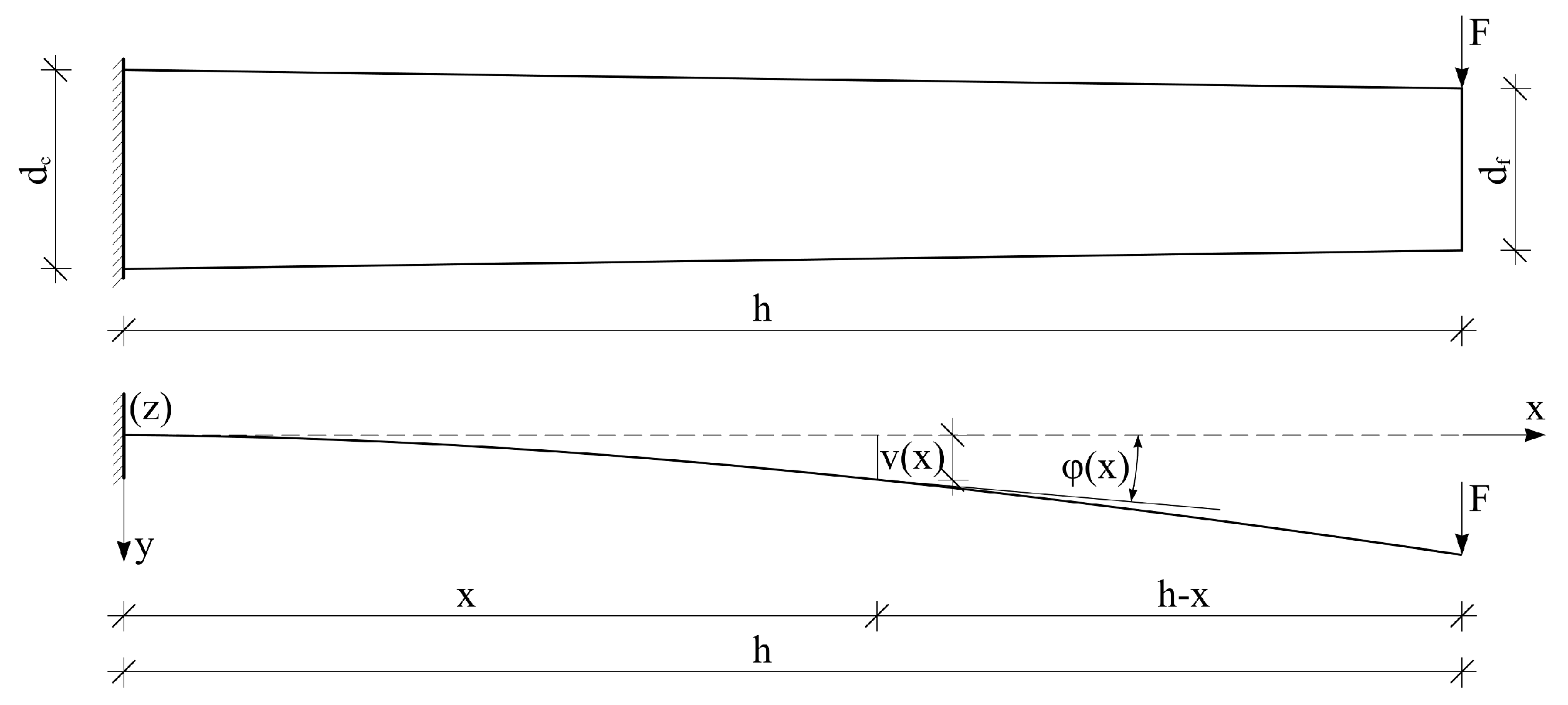
2. Solution for the Elastoplastic Bending of the Cantilever Beam
2.1. Elastic Regime
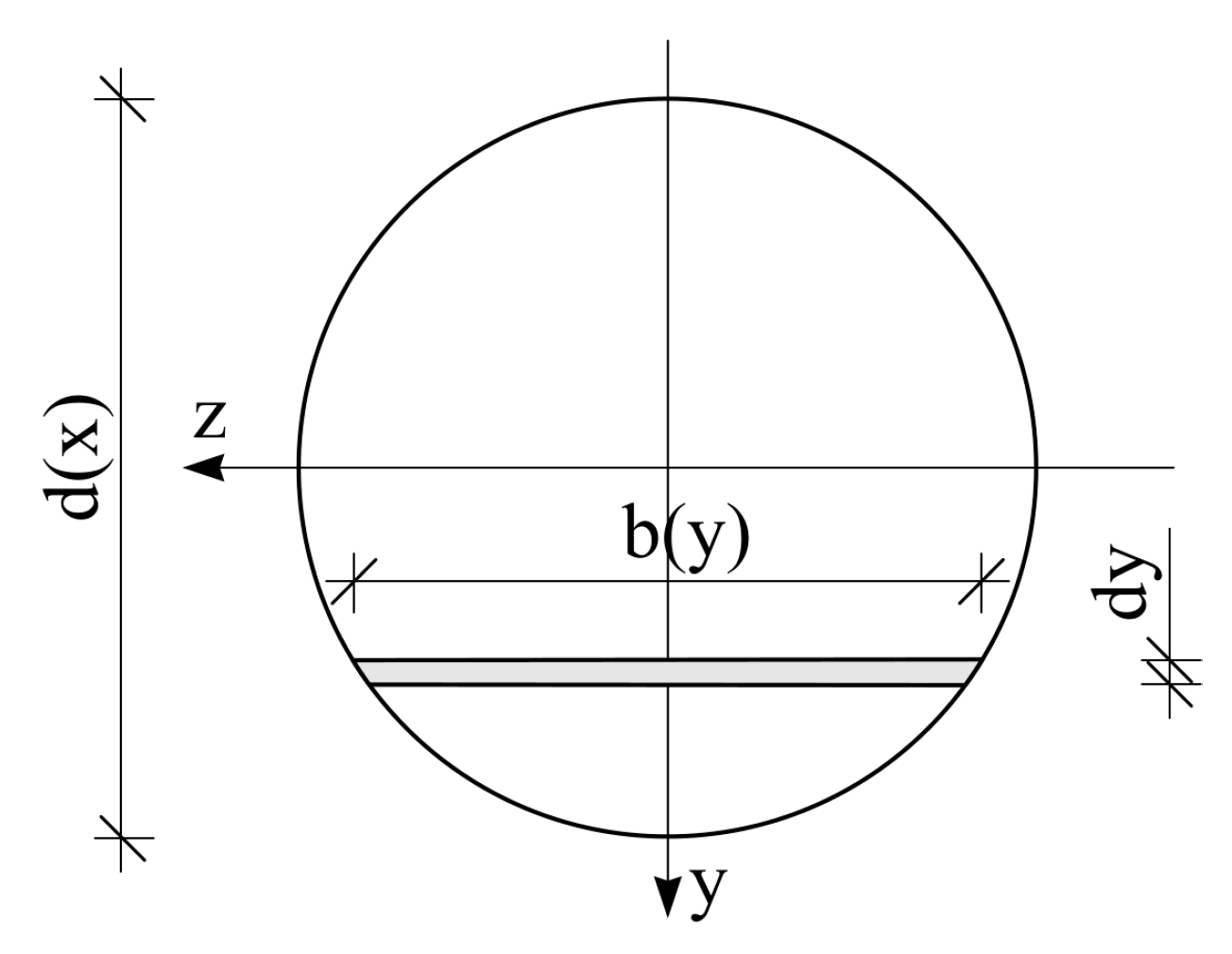
2.2. Plastic Regime
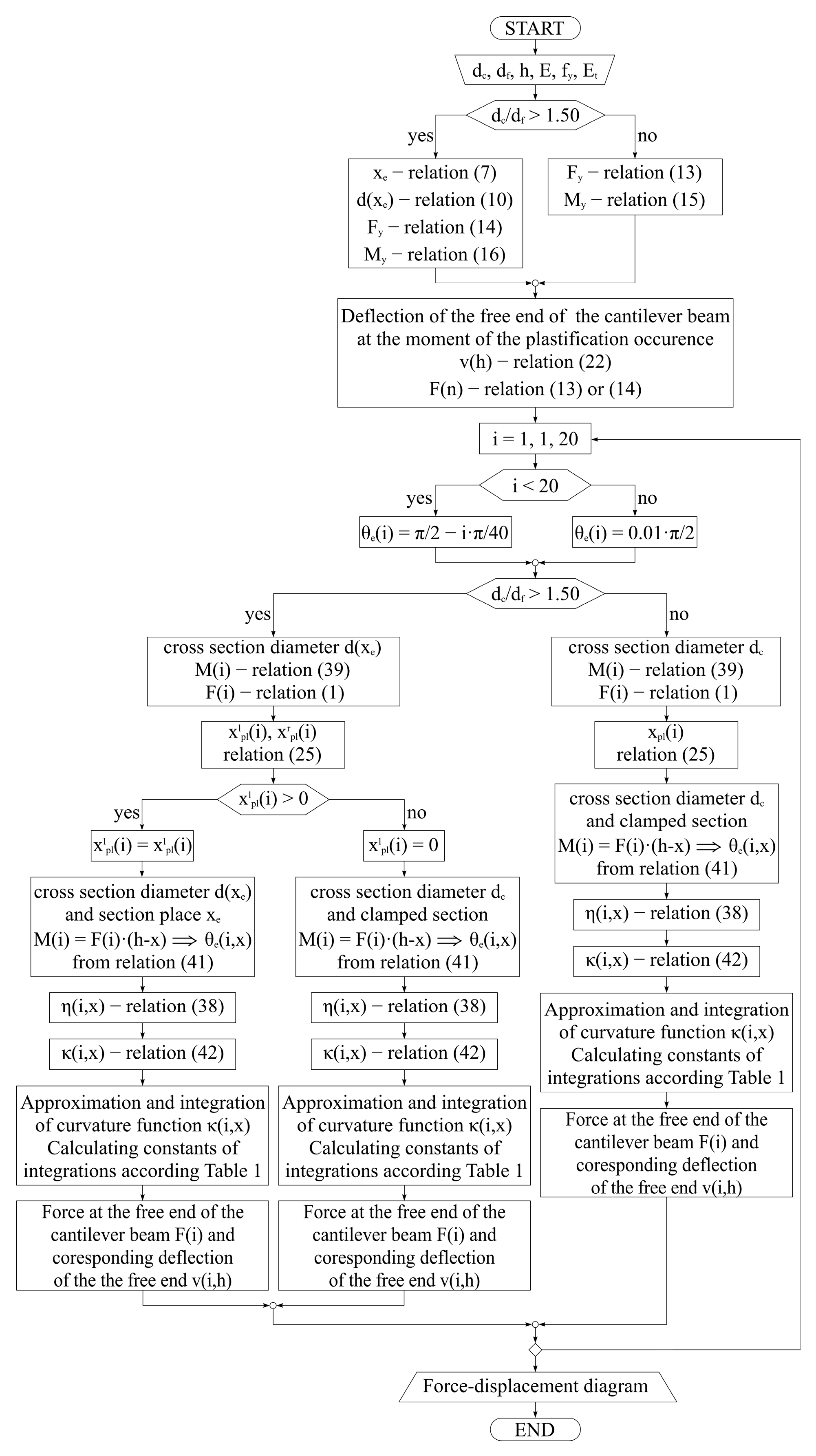
2.3. Incremental Analysis
3. Validation of the Proposed Semi-Analytical Solution
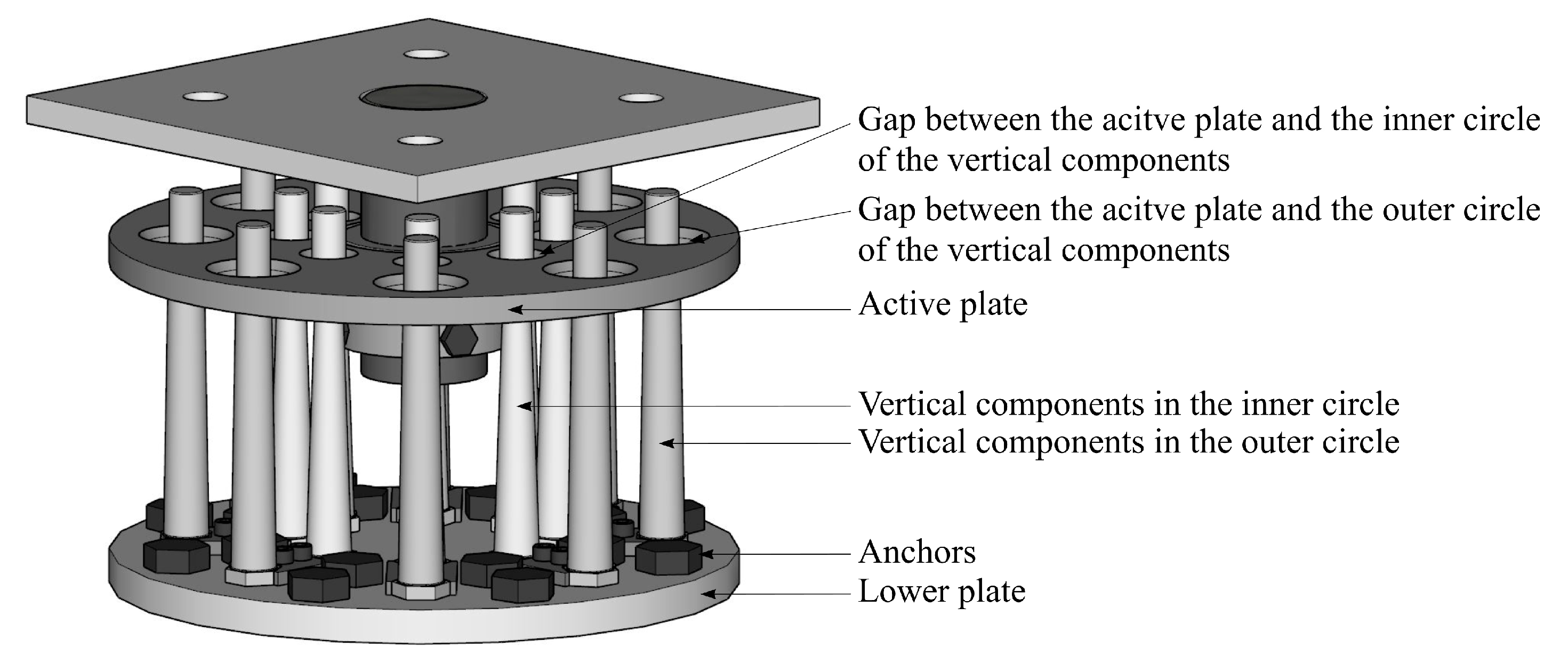
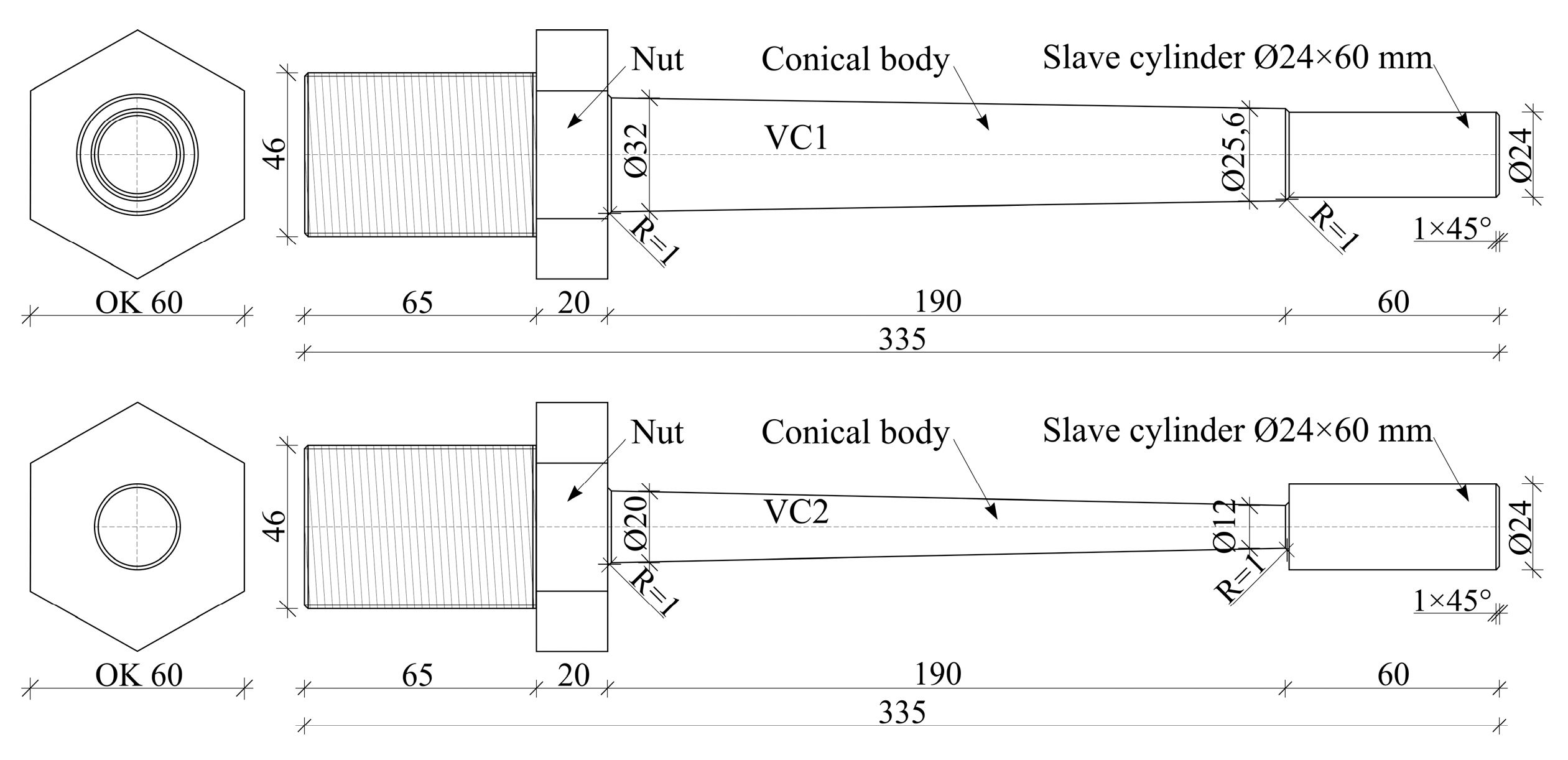
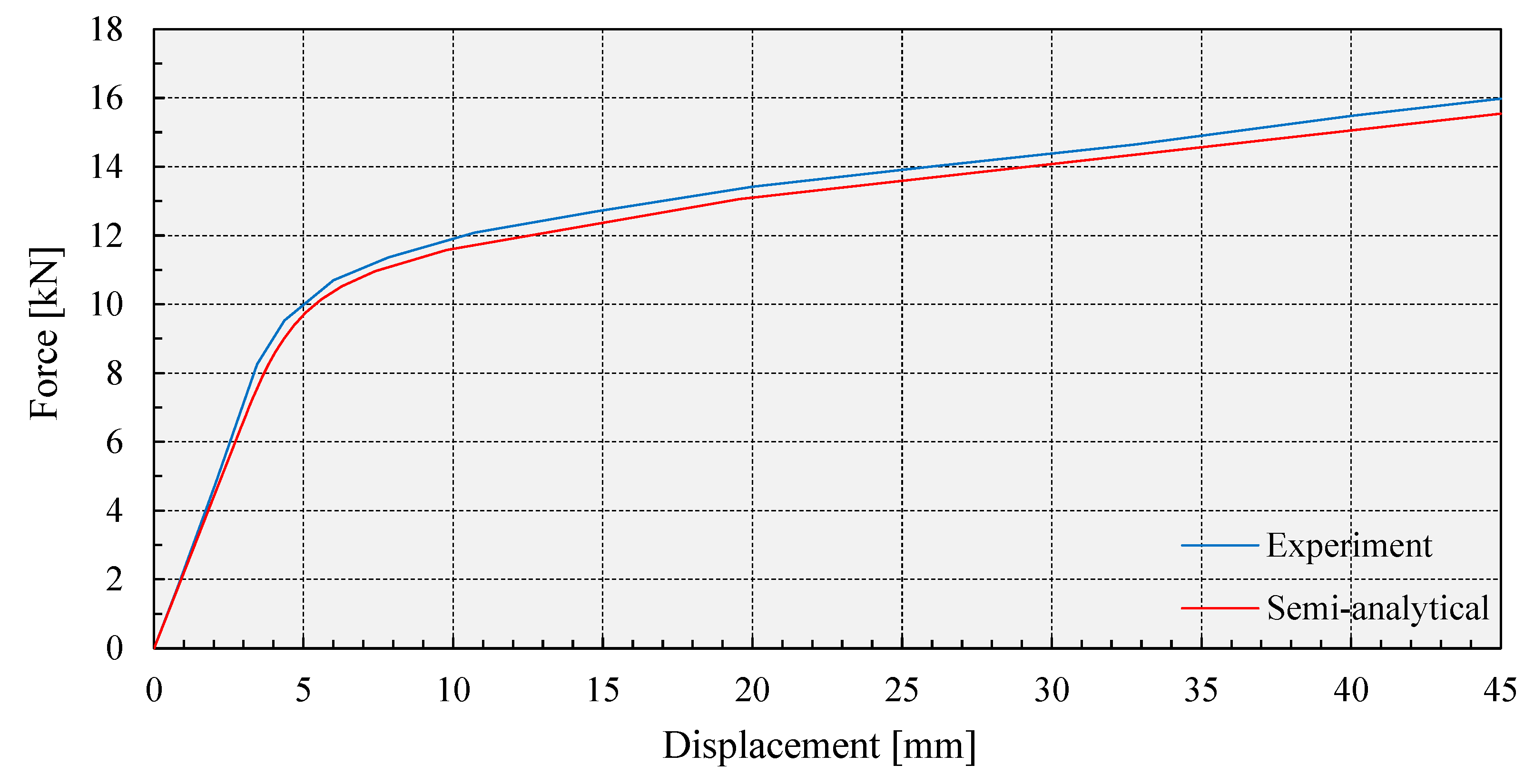
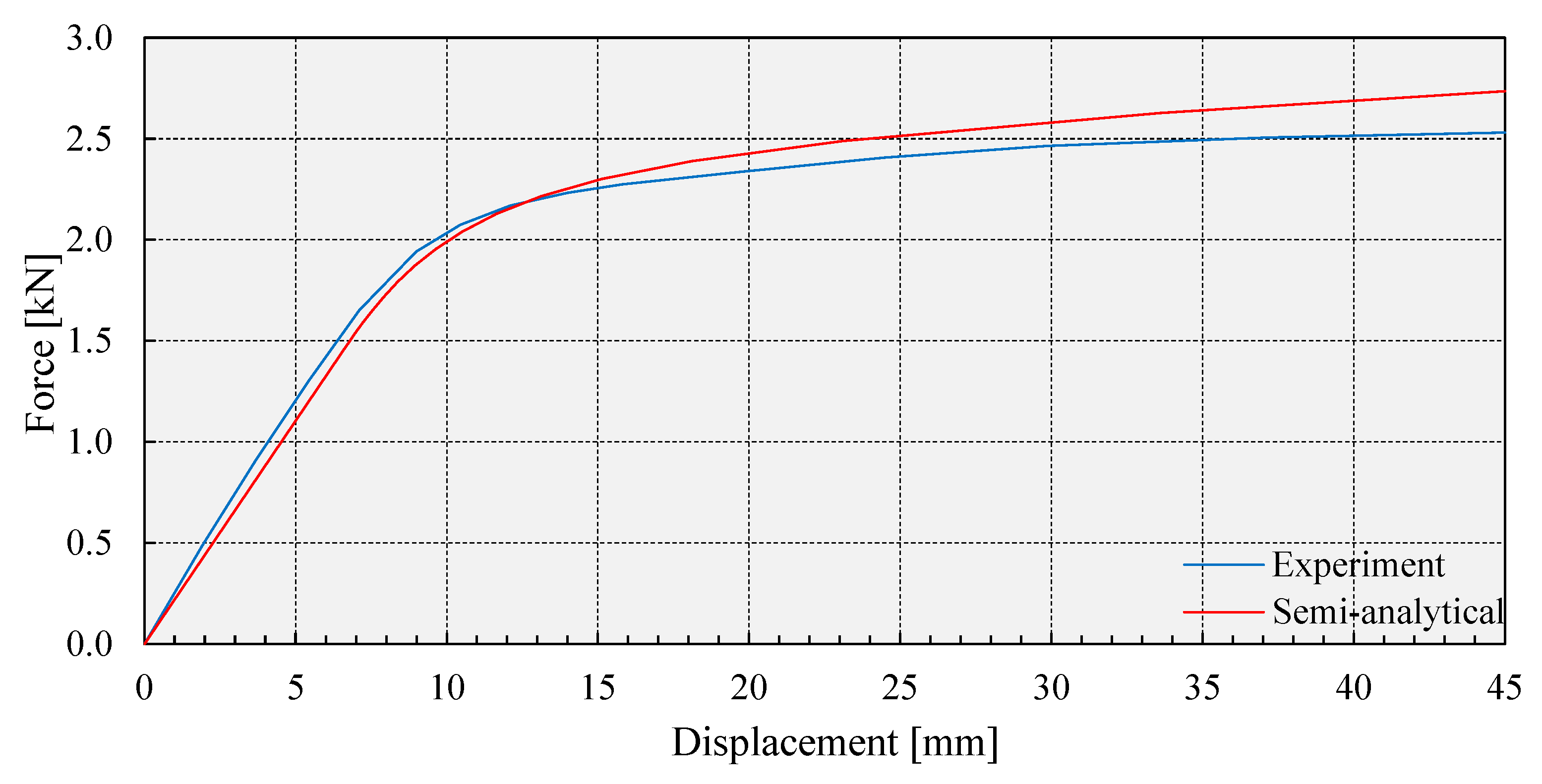
3.1. Validation of the Proposed Semi-Analytical Solution Regarding Experimental Results
3.2. Validation of the Proposed Semi-Analytical Solution Regarding Numerical Results
4. Conclusions
- it is confirmed that the Bernoulli–Euler formula grants satisfying results for the analysis of the deflection of the cantilever beam in the elastic regime, while in the plastic regime the differential equation of beam bending has no solution in the closed form; therefore, the problem needs to be solved via incremental analysis;
- the results of the proposed semi-analytical solution are in good correlation with the experimental results of two models of vertical components of a seismic energy dissipation device;
- the results of the proposed semi-analytical solution are in good correlation with the numerical results of several cantilever beam models, where the cross-section diameter, beam span, and mechanical characteristics of material vary;
- taking into account the above-mentioned conclusions, the proposed semi-analytical solution is considered as validated;
- the proposed semi-analytical solution is a simple method for application in practical engineering.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Symbols
| E | Young’s modulus |
| Et | tangent modulus |
| F | force |
| Fy | yield force |
| Iz | cross-section moment of inertia related to the z axis |
| Ke | elastic stiffness |
| Ky | post-yield stiffness |
| M | bending moment |
| Mmax | maximum bending moment |
| My | yield bending moment |
| b | width of elemental integration area |
| d | diameter of circular cross-section |
| dc | diameter of circular cross-section at the clamped end of the cantilever beam |
| df | diameter of circular cross-section at the free end of the cantilever beam |
| fu | ultimate stress of material |
| fy | yield stress of material |
| h | length of the cantilever beam |
| r | radius of circular cross-section |
| v | deflection of the cantilever beam |
| vel | deflection of the cantilever beam in the elastic regime |
| vlel | deflection of the elastic region from the fixed support to the boundary between the elastic and the plastic region of the cantilever beam |
| vrel | deflection of the elastic region from the boundary between the elastic and the plastic region to the free end of the cantilever beam |
| vpl | deflection of the cantilever beam in the plastic regime |
| xe | position of the critical cross-section |
| xp | boundary between the elastic and the plastic region of the cantilever beam |
| xpl | boundary between the elastic and the plastic region from the fixed support to critical cross-section of the cantilever beam |
| xpr | boundary between the elastic and the plastic region from the critical cross-section to the free end of the cantilever beam |
| ymax | maximum distance of fibers from neutral axis |
| ε | strain |
| εpl | plastic strain |
| εy | yield strain |
| η | cross-section part from neutral axis in elastic regime |
| θ | angle in polar coordinate system |
| θe | angle defining elastic part of the cross-section |
| κ | curvature |
| ν | Poisson’s ratio |
| π | Archimedes’ constant |
| σ | normal stress |
| σmax | maximum normal stress |
| φ | slope of the cantilever beam |
| φel | slope of the cantilever beam in the elastic regime |
| φlel | slope of the elastic region from the fixed support to the boundary between the elastic and the plastic region of the cantilever beam |
| φdel | slope of the elastic region from the boundary between the elastic and the plastic region to the free end of the cantilever beam |
| φpl | slope of the cantilever beam in the plastic regime |
References
- Levien, R. The Elastica: A Mathematical History; Technical Report No. UCB/EECS-2008-103, Electrical Engineering and Computer Sciences; University of California: Berkeley, CA, USA, 2008. [Google Scholar]
- Bisshopp, K.E.; Drucker, D.C. Large deflection of cantilever beams. Q. Appl. Math. 1945, 3, 272–275. [Google Scholar] [CrossRef]
- Banerjee, A.; Bhattacharya, B.; Mallik, A.K. Large deflection of cantilever beams with geometric non-linearity: Analytical and numerical approaches. Int. J. Non Linear Mech. 2008, 43, 366–376. [Google Scholar] [CrossRef]
- Lee, S.Y.; Kuo, Y.H. Deflection and Stability of Elastically Restrained Nonuniform Beam. J. Eng. Mech. 1991, 117, 674–692. [Google Scholar] [CrossRef]
- Dong, L.; Alotaibi, A.; Mohiuddine, S.A.; Atluri, S.N. Computational Methods in Engineering: A Variety of Primal & Mixed Methods, with Global & Local Interpolations, for Well-Posed or Ill-Posed BCs. Comput. Model. Eng. Sci. 2014, 99, 1–85. [Google Scholar] [CrossRef]
- Lee, J.K.; Lee, B.K. Elastica of Non-Prismatic and Nonlinear Elastic Cantilever Beams unde Combined Loading. Appl. Sci. 2019, 9, 877. [Google Scholar] [CrossRef]
- Latalski, J.; Zulli, D. Generalized Beam Theory for Thin-Walled Beams with Curvilinear Open Cross-Sections. Appl. Sci. 2020, 10, 7802. [Google Scholar] [CrossRef]
- Yu, T.X.; Johnson, W. The plastica: The large elastic-plastic deflection of a strut. Int. J. Non-Linear Mech. 1982, 17, 195–209. [Google Scholar] [CrossRef]
- Xiaoqiang, W.; Tongxi, Y. The Complete Process of Large Elastic-Plastic Deflection of a Cantilever. Acta Mech. Sin. 1986, 2, 333–341. [Google Scholar] [CrossRef]
- Gere, J.; Timoshenko, S. Mechanics of Materials, 4th ed.; PWS: Boston, MA, USA, 1997. [Google Scholar]
- Štok, B.; Halilovič, M. Analytical solutions in elasto-plastic bending of beams with rectangular cross section. Appl. Math. Model. 2009, 33, 1749–1760. [Google Scholar] [CrossRef]
- Ghosh, S.; Roy, D. Numerical-Analytic Form of the Adomian Decomposition Method for Two-Point Boundary Value Problems in Nonlinear Mechanics. J. Eng. Mech. 2007, 133, 1124–1133. [Google Scholar] [CrossRef]
- Huang, X.; Wang, B.; Lu, G.; Yu, T.X. Large deflection of elastoplastic, non-linear strain-hardening cantilevers. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2001, 216, 433–446. [Google Scholar] [CrossRef]
- Liu, J.H.; Atkins, A.G.; Pretlove, A.J. The effect of inclined loads on the large deflection behaviour of elastoplastic work-hardening straight and pre-bent cantilevers. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1995, 209, 87–96. [Google Scholar] [CrossRef]
- Solano-Carrillo, E. Semi-exact solutions for large deflections of cantilever beams of non-linear elastic behaviour. Int. J. Non-Linear Mech. 2009, 44, 253–256. [Google Scholar] [CrossRef]
- Kang, Y.-A.; Li, X.-F. Bending of functionally graded cantilever beam with power-law non-linearity subjected to an end force. Int. J. Non-Linear Mech. 2009, 44, 696–703. [Google Scholar] [CrossRef]
- Pascon, J.P. Numerical analysis of highly deformable elastoplastic beams. Lat. Am. J. Solids Struct. 2015, 12, 1595–1615. [Google Scholar] [CrossRef]
- Pandit, D.; Thomas, N.; Patel, B.; Srinivasan, S.M. Finite Deflection of Slender Cantilever with Predefined Load Application Locus using an Incremental Formulation. Comput. Mater. Contin. 2015, 45, 127–144. [Google Scholar] [CrossRef]
- Pandit, D.; Srinivasan, S.M. Numerical analysis of large elasto-plastic deflection of constant curvature beam under follower load. Int. J. Non-Linear Mech. 2016, 84, 46–55. [Google Scholar] [CrossRef]
- Romano, F.; Ganduscio, S.; Zingone, G. Elastoplastic Deflection for Prismatic and Nonprismatic Beams. J. Eng. Mech. 1993, 119, 1117–1135. [Google Scholar] [CrossRef]
- Milligan, R. Moment-Strain Relationships in Elastic-Plastic Bending of Beams; Report No. ARLCB-TR-81025, US Army Armament Research & Development Command; Large Caliber Wapon Systems Laboratory: New York, NY, USA, 1981. [Google Scholar]
- Daunys, M.; Rimovskis, S. Analysis of circular cross-section element, loaded by static and cyclic elastic-plastic pure bending. Int. J. Fatigue 2006, 28, 211–222. [Google Scholar] [CrossRef]
- Rimovskis, S.; Sabaliauskas, A. Analysis of Rectangular and Circular Cross-section Power Hardening Elements Under Pure Bending. Int. J. Mater. Eng. 2012, 2, 84–89. [Google Scholar] [CrossRef][Green Version]
- Abdallah, S.; Rees, D. Elastic-plastic bending analysis of a circular cross section. In Proceedings of the 7th International Colloquium on Performance, Protection and Strengthening of Structures under Extreme Loading and Events, Whisler, BC, Canada, 16–17 September 2019. [Google Scholar]
- Gohari, S.; Sharifi, S.; Vrcelj, Z. New explicit solution for static shape control of smart laminated cantilever piezo-composite-hzbrid plates/beams under thermo-electro-mechanical loads using piezoelectric actuators. Compos. Struct. 2016, 145, 89–112. [Google Scholar] [CrossRef]
- Zlatkov, D.; Projektinženjering Tim Ltd. Seismo-Safe 2G3-GOSEB Buidling System, Project ID 476, Report No. 1–4; Innovation Fund of the Republic of Serbia: Niš, Serbia, 2015. [Google Scholar]
- Ristić, D.; Ristić, J.; Zlatkov, D. Adaptivni Sistem za Seizmičku Zaštitu Objekata Zgrada od Dejstva Jakih Zemljotresa Putem Konstruktivno Obezbeđene Globalne Optimizacije Seizmo-Energetskog Balansa. Republic of Serbia Patent 57554, 31 October 2018. [Google Scholar]
- MacCullough, G.H. An Experimental and Analytical Investigation of Creep in Bending. J. Appl. Mech. 1933, 1, 55–60. [Google Scholar] [CrossRef]
- Syed, J.I.A.; Kumar, P.; Jayaram, V. Creep of Metallic Materials in Bending. JOM 2019, 71, 3565–3583. [Google Scholar] [CrossRef]
- Hamming, R.W. Numerical Methods for Scientists and Engineers, 2nd ed.; Dover Publications Inc.: New York, NY, USA, 1973. [Google Scholar]
- EN ISO 683-1:2018; Heat-Treatable Steels, Alloy Steels and Free-Cutting Steels—Part 1: Non-Alloy Steels for Quenching and Tempering. European Committee for Stadardization: Brussels, Belgium, 2018.
- Abaqus Theory Manual; Dassault Systèmes Simulia Corporation: Providence, RI, USA, 2014.
- Zienkiewicz, O.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Basis and Fundamentals, 6th ed.; Elsevier: Holland, The Netherlands, 2005; pp. 398–404. [Google Scholar]
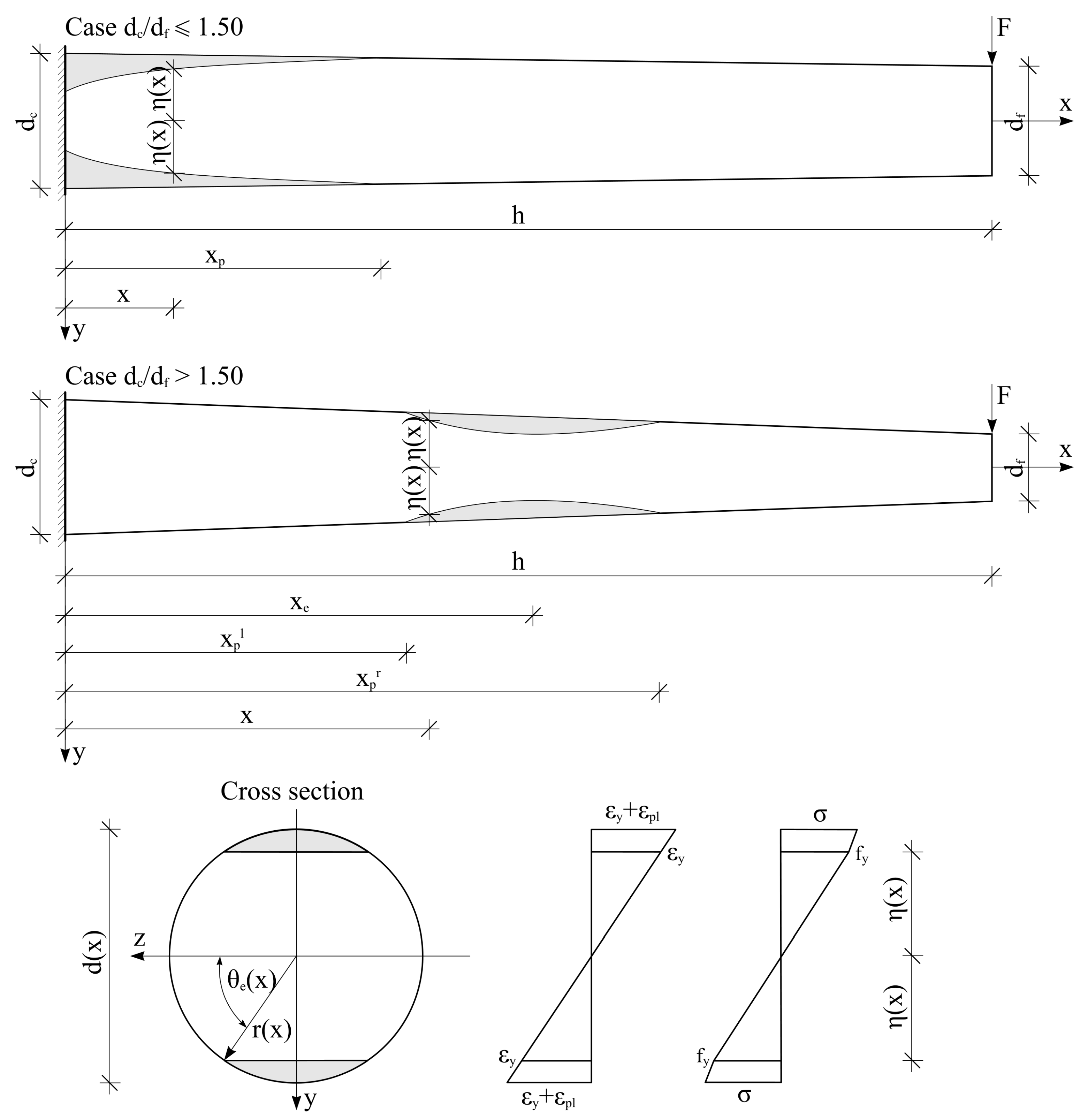


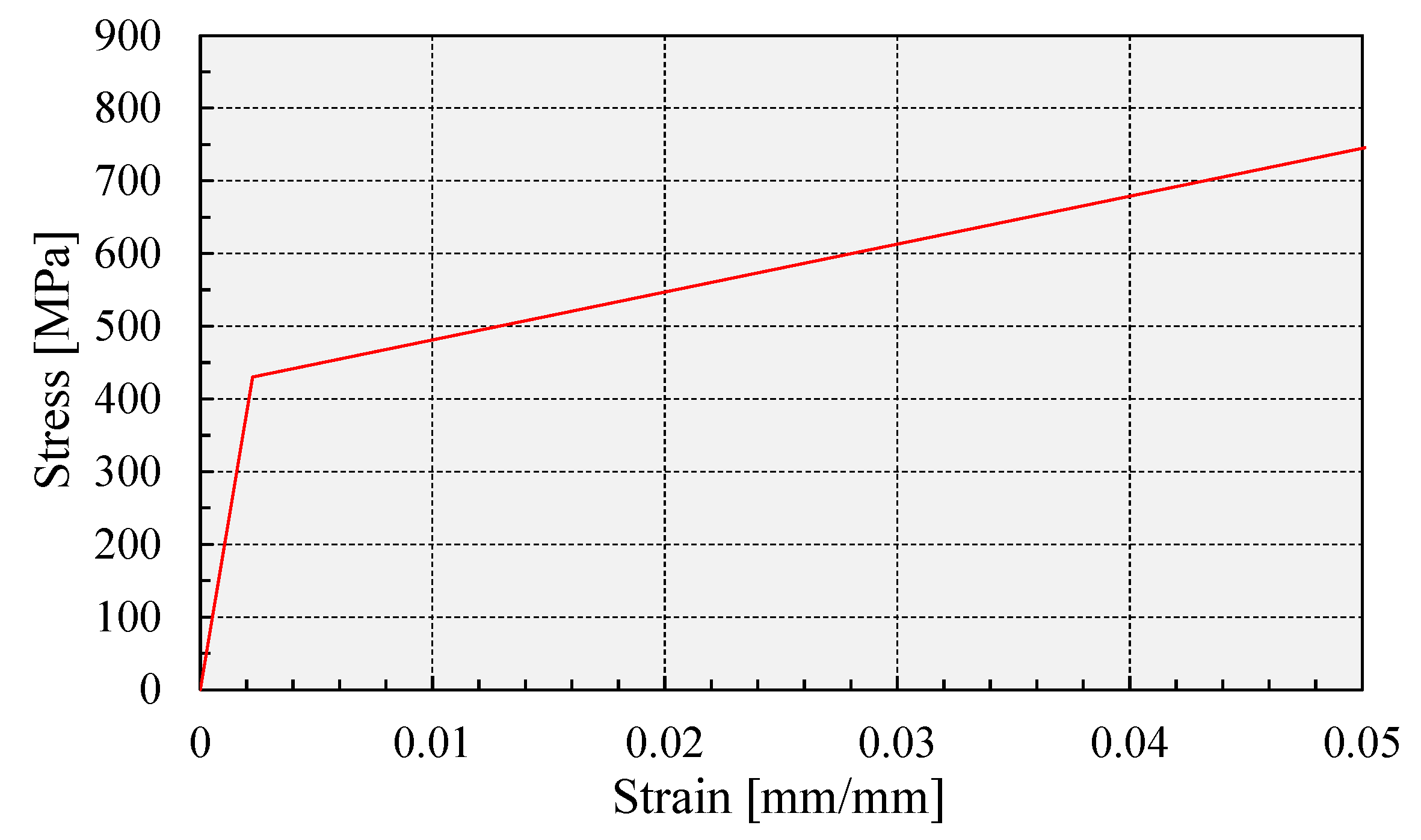

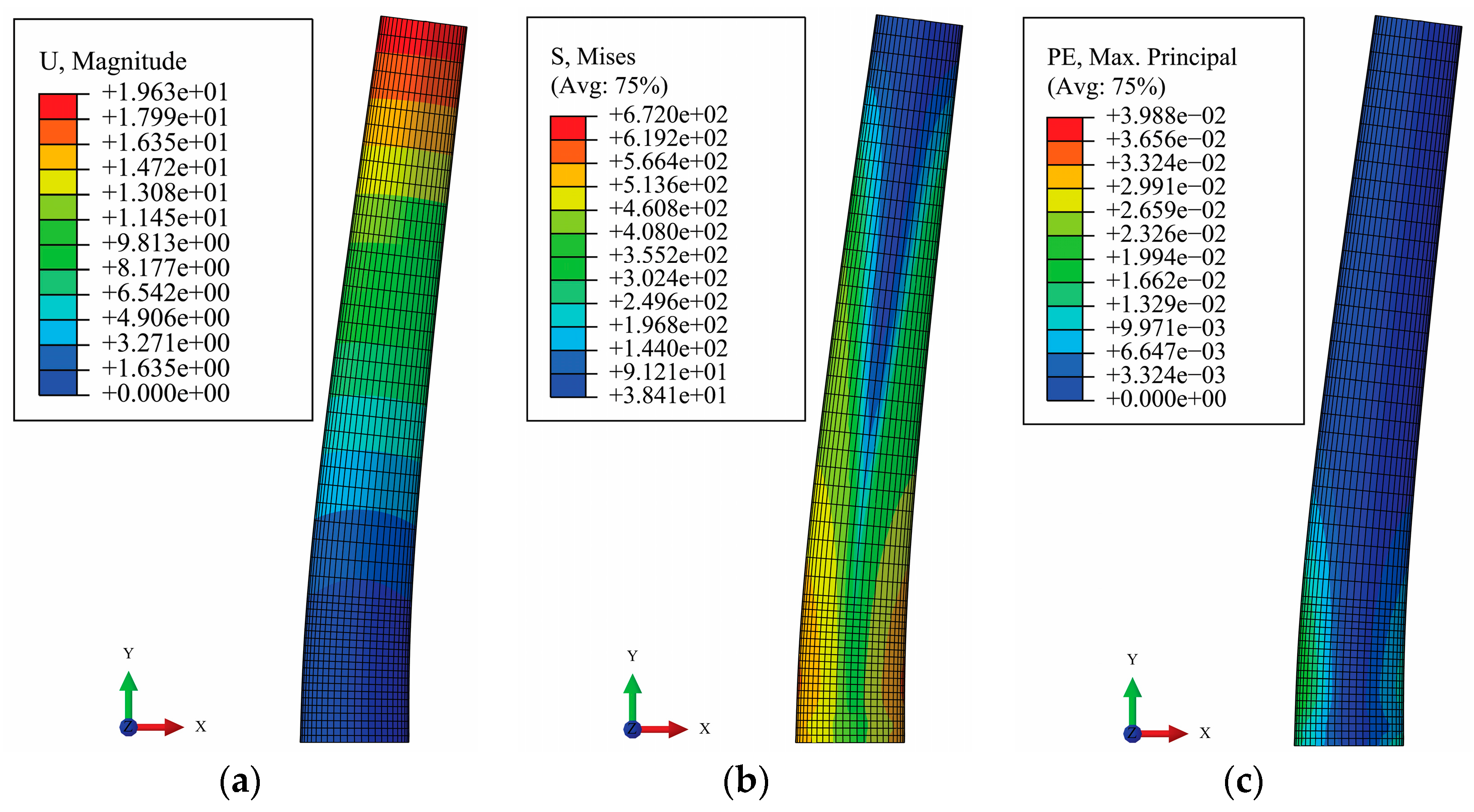

| dc/df | ≤1.50 | >1.50 | |
|---|---|---|---|
| Cross-Section at Clamped End | Plastified | Elastic | Plastified |
| Boundary conditions | |||
| Continuity conditions | |||
| Model | VC1 | VC2 | ||||
|---|---|---|---|---|---|---|
| Results | Semi-Analytical | Experiment | Difference [%] | Semi-Analytical | Experiment | Difference [%] |
| Force [kN] at displacement of 45 mm | 15.55 | 15.98 | 2.77 | 2.74 | 2.53 | 8.30 |
| Elastic stiffness Ke [kN/mm] | 2.18117 | 2.36899 | 8.61 | 0.21651 | 0.23122 | 6.79 |
| Post-yield stiffness Ky [kN/mm] | 0.11570 | 0.11616 | 0.40 | 0.01205 | 0.01183 | 1.86 |
| Model | dc [mm] | df [mm] | h [mm] | E [GPa] | Et [MPa] | fy [MPa] |
|---|---|---|---|---|---|---|
| C1 | 30 | 24 | 200 | 190 | 6600 | 430 |
| C2 | 30 | 24 | 500 | |||
| C3 | 30 | 15 | 200 | |||
| C4 | 30 | 15 | 500 | |||
| C5 | 30 | 24 | 200 | 2000 | 350 | |
| C6 | 30 | 24 | 500 |
| Case | Number of Divisions of the Circle | Size of the FE * along the Cantilever Beam | Number of Nodes per FE * | Displacement of the Free End | Normalized Mises Stress Error Indicator |
|---|---|---|---|---|---|
| I | 48 | 5 mm (2 mm) | 8 | 6.43 mm | 0.97% |
| II | 48 | 5 mm (2 mm) | 20 | 6.27 mm | 2.19% |
| III | 64 | 3.5 mm (1.5 mm) | 8 | 6.38 mm | 0.94% |
| IV | 64 | 3.5 mm (1.5 mm) | 20 | 6.23 mm | 1.29% |
| Model | Number of Elements | Number of Nodes | Number of Degrees of Freedom |
|---|---|---|---|
| C1 | 9984 | 11,501 | 34,503 |
| C2 | 24,960 | 28,427 | 85,281 |
| C3 | 8112 | 9593 | 28,779 |
| C4 | 20,280 | 23,711 | 71,133 |
| C5 | 9984 | 11,501 | 34,503 |
| C6 | 24,960 | 28,427 | 85,281 |
| Model | Force at Limit Displacement [kN] | Elastic Stiffness Ke [kN/mm] | Post-Yield Stiffness Ky [kN/mm] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Semi Analytical | FEM | Difference [%] | Semi Analytical | FEM | Difference [%] | Semi Analytical | FEM | Difference [%] | |
| C1 | 13.19 | 13.43 | 1.82 | 2.26342 | 2.17084 | 4.26 | 0.11095 | 0.12025 | 8.38 |
| C2 | 4.44 | 4.50 | 1.35 | 0.14486 | 0.14338 | 1.03 | 0.01120 | 0.01221 | 9.02 |
| C3 | 9.83 | 9.93 | 1.02 | 1.40488 | 1.33542 | 5.20 | 0.06873 | 0.07465 | 8.61 |
| C4 | 3.40 | 3.47 | 2.06 | 0.09059 | 0.08884 | 1.97 | 0.00906 | 0.00973 | 7.40 |
| C5 | 9.21 | 9.66 | 4.89 | 2.24202 | 2.15625 | 3.98 | 0.04155 | 0.04522 | 8.83 |
| C6 | 3.41 | 3.50 | 2.64 | 0.14427 | 0.14341 | 0.60 | 0.00532 | 0.00582 | 9.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zorić, A.; Trajković-Milenković, M.; Zlatkov, D.; Vacev, T. Semi-Analytical Solution for Elastoplastic Deflection of Non-Prismatic Cantilever Beams with Circular Cross-Section. Appl. Sci. 2022, 12, 5439. https://doi.org/10.3390/app12115439
Zorić A, Trajković-Milenković M, Zlatkov D, Vacev T. Semi-Analytical Solution for Elastoplastic Deflection of Non-Prismatic Cantilever Beams with Circular Cross-Section. Applied Sciences. 2022; 12(11):5439. https://doi.org/10.3390/app12115439
Chicago/Turabian StyleZorić, Andrija, Marina Trajković-Milenković, Dragan Zlatkov, and Todor Vacev. 2022. "Semi-Analytical Solution for Elastoplastic Deflection of Non-Prismatic Cantilever Beams with Circular Cross-Section" Applied Sciences 12, no. 11: 5439. https://doi.org/10.3390/app12115439
APA StyleZorić, A., Trajković-Milenković, M., Zlatkov, D., & Vacev, T. (2022). Semi-Analytical Solution for Elastoplastic Deflection of Non-Prismatic Cantilever Beams with Circular Cross-Section. Applied Sciences, 12(11), 5439. https://doi.org/10.3390/app12115439








