Kalman Filter Implementation of Subglottal Impedance-Based Inverse Filtering to Estimate Glottal Airflow during Phonation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Standard IBIF Implementation
2.2. Formulation of IBIF Model Based on a Kalman Filter
| Algorithm 1 Kalman Filter Algorithm. |
|
2.3. Glottal Flow Model for the Kalman Filter
Rosenberg Model for the Glottal Pulse
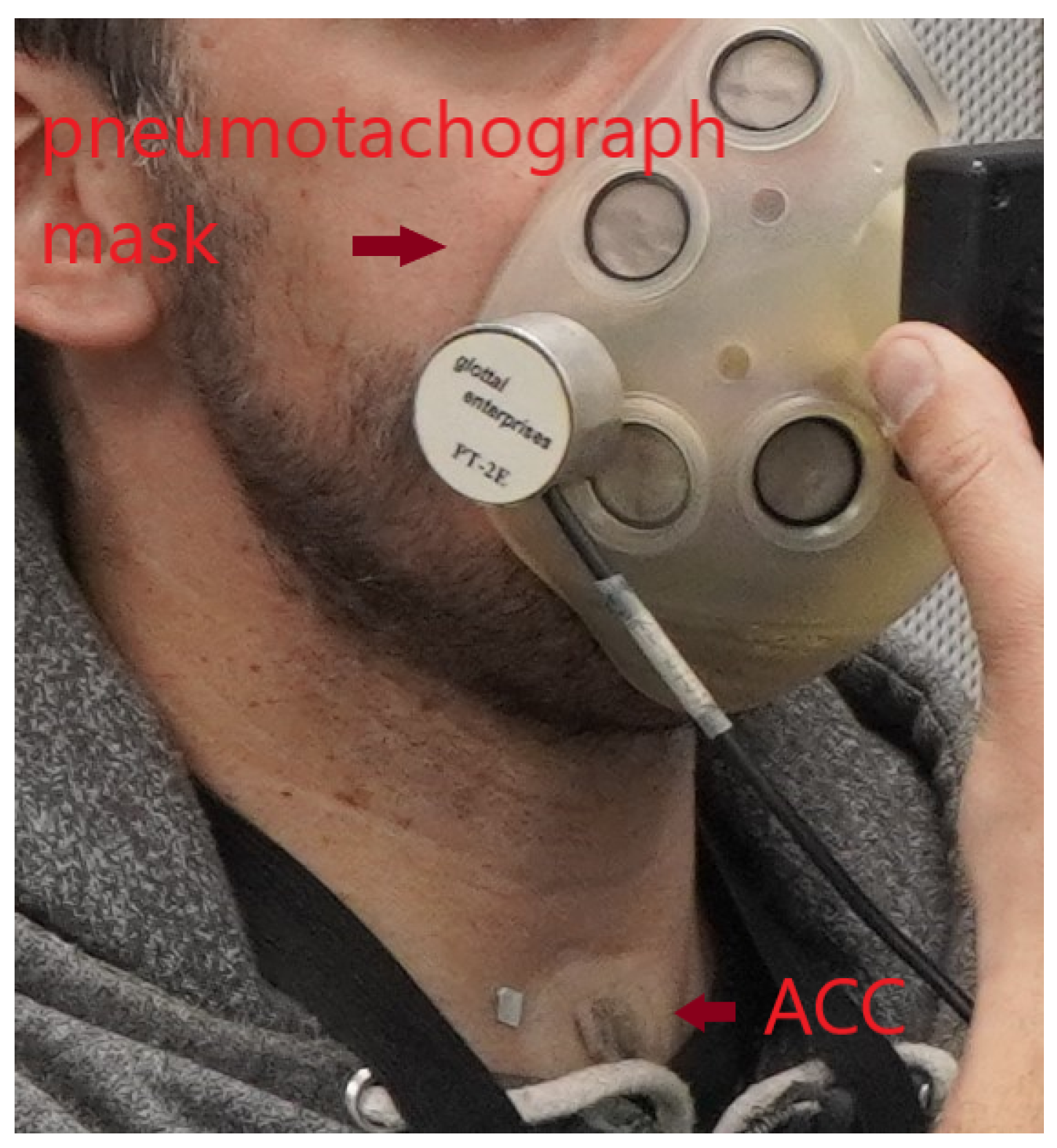
3. Experimental Setup
3.1. IBIF Calibration
3.2. Ground Truth GVV
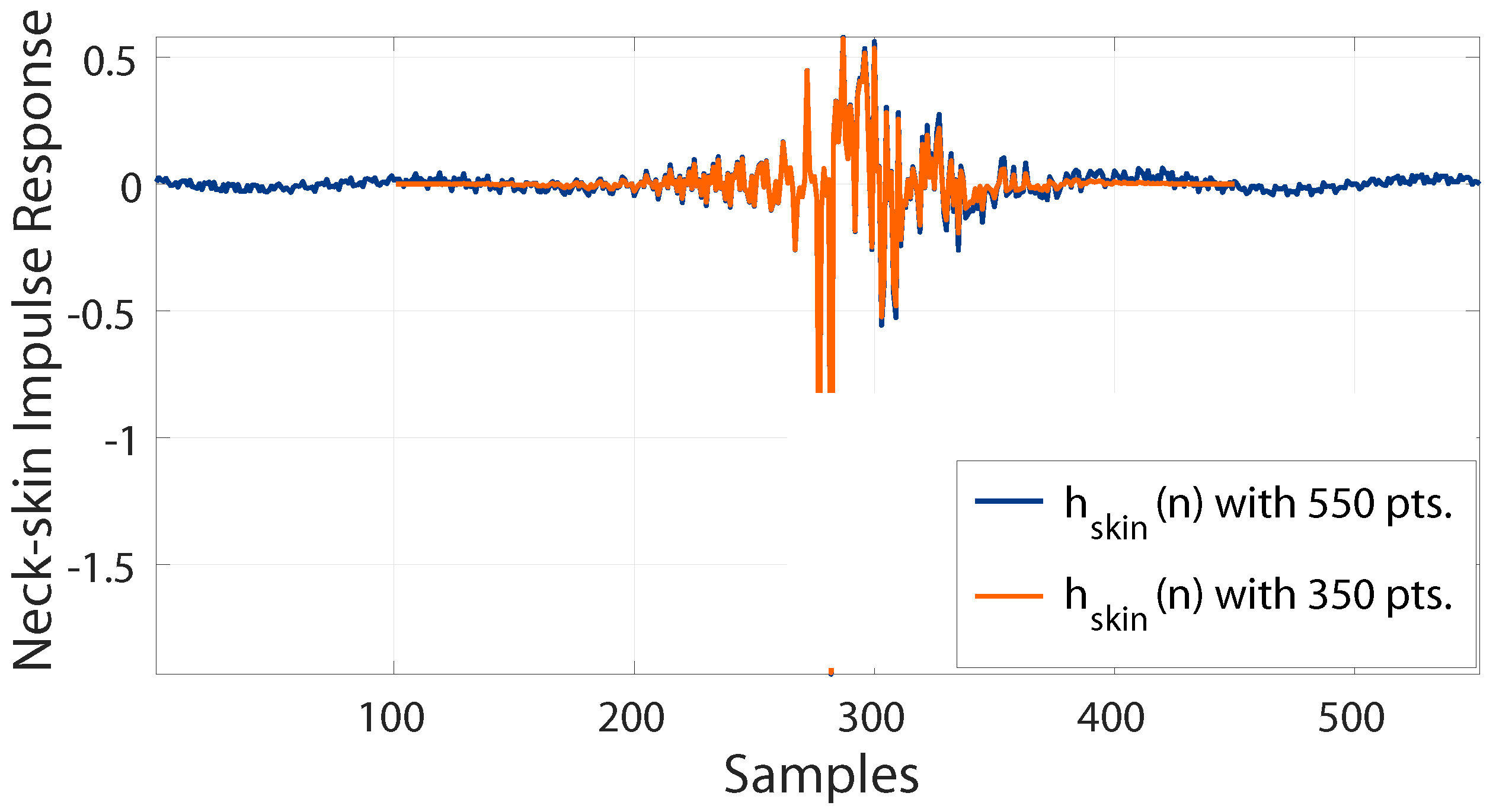
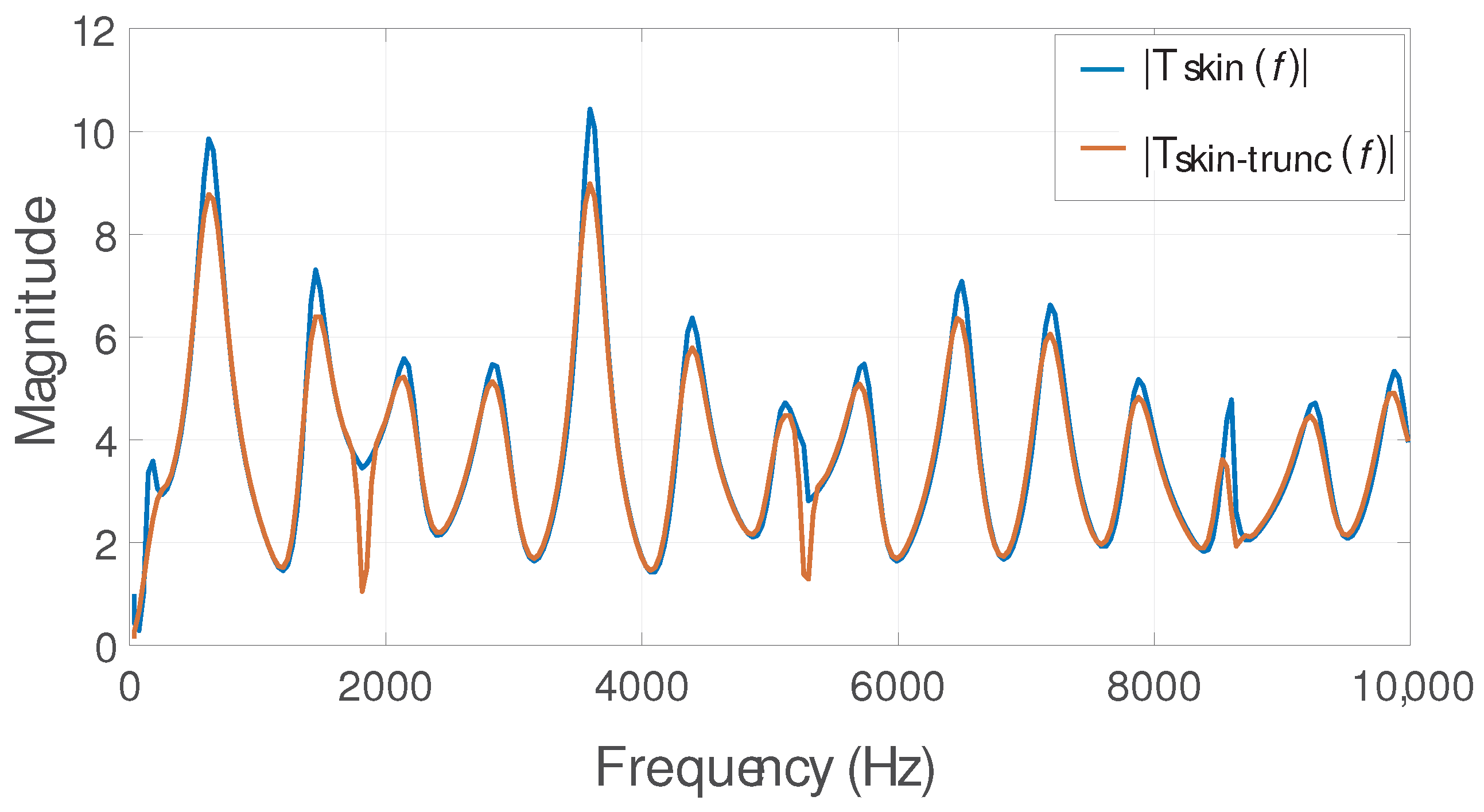
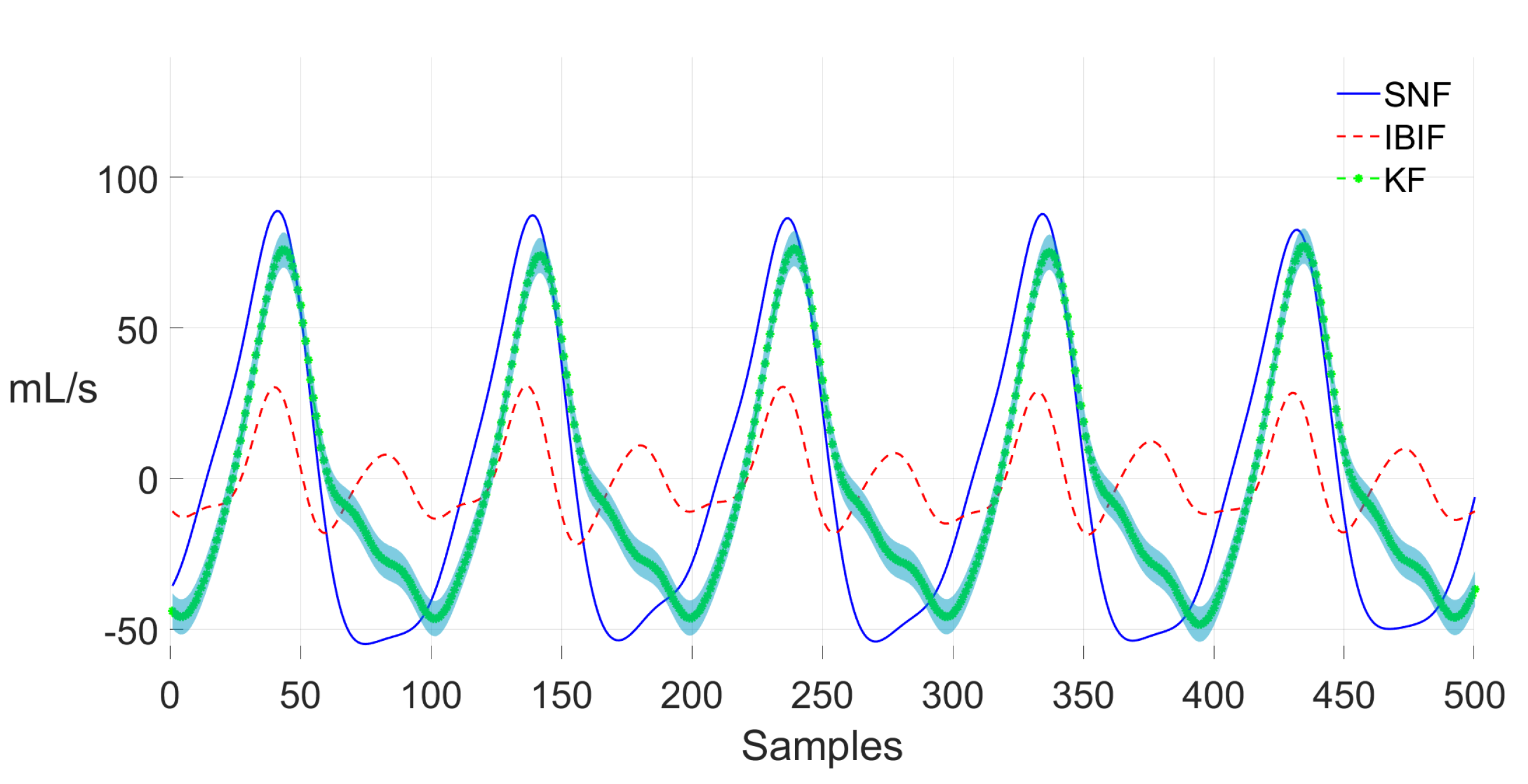
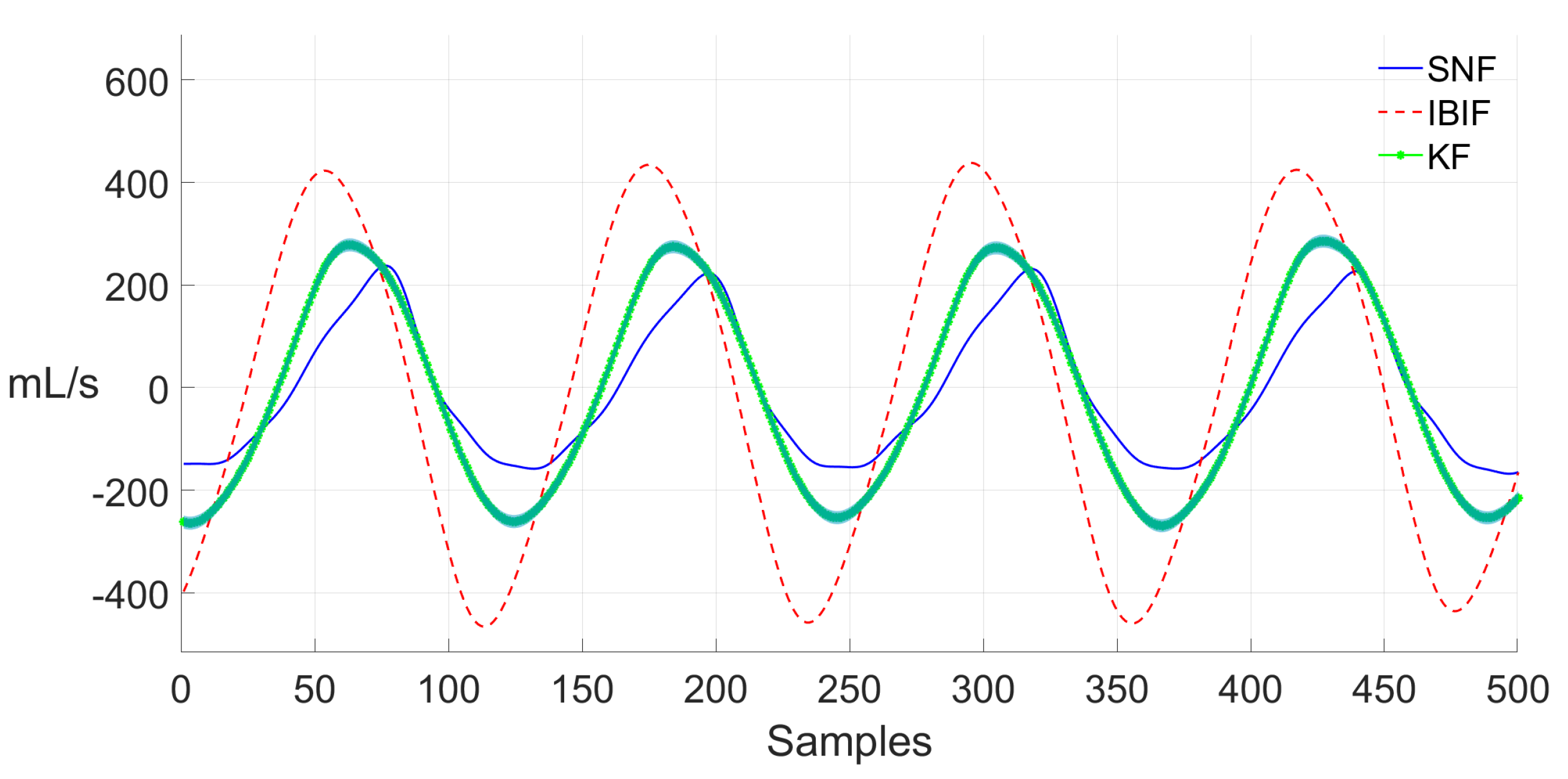
3.3. Reducing Order of the IBIF Filter
3.4. Aerodynamic Features
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACC | Neck Surface Accelerometer |
| ACFL | AC Flow, i.e., Unsteady Flow Peak-to-Peak Amplitude |
| ANOVA | Analysis of Variance |
| FFT | Fast Fourier Transform |
| FIR | Finite Impulse Response |
| Fundamental Frequency | |
| H1-H2 | Difference of Magnitudes between First and Second Harmonic |
| KF | Kalman Filter |
| MA | Moving Average |
| MFDR | Maximum Flow Declination Rate |
| NAQ | Normalized Amplitude Quotient |
| OVV | Oral Volume Velocity |
| PVH | Phonotraumatic Vocal Hyperfunction |
| RMSE | Root-Mean-Square-Error |
| SNF | Single Notch Filter |
| VH | Vocal Hyperfunction |
References
- Bhattacharyya, N. The prevalence of voice problems among adults in the United States. Laryngoscope 2014, 124, 2359–2362. [Google Scholar] [CrossRef] [PubMed]
- Coyle, S.M.; Weinrich, B.D.; Stemple, J.C. Shifts in Relative Prevalence of Laryngeal Pathology in a Treatment-Seeking Population. J. Voice 2001, 15, 424–440. [Google Scholar] [CrossRef]
- Herrington-Hall, B.; Lee, L.; Stemple, J.C.; Niemi, K.R.; McHone, M.M. Description of laryngeal pathologies by age, sex, and occupation in a treatment-seeking sample. J. Speech Hear. Disord. 1988, 53, 57–64. [Google Scholar] [CrossRef] [PubMed]
- Kridgen, S.; Hillman, R.E.; Stadelman-Cohen, T.; Zeitels, S.; Burns, J.A.; Hron, T.; Krusemark, C.; Muise, J.; Stan, J.H.V. Patient-Reported Factors Associated with the Onset of Hyperfunctional Voice Disorders. Ann. Otol. Rhinol. Laryngol. 2021, 130, 389–394. [Google Scholar] [CrossRef]
- Hillman, R.E.; Holmberg, E.B.; Perkell, J.S.; Walsh, M.; Vaughan, C. Objective Assessment of Vocal Hyperfunction: An Experimental Framework and Initial Results. J. Speech Lang. Hear. Res. 1989, 32, 373–392. [Google Scholar] [CrossRef]
- Mehta, D.D.; Hillman, R.E. Use of Aerodynamic Measures in Clinical Voice Assessment. Voice Voice Disord. 2007, 17, 14–18. [Google Scholar] [CrossRef]
- Hillman, R.E.; Stepp, C.E.; Stan, J.H.V.; Zañartu, M.; Mehta, D.D. An Updated Theoretical Framework for Vocal Hyperfunction. Am. J. Speech-Lang. Pathol. 2020, 29, 2254–2260. [Google Scholar] [CrossRef]
- Franco, R.A.; Andrus, J.G. Common Diagnoses and Treatments in Professional Voice Users. Otolaryngol. Clin. N. Am. 2007, 40, 1025–1061. [Google Scholar] [CrossRef] [PubMed]
- Espinoza, V.M.; Zañartu, M.; Van Stan, J.H.; Mehta, D.D.; Hillman, R.E. Glottal Aerodynamic Measures in Women With Phonotraumatic and Nonphonotraumatic Vocal Hyperfunction. J. Speech Lang. Hear. Res. 2017, 60, 2159–2169. [Google Scholar] [CrossRef]
- Holmberg, E.B.; Doyle, P.; Perkell, J.S.; Hammarberg, B.; Hillman, R.E. Aerodynamic and Acoustic Voice Measurements of Patients with Vocal Nodules: Variation in Baseline and Changes Across Voice Therapy. J. Voice 2003, 17, 269–282. [Google Scholar] [CrossRef]
- Lien, Y.A.S.; Calabrese, C.R.; Michener, C.M.; Murray, E.H.; Van Stan, J.H.; Mehta, D.D.; Hillman, R.E.; Noordzij, J.P.; Stepp, C.E. Voice Relative Fundamental Frequency Via Neck-Skin Acceleration in Individuals With Voice Disorders. J. Speech Lang. Hear. Res. 2015, 58, 1482–1487. [Google Scholar] [CrossRef] [Green Version]
- Mehta, D.D.; Espinoza, V.M.; Van Stan, J.H.; Zañartu, M.; Hillman, R.E. The difference between first and second harmonic amplitudes correlates between glottal airflow and neck-surface accelerometer signals during phonation. J. Acoust. Soc. Am. 2019, 145, 386–392. [Google Scholar] [CrossRef] [PubMed]
- Narasimhan, S.V.; Vishal, K. Spectral Measures of Hoarseness in Persons with Hyperfunctional Voice Disorder. J. Voice 2016, 31, 57–61. [Google Scholar]
- Mehta, D.D.; Van Stan, J.H.; Zañartu, M.; Ghassemi, M.; Guttag, J.V.; Espinoza, V.M.; Cortés, J.P.; Cheyne, H.A.I.; Hillman, R.E. Using ambulatory voice monitoring to investigate common voice disorders: Research update. Front. Bioeng. Biotechnol. 2015, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghassemi, M.; Van Stan, J.; Mehta, D.; Zañartu, M.; Cheyne, H.; Hillman, R.; Guttag, J. Learning to Detect Vocal Hyperfunction From Ambulatory Neck-Surface Acceleration Features: Initial Results for Vocal Fold Nodules. IEEE Trans. Biomed. Eng. 2014, 61, 1668–1675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cortés, J.P.; Espinoza, V.M.; Ghassemi, M.; Mehta, D.D.; Van Stan, J.H.; Hillman, R.E.; Guttag, J.V.; Zañartu, M. Ambulatory assessment of phonotraumatic vocal hyperfunction using glottal airflow measures estimated from neck-surface acceleration. PLoS ONE 2018, 13, e0209017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Stan, J.H.; Mehta, D.D.; Ortiz, A.J.; Burns, J.A.; Toles, L.E.; Marks, K.L.; Vangel, M.; Hron, T.; Zeitels, S.; Hillman, R.E. Differences in Weeklong Ambulatory Vocal Behavior Between Female Patients With Phonotraumatic Lesions and Matched Controls. J. Speech Lang. Hear. Res. 2020, 63, 372–384. [Google Scholar] [CrossRef] [PubMed]
- Van Stan, J.H.; Mehta, D.D.; Ortiz, A.J.; Burns, J.A.; Marks, K.L.; Toles, L.E.; Stadelman-Cohen, T.; Krusemark, C.; Muise, J.; Hron, T.; et al. Changes in a Daily Phonotrauma Index After Laryngeal Surgery and Voice Therapy: Implications for the Role of Daily Voice Use in the Etiology and Pathophysiology of Phonotraumatic Vocal Hyperfunction. J. Speech Lang. Hear. Res. 2020, 63, 3934–3944. [Google Scholar] [CrossRef] [PubMed]
- Van Stan, J.H.; Ortiz, A.J.; Cortes, J.P.; Marks, K.L.; Toles, L.E.; Mehta, D.D.; Burns, J.A.; Hron, T.; Stadelman-Cohen, T.; Krusemark, C.; et al. Differences in Daily Voice Use Measures Between Female Patients With Nonphonotraumatic Vocal Hyperfunction and Matched Controls. JSLHR Res. Artic. J. Speech Lang. Hear. Res. 2021, 64, 1457–1470. [Google Scholar] [CrossRef]
- Toles, L.E.; Ortiz, A.J.; Marks, K.L.; Burns, J.A.; Hron, T.; Stan, J.H.V.; Mehta, D.D.; Hillman, R.E. Differences Between Female Singers With Phonotrauma and Vocally Healthy Matched Controls in Singing and Speaking Voice Use During 1 Week of Ambulatory Monitoring. Am. J. Speech-Lang. Pathol. 2021, 30, 199–209. [Google Scholar] [CrossRef]
- Manfredi, C.; Bruschi, T.; Dallai, A.; Ferri, A.; Tortoli, P.; Calisti, M. Voice quality monitoring: A portable device prototype. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; pp. 997–1000. [Google Scholar]
- Smith, N.R.; Rivera, L.A.; Dietrich, M.; Shyu, C.R.; Page, M.P.; DeSouza, G.N. Detection of Simulated Vocal Dysfunctions Using Complex sEMG Patterns. IEEE J. Biomed. Health Inform. 2016, 20, 787–801. [Google Scholar] [CrossRef] [PubMed]
- Cheyne, H.A.; Hanson, H.M.; Genereux, R.P.; Stevens, K.N.; Hillman, R.H. Development and Testing of a Portable Vocal Accumulator. J. Speech Hear. Res. 2003, 46, 1457–1467. [Google Scholar] [CrossRef]
- Carroll, T.; Nix, J.; Hunter, E.; Titze, I.; Abaza, M. Objective Measurement of Vocal Fatigue in Classically Trained Singers: A Pilot Study of Vocal Dosimetry Data. Otolaryngol.-Head Neck Surg. 2006, 135, 595–602. [Google Scholar] [CrossRef] [PubMed]
- Titze, I.R.; Hunter, E.J.; Svec, J.G. Voicing and Silence Periods in Daily and Weekly Vocalizations of Teachers. J. Acoust. Soc. Am. 2007, 121, 469–478. [Google Scholar] [CrossRef]
- Mehta, D.D.; Zañartu, M.; Feng, S.W.; Cheyne, H.A.; Hillman, R.E. Mobile Voice Health Monitoring Using a Wearable Accelerometer Sensor and a Smartphone Platform. IEEE Trans. Biomed. Eng. 2012, 59, 3090–3096. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Stan, J.H.; Mehta, D.D.; Zeitels, S.M.; Burns, J.A.; Barbu, A.M.; Hillman, R.E. Average Ambulatory Measures of Sound Pressure Level, Fundamental Frequency, and Vocal Dose Do Not Differ Between Adult Females With Phonotraumatic Lesions and Matched Control Subjects. Ann. Otol. Rhinol. Laryngol. 2015, 124, 864–874. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bottalico, P.; Graetzer, S.; Astolfi, A.; Hunter, E. Silence and Voicing Accumulations in Italian Primary School Teachers With and Without Voice Disorders. J. Voice 2017, 31, 260.e11–260.e20. [Google Scholar] [CrossRef] [Green Version]
- Espinoza, V.M.; Mehta, D.D.; Stan, J.H.V.; Hillman, R.E.; Zañartu, M. Glottal aerodynamics estimated from neck-surface vibration in women with phonotraumatic and nonphonotraumatic vocal hyperfunction. J. Speech Lang. Hear. Res. 2020, 63, 2861–2869. [Google Scholar] [CrossRef] [PubMed]
- Zañartu, M.; Galindo, G.; Erath, B.D.; Peterson, S.D.; Wodicka, G.R.; Hillman, R.E. Modeling the effects of a posterior glottal opening on vocal fold dynamics with implications for vocal hyperfunction. J. Acoust. Soc. Am. 2014, 136, 3262–3271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Galindo, G.E.; Peterson, S.D.; Erath, B.D.; Castro, C.; Hillman, R.E.; Zañartu, M. Modeling the pathophysiology of phonotraumatic vocal hyperfunction with a triangular glottal model of the vocal folds. J. Speech Lang. Hear. Res. 2017, 60, 2452–2471. [Google Scholar] [CrossRef]
- Rothenberg, M. A new inverse filtering technique for deriving the glottal air flow waveform during voicing. J. Acoust. Soc. Am. 1973, 53, 1632–1645. [Google Scholar] [CrossRef] [Green Version]
- Zañartu, M.; Ho, J.C.; Mehta, D.D.; Hillman, R.E.; Wodicka, G.R. Subglottal Impedance-Based Inverse Filtering of Voiced Sounds Using Neck Surface Acceleration. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 1929–1939. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Espinoza, V. Stationary and Dynamic Aerodynamic Assessment of Vocal Hyperfunction Using Enhanced Supraglottal and Subglottal Inverse Filtering Methods. Ph.D. Thesis, Universidad Técnica Federico Santa María, Valparaíso, Chile, 2018. [Google Scholar]
- Perkell, J.S.; Holmberg, E.B.; Hillman, R.E. A system for signal processing and data extraction from aerodynamic, acoustic, and electroglottographic signals in the study of voice production. J. Acoust. Soc. Am. 1991, 89, 1777–1781. [Google Scholar] [CrossRef] [PubMed]
- Perkell, J.S.; Hillman, R.E.; Holmberg, E.B. Group differences in measures of voice production and revised values of maximum airflow declination rate. J. Acoust. Soc. Am. 1994, 96, 695–698. [Google Scholar] [CrossRef]
- Stevens, K.N. Acoustic Phonetics; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Ho, J.C.; Zañartu, M.; Wodicka, G.R. An Anatomically Based, Time-Domain Acoustic Model of the Subglottal System for Speech Production. J. Acoust. Soc. Am. 2011, 129, 1531–1547. [Google Scholar] [CrossRef]
- Zañartu, M.; Espinoza, V.M.; Mehta, D.D.; Van Stan, J.H.; Cheyne, H.A., III; Ghassemi, M.; Guttag, J.V.; Hillman, R.E. Toward An Objective Aerodynamic Assessment Of Vocal Hyperfunction Using A Voice Health Monitor. In Proceedings of the 8th International Workshop on Models and Analysis of Vocal Emissions for Biomedical Applications, MAVEBA 2013, Firenze, Italy, 16–18 December 2013. [Google Scholar]
- Zañartu, M. Acoustic Coupling in Phonation and Its Effect on Inverse Filtering of Oral Airflow and Neck Surface Acceleration. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2010. [Google Scholar]
- Espinoza, V.M.; Mehta, D.D.; Van Stan, J.H.; Hillman, R.E.; Zañartu, M. Uncertainty of glottal airflow estimation during continuous speech using impedance-based inverse filtering of the neck-surface acceleration signal. Proc. Acoust. Soc. Am. 2017, 141, 3579. [Google Scholar] [CrossRef] [Green Version]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Benesty, J.; Sondhi, M.; Huang, Y. Springer Handbook of Speech Processing; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Grewal, M.; Andrews, A. Kalman Filtering: Theory and Practice Using MATLAB; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Fant, G. The Acoustic Theory of Speech Production; Mouton & Co. N.V. Publishers: The Hague, The Netherlands, 1960. [Google Scholar]
- Rosenberg, A.E. Effect of Glottal Pulse Shape on the Quality of Natural Vowels. J. Acoust. Soc. Am. 1971, 49, 583–590. [Google Scholar] [CrossRef] [PubMed]
- Fant, G.; Liljencrants, J.; Lin, Q. A Four-Parameter Model of Glottal Flow. STL-QPSR 1985, 4, 1–3. [Google Scholar]
- Alzamendi, G.; Schlotthauer, G. Modeling and joint estimation of glottal source and vocal tract filter by state-space methods. Biomed. Signal Process. Control. 2017, 37, 5–15. [Google Scholar] [CrossRef]
- Doval, B.; D’Alessandro, C.; Henrich Bernardoni, N. The spectrum of glottal flow models. Acta Acust. United Acust. 2006, 92, 1026–1046. [Google Scholar]
- Quatieri, T.F. Discrete-Time Speech Signal Processing: Principles and Practice; Pearson Education Inc.: London, UK, 2012. [Google Scholar]
- Rabiner, L.R.; Schafer, R.W. Theory and Applications of Digital Speech Processing; Prentice Hall: Hoboken, NJ, USA, 2010. [Google Scholar]
- Kunduk, M.; Mcwhorter, A. True vocal fold nodules: The role of differential diagnosis. Curr. Opin. Otolaryngol. Head Neck Surg. 2009, 17, 449–452. [Google Scholar] [CrossRef]
- Alisa, Z.; Danielle, B.; Khosla, S.M.; Thomas, M.; Lucian, S. Gender and age in benign vocal fold lesions. Laryngoscope 2015, 125, 191–196. [Google Scholar]
- Mehta, D.D.; Hillman, R.E. Voice Assessment: Updates on Perceptual, Acoustic, Aerodynamic, and Endoscopic Imaging Methods. Curr. Opin. Otolaryngol. Head Neck Surg. 2008, 16, 211–215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hogikyan, N.D.; Sethuraman, G. Validation of an instrument to measure voice-related quality of life (V-RQOL). J. Voice 1999, 13, 557–569. [Google Scholar] [CrossRef]
- Kempster, G.B.; Gerratt, B.R.; Abbott, K.V.; Barkmeier-Kraemer, J.; Hillman, R.E. Consensus Auditory-Perceptual Evaluation of Voice: Development of a Standardized Clinical Protocol. Am. J. Speech-Languaje Pathol. 2009, 18, 124–132. [Google Scholar] [CrossRef] [Green Version]
- Fairbanks, G. Voice and Articulation Drillbook; Harper and Row: New York, NY, USA, 1960. [Google Scholar]
- Holmberg, E.B.; Hillman, R.E.; Perkell, J.S. Glottal Air-Flow and Transglottal Air-Pressure Measurements for Male and Female Speakers in Soft, Normal, and Loud Voice. J. Acoust. Soc. Am. 1988, 84, 511–529. [Google Scholar] [CrossRef]
- Alku, P.; Bäckström, T.; Vilkman, E. Normalized amplitude quotient for parametrization of the glottal flow. J. Acoust. Soc. Am. 2002, 112, 701–710. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manriquez, R.; Espinoza, V.; Castro, C.; Cortes, J.; Zañartu, M. Parameter analysis and uncertainties of impedance-based inverse filtering from neck surface acceleration. In Proceedings of the 14th International Conference on Advances in Quantitative Laryngology, Voice and Speech Research (AQL 2021), Online, 7–10 June 2021. [Google Scholar]
- May, N.A.; Scherer, R.C. Airflow Error Measurement Due to Pneumotachograph Mask Rim Leaks. J. Voice 2018, 32, 403–419. [Google Scholar] [CrossRef]
- Drugman, T.; Alku, P.; Alwan, A.; Yegnanarayana, Y. Glottal source processing: From analysis to applications. Comput. Speech Lang. 2014, 28, 1117–1138. [Google Scholar] [CrossRef] [Green Version]
- Alku, P.; Magi, C.; Yrttiaho, S.; Bäckström, T.; Story, B. Closed phase covariance analysis based on constrained linear prediction for glottal inverse filtering. J. Acoust. Soc. Am. 2009, 125, 3289–3305. [Google Scholar] [CrossRef]
- Cortés, J.; Alzamendi, G.; Weinstein, A.; Yuz, J.; Espinoza, V.; Mehta, D.; Van Stan, J.; Hillman, R.; Zañartu, M. Uncertainty of ambulatory airflow estimates and its effect on the classification of phonotraumatic vocal hyperfunction. In Proceedings of the 13th International Conference on Advances in Quantitative Laryngology, Voice and Speech Research (AQL 2019), Montreal, QC, Canada, 2–4 June 2019. [Google Scholar]
- Ibarra, E.J.; Parra, J.A.; Alzamendi, G.A.; Cortés, J.P.; Espinoza, V.M.; Mehta, D.D.; Hillman, R.E.; Zañartu, M. Estimation of Subglottal Pressure, Vocal Fold Collision Pressure, and Intrinsic Laryngeal Muscle Activation From Neck-Surface Vibration Using a Neural Network Framework and a Voice Production Model. Front. Physiol. 2021, 12, 1419. [Google Scholar] [CrossRef]
- Morales, A.; Yuz, J.I. Reduced order modeling for glottal airflow estimation using a Kalman smoother. In Proceedings of the 2021 IEEE International Conference on Automation/XXIV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Valparaíso, Chile, 22–26 March 2021; pp. 1–6. [Google Scholar]
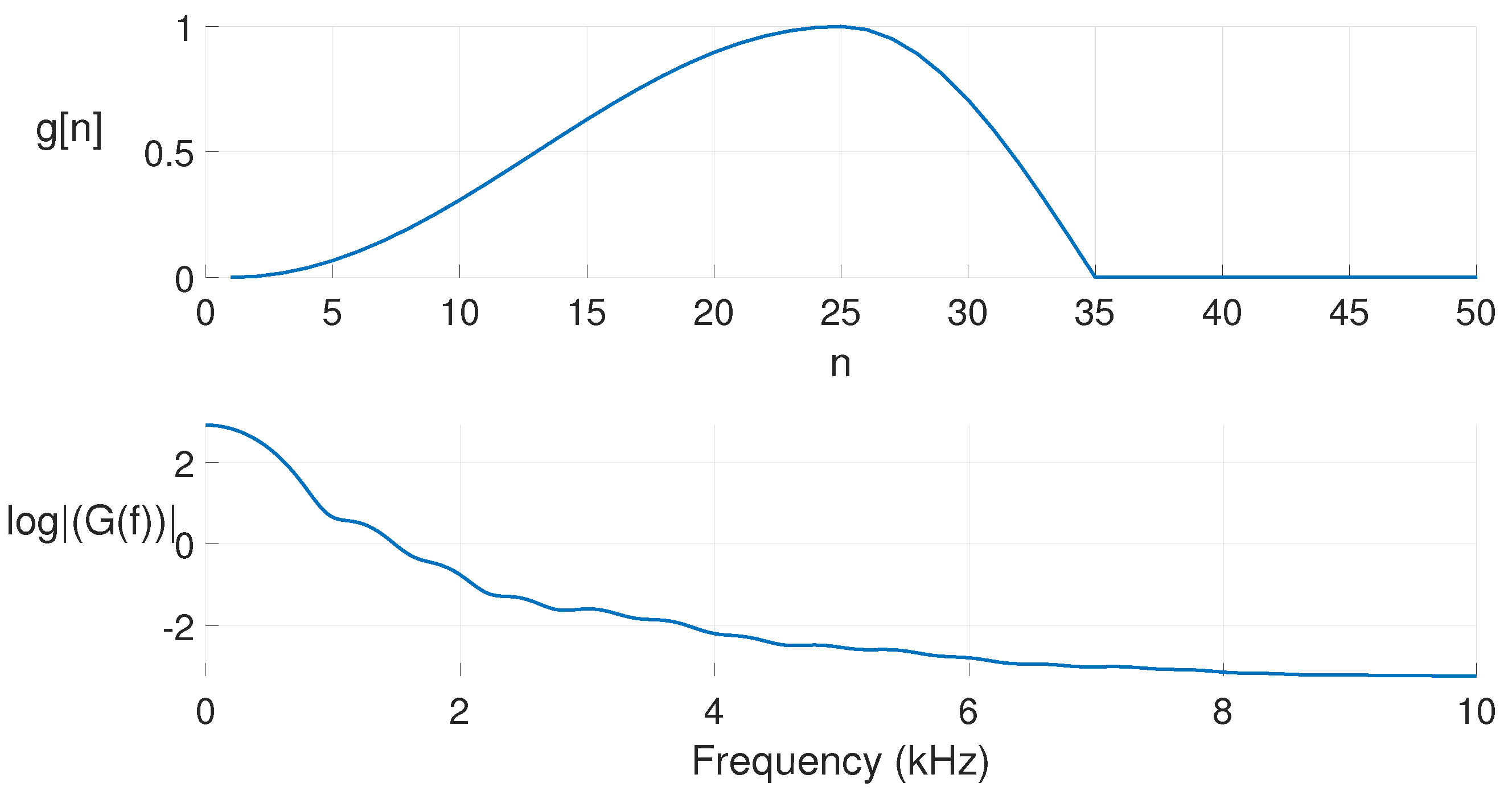
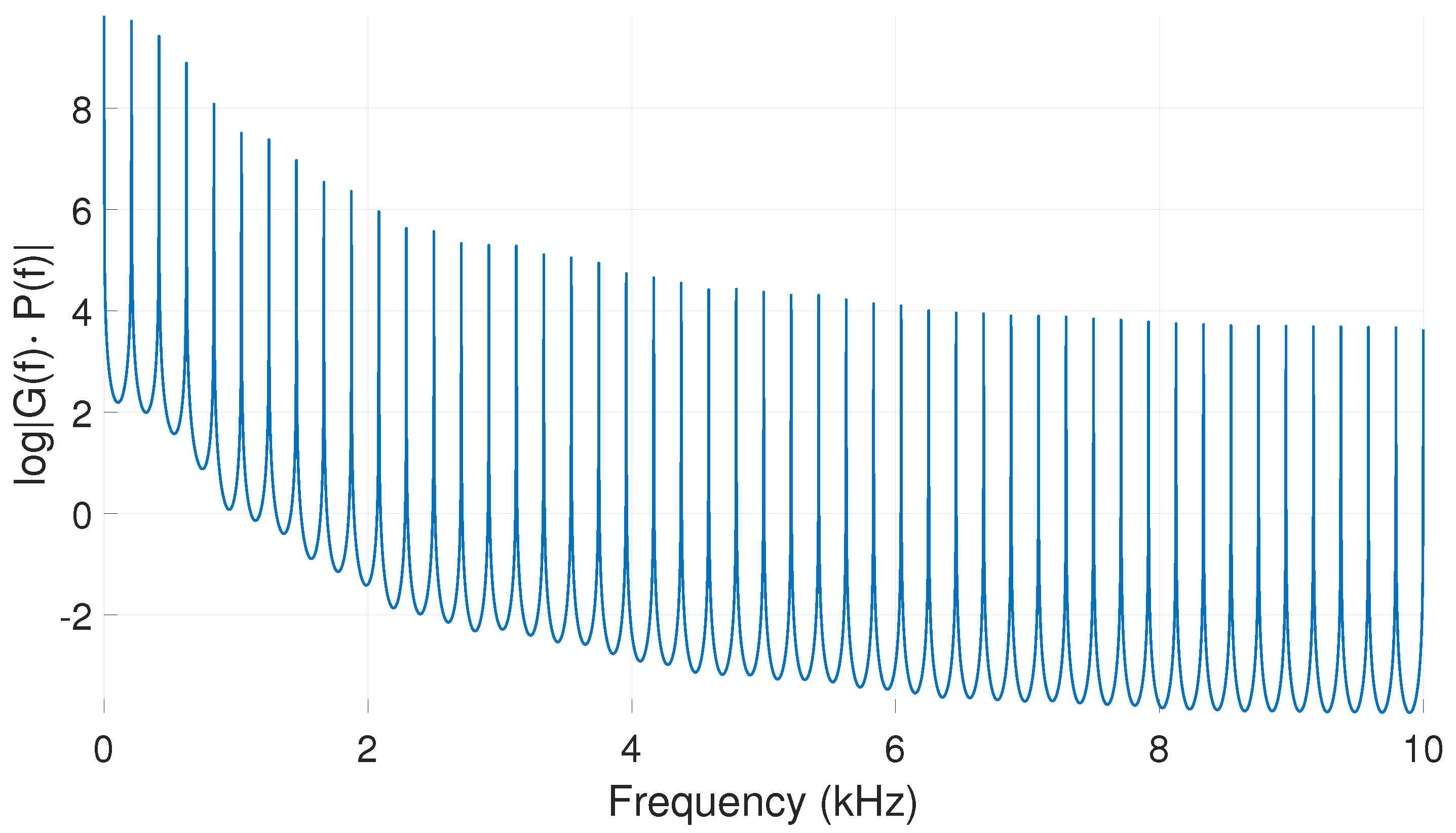
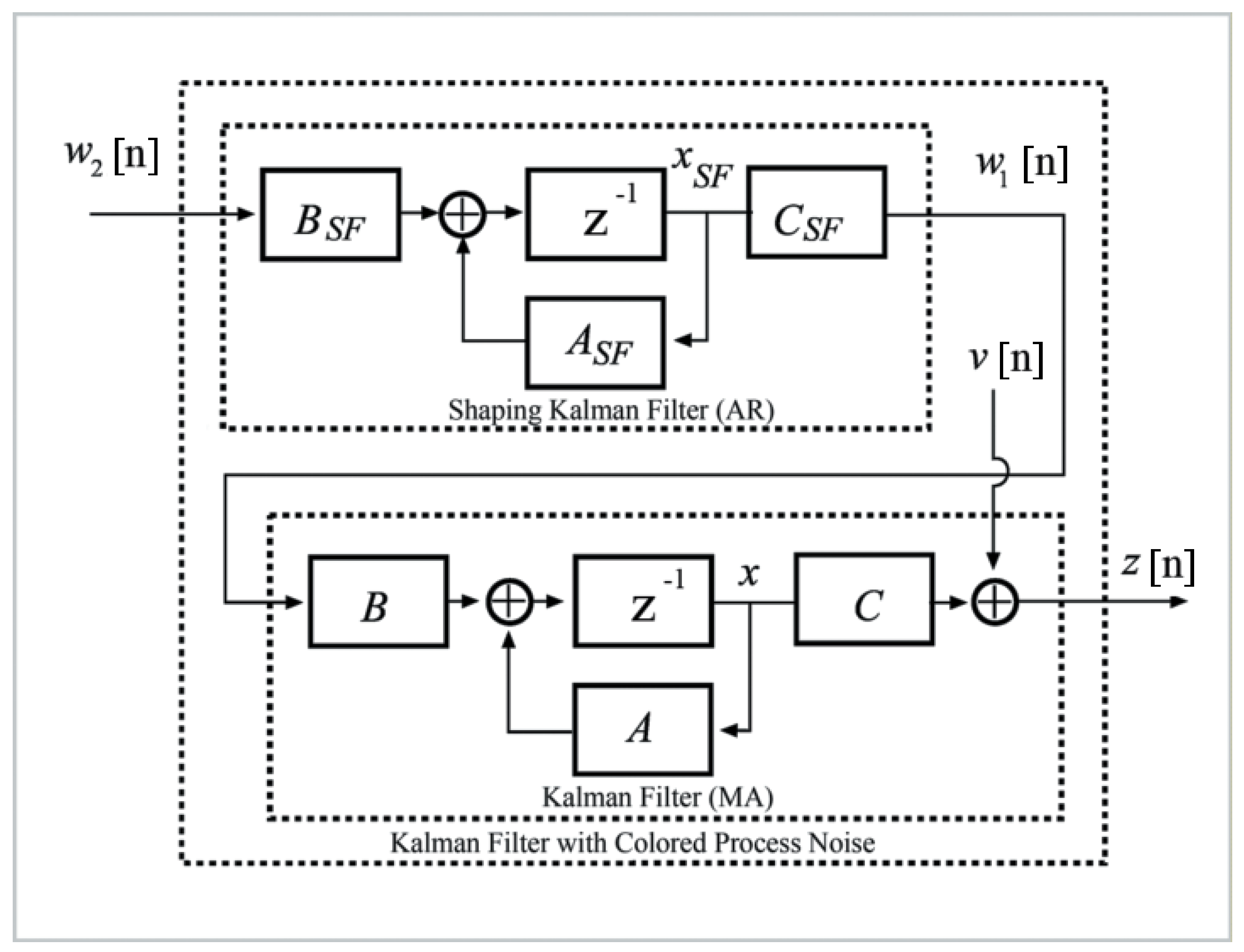
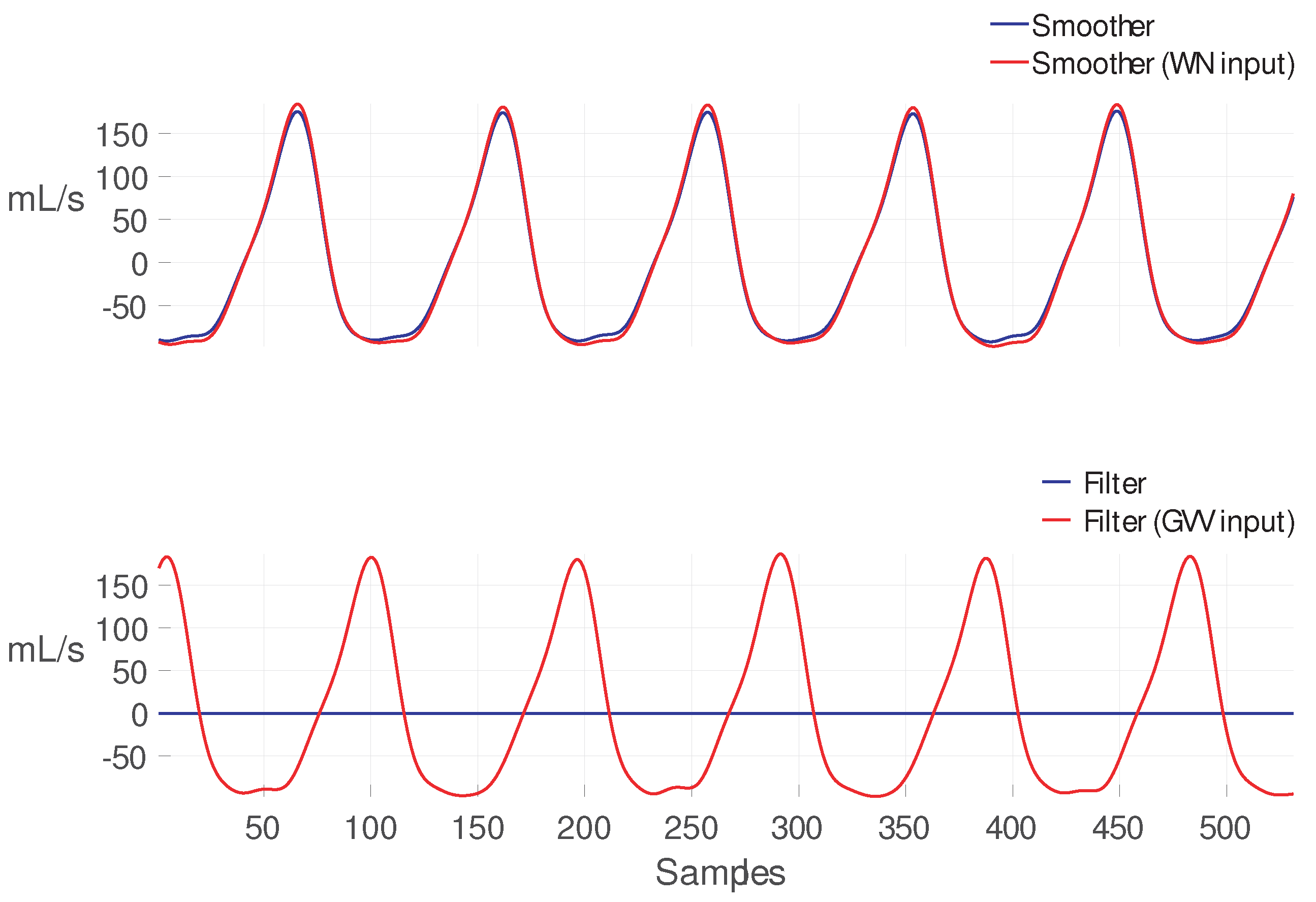
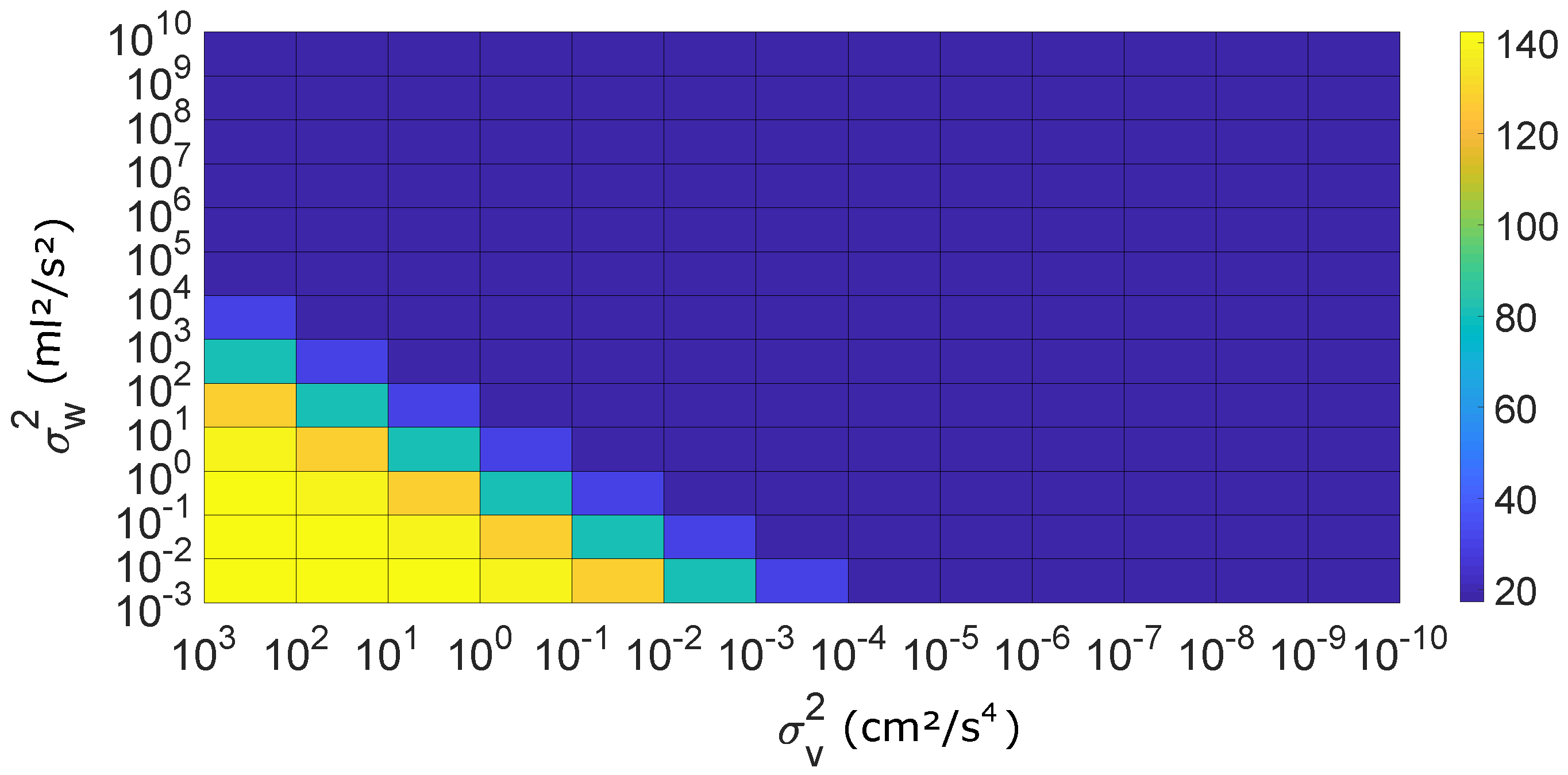
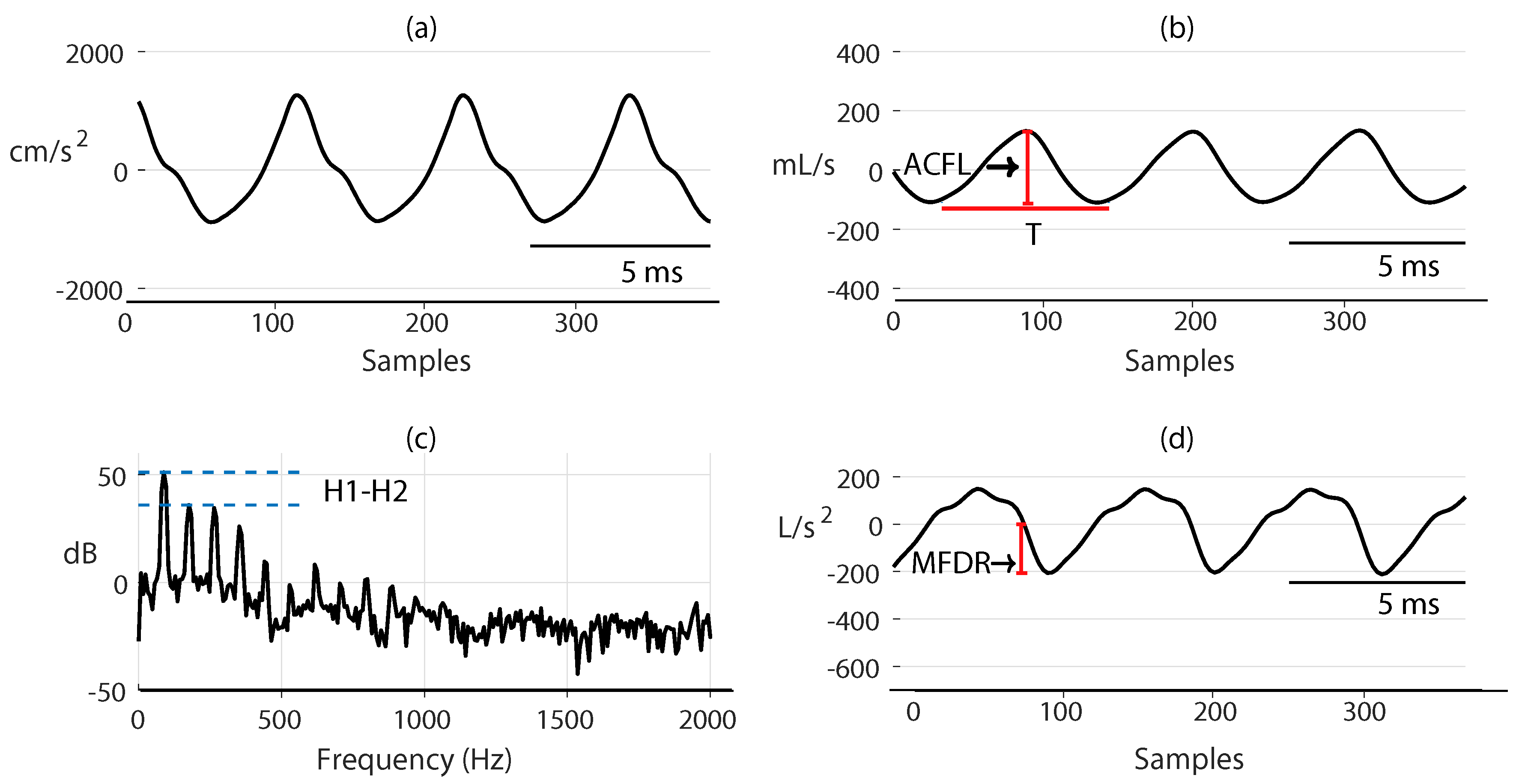
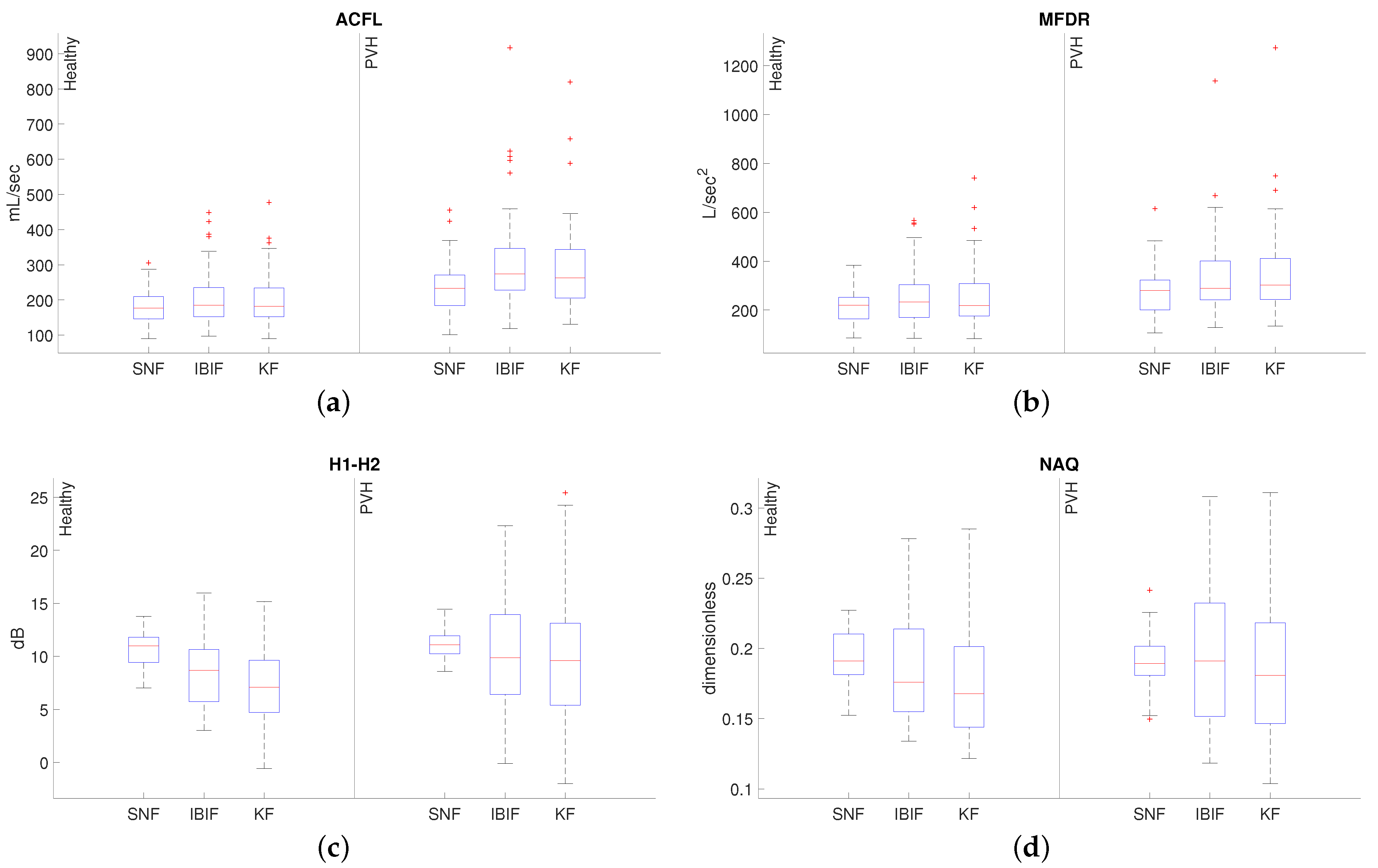
| Glottal Airflow Measures | Description | Units |
|---|---|---|
| ACFL | Peak-to-peak glottal airflow | mL/s |
| MFDR | Negative peak of the first derivative of the glottal waveform | L/s |
| H1-H2 | Difference between the magnitude of the first two harmonics | dB |
| Normalized Amplitude Quotient (NAQ) | Ratio of ACFL to MFDR divided by the glottal period | − |
| Fundamental frequency () | Inverse of the glottal period | Hz |
| ACFL | MFDR | H1-H2 | NAQ | |||
|---|---|---|---|---|---|---|
| PVH | SNF | |||||
| IBIF | ||||||
| Kalman | ||||||
| Healthy | SNF | |||||
| IBIF | ||||||
| Kalman |
| ANOVA | ACFL | MFDR | H1-H2 | NAQ | |
|---|---|---|---|---|---|
| Healthy | F | ||||
| p-value | * >0.001 | ||||
| PVH | F | ||||
| p-value | * 0.02 | * 0.04 |
| ACFL | MFDR | H1-H2 | NAQ | |
|---|---|---|---|---|
| Healthy | ||||
| PVH |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortés, J.P.; Alzamendi, G.A.; Weinstein, A.J.; Yuz, J.I.; Espinoza, V.M.; Mehta, D.D.; Hillman, R.E.; Zañartu, M. Kalman Filter Implementation of Subglottal Impedance-Based Inverse Filtering to Estimate Glottal Airflow during Phonation. Appl. Sci. 2022, 12, 401. https://doi.org/10.3390/app12010401
Cortés JP, Alzamendi GA, Weinstein AJ, Yuz JI, Espinoza VM, Mehta DD, Hillman RE, Zañartu M. Kalman Filter Implementation of Subglottal Impedance-Based Inverse Filtering to Estimate Glottal Airflow during Phonation. Applied Sciences. 2022; 12(1):401. https://doi.org/10.3390/app12010401
Chicago/Turabian StyleCortés, Juan P., Gabriel A. Alzamendi, Alejandro J. Weinstein, Juan I. Yuz, Víctor M. Espinoza, Daryush D. Mehta, Robert E. Hillman, and Matías Zañartu. 2022. "Kalman Filter Implementation of Subglottal Impedance-Based Inverse Filtering to Estimate Glottal Airflow during Phonation" Applied Sciences 12, no. 1: 401. https://doi.org/10.3390/app12010401
APA StyleCortés, J. P., Alzamendi, G. A., Weinstein, A. J., Yuz, J. I., Espinoza, V. M., Mehta, D. D., Hillman, R. E., & Zañartu, M. (2022). Kalman Filter Implementation of Subglottal Impedance-Based Inverse Filtering to Estimate Glottal Airflow during Phonation. Applied Sciences, 12(1), 401. https://doi.org/10.3390/app12010401






