Abstract
In the Industrial Internet of Things (IIoT), various tasks are created dynamically because of the small quantity batch production. Hence, it is difficult to execute tasks only with devices that have limited battery lives and computation capabilities. To solve this problem, we adopted the mobile edge computing (MEC) paradigm. However, if there are numerous tasks to be processed on the MEC server (MECS), it may not be suitable to deal with all tasks in the server within a delay constraint owing to the limited computational capability and high network overhead. Therefore, among cooperative computing techniques, we focus on task offloading to nearby devices using device-to-device (D2D) communication. Consequently, we propose a method that determines the optimal offloading strategy in an MEC environment with D2D communication. We aim to minimize the energy consumption of the devices and task execution delay under certain delay constraints. To solve this problem, we adopt a Q-learning algorithm that is part of reinforcement learning (RL). However, if one learning agent determines whether to offload tasks from all devices, the computing complexity of that agent increases tremendously. Thus, we cluster the nearby devices that comprise the job shop, where each cluster’s head determines the optimal offloading strategy for the tasks that occur within its cluster. Simulation results show that the proposed algorithm outperforms the compared methods in terms of device energy consumption, task completion rate, task blocking rate, and throughput.
1. Introduction
The Internet of Things (IoT) is a technology that is currently popular and applied in various domains, such as intelligent transportation and smart cities. Industrial IoT (IIoT) is part of the IoT domain and deals with industrial apparatus, especially in the manufacturing sector. IIoT has different features and requirements from IoT. IoT connects sensors or devices to improve human awareness of the surrounding environment, while IIoT connects them to improve industrial efficiency and productivity. Therefore, the devices are often less mobile or even fixed. It is necessary to reduce the delay time to improve the reliability of work execution, with high energy efficiency required due to the characteristics of IoT devices having limited battery life. In addition, as industrial process is time-varying, the computing system must be quickly adapted and realized to new situations [1,2,3]. Smart factory, an example of an IIoT application, has certain manufacturing characteristics, such as job shop and division of work [4]. Therefore, we can observe that devices that deal with similar tasks are gathered in close proximity. When computation-intensive or delay-sensitive tasks are created, it may be challenging to complete the task execution on a local device. Because a device has limited computation capability and battery life, cloud computing technology has been proposed to solve this problem. However, because a cloud data center is far from the device, it is difficult to satisfy the delay constraints of delay-sensitive tasks. Therefore, mobile edge computing (MEC), which places data centers close to terminal devices, is emerging [5]. Computation offloading is essential when using this paradigm. Computation offloading includes full offloading, a method that sends all tasks to the MEC server (MECS) at once, and partial offloading, a method that partitions and sends tasks to the MECS. The former processes tasks locally or on the MECS, while the latter processes partitioned tasks simultaneously locally and on the MECS. There are two types of computation offloading that can be adopted in the execution step. One is single-hop computation offloading, which sends the task directly to the MECS or cloud data center. The other is multi-hop computation offloading, where tasks are sent to nearby devices and then to the MECS or cloud data center [6]. However, MECS also has limited computation capability, making it unsuitable for processing many tasks compared to the cloud. Furthermore, the more tasks processed in MECS, the greater the burden on the cellular network for task transfer between the device and MECS [7]. Therefore, the paradigm of cooperative computing has recently been proposed, in which device-to-device (D2D) communication has garnered increasing popularity as a prominent technology that addresses the shortcomings of MECS [8].
MEC paradigm is a technology that is being used to support the limited computation capability and battery life of devices, and computation-intensive or delay-sensitive tasks. Therefore, computational offloading technology is one of the essential elements in the MEC paradigm. In [9], offloading decision is defined as a resource allocation problem with a single objective function that minimizes task execution time. However, this study did not take into account the energy consumption and load conditions of MECSs, which are particularly important in the IIoT environment during offloading decisions. Selecting offloading nodes that minimize task execution time using reinforcement learning is studied in [10]. However, this study also has limitations that do not take into account energy consumption. In [11], energy consumption and task execution time are defined as offloading cost, with game theory used to minimize offloading cost and optimize offloading. However, if the offloading target is limited to MECS, there is a limit to minimizing offloading costs. If the MECS is not close to the device, energy consumption may increase for task transmission. In addition, if multiple tasks are simultaneously offloaded into a MECS, the load on the server sharply increases and task execution time increases, which may not satisfy the latency constraints. Thus, D2D communication is used to solve this problem in consideration of computing resources. The focus of [12] is on formulating the computation resource allocation problem that reduces offloading costs in the IIoT field. However, the study does not consider cooperative computing. Minimizing the energy consumption of devices while ensuring reliability and latency requirements is studied in [13]. The research uses a technique of partial offloading rather than the full offloading of tasks. In [14], the aim is to maximize the utility function by calculating revenues and costs using energy consumption and task execution delay. Since it considered the mobility of users, migration was also considered. The aim of [15] is to improve the efficiency of energy consumption and the cost of offloading. The consumption of computing resources of a MECS were used as the offloading cost so that tasks were not concentrated on a specific MECS in a smart home environment. In [16], the focus was on formulating the offloading assignment problem to minimize the total system cost within delay constraints of each application. It heuristically solves the problem by using the dependence between tasks. In summary, except for [12], which deals with the IIoT field, all studies relate to the IoT field and vehicle field. However, due to the characteristics of the IIoT environment, which requires low device mobility, latency constraint, and energy efficiency, the proposed techniques in IoT and vehicle environments are not suitable.
We propose an algorithm that determines the optimal offloading strategy of tasks to minimize the task execution delay and energy consumption of devices to satisfy energy efficiency and delay constraint, which are important requirements in the IIoT field. However, it is not easy to manage because of the difficulty in predicting how many tasks will occur and the load situation of MECSs and devices. In addition, devices have limited computational power and battery life. To solve this problem, Reinforcement Learning (RL) is adopted while using the MEC paradigm and D2D communication. RL follows a Markov decision process (MDP) that models a decision-making problem and learns by mapping the state to action to maximize reward value. Among RL algorithms, Q-learning is model-free RL that deals with the MDP problem in which the probability of state transition is unknown. Therefore, in our problem of finding an optimal offloading strategy by reflecting only the current state, using Q-learning to make optimal decisions is suitable without requiring prior knowledge. Since Q-learning requires a relatively low computational complexity compared to other reinforcement learning techniques, it is suitable for application to IIoT devices that do not have high computing capabilities. Nevertheless, since Q-learning stores and maintains the Q-value for the state-action pair in the Q-table, as the Q-table increases, increasing the time complexity to search for the Q-table and the space complexity to maintain it is inevitable [17]. Therefore, we adopt device clustering to manage devices with low complexity, then perform Q-learning to obtain an optimal offloading strategy in the IIoT field.
2. System Model
As shown in Figure 1, the system consists of base stations (BSs), MECSs, and IIoT devices. As mentioned in Section 1, we do not consider the mobility of the device because the devices are fixed in the IIoT field. We assume that tasks of the same type are located close to each other. Therefore, IIoT devices are clustered based on distance. The cluster head (CH) is then selected for each cluster. The CH is the device with the highest computation capability within the cluster. The role of the CH is to run the proposed algorithm to determine offloading strategies for devices within the cluster. The reason why the device with the highest computation capability is selected as the CH is that it communicates the information of devices in the cluster and the information of MECSs, in addition to executing the task. Thus, the CH makes an offloading decision regarding the tasks occurring in its own cluster. Each BS is equipped with one MECS, where the task queue of the MECS consists of tasks to be executed on it. The device task queue holds tasks that are to be processed on the device.
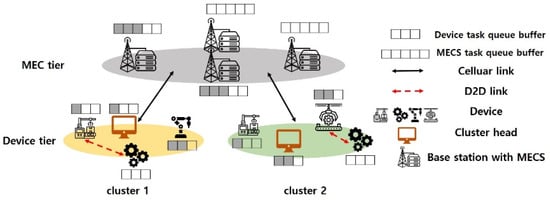
Figure 1.
The proposed system architecture of an IIoT environment.
We use the task execution time model and the energy consumption model to minimize the task execution time and energy consumption and that are the objectives of our proposed paper. represents a set of MECSs, with the number of MECSs equal to . represents a set of devices, with the number of devices equal to . represents a set of tasks, with the number of tasks equal to . A device generates a task with a delay constraint given by a Poisson distribution in each time slot. We assume that the task is not divided and is processed locally or offloaded. The task set created in a time slot t is . Each task that is created by the device d () in a time slot t consists of a tuple with three properties: , where (in Kbits) is the data size of the task and (in cycles/bit) is the number of CPU cycles used per bit to process the task. (in seconds) is the delay constraint of the task. Task execution delay is defined differently according to the offloading strategy of the task. To calculate task execution delay, the task transmission rate is essential if the task is transmitted to an MECS or another device. The task transmission rate depends on the offload location because of using different links. The communication between the devices and MECS uses a cellular link, while the communication between devices is performed through a D2D link. The task transmission rate is computed using the Shannon–Hartley formula, which is a general communication model. The task transmission rate between device d () and MECS m () in time slot t can be described as:
where denotes the channel bandwidth of cellular communication at time slot t and is the power required by device d to transmit data to MECS m with the least load. indicates the channel gain between device d and MECS m and is the noise power. The task transmission rate between devices i and j () in time slot t is described as:
where denotes the channel bandwidth of the D2D communication at time slot t and is the power required by device i to transmit data to device j with the least load. indicates the channel gain between devices i and j. The downlink rate is not considered because the data output size of the task is relatively small. The task execution delay of a task created by device d in time slot t is given as:
where denotes the offloading strategy for . is determined by the CH of the cluster where the task occurs. indicates that is executed locally on the device where it first occurs, means that is offloaded to the MECS with the least load, and denotes that is executed by device with the least load. denotes , the number of CPU cycles required to process the task. Let , , and be the computation capabilities of devices d, j, and MECS m, respectively. , , and are the queuing delays of devices d, j, and MECS m, respectively, in a time slot t. In addition, as per the task execution delay (Equation (3)), the energy consumption of the device is defined differently according to the offloading strategy. When the task generated by device d in a time slot t is executed according to the offloading strategy , the energy consumption with respect to the device is stated as follows:
where denotes the energy consumption per CPU cycle and is a constant dependent on the hardware architecture [5].
3. Problem Definition and Proposed Algorithm
In this section, we formulate the problem and describe its solution. We propose an algorithm to improve the system throughput and satisfaction degree associated with the quality of service (QoS) by reducing the total task execution delay and total energy consumption of devices in an IIoT environment, where devices and MECSs have limited computing capability and queue length for processing tasks. The objectives and constraints of this study can be summarized as follows:
where is a factor that balances the energy consumption and task execution delay and denotes the offloading strategy set of all tasks. Any belonging to the set means an offloading strategy of a task generated in the device d in a time slot, thus, it can assume a value between 0, 1, and 2, such as C1. At O1 in Equation (5), indicates an offloading cost created by combining the energy consumption of a device and the task execution delay. Since the goal of the proposed method is to minimize the offloading cost, it is used as a reward function in a Markov decision process when learning progresses. Through C1, observe that the problem is an integer problem. and represent the energy consumption and task execution delay for processing task c, respectively. C2 demonstrates that the task execution delay must satisfy the delay constraints. Let and be the loads of device d and MECS m, respectively, while and denote the maximum loads of device d and MECS m, respectively.
We assume an IIoT scenario that is characterized by a division of work and a job shop. According to such characteristics, cooperating devices close to each other are clustered. After clustering, a CH in each cluster is selected considering the working characteristics and computational capabilities of the devices in the cluster. It is assumed that the selected CH does not change. However, it is difficult to find the optimal offloading strategy in an environment where the states of MECSs and devices change dynamically over time. In a dynamic environment, it is not appropriate to use conventional heuristic methods owing to a high computational complexity. Thus, we use the Q-learning algorithm, a model-free reinforcement learning (RL) scheme that can be executed on a CH without requiring prior knowledge of the environment and high computational resources. Prior to executing Q-learning, each CH determines its serving MECS and D2D device that execute the new tasks in the cluster. Its serving MECS and D2D device are selected considering their respective workloads. The CH determines whether the task is offloaded; if so, the task is offloaded to the serving D2D device or MECS. This approach ensures that the system throughput is improved and delay constraints are satisfied via reducing task blocking and queuing delay. We define the subsequent Markov decision process (MDP) as follows:
- Agent: The CH(),
- State: being the state of the created task at time slot t in cluster i.-: the task created by device d at time slot t,-: the load of device d, serving MECS m, and serving D2D device j at time slot t, ,-: the location of device d, serving MECS m, and serving D2D device j at time slot t, ,
- Action: being the offloading strategy of a task at time t in cluster i.
- Reward (Penalty): where is the weighting factor between 0 and 1. indicates a normalized value of the total of computing and transmission energy consumed by the device when executing the task in a time slot t. denotes the normalized value of the execution delay of the task from the time slot t where it occurs until the job execution is completed.
According to the above mentioned MDP, we update the Q-value as follows:
where is the learning rate. Our proposed algorithm does not consider multi-hop transmissions.
4. Numerical Results
To evaluate the performance of our proposed algorithm, the effects of various indicators, such as the task arrival rate per device and cluster type, were tested. For experimental evaluation, we deployed four MECSs and 52 devices in an MEC system, with the locations of these devices randomly distributed in a 250 m × 250 m square area. The values of the parameters required for the experiments are reported in Table 1.

Table 1.
Simulation parameters.
Figure 2 shows the performance comparison according to the task arrival rate per device when the number of devices is 52 and the cluster type is homogeneous. A homogeneous cluster type denotes that the cluster sizes are similar. In Figure 2, there are three methods to compare with the proposed algorithm, load_QL(0.7). The proposed algorithm load_QL(0.7) sets the α for Q-value computation as reward to 0.7. The first method was all MEC offloading (AMO), which is a method of offloading all tasks to the MECS with the least load. The second was all D2D offloading (ADO), which is a method of offloading all tasks to the device with the least load through D2D communication without executing them locally. The third comparison method, load_random, firstly selects the MECS and D2D device with the least load as offloading targets, such as load_QL, and then the offloading strategy is randomly determined. This is to show that performance can be improved through an optimized offloading strategy by comparing these three methods. In Figure 2a, when the task arrival rate is 0.8, the performance of the proposed algorithm is approximately 59%, 28.6%, and 18.9% better than those of AMO, ADO, and load_random, respectively. When the task arrival rate is 0.3, the performance of the proposed algorithm is approximately 41.7% and 31.4% better than those of AMO and load_random, respectively. However, compared to ADO, the task blocking rate of the proposed algorithm is slightly higher. This shows that ADO may perform temporarily better because the system load decreases when the task arrival rate is low. However, observe that simple D2D offloading rapidly increases the load of neighboring devices in the cluster, resulting in a sharp decrease in performance. Figure 2b illustrates the task completion rate within the delay constraints according to the task arrival rate per device. When the task arrival rate is 0.8, the performance of the proposed algorithm is approximately 59.3%, 16.5%, and 9.8% better than those of AMO, ADO, and load_random, respectively. When the task arrival rate is 0.3, the performance of the proposed algorithm is approximately 4.9% and 5.6% better than those of AMO and load_random, respectively. However, compared to ADO, the task completion rate of the proposed algorithm is slightly worse. When the task arrival rate is 0.3, the load of the MECS and D2D devices are low because the number of tasks is small. The comparison algorithms select the MECS or D2D devices for task offloading considering the load. However, only the proposed algorithm(load_QL(0.7)) considers the energy consumption of the devices and task execution delay. Therefore, because the load is less affected when the task arrival rate is 0.3, and the proposed algorithm is affected by the energy consumption of the device, there is a difference in performance compared to ADO. In Figure 2c, for AMO, only the energy consumption during data transmission from the devices to MECS, and not the computation energy consumption of the MECS, is considered to calculate the total energy consumption. This is because the energy consumption we focus on is the device energy consumption. Therefore, because the computational energy of the MECS is excluded, the energy consumption seems relatively small. When the task arrival rate is 0.8, the performance regarding the energy consumption of devices is approximately 21.15% and 11.22% better than those of ADO and load_random, respectively. In Figure 2d, AMO shows a relatively low throughput trend because the task blocking rate in MECS increases as the task arrival rate increases. When the task arrival rate is 0.8, the throughput of the proposed algorithm is approximately 13.5% and 8.8% better than those of ADO and load_random, respectively. Compared to ADO, the proposed algorithm achieves better throughput because the blocking rate is low and completion rate is high when the task arrival rate increases. Since Figure 2 shows a performance comparison according to the system architecture, there seems to be no significant difference in performance between load_random and load_QL(0.7). However, through Figure 3, the performance difference among the methods in the same system architecture will be shown. As a result, through Figure 2, load_random and load_QL(0.7) considering both MEC and D2D communication showed better performance in terms of task throughput, task completion rate, task blocking rate, and energy than AMO and ADO considering only MEC or D2D communication.
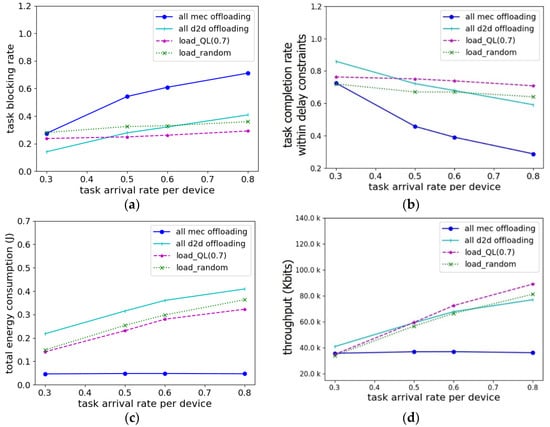
Figure 2.
Performance comparison according to task arrival rate per device and the system architecture: (a) task blocking rate; (b) task completion rate within delay constraints; (c) total energy consumption (J); (d) throughput.
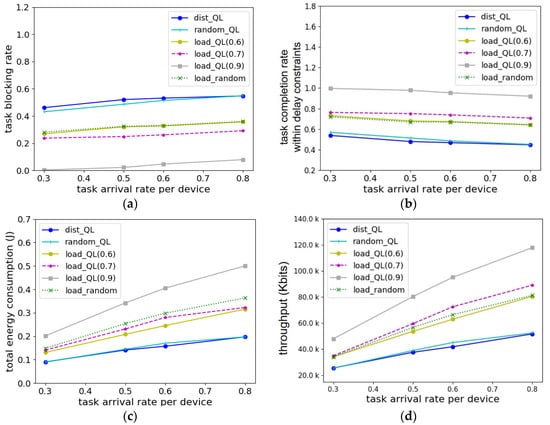
Figure 3.
Performance comparison according to task arrival rate per device and the method of selecting the MECS and D2D device and determining offloading strategy decision: (a) task blocking rate; (b) task completion rate within delay constraints; (c) total energy consumption (J); (d) throughput.
Figure 3 shows the performance comparison according to the task arrival rate per device when the number of devices is 52 and the cluster type is homogeneous. In Figure 3, the comparison methods are described as follows. The first was dist_QL, which is a method for selecting the nearest D2D device and MECS as the offloading targets with the distance from the device which originally generated the task. The second was random_QL, which is a method that randomly selects the MECS and D2D device as offloading targets. Both dist_QL and random_QL use the Q-learning algorithm in the same way as the proposed algorithm to determine the optimal offloading strategy, after selecting offloading targets. The methods were compared with the proposed algorithm (load_QL), with the proposed algorithm used with different weight values, α, for Q-value computation with load_QL(0.6), load_QL(0.7), and load_QL(0.9). The proposed algorithm may set α differently according to the application requirements in terms of the task execution delay and energy. Therefore, different α values (0.6, 0.7, and 0.9) were used for performance comparison of the proposed algorithm load_QL, whilethe average value of the performance when different α values were used for comparison with other methods was used. The performance comparison among these methods was to analyze the performance in selecting an offloading target MECS and D2D device. The dist_QL and random_QL methods were compared as different MECS and D2D device selection methods. In addition, we compared the performance of load_random as the method that does not use Q-learning for the offloading strategy decision method. In Figure 3a, when the task arrival rate is 0.8, the average performance of the proposed algorithm(load_QL) is approximately 55% better than those of dist_QL and random_QL. When the task arrival rate is 0.3, the average performance of the proposed algorithm is approximately 63.2% and 60.1% better than those of dist_QL and random_QL, respectively. As a result, it can be seen that the method of considering the load in the MECS and D2D device selection methods is better in terms of task blocking rate than dist_QL and random_QL with the different MECS and D2D device selection methods. This is because the loads are evenly distributed and not concentrated on a few MECSs or D2D devices. When the task arrival rate is 0.8, the average performance of the proposed algorithm is approximately 33% better than that of load_random. When the task arrival rate is 0.3, the average performance of the proposed algorithm is approximately 39.4% better than that of load_random. The comparison with load_random was to evaluate the performance of the Q-learning algorithm as the offloading strategy method; the proposed algorithm showed better performance in terms of task blocking rate. In the case of Q-learning, the Q-value is updated according to the reward that combines task execution time and energy consumption of devices, and it shows much better performance than when randomly selected. In Figure 3b, when the task arrival rate is 0.8, the average task completion rate within delay constraints of the proposed algorithm (load_QL(0.6), load_QL(0.7), and load_QL(0.9)) is approximately 69.1% and 67.8% better than those of dist_QL and random_QL, respectively. When the task arrival rate is 0.3, the average performance of the proposed algorithm is approximately 85.4% and 45.9% better than those of dist_QL and random_QL, respectively. As a result, load_QL shows much better performance because queuing delay can be reduced by selecting MECS and D2D devices based on the load. When the task arrival rate is 0.8 and 0.3, the performance of the proposed algorithm is approximately 18.2% and 15.3% better, respectively, than those of load_random. The load_QL and load_random algorithms have the same target selection method of the MECS and D2D device, but load_QL using Q-learning, which extracts the optimal offloading strategy depending on the dynamic situation, performs better than load_random, which randomly determines the offloading strategy. Therefore, the performance of load_QL is much better than that of load_random. In Figure 3c, dist_QL and random_QL perform relatively well in terms of energy consumption of devices, but this is because, as Figure 3a shows, a large number of tasks processed were blocked. The average performance of the proposed algorithm for all task arrival rates was worse than load_random. However, this does not necessarily suggest poor performance. The reason is that load_QL(0.9) focused on increasing task completion rate through reducing latency rather than energy. In terms of task blocking rate and task completion rate, the performance of load_random is similar to load_QL(0.6). Comparing load_QL(0.6) and load_random in terms of total energy consumption, load_QL(0.6) performs approximately 13.16% better than load_random at task arrival rate 0.8. As a result, it can be seen that the proposed algorithm has better performance in terms of total energy consumption when the number of tasks is similarly processed. In Figure 3d, when the task arrival rate is 0.8, the performance of the proposed algorithm is approximately 46%, 45.2%, and 15.2% better than those of dist_QL, random_QL, and load_random, respectively. When the task arrival rate is 0.3, the performance of the proposed algorithm is approximately 34.4%, 35%, and 12.6% better than those of dist_QL, random_QL, and load_random, respectively. Because the proposed algorithm has a relatively low task blocking rate and a high task completion rate within delay constraints, it shows higher throughput. As a result, Figure 3 shows that the method of selecting the MECS and D2D device and determining offloading strategy decision for the proposed algorithm are effective with different task arrival rates.
Figure 4 demonstrates the performance comparison according to the cluster types when the number of devices is 52 and task arrival rate is 0.8. In the cluster type, hetero indicates that in the given environment clusters with different sizes are arranged, while homo refers to an environment in which same-sized clusters are arranged. Figure 4 shows the performance of different cluster types when using different target MECS and D2D device selection methods with the same optimal offloading strategy. When the cluster type is homo, detailed performance comparison was already conducted as shown in Figure 3. In Figure 4a, when the cluster type is hetero, the average performance of the proposed algorithm load_QL is approximately 53.4% and 54.7% better than those of dist_QL and random_QL, respectively. In Figure 4b, when the cluster type is hetero, the performance of the proposed algorithm is approximately 38.28% and 39.9% better than those of dist_QL and random_QL, respectively. Even if the cluster type is hetero, the performance of the proposed algorithm is still better than those of dist_QL and random_QL. Since the proposed algorithm considers the load of the MECS and D2D device when it selects the offloading target, it shows better performance by properly distributing the load on the system. In Figure 4c, when the cluster type is hetero, the average value reported regarding the proposed algorithm is higher than those of dist_QL and random_QL, respectively. The reason is that there are more blocked tasks of dist_QL and random_QL than that of the proposed algorithm, as shown in Figure 4a, hence, the number of computed tasks is smaller and the total energy of task computing is lower. Similarly, in Figure 4d, when the cluster type is hetero, the proposed algorithm performs approximately 29.3% and 31.87% better compared to dist_QL and random_QL, respectively. This is because the proposed algorithm has a lower blocking rate and a higher task completion rate than other algorithms.
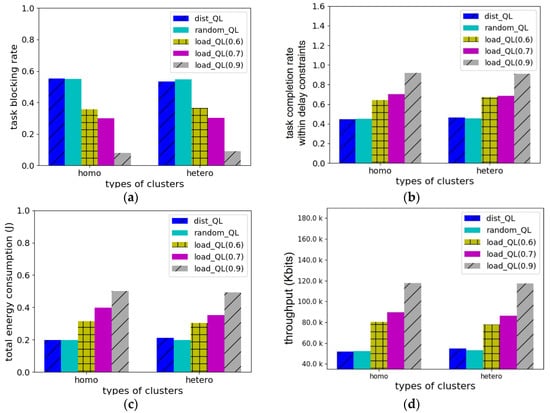
Figure 4.
Performance comparison according to cluster types when using different target MECS and D2D device selection methods with the same optimal offloading strategy (the number of devices is 52 and task arrival rate is 0.8): (a) task blocking rate; (b) task completion rate within delay constraints; (c) total energy consumption(J); (d) throughput.
Figure 5 shows the performance when the methods of determining the offloading target are the same based on load and the methods of selecting the optimal offloading strategy are different. In Figure 5a, when the cluster type is hetero, the average performance of the proposed algorithm is approximately 35.2% better than load_random. In Figure 5b, when the cluster type is hetero, the average performance of the proposed algorithm is approximately 19.4% better than load_random. In addition, it can be seen that the larger the weight used on the latency side when calculating the reward in learning, the better the task blocking rate or task completion rate within delay constraints. In Figure 5c, the performance of the proposed algorithm is higher than that of load_random. The reason is that there are more blocked tasks when load_random is used, as shown in Figure 5a. As a result, the number of computed tasks is smaller and the total energy consumption decreases. It can be observed that energy consumption increases by processing relatively more tasks because the task blocking rate is reduced if a larger weight is used on the latency side when calculating rewards in learning. Conversely, it can be seen that the energy consumption improves as the weight on the energy side increases. In Figure 5d, when the cluster type is hetero, the proposed algorithm has a lower blocking rate and a higher task completion rate than other algorithms. As a result, regardless of the cluster type, the proposed method performs well for various performance indicators.
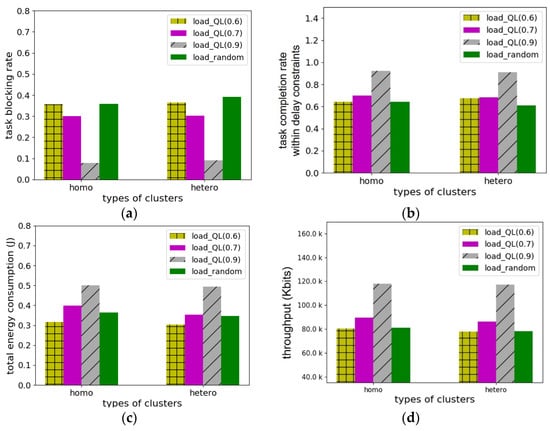
Figure 5.
Performance comparison according to cluster types when using same-target MECS and D2D device selection methods with the different optimal offloading strategy (the number of devices is 52 and task arrival rate is 0.8): (a) task blocking rate; (b) task completion rate within delay constraints; (c) total energy consumption(J); (d) throughput.
5. Conclusions
In this study, we proposed an algorithm that determines the optimal offloading strategy of tasks in terms of the energy consumption of devices and task execution delay using Q-learning in an IIoT environment. Because we clustered the nearby devices together, and each CH determined the optimal offloading strategy for the tasks that occurred within its cluster, we effectively reduced the time and space complexity of determining the optimal strategy. The algorithm outperforms the compared algorithms in terms of energy consumption of devices, task completion rate, task blocking rate, and throughput with different cluster types and task arrival rates per device. This is because the load is considered when selecting the MECS and D2D device for task offloading. Future research will focus on the optimal offloading strategy for multi-hop computation offloading.
Author Contributions
Conceptualization, S.K. and Y.L.; Methodology, S.K.; Software, S.K.; Writing—Review Editing, S.K. and Y.L.; Supervision. Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea Government(MSIT) (No.2021R1F1A1047113).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sisinni, E.; Saifullah, A.; Han, S.; Jennehag, U.; Gidlund, M. Industrial Internet of Things: Challenges, Opportunities, and Directions. IEEE Trans. Ind. Inform. 2018, 14, 4724–4734. [Google Scholar] [CrossRef]
- Sun, W.; Liu, J.; Yue, Y. AI-Enhanced Offloading in Edge Computing: When Machine Learning Meets Industrial IoT. IEEE Netw. 2019, 33, 68–74. [Google Scholar] [CrossRef]
- Li, X.; Wan, J.; Dai, H.N.; Imran, M.; Xia, M.; Celesti, A. A Hybrid Computing Solution and Resource Scheduling Strategy for Edge Computing in Smart Manufacturing. IEEE Trans. Ind. Inform. 2019, 15, 4225–4234. [Google Scholar] [CrossRef]
- Lin, C.; Deng, D.; Chih, Y.; Chiu, H. Smart Manufacturing Scheduling with Edge Computing using Multiclass Deep Q Network. IEEE Trans. Ind. Inform. 2019, 15, 4276–4284. [Google Scholar] [CrossRef]
- Mao, Y.; You, C.; Zhang, J.; Huang, K.; Letaief, K.B. A Survey on Mobile Edge Computing: The Communication Perspective. IEEE Commun. Surv. Tutor. 2017, 19, 2322–2358. [Google Scholar] [CrossRef] [Green Version]
- Hong, Z.; Chen, W.; Huang, H.; Guo, S.; Zheng, Z. Multi-Hop Cooperative Computation Offloading for Industrial IoT–Edge–Cloud Computing Environments. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 2759–2774. [Google Scholar] [CrossRef]
- Xie, J.; Jia, Y.; Chen, Z.; Nan, Z.; Liang, L. D2D Computation Offloading Optimization for Precedence-Constrained Tasks in Information-Centric IoT. IEEE Access 2019, 7, 94888–94898. [Google Scholar] [CrossRef]
- Mehrabi, M.; You, D.; Latzko, V.; Salah, H.; Reisslein, M.; Fitzek, F.H.P. Device-Enhanced MEC: Multi-Access Edge Computing (MEC) Aided by End Device Computation and Caching: A Survey. IEEE Access 2019, 7, 166079–166108. [Google Scholar] [CrossRef]
- Zhi, L.; Zhu, Q. Genetic Algorithm-Based Optimization of Offloading and Resource Allocation in Mobile-Edge Computing. Information 2020, 11, 83. [Google Scholar] [CrossRef] [Green Version]
- Yang, G.; Hou, L.; He, X.; He, D.; Chan, S.; Guizani, M. Offloading Time Optimization via Markov Decision Process in Mobile-Edge Computing. IEEE Internet Things J. 2021, 8, 2483–2493. [Google Scholar] [CrossRef]
- Yang, Y.; Long, C.; Wu, J.; Peng, S.; Li, B. D2D-Enabled Mobile-Edge Computation Offloading for Multiuser IoT Network. IEEE Internet Things J. 2021, 8, 12490–12504. [Google Scholar] [CrossRef]
- Hossain, M.S.; Nwakanma, C.I.; Lee, J.M.; Kim, D.S. Edge Computational Task Offloading Scheme using Reinforcement Learning for IIoT Scenario. ICT Express 2020, 6, 291–299. [Google Scholar] [CrossRef]
- Liu, H.; Cao, L.; Pei, T.; Deng, Q.; Zhu, J. A Fast Algorithm for Energy-saving Offloading with Reliability and Latency Requirements in Multi-Access Edge Computing. IEEE Access 2020, 8, 151–161. [Google Scholar] [CrossRef]
- Wang, D.; Tian, X.; Cui, H.; Liu, Z. Reinforcement Learning-based Joint Task Offloading and Migration Schemes Optimization in Mobility-aware MEC Network. China Commun. 2020, 17, 31–44. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, X.; You, I.; Khan, U.S. Efficient Computation Offloading in Edge Computing Enabled Smart Home. IEEE Access 2021, 9, 48631–48639. [Google Scholar] [CrossRef]
- Fan, Y.; Zhai, L.; Wang, H. Cost-Efficient Dependent Task Offloading for Multiusers. IEEE Access 2019, 7, 115843–115856. [Google Scholar] [CrossRef]
- Qian, Y.; Wu, J.; Wang, R.; Zhu, F.; Zhang, W. Survey on Reinforcement Learning Applications in Communication Networks. J. Commun. Inf. Netw. 2019, 4, 30–39. [Google Scholar]
- Liao, Z.; Peng, J.; Xiong, B.; Huang, J. Adaptive Offloading in Mobile-Edge Computing for Ultra-dense Cellular Networks based on Genetic Algorithm. J. Cloud Comput. 2021, 10, 15. [Google Scholar] [CrossRef]
- Hu, G.; Jia, Y.; Chen, Z. Multi-User Computation Offloading with D2D for Mobile Edge Computing. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).