Analysis of the Causes of the Collapse of a Deep-Buried Large Cross-Section of Loess Tunnel and Evaluation of Treatment Measures

Abstract

To address the problem of the collapse of the roof of the Bailuyuan tunnel during construction, the causes of collapse were analyzed, targeted treatment measures were proposed, and the effects of the treatment measures were evaluated through on-site monitoring and three-dimensional numerical simulations. The results showed that the particular characteristics of loess and the synergy of groundwater were the internal causes of the tunnel’s collapse as well as, to a certain extent, atmospheric precipitation. Therefore, the combination of multiple factors contributed to the tunnel’s collapse. Untimely monitoring and measurement, as well as the low initial support parameters, reflect a lack of human understanding of the collapse. Based on the analysis of the causes of the collapse, comprehensive treatment measures for inside and outside the tunnel are proposed, which are shown to be effective and to be capable of preventing the occurrence of further collapses. After the collapse treatment, the measured maximum settlement of the tunnel vault was 65.1 mm, the maximum horizontal convergence was 25 mm, the maximum surrounding rock pressure was 0.56 MPa, and the maximum stress on the steel arch frame was 54.34 MPa. Compared with the original design plan, the vertical stress, horizontal stress, and shear stress of the surrounding rock obtained from numerical simulation after the collapse treatment were greatly reduced, the reduction rate at the vault reached 50%, and the safety factors of the initial support positions after treatment met the specification requirements. The research results can provide engineering guidance for the design and construction of large-section tunnels crossing deep-loess strata, and they are of important engineering significance.

1. Introduction

China is the country with the largest loess area in the world, covering an area of nearly 640,000 km² and accounting for 6.6% of the total land area of the country [1,2]. The Loess Plateau in north-central China is the largest loess sedimentary area on earth, accounting for about 70% of the total loess area in China (Figure 1). In recent years, through the continuous promotion of the western development strategy, a growing number of long and deep-buried tunnels have been constructed on the loess stratum [3,4,5]. However, tunnel construction in this stratum is extremely prone to tunnel collapse accidents, which not only extend the construction period and cause economic losses and casualties, but also create safety hazards once improperly handled [6,7,8]. The prevention and control of collapses are the primary tasks of underground engineering. Therefore, studying the causes of tunnel collapse and effective engineering measures is essential in tunnel design and construction.

Researchers around the world have performed considerable research on the causes of and treatment measures for tunnel collapse. Mete et al. [9] studied the influence mechanism of geological structures on shallow tunnel collapse. Zarei et al. [10] studied the causes of collapse when a tunnel crosses the surrounding rock of a fault section under the action of groundwater. Wolfhard [11] found that the combination of unfavorable structural planes was the leading cause the collapse of a German Federal Railway during construction. Fraldi et al. [12,13,14] used the upper bound theorem of limit analysis to study the influence of the tunnel collapse width and height on rock mass mechanical parameters and tunnel section parameters. Zhu et al. [15] conducted indoor tests and a numerical simulation analysis on the collapse mechanism of tunnels in soft and broken rock mass at buried depths of 25–60 m. Shin et al. [16] established a tunnel collapse evaluation system based on the existing collapse data and neural network technology, which was successfully applied to the SKY tunnel project. Yang et al. [17] studied the collapse mechanism of shallow tunnels based on the nonlinear Hoek–Brown yield criterion, discussed the influence of different parameters on the collapse mechanism, and presented a critical expression for the division of deep and shallow buried depths. Wang et al. [18], using catastrophe theory, studied the collapse reason of the loose surrounding rock of a shallow tunnel under the action of rainfall. Huang et al. [19] combined the upper bound theorem of limit analysis to derive the two-dimensional collapse contour curve equation of a deep-buried tunnel. In terms of tunnel collapse treatment measures. Li et al. [20] and Yang et al. [21] proposed corresponding treatment measures for water gushing and collapse accidents that occur when a tunnel passes through different strata. Wang et al. [22] proposed treatment measures involving a pipe shed and small conduit grouting to strengthen the surrounding rock during collapse accidents in which a tunnel passes through a soil–stone composite stratum. Zuo et al. [23] proposed comprehensive treatment measures inside and outside of the tunnel for collapse accidents that occur when a tunnel crosses a fault section. Liu et al. [24] proposed corresponding treatment measures for a collapse accident that occurs when a tunnel passes through a water-rich soil area. Zhang [25] used similar model tests to study the characteristics and evolution of the collapse of deep and shallow tunnels in weak surrounding rock and proposed targeted prevention and control measures.

In summary, scholars have analyzed the causes of the collapse of deep and shallow tunnels from different perspectives and proposed corresponding measures. However, the deep-buried tunnels studied previously did not undergo roof collapse. Typically, the surrounding rock at the top of a deep-buried tunnel will stabilize itself and form an arch structure after collapsing to a certain height, but the deep-buried loess tunnel examined in this study underwent collapse and roof fall in the construction process for collapse depths up to 120 m. This kind of collapse had not occurred previously in China. Therefore, it is necessary to study the causes of the collapse and roof fall of deep-buried loess tunnels and to propose corresponding treatment measures.

Based on an engineering example of a deep-buried large-section loess tunnel collapse section of the Xi’an Outer Ring Expressway, a collapse treatment scheme is proposed based on the analysis of the cause of the tunnel collapse and roof failure. The rationality of the collapse treatment measures is evaluated through on-site monitoring and numerical simulations to provide a reference for subsequent excavation and to support other similar deep-buried tunnels and mines with loess zone engineering design and construction.

2. Project Overview

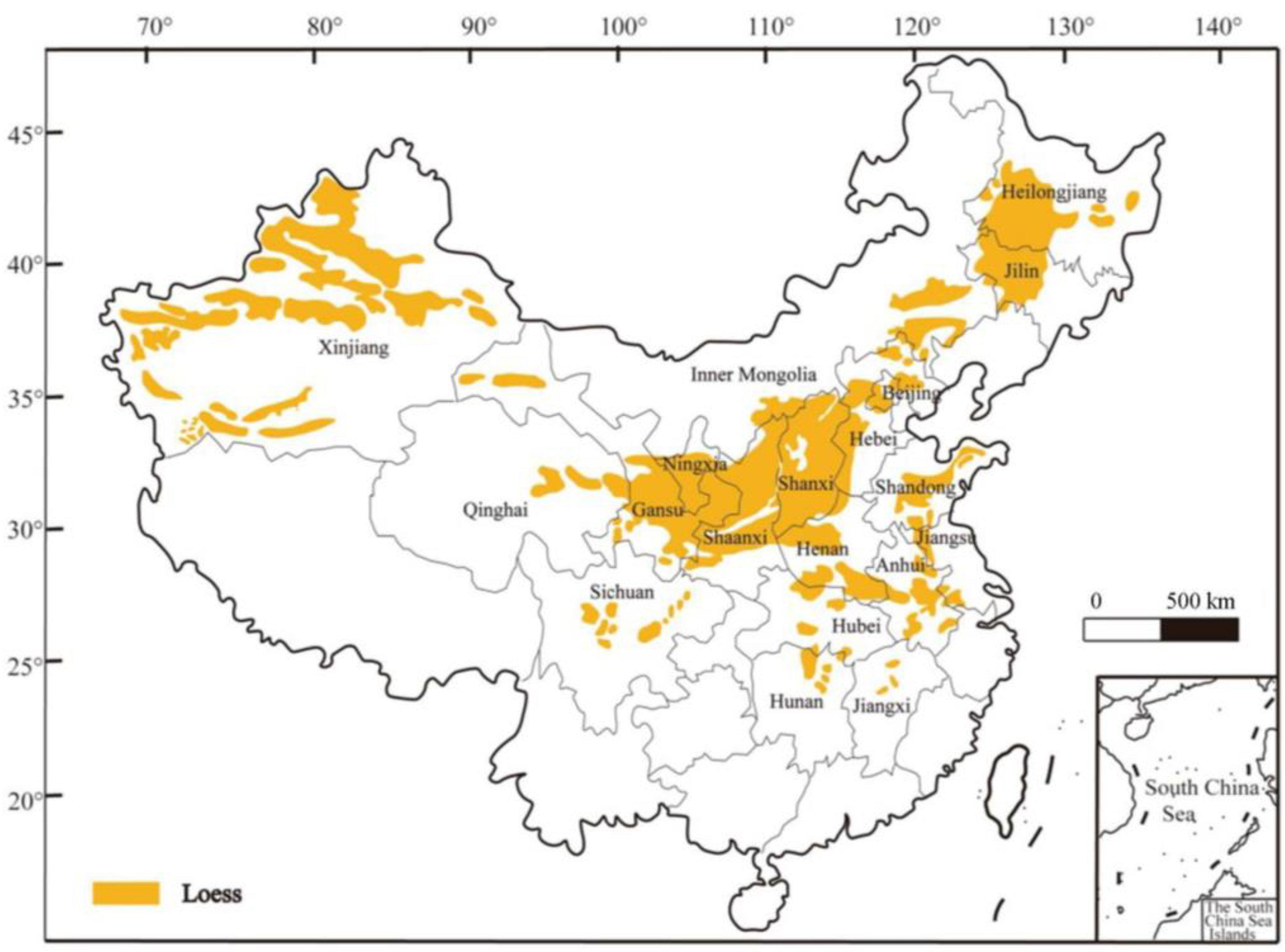
2.1. General Engineering Scenario

Bailuyuan tunnel is located in the south section of Xi’an Outer Ring Expressway, beginning at the village entrance on the east side of the Yangmuzhai, and ending on the north side of Taoyuhe Village. The right tunnel is 2819 m long (from YK56 + 755 to YK59 + 574), with a maximum buried depth of 135 m; and the left tunnel is 2725 m long (from ZK56 + 755 to ZK59 + 510), with a maximum buried depth of 133 m. The tunnel is a large-section loess tunnel with a complex engineering geology, poor hydrogeological conditions, and V-class surrounding rock throughout the entire area. The exposed strata in the tunnel area are Neogene (N₂) mudstone, conglomerate, Middle Pleistocene ($Q_2^{\mathrm{eol}}$) Lishi loess, and upper Pleistocene ($Q_3^{\mathrm{eol}}$) Malan loess, from oldest to youngest, respectively. The loess contains a thin layer of ancient soil that is locally intercalated with calcareous nodules. The south side of the gully bottom on both sides of the tunnel is covered with 3 to 7 m-thick loose slope deposits, mainly composed of quaternary slope residual silty clay and broken stones. The groundwater in the tunnel site is predominantly composed of pore water, which is mainly replenished by atmospheric precipitation and surface water. When atmospheric rainfall is heavy, affected by the large catchment area, the water flow becomes turbulent over a short period of time. The consequent erosion and damage are severe. Rainfall is the main source of groundwater replenishment, increasing the rich stock of groundwater. The amount of water inflow in the tunnel is relatively large, with the maximum reaching 13,494 m³/d on the left line and 13,477 m³/d on the right line. The design portal section and the shallow buried section of the V-class surrounding rock adopted the double-side-wall heading method. At present, the tunnel is excavated using the three-bench seven-step excavation method. The Bailuyuan tunnel is the largest three-lane loess tunnel in China, with a design section width of 17.54 m, a height of 10.56 m and an excavation area of 192.3 m². The tunnel section and support parameters are shown in Figure 2.

2.2. Scenario Status of Collapsed Tunnel Section

Before the collapse, the tunnel face of the right tunnel was constructed to YK58 + 550, the lower heading was constructed to YK58 + 574, the inverted arch was constructed to YK58 + 584, and the second lining was constructed to YK58 + 613. A stream of water appeared at the left arch of the tunnel, and the amount of water inflow continued to increase. At 11 p.m. on 5 August 2020, the vault settlements of the monitored sections YK58 + 560, YK58 + 565, YK58 + 575, and YK58 + 580 reached 223.6, 287.4, 262.1 and 251.9 mm, respectively, far exceeding the warning value. The project department launched an emergency plan to evacuate all the people in the tunnel. At 2:30 a.m. on 6 August the initial support section between YK58 + 550 and YK58 + 584, which had been completed, collapsed and formed a large area of pits on the surface. At the same time, three residential houses collapsed and staggered cracks appeared on the surface. In addition, due to the impact of the collapse and the continuous erosion of groundwater, the rock mass strength of the tunnel decreased, as did the foundation bearing capacity, resulting in the cracking and peeling of shotcrete along the longitudinal direction at the bottom of both sides of the upper steps of YK58 + 584 to YK58 + 601 (Figure 3).

2.3. Analysis on the Causes of the Tunnel’s Collapse

(1)

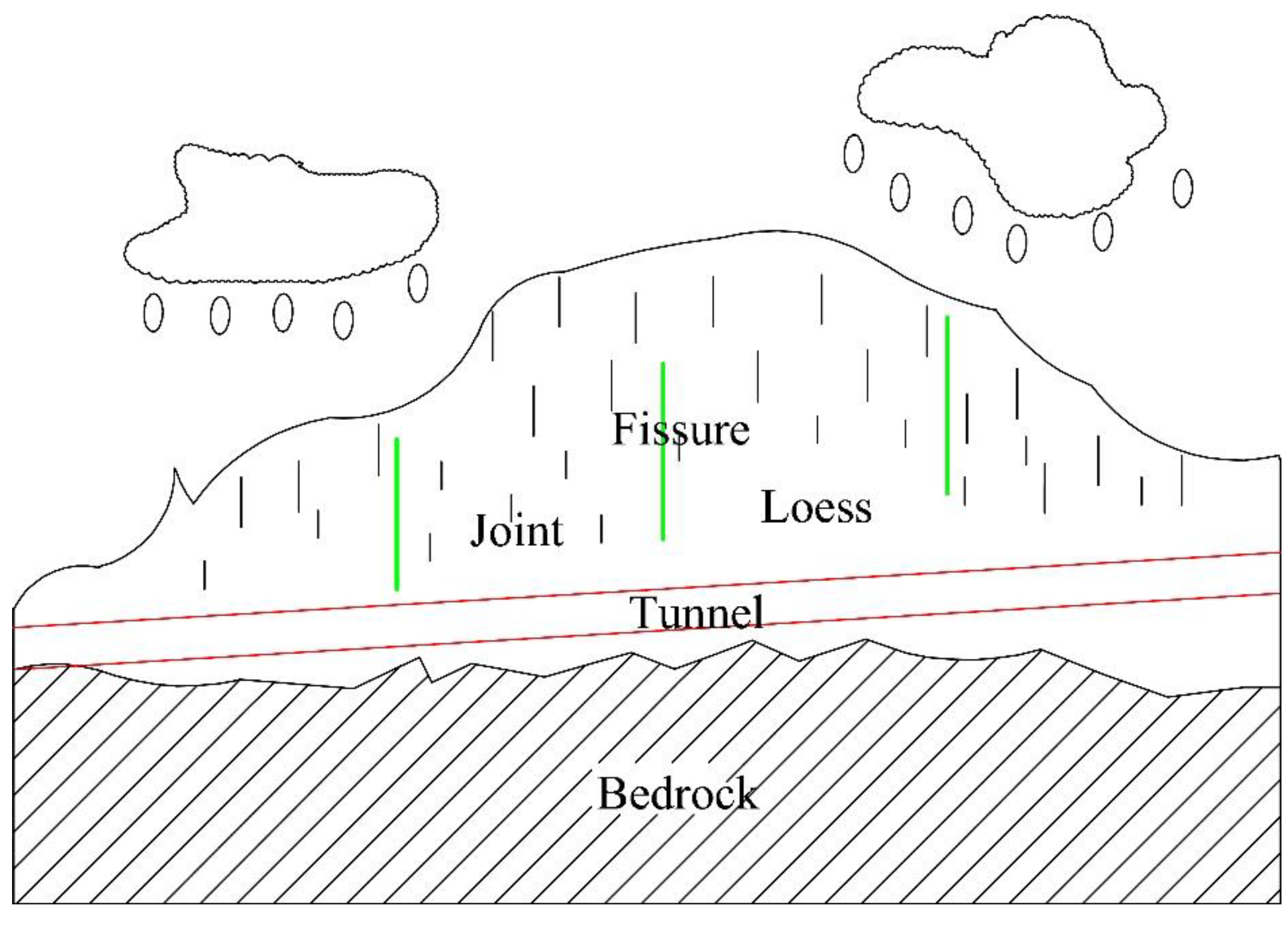
Geological factors

The overburden above the tunnel contains Malan loess, Lishi loess, and paleosol. The soil is relatively loose and characterized by the development of vertical joints, high porosity and strong water sensitivity [26,27]. After the tunnel was excavated, the stability of the loess was poor. As a result, the kind of soil in the tunnel could not resist the additional stress caused by secondary stress adjustment during the tunnel excavation, and the arch effect of the tunnel excavation contour could not be formed [28]. The weakness of the loess was the internal cause of this collapse.

(2)

Impact of groundwater

Tunnel excavation in the water-rich loess stratum destroyed the balance of groundwater and caused water to collect in the rock surrounding the tunnel, which scoured the soil around the tunnel and caused soil particle loss. In addition, the dynamic water pressure during the process of groundwater seepage significantly affected the stability of the soil. The unloading and rebound effect of the tunnel excavation caused a certain degree of relaxation of the rock mass around the tunnel, improved the seepage effect of the groundwater, weakened the self-supporting capacity of the loess and led to the tunnel’s collapse [29,30].

(3)

Influence of atmospheric precipitation

According to the geological field survey, the collapse section is a good groundwater enrichment zone. A few days before the collapse, Xi’an experienced heavy rain for several days and the collapse area received a long-term replenishment of atmospheric precipitation (Figure 4). In the case of insufficient drainage equipment and insufficient drainage time, rainwater seeped along the vertical joints and cracks of the loess. The infiltration of rainwater made the loess collapsible, increased the weight of the loess and increased the underground water level and pores of the tunnel. According to the Mohr–Coulomb strength criterion, under pore water pressure, the expression of the shear strength of saturated rock is as follows [31,32,33]:

$${\tau }_f=(\sigma -p_w)\tan {\phi }^{\prime }+c^{\prime }$$

(1)

where $\sigma$ is the total stress, $p_w$ is the pore water pressure, ${\tau }_f$ is the shear strength of the rock, ${\phi }^{\prime }$ is the internal friction angle, and $c^{\prime }$ is the cohesion of the rock.

Equation (1) shows that pore water pressure in the rock reduces its shear strength, resulting in large deformation of the surrounding rock and collapse of the tunnel. During severe rainfall, the large-scale and centralized rainstorm increases the instability of the tunnel surrounding rock, which is the external factor causing tunnel collapse accidents.

(4)

Design and Construction Factors

The burrow excavation width of this project exceeds 18 m, the height is 12 m and the excavation area exceeds 195 m². It is currently the largest three-lane loess tunnel in China, with the largest cross-section. When the deep-buried section was excavated, there was no awareness of the presence of unfavorable loess. When the tunnel collapsed, the tunnel face was constructed to YK58 + 550, and the second lining was constructed to YK58 + 613. The distance between the secondary lining and the tunnel face was 63 m, which did not meet the specification requirements for class V surrounding rock. During the measurement process, the vault settlement measurement was not timely and did not attract sufficient attention. Therefore, human factors, such as the untimely application of secondary lining, low initial support parameters, and untimely measurements, are primary causes of accidents [34,35].

2.4. Collapse Treatment Measures

At present, there is no similar case of collapse treatment in China. Therefore, based on previous experience, this paper proposes the following treatment measures for the collapse of large-section deep-buried loess tunnels in terms of two aspects, inside and outside the tunnel, for the first time:

(1)

Backfill the tunnel mileage from YK58 + 616 to YK58 + 584 with gravel, and at the same time perform back arch treatment on sections YK58 + 616 to YK58 + 599. The back arch should feature I25a steel with a spacing of 75 cm, and the inner diameter of the tunnel should be grouted upward.

(2)

Adopt full-face advanced pre-grouting and an advanced large pipe shed pre-support to cross the collapsed body. The reinforcement treatment range is YK58 + 540 to YK58 + 599 (Figure 5). At the same time, strengthen the feet-lock bolt, increase the drain hole and strengthen the drainage in the tunnel.

(1)

The full-face advanced pre-grouting requires a total of three cycles, where each cycle is 25 m long, and the actual excavation is 17 m. An 8 m grouting plate is reserved, and a 3 m thick grouting plate is set. There are 106 grouting holes in a single cycle. The grouting material should be mainly made from an early-strength sulfoaluminate cement single-liquid slurry (not less than 90%), supplemented by an ordinary-cement, water, and glass double slurry. The grouting pressure is 5.0–8.0 MPa. The grouting method should be a combination of a drill pipe with retreat-type segmented grouting and a clustered horizontal sleeve valve tube with segmented grouting.

(2)

The pre-support of the leading large pipe shed should be implemented after the full-section grouting is completed. The layout range is 100° for the arch, 5° for the extrapolation angle, 37 cm in the circumferential direction and 25 m in length. In total, 47 pieces are arranged in a single cycle, and the large pipe shed is built with Φ89 × 5 seamless steel pipes. After the reinforcement is complete, the three-bench seven-step excavation method is adopted (Figure 6).

(3)

All the damaged houses in the surface subsidence area were demolished, and the cavities in the subsidence holes was filled with pouring mortar. The original surface soil was mixed with 8% lime and backfill as a water-sealing layer with a thickness of 20 cm, followed by backfilling with plain soil to a thickness of 30 cm. Drainage measures, such as drainage ditches and intercepting ditches to prevent surface water from collecting and infiltrating, were adopted (Figure 7).

3. Evaluation of Reinforcement Effect of Collapse Section

On the third day after the tunnel collapsed, the collapsed section was reinforced. After the collapse was treated, the three-step seven-step excavation method was used for construction. The initial support was made of I25a steel, with a spacing of 50 cm and 32 cm-thick C25 shotcrete. The system used Φ22 drug coil bolts, with circumferential spacing of 1 m and longitudinal spacing of 1 m, while the secondary lining used a 65 cm-thick C35 reinforced concrete support system for the tunnel. The foot locking anchor bolts were driven into the tunnel, and two Φ50X4 feet-lock bolts, each with a length of 5 m, were used for each of the upper and lower steps.

In order to test the actual effect of the treatment measures for the collapsed section, on-site monitoring of section YK58 + 570 was carried out. The monitoring items included vault settlement, horizontal convergence, the pressure between the initial support and surrounding rock and the steel arch stress (Figure 8).

3.1. Introduction to On-Site Measurement Equipment and Procedures

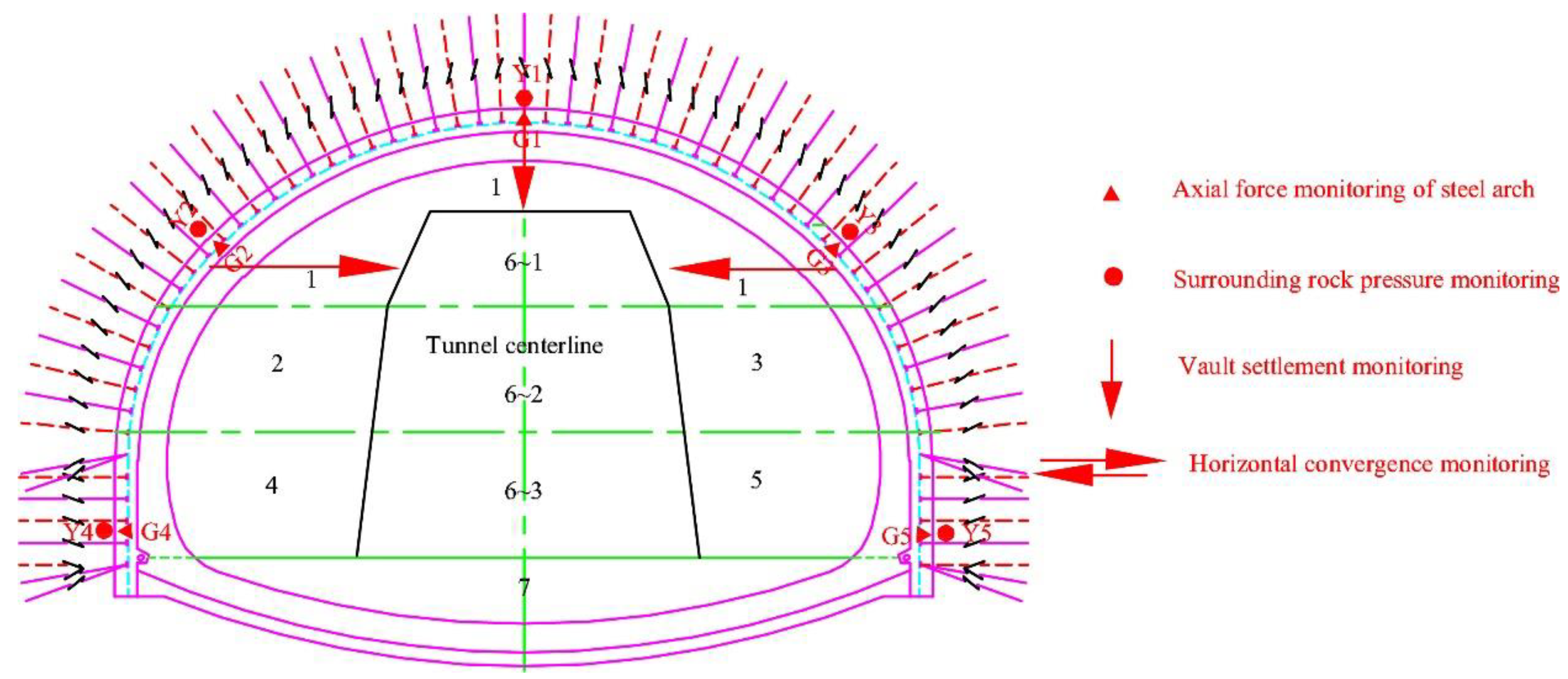
3.1.1. Surrounding Rock Pressure Measurement Equipment and Procedures

The surrounding rock pressure adopted XYJ-4 type vibrating wire double diaphragm pressure cells, which outputs signals through frequency and offers strong resistance to interference. It is measured by a ZXY-2 frequency reading instrument.

When the instrument is buried, a circular slot similar in size to the pressure box should be dug into the surrounding excavated rock to ensure that the pressure box can be inserted. The depth of the circular slot should be about 10 cm to ensure that the pressure box is stressed. Full contact should be established with surrounding rock to ensure accurate measurement results. After digging the empty slot, the pressure box should be inserted and the surroundings of the pressure box should be sealed with mud to ensure that the pressure box does not fall off due to vibration. After the test piece is buried, the test line should be organized and fully protected to prevent damage to the instrument and connecting line caused by blasting and excavation. The installation of on-site monitoring equipment is shown in Figure 9.

3.1.2. Stress Test of Steel Arch Frame Measurement Equipment and Procedures

The stress test of the steel arch frame adopts CL-XZ-B type steel bar dynamometer, and this component adopts a ZXY-2 type frequency reading instrument for measurement. Each measuring point is equipped with instruments inside and outside the corresponding section steel, and the components are fully welded to the broken steel bars by welding two sections of connecting rods. After installation, the instrument should be protected to ensure that the welding at both ends does not cause the instrument to fall off due to vibration or other reasons. The installation of on-site monitoring equipment is shown in Figure 10.

3.2. Deformation Analysis of Surrounding Rock

After the collapsed section of the tunnel was treated, the three-step seven-step excavation method was used for construction; the time history curve of the surrounding rock deformation is shown in Figure 11. The following points are evident in Figure 11:

(1)

The cumulative settlement of the tunnel vault $X_{vcs}$ was 65.1 mm, and the maximum settlement rate $V_{sr max}$ was 12.8 mm/d, which occurred on the second day. The settlement of the vault reached 39.7 mm within 10 days before construction, accounting for 61% of the total settlement. Subsequently, the variation trend of the tunnel vault settlement could be roughly divided into three stages of rapid increase, which corresponded to the successive excavation of the upper, middle and lower steps of the tunnel. After 35 days, the vault settlement and the settlement rate tended to be stable. The horizontal convergence of the surrounding rock of the tunnel $X_{hc}$ was 25 mm in total, and the maximum convergence rate $V_{cr max}$ was 4.3 mm/d, which was measured on the third day after the tunnel excavation. The horizontal convergence of the surrounding rock was large in the first 10 days before the construction, reaching 13.5 mm in total and accounting for 54% of the total convergence. With the blasting excavation of the upper, middle and lower steps, the blasting impact and load release further deformed the surrounding rock and the horizontal convergence continued to increase, but the convergence rate showed an overall decreasing trend. After 35 days, the horizontal convergence and convergence rate of the surrounding rock tended to be stable. The vault settlement and horizontal convergence were within the standard range, indicating that the treatment measures were reasonable and effective.

(2)

When a tunnel is excavated in the loess stratum, vault settlement is considered to be the main displacement caused by the excavation. The final vault settlement of the monitoring section reached 65.1 mm, the horizontal convergence $X_{hc}$ was 25 mm and the vault settlement was 2.6 times the horizontal convergence. This showed that there were significant directional differences in the tunnel displacement in the loess stratum. Thus, it is very important to control vault settlement to ensure tunnel safety.

(3)

There were significant differences in the tunnel displacement at different excavation stages. The vault settlement of the first five parts (Figure 8), the upper step part, the middle step part and the lower step part accounted for 61%, 26.7%, 7.3% and 5% of the total settlement, respectively. The horizontal convergence of each stage accounted for 54%, 31.5%, 10.5% and 4% of the total horizontal convergence, respectively. This showed that the displacement of the tunnel was mainly affected by the excavation of the preliminary pilot pit, upper bench and middle bench. Therefore, it is necessary to limit the length of the middle and upper steps and to close the support in time to achieve better control of tunnel displacement.

3.3. Surrounding Rock Pressure Analysis

Figure 11 shows the time history curve of surrounding rock pressure at monitoring section YK58 + 570. From Figure 12, the following conclusions can be drawn:

(1)

With the excavation of each step, the surrounding rock pressure of the section experienced three stages: a rapid increase, a slow increase, and stabilization, and the increases occurred in a stepped manner. The rock pressure surrounding the section was distributed discretely around the tunnel, and the maximum surrounding rock pressure in each part showed significant asymmetry. The order of the surrounding rock pressures $F_{sr}$ from large to small was vault Y1 (0.56 MPa) > left arch waist Y2 (0.40 MPa) > right arch waist Y3 (0.31 MPa) > left arch foot Y4 (0.19 MPa) > right arch foot Y5 (0.13 MPa).

(2)

The surrounding rock pressure of the vault was greater than that on both sides. This was because the super-large-section tunnel was flat and featured a large span, while the vault experienced a greater vertical pressure and settlement. The left arch waist was larger than the right arch waist because the measurement point of the left arch waist was on the side closest to the left line of the tunnel. The self-supporting capacity of the rock mass was poor and the surrounding rock pressure acting on the initial support was relatively large.

(3)

The construction of each step disturbed the surrounding rock, and the maximum rate of increase of the surrounding rock pressure was 0.196 MPa/d. On the 35th day of monitoring, the surrounding rock pressure at each measurement point was essentially stable, indicating that the supporting structure played a supporting role.

3.4. Stress Analysis of Steel Arch

Figure 13 shows the stress time history curve of the steel arch of monitoring section YK58 + 570. The following conclusions can be drawn from Figure 13:

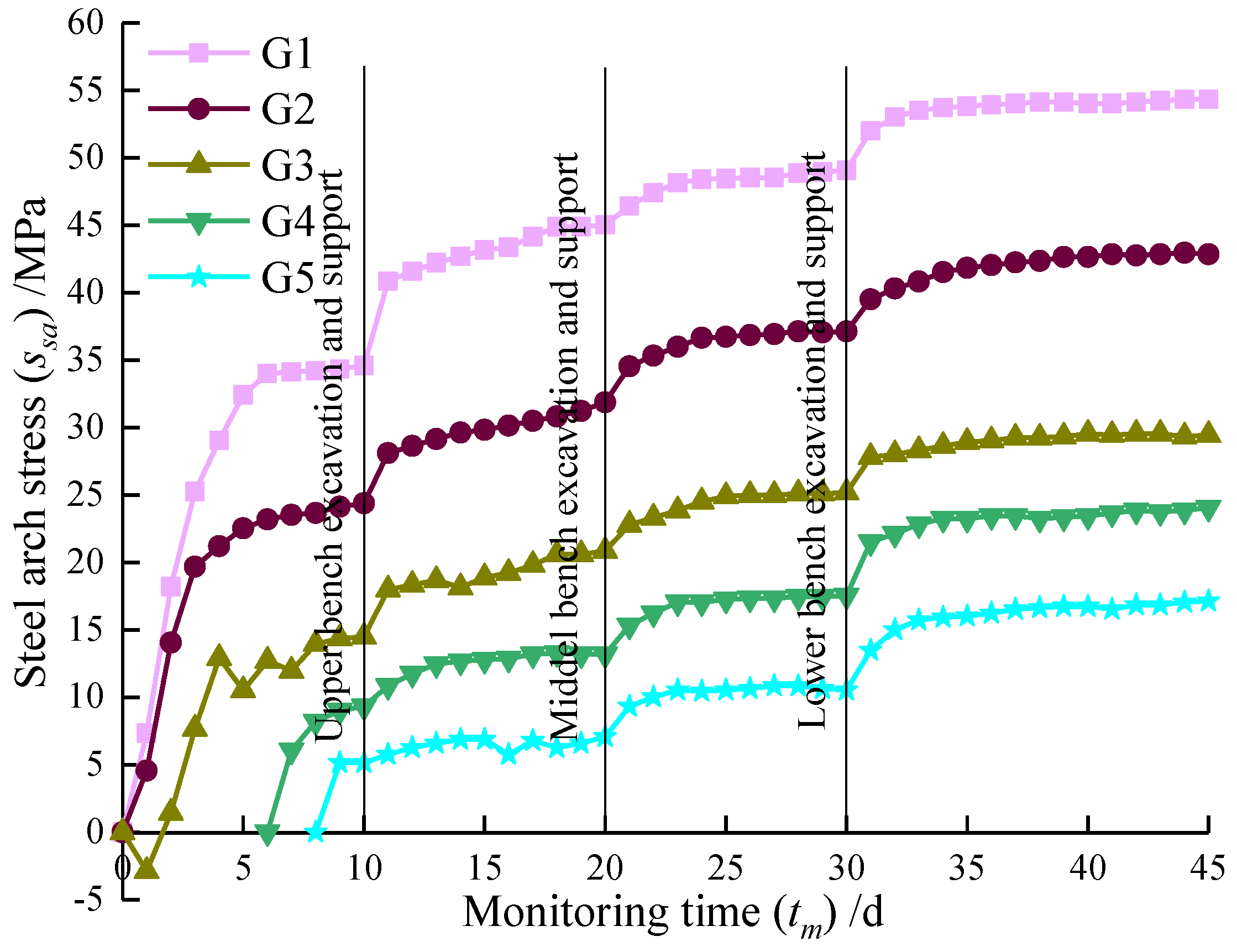
(1)

The stress change trends of the steel arch at each monitoring point of this section were roughly the same, and they were divided into three stages. The first stage, the stress growth stage of the steel arch, occurred before the core soil excavation. The stress value of the arch crown ${\sigma }_{ac}$ in this stage reached 34.68 MPa, accounting for 63.8% of the total stress value of 54.34 MPa. In the second stage, the stress of the steel arch slowly increased, which occurred in the core soil section of the excavation. The excavation and blasting of each step produced a certain disturbance effect on the steel arch and increased the stress value of the steel arch. The construction disturbance stress of the next stage was superimposed on that in this stage. At this stage, the cumulative stress of the vault ${\sigma }_{vc}$ was 14.46 MPa, accounting for 26.6% of the total stress. In the third stage, the stress of the steel arch increased slowly and the stress of the steel arch tended to be stable.

(2)

Overall, the stress of the steel arch at the monitoring point was in the following order, from large to small: arch crown G1 (54.34 MPa) > left arch waist G2 (42.86 MPa) > right arch waist G3 (29.45 MPa) > left arch foot G4 (24.06 MPa) > right arch foot G5 (17.14 MPa), showing asymmetry. The maximum growth rate occurred in the first stage of stress growth of the arch crown steel arch frame, and the growth rate was 9.63 MPa/d.

(3)

Due to the effect of the surrounding rock on the support system, the overall stress of the steel arch increased step by step with time, but the growth rate gradually decreased and eventually stabilized. The measured maximum stress of the steel arch frame ${\sigma }_{saf max}$ was 54.34 MPa, which was located at the arch crown and did not reach the yield strength value of the I-beam.

3.5. Analysis of Tunnel Water Inflow

Figure 14 shows the variation of the water inflow with time in the water inflow collapse section of the right tunnel. The daily water inflow of the tunnel roughly experienced three stages: slow growth, rapid increase, and gradual decrease from 1 July to 10 November 2020. The tunnel water inflow was relatively flat from 1 to 15 July, at an average of 7438 m³/d. From 15 July to 1 August, the tunnel water inflow continued to increase due to the influence of atmospheric rainfall and the maximum water inflow reached 13,697 m³/d on 2 August. From 2 to 5 August, the tunnel water inflow was maintained at a stable level, with an average of 12,769 m³/d. The continuous groundwater drove the scattered and broken surrounding rocks to pour downward. The surrounding rock of the tunnel face continued to collapse, forming mud inrush, while the collapse cavity gradually extended and expanded directly in front of the tunnel excavation, resulting in collapse of the tunnel. With the implementation of engineering measures, the continuous advancement of the tunnel area, and the reduction of local rainfall, the tunnel water inflow gradually decreased, declining the fastest from 2 to 23 September, with a maximum rate of 463 m³/d. Until 31 October, the tunnel water inflow decreased to 0.

Based on Figure 11, Figure 12, Figure 13 and Figure 14, after measures were taken to treat the collapsed section of the tunnel, such as advanced pre-grouting and the installation of an advanced large pipe shed to reinforce the surrounding rock and strengthen the initial support, the vault settlement and the horizontal convergence values of the surrounding rock were both low. The surrounding rock pressure was more consistent with the variation trends of the steel arch stress, the curve change was relatively stable, the value did not exhibit a large sudden increase or decrease and the tunnel water inflow gradually decreased to 0. The surrounding rock tended to be in a stable state, indicating that the disposal measures of the collapse section were effective.

4. Numerical Simulation

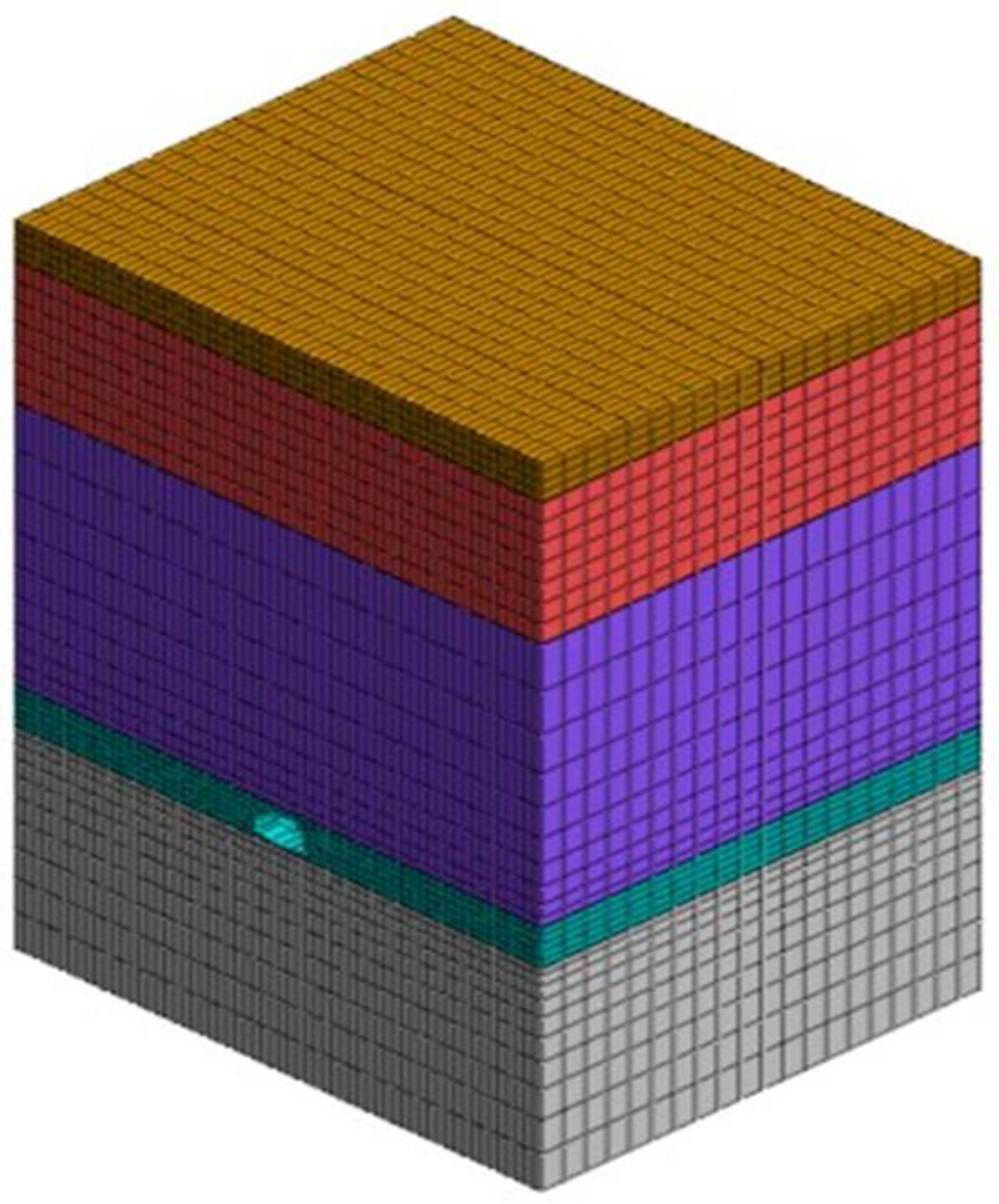
4.1. Numerical Model Establishment and Verification

Based on the actual tunnel project, considering the influence of water pressure, the following numerical model was established by using the finite element software Midas-GTS. According to the Saint-Venant’s Principle, the stress redistribution area generally appears within 3 to 5 times the width of the excavation. Therefore, in this model, the left and right sides of the model were four times the hole diameter, and the lower part was four times the hole diameter. The tunnel length was 100 m, the buried depth was 120 m, and the overall size was 120 m (X-direction) × 100 m (Y-direction) × 180 m (Z-direction), as shown in Figure 15.

Model boundary conditions: The upper surface boundary conditions of the model are free, and the remaining surface boundary conditions are all normal constraints.

Constitutive model: In previous studies, the Mohr–Coulomb (M–C) model, which does not fully consider the engineering characteristics of loess, has been widely used in the numerical analysis of loess tunnels. In this study, in order to improve the simulation accuracy, the Drucker–Prager (D-P) criterion was used. The D–P criterion considers the influence of the intermediate principal stress on the yield and failure; the yield surface is smooth, which can help to avoid the difficulty in the numerical calculation caused by the M–C criterion yield surface at the corners; that is, it avoids the so-called singularity [36,37].

Drucker and Prager put forward the Drucker–Prager criterion [38] in 1952. The expression is

$$\alpha I_1+\sqrt{J_2}-k=0$$

(2)

In the π plane, if the D–P criterion is the inscribed circle of the M–C, then $\alpha$ and $k$ can be expressed by the following formulas:

$$\alpha =\frac{\sin \phi }{\sqrt{3}\sqrt{3+{\sin }^2\phi }}$$

(3)

$$k=\frac{3c\cos \phi }{\sqrt{3}\sqrt{3+{\sin }^2\phi }}$$

(4)

where $I_1$ is the stress tensor first invariant, $J_2$ is the second invariant of stress deviation, $\phi$ is the internal friction angle and $c$ is cohesion.

The loess was cored on-site, and the surrounding rock parameters were determined through laboratory tests (

Table 1. Physical and mechanical parameters of surrounding rock and supporting structure.

Surrounding Rock	Density ρ/(kg·m−3)	Elastic Modulus E/MPa	Poisson’s Ratio (μ)	Internal Friction Angle φ/(°)	Cohesion c/kPa
Q3 loess	1420	12.6	0.38	15.1	20.1
Q2 loess	1460	16.8	0.34	26.6	30.5
Q2 loess	1630	18.9	0.41	30.1	41.3
Reinforcement area	2500	300	0.28	32.3	150.36
Mudstone	2010	48	0.32	33.1	66.2
Primary support	2500	50,500	0.28
Secondary lining	2500	60,000	0.28
Pipe shed support	4840	97,100	0.30

Note: 1. The physical and mechanical parameters of Q₂ loess are divided into two layers, as shown in the table through field coring and laboratory tests. 2. The reinforcement area refers to the range of surrounding rock reinforced by advanced pre-grouting. This range is expressed by improving the elastic modulus, cohesion, and internal friction angle of the surrounding rock.

). The elastoplastic constitutive model was used for the initial support and secondary lining. Because the role of the advanced pre-grouting was to squeeze and strengthen the rock and soil through slurry veins, the simulation was carried out by improving the elastic modulus, cohesion and internal friction angle of the surrounding rock.

The specific steps of the numerical simulation are as follows:

(1)

Establish model grids, assign rock mass parameters, apply static boundary conditions, and then generate the initial ground stress field. Considering the influence of groundwater, apply hydrostatic pressure at the groundwater level.

(2)

Simulate the excavation process, using the three-step-seven-step method for excavation. The width of the upper step is 5 m, the height of the upper step from the vault is 2.2 m, the length of the upper step is 5 m, and the length of the lower step is 9 m. During the excavation process, each cycle of excavation footage is 1 steel arch with a spacing of 0.5 m. The upper arch, upper left pilot pit, upper right pilot pit, core soil and lower bench excavation are each staggered 3 m for parallel operation. The invert closed distance is 12 m from the tunnel face and the excavation step is 3 m.

(3)

The model grid is divided into excavation grid, primary support grid and secondary lining grid. When the tunnel is excavated, to which part of the excavation, the required part is passivated. After the excavation of each part of the steps is completed, the initial support grid is activated by the activation plate, the excavation module is passivated, the initial support is performed, before releasing 30% of the ground stress. In the same way, during the secondary lining construction, the secondary lining grid is activated by the activation plate to passivate the excavation module and the release of 70% of the ground stress.

To simplify the calculation, an equivalent method was adopted to combine the influences of the section steel frame and shotcrete [39]. The formula for this method is as follows:

$$E_c=E_0+\frac{A_s{E}_s}{A_c}$$

(5)

where $E_c$ is the converted concrete elastic modulus, $E_0$ is the original concrete elastic modulus, $A_s$ is the steel arch cross-sectional area, $E_s$ is the steel elastic modulus and $A_c$ is the concrete area. The surrounding rock and support parameters are shown in Table 1.

In order to verify the correctness of the numerical model, the vault settlement and horizontal convergence of the field monitoring data (Figure 11) and the numerical simulation results after reinforcement (Figure 16) were compared and analyzed (

Table 2. Displacement comparison of monitoring points.

Monitoring Position	Measured Value Vm/mm	Numerical Simulation Value Vns/mm	Difference/mm	Relative Error Er/%
Vault settlement	65.1	63.8	1.3	2.00
Horizontal convergence	25	21.9	3.1	12.4

). As shown in Table 2, the measured value of the surrounding rock vault settlement $X_{vs}$ was 65 mm and the simulated value $X_{vs}$ was 63.8 mm, corresponding to a relative error of 2.00%. The measured value of the horizontal convergence of the surrounding rock $X_{hc}$ was 25 mm, the simulated value $X_{hc}$ was 21.9 mm and the relative error was 12.4%, which were all within the allowable error range. This shows that the numerical model described in this article was reliable.

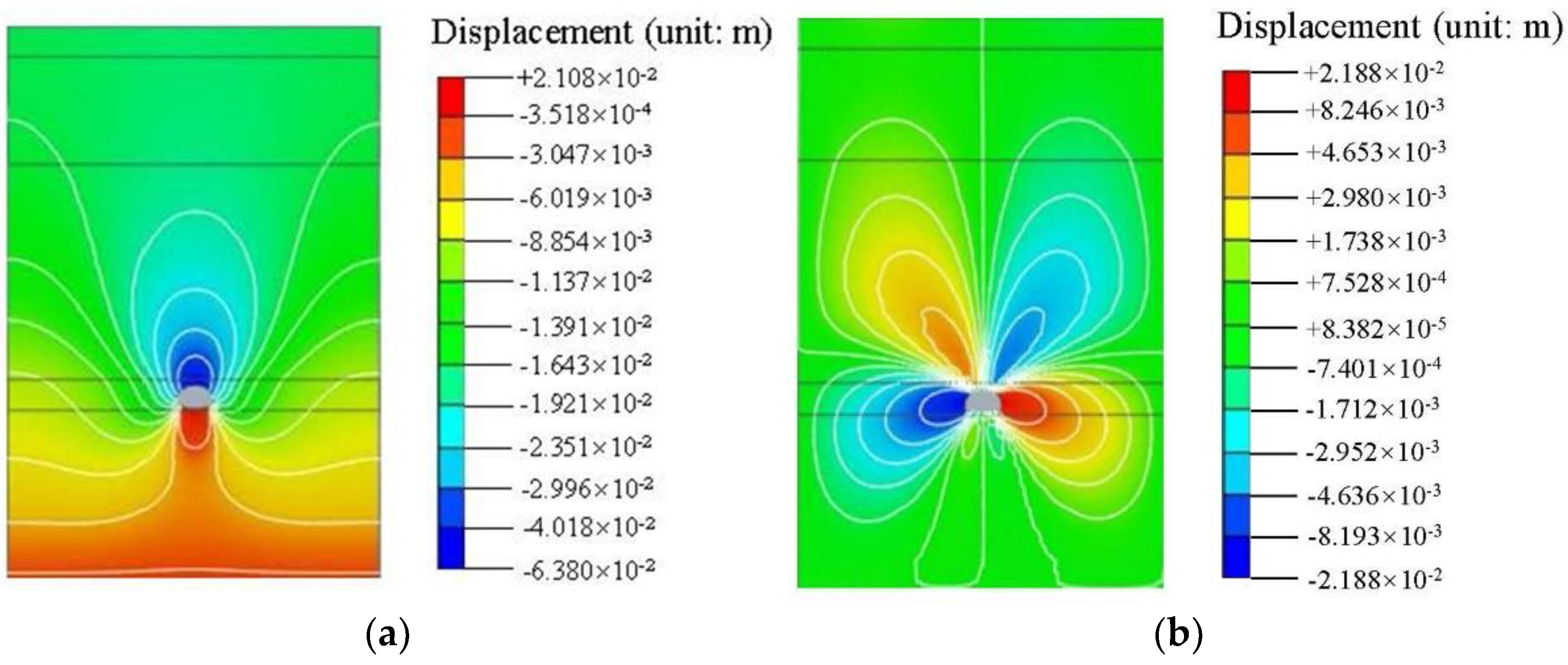
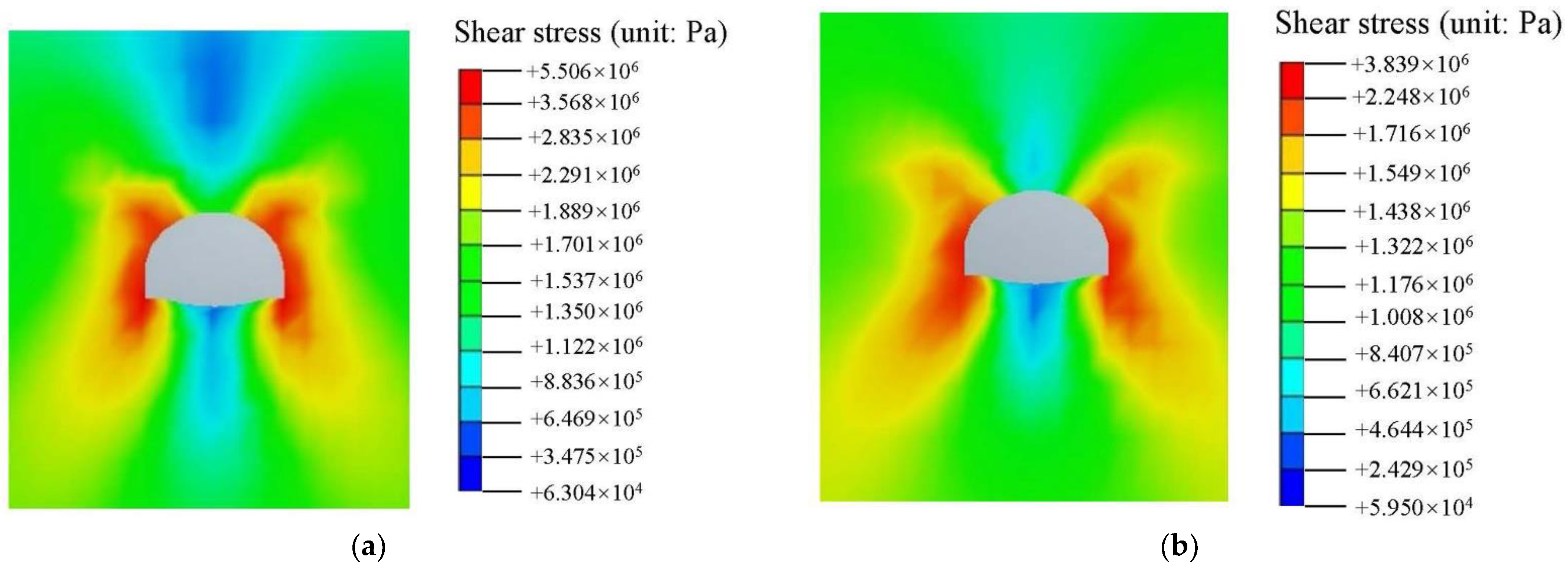
4.2. Stress Analysis of Surrounding Rock

Considering the two calculation work conditions of the original design scheme and the scheme after the collapse treatment, the stress nephograms of the tunnel surrounding rock after excavation under the two conditions were obtained by numerical simulations, as shown in Figure 17, Figure 18 and Figure 19. The surrounding rock stress was extracted at each position on the left side of the tunnel center line in the figures. The results are shown in

Table 3. Comparison of surrounding rock stress before and after reinforcement.

Monitoring Position	Vertical Stress Sv/MPa			Horizontal Stress Sh/MPa			Shear Stress Ss/MPa
	Original Case Co/MPa	Reinforced Case Cr/MPa	Difference (%)	Original Case Co/MPa	Reinforced Case Cr/MPa	Difference (%)	Original Case Co/MPa	Reinforced Case Cr/MPa	Difference (%)
Vault	2.6	1.3	50.0	1.0	0.5	50.0	1.6	0.8	50.0
Left shoulder	7.3	3.8	47.9	1.2	0.6	50.0	3.9	2.0	48.7
Left arch waist	8.3	5.2	37.3	1.8	0.9	50.0	3.7	2.4	35.1
Left wall	10.0	7.6	24.0	2.0	1.3	35.0	4.4	3.3	25.0
Left arch foot	10.5	6.3	40.0	0.9	0.6	33.3	5.4	3.1	42.6
Invert center line	0.82	0.51	39	1.1	0.85	22.7	0.65	0.46	29.2

.

Based on the results in Figure 17, Figure 18 and Figure 19 and Table 3, tensile stress appeared at the top and bottom of the tunnel. After the collapse treatment, the vertical stress, horizontal stress, and shear stress decreased significantly. The stress of the surrounding rock above the arch waist decreased by more than 35% and that at the arch crown reached 50%. There was no stress concentration in various parts of the tunnel. Therefore, the treatment measures for the collapse section described in this paper were effective.

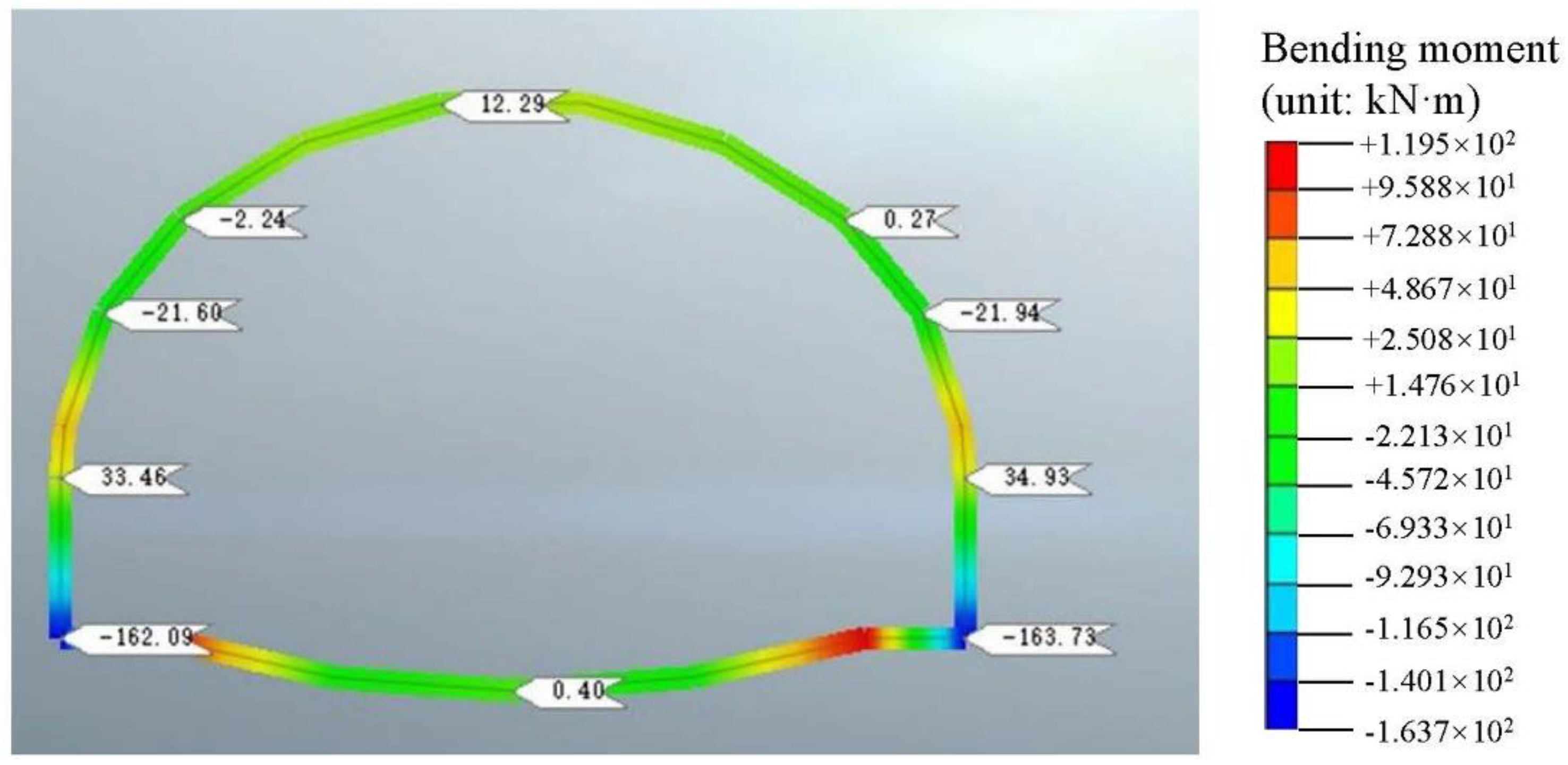
4.3. Internal Force Analysis of Initial Support

The initial support axial force and bending moment diagrams of the tunnel are shown in Figure 20 and Figure 21, respectively (taking the collapse treatment as an example). The axial forces on the vault, arch waist, and sidewall were all pressure forces, while the middle part of the inverted arch experienced tension forces. After treatment, the maximum axial compression force of the initial support occurred at the arch waist, with a value of −5253.45 kN/m. The thickness of the concrete slab element in the model was 0.32 m, so the maximum axial compressive force at the arch waist was −1681.1 kN. The maximum axial tensile force occurring at the inverted arch was 552.08 kN. The maximum bending moment occurred at the right corner, with a value of −163.73 kN·m/m. The thickness of the concrete slab element in the model was 0.32 m, so the maximum bending moment at the right corner was −52.13 kN·m.

According to the Code for the Design of Highway Tunnels [40], the strengths of the concrete eccentric compression members were checked according to the failure stage. The formula was as follows:

$$K=\frac{N_{limit}}{N}\ge K_{regulations}$$

(6)

where $K$ is the safety factor of the tunnel lining structure. When the concrete reaches the ultimate compressive or shear strength, the safety factor should be ≥2.0. When the concrete reaches the ultimate tensile strength, the safety factor should be ≥2.4.

When controlled by compressive strength, that is, $e=\frac{M}{N}\le 0.2h$, the ultimate bearing capacity is calculated as follows:

$$N_{{}_{limit}}=\phi \alpha R_{a}bh$$

(7)

where $e$ is the eccentricity, $M$ is the bending moment, $N$ is the axial force, $\phi$ is the longitudinal coefficient of the member, taken as $\phi =1$, $R_a$ is the ultimate compressive strength of concrete, $b$ is the section width and $\alpha$ is the eccentricity influence coefficient of the axial force. The value $\alpha$ is determined according to the following empirical formula:

$$\alpha =1-1.5\frac{e}{h}$$

(8)

where $h$ is the section thickness.

When controlled by tensile strength, that is, $e=\frac{M}{N}\le 0.2h$, the ultimate bearing capacity is calculated as follows:

$$N_{{}_{{}_{{}_{limit}}}}=\phi \frac{1.75R_{1}bh}{\frac{6e}{h}-1}$$

(9)

where $R_1$ is the ultimate tensile strength of concrete.

According to the above formula, the safety factors of each position in the original design scheme (

Table 4. Safety factor of each position in the original design scheme.

Monitoring Position	Axial Force Fz/kN	Bending Moment Mb/(kN·m)	Failure Type	K	Meets Safety Factor Requirement?
Vault	−534.32	77.32	Tensile	1.2	No
Left 45°	−2501.31	−43.80	Compressive	2.3	Yes
Left 60°	−2788.58	−60.58	Compressive	2.1	Yes
Left 90°	−772.67	44.05	Compressive	5.9	Yes
Left footwall	−406.47	−222.08	Tensile	0.3	No
Right 45°	−2540.80	−37.80	Compressive	2.3	Yes
Right 60°	−2835.99	−61.98	Compressive	2.1	Yes
Right 90°	−758.49	45.87	Compressive	5.9	Yes
Right footwall	−418.17	−224.23	Tensile	0.3	No
Invert center line	775.72	−0.43	Compressive	8.2	Yes

) and reinforcement treatment (

Table 5. Safety factor of each position after collapse treatment.

Monitoring Position	Axial Force Fz/kN	Bending Moment Mb/(kN·m)	Failure Type	K	Meets Safety Factor Requirement?
Vault	−38.29	3.91	Tensile	3.7	Yes
Left 45°	−953.28	−0.72	Compressive	6.5	Yes
Left 60°	−1435.70	−6.87	Compressive	4.2	Yes
Left 90°	−549.84	10.61	Compressive	10.3	Yes
Left footwall	−314.32	−51.61	Tensile	2.7	Yes
Right 45°	−959.65	0.08	Compressive	6.5	Yes
Right 60°	−1444.89	−6.98	Compressive	4.2	Yes
Right 90°	−540.27	11.08	Compressive	10.4	Yes
Right footwall	−316.01	−52.13	Tensile	2.6	Yes
Invert center line	552.08	0.11	Compressive	11.3	Yes

) were calculated. As shown in Table 4, when using the original design scheme, the safety factors of the arch crown and the left and right corners did not meet the required value of 2.4 specified in the code [26]. Other locations were resistant to compression damage. Although the safety factor met the required value of 2.0, the safety factor was generally low. After the collapse treatment, the safety factors at each position of the initial support met the requirements. The minimum safety factors at the left and right wall feet were 2.7 and 2.6, respectively, but they were also greater than the tensile strength safety factor of the reinforced concrete structure of 2.4. Thus, the collapse treatment measures proposed in this paper meet the engineering requirements and can serve as references for similar projects.

4.4. Discussion

When a deep-buried tunnel collapses, a collapsed arch is generally formed and no roof fall occurs. The cause of the deep-buried loess tunnel and its 120 m roof described in this study (the first case in China) was only preliminarily examined. More in-depth research needs to be carried out. The collapse treatment measures proposed in this paper are highly reliable and ensure a one-time passage through the collapsed section, but the cost is high and the construction period is long. The cost of this scheme was about 16.64 million CNY (including 14.64 million CNY for collapse treatment and 2 million CNY for secondary excavation construction) and the construction period was 135 days. Better treatment measures need to be proposed. However, the research results in this article offer a certain reference value for the treatment of tunnel collapse accidents when crossing loess under similar conditions. They also provide reliable support for the design of parameters and construction methods for similar section tunnel excavations in the future. From the loess tunnel collapse case described in this article, the following recommendations can be proposed.

(1)

Exploration stage. Determine the geological and hydrogeological engineering conditions of the location of the tunnel. On this basis, the influence of the local climate in particular should be taken into account, while the timing of the rainy season and the amount of rainfall should be ascertained to guide the design and construction.

(2)

Design stage. According to the survey results and tunnel design specifications, two tunnel support parameters should be proposed. One is the tunnel support parameter through the dry section, and the other is the tunnel support parameter through the water-rich section.

(3)

Construction stage. Increase the frequency of on-site monitoring and measurement, and implement the primary support and secondary lining in time. Learn to be flexible in extreme weather (such as continuous rainfall) and implement advanced support in a timely manner to prevent the tunnel from collapsing.

5. Conclusions

The collapse of the deep-buried loess tunnel with the largest cross-section in China was examined in this paper. The tunnel collapse scenario was described, corresponding engineering measures were proposed and the collapse treatment measures were comprehensively evaluated. The main conclusions were as follows:

(1)

The development of vertical joints in loess makes it highly water sensitive; the strength decreases significantly after encountering water. The special properties of loess and the synergistic effect of groundwater were internal causes of the tunnel’s collapse. Atmospheric precipitation contributed to the collapse to a certain extent and limited initial support, which is an external inducing factor of tunnel collapse. Human factors, such as low support parameters, the untimely application of the secondary lining, and untimely measurement, were important reasons for this water gushing and collapse accident.

(2)

Comprehensive treatment measures inside and outside the tunnel were proposed (advanced pre-grouting of the collapse body, reinforcement of the advance pipe shed, drilling of drainage holes to strengthen drainage, radial grouting in the tunnel, backfill of gravel back pressure, filling in the cavities in the caves with mortar, using the ground surface as a water-sealing layer and setting up drainage and interception ditches).

(3)

The field monitoring results showed that after the collapse treatment, the maximum settlement of the tunnel vault $X_{vs max}$ was 65.1 mm, the maximum settlement rate $V_{sr max}$ was 12.8 mm/d, the maximum horizontal convergence $X_{hc max}$ was 25 mm, the maximum convergence rate $X_{cr max}$ was 4.3 mm/d, the maximum surrounding rock pressure $F_{sr max}$ was 0.56 MPa and the maximum stress of steel arch frame ${\sigma }_{saf max}$ was 54.34 MPa. The variation of the curve was relatively stable and the value did not show a large sudden increase or decrease, indicating that the treatment measures effectively controlled the pressure and deformation of the surrounding rock and reduced the construction risk.

(4)

The numerical simulation results showed that after the collapse treatment, the vertical stress, horizontal stress and shear stress of the surrounding rock were greatly reduced. The safety factors on the left and right sides of the wall foot of the initial support were the smallest, with values of 2.7 and 2.6, respectively, but they also met the requirements of the specifications. During tunnel construction, attention should be paid to the advanced reinforcement of the tunnel face.