Tailored Magnetic Linear Birefringence in Wedge-Shaped Co Nanocluster Assemblies
Abstract
1. Introduction
2. Materials and Methods
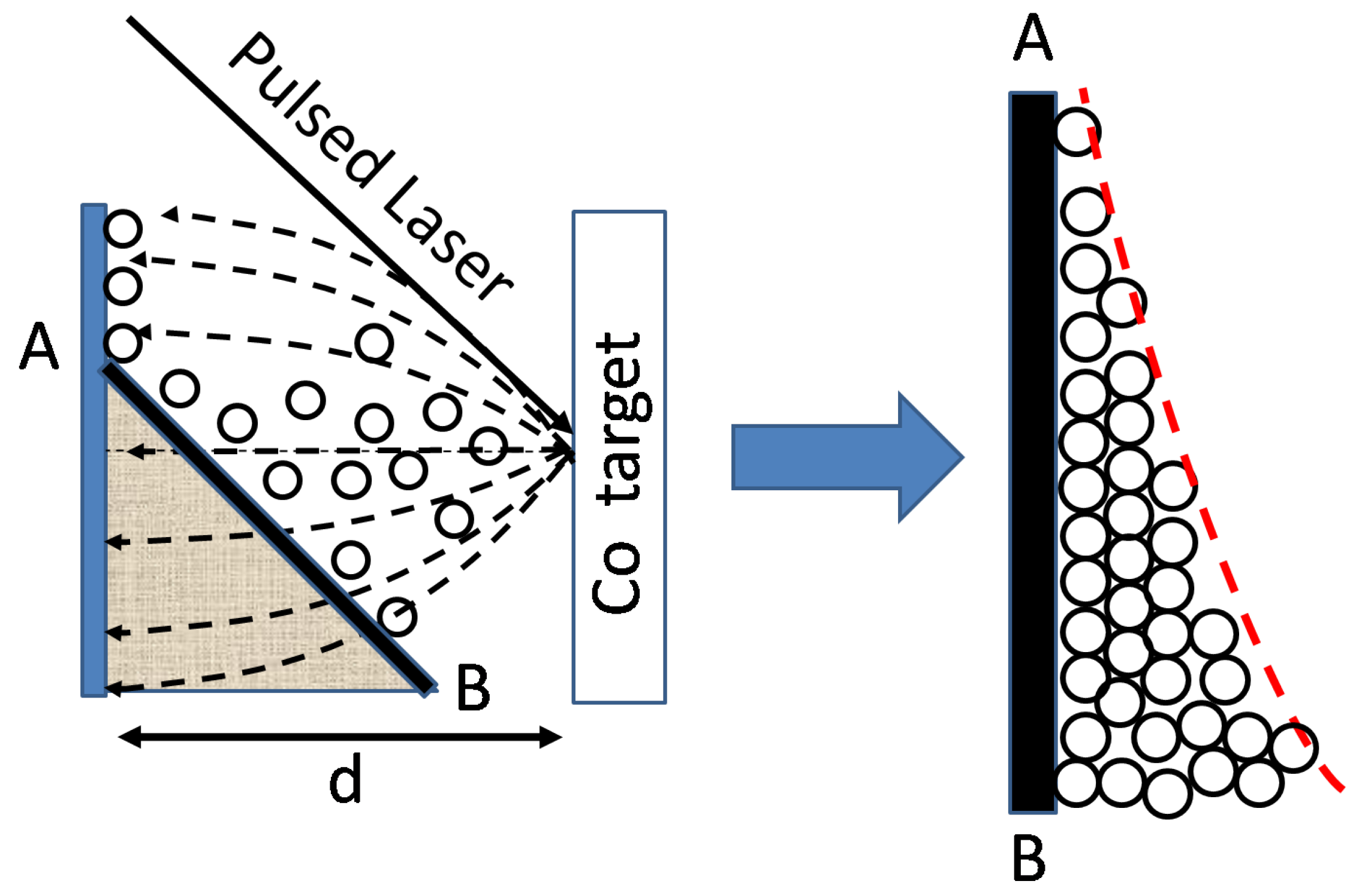
2.1. Preparation of Wedged 2D Assemblies of Co Nanoclusters in Off-Axis Geometry
2.2. Topography and Thickness Characterization
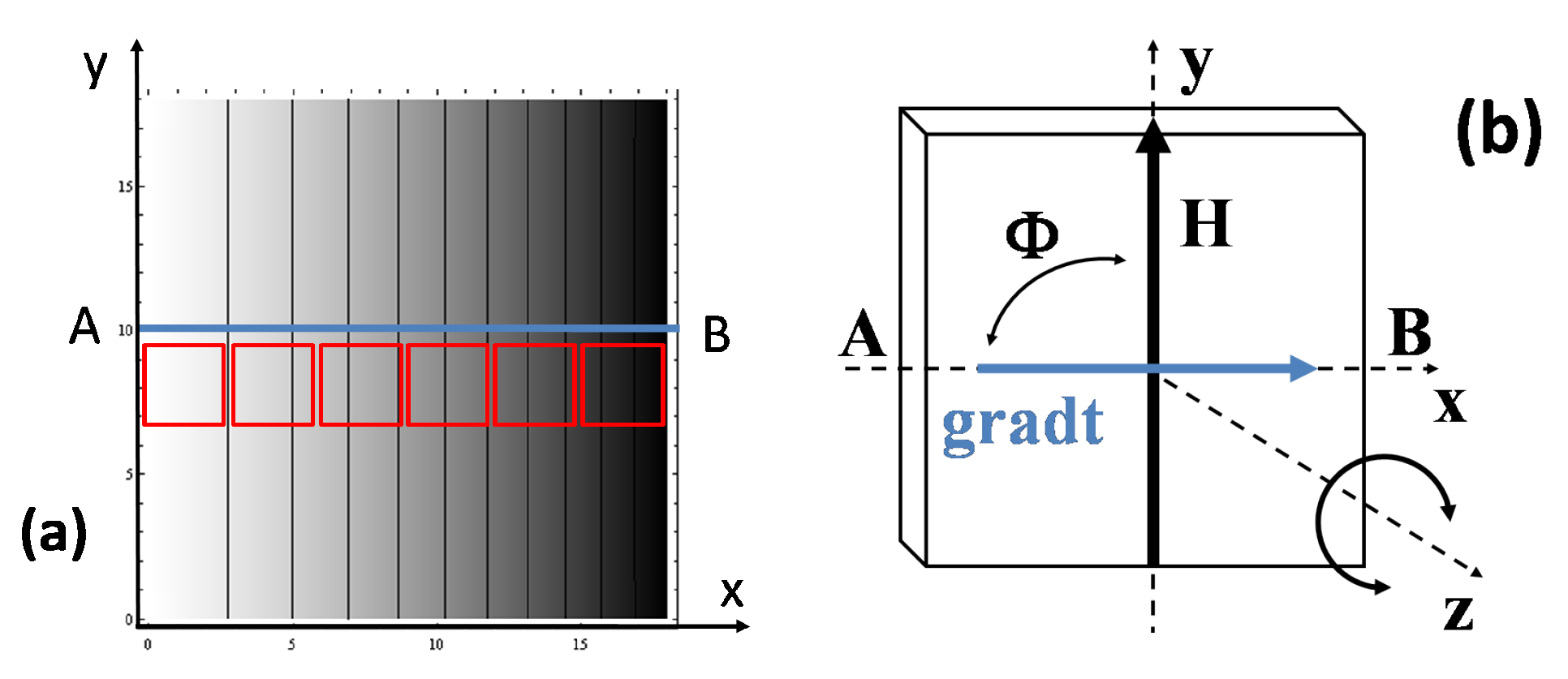
2.3. Surface Magnetization Characterization
3. Results
3.1. Thickness Profile
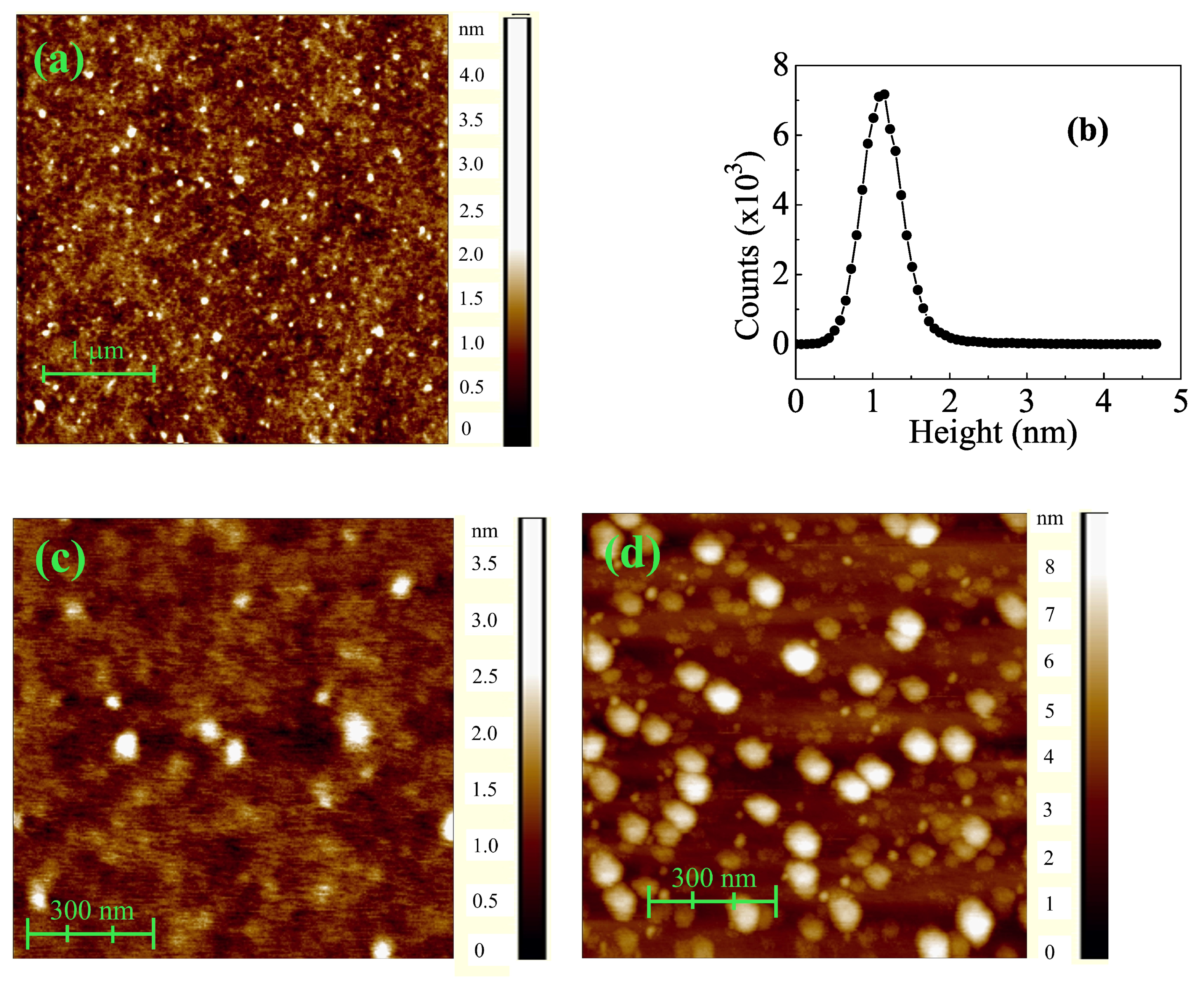
3.2. AFM Topography
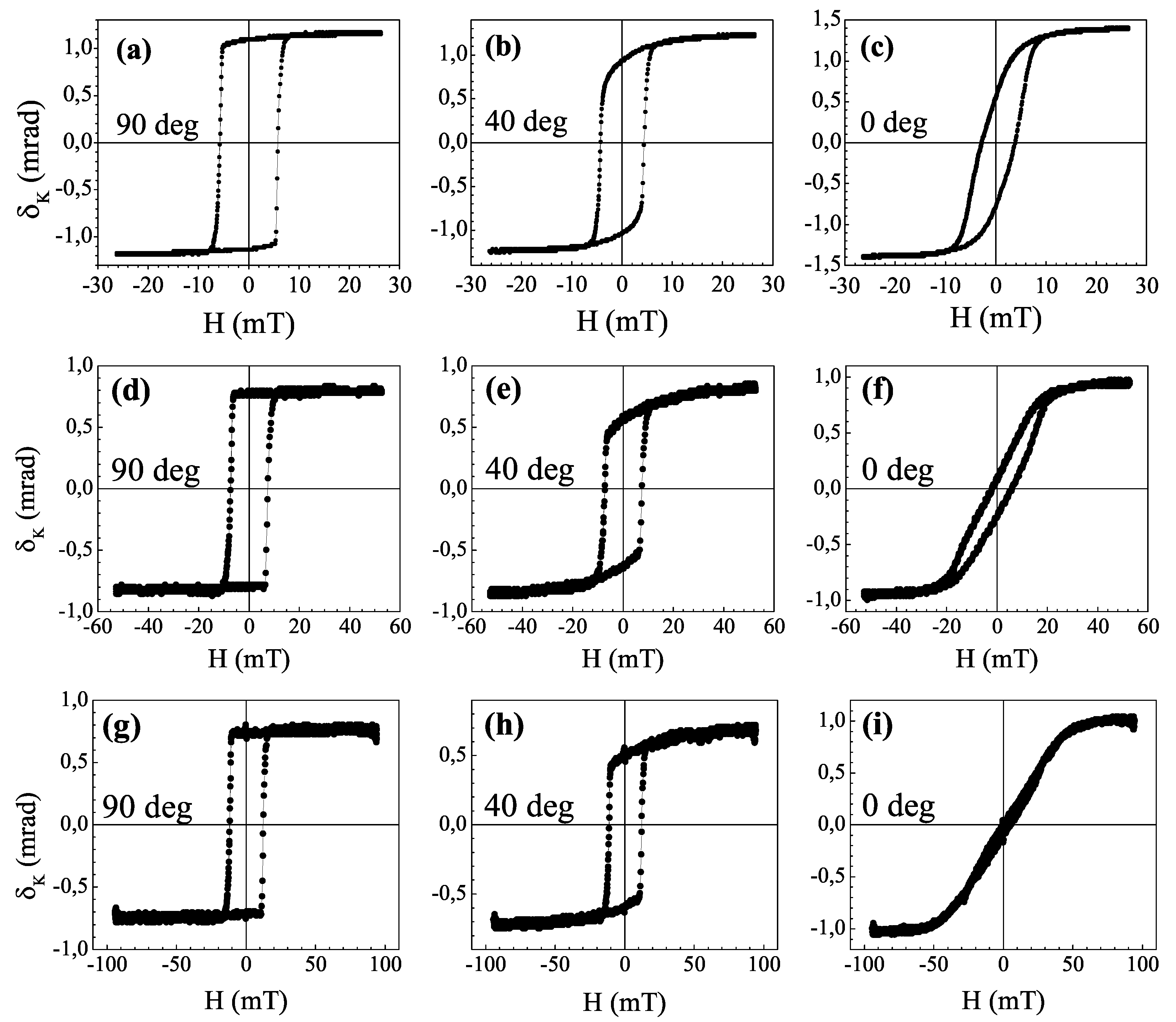
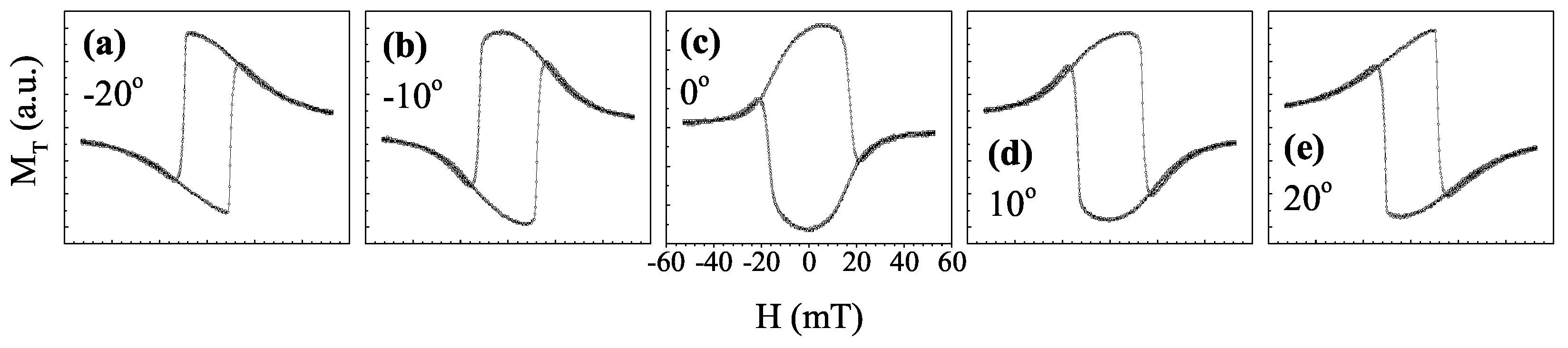
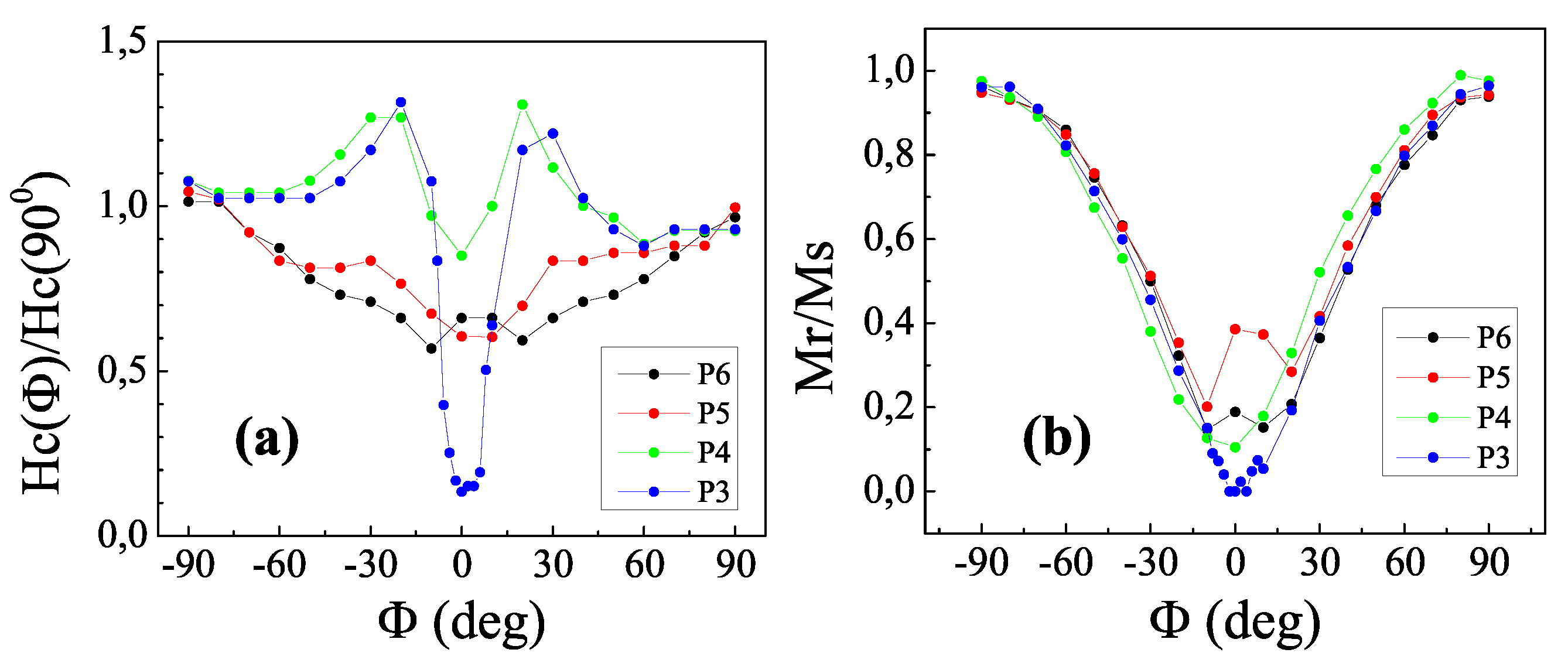
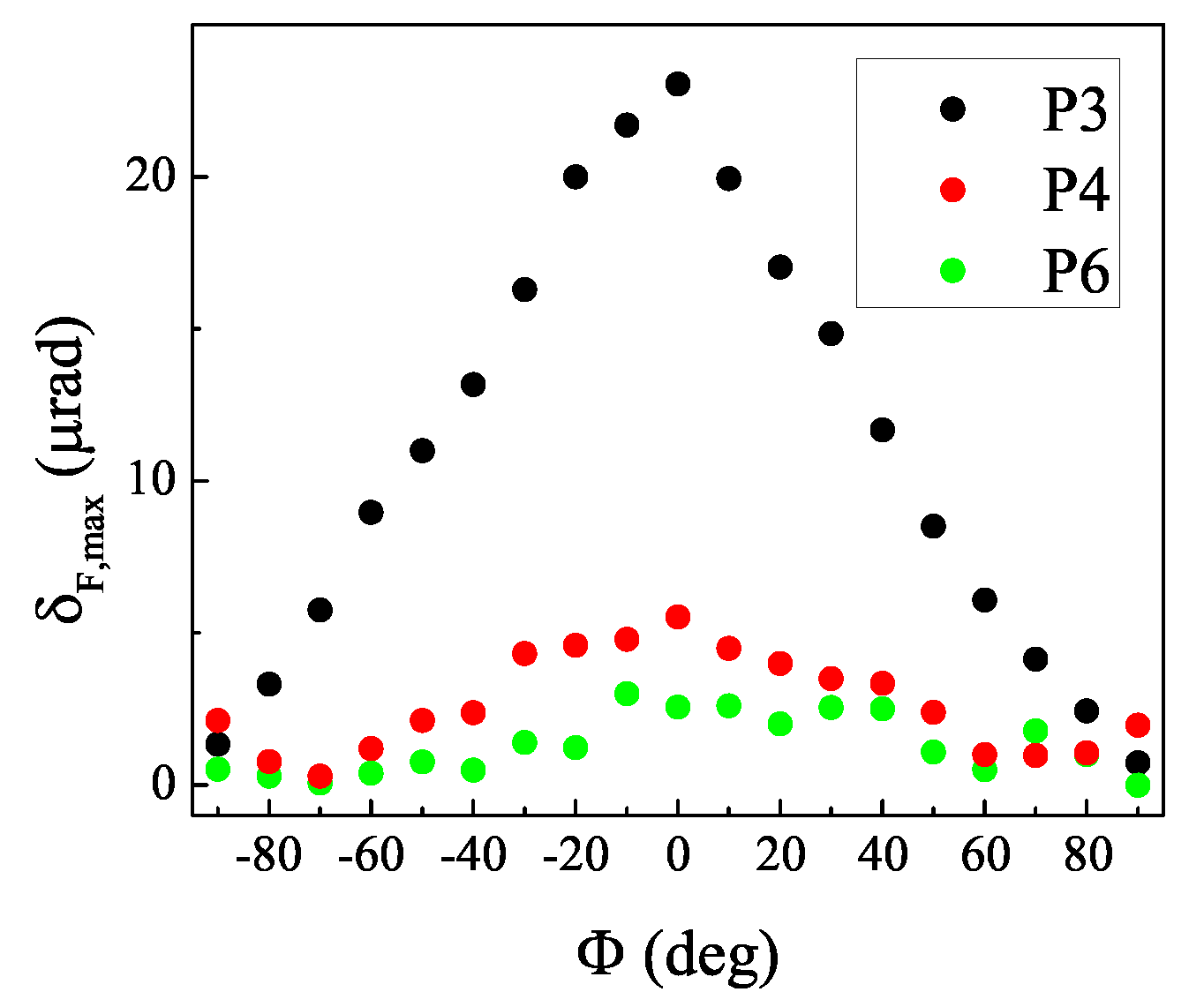
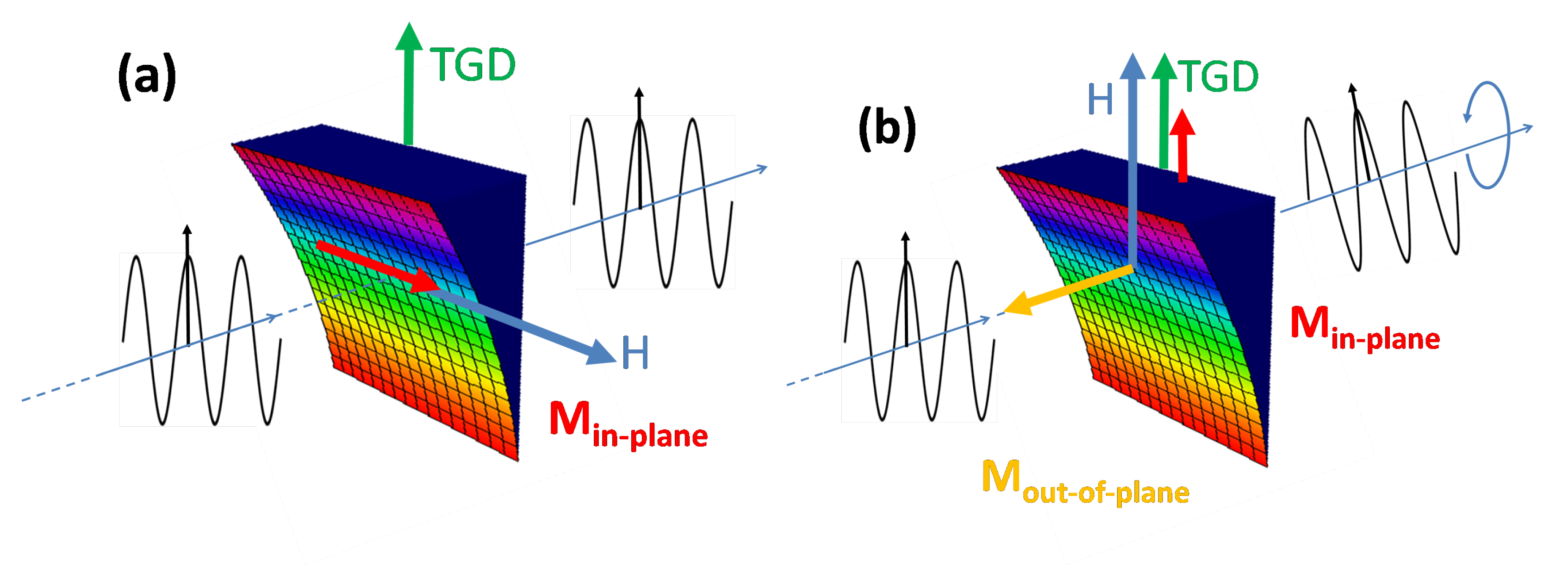
3.3. Magneto-Optical Effect in Reflection Configuration
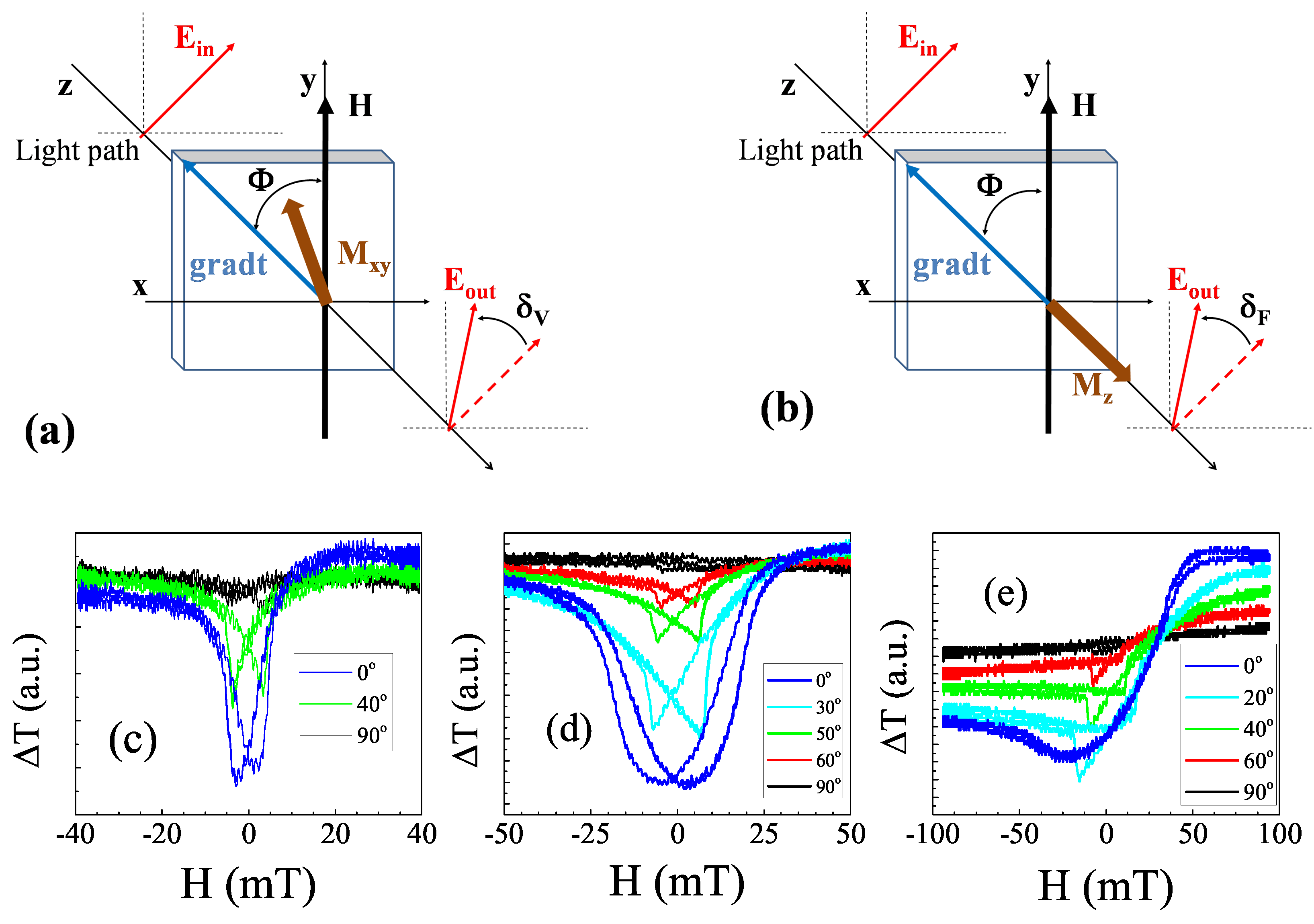
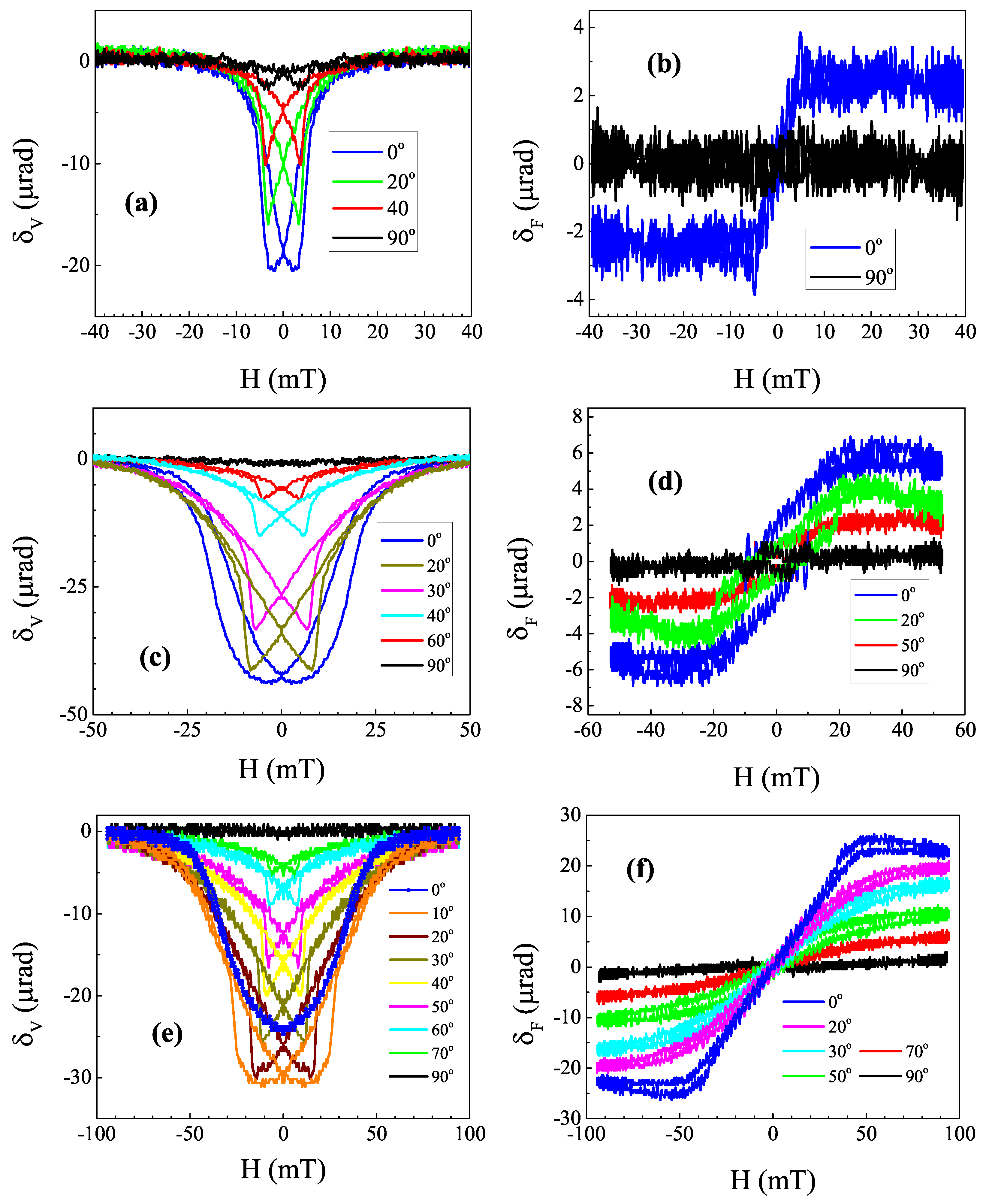
3.4. Magneto-Optical Effect in Transmission Configuration
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PLA | Pulsed laser ablation |
| TGD | Thickness gradient direction |
| UMA | Uniaxial magnetic anisotropy |
| MLB | Magnetic linear birefringence |
| MOKE | Magneto-optical Kerr effect |
| MOFE | Magneto-optical Faraday effect |
| MOVE | Magneto-optical Voigt effect |
References
- Chen, X.Y.; Lu, Y.F.; Cho, B.J.; Zeng, Y.P.; Zeng, J.N.; Wu, Y.H. Pattern-induced ripple structures at silicon-oxide/silicon interface by excimer laser irradiation. Appl. Phys. Lett. 2002, 81, 1344–1347. [Google Scholar] [CrossRef]
- Harzic, R.L.; Schuck, H.; Sauer, D.; Anhut, T.; Riemann, I.; König, K. Sub-100 nm nanostructuring of silicon by ultrashort laser pulses. Opt. Express 2005, 13, 6651–6655. [Google Scholar] [CrossRef] [PubMed]
- Arranz, M.A.; Sánchez, E.H.; Rebollar, E.; Castillejo, M.; Colino, J.M. Form and magnetic birefringence in undulated Permalloy/PET films. Opt. Express 2019, 27, 21285–21294. [Google Scholar] [CrossRef]
- Richter, S.; Miese, C.; Döring, S.; Zimmermann, F.; Withford, M.J.; Tünnermann, A.; Nolte, S. Laser induced nanogratings beyond fused silica-periodic nanostructures in borosilicate glasses and ULETM. Opt. Mat. Express 2013, 3, 1161–1166. [Google Scholar] [CrossRef]
- Yang, P.; Burns, G.R.; Guo, J.; Luk, T.S.; Vawter, G.A. Femtosecond laser-pulse-induced birefringence in optically isotropic glass. J. Appl. Phys. 2004, 95, 5280–5283. [Google Scholar] [CrossRef]
- Ali, M. Growth and Study of Magnetostrictive FeSiBC thin Films for Device Applications. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 1999. [Google Scholar]
- Sokolov, A. Optical Properties of Metals, 1st ed.; Blackie: London, UK, 1967. [Google Scholar]
- Carey, R.; Thomas, B.W.J.; Viney, I.V.F.; Weaver, G.H. Magnetic birefringence in thin ferromagnetic films. J. Phys. D 1968, 1, 1679. [Google Scholar] [CrossRef]
- Moroni, R.; Sekiba, D.; de Mongeot, F.B.; Gonella, G.; Boragno, C.; Mattera, L.; Valbusa, U. Uniaxial magnetic anisotropy in nanostructured Co/Cu(001): From surface ripples to nanowires. Phys. Rev. Lett. 2003, 91, 7027–7030. [Google Scholar] [CrossRef]
- Arranz, M.A.; Colino, J.M. Angular tuning of the magnetic birefringence in rippled cobalt films. Appl. Phys. Lett. 2015, 106, 3102–3105. [Google Scholar] [CrossRef]
- Carcia, P.F.; Mcinhaldt, A.D.; Suna, A. Perpendicular magnetic anisotropy in Pd/Co thin film layered structure. Appl. Phys. Lett. 1985, 47, 178–180. [Google Scholar] [CrossRef]
- Johnson, M.T.; Bloemen, P.J.H.; den Broeder, F.J.A.; de Vries, J.J. Magnetic anisotropy in metallic multilayers. Rep. Prog. Phys. 1996, 59, 1409–1458. [Google Scholar] [CrossRef]
- Jungblut, R.; Johnson, M.T.; aan de Stegge, J.; Reinders, A.; den Broeder, F.J.A. Orientational and structural dependence of magnetic anisotropy of Cu/Ni/Cu sandwiches: Misfit interface anisotropy. J. Appl. Phys. 1994, 75, 6425. [Google Scholar] [CrossRef]
- Gradmann, U. Surface Magnetism. J. Magn. Magn. Mater. 1991, 100, 481–496. [Google Scholar] [CrossRef]
- Nguyen, T.V.A.; Shiratsuchi, Y.; Sato, H.; Ikeda, S.; Endoh, T.; Endo, Y. Magnetic properties of Co film in Pt/Co/Cr2O3/Pt structure. AIP Adv. 2020, 10, 015152. [Google Scholar] [CrossRef]
- Kisielewski, M.; Maziewski, A.; Kurant, Z.; Tekielak, M.; Wawro, A.; Baczewski, L.T. Magnetic ordering in ultrathin cobalt film covered by an overlayer of noble metal. J. Appl. Phys. 2003, 93, 7628. [Google Scholar] [CrossRef]
- Jamal, M.S.; Guptab, P.; Kumara, D. Preferential alignment of Co moments at Oxide/Co interface in Si/Co/Co-oxide/CoWedge/Pt structure. Thin Solid Films 2020, 709, 138246. [Google Scholar] [CrossRef]
- Stupakiewicz, A.; Maziewski, A.; Matlak, K.; Spiridis, N.; Ślȩzak, M.; Ślȩzak, T.; Zaja, M.; Korecki, J. Tailoring of the Perpendicular Magnetization Component in Ferromagnetic Films on a Vicinal Substrate. Phys. Rev. Lett. 2008, 101, 217202. [Google Scholar] [CrossRef] [PubMed]
- Laidler, H.; Hickey, B.J. Anisotropy of an ultrathin Cu(111)/Co(111)/Cu(111) wedge. J. Phys. Condens. Matter 2000, 12, 8401–8410. [Google Scholar] [CrossRef]
- Suess, D. Multilayer exchange spring media for magnetic recording. Appl. Phys. Lett. 2006, 89, 113105. [Google Scholar] [CrossRef]
- Kirby, B.J.; Davies, J.E.; Liu, K.; Watson, S.M.; Zimanyi, G.T.; Shull, R.D.; Kienzle, P.A.; Borchers, J.A. Vertically graded anisotropy in Co/Pd multilayers. Phys. Rev. B 2010, 81, 100405. [Google Scholar] [CrossRef]
- Arranz, M.A.; Colino, J.M.; Palomares, F.J. On the limits of uniaxial magnetic anisotropy tuning by a ripple surface pattern. J. Appl. Phys. 2014, 115, 3906–3914. [Google Scholar] [CrossRef]
- Palik, E.D. The use of polarized infrared radiation in magneto-optical studies of semiconductors. Appl. Opt. 1963, 2, 527. [Google Scholar] [CrossRef]
- Krebs, H.U. Pulsed Laser Deposition of Thin Films. Applications-Led Growth of Functional Materials, 1st ed.; Chapter 16: Pulsed Laser Deposition of Metals; Wiley: Hoboken, NJ, USA, 2007; p. 363. [Google Scholar]
- Yamamuro, S.; Sumiyama, K.; Kamiyama, T.; Suzuki, K. Morphological and magnetic characteristics of monodispersed Co-cluster assemblies. J. Appl. Phys. 1999, 86, 5726. [Google Scholar] [CrossRef]
- Stupakiewicz, A.; Fleurence, A.; Maziewski, A.; Maroutian, T.; Gogol, P.; Bartenlian, B.; Mégy, R.; Beauvillain, P. Magnetization Processes in Ultrathin Co Film Grown on Stepped Si(111) Substrate. IEEE Trans. Magn. 2008, 44, 2887. [Google Scholar] [CrossRef]
- Vinogradov, A.; Dorofeenko, A.; Merzlikin, A.; Strelniker, Y.; Lisyansky, A.; Granovsky, A.; Bergman, D. Magnetophotonics: From Theory to Applications, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2013; p. 24. [Google Scholar]
- Muduli, P.; Rice, W.; He, L.; Collins, B.; Chu, Y.; Tsui, F. Study of magnetic anisotropy and magnetization reversal using the quadratic magnetooptical effect in epitaxial CoxMnyGez(111) films. J. Phys. Condens. Matter. 2009, 21, 296005. [Google Scholar] [CrossRef][Green Version]
- Hamrle, J.; Blomeier, S.; Gaier, O.; Hillebrands, B.; Schneider, H.; Jakob, G.; Postava, K.; Felser, C. Huge quadratic magneto-optical Kerr effect and magnetization reversal in the Co2FeSi Heusler compound. J. Phys. D Appl. Phys. 2007, 40, 1563. [Google Scholar] [CrossRef][Green Version]
- Arranz, M.A.; Colino, J.M. Magnetooptical Voigt effect in rippled polycrystalline Co films. J. Phys. D Appl. Phys. 2016, 49, 5306–5313. [Google Scholar] [CrossRef]
- Fallarino, L.; Riego, P.; Kirby, B.; Miller, C.; Berger, A. Modulation of Magnetic Properties at the Nanometer Scale in Continuously Graded Ferromagnets. Materials 2018, 11, 251. [Google Scholar] [CrossRef]
- Zha, C.; Dumas, R.; Fang, Y.; Bonanni, V.; Nogués, J.; Åkerman, J. Continuously graded anisotropy in single (Fe53Pt47)100-xCux films. Appl. Phys. Lett. 2010, 97, 182504. [Google Scholar] [CrossRef]
- Gräfe, J.; Haering, F.; Tietze, T.; Audehm, P.; Weigand, M.; Wiedwald, U.; Ziemann, P.; Gawroński, P.; Schütz, G.; Goering, E.J. Perpendicular magnetisation from in-plane fields in nano-scaled antidot lattices. Nanotechnology 2015, 26, 225203. [Google Scholar] [CrossRef]

| Square | P1 | P2 | P3 | P4 | P5 | P6 |
| Thickness (nm) | 1.58 | 2.32 | 5.41 | 11.5 | 18.26 | 24.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arranz, M.A.; Sánchez, E.H.; Ruiz-Díez, V.; Sánchez-Rojas, J.L.; Colino, J.M. Tailored Magnetic Linear Birefringence in Wedge-Shaped Co Nanocluster Assemblies. Appl. Sci. 2022, 12, 100. https://doi.org/10.3390/app12010100
Arranz MA, Sánchez EH, Ruiz-Díez V, Sánchez-Rojas JL, Colino JM. Tailored Magnetic Linear Birefringence in Wedge-Shaped Co Nanocluster Assemblies. Applied Sciences. 2022; 12(1):100. https://doi.org/10.3390/app12010100
Chicago/Turabian StyleArranz, Miguel A., Elena H. Sánchez, Víctor Ruiz-Díez, José L. Sánchez-Rojas, and José M. Colino. 2022. "Tailored Magnetic Linear Birefringence in Wedge-Shaped Co Nanocluster Assemblies" Applied Sciences 12, no. 1: 100. https://doi.org/10.3390/app12010100
APA StyleArranz, M. A., Sánchez, E. H., Ruiz-Díez, V., Sánchez-Rojas, J. L., & Colino, J. M. (2022). Tailored Magnetic Linear Birefringence in Wedge-Shaped Co Nanocluster Assemblies. Applied Sciences, 12(1), 100. https://doi.org/10.3390/app12010100








