Noise Reduction Effect of Superhydrophobic Surfaces with Streamwise Strip of Channel Flow
Abstract
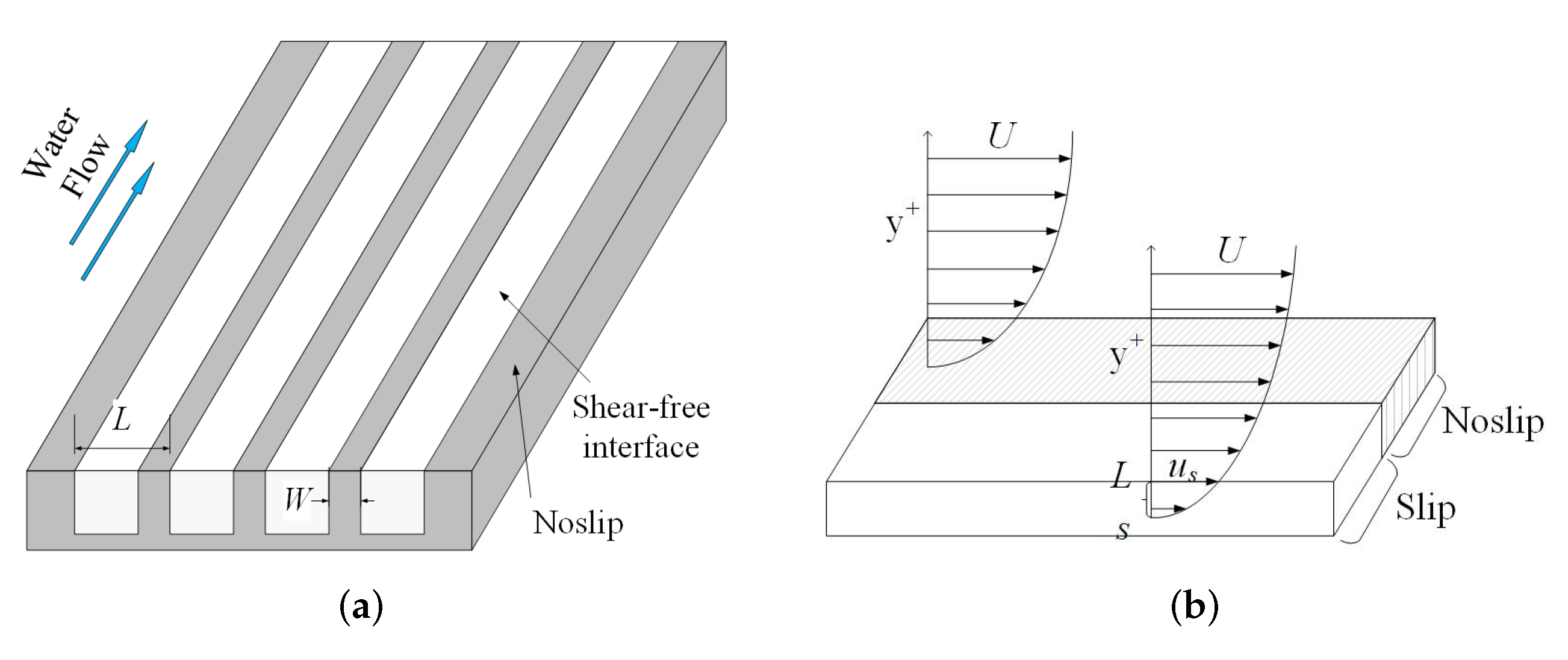
1. Introduction and Principle Headings
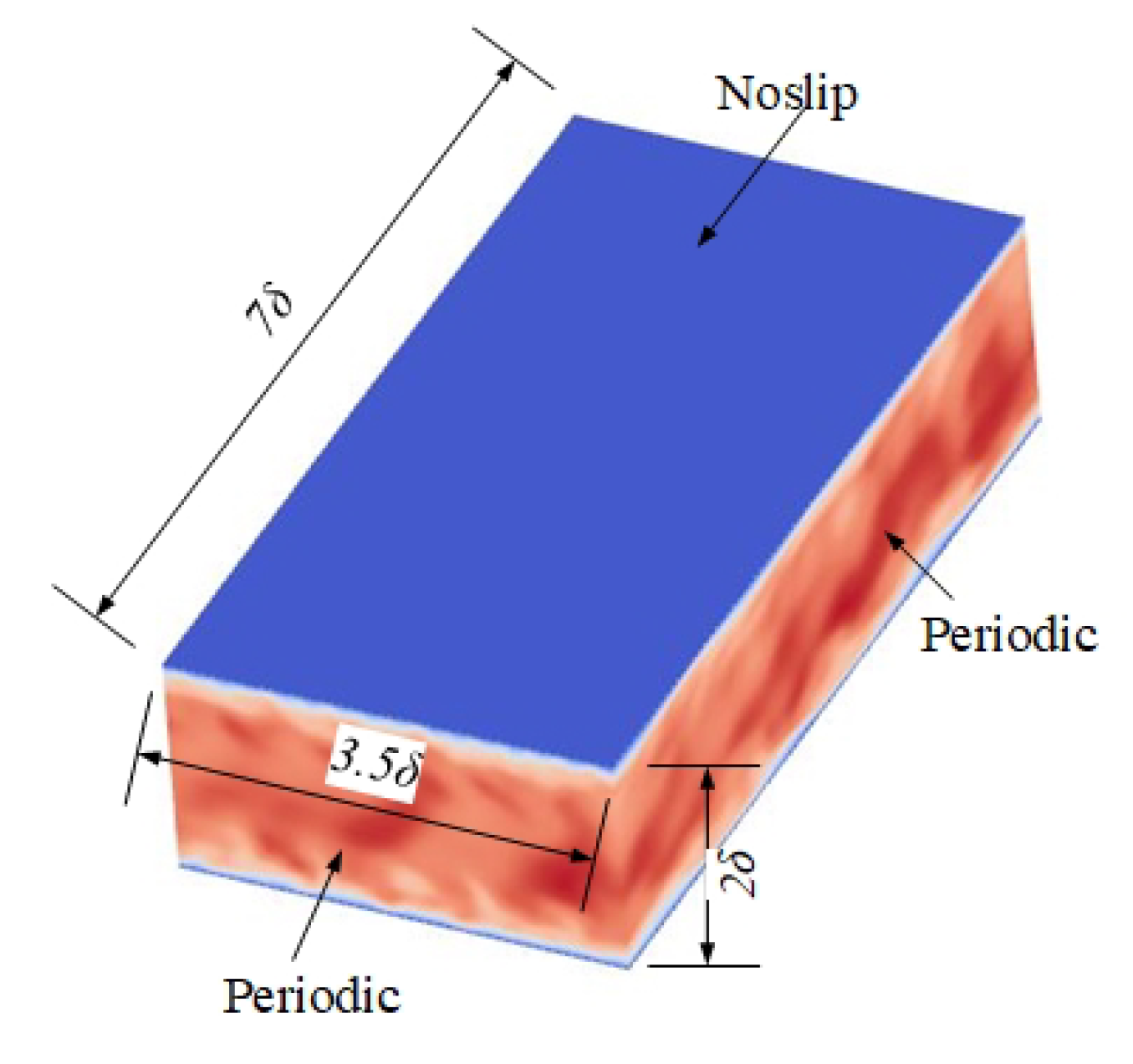
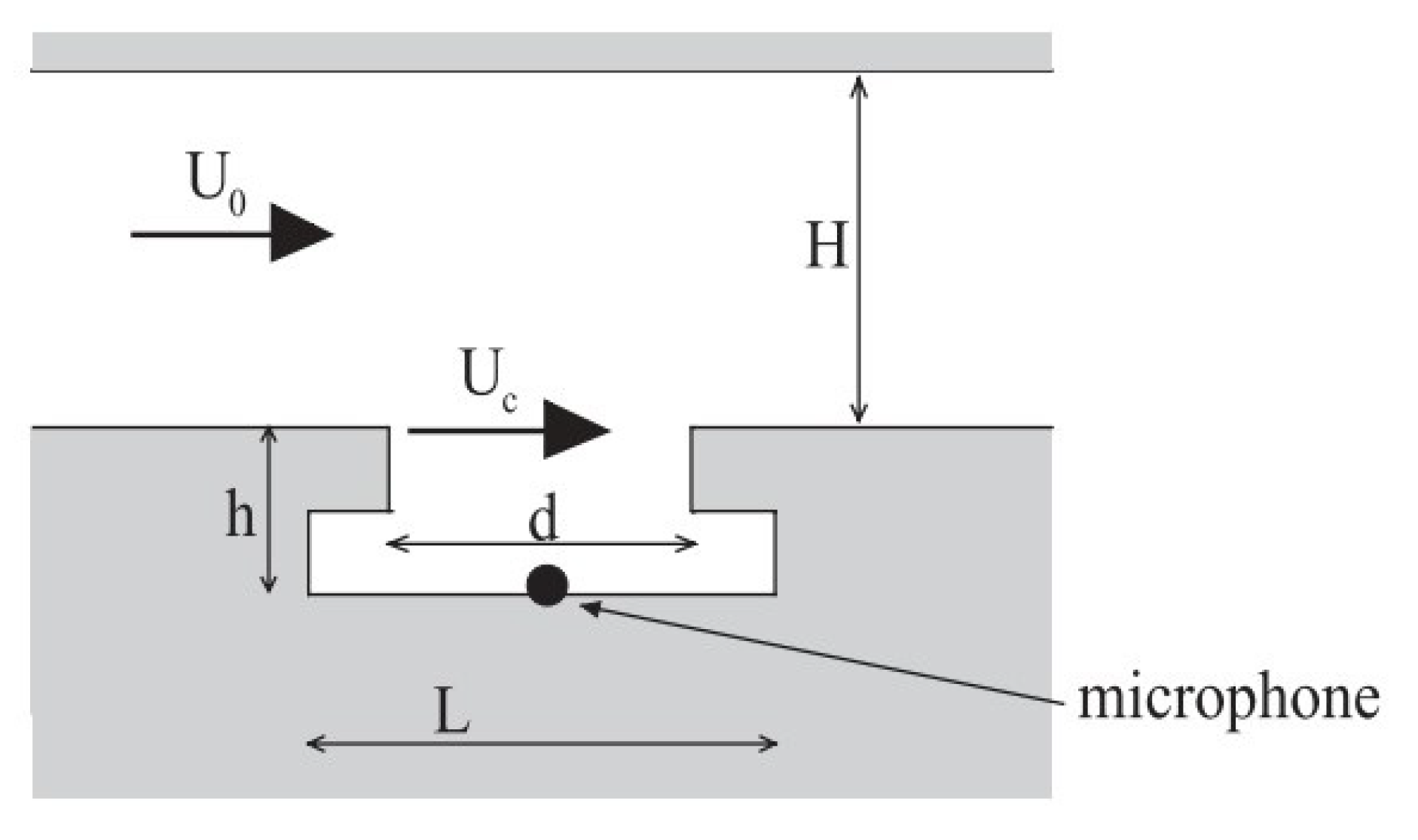
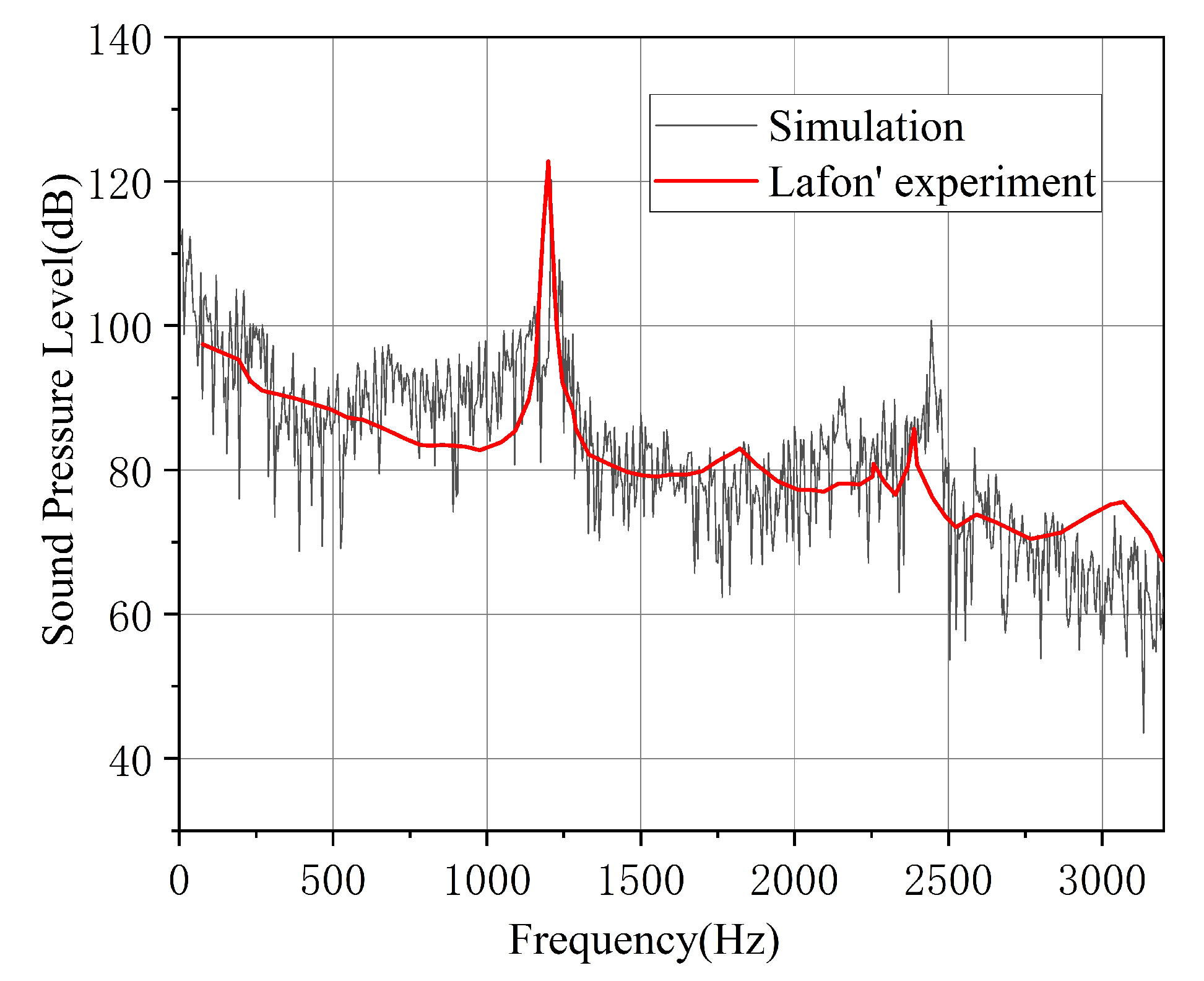
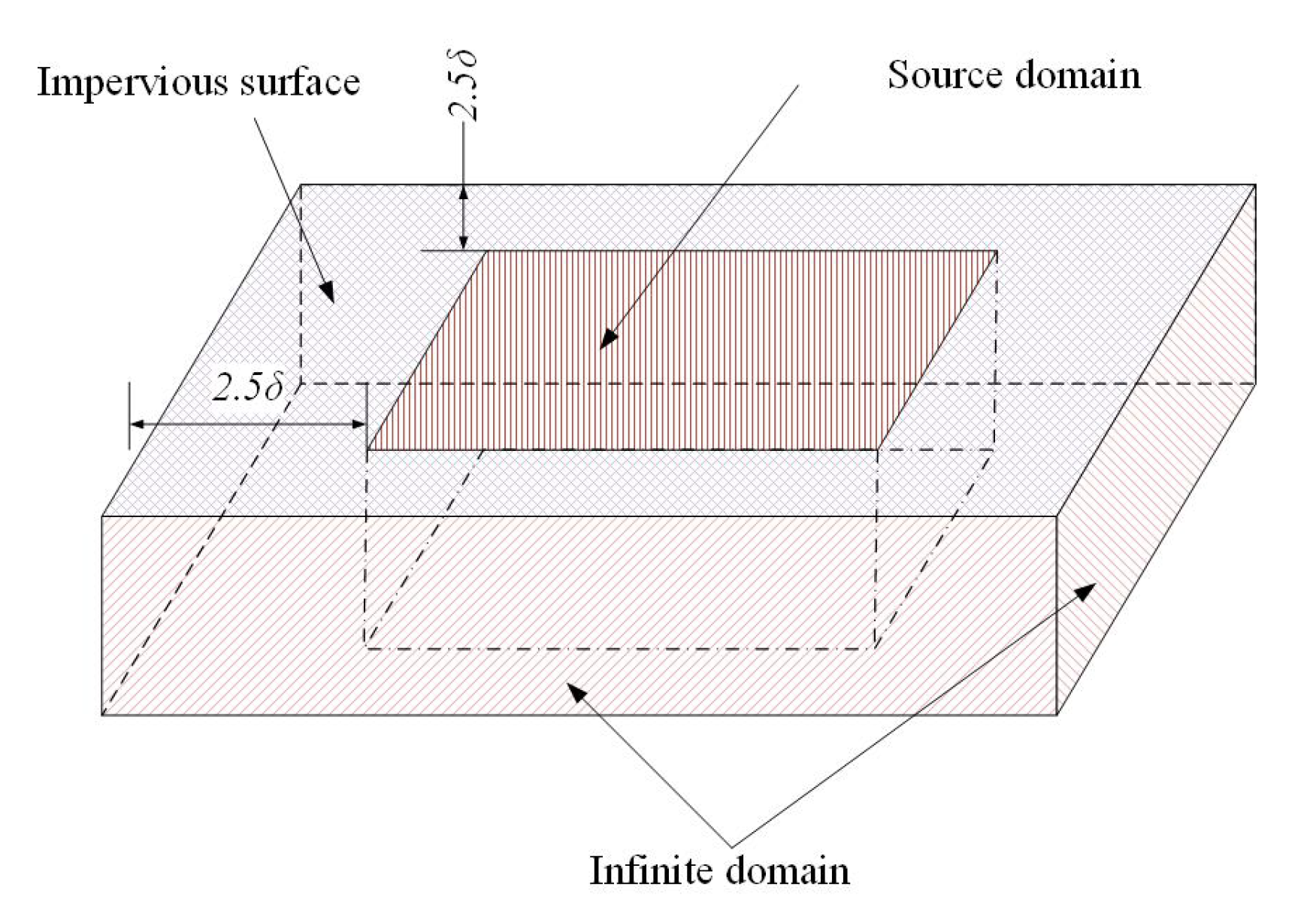
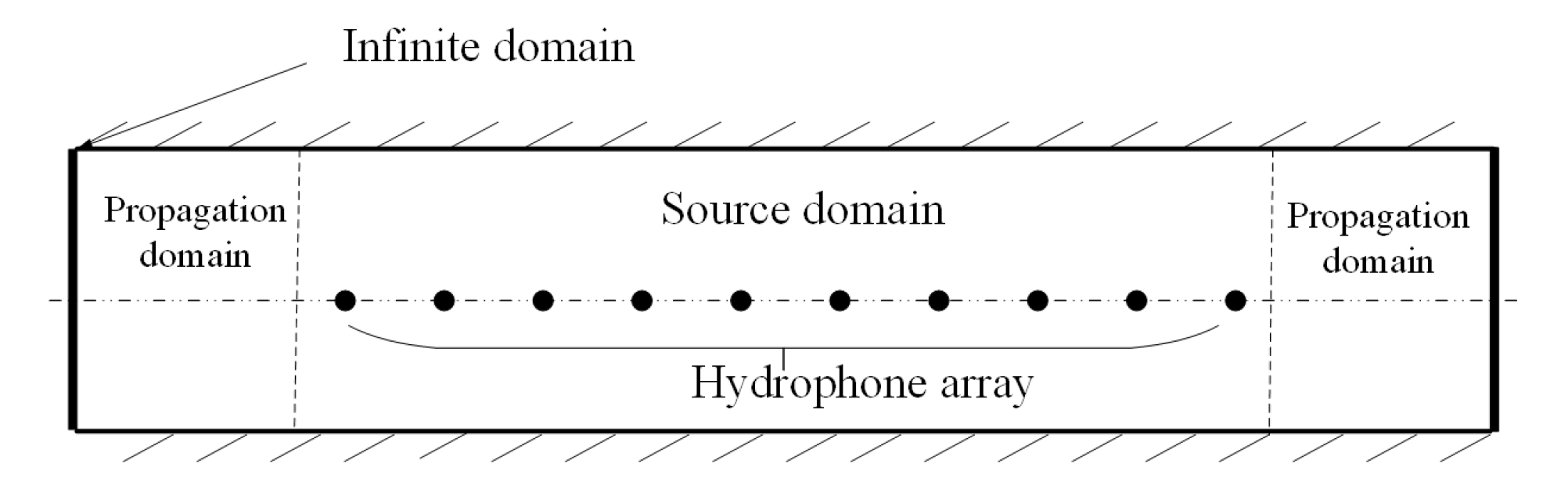
2. Problem Formulation and Simulation Methods
3. Discussion
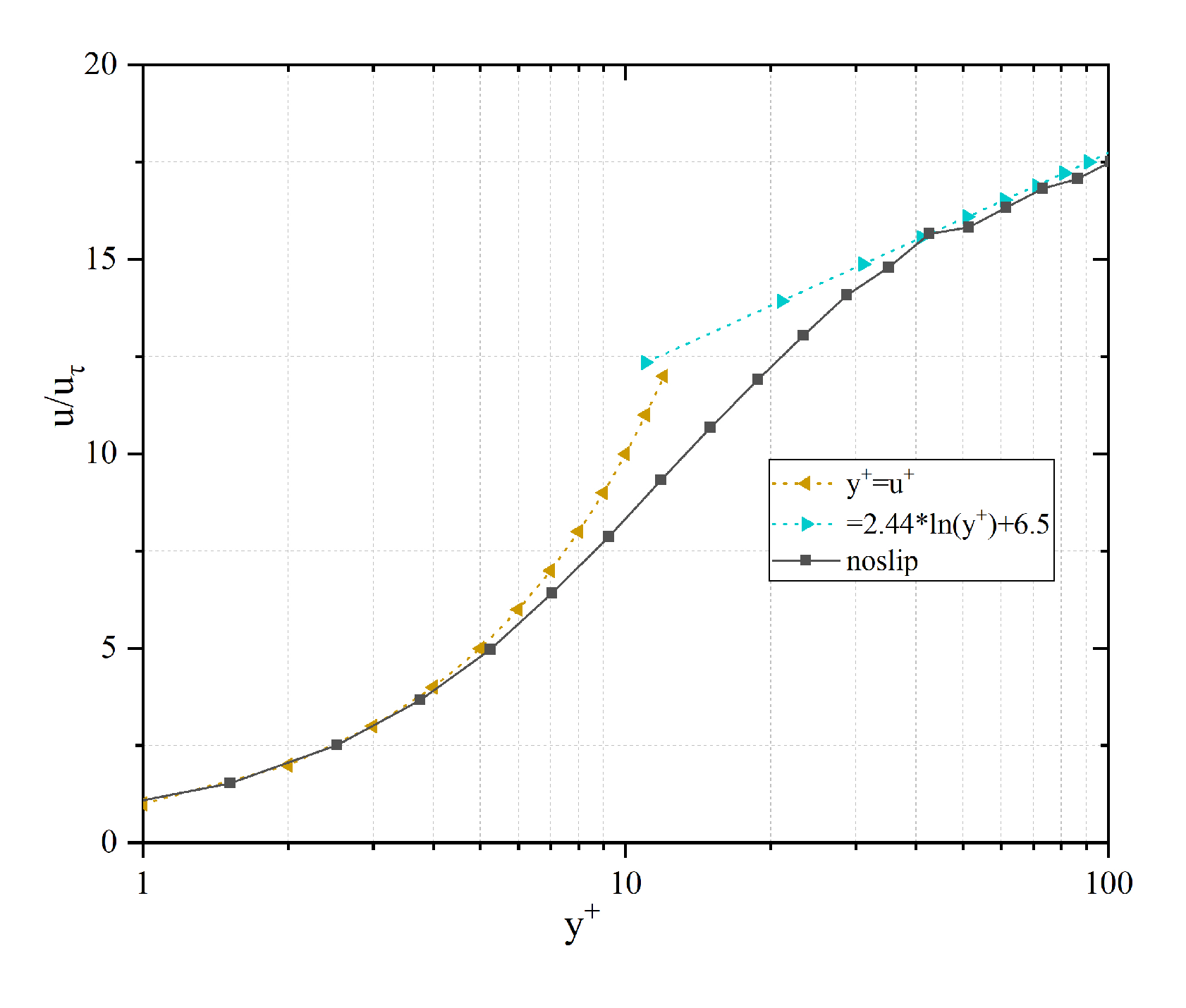
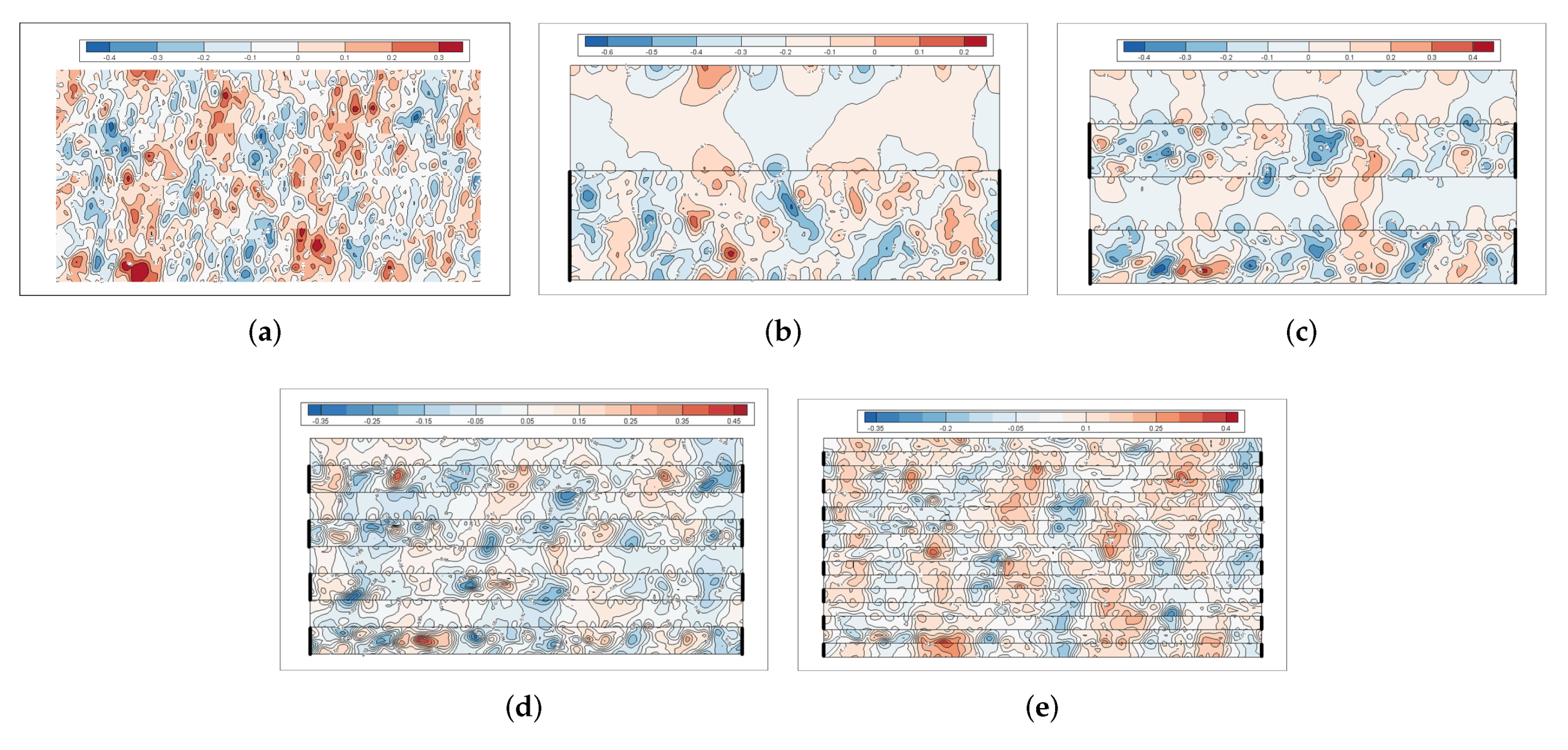
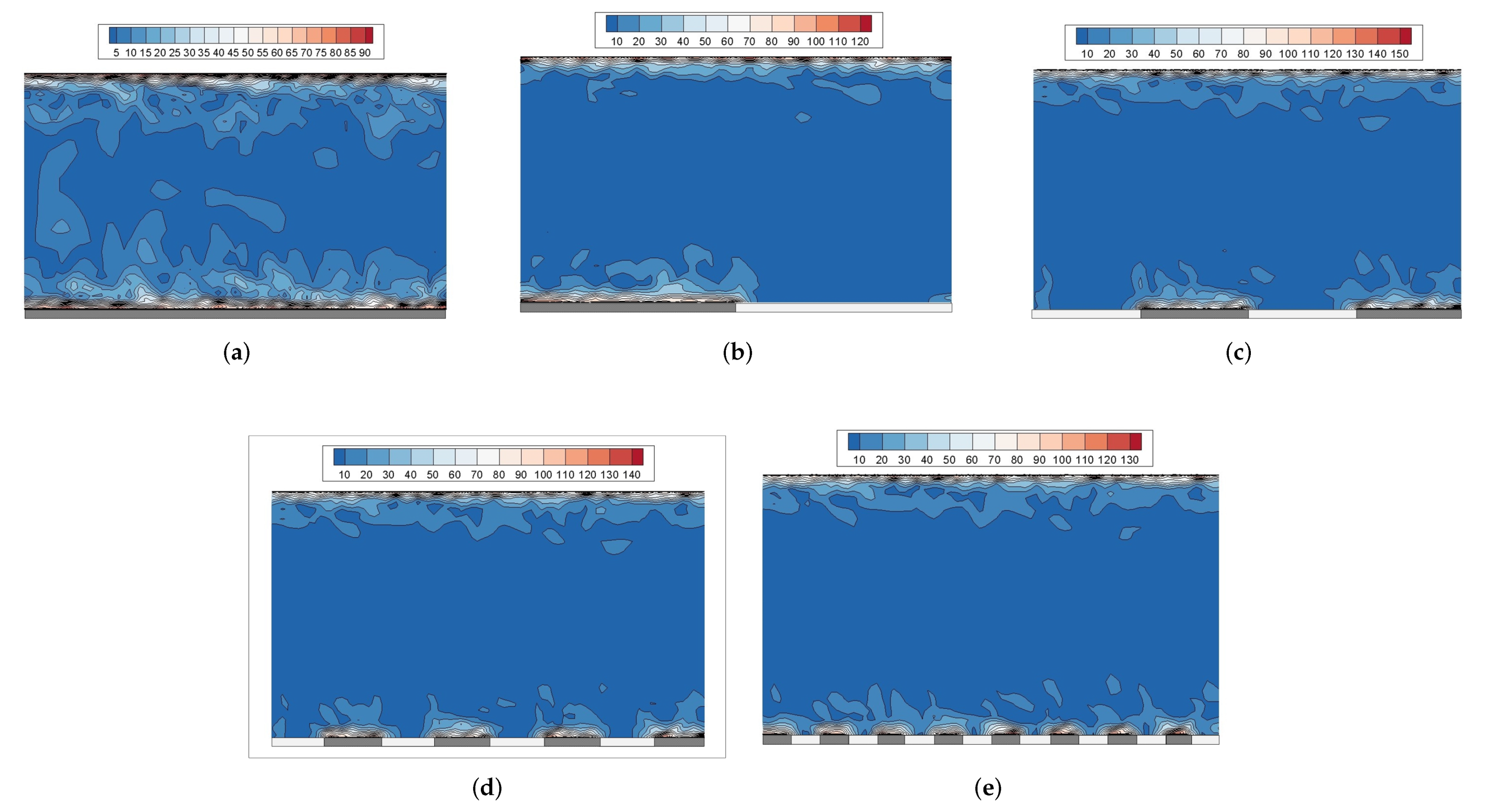
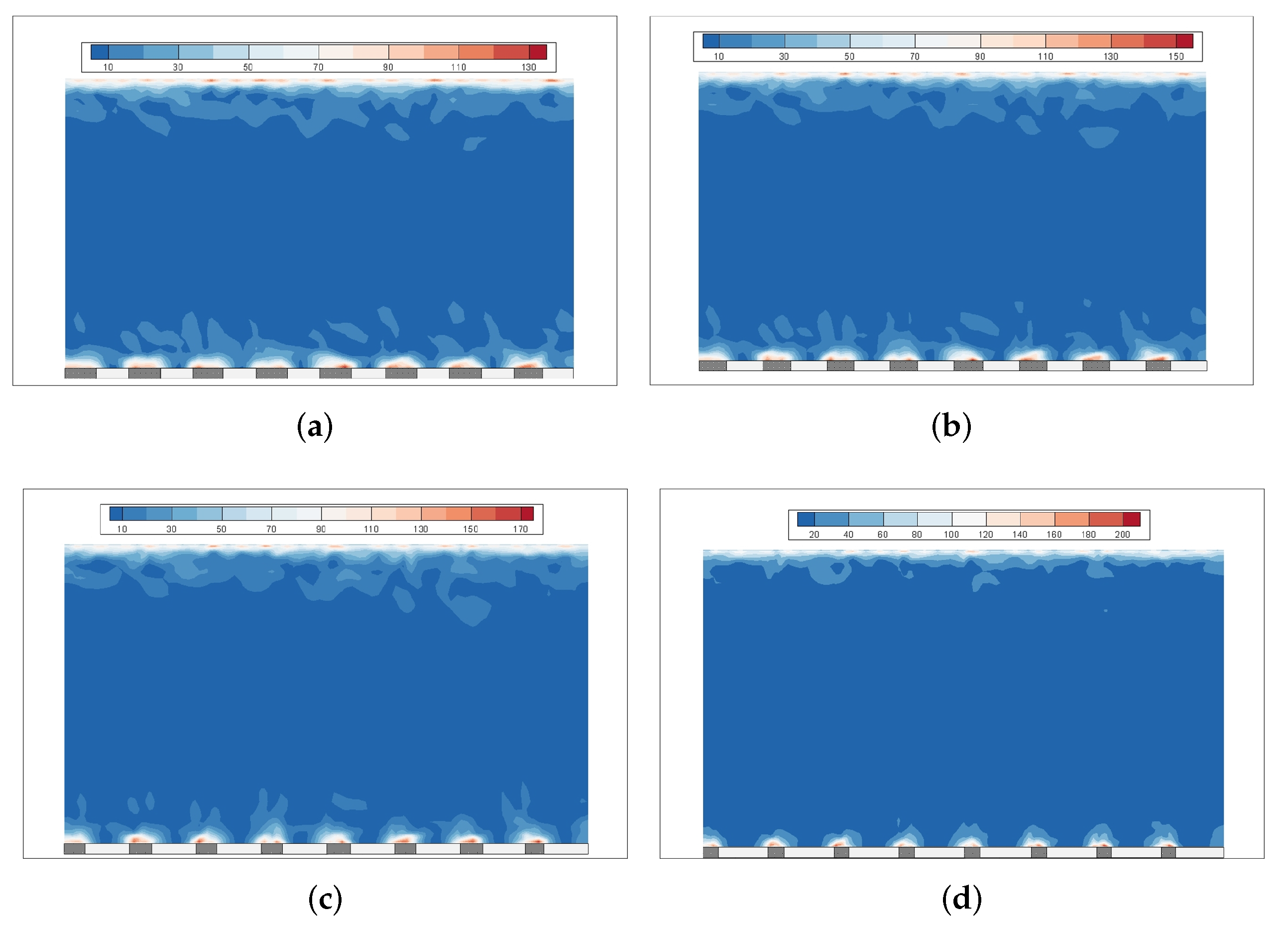
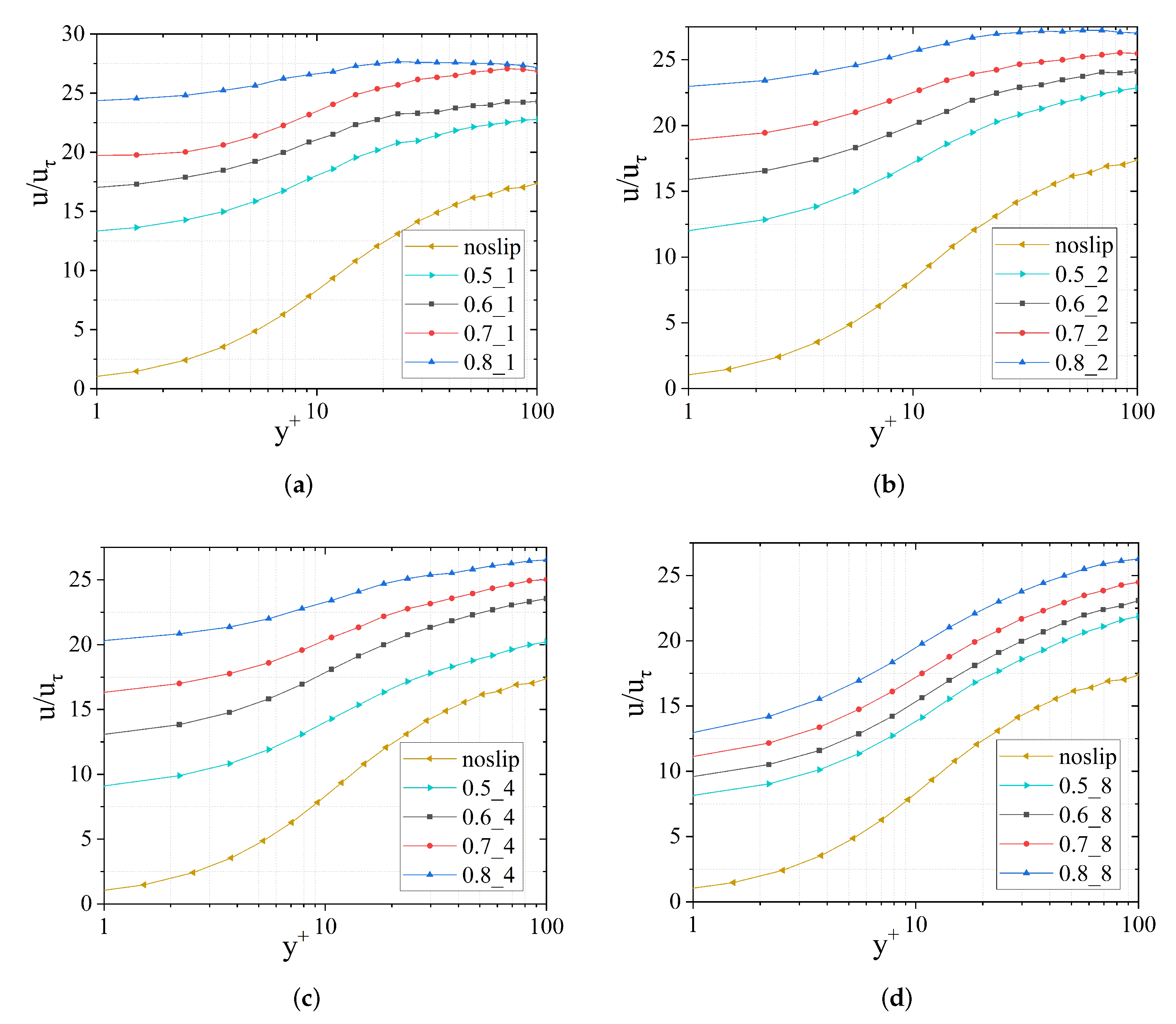
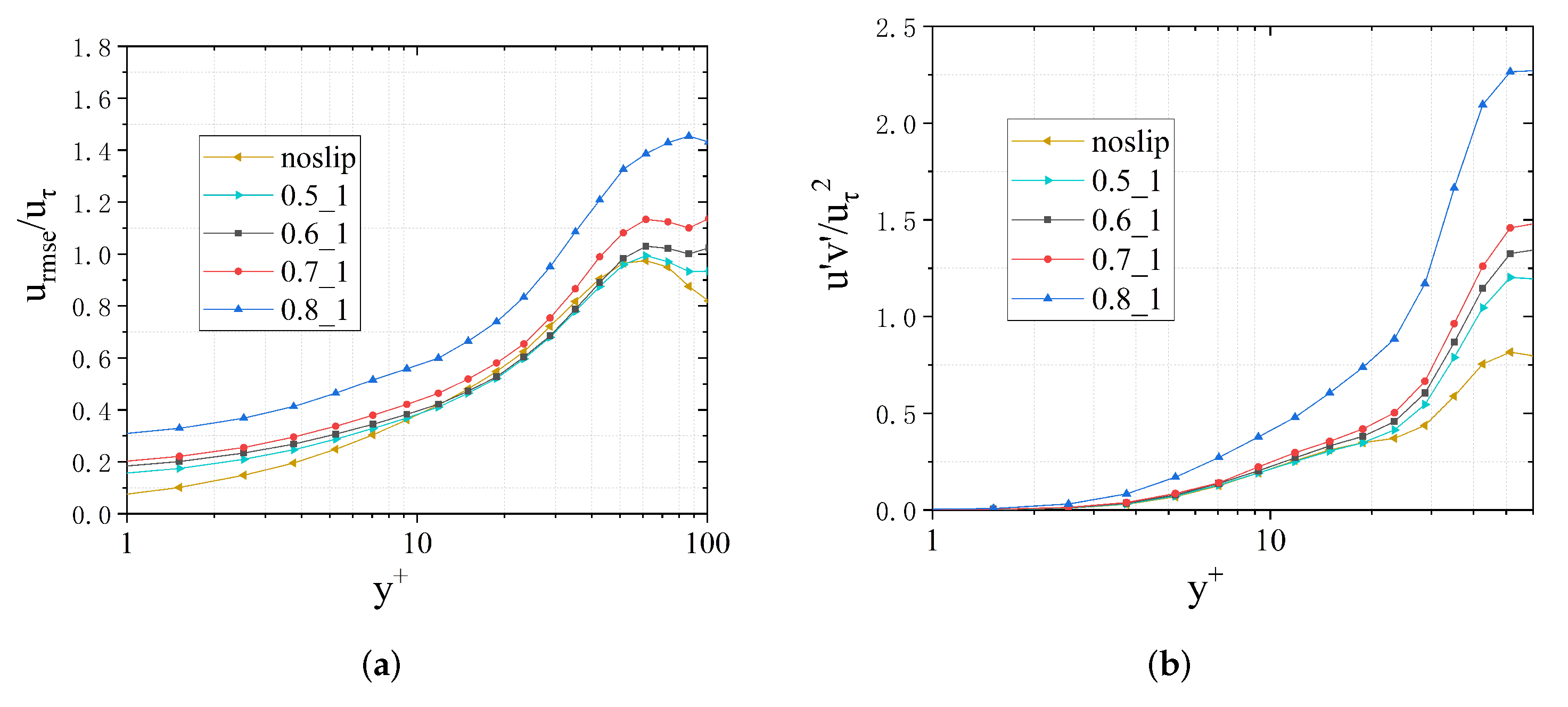
3.1. Turbulent Structures Changes on Superhydrophobic Surfaces
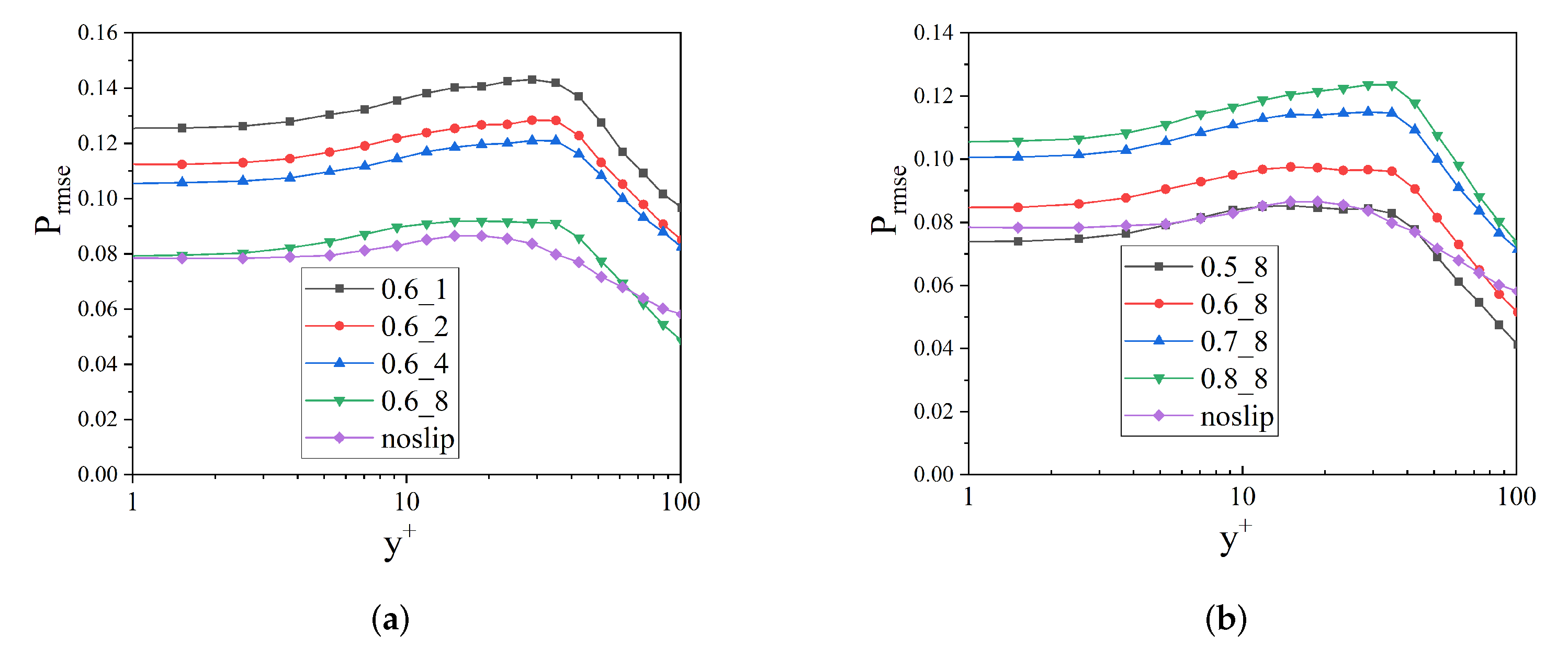
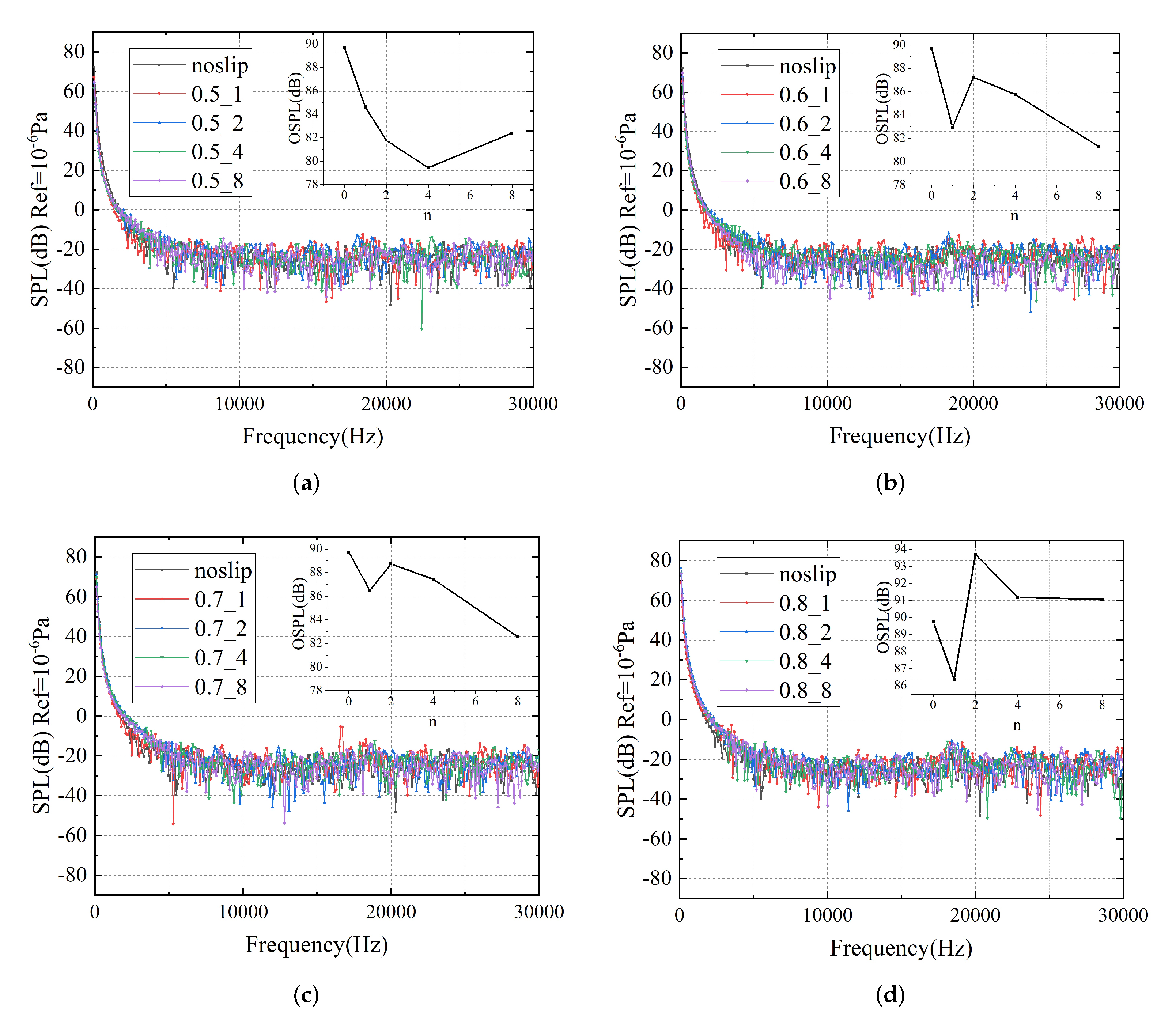
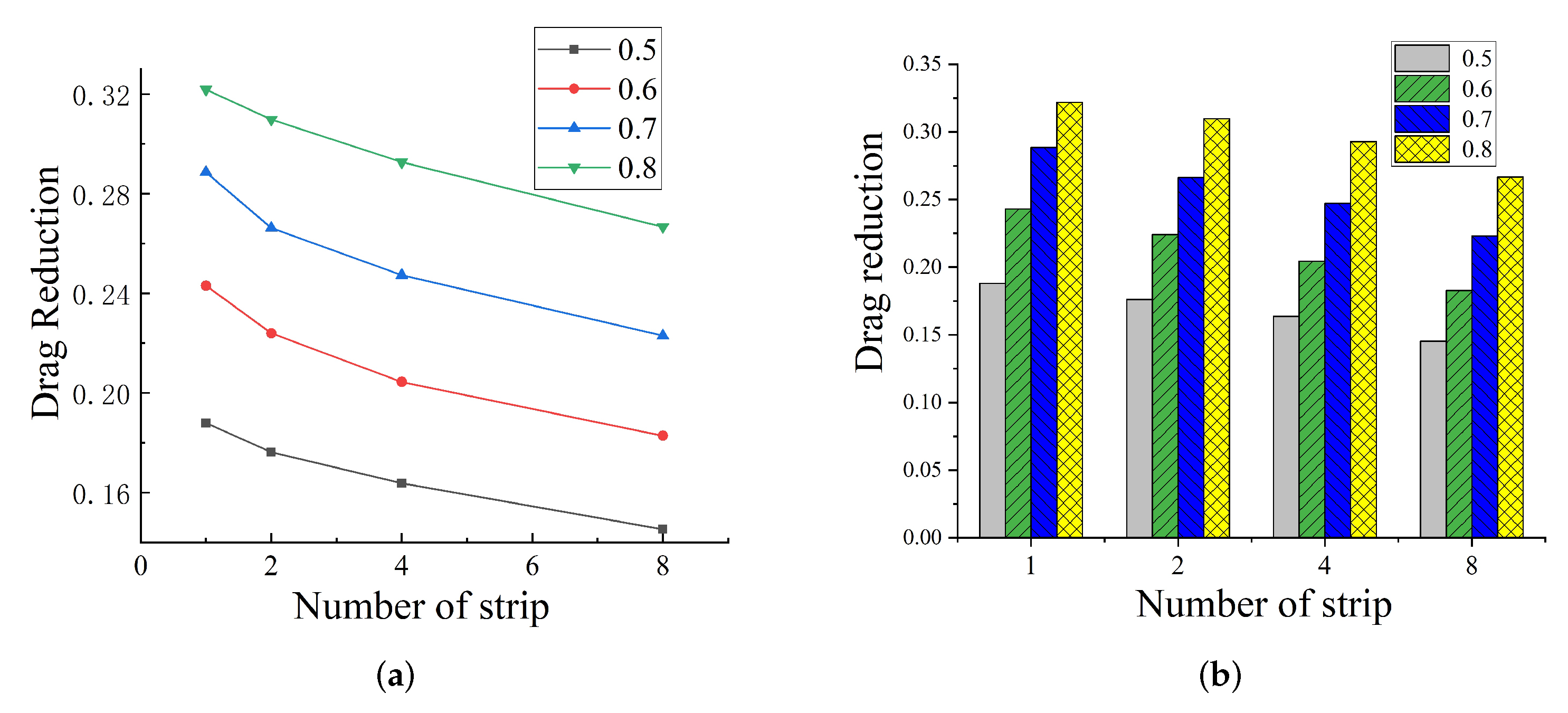
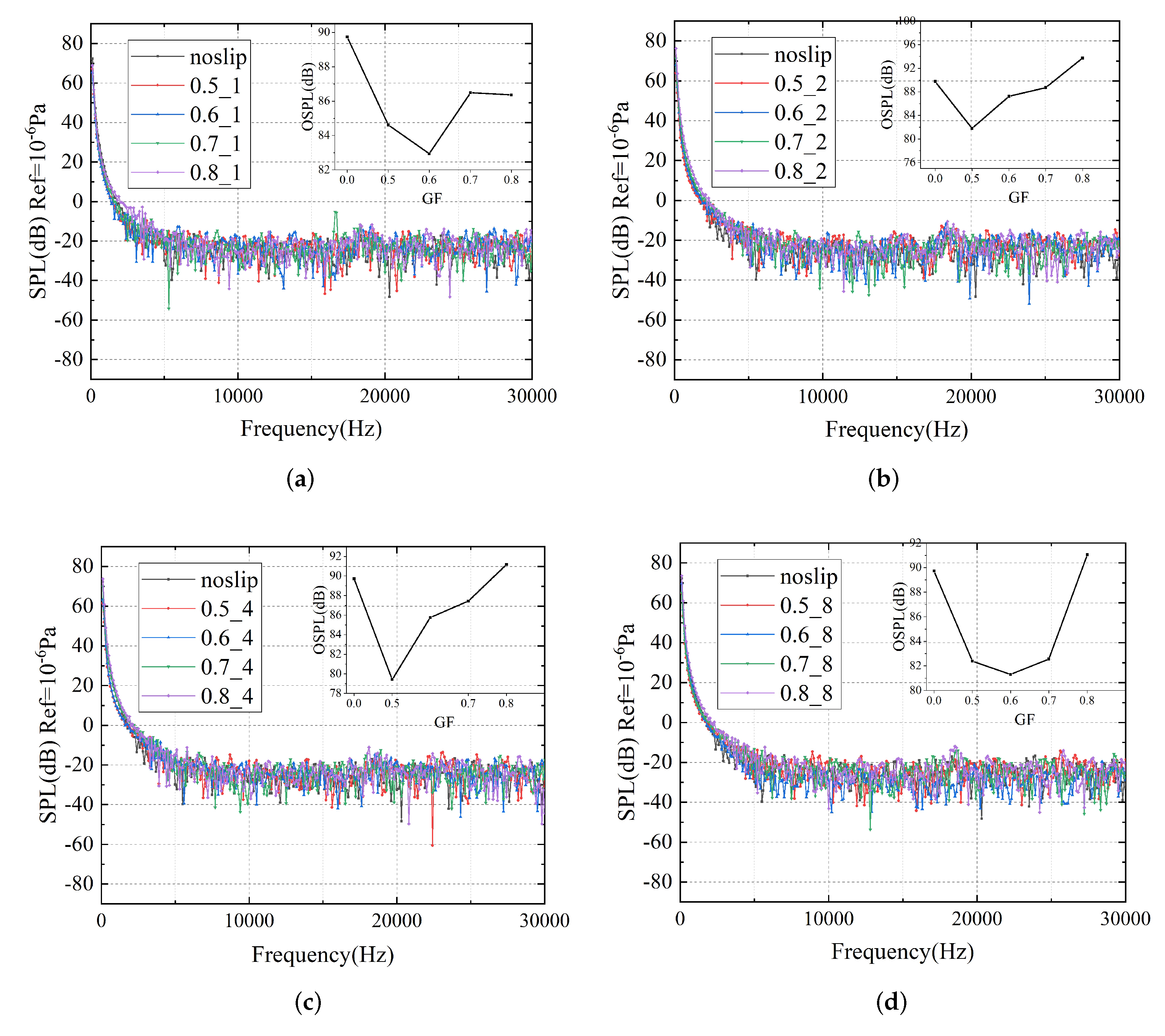
3.2. Noise Reduction Effect of Strip Numbers
3.3. Noise Reduction Effect of Free-Slip Fraction
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, S.; Kinnas, S.A. Prediction of Unsteady Developed Tip Vortex Cavitation and Its Effect on the Induced Hull Pressures. J. Mar. Sci. Eng. 2020, 8, 114. [Google Scholar] [CrossRef]
- Gloerfelt, X.; Perot, F.; Bailly, C.; Juve, D. Flow-induced cylinder noise formulated as a diffraction problem for low Mach numbers. J. Sound Vib. 2005, 287, 129–151. [Google Scholar] [CrossRef]
- Han, T.; Wang, L.; Cen, K.; Song, B.; Shen, R.Q.; Liu, H.B.; Wang, Q.S. Flow-induced noise analysis for natural gas manifolds using LES and FW-H hybrid method. Appl. Acoust. 2020, 159, 107101. [Google Scholar] [CrossRef]
- Lu, Z.B.; Halim, D.; Cheng, L. Flow-induced noise control behind bluff bodies with various leading edges using the surface perturbation technique. J. Sound Vib. 2016, 369, 1–15. [Google Scholar] [CrossRef]
- Rui, D.; Zezhen, Z.; Fuzhen, P.; Tiecheng, W.; Wanzhen, L. Investigating the sound power level of a simplified underwater vehicle induced by flow separation. Ocean. Eng. 2020, 204, 107286. [Google Scholar] [CrossRef]
- Barbarino, M.; Ilsami, M.; Tuccillo, R.; Federico, L. Combined CFD-Stochastic Analysis of an Active Fluidic Injection System for Jet Noise Reduction. Appl. Sci. 2017, 7, 623. [Google Scholar] [CrossRef]
- Kim, K.S.; Ku, G.r.; Lee, S.J.; Park, S.G.; Cheong, C. Wavenumber-Frequency Analysis of Internal Aerodynamic Noise in Constriction-Expansion Pipe. Appl. Sci. 2017, 7, 1137. [Google Scholar] [CrossRef]
- Al-Okbi, Y.; Chong, T.P.; Stalnov, O. Leading Edge Blowing to Mimic and Enhance the Serration Effects for Aerofoil. Appl. Sci. 2021, 11, 2593. [Google Scholar] [CrossRef]
- Dang, Z.; Mao, Z.; Tian, W. Reduction of Hydrodynamic Noise of 3D Hydrofoil with Spanwise Microgrooved Surfaces Inspired by Sharkskin. J. Mar. Sci. Eng. 2019, 7, 136. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Shang, D. The Hydrodynamic Noise Suppression of a Scaled Submarine Model by Leading-Edge Serrations. J. Mar. Sci. Eng. 2019, 7, 68. [Google Scholar] [CrossRef]
- Chandrika, U.K.; Pallayil, V.; Lim, K.M.; Chew, C.H. Flow noise response of a diaphragm based fibre laser hydrophone array. Ocean. Eng. 2014, 91, 235–242. [Google Scholar] [CrossRef]
- Corcos, G. Resolution of pressure in turbulence. J. Acoust. Soc. Am. 1963, 35, 192–199. [Google Scholar] [CrossRef]
- Jordan, S.A. A simple model of axisymmetric turbulent boundary layers along long thin circular cylinders. Phys. Fluids 2014, 26, 085110. [Google Scholar] [CrossRef]
- Karthik, K.; Vengadesan, S.; Bhattacharyya, S.K. Prediction of flow induced sound generated by cross flow past finite length circular cylinders. J. Acoust. Soc. Am. 2018, 143, 260. [Google Scholar] [CrossRef]
- Pallayil, V.; Chotiros, N.P. AUV-Based Seabed Characterisation Using a Lightweight Towed Array System. In Proceedings of the Offshore Technology Conference Asia, Houston, TX, USA, 2–5 May 2016. [Google Scholar]
- Willmarth, W.; Yang, C. Wall-pressure fluctuations beneath turbulent boundary layers on a flat plate and a cylinder. J. Fluid Mech. 1970, 41, 47–80. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Philip, J.R. Flows satisfying mixed no-slip and no-shear conditions. Z. Für Angew. Math. Und Phys. ZAMP 1972, 23, 353–372. [Google Scholar] [CrossRef]
- Choi, C.H.; Westin, K.J.A.; Breuer, K.S. Apparent slip flows in hydrophilic and hydrophobic microchannels. Phys. Fluids 2003, 15, 2897–2902. [Google Scholar] [CrossRef]
- Ou, J.; Perot, B.; Rothstein, J.P. Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 2004, 16, 4635–4643. [Google Scholar] [CrossRef]
- Joseph, P.; Tabeling, P. Direct measurement of the apparent slip length. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005, 71, 035303. [Google Scholar] [CrossRef]
- Park, H.; Park, H.; Kim, J. A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids 2013, 25, 66001. [Google Scholar] [CrossRef]
- Truesdell, R.; Mammoli, A.; Vorobieff, P.; van Swol, F.; Brinker, C.J. Drag reduction on a patterned superhydrophobic surface. Phys. Rev. Lett. 2006, 97, 044504. [Google Scholar] [CrossRef]
- Min, T.G.; Kim, J. Effects of hydrophobic surface on skin-friction drag. Phys. Fluids 2004, 16, L55–L58. [Google Scholar] [CrossRef]
- Martell, M.B.; Perot, J.B.; Rothstein, J.P. Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 2009, 620, 31–41. [Google Scholar] [CrossRef]
- Martell, M.B.; Rothstein, J.P.; Perot, J.B. An analysis of superhydrophobic turbulent drag reduction mechanisms using direct numerical simulation. Phys. Fluids 2010, 22, 065102. [Google Scholar] [CrossRef]
- Jalalabadi, R.; Hwang, J.; Nadeem, M.; Yoon, M.; Sung, H.J. Turbulent boundary layer over a divergent convergent superhydrophobic surface. Phys. Fluids 2017, 29, 085112. [Google Scholar] [CrossRef]
- Turk, S.; Daschiel, G.; Stroh, A.; Hasegawa, Y.; Frohnapfel, B. Turbulent flow over superhydrophobic surfaces with streamwise grooves. J. Fluid Mech. 2014, 747, 186–217. [Google Scholar] [CrossRef]
- Seo, J.; García-Mayoral, R.; Mani, A. Pressure fluctuations and interfacial robustness in turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 2015, 783, 448–473. [Google Scholar] [CrossRef]
- Fairhall, C.T.; Abderrahaman-Elena, N.; Garcia-Mayoral, R. The effect of slip and surface texture on turbulence over superhydrophobic surfaces. J. Fluid Mech. 2019, 861, 88–118. [Google Scholar] [CrossRef]
- Rastegari, A.; Akhavan, R. The common mechanism of turbulent skin-friction drag reduction with superhydrophobic longitudinal microgrooves and riblets. J. Fluid Mech. 2018, 838, 68–104. [Google Scholar] [CrossRef]
- Rastegari, A.; Akhavan, R. On drag reduction scaling and sustainability bounds of superhydrophobic surfaces in high Reynolds number turbulent flows. J. Fluid Mech. 2019, 864, 327–347. [Google Scholar] [CrossRef]
- Im, H.J.; Lee, J.H. Comparison of superhydrophobic drag reduction between turbulent pipe and channel flows. Phys. Fluids 2017, 29, 095101. [Google Scholar] [CrossRef]
- Costantini, R.; Mollicone, J.P.; Battista, F. Drag reduction induced by superhydrophobic surfaces in turbulent pipe flow. Phys. Fluids 2018, 30, 025102. [Google Scholar] [CrossRef]
- Daniello, R.J.; Waterhouse, N.E.; Rothstein, J.P. Drag reduction in turbulent flows over superhydrophobic surfaces. Phys. Fluids 2009, 21, 085103. [Google Scholar] [CrossRef]
- Fukagata, K.; Kasagi, N.; Koumoutsakos, P. A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces. Phys. Fluids 2006, 18, 051703. [Google Scholar] [CrossRef]
- Zhang, J.X.; Tian, H.P.; Yao, Z.H.; Hao, P.F.; Jiang, N. Mechanisms of drag reduction of superhydrophobic surfaces in a turbulent boundary layer flow. Exp. Fluids 2015, 56, 179. [Google Scholar] [CrossRef]
- Abu Rowin, W.; Ghaemi, S. Streamwise and spanwise slip over a superhydrophobic surface. J. Fluid Mech. 2019, 870, 1127–1157. [Google Scholar] [CrossRef]
- Gose, J.W.; Golovin, K.; Boban, M.; Mabry, J.M.; Tuteja, A.; Perlin, M.; Ceccio, S.L. Characterization of superhydrophobic surfaces for drag reduction in turbulent flow. J. Fluid Mech. 2018, 845, 560–580. [Google Scholar] [CrossRef]
- Aljallis, E.; Sarshar, M.A.; Datla, R.; Sikka, V.; Jones, A.; Choi, C.H. Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow. Phys. Fluids 2013, 25, 025103. [Google Scholar] [CrossRef]
- Ybert, C.; Barentin, C.; Cottin-Bizonne, C.; Joseph, P.; Bocquet, L. Achieving large slip with superhydrophobic surfaces: Scaling laws for generic geometries. Phys. Fluids 2007, 19, 123601. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically. Philos. Trans. R. Soc. A 1952, 211, 564–587. [Google Scholar]
- Bossart, R.; Joly, N.; Bruneau, M. Hybrid numerical and analytical solutions for acoustic boundary problems in thermo-viscous fluids. J. Sound Vib. 2003, 263, 69–84. [Google Scholar] [CrossRef]
- Lafon, P.; Caillaud, S.; Devos, J.P.; Lambert, C. Aeroacoustical coupling in a ducted shallow cavity and fluid/structure effects on a steam line. J. Fluids Struct. 2003, 18, 695–713. [Google Scholar] [CrossRef]



| Domain Size | Gas Fraction | Strip Number | Grid Number () | ||||
|---|---|---|---|---|---|---|---|
| GF = 0.5 | 1, 2, 4, 8 | 150 × 60 × 80 | 180 | 3 | 0.3 | 3 | |
| GF = 0.6 | 1, 2, 4, 8 | 150 × 60 × 80 | 180 | 3 | 0.3 | 3 | |
| GF = 0.7 | 1, 2, 4, 8 | 150 × 60 × 96 | 180 | 3 | 0.3 | 3 | |
| GF = 0.8 | 1, 2, 4, 8 | 150 × 60 × 112 | 180 | 3 | 0.3 | 3 |
| Mesh Size | Mesh Size | ||||
|---|---|---|---|---|---|
| 130 × 40 × 60 | 0.001307 | 150 × 60 × 80 | 0.1 | 0.32 | 0.001294 |
| 140 × 50 × 70 | 0.001291 | ||||
| 150 × 60 × 80 | 0.001294 | 0.18 | 0.55 | 0.001288 | |
| 160 × 70 × 90 | 0.001288 |
| = 61.2 m/s | h = 0.02 m | H = 0.137 m |
| d = 0.05 m | L = 0.073 m |
| Strips Number | 1 | 2 | 4 | 8 |
|---|---|---|---|---|
| GF = 0.5 | 84.6 | 81.5 | 79.2 | 82.6 |
| GF = 0.6 | 83.1 | 87.1 | 85.9 | 81.2 |
| GF = 0.7 | 86.5 | 88.6 | 87.5 | 82.5 |
| GF = 0.8 | 86.2 | 93.5 | 91.1 | 90.8 |
| no-slip | 89.9 dB | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, C.; Liu, Y.; Shang, D.; Zhang, C. Noise Reduction Effect of Superhydrophobic Surfaces with Streamwise Strip of Channel Flow. Appl. Sci. 2021, 11, 3869. https://doi.org/10.3390/app11093869
Niu C, Liu Y, Shang D, Zhang C. Noise Reduction Effect of Superhydrophobic Surfaces with Streamwise Strip of Channel Flow. Applied Sciences. 2021; 11(9):3869. https://doi.org/10.3390/app11093869
Chicago/Turabian StyleNiu, Chen, Yongwei Liu, Dejiang Shang, and Chao Zhang. 2021. "Noise Reduction Effect of Superhydrophobic Surfaces with Streamwise Strip of Channel Flow" Applied Sciences 11, no. 9: 3869. https://doi.org/10.3390/app11093869
APA StyleNiu, C., Liu, Y., Shang, D., & Zhang, C. (2021). Noise Reduction Effect of Superhydrophobic Surfaces with Streamwise Strip of Channel Flow. Applied Sciences, 11(9), 3869. https://doi.org/10.3390/app11093869






