Spectrum Awareness for Cognitive Radios Supported by Radio Environment Maps: Zonal Approach †
Abstract
1. Introduction
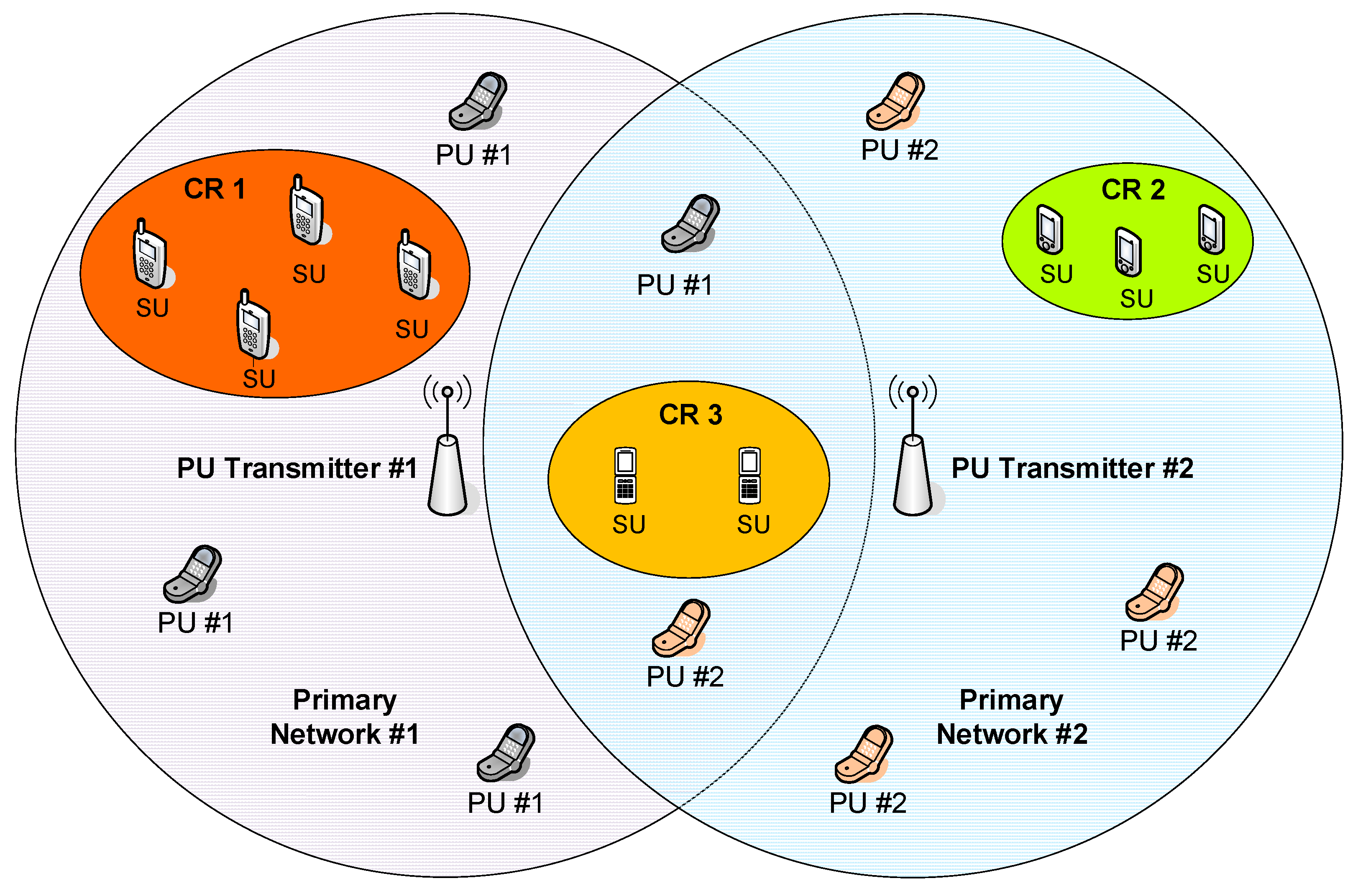
2. Related Works
- When the RSS from PU was overestimated, the transmission from SU was needlessly restrained to avoid interferences,
- when the RSS from PU was underestimated, the transmission from SU was allowed and resulted in interferences.
3. Map Construction Techniques
- Indirect (transmitter location based methods)—applying transmitter location and propagation model to obtain the estimated value,
- direct (spatial statistics based methods)—applying interpolation techniques and sampled data,
- hybrid—combining the two approaches.
- is the predicted signal level for point x0,
- N is the number of points at which the signal level was measured,
- 0) is the weighing factor for point x0,
- is the signal level measured at location xi.
- h = xi–xj is the distance between points xi and xj,
- V(xi) and V(xj) are the levels of the signal measured at points xi and xj,
- N is the number of measurement points, while N(h) is the set of pairs of points separated by the distance h, and |N(h)| denotes its cardinality.
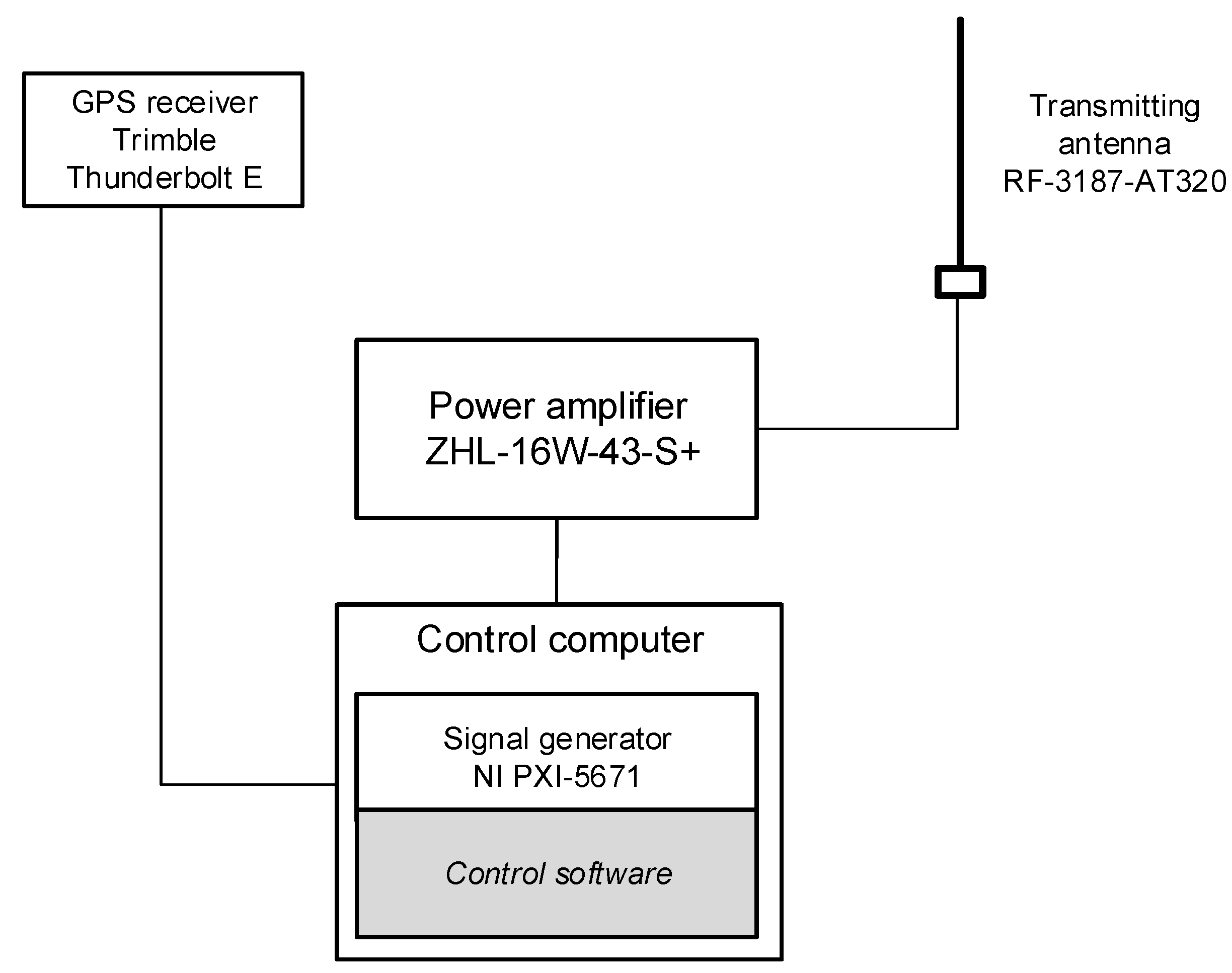
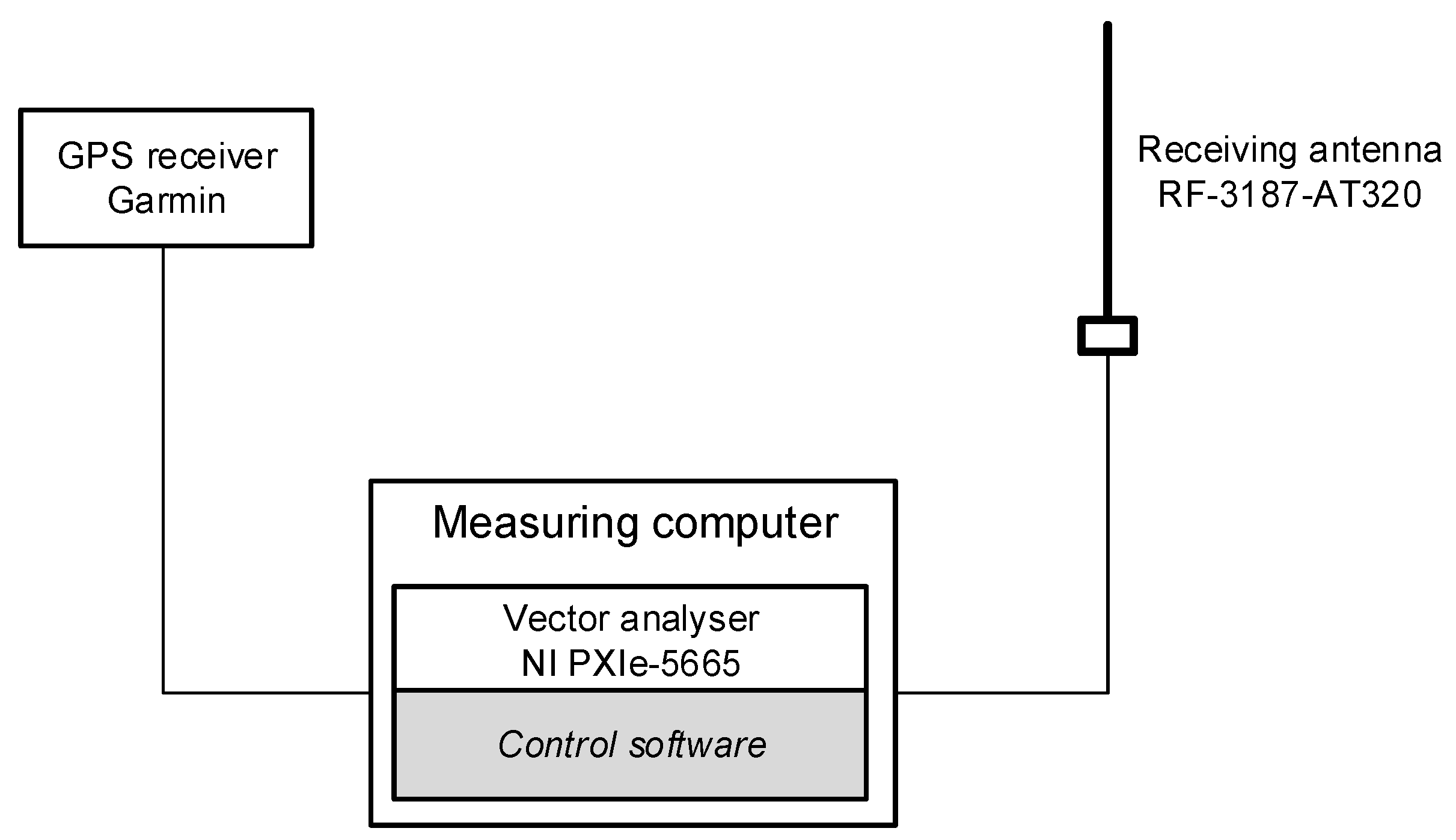
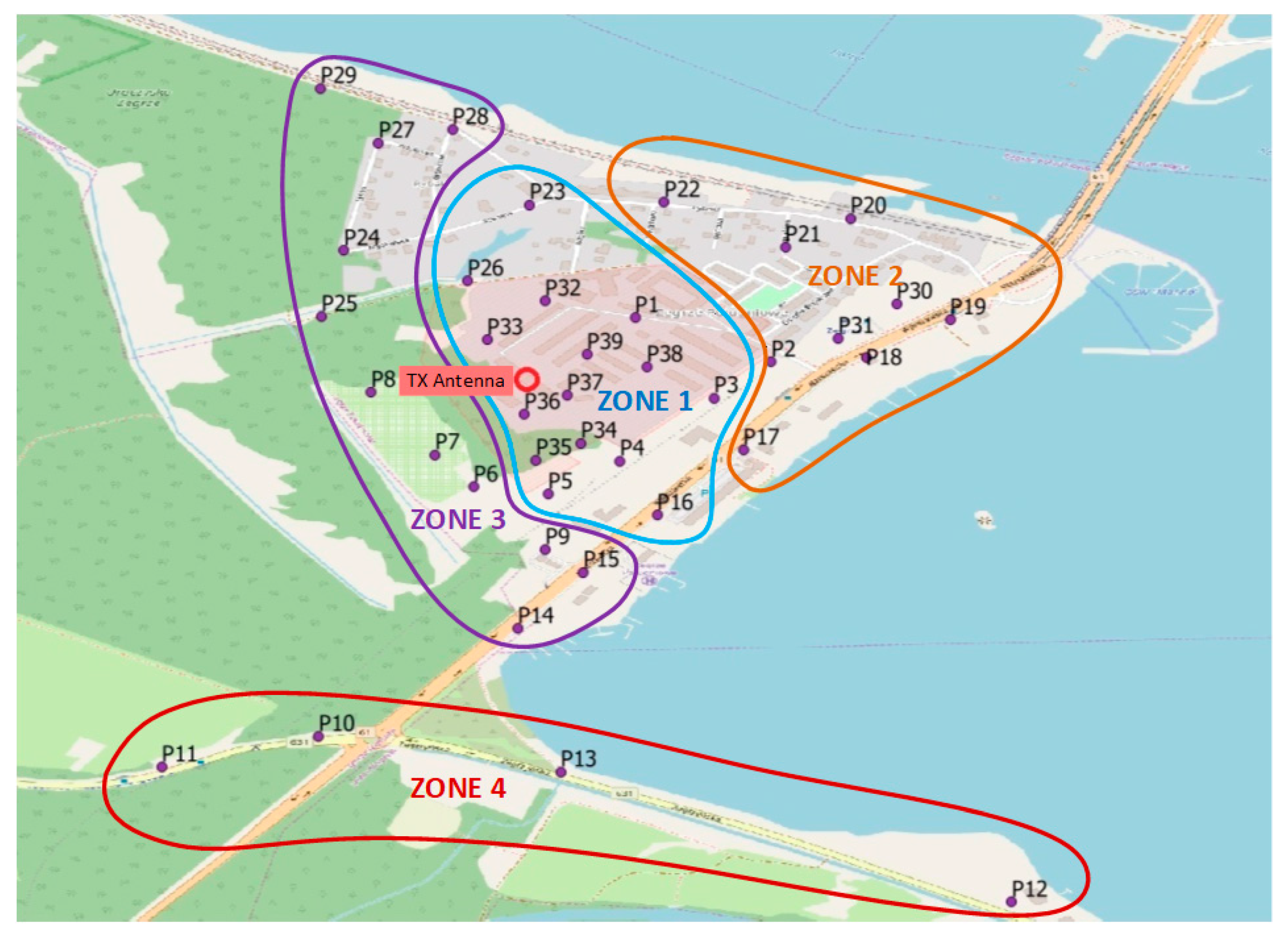
4. Test Scenario and Exemplary Maps
- P6–P8, P10, P11, P24, P25, P27, and P29—the average height of the forest separating sensors is about 25 m,
- P2, P18–P22, P30, and P31—the approximate height of the buildings separating sensors is between 12 m and 15 m,
- P1, P3–P5, P9, P12–P17, P23, P26, P28, P35, and P36—the approximate height of the buildings and single trees separating sensors ranges from 8 m to 10 m.
5. Analysis of the Results
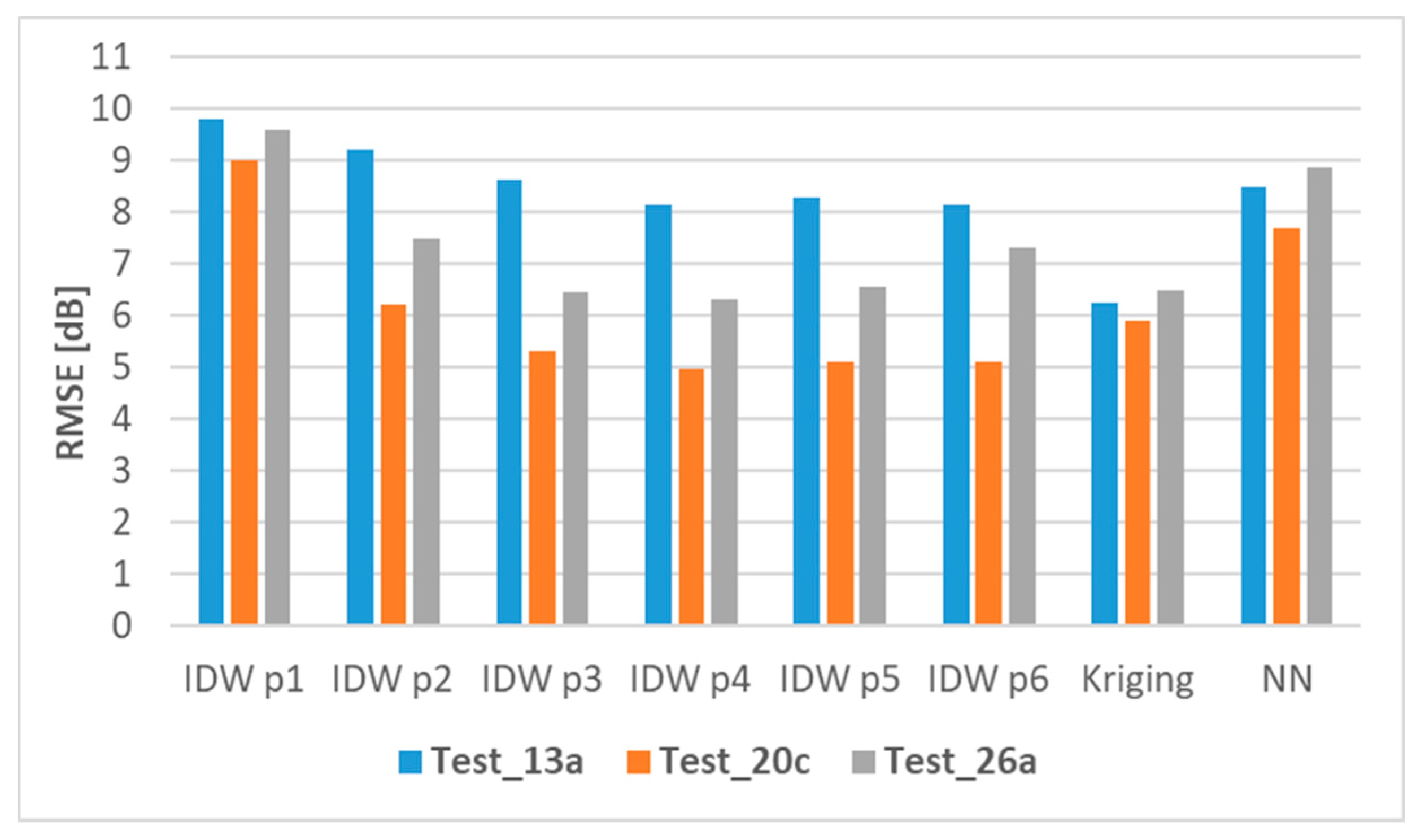
- Globally, for the “lowest RMSE” test case for each scenario with 13, 20, and 26 sensors, i.e., for selected tests with the lowest RMSE value.
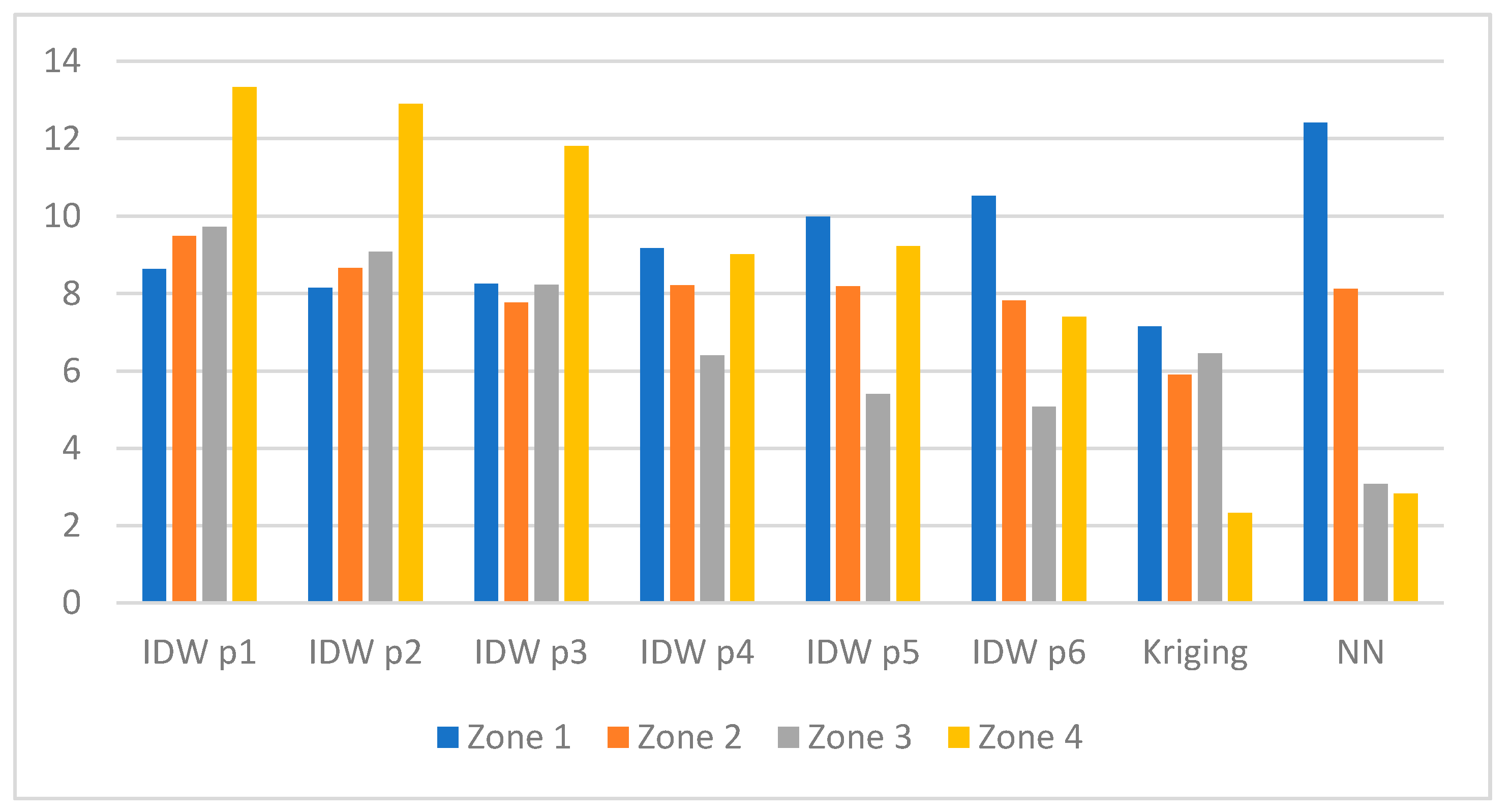
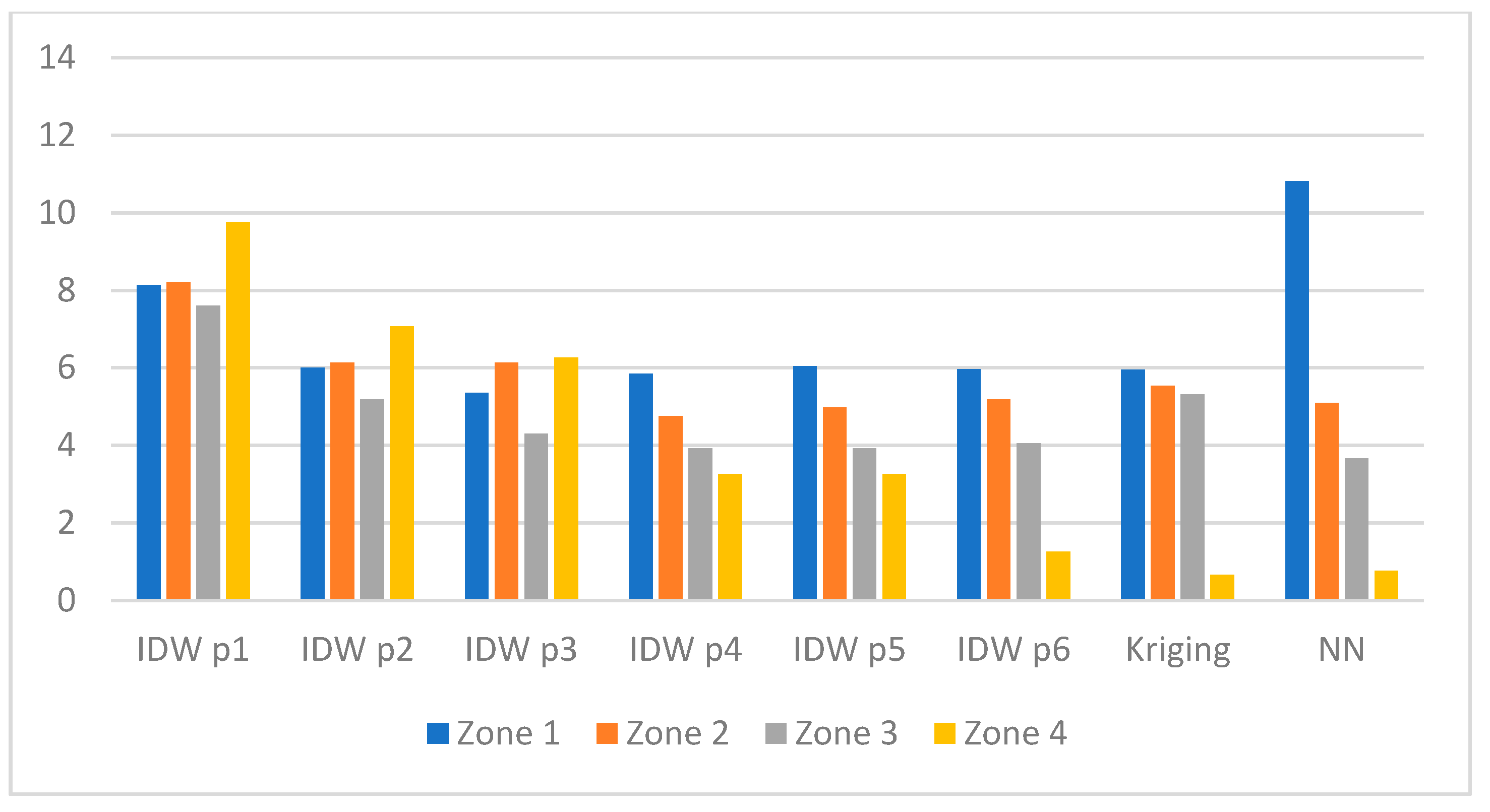
- Separately, for each of the zones presented in Figure 2.
- n is the number of control sensors,
- Sri is the signal level [dBm] measured by i-th control sensor,
- Soi is the signal level [dBm] interpolated for i-th control sensor,
- is the difference between measured and interpolated signal level [dB] for i-th control sensor,
- is the average value of .
- Test_13a for the scenario with 13 sensors,
- Test_20c for the scenario with 20 sensors,
- Test_26a for the scenario with 26 sensors.
- Kriging in Test_13a (6.3 dB),
- IDW p4 in Test_20c (5.0 dB),
- IDW p4 in Test_26a (6.3 dB), and was comparable with the result for IDW p3 (6.4 dB) and for Kriging (6.5 dB).
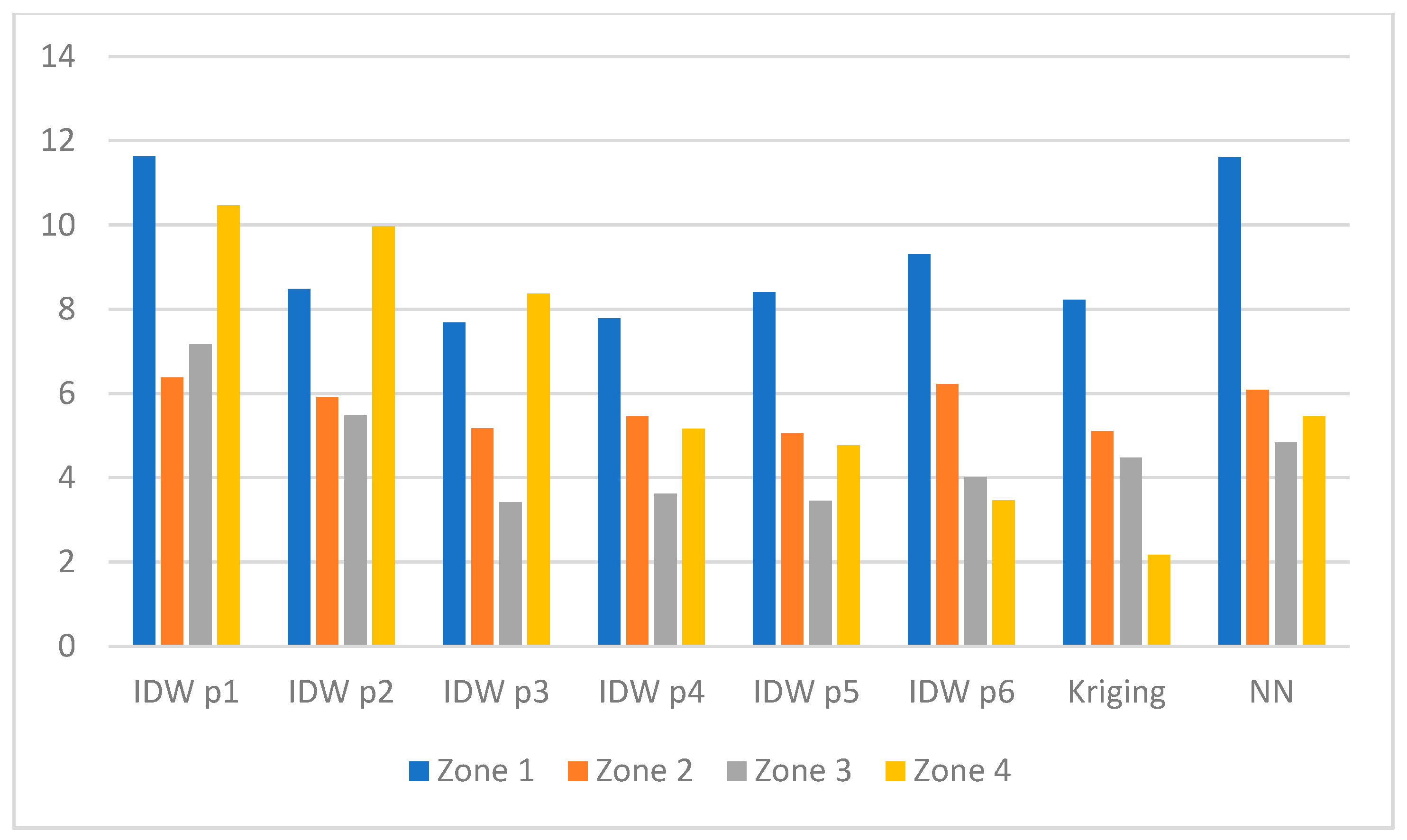
- IDW p3 method in Zone 1 (RMSE approx. 5.3 dB),
- IDW p4 method in Zone 2 (RMSE approx. 4.7 dB),
- NN method in Zone 3 (RMSE approx. 3.7 dB),
- Kriging method in Zone 4 (RMSE approx. 0.65 dB).
- Around 5.0 dB for IDW p5 and 5.1 dB for Kriging in Zone 2,
- approximately 3.4 dB for IDW p3 in Zone 3.
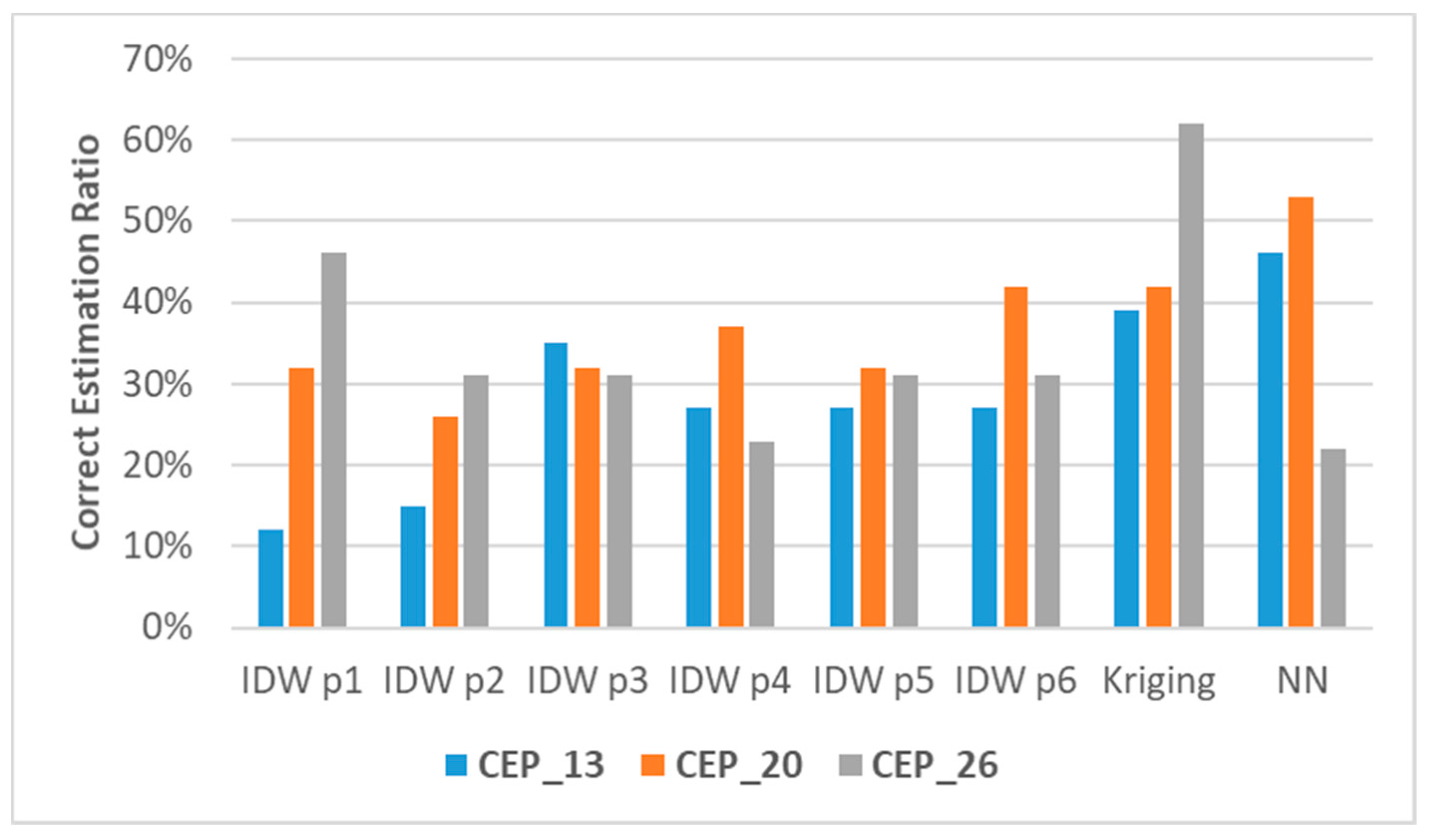
- ±3 dB—Correct Estimation Point (CEP), green color,
- >3 dB—Overestimation Point (OEP), blue color,
- <−3 dB—Underestimation Point (UEP), orange color.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Sensor ID | LATITUDE | LONGITUDE | Signal Level [dBm] | Sensor ID | LATITUDE | LONGITUDE | Signal Level [dBm] |
|---|---|---|---|---|---|---|---|
| P1 | 52.45390833 | 21.00674833 | −72.087 | P21 | 52.45544333 | 21.01000833 | −101.29 |
| P2 | 52.45294833 | 21.00970667 | −94.82 | P22 | 52.456415 | 21.00738333 | −104.27 |
| P3 | 52.45216833 | 21.00846667 | −77.935 | P23 | 52.456365 | 21.00446 | −87.69 |
| P4 | 52.4508 | 21.00642 | −88.057 | P24 | 52.45536333 | 21.00042833 | −93.598 |
| P5 | 52.45008167 | 21.00486167 | −88.625 | P25 | 52.453935 | 20.99994167 | −100.31 |
| P6 | 52.450235 | 21.003245 | −100.77 | P26 | 52.45470667 | 21.003115 | −86.089 |
| P7 | 52.450935 | 21.00240833 | −96.821 | P27 | 52.45770167 | 21.00118167 | −98.633 |
| P8 | 52.45229167 | 21.00102 | −93.106 | P28 | 52.45799667 | 21.00278667 | −97.605 |
| P9 | 52.44887833 | 21.00480167 | −96.386 | P29 | 52.45889 | 20.99992167 | −98.734 |
| P10 | 52.44482 | 20.99988167 | −100.76 | P30 | 52.45421 | 21.01242667 | −100.80 |
| P11 | 52.44415833 | 20.996475 | −100.73 | P31 | 52.45346 | 21.01116 | −101.11 |
| P12 | 52.44123 | 21.01492667 | −102.20 | P32 | 52.45427333 | 21.004795 | −69.633 |
| P13 | 52.44405 | 21.005135 | −100.97 | P33 | 52.45342833 | 21.00353667 | −67.873 |
| P14 | 52.44716167 | 21.004205 | −96.756 | P34 | 52.451185 | 21.00557333 | −70.594 |
| P15 | 52.448385 | 21.00562833 | −100.3 | P35 | 52.45081667 | 21.00459667 | −87.471 |
| P16 | 52.44962333 | 21.00723 | −85.686 | P36 | 52.45181167 | 21.004345 | −80.195 |
| P17 | 52.45104 | 21.0091 | −99.576 | P37 | 52.45222167 | 21.005275 | −59.779 |
| P18 | 52.45305333 | 21.01176333 | −90.147 | P38 | 52.45284167 | 21.00700333 | −71.768 |
| P19 | 52.453865 | 21.01358833 | −95.426 | P39 | 52.45311167 | 21.005705 | −64.569 |
| P20 | 52.45606667 | 21.011425 | −97.96 | - | - | - | - |
Appendix B
References
- Matyszkiel, R.; Grochowina, B.; Namiotko, R.; Wiśniewski, M.; Dobkowski, A.; Pater, G. The Tool to Support the Frequency Planning Process in the HF Range. In Proceedings of the 2018 New Trends in Signal Processing (NTSP), Demanovska Dolina, Slovakia, 10–12 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Romanik, J.; Golan, E.; Zubel, K.; Kaniewski, P. Electromagnetic Situational Awareness of Cognitive Radios supported by Radio Environment Maps. In Proceedings of the 2019 Signal Processing Symposium (SPSympo), Krakow, Poland, 17–19 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Luo, G.; Shi, M.; Zhao, C.; Shi, Z. Hash-Chain-Based Cross-Regional Safety Authentication for Space-Air-Ground Integrated VANETs. Appl. Sci. 2020, 10, 4206. [Google Scholar] [CrossRef]
- IEEE Standard for Information technology—Local and metropolitan area networks—Specific requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 6: Wireless Access in Vehicular Environments. In IEEE Std 802.11p-2010; (Amendment to IEEE Std 802.11-2007 as amended by IEEE Std 802.11k-2008, IEEE Std 802.11r-2008, IEEE Std 802.11y-2008, IEEE Std 802.11n-2009, and IEEE Std 802.11w-2009); IEEE: New York, NY, USA, 2010; pp. 1–1465.
- Paul, A.; Chilamkurti, N.; Daniel, A.; Rho, S. Intelligent Vehicular Networks and Communications: Fundamentals, Architectures and Solutions; Elsevier: Amsterdam, The Netherlands; Boston, MA, USA; Heidelberg, Germany, 2017; ISBN 9780128092668. [Google Scholar]
- IEEE Standard—Information Technology—Telecommunications and information exchange between systems—Wireless Regional Area Networks—Specific requirements—Part 22: Cognitive Wireless RAN MAC and PHY specifications: Policies and Procedures for Operation in the Bands that Allow Spectrum Sharing where the Communications Devices May Opportunistically Operate in the Spectrum of Primary Service. In IEEE Std 802.22-2019; (Revision of IEEE Std 802.22-2011); IEEE: New York, NY, USA, 2020; pp. 1–1465.
- Bahaghighat, M.; Motamedi, S.A.; Xin, Q. Image Transmission over Cognitive Radio Networks for Smart Grid Applications. Appl. Sci. 2019, 9, 5498. [Google Scholar] [CrossRef]
- Garcia, C.E.; Camana, M.R.; Koo, I. Secrecy Energy Efficiency Maximization in an Underlying Cognitive Radio–NOMA System with a Cooperative Relay and an Energy-Harvesting User. Appl. Sci. 2020, 10, 3630. [Google Scholar] [CrossRef]
- Kustra, M.; Kosmowski, K.; Suchański, M. Hybrid sensing method of real OFDM signal. In Proceedings of the 2018 International Conference on Military Communications and Information Systems (ICMCIS), Warsaw, Poland, 22–23 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Kosmowski, K.; Prawdzik, K.; Baranowski, G. Immunity of automatic modulation classification algotithms against inaccurate estimation of signal parameters. In Proceedings of the 2017 Communication and Information Technologies (KIT), Vysoke Tatry, Slovakia, 4–6 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Arshid, K.; Hussain, I.; Bashir, M.K.; Naseem, S.; Ditta, A.; Mian, N.A.; Zahid, M.; Khan, I.A. Primary User Traffic Pattern Based Opportunistic Spectrum Handoff in Cognitive Radio Networks. Appl. Sci. 2020, 10, 1674. [Google Scholar] [CrossRef]
- Erdogan, E.; Çolak, S.; Alakoca, H.; Namdar, M.; Basgumus, A.; Durak-Ata, L. Interference Alignment in Multi-Hop Cognitive Radio Networks under Interference Leakage. Appl. Sci. 2018, 8, 2486. [Google Scholar] [CrossRef]
- Arjoune, Y.; Mrabet, Z.; Kaabouch, N. Multi-Attributes, Utility-Based, Channel Quality Ranking Mechanism for Cognitive Radio Networks. Appl. Sci. 2018, 8, 628. [Google Scholar] [CrossRef]
- Yilmaz, H.B.; Tugcu, T. Location estimation-based radio environment map construction in fading channels: REM construction in fading channels. Wirel. Commun. Mob. Comput. 2015, 15, 561–570. [Google Scholar] [CrossRef]
- IEEE Standard for Information technology—Telecommunications and information exchange between systems—Local and metropolitan area networks—Specific requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 5: Television White Spaces (TVWS) Operation. In IEEE Std 802.11af-2013; (Amendment to IEEE Std 802.11-2012, as amended by IEEE Std 802.11ae-2012, IEEE Std 802.11aa-2012, IEEE Std 802.11ad-2012, and IEEE Std 802.11ac-2013); IEEE: New York, NY, USA, 2014; pp. 1–198.
- Corral-De-Witt, D.; Ahmed, S.; Awin, F.; Rojo-Álvarez, J.L.; Tepe, K. An Accurate Probabilistic Model for TVWS Identification. Appl. Sci. 2019, 9, 4232. [Google Scholar] [CrossRef]
- International Telecommunication Union. Recommendation 76, Deployment and use of cognitive radio systems. In Final Acts WRC-12, World Radiocommunication Conference; ITU: Geneva, Switzerland, 2012; ISBN 978-92-61-14141-7. [Google Scholar]
- EN 301 598 V1.1.1 White Space Devices (WSD); Wireless Access Systems Operating in the 470 MHz to 790 MHz TV Broadcast Band; Harmonized EN Covering the Essential Requirements of Article 3.2 of the R&TTE Directive; ETSI: Valbonne, France, 2014.
- Zhang, J.; Zhao, Q.; Zou, J. The IEEE802.22 WRAN System Based on Radio Environment Map (REM). In Proceedings of the First International Workshop on Education Technology and Computer Science, Wuhan, China, 7–8 March 2009; pp. 98–101. [Google Scholar] [CrossRef]
- Pesko, M.; Javornik, T.; Kosir, A.; Stular, M.; Mohorcic, M. Radio Environment Maps: The Survey of Construction Methods. KSII TIIS 2014, 8. [Google Scholar] [CrossRef]
- Bednarek, P.; Bicki, D.; Łopatka, J. Radio Environment Map for the Cognitive Radio Network Simulator. INTL J. Electron. Telecommun. 2018, 64, 45–49. [Google Scholar] [CrossRef]
- Kliks, A.; Kryszkiewicz, P.; Umbert, A.; PéRez-Romero, J.; Casadevall, F.; Kułacz, Ł. Application of Radio Environment Maps for Dynamic Broadband Access in TV Bands in Urban Areas. IEEE Access 2017, 5. [Google Scholar] [CrossRef]
- Bi, S.; Lyu, J.; Ding, Z.; Zhang, R. Engineering Radio Maps for Wireless Resource Management. IEEE Wireless Commun. 2019, 26, 133–141. [Google Scholar] [CrossRef]
- Ureten, S.; Yongacoglu, A.; Petriu, E. A comparison of Interference Cartography Generation Techniques in Cognitive Radio Networks. In Proceedings of the IEEE International Conference on Communications, Ottawa, ON, Canada, 10–15 June 2012; pp. 1879–1883. [Google Scholar] [CrossRef]
- Suchański, M.; Kaniewski, P.; Romanik, J.; Golan, E. Radio environment maps for military cognitive networks: Construction techniques vs. map quality. In Proceedings of the 2018 International Conference on Military Communications and Information Systems (ICMCIS), Warsaw, Poland, 22–23 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, R. Secure crowdsourced radio environment map construction. In Proceedings of the 2017 IEEE 25th International Conference on Network Protocols (ICNP), Toronto, ON, Canada, 10–13 October 2017; pp. 1–10. [Google Scholar] [CrossRef]
- Phillips, C.; Ton, M.; Sicker, D.; Grunwald, D. Practical radio environment mapping with geostatistics. In Proceedings of the IEEE International Symposium on Dynamic Spectrum Access Networks, Bellevue, WA, USA, 16–19 October 2012; pp. 422–433. [Google Scholar] [CrossRef]
- Zhang, T.; Ji, X.; Zhuang, Z.; Xu, W. JamCatcher: A Mobile Jammer Localization Scheme for Advanced Metering Infrastructure in Smart Grid. Sensors 2019, 19, 909. [Google Scholar] [CrossRef]
- Mao, D.; Shao, W.; Qian, Z.; Xue, H.; Lu, X.; Wu, H. Constructing accurate Radio Environment Maps with Kriging Interpolation in Cognitive Radio Networks. In Proceedings of the 2018 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC), Xuzhou, China, 21–24 July 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Camarinha-Matos, L.M.; Oliveira, L.B. Distributed Localization with Complemented RSS and AOA Measurements: Theory and Methods. Appl. Sci. 2019, 10, 272. [Google Scholar] [CrossRef]
- Yilmaz, H.B.; Chae, C.-B.; Tugcu, T. Sensor placement algorithm for radio environment map construction in cognitive radio networks. In Proceedings of the 2014 IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 6–9 April 2014; pp. 2096–2101. [Google Scholar] [CrossRef]
- Pesko, M.; Javornik, T.; Vidmar, L.; Košir, A.; Štular, M.; Mohorčič, M. The indirect self-tuning method for constructing radio environment map using omnidirectional or directional transmitter antenna. EURASIP J. Wirel. Com. Netw. 2015, 50. [Google Scholar] [CrossRef]
- Yilmaz, H.; Tugcu, T.; Alagöz, F.; Bayhan, S. Radio environment map as enabler for practical cognitive radio networks. IEEE Commun. Mag. 2013, 51, 162–169. [Google Scholar] [CrossRef]
- Kosmowski, K.; Romanik, J. Hybrid Method of the Radio Environment Map Construction to Increase Spectrum Awareness of Cognitive Radios. In Theory and Applications of Dependable Computer Systems. DepCoS-RELCOMEX 2020; Zamojski, W., Mazurkiewicz, J., Sugier, J., Walkowiak, T., Kacprzyk, J., Eds.; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2020; Volume 1173, pp. 378–388. [Google Scholar] [CrossRef]
- Reddy, K.B.; Ramana, P.V.; Sumiya, K. Comparative analysis of spatial interpolation methods of different field measurements for cognitive radio. In Proceedings of the 2017 2nd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Belgrade, Serbia, 22–24 November 2011; pp. 2212–2216. [Google Scholar] [CrossRef]
- Le Nir, V.; Scheers, B. Multiple jammer localization and transmission power estimation for radio environment map. In Proceedings of the 2018 International Conference on Military Communications and Information Systems (ICMCIS), Warsaw, Poland, 22–23 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Dwarakanath, R.C.; Naranjo, J.D.; Ravanshid, A. Modeling of interference maps for Licensed Shared Access in LTE-advanced networks supporting Carrier Aggregation. In Proceedings of the IFIP Wireless Days (WD), Valencia, Spain, 13–15 November 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Denkovski, D.; Atanasovski, V.; Gavrilovska, L.; Riihijaervi, J.; Maehoenen, P. Reliability of a Radio Environment Map: Case of Spatial Interpolation Techniques. In Proceedings of the 7th International Conference on Cognitive Radio Oriented Wireless Networks, Stockholm, Sweden, 18–20 June 2012. [Google Scholar] [CrossRef]
- Xiang, T.; Wang, H. Research on Distributed 5G Signal Coverage Detection Algorithm Based on PSO-BP-Kriging. Sensors 2018, 18, 4390. [Google Scholar] [CrossRef] [PubMed]
- Boccolini, G.; Hernández-Peñaloza, G.; Beferull-Lozano, B. Wireless sensor network for Spectrum Cartography based on Kriging interpolation. In Proceedings of the IEEE 23rd International Symposium on Personal, Indoor and Mobile Radio Communications—(PIMRC), Sydney, NSW, Australia, 9–12 September 2012; pp. 1565–1570. [Google Scholar] [CrossRef]
- Roger, S.; Botella, C.; Pérez-Solano, J.J.; Perez, J. Application of Radio Environment Map Reconstruction Techniques to Platoon-based Cellular V2X Communications. Sensors 2020, 20, 2440. [Google Scholar] [CrossRef] [PubMed]
- Suchański, M.; Kaniewski, P.; Romanik, J.; Golan, E. Radio environment map to support frequency allocation in military communications systems. In Proceedings of the 2018 Baltic URSI Symposium (URSI), Poznan, Poland, 15–17 May 2018; pp. 230–233. [Google Scholar] [CrossRef]
- Romanik, J.; Zubel, K. Radio Environment Maps for Military Cognitive Networks: Analysis of Measurement-based Maps for UHF Band. In Proceedings of the 2019 Communication and Information Technologies (KIT), Vysoke Tatry, Slovakia, 9–11 October 2019. [Google Scholar] [CrossRef]
- Zubel, K.; Romanik, J.; Golan, E.; Wilgucki, K. Measurement method for construction of the radio environment maps supporting cognitive radios. In Proceedings of the Radioelectronic Systems Conference 2019; Kaniewski, P., Matuszewski, J., Eds.; SPIE: Jachranka, Poland, 2020; p. 29. [Google Scholar] [CrossRef]
- Suchański, M.; Kaniewski, P.; Romanik, J.; Golan, E.; Zubel, K. Radio environment maps for military cognitive networks: Density of small-scale sensor network vs. map quality. EURASIP J. Wirel. Com. Netw. 2020, 189. [Google Scholar] [CrossRef]
- Suchański, M.; Kaniewski, P.; Romanik, J.; Golan, E.; Zubel, K. Radio Environment Maps for Military Cognitive Networks: Deployment of Sensors vs. Map Quality. In Proceedings of the 2019 International Conference on Military Communications and Information Systems (ICMCIS), Budva, Montenegro, 14–15 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
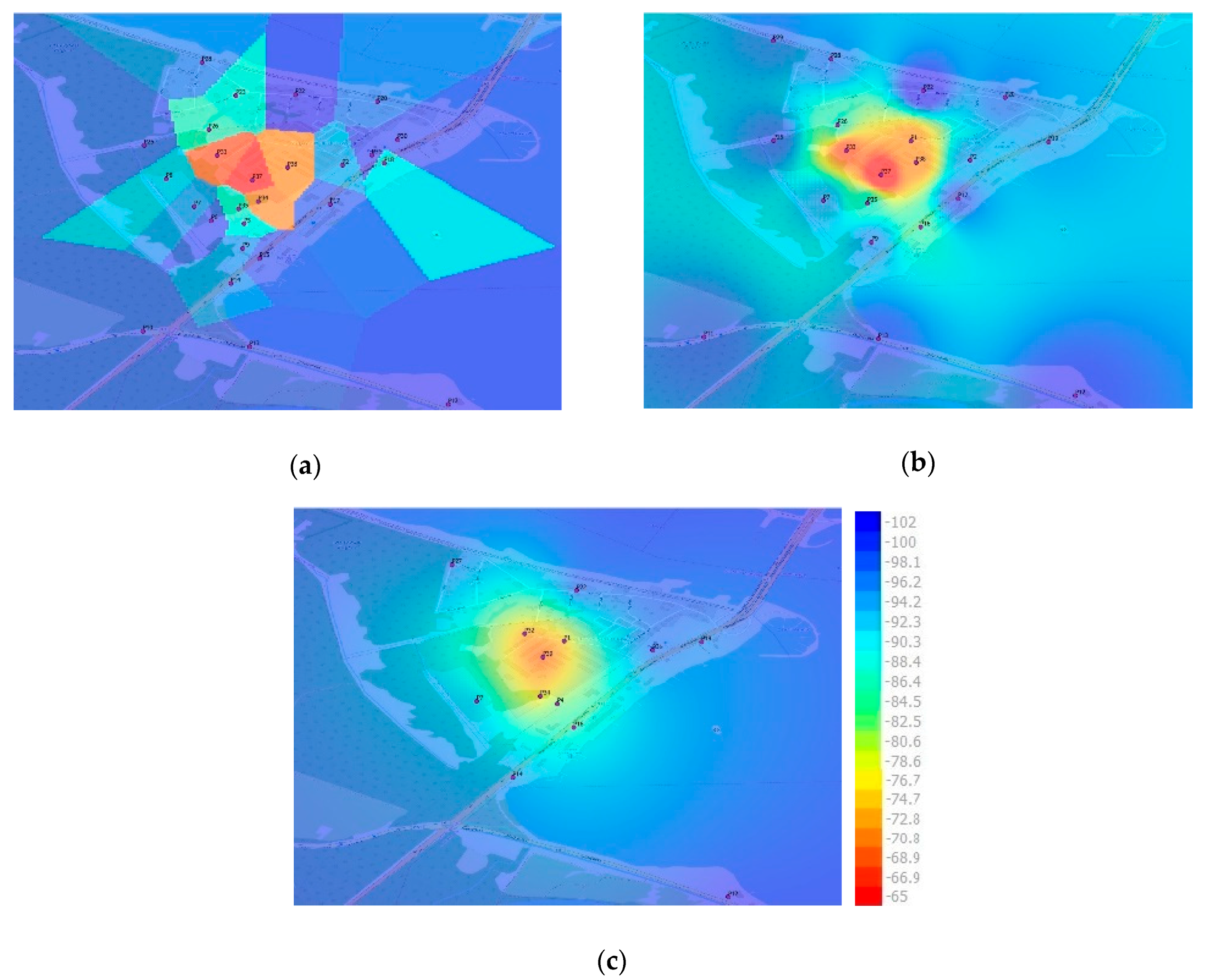
| Scenario 13 | Scenario 20 | Scenario 26 | ||||||
|---|---|---|---|---|---|---|---|---|
| Test_13a | Test_13b | Test_13c | Test_20a | Test_20b | Test_20c | Test_26a | Test_26b | Test_26c |
| P2 | P1 | P1 | P2 | P1 | P3 | P5 | P2 | P1 |
| P3 | P4 | P4 | P5 | P4 | P4 | P8 | P6 | P3 |
| P5 | P6 | P5 | P6 | P6 | P5 | P13 | P7 | P4 |
| P6 | P7 | P6 | P8 | P7 | P6 | P15 | P9 | P11 |
| P8 | P8 | P8 | P10 | P9 | P8 | P18 | P10 | P16 |
| P9 | P9 | P9 | P13 | P11 | P10 | P20 | P12 | P19 |
| P10 | P11 | P11 | P15 | P13 | P14 | P23 | P14 | P21 |
| P11 | P13 | P13 | P18 | P14 | P15 | P26 | P17 | P24 |
| P13 | P14 | P14 | P20 | P17 | P18 | P28 | P22 | P27 |
| P15 | P15 | P16 | P21 | P18 | P21 | P31 | P25 | P29 |
| P17 | P16 | P17 | P23 | P20 | P23 | P33 | P30 | P32 |
| P18 | P17 | P18 | P24 | P22 | P24 | P35 | P34 | P36 |
| P20 | P18 | P20 | P28 | P23 | P27 | P37 | P38 | P39 |
| P21 | P20 | P22 | P29 | P25 | P30 | |||
| P23 | P22 | P24 | P30 | P27 | P31 | |||
| P24 | P24 | P25 | P31 | P30 | P32 | |||
| P25 | P25 | P26 | P33 | P34 | P34 | |||
| P26 | P26 | P27 | P35 | P36 | P36 | |||
| P28 | P27 | P28 | P37 | P39 | P39 | |||
| P29 | P28 | P30 | ||||||
| P30 | P30 | P31 | ||||||
| P33 | P31 | P34 | ||||||
| P35 | P34 | P35 | ||||||
| P36 | P36 | P36 | ||||||
| P37 | P38 | P38 | ||||||
| P38 | P39 | P39 | ||||||
| Test ID | RMSE for Various Interpolation Methods | Avg. RMSE | |||||||
|---|---|---|---|---|---|---|---|---|---|
| IDW p1 | IDW p2 | IDW p3 | IDW p4 | IDW p5 | IDW p6 | Kriging | NN | ||
| Test_13a | 9.81 | 9.22 | 8.63 | 8.16 | 8.29 | 8.16 | 6.26 | 8.50 | 8.38 |
| Test_13b | 11.44 | 10.74 | 10.93 | 11.63 | 10.97 | 11.07 | 9.57 | 11.90 | 11.03 |
| Test_13c | 9.59 | 8.69 | 9.17 | 9.60 | 10.0 | 10.26 | 7.83 | 11.75 | 9.61 |
| Test_20a | 11.00 | 9.11 | 8.48 | 7.76 | 7.62 | 7.62 | 6.72 | 8.60 | 8.36 |
| Test_20b | 10.41 | 9.52 | 8.81 | 8.47 | 8.64 | 8.23 | 8.02 | 9.24 | 8.92 |
| Test_20c | 9.02 | 6.23 | 5.31 | 4.97 | 5.11 | 5.10 | 5.89 | 7.70 | 6.17 |
| Test_26a | 9.60 | 7.48 | 6.44 | 6.32 | 6.56 | 7.32 | 6.50 | 8.86 | 7.39 |
| Test_26b | 12.56 | 11.42 | 11.23 | 11.04 | 11.18 | 11.19 | 8.43 | 12.32 | 11.17 |
| Test_26c | 10.55 | 6.75 | 6.55 | 6.55 | 6.64 | 6.71 | 6.25 | 11.07 | 7.64 |
| Zone ID | Point ID | Difference between Interpolated and True Values [dB] | True [dBm] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IDW p1 | IDW p2 | IDW p3 | IDW p4 | IDW p5 | IDW p6 | Kriging | NN | |||
| 1 | P3 | −5.6 | −4.6 | −2.7 | −3.1 | −1.1 | −2.7 | −7.6 | 4.9 | −77.9 |
| P5 | 6.1 | 8.4 | 10.1 | 12.1 | 13.4 | 13.9 | 4.1 | 17.6 | −88.6 | |
| P23 | 2.7 | 7.1 | 7.2 | 10.7 | 13.7 | 14.2 | −0.1 | 18.7 | −87.7 | |
| P26 | 3.6 | 7.5 | 11.6 | 13.3 | 13.9 | 15.1 | 2.8 | 17.1 | −86.1 | |
| P33 | −12.9 | −7.8 | −6.1 | −5.1 | −3.9 | −3.1 | −11.4 | −1.1 | −67.9 | |
| P35 | 5.0 | 10.5 | 13.0 | 12.8 | 14.7 | 15.5 | 6.0 | 16.5 | −87.5 | |
| P36 | −1.3 | 3.5 | 5.2 | 5.2 | 7.0 | 7.7 | 1.8 | 9.2 | −80.2 | |
| P37 | −17.9 | −14.4 | −9.1 | −9.4 | −7.4 | −7.4 | −13.6 | −7.2 | −59.8 | |
| P38 | −8.2 | −2.9 | 1.5 | 1.8 | 0.0 | 2.0 | −5.0 | −1.2 | −71.8 | |
| 2 | P2 | 5.8 | 2.5 | −2.2 | −3.4 | −4.9 | −5.7 | 3.1 | −6.2 | −94.8 |
| P17 | 13.9 | 15.1 | 15.1 | 16.6 | 15.1 | 14.1 | 10.8 | 14.6 | −99.6 | |
| P18 | −1.9 | −9.4 | −9.9 | −9.9 | −10.9 | −10.9 | −7.4 | −10.9 | −90.1 | |
| P20 | 8.5 | 5.3 | 1.3 | −1.0 | −1.0 | −2.0 | −1.2 | −3.0 | −98.0 | |
| P21 | 12.3 | 9.1 | 5.1 | 2.8 | 2.8 | 2.0 | 4.3 | 0.3 | −101.3 | |
| P30 | 9.3 | 4.3 | 2.3 | 3.6 | 5.0 | 3.3 | 2.8 | 4.3 | −100.8 | |
| 3 | P6 | 13.3 | 8.8 | 8.1 | 6.5 | 6.1 | 6.3 | 11.0 | 2.8 | −100.8 |
| P8 | 5.1 | 2.6 | 0.9 | −0.9 | −1.1 | −1.1 | 1.3 | −4.9 | −93.1 | |
| P9 | 8.9 | 9.9 | 9.4 | 6.1 | 4.7 | 3.9 | 7.0 | −1.6 | −96.4 | |
| P15 | 12.8 | 13.8 | 13.9 | 10.3 | 9.1 | 8.8 | 10.3 | 2.3 | −100.3 | |
| P24 | 5.1 | 3.6 | 0.9 | −1.6 | −4.9 | −3.9 | 0.3 | −5.4 | −93.6 | |
| P25 | 12.3 | 15.8 | 13.9 | 11.8 | 8.0 | 7.3 | 7.1 | 2.3 | −100.3 | |
| P28 | 8.6 | 4.4 | −0.4 | −0.1 | −1.7 | −1.9 | 2.6 | −1.4 | −97.6 | |
| P29 | 7.7 | 2.2 | 0.2 | 0.5 | −0.5 | −0.8 | −0.1 | −0.3 | −98.7 | |
| 4 | P10 | 13.3 | 12.8 | 12.8 | 8.8 | 8.5 | 6.6 | 1.9 | 2.8 | −100.8 |
| P11 | 13.7 | 13.2 | 13.2 | 9.7 | 10.7 | 9.2 | 0.9 | 2.7 | −100.7 | |
| P13 | 13.0 | 12.7 | 9.0 | 8.5 | 8.3 | 6.0 | 3.5 | 3.0 | −101.0 | |
| Zone ID | Point ID | Difference between Interpolated and True Values [dB] | True [dBm] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IDW p1 | IDW p2 | IDW p3 | IDW p4 | IDW p5 | IDW p6 | Kriging | NN | |||
| 1 | P3 | −11.1 | −10.6 | −9.6 | −11.7 | −11.6 | −13.6 | −9.5 | −21.6 | −77.9 |
| P4 | 1.1 | 4.7 | 6.1 | 6.7 | 9.1 | 5.1 | 5.8 | 2.1 | −88.1 | |
| P5 | 0.6 | 2.6 | 0.6 | −0.9 | 2.6 | 0.6 | 1.2 | 1.0 | −88.6 | |
| P23 | −1.3 | 1.7 | 2.7 | 2.2 | 0.2 | 0.7 | −1.7 | 0.1 | −87.7 | |
| P32 | −14.4 | −8.4 | −6.4 | −3.9 | −3.4 | −1.9 | −8.9 | 1.6 | −69.6 | |
| P34 | −13.9 | −8.4 | −5.9 | −2.4 | −4.4 | −4.4 | −8.6 | −17.0 | −70.6 | |
| P36 | −2.1 | 2.0 | 4.2 | 8.2 | 6.2 | 7.2 | 2.0 | 13.2 | −80.2 | |
| P39 | −17.4 | −9.4 | −2.4 | −1.4 | −1.4 | −1.4 | −9.1 | −2.4 | −64.6 | |
| 2 | P18 | −1.2 | −3.9 | −3.4 | −6.4 | −5.9 | −4.4 | −5.7 | −5.9 | −90.1 |
| P21 | 9.9 | 6.6 | 6.3 | 3.8 | 4.3 | 3.3 | 6.1 | 3.0 | −101.3 | |
| P30 | 8.5 | 6.2 | 5.8 | 3.8 | 4.5 | 5.8 | 4.4 | 4.8 | −100.8 | |
| P31 | 9.9 | 7.3 | 8.1 | 4.6 | 5.1 | 6.6 | 5.8 | 6.1 | −101.1 | |
| 3 | P6 | 12.3 | 9.0 | 7.3 | 6.8 | 6.8 | 5.3 | 10.3 | 3.0 | −100.8 |
| P8 | 3.1 | 1.6 | 0.6 | −2.4 | −0.9 | −2.4 | 0.6 | −4.7 | −93.1 | |
| P14 | 6.3 | 3.5 | 2.8 | 0.8 | 0.8 | 0.8 | 0.4 | 0.3 | −96.8 | |
| P15 | 10.1 | 7.5 | 5.8 | 3.8 | 3.8 | 4.8 | 7.5 | 3.8 | −100.3 | |
| P24 | 2.4 | −1.6 | −3.9 | −4.9 | −5.4 | −6.4 | −1.6 | −5.9 | −93.6 | |
| P27 | 6.3 | 2.6 | 1.1 | 1.1 | 1.1 | 0.6 | 2.1 | 0.6 | −98.6 | |
| 4 | P10 | 9.8 | 7.1 | 6.3 | 3.3 | 3.3 | 1.3 | 0.7 | 0.8 | −100.8 |
| Zone ID | Point ID | Difference between Interpolated and True Values [dB] | True [dBm] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IDW p1 | IDW p2 | IDW p3 | IDW p4 | IDW p5 | IDW p6 | Kriging | NN | |||
| 1 | P5 | 0.6 | 1.6 | 1.1 | 3.1 | −0.4 | −1.4 | 0.5 | −4.9 | −88.6 |
| P23 | −0.8 | 2.2 | 4.7 | 8.2 | 11.5 | 13.0 | −0.1 | 19.5 | −87.7 | |
| P26 | −2.1 | 0.6 | 6.1 | 9.8 | 11.4 | 12.1 | 1.5 | 17.9 | −86.1 | |
| P33 | −17.6 | −11.6 | −9.6 | −6.6 | −4.9 | −6.8 | −13.4 | −0.3 | −67.9 | |
| P35 | 1.5 | 4.5 | 6.3 | 8.5 | 7.3 | 8.5 | 2.9 | 6.7 | −87.5 | |
| P37 | −22.2 | −16.4 | −12.7 | −8.7 | −9.2 | −9.2 | −14.7 | −6.3 | −59.8 | |
| 2 | P18 | −1.9 | −3.5 | −7.4 | −8.9 | −8.4 | −9.9 | −7.5 | −9.7 | −90.1 |
| P20 | 6.0 | 4.4 | −0.2 | −2.0 | −2.0 | −4.0 | −2.8 | −4.0 | −98.0 | |
| P31 | 9.1 | 8.6 | 5.1 | 2.6 | 1.6 | 1.6 | 3.8 | 1.3 | −101.1 | |
| 3 | P8 | 2.1 | 1.3 | −0.4 | −3.9 | −4.4 | −5.9 | −2.1 | −4.4 | −93.1 |
| P15 | 10.3 | 8.5 | 5.8 | 4.3 | 3.8 | 2.8 | 7.0 | 6.8 | −100.3 | |
| P28 | 6.6 | 4.0 | 1.1 | −2.4 | −1.4 | −2.4 | 2.6 | −2.2 | −97.6 | |
| 4 | P13 | 10.5 | 10.0 | 8.4 | 5.2 | 4.8 | 3.5 | 2.2 | 5.5 | −101.0 |
| Scenario | IDW p1 | IDW p2 | IDW p3 | IDW p4 | IDW p5 | IDW p6 | Kriging | NN |
|---|---|---|---|---|---|---|---|---|
| CEP_13 | 12% | 15% | 35% | 27% | 27% | 27% | 39% | 46% |
| OEP_13 | 73% | 70% | 54% | 54% | 54% | 54% | 42% | 31% |
| UEP_13 | 15% | 15% | 11% | 19% | 19% | 19% | 19% | 23% |
| CEP_20 | 32% | 26% | 32% | 37% | 32% | 42% | 42% | 53% |
| OEP_20 | 47% | 48% | 42% | 42% | 42% | 37% | 32% | 21% |
| UEP_20 | 21% | 26% | 26% | 21% | 26% | 21% | 26% | 26% |
| CEP_26 | 46% | 31% | 31% | 23% | 31% | 31% | 62% | 22% |
| OEP_26 | 39% | 46% | 46% | 46% | 38% | 31% | 15% | 39% |
| UEP_26 | 15% | 23% | 23% | 31% | 31% | 38% | 23% | 39% |
| Zone | IDW p1 | IDW p2 | IDW p3 | IDW p4 | IDW p5 | IDW p6 | Kriging | NN |
|---|---|---|---|---|---|---|---|---|
| 1 | 43% | 30% | 26% | 21% | 26% | 30% | 43% | 35% |
| 2 | 23% | 8% | 31% | 31% | 31% | 23% | 23% | 23% |
| 3 | 12% | 35% | 53% | 47% | 41% | 47% | 59% | 59% |
| 4 | 0% | 0% | 0% | 0% | 0% | 20% | 80% | 80% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaniewski, P.; Romanik, J.; Golan, E.; Zubel, K. Spectrum Awareness for Cognitive Radios Supported by Radio Environment Maps: Zonal Approach. Appl. Sci. 2021, 11, 2910. https://doi.org/10.3390/app11072910
Kaniewski P, Romanik J, Golan E, Zubel K. Spectrum Awareness for Cognitive Radios Supported by Radio Environment Maps: Zonal Approach. Applied Sciences. 2021; 11(7):2910. https://doi.org/10.3390/app11072910
Chicago/Turabian StyleKaniewski, Paweł, Janusz Romanik, Edward Golan, and Krzysztof Zubel. 2021. "Spectrum Awareness for Cognitive Radios Supported by Radio Environment Maps: Zonal Approach" Applied Sciences 11, no. 7: 2910. https://doi.org/10.3390/app11072910
APA StyleKaniewski, P., Romanik, J., Golan, E., & Zubel, K. (2021). Spectrum Awareness for Cognitive Radios Supported by Radio Environment Maps: Zonal Approach. Applied Sciences, 11(7), 2910. https://doi.org/10.3390/app11072910






