Behavioral Modeling of Memristor-Based Rectifier Bridge
Abstract
1. Introduction
- Being an analog element, its resistance can take any values. This is a positive property in comparison with any binary element whose value can be either 0 or 1. Such variability of resistance is realized in one element, the memristor size is reduced to several nanometers and the response rate is reduced to nanoseconds.
- The memristor does not store a charge. This means that it is not prone to charge leaks, which must be dealt with when going to nanometer-scale microcircuits.
- The memristor is a non-volatile element, and data can be stored as long as the materials from which it is made exist.
- Memristors placed on crossing conductors (crossbars) can be used to form densely packed memory.
- Many memristor materials are compatible with complementary metal-oxide-semiconductor (CMOS) technology.
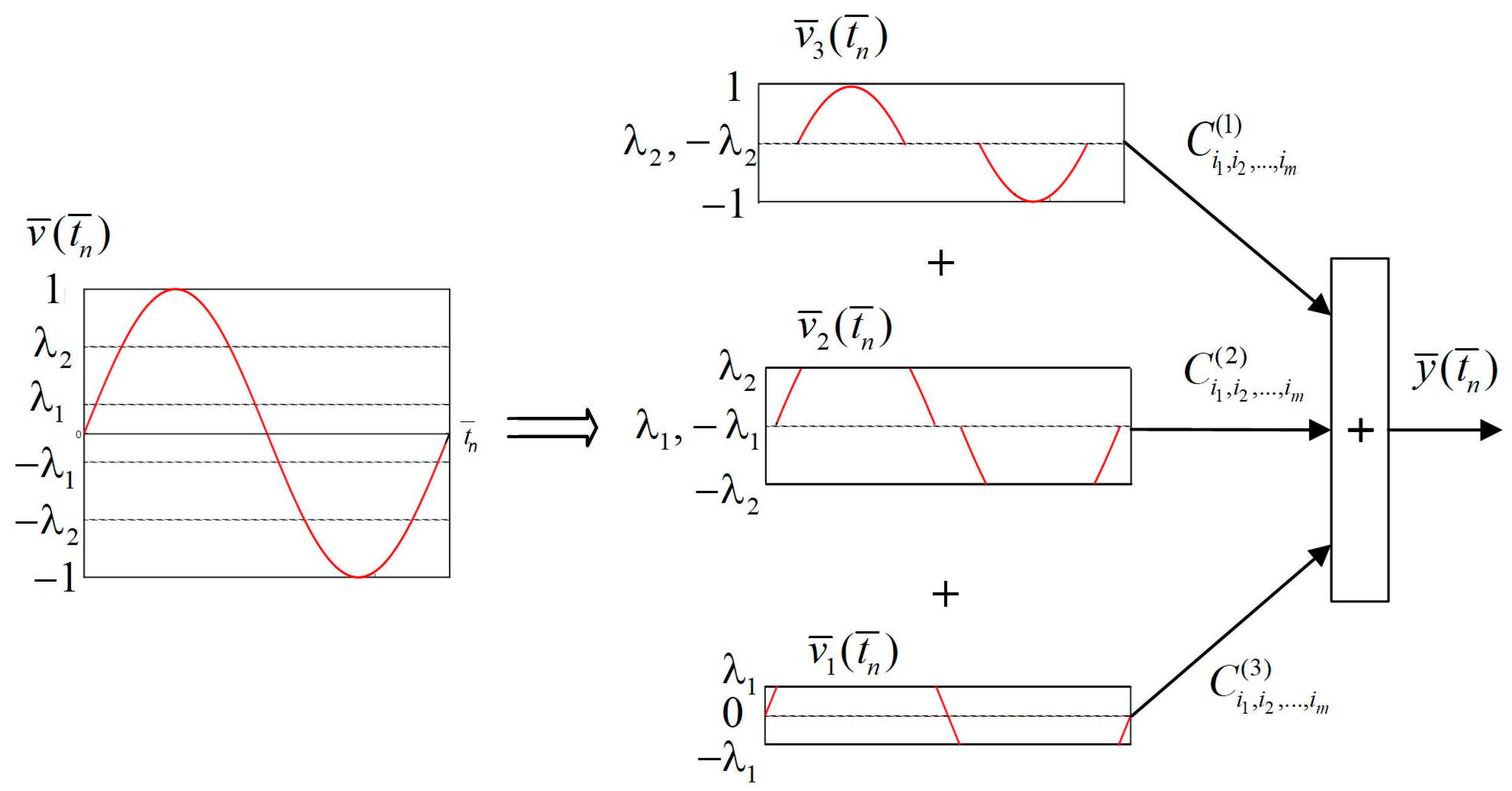
2. Multi-Dimensional Split Polynomial as a Behavioral Nonlinear Model
- for all , , there is an inequality
- for any , , , , , , there is an inequality
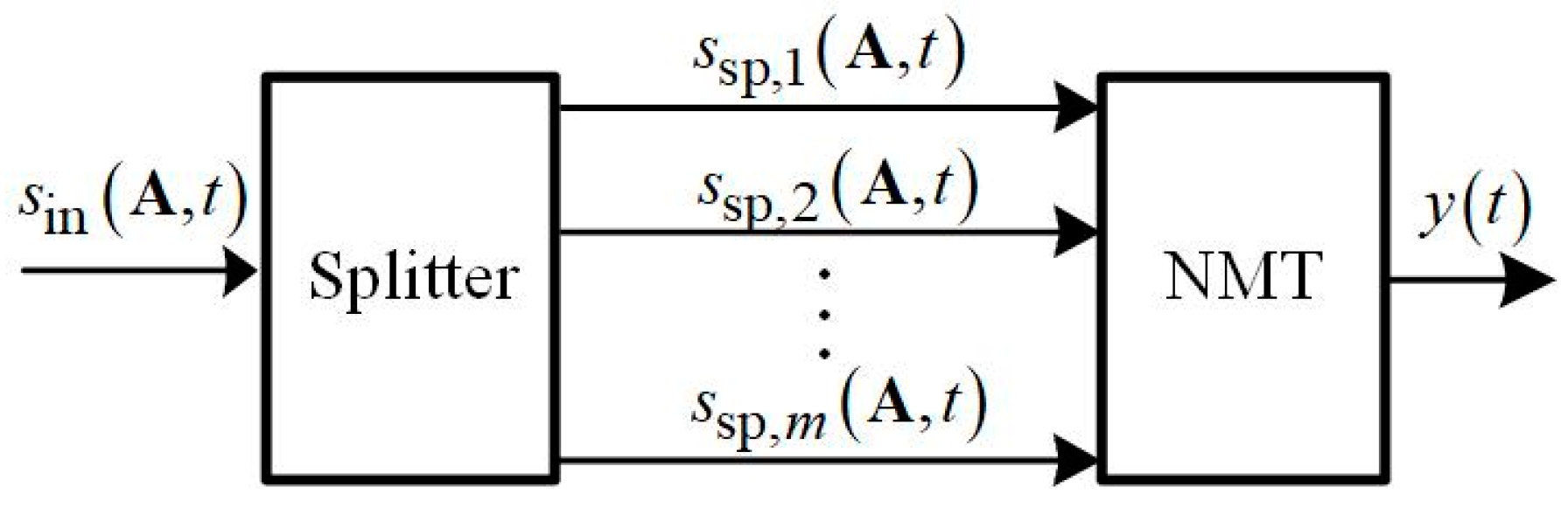
3. Forming the Sets of Input and Output Signals of the Memristor-Based Rectifier Bridge
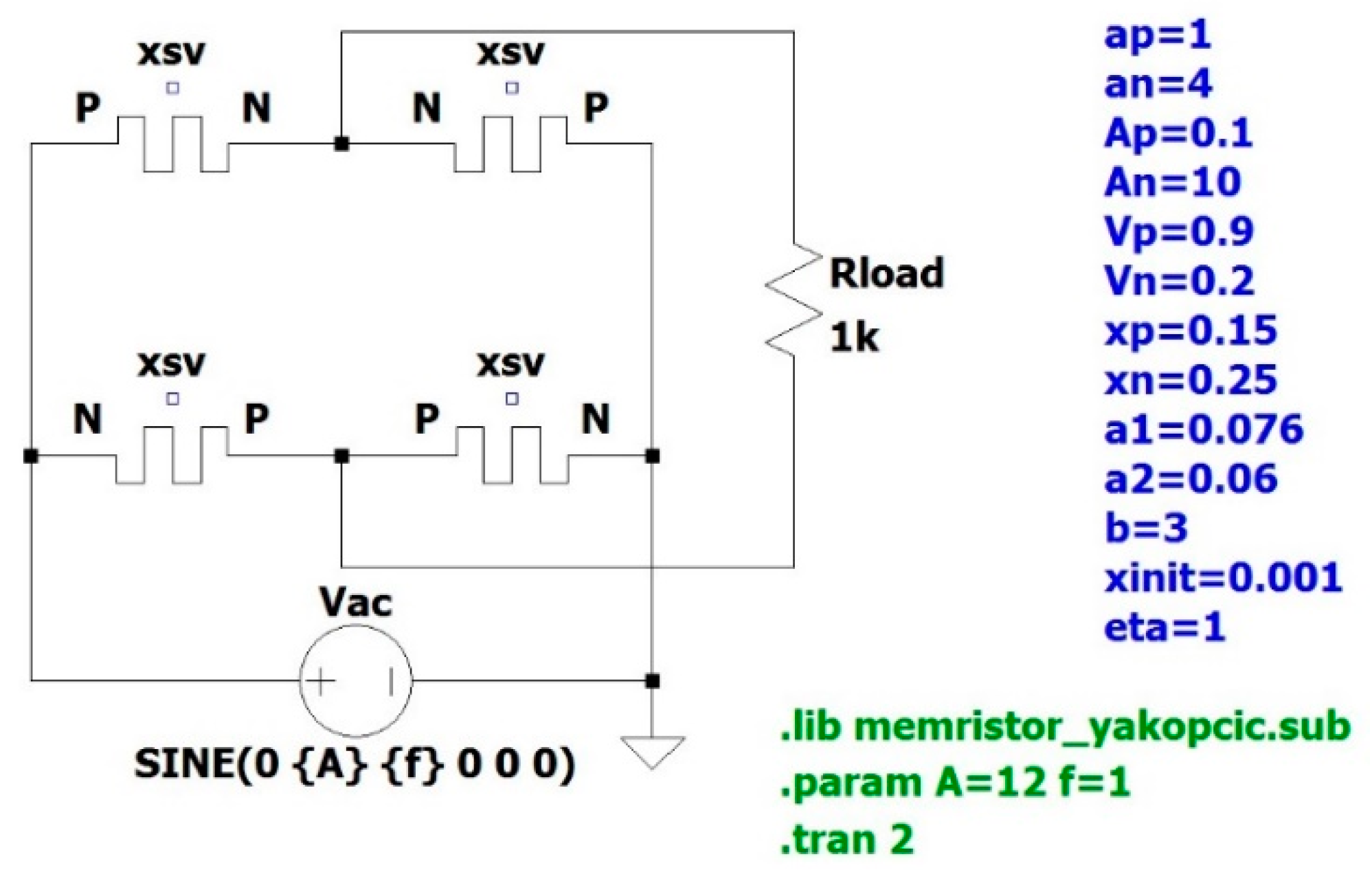
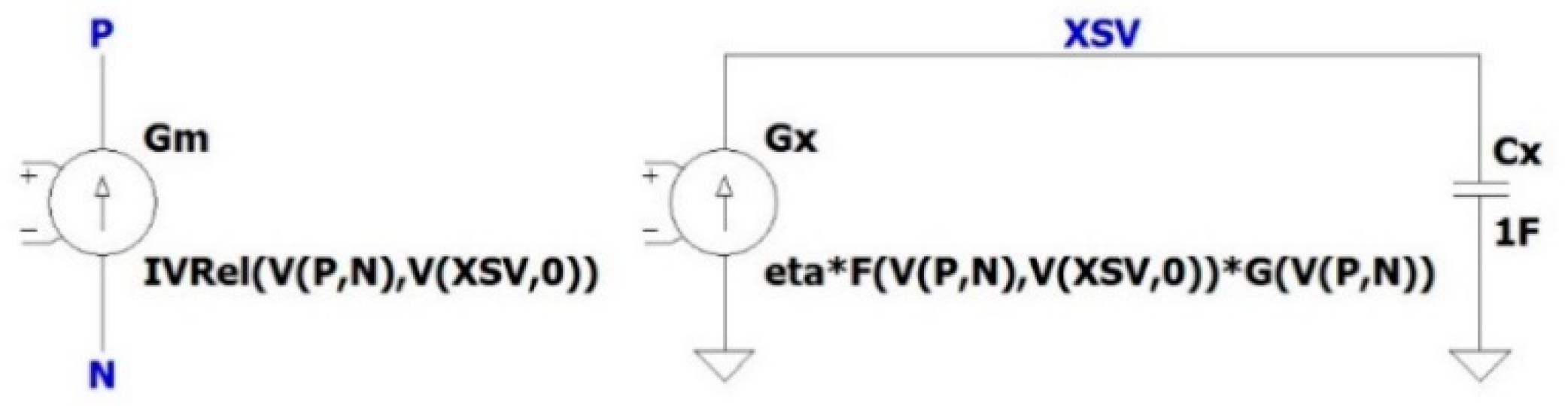
3.1. The Yakopcic Model of a Memristor in LTspice
- Cx XSV 0 {1}
- .ic V(XSV) = xo
- .func F(V1,V2) = IF(eta*V1 >= 0, IF(V2 >= xp,exp(−alphap*(V2−xp))*wp(V2),1), IF(V2 <= (1−xn), exp(alphan*(V2+xn−1))*wn(V2),1))
- .func wp(V) = (xp−V)/(1−xp) + 1
- .func wn(V) = V/(1−xn)
- Gx 0 XSV value = {eta*F(V(P,N),V(XSV,0))*G(V(P,N))}
- Gm P N value = {IVRel(V(P,N),V(XSV,0))}
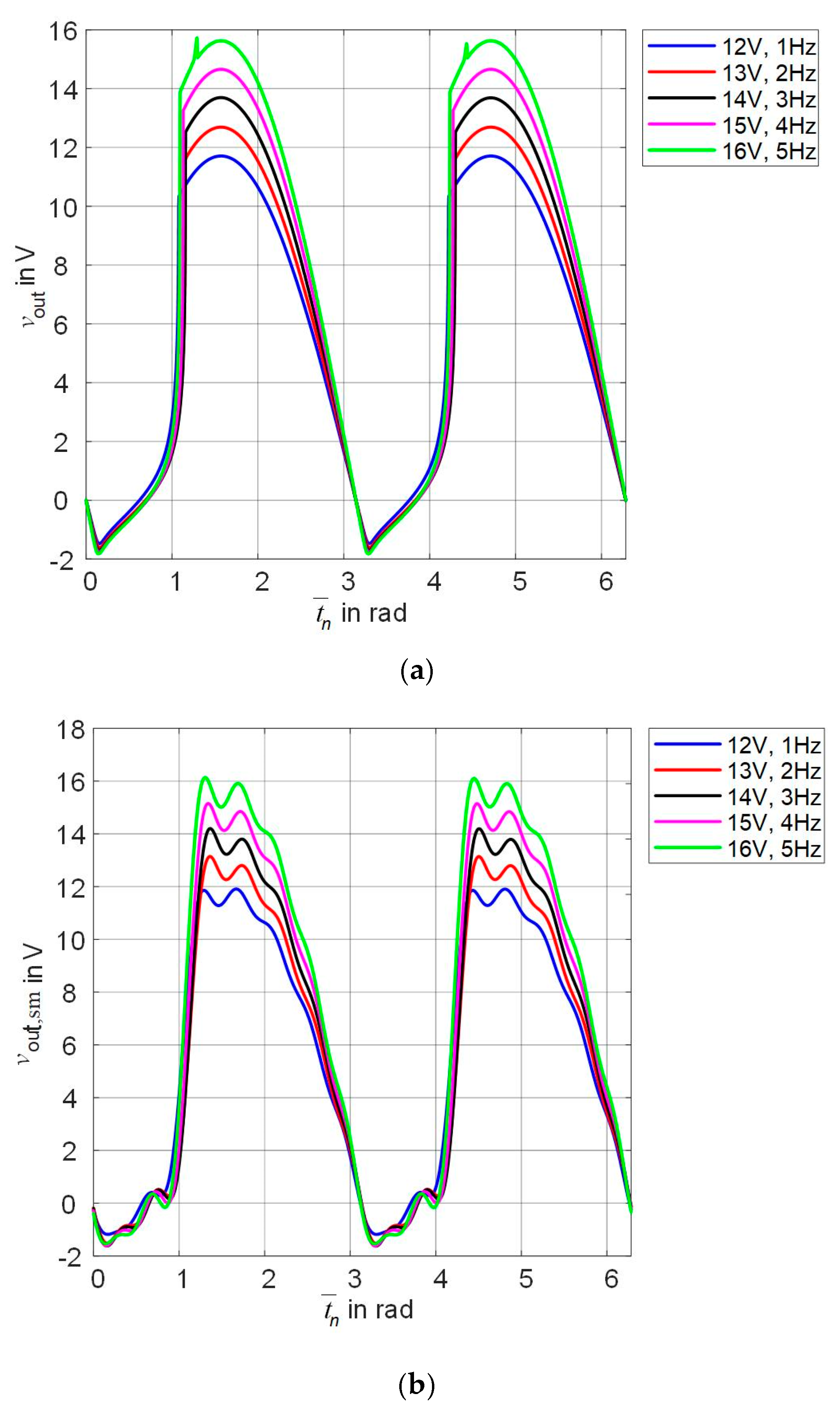
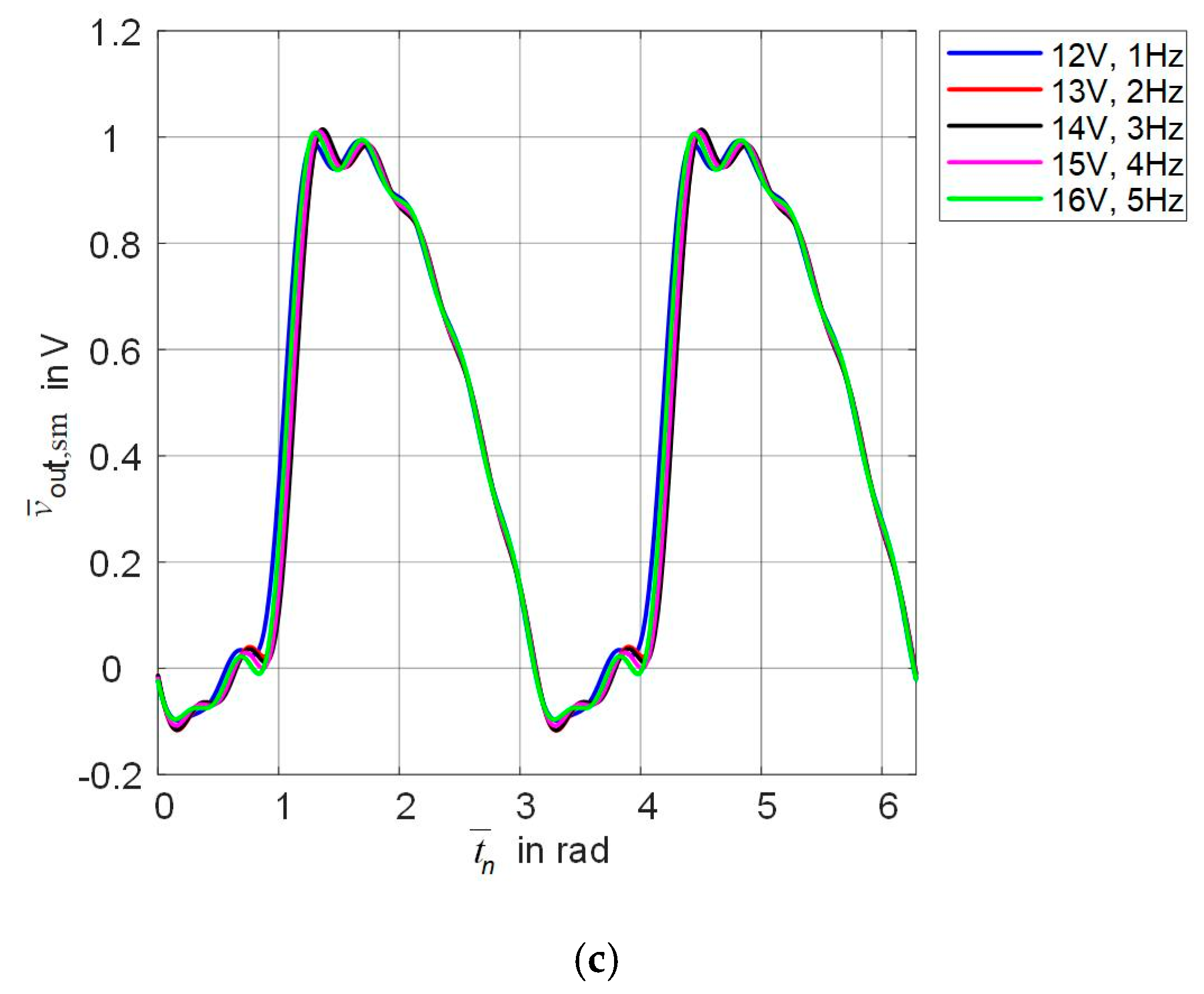
3.2. Smoothing Output Signals of the Memristor-Based Rectifier Bridge
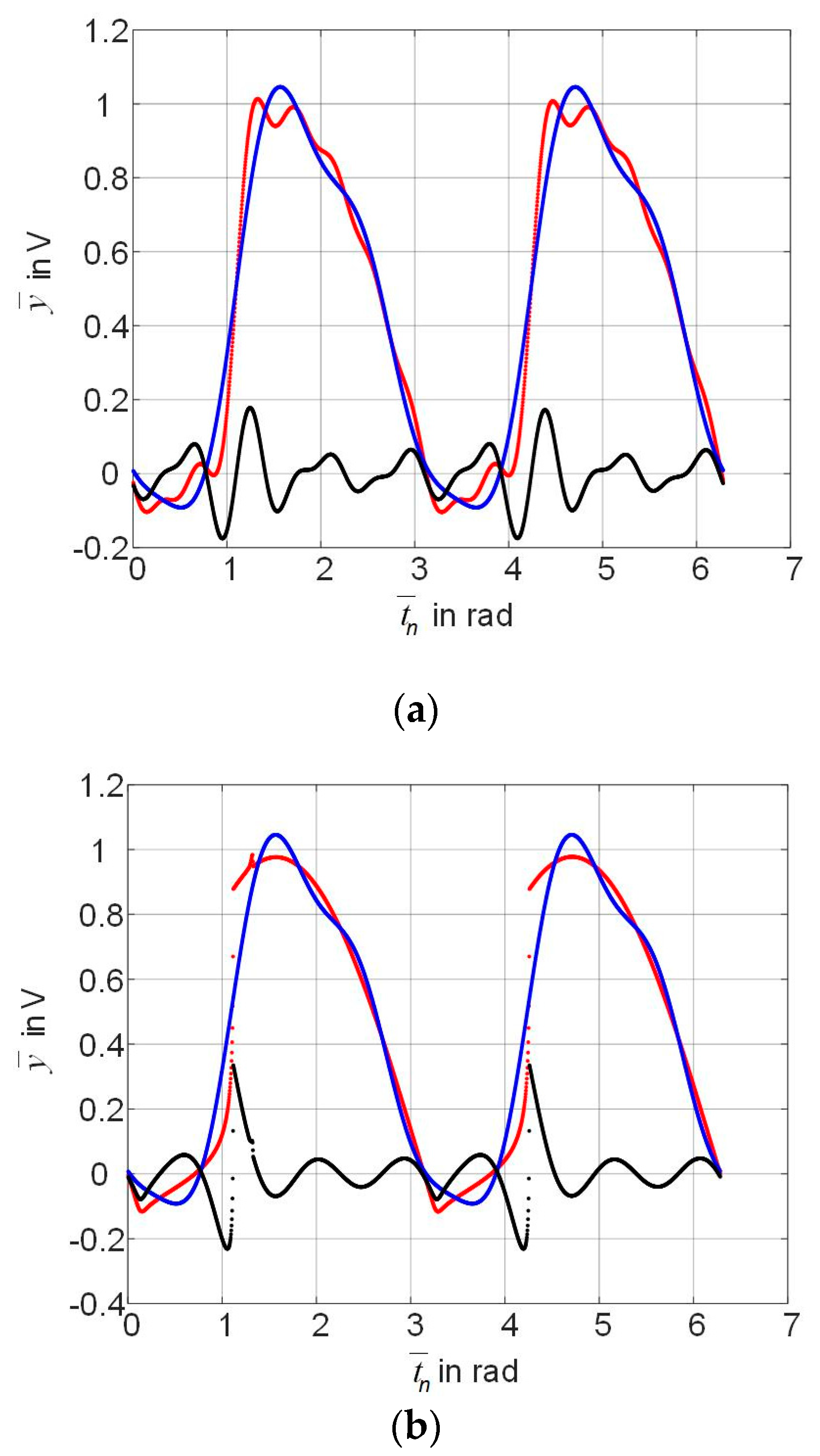
4. Results of the Rectifier Modeling Based on Multi-Dimensional Polynomials
- the uniform error
- the maximum absolute error
- the root-mean-square error
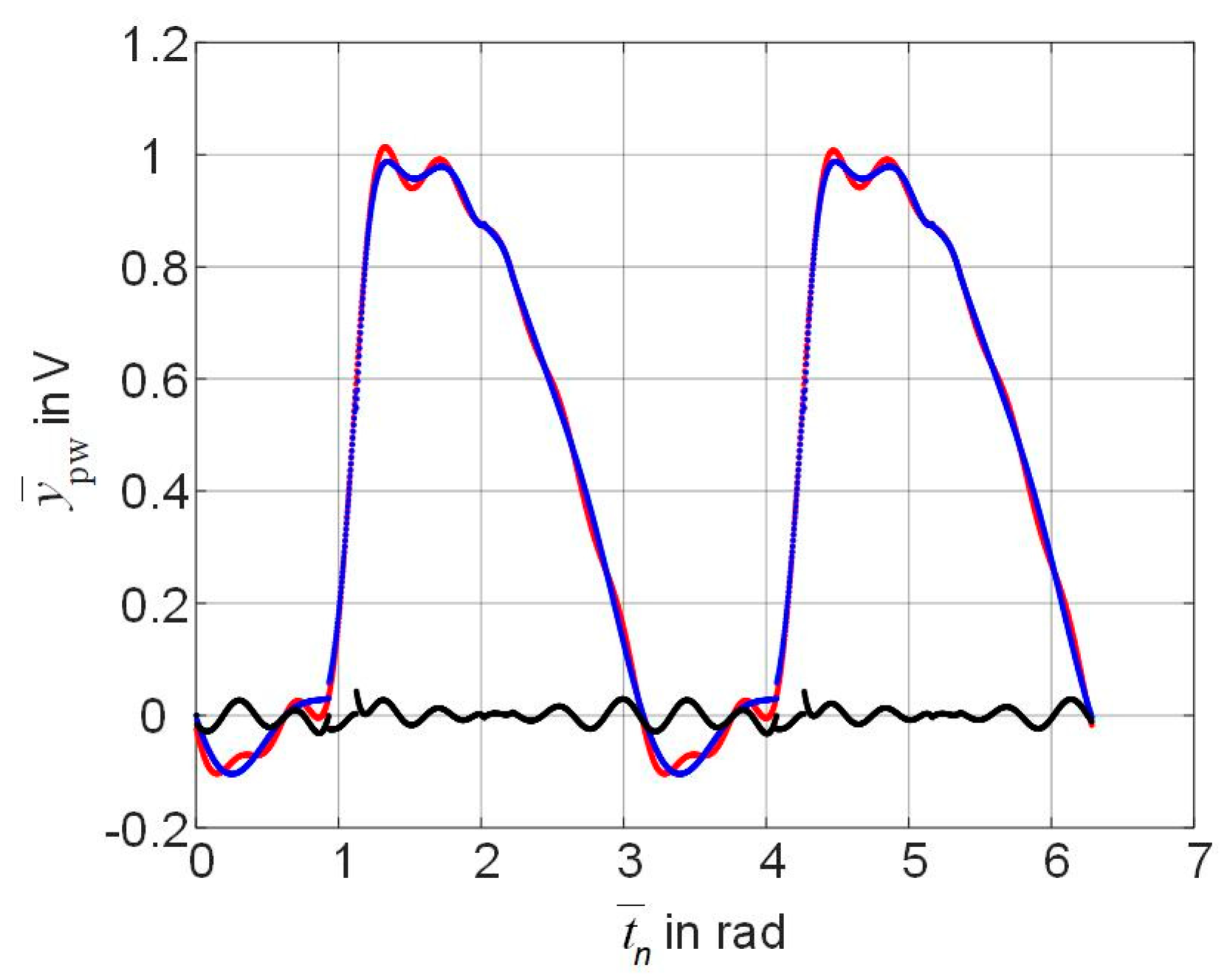
5. Results of the Rectifier Modeling Based on Piecewise Multi-Dimensional Polynomials
6. Conclusions
- The form of the model and the method of its construction are universal, because they do not depend on the technology of memristor implementation.
- Since a polynomial is linear-in-parameters, these parameters are defined as globally optimal by solving the approximation problem.
- The splitting property allows the polynomial to be adapted to the assigned signal class, hence to construct a simpler model than other behavioral models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Corinto, F.; Forti, M.; Chua, L.O. Nonlinear Circuits and Systems with Memristors: Nonlinear Dynamics and Analogue Computing via the Flux-Charge Analysis Method; Springer Nature Switzerland AG: Cham, Switzerland, 2021; p. 438. [Google Scholar]
- Mladenov, V. Advanced Memristor Modeling: Memristor Circuits and Networks; MDPI: Basel, Switzerland, 2019; p. 170. [Google Scholar]
- Rahma, F.; Muneam, S. Memristive Nonlinear Electronic Circuits: Dynamics, Synchronization and Applications; Springer Nature Switzerland AG: Cham, Switzerland, 2019; p. 98. [Google Scholar]
- Vaidyanathan, S.; Volos, C. Advances in Memristors, Memristive Devices and Systems; Springer International Publishing AG: Cham, Switzerland, 2017; p. 511. [Google Scholar]
- Chua, L.O. Memristor—The missing circuit element. IEEE Trans. Circuit Theory 1971, CT-18, 507–519. [Google Scholar] [CrossRef]
- Kund, M.; Beitel, G.; Pinnow, C.U.; Roehr, T.; Schumann, J.; Symanczyk, R.; Ufert, K.D.; Mueller, G. Conductive bridging RAM (CBRAM): An emerging non-volatile memory technology scalable to sub 20nm. In Proceedings of the IEEE International Electron Devices Meeting, Washington, DC, USA, 5 December 2005; pp. 754–757. [Google Scholar]
- Kozicki, M.N.; Yun, M.; Hilt, L.; Singh, A. Applications of programmable resistance changes in metal-doped chalcogenides. Electrochem. Soc. 1999, 298, 298–309. [Google Scholar]
- Terabe, K.; Hasegaw, T.; Nakayama, T.; Aono, M. Quantum point contact switch realized by solid electrochemical reaction. Riken Rev. 2001, 37, 7–8. [Google Scholar]
- Beck, A.; Bednorz, J.G.; Gerber, C.; Rossel, C.; Widmer, D. Reproducible switching effect in thin oxide films for memory applications. Appl. Phys. Lett. 2000, 77, 139–141. [Google Scholar] [CrossRef]
- Jeong, D.S.; Schroeder, H.; Waser, R. Impedance spectroscopy of TiO thin films showing resistive switching. Appl. Phys. Lett. 2006, 89, 082909. [Google Scholar] [CrossRef]
- Szot, K.; Speier, W.; Bihlmayer, G.; Waser, R. Switching the electrical resistance of individual dislocations in single-crystalline SrTiO. Nat. Mater. 2006, 5, 312–320. [Google Scholar] [CrossRef] [PubMed]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Linn, E.; Siemon, A.; Waser, R.; Menzel, S. Applicability of well-established memristive models for simulations of resistive switching devices. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 2402–2410. [Google Scholar] [CrossRef]
- Vourkas, I.; Sirakoulis, G.C. Memristor-Based Nanoelectronic Computing Circuits and Architectures; Springer International Publishing: Cham, Switzerland, 2016; p. 241. [Google Scholar]
- Zheng, N.; Mazumder, P. Learning in Energy-Efficient Neuromorphic Computing: Algorithm and Architecture Co-Design; John Wiley & Sons Ltd: Hoboken, NJ, USA, 2020; p. 276. [Google Scholar]
- Gao, Y.; Ranasinghe, D.; Al-Sarawi, S. Memristive crypto primitive for building highly secure physical unclonable functions. Sci. Rep. 2015, 5, 1–14. [Google Scholar] [CrossRef]
- Reuben, J.; Pechmann, S. A Parallel-friendly majority gate to accelerate in-memory computation. In Proceedings of the 2020 IEEE 31st International Conference on Application-specific Systems, Architectures and Processors (ASAP), Manchester, UK, 6–8 July 2020; pp. 93–100. [Google Scholar]
- Maan, A.K.; Jayadevi, D.A.; James, A.P. A survey of memristive threshold logic circuits. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 1734–1746. [Google Scholar] [CrossRef]
- Vourkas, I.; Sirakoulis, G.C. Emerging memristor-based logic circuit design approaches: A review. IEEE Circuits Syst. Mag. 2016, 16, 15–30. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Li, Y.; Friedman, E.G. Memristive model for synaptic circuits. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 767–771. [Google Scholar] [CrossRef]
- Corinto, F.; Torcini, A. Nonlinear Dynamics in Computational Neuroscience; Springer International Publishing AG: Cham, Switzerland, 2019; p. 152. [Google Scholar]
- Hu, X.; Feng, G.; Duan, S.; Liu, L. A memristive multilayer cellular neural network with applications to image processing. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1889–1902. [Google Scholar] [CrossRef] [PubMed]
- Wen, S.; Xiao, S.; Yang, Y.; Yan, Z.; Zeng, Z.; Huang, T. Adjusting learning rate of memristor-based multilayer neural networks via fuzzy method. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2019, 38, 1084–1094. [Google Scholar] [CrossRef]
- Wang, H.; Duan, S.; Huang, T.; Wang, L.; Li, C. Exponential stability of complex-valued memristive recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 766–771. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Duan, S.; Liu, J.; Wang, L.; Huang, T. A spintronic memristor-based neural network with radial basis function for robotic manipulator control implementation. IEEE Trans. Syst. Manand Cybern. Syst. 2016, 46, 582–588. [Google Scholar] [CrossRef]
- James, A.P. Deep Learning Classifiers with Memristive Networks. Theory and Applications; Springer Nature Switzerland AG: Cham, Switzerland, 2020; p. 213. [Google Scholar]
- Pham, V.T.; Vaidyanathan, S.; Volos, C.; Kapitaniak, T. Nonlinear Dynamical Systems with Self-Excited and Hidden Attractors; Springer International Publishing AG: Cham, Switzerland, 2018; p. 506. [Google Scholar]
- Corinto, F.; Krulikovskyi, O.V.; Haliuk, S.D. Memristor-based chaotic circuit for pseudo-random sequence generators. In Proceedings of the 2016 18th Mediterranean Electrotechnical Conference (MELECON), Lemesos, Cyprus, 18–20 April 2016; pp. 1–3. [Google Scholar]
- Ascoli, A.; Tetzlaff, R.; Biey, M. Memristor and memristor circuit modelling based on methods of nonlinear system theory. In Nonlinear Dynamics in Computational Neuroscience; Corinto, F., Torcini, A., Eds.; Springer International Publishing AG: Cham, Switzerland, 2019; pp. 99–132. [Google Scholar]
- Abunahla, H.; Mohammad, B. Memristor Technology: Synthesis and Modeling for Sensing and Security Applications; Springer International Publishing: Cham, Switzerland, 2018; p. 106. [Google Scholar]
- Jing, X.; Lang, Z. Frequency Domain Analysis and Design of Nonlinear Systems Based on Volterra Series Expansion. A Parametric Characteristic Approach; Springer Science + Business Media: New York, NY, USA, 2015; p. 331. [Google Scholar]
- Ogunfunmi, T. Adaptive Nonlinear System Identification: The Volterra and Wiener Model Approaches; Springer Science + Business Media: New York, NY, USA, 2007; p. 229. [Google Scholar]
- Janczak, A. Identification of Nonlinear Systems Using Neural Networks and Polynomial Models. A Block-Oriented Approach; Springer-Verlag: Berlin/Heidelberg, Germany, 2005; p. 197. [Google Scholar]
- Mathews, V.J.; Sicuranza, G.L. Polynomial Signal Processing; John Wiley & Sons: New York, NY, USA, 2000; p. 452. [Google Scholar]
- Solovyeva, E. A split signal polynomial as a model of an impulse noise filter for speech signal recovery. J. Phys. Conf. Ser. (JPCS) 2017, 803, 012156. [Google Scholar] [CrossRef]
- Solovyeva, E. Cellular neural network as a non-linear filter of impulse noise. In Proceedings of the 20th Conference of Open Innovation Association FRUCT (FRUCT20), Saint-Petersburg, Russia, 3–7 April 2017; pp. 420–426. [Google Scholar]
- Solovyeva, E. Types of recurrent neural networks for non-linear dynamic system modelling. In Proceedings of the 2017 IEEE International Conference on Soft Computing and Measurements (SCM2017), Saint-Petersburg, Russia, 24−26 May 2017; pp. 1–4. [Google Scholar]
- Solovyeva, E. Operator approach to nonlinear compensator synthesis for communication systems. In Proceedings of the International Siberian Conference on Control and Communications (SIBCON) 2016, Moscow, Russia, 12−14 May 2016; pp. 1–5. [Google Scholar]
- Billings, S.A. Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains; John Wiley & Sons: Chichester, UK, 2013; p. 574. [Google Scholar]
- Bittanti, S. Model Identification and Data Analysis; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2019; p. 416. [Google Scholar]
- Graupe, D. Principles of Artificial Neural Networks; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2013; p. 363. [Google Scholar]
- International Standard IEC 61000-3-2: Electromagnetic Compatibility (EMC)—Part 3-2: Limits—Limits for Harmonic Current Emissions (Equipment Input Current ≤ 16 A per Phase), 5th ed.; BSI: London, UK, 2018.
- Pabst, O.; Schmidt, T. Sinusoidal analysis of memristor bridge circuit-rectifier for low frequencie. arXiv 2012, arXiv:1208.3620. [Google Scholar]
- Wu, C.; Yang, N.; Xu, C.; Jia, R.; Liu, C. A novel generalized memristor based on three-phase diode bridge rectifier. Complex. J. 2019, 2019, 1084312. [Google Scholar] [CrossRef]
- Adhikari, S.P.; Yang, C.; Kim, H.; Chua, L.O. Memristor bridge synapse-based neural network and its learning. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1426–1435. [Google Scholar] [CrossRef]
- Pabst, O.; Schmidt, T. Frequency dependent rectifier memristor bridge used as a programmable synaptic membrane voltage generator. J. Electr. Bioimpedance 2013, 4, 23–32. [Google Scholar] [CrossRef]
- Yu, Y.; Yang, N.; Yang, C.; Nyima, T. Memristor bridge-based low pass filter for image processing. J. Syst. Eng. Electron. 2019, 30, 448–455. [Google Scholar] [CrossRef]
- González-Cordero, G.; González, M.B.; García, H.; Campabadal, F.; Dueñas, S.; Castán, H.; Jiménez-Molinos, F.; Roldán, J.B. A physically based model for resistive memories including a detailed temperature and variability description. Mircoelectron. Eng. 2017, 178, 26–29. [Google Scholar] [CrossRef]
- Puglisi, F.M.; Larcher, L.; Padovani, A.; Pavan, P. Bipolar resistive RAM based on HfO2: Physics, compact modeling, and variability control. IEEE J. Emerg. Sel. Top. Circuits Syst. 2016, 6, 171–184. [Google Scholar] [CrossRef]
- Bengel, C.; Siemon, A.; Cüppers, F.; Hoffmann-Eifert, S.; Hardtdegen, A.; Witzleben, M.; Helllmich, L.; Waser, R.; Menzel, S. Variability-aware modeling of filamentary oxide-based bipolar resistive switching cells using SPICE level compact models. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4618–4630. [Google Scholar] [CrossRef]
- Menzel, S.; Böttger, U.; Waser, R. Simulation of multilevel switching in electrochemical metallization memory cells. J. Appl. Phys. 2012, 111, 014501. [Google Scholar] [CrossRef]
- Guan, X.; Yu, S.; Wong, H.-S.P. A SPICE compact model of metal oxide resistive switching memory with variations. IEEE Electron Device Lett. 2012, 33, 1405–1407. [Google Scholar] [CrossRef]
- Bocquet, M.; Deleruyelle, D.; Aziza, H.; Muller, C.; Portal, J.M.; Cabout, T.; Jalaguier, E. Robust compact model for bipolar oxide-based resistive switching memories. IEEE Trans. Electron Devices 2014, 61, 674–681. [Google Scholar] [CrossRef]
- Majetta, K.; Clauss, C.; Schmidt, T. Towards a memristor model in Modelica. In Proceedings of the 9th International Modelica Conference, Munich, Germany, 3–5 September 2012; pp. 507–512. [Google Scholar]
- Yakopcic, C.; Taha, T.M.; Subramanyam, G.; Pino, R.E. Memristor SPICE Modeling. Advances in Neuromorphic Memristor Science and Applications; Springer: Berlin, Germany, 2012; pp. 211–244. [Google Scholar]
- Joglekar, Y.N.; Wolf, S.J. The elusive memristor: Properties of basic electrical circuits. Eur. J. Phys. 2009, 30, 661. [Google Scholar] [CrossRef]
- Biolek, Z.; Biolek, D.; Biolková, V. Spice model of memristor with nonlinear dopant drift. Radioengineering 2009, 18, 210–214. [Google Scholar]
- Pino, R.E.; Bohl, J.W.; McDonald, N.; Wysocki, B.; Rozwood, P.; Campbell, K.A.; Oblea, A.; Timilsina, A. Compact method for modeling and simulation of memristor devices: Ion conductor chalcogenide-based memristor devices. In Proceedings of the 2010 IEEE/ACM International Symposium on Nanoscale Architectures, Anaheim, CA, USA, 17–18 June 2010; pp. 1–4. [Google Scholar]
- Chang, T.; Jo, S.H.; Kim, K.H.; Sheridan, P.; Gaba, S.; Lu, W. Synaptic behaviors and modeling of a metal oxide memristor device. Appl. Phys. A 2011, 102, 857–863. [Google Scholar] [CrossRef]
- Menzel, S.; Böttger, U.; Wimmer, M.; Salinga, M. Physics of the switching kinetics in resistive memories. Adv. Funct. Mater. 2015, 25, 6306–6325. [Google Scholar] [CrossRef]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Frasca, M. Control of imperfect dynamical systems. Nonlinear Dyn. 2019, 98, 2989–2999. [Google Scholar] [CrossRef]
- Fortuna, L.; Buscarino, A.; Frasca, M.; Famoso, C. Control of Imperfect Nonlinear Electromechanical Large Scale Systems. From Dynamics to Hardware Implementation; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2017; p. 148. [Google Scholar]
| Signal Number | Amplitude and Frequency of Trial Input Signal | Errors | |
|---|---|---|---|
| 1 | 12.5 V, 1.5 Hz | 1.5616 × 10−1 | 3.4918 × 10−3 |
| 2 | 14.5 V, 3.6 Hz | 2.1941 × 10−1 | 4.9062 × 10−3 |
| 3 | 15.5 V, 4.6 Hz | 1.7786 × 10−1 | 3.9771 × 10−3 |
| Signal Number | Amplitude and Frequency of Trial Input Signal | Errors | |
|---|---|---|---|
| 1 | 12.5 V, 1.5 Hz | 3.0720 × 10−2 | 6.8692 × 10−4 |
| 2 | 14.5 V, 3.6 Hz | 1.0967 × 10−1 | 2.4522 × 10−3 |
| 3 | 15.5 V, 4.6 Hz | 1.0967 × 10−1 | 9.6150 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solovyeva, E.; Schulze, S.; Harchuk, H. Behavioral Modeling of Memristor-Based Rectifier Bridge. Appl. Sci. 2021, 11, 2908. https://doi.org/10.3390/app11072908
Solovyeva E, Schulze S, Harchuk H. Behavioral Modeling of Memristor-Based Rectifier Bridge. Applied Sciences. 2021; 11(7):2908. https://doi.org/10.3390/app11072908
Chicago/Turabian StyleSolovyeva, Elena, Steffen Schulze, and Hanna Harchuk. 2021. "Behavioral Modeling of Memristor-Based Rectifier Bridge" Applied Sciences 11, no. 7: 2908. https://doi.org/10.3390/app11072908
APA StyleSolovyeva, E., Schulze, S., & Harchuk, H. (2021). Behavioral Modeling of Memristor-Based Rectifier Bridge. Applied Sciences, 11(7), 2908. https://doi.org/10.3390/app11072908






