Performance Analysis of Partitioned Step Particle Swarm Optimization in Function Evaluation
Abstract
:1. Introduction
1.1. Review of Related Algorithms
1.1.1. Genetic Algorithm
1.1.2. Particle Swarm Optimization
1.1.3. Harmony Search
1.2. Particle Swarm Optimization Components
1.2.1. Velocity Rule
1.2.2. Inertia Weight
1.2.3. Crossover
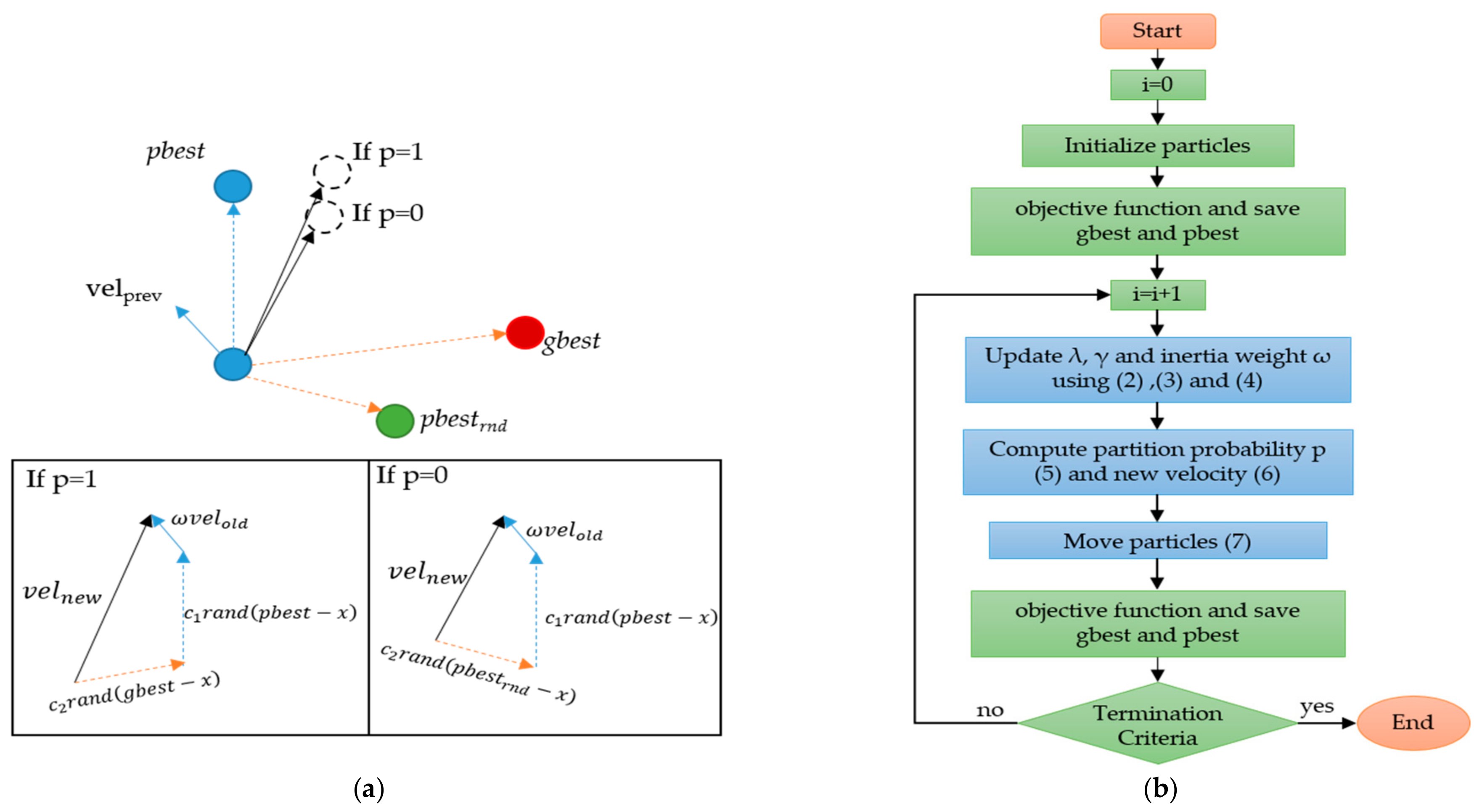
2. Partitioned Step Particle Swarm Optimization
2.1. Theory
2.2. Parameter Setting
2.3. Performance Tests
2.3.1. PSO Variants
2.3.2. Benchmark Functions
2.3.3. Unit Commitment Problem
2.3.4. Function Evaluation Tests
3. Data and Results
3.1. Variables and Parameter Setting
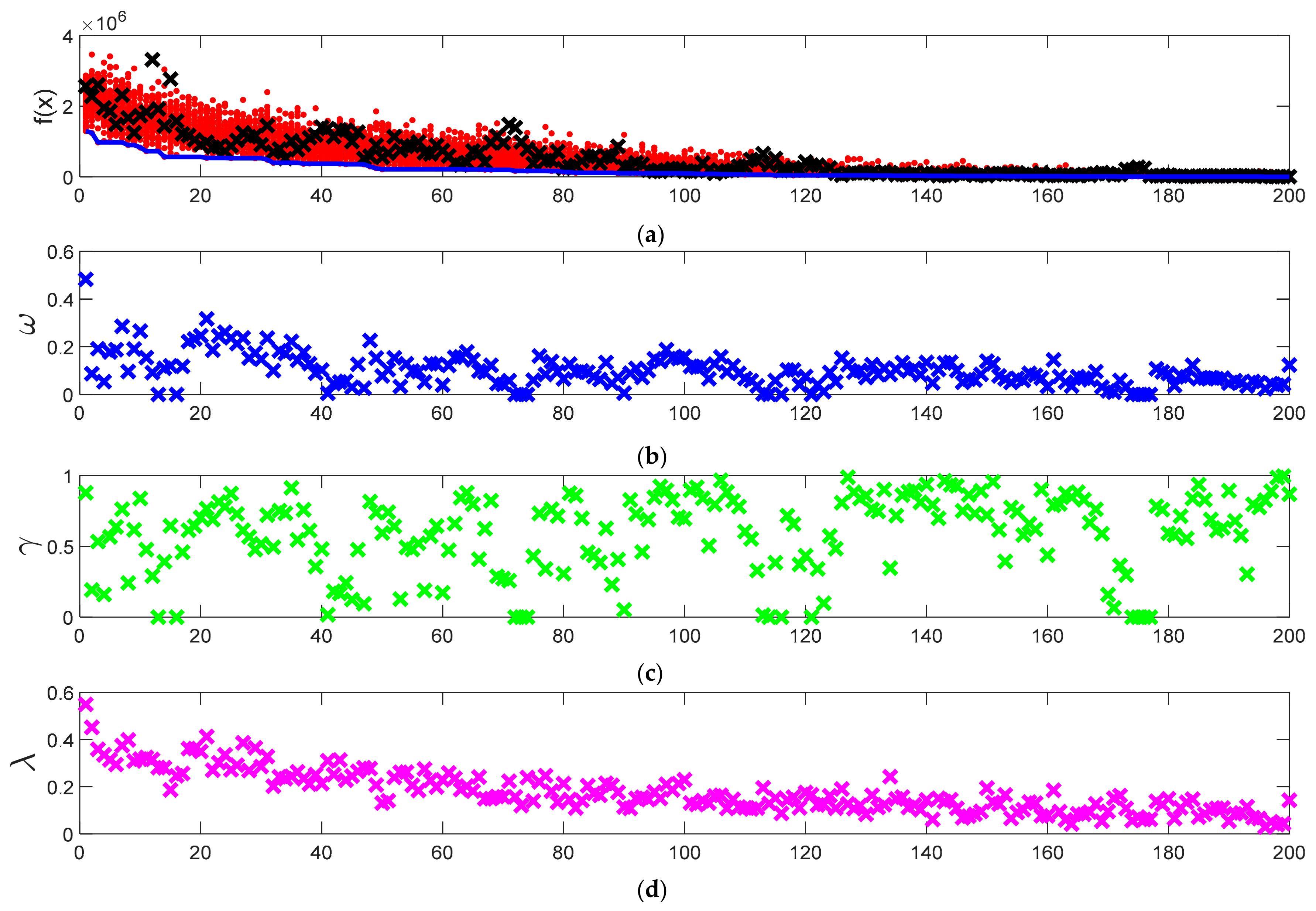
3.2. PSPSO
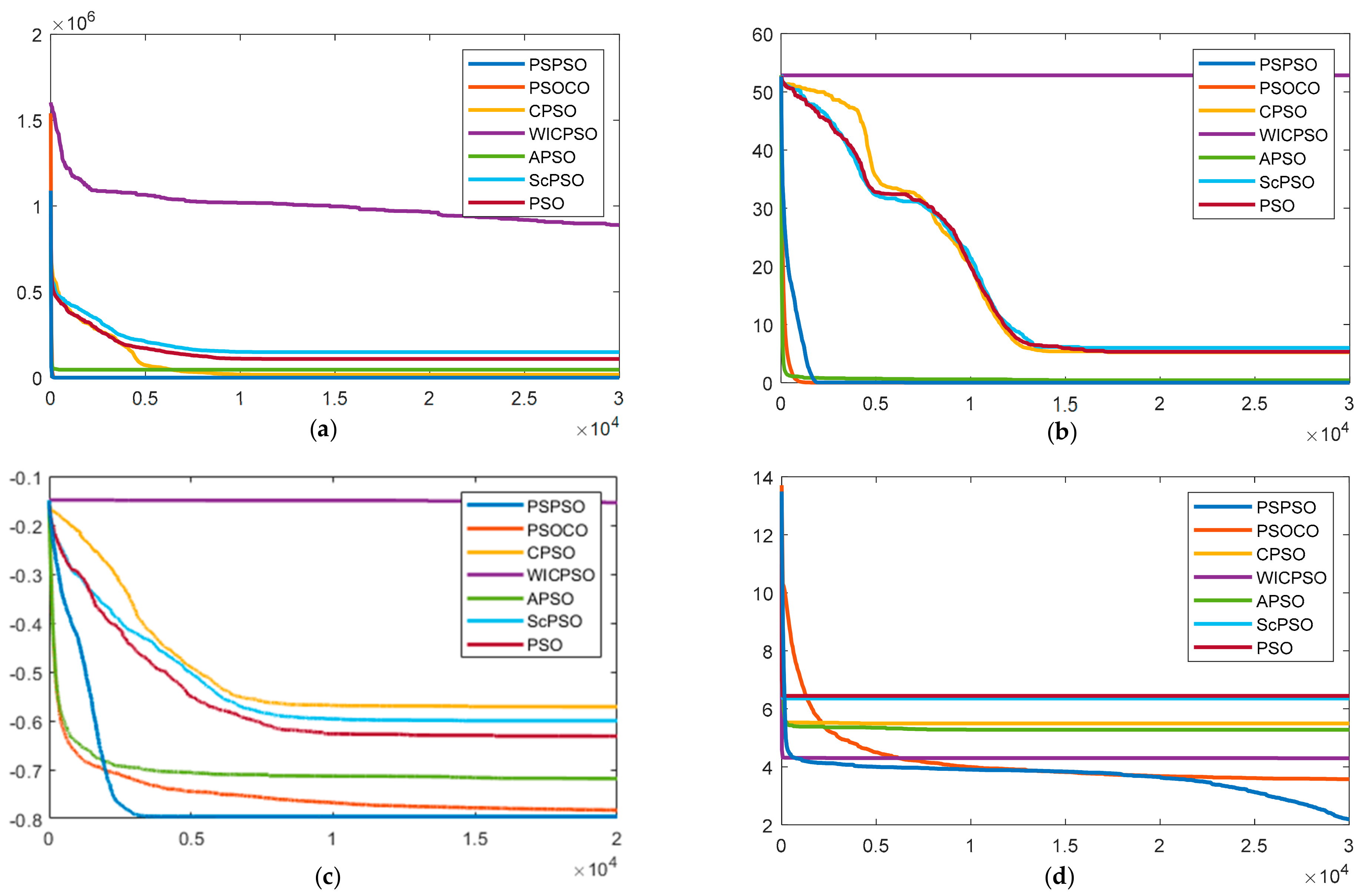
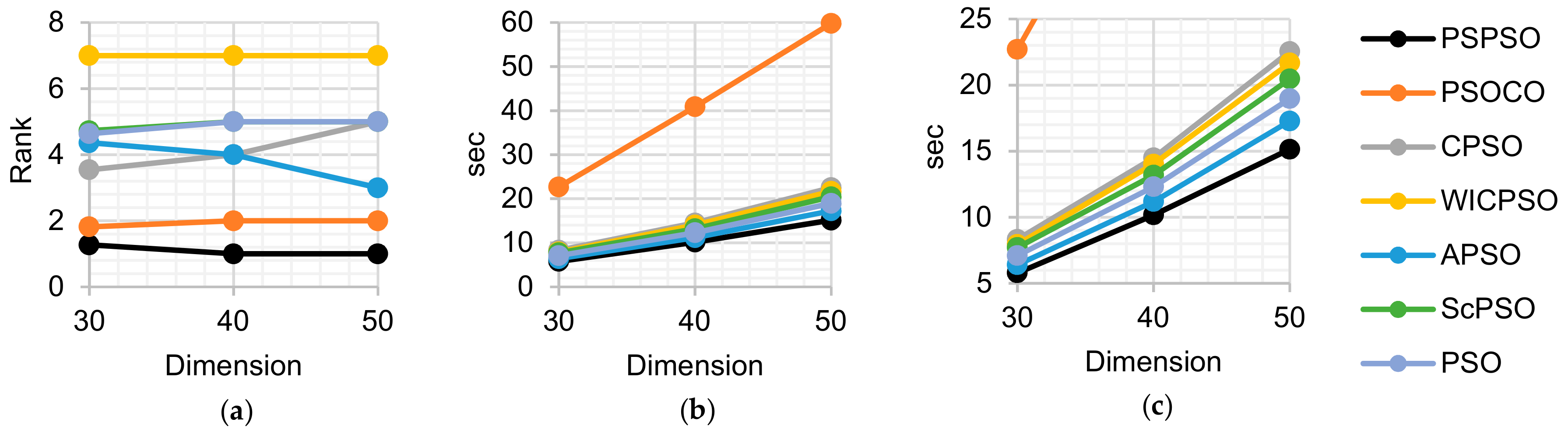
3.3. Benchmark Functions
3.4. Unit Commitment Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Beckington, UK, 2010. [Google Scholar]
- Abujarad, S.Y.; Mustafa, M.W.; Jamian, J.J. Recent approaches of unit commitment in the presence of intermittent renewable energy resources: A review. Renew. Sustain. Energy Rev. 2017, 70, 215–223. [Google Scholar] [CrossRef]
- Abdmouleh, Z.; Gastli, A.; Ben-Brahim, L.; Haouari, M.; Al-Emadi, N.A. Review of optimization techniques applied for the integration of distributed generation from renewable energy sources. Renew. Energy 2017, 113, 266–280. [Google Scholar] [CrossRef]
- Chou, J.-S.; Truong, D.-N. A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean. Appl. Math. Comput. 2021, 389, 125535. [Google Scholar] [CrossRef]
- Portilla-Flores, E.A.; Sanchez-Marquez, A.; Flores-Pulido, L.; Vega-Alvarado, E.; Yanez, M.B.C.; Aponte-Rodriguez, J.A.; Nino-Suarez, P.A. Enhancing the Harmony Search Algorithm Performance on Constrained Numerical Optimization. IEEE Access 2017, 5, 25759–25780. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution–A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Mirjalili, S. Hybrid Whale Optimization Algorithm with simulated annealing for feature selection. Neurocomputing 2017, 260, 302–312. [Google Scholar] [CrossRef]
- Xiong, H.; Wu, Z.; Fan, H.; Li, G.; Jiang, G. Quantum rotation gate in quantum-inspired evolutionary algorithm: A review, analysis and comparison study. Swarm Evol. Comput. 2018, 42, 43–57. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Kamboj, V.K.; Bath, S.K.; Dhillon, J.S. Implementation of hybrid harmony search/random search algorithm for single area unit commitment problem. Int. J. Electr. Power Energy Syst. 2016, 77, 228–249. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Fakhim-Babaei, A.; Mohammadi-Ivatloo, B. A novel hybrid harmony search and particle swarm optimization method for solving combined heat and power economic dispatch. In Proceedings of the 2017 Smart Grid Conference (SGC), Tehran, Iran, 20–21 December 2017; pp. 1–9. [Google Scholar] [CrossRef]
- Liang, Y.; Juarez, J.R.C. Harmony search and virus optimization algorithm for multi-objective combined economic energy dispatching problems. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 3947–3954. [Google Scholar] [CrossRef]
- Ocampo, E.; Huang, Y.-C.; Kuo, C.-C. Feasible Reserve in Day-Ahead Unit Commitment Using Scenario-Based Optimization. Energies 2020, 13, 5239. [Google Scholar] [CrossRef]
- Victoire, T.A.A.; Jeyakumar, A.E. Reserve constrained dynamic dispatch of units with valve-point effects. IEEE Trans. Power Syst. 2005, 20, 1273–1282. [Google Scholar] [CrossRef]
- Bonyadi, M.R.; Michalewicz, Z. Analysis of Stability, Local Convergence, and Transformation Sensitivity of a Variant of the Particle Swarm Optimization Algorithm. IEEE Trans. Evol. Comput. 2016, 20, 370–385. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Chen, Y.; Li, L.; Xiao, J.; Yang, Y.; Liang, J.; Li, T. Particle swarm optimizer with crossover operation. Eng. Appl. Artif. Intell. 2018, 70, 159–169. [Google Scholar] [CrossRef]
- Shukla, A.; Singh, S.N. Multi-objective unit commitment with renewable energy using hybrid approach. IET Renew. Power Gener. 2016, 10, 327–338. [Google Scholar] [CrossRef]
- Khokhar, B.; Parmar, K. A novel weight-improved particle swarm optimization for combined economic and emission dispatch problems. Int. J. Eng. Sci. Technol. 2012, 4, 2012. [Google Scholar]
- Sedighizadeh, D.; Masehian, E.; Sedighizadeh, M.; Akbaripour, H. GEPSO: A new generalized particle swarm optimization algorithm. Math. Comput. Simul. 2021, 179, 194–212. [Google Scholar] [CrossRef]
- Li, D.; Guo, W.; Lerch, A.; Li, Y.; Wang, L.; Wu, Q. An adaptive particle swarm optimizer with decoupled exploration and exploitation for large scale optimization. Swarm Evol. Comput. 2021, 60, 100789. [Google Scholar] [CrossRef]
- Han, H.; Lu, W.; Hou, Y.; Qiao, J. An Adaptive-PSO-Based Self-Organizing RBF Neural Network. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 104–117. [Google Scholar] [CrossRef]
- Koyuncu, H.; Ceylan, R. A PSO based approach: Scout particle swarm algorithm for continuous global optimization problems. J. Comput. Des. Eng. 2019, 6, 129–142. [Google Scholar] [CrossRef]
- Jamil, M.; Yang, X. A literature survey of benchmark functions for global optimisation problems. arXiv 2013, arXiv:abs/1308.4008. [Google Scholar] [CrossRef] [Green Version]
- Saber, N.A.; Salimi, M.; Mirabbasi, D. A priority list based approach for solving thermal unit commitment problem with novel hybrid genetic-imperialist competitive algorithm. Energy 2016, 117, 272–280. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khosravi, A. Integration of renewable generation uncertainties into stochastic unit commitment considering reserve and risk: A comparative study. Energy 2016, 103, 735–745. [Google Scholar] [CrossRef]
- Srikanth, K.; Panwar, L.K.; Panigrahi, B.K.; Herrera-Viedma, E.; Sangaiah, A.K.; Wang, G.-G. Meta-heuristic framework: Quantum inspired binary grey wolf optimizer for unit commitment problem. Comput. Electr. Eng. 2018, 70, 243–260. [Google Scholar] [CrossRef]
- Wang, W.; Li, C.; Liao, X.; Qin, H. Study on unit commitment problem considering pumped storage and renewable energy via a novel binary artificial sheep algorithm. Appl. Energy 2017, 187, 612–626. [Google Scholar] [CrossRef]
- Panwar, L.K.; Reddy, K.S.; Verma, A.; Panigrahi, B.K.; Kumar, R. Binary Grey Wolf Optimizer for large scale unit commitment problem. Swarm Evol. Comput. 2018, 38, 251–266. [Google Scholar] [CrossRef]
- Soltani, Z.; Ghaljehei, M.; Gharehpetian, G.B.; Aalami, H.A. Integration of smart grid technologies in stochastic multi-objective unit commitment: An economic emission analysis. Int. J. Electr. Power Energy Syst. 2018, 100, 565–590. [Google Scholar] [CrossRef]
- MATLAB. MATLAB Documenation: Solve a Constrained Non-Linear Problem. Available online: https://www.mathworks.com/help/optim/ug/example-nonlinear-constrained-minimization.html (accessed on 5 October 2020).
- Bird Problem (Constrained). Available online: https://web.archive.org/web/20150506143633/http://www.phoenixint.com/software/benchmark_report/index.php (accessed on 5 October 2020).
- Constrained Optimization in Chebfun. Available online: http://www.chebfun.org/examples/opt/ConstrainedOptimization.html (accessed on 5 October 2020).
- Ma, H.; Simon, D. Constrained Benchmark Functions. In Evolutionary Computation with Biogeography-based Optimization; ISTE Ltd and John Wiley & Sons, Inc: New York, NY, USA, 2017; pp. 265–287. [Google Scholar]
| Algorithms | Parameter Setting |
|---|---|
| PSO | c1 = c2 = 2, ωmin = 0.4, ωmax = 0.9 |
| CPSO | c1 = c2 = 2, ωmin = 0.4, ωmax = 0.9 |
| PSOCO | c = 1.49618, ω = 0.7298, CR = 0.05, G = 7 |
| WICPSO | c1max = 2.2, c1min = 1.5, c1max = 2.2, c1min = 1.5, ωmin = 0.4, ωmax = 0.9 |
| APSO | c1 = c2 = 2, L = 3, C = 1 |
| ScPSO | c1 = c2 = 2, ωmin = 0.4, ωmax = 0.9 |
| No. | Function Name | Characteristics | Range |
|---|---|---|---|
| f1 | Sphere | C, D, S, Sc, U | [−10, 10] |
| f2 | Rosenbrock | C, D, NS, Sc, U | [−30, 30] |
| f3 | Chung Reynolds | C, D, PS, Sc, U | [−100, 100] |
| f4 | Dixon and Price | C, D, NS, Sc, U | [−10, 10] |
| f5 | Powell Singular | C, D, NS, Sc, U | [−4, 5] |
| f6 | Step | DC, ND, S, Sc, U | [−100, 100] |
| f7 | Cosine Mixture | DC, ND, S, Sc, M | [−1, 1] |
| f8 | Ackley 1 | C, D, NS, Sc, M | [−35, 35] |
| f9 | Alpine | C, ND, S, NSc, M | [−10, 10] |
| f10 | Egg Holder | C, D, NS, Sc, M | [−512, 512] |
| f11 | Griewank | C, D, NS, Sc, M | [−100, 100] |
| f12 | Pathological | C, D, NS, NSc, M | [−100, 100] |
| f13 | Weierstrass | C, D, S, Sc, M | [−0.5, 0.5] |
| f14 | Schwefel | C, D, S, NSc, M | [−500, 500] |
| f15 | Pinter | C, D, NS, Sc, M | [−100, 100] |
| f16 | Qing | C, D, S, Sc, M | [−500, 500] |
| f17 | Quintic | C, D, S, NSc, M | [−10, 10] |
| f18 | Stretched V Sine Wave Function | C, D, NS, Sc, U | [−10, 10] |
| f19 | Styblinski-Tang | C, D, NS, NSc, M | [−5, 5] |
| f20 | Trigonometric 2 | C, D, NS, Sc, M | [−500, 500] |
| Nomenclature: Continuous (C), Differentiable (D), Discontinuous (DC), Multimodal (M), Non-Differentiable (ND), Non-Separable (NS), Non-Scalable (NSc), Partially Separable (PS), Separable (S), Scalable (Sc), and Unimodal (U) | |||
| No. | Function Name | Dimension |
|---|---|---|
| c1 | Rosenbrock [31] | 2 |
| c2 | Bird Problem [32] | 2 |
| c3 | Townsend [33] | 2 |
| c4 | G01 [34] | 13 |
| c5 | G02 [34] | 20 |
| Gen | MAX OP (kW) | MIN OP (kW) | a ($) | b ($/MW) | c ($/MW2) | Hot Start Cost (HSC) | Cold Start Cost (CSC) | Cold Start Hour (CSH) | MUT (h) | MDT (h) | tini (h) | Ramp Up/ Down (kW) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 455 | 150 | 1000 | 16.19 | 0.00048 | 4500 | 9000 | 5 | 8 | 8 | 8 | 160 |
| 2 | 455 | 150 | 970 | 17.26 | 0.00031 | 5000 | 10,000 | 5 | 8 | 8 | 8 | 160 |
| 3 | 130 | 20 | 700 | 16.60 | 0.00200 | 550 | 1100 | 5 | 5 | 4 | −5 | 100 |
| 4 | 130 | 20 | 680 | 16.50 | 0.00211 | 560 | 1120 | 5 | 5 | 4 | −5 | 100 |
| 5 | 162 | 25 | 450 | 19.70 | 0.00398 | 900 | 1800 | 6 | 6 | 4 | −6 | 100 |
| 6 | 80 | 20 | 370 | 22.25 | 0.00712 | 170 | 340 | 2 | 3 | 3 | −3 | 60 |
| 7 | 85 | 25 | 480 | 27.74 | 0.00079 | 260 | 520 | 2 | 3 | 3 | −3 | 60 |
| 8 | 55 | 10 | 660 | 25.92 | 0.00413 | 30 | 60 | 0 | 1 | 1 | −1 | 40 |
| 9 | 55 | 10 | 665 | 27.27 | 0.00222 | 30 | 60 | 0 | 1 | 1 | −1 | 40 |
| 10 | 55 | 10 | 670 | 27.79 | 0.00173 | 30 | 60 | 0 | 1 | 1 | −1 | 40 |
| Hour | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Load | 700 | 750 | 850 | 950 | 1000 | 1100 | 1150 | 1200 | 1300 | 1400 | 1450 | 1500 |
| Hour | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Load | 1400 | 1300 | 1200 | 1050 | 1000 | 1100 | 1200 | 1400 | 1300 | 1100 | 900 | 800 |
| Objective | 6-a |
| s.t. | 6-b |
| 6-c | |
| 6-d 6-e | |
| 6-f | |
| 6-g | |
| 6-h |
| (a) N = 50 | (b) C1 = C2 = 1.50 | ||||||
|---|---|---|---|---|---|---|---|
| C | Mean | Std Dev | Time (s) | N | Mean | Std Dev | Time(s) |
| 1.00 | 65.6091 | 14.3104 | 8.773 | 30 | 1.0940 | 5.1989 | 5.303 |
| 1.25 | 30.4968 | 29.3233 | 8.020 | 40 | 0.0546 | 0.0282 | 6.353 |
| 1.50 | 0.0447 | 0.0006 | 7.625 | 50 | 0.0446 | 0.0006 | 7.591 |
| 1.75 | 2.5755 | 0.7062 | 9.687 | 60 | 0.0445 | 0.0002 | 8.868 |
| 2.00 | 13,050.09 | 15,406.5 | 10.373 | 70 | 0.0444 | 7.16 × 10−6 | 10.131 |
| 2.25 | 5.69 × 1029 | 3.11 × 1030 | 10.358 | 80 | 0.0445 | 1.37 × 10−4 | 11.622 |
| 2.50 | 1.07 × 1036 | 2.64 × 1036 | 10.107 | 90 | 0.0445 | 9.62 × 10−5 | 12.995 |
| PSPSO | PSOCO | CPSO | WICPSO | APSO | ScPSO | PSO | PSPSO | PSOCO | CPSO | WICPSO | APSO | ScPSO | PSO | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f1 | mean | 0.0 × 100 | 5.6 × 10-296 | 6.7 × 102 | 7.0 × 104 | 3.9 × 102 | 1.4 × 10-208 | 3.3 × 102 | f11 | mean | 1.3 × 10-3 | 0.0 × 100 | 1.9 × 10-1 | 1.8 × 101 | 2.8 × 10-1 | 1.9 × 10-2 | 1.8 × 10-2 |
| std | 0.0 × 100 | 0.0 × 100 | 2.5 × 103 | 2.2 × 103 | 1.8 × 103 | 0.0 × 100 | 1.8 × 103 | std | 3.0 × 10-3 | 0.0 × 100 | 6.8 × 10-1 | 6.3 × 10-1 | 7.2 × 10-1 | 2.5 × 10-2 | 2.0 × 10-2 | ||
| time | 2.597 | 5.746 | 2.84 | 3.264 | 1.805 | 2.423 | 1.778 | time | 4.741 | 10.487 | 5.596 | 5.933 | 3.107 | 4.845 | 3.837 | ||
| f2 | mean | 5.0 × 10-4 | 2.5 × 10-2 | 1.7 × 104 | 8.9 × 105 | 4.6 × 104 | 1.5 × 105 | 1.1 × 105 | f12 | mean | 2.2 × 100 | 3.6 × 100 | 5.5 × 100 | 4.3 × 100 | 5.3 × 100 | 6.4 × 100 | 6.4 × 100 |
| std | 1.6 × 10-3 | 3.5 × 10-2 | 2.5 × 104 | 7.2 × 104 | 5.7 × 104 | 7.6 × 104 | 7.2 × 104 | std | 6.9 × 10-1 | 3.9 × 10-1 | 1.0 × 100 | 4.7 × 10-1 | 8.7 × 10-1 | 7.5 × 10-01 | 7.0 × 10-1 | ||
| time | 2.766 | 6.956 | 3.028 | 3.4 | 1.957 | 2.76 | 2.058 | time | 4.678 | 16.267 | 8.084 | 5.603 | 3.875 | 6.406 | 5.487 | ||
| f3 | mean | 0.0 × 100 | 0.0 × 100 | 3.3 × 106 | 4.9 × 109 | 3.3 × 106 | 1.0 × 107 | 3.3 × 106 | f13 | mean | 0.0 × 100 | 6.9 × 10-1 | 2.3 × 100 | 5.2 × 101 | 7.1 × 100 | 3.6 × 100 | 3.2 × 100 |
| std | 0.0 × 100 | 0.0 × 100 | 1.8 × 107 | 3.2 × 108 | 1.8 × 107 | 3.1 × 107 | 1.8 × 107 | std | 0.0 × 100 | 4.6 × 10-1 | 2.5 × 100 | 6.1 × 10-01 | 4.5 × 100 | 3.0 × 100 | 3.5 × 100 | ||
| time | 2.712 | 5.459 | 2.796 | 3.292 | 1.867 | 2.488 | 1.798 | time | 58.365 | 305.531 | 94.078 | 76.381 | 86.413 | 92.411 | 91.694 | ||
| f4 | mean | 6.7 × 10-1 | 3.2 × 10-1 | 3.3 × 104 | 1.7 × 106 | 2.4 × 101 | 5.7 × 104 | 4.5 × 104 | f14 | mean | 1.2 × 10-219 | 5.6 × 10-165 | 7.3 × 102 | 1.9 × 1040 | 6.1 × 102 | 7.7 × 102 | 7.2 × 102 |
| std | 0.0 × 100 | 3.3 × 10-1 | 5.0 × 104 | 3.1 × 104 | 3.8 × 101 | 6.5 × 104 | 6.1 × 104 | std | 0.0 × 100 | 0.0 × 100 | 2.1 × 102 | 1.4 × 1040 | 2.1 × 102 | 2.2 × 102 | 1.9 × 102 | ||
| time | 2.665 | 9.563 | 3.536 | 3.435 | 1.992 | 2.889 | 2.214 | time | 3.616 | 8.159 | 4.998 | 4.067 | 2.298 | 3.884 | 2.982 | ||
| f5 | mean | 2.3 × 10-7 | 3.5 × 10-4 | 5.7 × 102 | 5.0 × 103 | 6.5 × 101 | 9.4 × 102 | 8.9 × 102 | f15 | mean | 0.0 × 100 | 2.8 × 101 | 2.3 × 103 | 1.8 × 104 | 1.6 × 103 | 1.9 × 103 | 2.3 × 103 |
| std | 1.5 × 10-7 | 1.2 × 10-4 | 3.4 × 102 | 6.0 × 102 | 6.8 × 101 | 6.7 × 102 | 6.9 × 102 | std | 0.0 × 100 | 1.5 × 102 | 1.1 × 103 | 2.1 × 102 | 1.3 × 103 | 9.4 × 102 | 9.5 × 102 | ||
| time | 6.293 | 19.669 | 7.419 | 6.363 | 5.773 | 6.217 | 5.314 | time | 10.028 | 19.846 | 8.521 | 11.07 | 6.231 | 7.882 | 7.23 | ||
| f6 | mean | 0.0 × 100 | 0.0 × 100 | 1.0 × 103 | 7.0 × 104 | 3.6 × 102 | 3.3 × 102 | 6.7 × 102 | f16 | mean | 1.3 × 10-21 | 1.2 × 10-28 | 1.4 × 10-28 | 2.2 × 1011 | 9.7 × 10-11 | 1.5 × 10-28 | 1.5 × 10-28 |
| std | 0.0 × 100 | 0.0 × 100 | 3.1 × 103 | 1.5 × 103 | 1.8 × 103 | 1.8 × 103 | 2.5 × 103 | std | 7.3 × 10-21 | 0.0 × 100 | 2.9 × 10-29 | 2.2 × 109 | 5.2 × 10-10 | 5.1 × 10-29 | 5.5 × 10-29 | ||
| time | 3.698 | 9.278 | 6.12 | 5.21 | 2.908 | 4.684 | 3.67 | time | 4.017 | 9.733 | 4.133 | 4.227 | 2.341 | 3.385 | 2.55 | ||
| f7 | mean | -1.8 × 100 | -1.8 × 100 | -1.8 × 100 | -1.8 × 100 | -1.8 × 100 | -1.8 × 100 | -1.8 × 100 | f17 | mean | 1.5 × 10-17 | 0.0 × 100 | 1.6 × 10-15 | 2.3 × 105 | 5.3 × 10-1 | 4.6 × 10-16 | 2.0 × 10-15 |
| std | 9 × 10-16 | 9 × 10-16 | 9 × 10-16 | 9 × 10-16 | 9 × 10-16 | 9 × 10-16 | 9.0 × 10-16 | std | 8.1 × 10-17 | 0.0 × 100 | 2.3 × 10-15 | 1.6 × 104 | 1.9 × 100 | 1.1 × 10-15 | 3.7 × 10-15 | ||
| time | 0.094 | 0.252 | 0.089 | 0.11 | 0.073 | 0.091 | 0.065 | time | 9.248 | 64.709 | 21.968 | 23.553 | 21.128 | 20.731 | 19.947 | ||
| f8 | mean | 3.7 × 10-15 | 3.8 × 10-15 | 2.0 × 101 | 2.0 × 101 | 1.8 × 101 | 2.0 × 101 | 2.0 × 101 | f18 | mean | 0.0 × 100 | 2.3 × 10-37 | 2.0 × 10-38 | 3.0 × 10-1 | 0.0 × 100 | 2.3 × 10-38 | 2.6 × 10-38 |
| std | 6.5 × 10-16 | 9.0 × 10-16 | 2.1 × 10-3 | 8.2 × 10-4 | 5.1 × 100 | 1.5 × 10-3 | 1.7 × 10-03 | std | 0.0 × 100 | 9.9 × 10-37 | 4.2 × 10-38 | 9.2 × 10-2 | 0.0 × 100 | 4.5 × 10-38 | 4.6 × 10-38 | ||
| time | 4.015 | 9.64 | 7.242 | 5.462 | 3.545 | 5.993 | 4.942 | time | 0.118 | 0.335 | 0.109 | 0.13 | 0.077 | 0.114 | 0.088 | ||
| f9 | mean | 5.8 × 10-20 | 4.2 × 10-9 | 5.2 × 100 | 5.3 × 101 | 4.1 × 10-1 | 6.0 × 100 | 5.3 × 100 | f19 | mean | -1.1 × 103 | -1.2 × 103 | -1.2 × 103 | -4.1 × 102 | -1.1 × 103 | -1.2 × 103 | -1.2 × 103 |
| std | 3.2 × 10-19 | 1.6 × 1008 | 4.2 × 100 | 3.6 × 10-14 | 1.0 × 100 | 4.0 × 100 | 4.3 × 100 | std | 1.7 × 101 | 4.2 × 10-13 | 1.0 × 101 | 7.9 × 100 | 4.1 × 101 | 1.1 × 101 | 1.1 × 101 | ||
| time | 4.089 | 11.099 | 5.508 | 5.503 | 3.254 | 4.73 | 3.74 | time | 9.642 | 29.122 | 9.991 | 10.628 | 3.294 | 9.697 | 8.744 | ||
| f10 | mean | -959.6 | -958 | -959.6 | -959.6 | -959.6 | -943.5 | -951.6 | f20 | mean | 1.0 × 100 | 1.0 × 100 | 1.7 × 104 | 1.8 × 106 | 1.7 × 104 | 1.7 × 104 | 4.5 × 100 |
| std | 5.8 × 10-13 | 5.4 × 100 | 5.8 × 10-13 | 2.8 × 10-5 | 5.8 × 10-13 | 6.1 × 101 | 4.4 × 101 | std | 1.0 × 10-16 | 9.2 × 10-17 | 6.3 × 104 | 4.1 × 104 | 6.3 × 104 | 6.3 × 104 | 3.4 × 100 | ||
| time | 0.096 | 0.267 | 0.09 | 0.113 | 0.078 | 0.096 | 0.07 | time | 5.278 | 10.321 | 6.108 | 15.027 | 3.591 | 5.658 | 4.728 | ||
| PSPSO | PSOCO | CPSO | WICPSO | APSO | ScPSO | PSO | ||
|---|---|---|---|---|---|---|---|---|
| c1 | mean | 7.90 × 10−28 | 8.25 × 10−6 | 2.53 × 10−29 | 1.65 × 10−3 | 1.00 × 10−29 | 2.92 × 10−28 | 6.23 × 10−28 |
| std | 4.28 × 10−27 | 1.30 × 10−5 | 7.39 × 10−29 | 1.33 × 10−3 | 4.00 × 10−29 | 8.95 × 10−28 | 1.89 × 10−27 | |
| time | 0.091 | 0.224 | 0.069 | 0.091 | 0.059 | 0.075 | 0.05 | |
| c2 | mean | −1.07 × 102 | −1.07 × 102 | −1.07 × 102 | −1.07 × 102 | −1.10 × 102 | −1.07 × 102 | −1.07 × 102 |
| std | 2.81 × 10−14 | 3.82 × 10−14 | 2.84 × 10−14 | 2.27 × 10−1 | 3.90 × 10−14 | 3.07 × 10−14 | 3.02 × 10−14 | |
| time | 0.127 | 0.277 | 0.084 | 0.11 | 0.072 | 0.089 | 0.064 | |
| c3 | mean | −2.13 × 100 | −2.08 × 100 | −2.13 × 100 | −2.13 × 100 | −2.10 × 100 | −2.13 × 100 | −2.13 × 100 |
| std | 1.17 × 10−15 | 1.42 × 10−1 | 8.96 × 10−16 | 3.83 × 10−4 | 6.00 × 10−16 | 9.72 × 10−16 | 1.06 × 10−15 | |
| time | 0.095 | 0.285 | 0.084 | 0.109 | 0.081 | 0.09 | 0.065 | |
| c4 | mean | −1.50 × 101 | −1.50 × 101 | −9.77 × 100 | −8.15 × 100 | −1.10 × 101 | −6.63 × 100 | −6.43 × 100 |
| std | 0.00 × 100 | 0.00 × 100 | 2.21 × 100 | 2.61 × 100 | 2.40 × 100 | 1.69 × 100 | 1.43 × 100 | |
| time | 1.207 | 3.389 | 1.557 | 1.298 | 0.841 | 1.36 | 1.027 | |
| c5 | mean | −7.96 × 10−1 | −7.83 × 10−1 | −5.71 × 10−1 | −1.54 × 10−1 | −7.20 × 10−1 | −6.00 × 10−1 | −6.32 × 10−1 |
| std | 1.10 × 10−2 | 8.73 × 10−3 | 1.31 × 10−1 | 9.32 × 10−3 | 9.80 × 10−2 | 1.50 × 10−1 | 1.28 × 10−1 | |
| time | 4.2 | 10.678 | 3.923 | 4.018 | 3.301 | 3.746 | 3.221 |
| PSPSO | PSOCO | CPSO | WICPSO | APSO | ScPSO | PSO | |
|---|---|---|---|---|---|---|---|
| Unconstrained function property | |||||||
| Continuous | 1 | 2 | 3 | 7 | 4 | 6 | 4 |
| Discontinuous | 1 | 1 | 6 | 7 | 4 | 3 | 4 |
| Differentiable | 1 | 2 | 3 | 7 | 5 | 5 | 4 |
| Non-differentiable | 1 | 2 | 5 | 7 | 3 | 4 | 5 |
| Separable | 2 | 1 | 4 | 7 | 6 | 3 | 5 |
| Non-separable | 1 | 2 | 3 | 7 | 4 | 6 | 5 |
| Scalable | 1 | 2 | 3 | 7 | 4 | 6 | 5 |
| Non-scalable | 2 | 1 | 3 | 7 | 6 | 5 | 4 |
| Unimodal | 1 | 2 | 4 | 7 | 3 | 5 | 5 |
| Multimodal | 2 | 1 | 3 | 7 | 6 | 5 | 4 |
| Constrained functions | 1 | 4 | 2 | 7 | 3 | 4 | 6 |
| Overall Ranking in Function Evaluation | 1 | 2 | 3 | 7 | 3 | 5 | 5 |
| Overall Ranking in Computational Time | 3 | 7 | 5 | 6 | 1 | 4 | 2 |
| hour\unit | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Fuel Cost | SU Cost |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 455 | 245 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13,683.13 | 0 |
| 2 | 455 | 295 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14,554.50 | 0 |
| 3 | 455 | 370 | 0 | 0 | 25 | 0 | 0 | 0 | 0 | 0 | 16,809.45 | 900 |
| 4 | 455 | 455 | 0 | 0 | 40 | 0 | 0 | 0 | 0 | 0 | 18,597.67 | 0 |
| 5 | 455 | 390 | 0 | 130 | 25 | 0 | 0 | 0 | 0 | 0 | 20,020.02 | 560 |
| 6 | 455 | 360 | 130 | 130 | 25 | 0 | 0 | 0 | 0 | 0 | 22,387.04 | 1100 |
| 7 | 455 | 410 | 130 | 130 | 25 | 0 | 0 | 0 | 0 | 0 | 23,261.98 | 0 |
| 8 | 455 | 455 | 130 | 130 | 30 | 0 | 0 | 0 | 0 | 0 | 24,150.34 | 0 |
| 9 | 455 | 455 | 130 | 130 | 85 | 20 | 25 | 0 | 0 | 0 | 27,250.86 | 860 |
| 10 | 455 | 455 | 130 | 130 | 162 | 33 | 25 | 10 | 0 | 0 | 30,057.22 | 60 |
| 11 | 455 | 455 | 130 | 130 | 162 | 73 | 25 | 10 | 10 | 0 | 31,915.33 | 60 |
| 12 | 455 | 455 | 130 | 130 | 162 | 80 | 25 | 43 | 10 | 10 | 33,889.36 | 60 |
| 13 | 455 | 455 | 130 | 130 | 162 | 33 | 25 | 10 | 0 | 0 | 30,057.22 | 0 |
| 14 | 455 | 455 | 130 | 130 | 85 | 20 | 25 | 0 | 0 | 0 | 27,250.86 | 0 |
| 15 | 455 | 455 | 130 | 130 | 30 | 0 | 0 | 0 | 0 | 0 | 24,150.34 | 0 |
| 16 | 455 | 310 | 130 | 130 | 25 | 0 | 0 | 0 | 0 | 0 | 21,513.66 | 0 |
| 17 | 455 | 260 | 130 | 130 | 25 | 0 | 0 | 0 | 0 | 0 | 20,641.82 | 0 |
| 18 | 455 | 360 | 130 | 130 | 25 | 0 | 0 | 0 | 0 | 0 | 22,387.04 | 0 |
| 19 | 455 | 455 | 130 | 130 | 30 | 0 | 0 | 0 | 0 | 0 | 24,150.34 | 0 |
| 20 | 455 | 455 | 130 | 130 | 162 | 33 | 25 | 10 | 0 | 0 | 30,057.22 | 490 |
| 21 | 455 | 455 | 130 | 130 | 85 | 20 | 25 | 0 | 0 | 0 | 27,250.86 | 0 |
| 22 | 455 | 455 | 0 | 0 | 145 | 20 | 25 | 0 | 0 | 0 | 22,735.32 | 0 |
| 23 | 455 | 425 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 0 | 17,645.16 | 0 |
| 24 | 455 | 345 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15,427.42 | 0 |
| 559,844.16 | 4090 | |||||||||||
| Total Cost ($) | 563,934.16 | |||||||||||
| (a) Without Ramp Constraint | ||||||
| Approach | Best ($) | Average ($) | Worst ($) | Avg. Time (s) | Max Iter | n |
| WICPSO [18] | 563,937.69 | - | - | 39.6 | 100 | 10 |
| HGICA [25] | 563,935.31 | - | - | 2.44 | 32 | 55 |
| GA [26] | 563,937.69 | - | - | - | 300 | 64 |
| QBGWO [27] | 563,936.30 | 563,963.30 | 563,936.30 | 62.3 | 500 | 30 |
| BASA [28] | 563,937 | 563,937 | 563,937 | - | - | - |
| BGWO [29] | 563,937.30 | 563,937.30 | 563,937.30 | 66.15 | 500 | 30 |
| MILP-SMOUC [30] | 56,3937 | - | - | - | - | - |
| PSPSO | 563,934.17 | 564,112.10 | 564,357.63 | 3.57 | 1000 | 50 |
| (b)With Ramp Constraint | ||||||
| Approach | Best ($) | Average ($) | Worst ($) | Avg. Time (s) | Max Iter | n |
| HGICA [25] | 564,186.63 | - | - | 1.61 | 32 | 55 |
| MILP- SMOUC [30] | 564,326.80 | - | - | 1.08 | - | - |
| PSPSO | 564,111.36 | 564,178.22 | 564,563.00 | 5.9 | 1000 | 50 |
| PSO | CPSO | PSOCO | WICPSO | PSPSO | |
|---|---|---|---|---|---|
| 10-unit DUC | |||||
| best | 564,112 | 564,278 | 566,485 | 563,974 | 563,934 |
| average | 564,966 | 564,892 | 569,874 | 564,623 | 564,039 |
| worst | 566,891 | 566,847 | 572,136 | 566,127 | 564,214 |
| time | 24.05 | 21.93 | 35.86 | 19.94 | 7.24 |
| 30-unit DUC | |||||
| best | 1,124,723 | 1,125,119 | 1,134,358 | 1,124,639 | 1,124,663 |
| average | 1,126,983 | 1,126,516 | 1,140,327 | 1,126,166 | 1,125,221 |
| worst | 1,131,985 | 1,129,734 | 1,144,489 | 1,128,543 | 1,126,375 |
| time | 46.01 | 42.26 | 65.07 | 38.14 | 27.80 |
| 40-unit DUC | |||||
| best | 2,249,498 | 2,250,868 | 2,273,559 | 2,246,659 | 2,245,909 |
| average | 2,254,239 | 2,255,014 | 2,282,112 | 2,249,593 | 2,248,930 |
| worst | 2,257,990 | 2,260,150 | 2,290,050 | 2,252,665 | 2,250,830 |
| time | 96.10 | 87.31 | 131.00 | 86.45 | 85.65 |
| 60-unit DUC | |||||
| best | 3,379,482 | 3,376,946 | 3,407,486 | 3,367,881 | 3,368,371 |
| average | 3,384,379 | 3,385,574 | 3,420,476 | 3,373,715 | 3,371,589 |
| worst | 3,392,098 | 3,392,595 | 3,430,814 | 3,379,109 | 3,375,929 |
| time | 164.85 | 152.47 | 217.43 | 176.86 | 146.83 |
| 80-unit DUC | |||||
| best | 4,508,627 | 4,509,984 | 4,550,595 | 4,495,549 | 4,495,053 |
| average | 4,517,806 | 4,521,129 | 4,567,651 | 4,502,553 | 4,497,875 |
| worst | 4,533,652 | 4,536,629 | 4,585,982 | 4,509,585 | 4,500,931 |
| time | 235.21 | 214.21 | 295.07 | 240.66 | 235.68 |
| 100-unit DUC | |||||
| best | 5,633,268 | 5,643,919 | 5,691,819 | 5,622,310 | 5,619,793 |
| average | 5,652,797 | 5,657,421 | 5,719,049 | 5,630,848 | 5,626,222 |
| worst | 5,669,649 | 5,669,151 | 5,826,662 | 5,636,712 | 5,631,809 |
| time | 318.28 | 280.12 | 368.28 | 309.69 | 319.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ocampo, E.; Liu, C.-H.; Kuo, C.-C. Performance Analysis of Partitioned Step Particle Swarm Optimization in Function Evaluation. Appl. Sci. 2021, 11, 2670. https://doi.org/10.3390/app11062670
Ocampo E, Liu C-H, Kuo C-C. Performance Analysis of Partitioned Step Particle Swarm Optimization in Function Evaluation. Applied Sciences. 2021; 11(6):2670. https://doi.org/10.3390/app11062670
Chicago/Turabian StyleOcampo, Erica, Chien-Hsun Liu, and Cheng-Chien Kuo. 2021. "Performance Analysis of Partitioned Step Particle Swarm Optimization in Function Evaluation" Applied Sciences 11, no. 6: 2670. https://doi.org/10.3390/app11062670
APA StyleOcampo, E., Liu, C.-H., & Kuo, C.-C. (2021). Performance Analysis of Partitioned Step Particle Swarm Optimization in Function Evaluation. Applied Sciences, 11(6), 2670. https://doi.org/10.3390/app11062670







