Abstract
Outliers are observations suspected of not having been generated by the underlying process of the remaining data. Many applications require a way of identifying interesting or unusual patterns in multivariate time series (MTS), now ubiquitous in many applications; however, most outlier detection methods focus solely on univariate series. We propose a complete and automatic outlier detection system covering the pre-processing of MTS data that adopts a dynamic Bayesian network (DBN) modeling algorithm. The latter encodes optimal inter and intra-time slice connectivity of transition networks capable of capturing conditional dependencies in MTS datasets. A sliding window mechanism is employed to score each MTS transition gradually, given the DBN model. Two score-analysis strategies are studied to assure an automatic classification of anomalous data. The proposed approach is first validated in simulated data, demonstrating the performance of the system. Further experiments are made on real data, by uncovering anomalies in distinct scenarios such as electrocardiogram series, mortality rate data, and written pen digits. The developed system proved beneficial in capturing unusual data resulting from temporal contexts, being suitable for any MTS scenario. A widely accessible web application employing the complete system is publicly available jointly with a tutorial.
1. Introduction
In recent times, the machine learning community has boomed coupled with the always-expanding desire to acquire maximum benefit from collected data, apparent in sectors such as biomedicine, socio-economics, and industry. Grubbs [1] has defined anomalies as observations that deviate appreciably from the sample in which they occur. In the current study, an outlier is described as a data element or segment which there is no explanation for it, being suspected of not have been generated by the data’s underlying processes. Outliers can mislead analysts to altogether different insights. However, their discovery is crucial in acquiring a better understanding of the behavior of the data, leading to the development of more efficient methods.
Multivariate time series (MTS) are defined as sets of observations measured along time, being a representation for time series analysis. Each observation depicts a collection of variables, which the combined evolution over time is the object of study. In this context, we propose METEOR—MultivariatE Time sEries OutlieR—an outlier detection method to identify abnormal entities among real-world MTS datasets. Outlier detection algorithms in MTS are typically not found in existing literature, which solely considers univariate case [2,3], overlooking anomalies arising from inter-variable temporal contexts.
Within the vast world of anomaly detection [4,5] extensity and versatility are craved traits. In time series (TS) data, temporal trends play a crucial role in anomaly discovery, where data patterns are not assumed to change abruptly through time. Most of the existing techniques do not take these temporal dependencies into account, leaving them less effective. When time is taken into consideration, mostly univariate temporal data is considered [6]. An example is autoregressive models, extensively used in TS data. In such cases, data points typically depend linearly on previous values and a stochastic term, representing a random process. Alternative procedures consider that outliers are high residual entities with respect to a model expressing the time-varying process [5,7]. Outlierness can be evaluated according to a distance or similarity measure. Anomalies are usually considered to be isolated from the rest of the data. An example is to use the distance of an element to its k-th nearest neighbor as a score [4]. Such reasoning can be applied to measure the distance between discrete sequences [8], which can easily represent TS data. Similarly, certain methods create a boundary between an anomalous and normal class. Data instances are scored given their distance to the boundary, typical in clustering and classification methods [9,10]. Recent efforts have been invested trying to satisfy the existing gap in MTS anomaly detection [11,12,13]; however, a complete and available implementation of such approaches is non-existing. This forces analysts to use typical univariate strategies.
Temporal dependencies within and between variables can be modeled using dynamic Bayesian networks (DBN) which extend traditional Bayesian networks to temporal processes described by MTS. These are probabilistic graphical methods capable of encoding conditional relationships of complex MTS structures via transition networks. A modeling technique, so-called tree-augmented DBN (tDBN) [14], is used to provide a network possessing optimum inter and intra-time slice dependencies between discrete variables for each transition network, verified to outperform existing methods in the literature. DBNs already proved to benefit anomaly detection [15] and gene expression data modeling [16]. Analogous to unsupervised learning, our fully automatic system, called METEOR, exempts the need for any prior knowledge. The latter resides in the statistical paradigm, providing a tDBN representing a normality standard for anomaly detection, where observations are scored using the transition networks. Both stationary and non-stationary tDBNs are studied.
Within METEOR, a tDBN is acquired to shape the general behavior of the data (a set of MTS). Each MTS is then scored according to a sliding window mechanism capable of capturing compelling patterns encoded by temporal dependencies amid variables, absent in existing literature. Outliers are ruled out as those with lower scores; these scores are based on the likelihood given by the joint probability distribution induced by the tDBN transition networks. The system can detect as outlier both an entire MTS, called a subject, or only some subject transition (a partial MTS comprising contiguous observations of the subject variables in a certain period of time).
In detail, data is comprised of a set of MTS known as subjects. For example, time series taken at discrete time with monthly temperature and humidity measurements at major cities would be composed of observations of both variables (temperature and humidity) where each city depicts a different subject. In its turn, each subject encompasses several observations of these two variables along time, where contiguous observations define transitions. For simplicity, consider a transition with lag 2, i.e., covering both temperature and humidity observations at time t and previous lagged observations at time and . Low scores depict transitions that are not explained by observation at time t and its lagged observations, according to the tDBN model. Likewise, whole subjects are scored using the average of all its transition scores.
Hence, METEOR is adapted to detect anomalous portions or entire MTS, fitting into numerous scenarios. A score-analysis phase is available to classify each score. Two main strategies are studied, namely Tukey’s Method [17,18] and Gaussian Mixture Models (GMM) [19]. A threshold is automatically selected to determine the outlierness disclosure boundary.
The system is validated through synthetic and real-world data sets demonstrating its performance in multiple scenarios. Furthermore, a multivariate probabilistic suffix tree (PST) technique is built and compared with METEOR, illustrating the contrast of the current system with typical univariate existing techniques. Due to the increasing demand for data science-related appliances aspiring not only promptness but also easily adaptable mechanisms, the current implementation of METEOR is made entirely free and accessible through a web application [20] available at https://meteor.jorgeserras.com/ (accessed on December 2020). The latter does not require any download and is accompanied by a tutorial video.
This paper is organized as follows. Theoretical background regarding dynamic Bayesian networks modeling is made available in Section 2 before the description of each phase of the proposed system from pre-processing to score-analysis in Section 3. The developed web application and software along with experimental validation are showcased in Section 4. Finally, we draw some conclusions in Section 5.
2. Theoretical Background
In this section we introduce some notation, while recalling relevant concepts and results concerning discrete Bayesian networks and their dynamics counterparts.
2.1. Bayesian Networks
Let X be a discrete random variable that takes values over a finite set . We denote an n-dimensional random vector by where each component is a random variable over . We denote the elements of by , where is the number of values can take.
A Bayesian network (BN) is a probabilistic graphical model which encodes conditional relationships among variables. It is composed by a directed acyclic graph (DAG) defined as , where the vertices V coincide with a set of random variables , also known as nodes, and the edgesE with their conditional dependencies. Variables are independent of all its non-descendant nodes given its parents. A node contains a local probability distribution, encoding the probabilities of every possible configuration of node given its set of parents ,
where is the k-th possible value from the domain of and the j-th configuration of . The set of conditional probabilities associated with each node denotes the BN parameters.
The joint probability distribution of the network is composed by several local probability distributions associated with each variable, as
and can be used to compute the probability of an evidence set.
Learning the structure of a BN [21] can be summarized as finding the DAG which better fits a training dataset. The goodness of fit of a network is measured using a scoring function. If the scoring function is decomposable over the network structure then local score-based algorithms can be employed, turning the DAG search extremely efficient [22,23,24]. A known decomposable scoring criterion is the log-likelihood (LL) [25]. Network parameters are computed by using the observed frequencies of each configuration.
2.2. Dynamic Bayesian Networks
The proposed method is designed to handle discrete multivariate temporal data. In this case, consider the discretization of time in time slices . Moreover, as for the BN case, variables are always discrete-valued.
A discrete multivariate time series (MTS) is a set of observations from n time-dependent variables. Consider a set of subjects of size N. Observations for each variable are measured over T time instants, gathered in a MTS dataset where . Hence, the overall size of D is given by single-valued observations.
Definition 1
(Subject observations). Given a dataset D, the observations of a subject h constitute the set of n variables measured throughout time .
To model MTS we considered inter-variable as well as temporal dependencies. DBNs [26] are BNs which relate variables over adjacent time slices, modeling probability distributions over time, and therefore can be used to model MTS. A time-dependent discrete random vector, , expresses the value of the set of variables at time t. From a graphical perspective, nodes represent the variables at specific time slices t, , and possess time-dependent parameters. Unlike standard BNs, DBNs are composed by a prior network , denoting the distribution of initial states, and multiple transition networks. A transition network has two types of connectivity among variables noted as inter-slice and intra-slice connectivities. The latter refers to variable dependencies at the same time frame. Inter-slice connectivity is responsible for the temporal aspect relating variables of different time slices, allowing only dependencies that follow forward in time.
Let denote the set of random vectors for the time interval . In addition, let denote the joint probability distribution over the trajectory of the process from to . Using the chain rule, the joint probability over is given by:
Common simplifying assumptions consider m- order Markov and stationary processes, which we describe next.
Definition 2
(m- order Markov DBN). A DBN is said to be a m- order Markov DBN if, for all ,
In a m- order Markov DBN, m is called the Markov lag. Considering both inter and intra-slices connectivity, attributes can admit parent nodes from to t, being transition networks expressed by .
Definition 3
(Stationarity DBN). A m- order Markov DBN is said to be stationary if, for all , the structure and parameters of each are the same.
For the stationary case, the only transition network is thus invariant over time, being unrolled through time. To address the non-stationary case, a different network for each transition is required.
In Figure 1, a stationary first-order Markov DBN is depicted, composed by a prior network , over , and a transition network , for all . The connections and represent the intra-slice connectivity of the transition network which correlates the attributes in the same time frame. Temporal relations are present in the inter-connectivity, being connections and . The transition network is unrolled for every slice . Considering Figure 1, the conditional joint probability of the attributes at slice t, given the attributes at slice , is
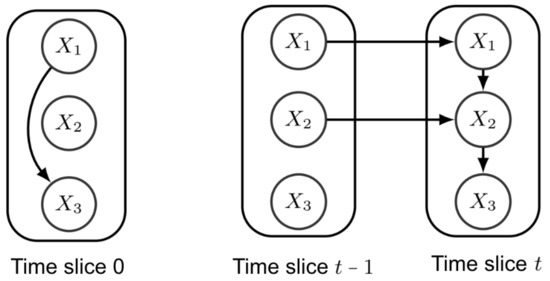
Figure 1.
Example of a stationary first-order Markov DBN. On the left, the prior network , for , and on the right, the transition network over slices and t, for all .
When learning a DBN, state-of-the-art algorithms focus mainly in modeling inter-slice dependencies, neglecting intra-slice connectivity or simply structuring it as a detached approach. The latter comes from the fact that obtaining an unrestricted network is NP-hard [27], contrary to learning solely the inter-connectivity [28]. In METEOR, an optimal tDBN structure learning algorithm [14] is used, providing an optimal inter/intra-slice connectivities simultaneously for each transition network. In this case, an attribute node at a certain time slice has a tree-like network structure, therefore containing at most one parent at that same slice, as seen in Figure 1. Furthermore, in each node, the maximum number of parents from preceding time slices is bounded by a parameter p. The tDBN learning algorithm limits the search space to tree-augmented networks, attaining polynomial-time bounds. These have proven to be effective, being one example the tree-augmented naive Bayes classifier [29]. Moreover, tDBN has motivated further research concerning the efficient learning of optimal DBNs [30,31].
3. Methods
METEOR is portioned in four phases including pre-processing, modeling, scoring, and score-analysis, which together form a complete and automatic anomaly detection system. Data is assumed to be complete, lacking missing values or hidden variables. A diagram comprising all phases is depicted in Figure 2. The pre-processing phase studied is comprised by (an optional) discretization and dimensionality reduction technique discussed in Section 3.1, especially relevant when considering data descendant from sensor devices. Discrete MTS datasets are then employed to the tDBN modeling algorithm, which generates a DBN according to the parameters chosen: the Markov lag m, the maximum number of parents p from preceding slices and a flag s deciding the stationarity of the model. Afterward, the MTS dataset, together with the trained model, are delivered to a scoring phase. The aforementioned capitalizes on the structure and parameters of the DBN to analyze each subject transition using a sliding window algorithm. Entire series are likewise scored. Subsequently, scores are delivered to a score-analysis strategy which creates a threshold differentiating abnormal and normal scores. Two possible strategies are discussed in Section 3.5 and later compared; both output a threshold for the final binary classification. Observations associated with scores below the threshold are classified as outliers, being suspected of not have been generated by the learned model.
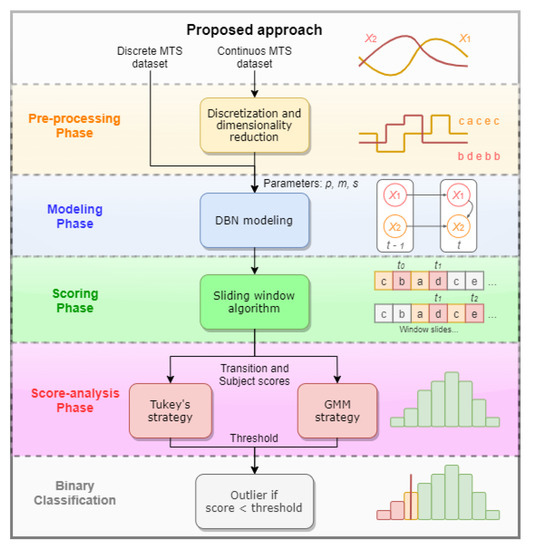
Figure 2.
Scheme of the proposed outlier detection approach comprised of four phases. Datasets formed by MTS data can be directly applied to the modeling phase when discrete; otherwise, the pre-processing phase is applied before modeling. Discrete data is delivered to the modeling phase along with parameters p, m, and s of the DBN to be modeled. Afterward, a sliding window algorithm outputs a score distribution for the data (scoring entire MTS, called subjects, or only portions of it, called transitions, depending on the user’s choice). The score-analysis phase considers two distinct strategies providing thus two possible routes for outlier disclosure.
3.1. Pre-Processing
METEOR modeling phase requires a discrete MTS. In the presence of an already discrete series, this phase can be skipped and follow directly to modeling (Section 3.2); the user can also pre-discretize its MTS with meaningful domain values or any other approach outside METEOR. However, if a continuous series is fed to METEOR, a representation known as Symbolic Aggregate approXimation (SAX) [32] is enforced prior to the modeling phase. SAX has already been validated in anomaly detection scenarios [33] providing discretization and dimensionality reduction. The procedure is applied separately to each univariate TS belonging to a continuous MTS. The processed series are then combined to form a discrete MTS dataset. The pseudo-code for the SAX pre-processing mechanism is available in Algorithm 1.
| Algorithm 1 Data Pre-Processing |
|
Input: A MTS dataset D of n variables along T instants; an alphabet size for each attribute , ; desired length of the resulting MTS. Output: The set of input MTS discretized. 1: procedure SAX(D, for all i,w) 2: for each subject h in D do 3: for each TS , with do 4: for each t, with do 5: Normhihi[t] ▹Normalization 6: function PAA() ▹Dimensionality reduction 7: 8: Partition the in contiguous blocks of size 9: for each block do 10: ▹ Compressed slices 11: 12: function Discretization () ▹ Symbolic discretization 13: ) 14: for each value in do 15: Discretehi[k] 16: ▹ Return discretized MTS dataset |
For each real-valued TS of length T (steps 2–3), normalization (steps 4–5), dimensionality reduction (steps 5–11) and symbolic discretization (steps 12–14) are performed. Normalization is done to present zero mean and a standard deviation of one by employing Z-normalization. The mean of each TS is subtracted from every data point. The result is then divided by the TS standard deviation. The dimensionality reduction compresses the TS into an equivalent sequence of size . Such is assured by piecewise aggregate approximation (PAA). The latter subdivides the normalized TS into w equally sized blocks. The mean of the data points in each block is computed, being the w mean values the new TS. Finally, symbolic discretization is done. In many applications, these normalized time series have a Gaussian distribution [34]. Hence, the TS domain can be divided into equiprobable regions according to a Gaussian distribution , where denotes the size of the alphabet . Regions are identified by boundaries, known as breakpoints . The goal is to resolve in which of the regions each data point resides. A value falling in interval is associated with the symbol , .
When choosing the most suitable value for the alphabet size , experiments conducted [32] demonstrate that a value in the range of 5 to 8 is optimal in most datasets. The latter means that the information loss during discretization is minimized. However, it is always advised to test different values when possible and consider the particularities of each domain.
3.2. Modeling
In the modeling phase, a DBN is learnt from data. The algorithm for non-stationary networks is sketched in Algorithm 2 as proposed in [14]. Since we want to model the distribution underlying the MTS discretized data the log-likelihood (LL) score is used to measure the fitness of the transition networks to the data. The output is a tree-like DBN allowing for one parent in the current time slice (intra-slice network) and at most p parents from the preceding m time slices (inter-slice network).
For each transition from time slices to time slice t a complete directed graph is built at time t (steps 3–4). Each edge in this graph is then weighted with a local LL score given by the optimal set of parents: up to p parents from the previous m time slices and the best parent from time slice t (step 5). Having the completed graph weighted, Edmond’s algorithm [35] is applied to obtain a maximum branching for the intra-slice network from which a transition network is easily extracted (step 6). In non-stationary DBNs, transition networks are collected in each for-loop iteration (step 7). In the case of a stationary network only one transition network is retrieved.
| Algorithm 2 Optimal Non-Stationary m-Order Markov tDBN Learning |
|
Input: A set of input MTS discretized over w time slices; the Markov lag m; the maximum number of parents p from preceding time slices. Output: A tree-augmented DBN structure. 1: procedure Tree-augmented DBN(MTS,m,p) 2: for each transition do 3: Build a complete directed graph in 4: Calculate the weight of all edges and the optimal set of parents 5: Apply a maximum branching algorithm 6: Extract transition network and the optimal set of parents 7: Collect transition networks to obtain a tDBN structure |
3.3. Scoring
After the pre-processing and modeling phases, the proposed method starts a scoring phase. Outliers are considered to be observations that do not fit well the DBN trained model. The goal is to score portions or entire subject observations according to the tDBN structure.
Definition 4
(Window). Given subject observations , a m--order window is defined as the subset of the h-th subject observations concerning time transition in D.
Please note that m--order windows have a size equal to . Given a m--order DBN, a window is scored according the its transition network as
where is the value of observed at time t for subject h and the observed configuration of the set of parents which comprises observations ranging from slices to t according to . Equation (4) is referred as a transition score, representing the log-likelihood (LL) of the observed window computed using the network’s conditional probabilities. Every procedure is akin when considering both stationary and non-stationary DBNs.
If a window possesses a configuration unseen in the modeling phase, the probability of that configuration is zero, nullifying the LL score associated to it. A technique known as probability smoothing is thus employed to prevent score disruption [36]. Probabilities are transformed according to
where is a conditional probability , a parameter expressing the degree of probability uncertainty and the granularity of the . Such means that when is zero, the new probability will be equal to , which is typically . Additionally, Equation (5) ensures that probabilities with value 1 are decreased according not only to but also the size of the alphabet related to that attribute, reducing thus overfitting. Consequently, the LL scores are computed using the smoothed probabilities.
To acquire the outlierness of every MTS transition, a sliding window is employed. The mechanism gradually captures all equally sized windows, with , of a subject to compute the LL scores for each transition. Since the trained model possesses an initial network , time frames cannot be explained by windows of size . Hence, according to the order of the model, only transitions from slice forward are captured. However, the initial frames influence the scores of the next consecutive windows which include them, having the ability of inducing anomalies. The whole procedure is depicted in Algorithm 3. It is worth noting that the stationarity of the DBN modeled influences the way data is scored. Non-stationary models adapt to each transition, meaning that windows are not scored according to the series general behavior. Such allows the adaptation of the system to data whose behavior is time variant.
| Algorithm 3 Transition Outlier Detection |
|
Input: A tDBN storing conditional probabilities for each transition network , a (discretized) MTS dataset D, and a threshold to discern abnormality. Output: The set of anomalous transitions with scores below . 1: procedure 2: for each time slice t do 3: for each subject do 4: function Scoring() 5: for each variable do 6: ΠXi[t] 7: whi[t] 8: phi 9: Phi ▹ Probability smoothing 10: sht−m:t ▹ Transition score 11: if then 12: outliers .append |
Furthermore, subject outlier detection can be easily computed from Algorithm 3, offering the detection of anomalous entire subject observations. In this case, a subject h outlierness is measured by the mean of every transition score of that subject. A subject is scored as
where represents the transition scores of all windows captured from subject h. The algorithm is straightforward, and so we do not present it, but it is available in the current implementation of METEOR.
With the computation of all transition/subject scores, a strategy must now discern normal and anomalous ones. The score-analysis phase is discussed next.
3.4. Parameter Tuning
A qualitative sensitivity analysis is presented to aid users in selecting the optimal set of parameters when employing METEOR with their own datasets. The Markov lag m is the most significant parameter when modeling a DBN structure. Increasing m causes the complexity of the network to increase, causing each window captured to include information of time slices, which decreases the number of windows available. Longer MTS analysts are thus advised to model a high order DBN correctly. Users should avoid a high value of m, being common values or . It is presumed that attributes are better explained by their immediate previous values, for most scenarios, than from long memory.
Also, for each node, the maximum number of connections from previous time slices, parameter p, is useful in datasets where there is a high temporal dependency between attributes, i.e., when a certain attribute is better explained by a set of values from previous time slices. These connections form the inter-slice dependencies of the transition network. Conducted experiments in Section 4 demonstrate that is sufficient in most cases; this typically leads for each attribute to have a connection to its previous value which is easily understandable. Inter-slice connections are normally between the same variable at different time slices. Please note that by using tDBNs, besides inter-slice connections, there are also intra-slice ones. Therefore, a large p value can easily cause overfitting since each network node begins to be allowed to connect with multiple nodes. Users are advised to experiment with or , yielding favorable results for the majority of the datasets tested.
The value s conveys the stationarity of the system and indicates if transitions should be modeled according to their temporal position on the series. In other words, if it is important that certain patterns occur on specific time slices. It is worth noting that the complexity is much larger in non-stationary models, and the learning phase could take a long time resulting in a large DBN encompassing the whole series time domain. Additionally, the trained model is more probable of overfitting to certain patterns at specific transitions. On the contrary, in a stationary DBN, every window captured is scored according to the general network modeling the whole MTS. Stationarity should always be active unless the analyst knows for sure that in its specific dataset, observations can be considered anomalous for occurring in specific time frames and not for their observed values.
3.5. Score-Analysis
Two score-analysis strategies are studied to elect an optimum threshold for outlier disclosure amid score arrays.
3.5.1. Tukey’s Strategy
Abnormal scores can be defined as values that are too far away from the norm, presuming the existence of a cluster comprising normality. The current technique has inspiration in John Tukey’s method [17,18], which determines the score’s interquartile range (IQR) as
where Q1 and Q3 are the first and third quartiles, respectively. The IQR measures statistical dispersion, depicting that 50% of the scores are within of the median. By ignoring the scores mean and standard deviation, the impact of extreme values does not influence the procedure. Hence, IQR is robust to the presence of outliers.
Tukey exploits the notion of fences [18], frontiers which separate outliers from normal data. METEOR typically generates negatively skewed score distributions. Hence, a lower fence computed as is used. The reason behind choosing is that for most cases, a value of IQR labels too many outliers (too exclusive) while begins to classify extreme values as normal (too inclusive), being such value fruit of conducted experiments [18]. Transition and subject scores are classified as anomalous if their value subsists below their respective lower fence. Formally, a score s holding inequality
is considered anomalous, being the threshold.
Tukey’s procedure prefers symmetric score distributions with a low ratio of outliers, having a breakdown at about 25% [37]. The aforementioned arises from the fact that the score distribution starts to be increasingly asymmetric with the increase of more extreme scores, and such has been confirmed in existing literature [38]. It is also worth noting that the nature of the outliers can influence Tukey’s assumptions. If outliers are generated by a different underlying process, the score distribution may display multiple clusters, causing Tukey’s threshold to avoid the main distribution and rising the number of false negatives. On the other hand, in scenarios with absence of anomalies, this mechanism is capable of completely eliminate false positive occurrences, since fences are not forced to be in the scores’ observed domain.
3.5.2. Gaussian Mixture Model
To handle disjoint score distributions, a method based on a Gaussian Mixture Model (GMM) [19] is employed. Commonly used in classification and clustering problems, GMMs are probabilistic models that assume data is generated from a finite mixture of Gaussian distributions with unknown parameters, a reasonable assumption in most scenarios [34].
Score distributions are modeled as mixtures of two Gaussian curves. Labeling each score becomes a classification problem among two classes and , representing abnormality and normality, respectively. The problem is defined as uncovering the value of for each score value s, which can be obtained by Bayes’ rule
where is the likelihood of score s belonging to class , the priors for each class and the evidence. The threshold is defined as the boundary that better separates both curves, which describes the point of maximum uncertainty. Evidence for each score is calculated according to
Combining Equations (9) and (10) leads to the conclusion that for a score s be classified as anomalous, it must hold inequality
Such is known as the Bayes’ classification rule which provides the desired boundary.
The GMM is defined as the sum of the two Gaussian distributions, i.e., . An Expectation-Maximization algorithm [39] is used to determine the values of parameters , and . In the current study, GMM is employed with the aid of the available R package mclust [40].
The GMM strategy can handle discontinued score distributions, however, it assumes the existence of an outlier cluster which may not always be appropriate. Thus, both Tukey’s and GMM strategies should be contemplated.
4. Experimental Results
With the intention of providing a fully automatic and adaptable outlier detection mechanism, the developed implementation is freely available online [20]. Most figures from undertaken experiments in the current study derive from the built web application. The latter offers support from data-formatting to score-analysis, together with a tutorial video. Sample datasets are likewise accessible for immediate usage. Results can be downloaded in each phase.
A score-analysis tab regarding subject/transition outlierness is available. The latter offers automatic thresholds considering the studied strategies as well as manual regulation. Users are capable of adjusting parameters in the midst of each phase influencing the outputted results. The graphical interface is adapted in real time. Furthermore, source code is available, allowing the installation of the application in any setup while supporting the adaptation of each phase for a particular endeavour.
To outline the performance of METEOR, several experiments are conducted using simulated as well as real-world datasets from distinct sources. To support the importance of the intra-slice connections in the modeling phase via tDBN, a comparison with a univariate outlier detection method is also provided.
4.1. Simulated Data
First, the performance is validated using simulated data, the latter consists of MTS of 5 variables () with a domain of 3 symbols ( for all i) along 10 time frames (). More specifically, the present experiments subsist on training two separate stationary first-order DBNs, one for generating normal data and another to produce outliers. All data is mixed together in a single dataset and fed to the system. A DBN is trained using the combined dataset, with the aim of locating the anomalous subjects.
To evaluate the performance of each experiment, the number of true positives (TP), false positives (FP) and false negatives (FN) is measured. Such are used to determine the Positive Predictive Value (PPV), representing precision, and True Positive Rate (TPR), representing recall. To conjointly consider both metrics, the score is computed along with the accuracy (ACC) of each test.
Experiments are identified by their outlier ratio , indicating the percentage of anomalous subjects in the dataset, the anomalous model, DBN B or C, used to generate anomalous subjects and the total number of subjects in the dataset D of size N. The transition networks of the anomalous models are displayed in Figure 3 together with their dissimilarities with respect to the normal model A.
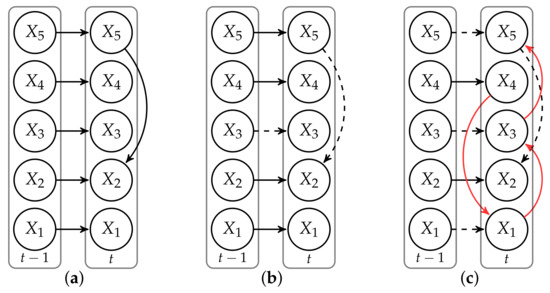
Figure 3.
Transition networks of stationary first-order DBNs (). The network (a) on the left represents the transition network of DBN A which generates normal subjects. Networks (b,c) represent DBN B and C, respectively, which generate anomalous subjects. Dashed connections represent links which are removed with respect to the normal network (a), while red links symbolize added dependencies. Solid black edges are connections which are common with respect to (a).
Experiments are divided in two groups according to the strategies in the score-analysis phase. Such means that both strategies are validating the proposed approach. Experiments considering a different approach are carried out afterwards.
4.1.1. Tukey’s Score-Analysis
Results employing Tukey’s method in the score-analysis phase are shown in Table 1, each row depicts an experiment. Every value is rounded down to two decimal places and represents an average among 5 trials.

Table 1.
Subject outlier detection of METEOR on simulated data using Tukey’s strategy.
The outcomes demonstrate that datasets with solely 100 subjects () perform generally poorly, since these do not possess enough information about the data’s underlying processes. Accuracy as well as scores tend to decline with the increase of outlier ratios, due to less normal data available for a correct modeling phase. The latter is observed by the decrease of measurements. The computed thresholds converge to more stable values with the increase of data, hence outputting more reliable values for every performance measure.
Discussing the impact of outlier ratios, Tukey’s method is recognized to be more effective in the presence of lower anomaly percentages due to the increasingly asymmetric score distribution when increasing the number of outliers, as already confirmed in [38]. Moreover, when is high enough and the majority of outliers are generated by a common process, the score distribution of abnormal data becomes visible, causing poor performance in experiments with 20% of outliers. Such explains why, for the same , scores may decrease with the increase of subjects. The breakpoint of Tukey’s method [37] prevents favorable results when in the presence of abundance outlierness. However, FP tend to disappear, reflecting high precision measurements.
Comparing experiments from both anomalous networks B and C, accuracy is in general higher in experiments with C, since the latter has fewer connections in common with the normal model A, resulting in a more dissimilar structure. However, such is not always true, since asymmetric distributions perturb Tukey’s analysis.
Control experiments performed using datasets solely comprised by normal subjects demonstrated favorable results with Tukey’s score-analysis, contrary to the GMM strategy, which divides the distribution in two classes creating an high number of FP.
4.1.2. Gaussian Mixture Model
Inspecting results using Tukey’s analysis, the performance of experiments with larger anomaly ratios bear low values due to high counts of FN. The main reason for the aforementioned is the presence of an outlier curve in the scores’ distribution. The latter occurs due to the high proportion of outliers formed by a specific mechanism, in this case an abnormal DBN. GMM score-analysis is thus employed in the same experiments, affecting solely the threshold computation in the score-analysis phase.
Results are available in Table 2, being noticeable the considerable increase in recall for experiments with of 20% when compared to results from Table 1. Such is confirmed in existing literature [38]. In general, the count of FP is higher when employing GMM. Such is caused by the GMM’s assumption of the existence of an abnormal model even in its absence. Due to similarities between DBNs, especially when considering model B, scores from both networks tend to mix together around the threshold being thus difficult to discern them. The GMM approach has typically higher recall but lower precision with thresholds smaller in module. The latter is more noticeable in higher outlier ratios, since in the presence of fewer anomalies Tukey’s method displays higher scores.

Table 2.
Subject outlier detection of METEOR on simulated data using GMM’s strategy.
4.1.3. Comparison between GMM and Tukey’s Score-Analysis
With the aim of giving additional insight on which method to choose when performing score-analysis and summarize the conclusions derived from the experimental results using simulated data, the scores for each method are compared in the presence of different outlier ratios.
In Figure 4, the average scores of every experiment using a specific method and outlier ratio is shown. Tukey’s method performs very poorly in datasets with 20% of anomalies while outperforming the GMM strategy in datasets with 5% of anomalies as well as control experiments.
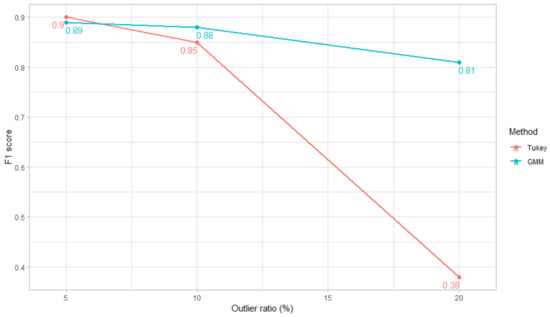
Figure 4.
Comparison between GMM and Tukey’s score-analysis scores for multiple outlier ratios. Each value is an average of all 15 trials performed for each outlier ratio.
To determine a priori which method will excel in the score-analysis of a specific dataset, analysts should understand the underlying process generating normal data and the ability to anticipate the type of outlier expected. Tukey’s method expects score distributions to be negatively skewed, meaning that anomalies are generated by the same underlying process as normal data but present the lowest distribution scores. These scenarios are the most common, being real-world examples studied in Section 4.2 and Section 4.3. Alternatively, if a different external process is generating abnormal data that contaminates the rest of the data, the score distribution of the whole dataset will present multiple clusters requiring the employment of the GMM method to separate both classes. An example is seen in the experiments using simulated data where GMM performs well regardless of the outlier ratio.
Although the present synthetic experiments seem to endorse the use of a GMM strategy, one should note that both normal and abnormal data are generated according to two defined models, which can, by some degree, be separated. Such is a favorable scenario for GMM. When considering other scenarios, Tukey’s method is not so susceptible to well-defined curves being thus always a strategy to consider. With that said, it is advised for the analyst to apply as much knowledge as possible with both strategies’ experimentation.
4.1.4. Comparison with Probabilistic Suffix Trees
To contrast the proposed system, an additional outlier detection mechanism is studied. The latter adopts probabilistic suffix trees (PST) [41], variable length Markovian techniques, with the aim of mining abnormal values in MTS. These structures are only capable of modeling univariate data, perceiving a discrete TS as a sequence of symbols . The temporal component is encoded in the position of each symbol, which assumes a value from the discrete set .
To tackle MTS, datasets are divided into multiple sets, each one containing data concerning one variable. Every set is used to model a PST . Subjects are seen as sets of sequences for each variable associated to its corresponding PST. Thus, subjects with five variables are modeled using five independent trees. Each PST computes an univariate score [42] for all subjects considering its variable, according to
where T is the maximum length of sequence . The probability of a sequence is computed using the - property as
with each state in the sequence, , being conditioned on its past observed states, also known as contexts. The conditional probabilities are retrieved efficiently from a tree structure. Scores, computed using Equation (12) for each PST , concerning every TS from a common subject are stored in an array. The mean of the array is the multivariate score for the subject, being obtained by
where is the sequence concerning variable i from subject .
An existing PST modeling software [42] was adapted to a MTS scenario. Each experiment using simulated data is compared with METEOR. Likewise, score-analysis is employed posterior to scoring, selecting one of the two considered strategies. Tests are available in Table 3, being models A, B and C the same used in Section 4.1. Results demonstrate the low performance of the PST approach when discerning anomalies generated by DBN B. Such is explained by the fact that B is much similar to the normal model A when compared with C. Furthermore, since inter-variable relations are not considered, subjects become identical when seen by the PSTs. Hence, the resulting score distributions display a single curve blending both classes. One exception are experiments considering 5% of anomalies, which indicate that with the increase of outlier ratios, the few dissimilarities among classes are modeled, causing outliers to fit each PST. Additionally, the superior results with model C can be explained by the its higher discrepancy with the normal model A.

Table 3.
PST results using Tukey and GMM strategies on simulated data for experiments with 10,000.
In Figure 5, a comparison between the METEOR and the PST approaches for a same experiment with 20% of outliers from model C is shown. The PST system cannot separate both classes as well as the DBN approach, blending normal and anomalous scores. Results demonstrate the importance of the inter-variable relationships present in model C for outlier disclosure in MTS data, of which the PST technique neglects. Moreover, the PST approach scales poorly with the increase of outlier ratios and never outperforms METEOR in the experiments conducted.
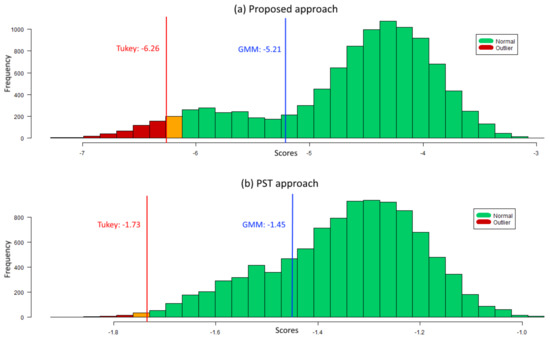
Figure 5.
Subject outlierness using METEOR (a) and PST approach (b) for a same experiment of a dataset of 10,000 subjects () with 20% anomalies generated by model C. Histograms display thresholds using both score-analysis strategies. Scores below the threshold are classified as abnormal (in red) while the rest are classified as normal (in green), being the presented color representation for the Tukey’s thresholds.
4.2. ECG
A common application of anomaly detection in medical scenarios is in electrocardiogram (ECG) alert systems [33]. These have the capability of detecting unusual patterns in signals measured from patients. Data is usually continuous and present expected patterns in healthy patients.
An ECG dataset, available at [43], is composed by 200 MTS () each with 2 distinct variables (). A representation of the normalized data can be seen in Figure 6 together with the breakpoints of the performed SAX discretization. The location of the ventricular contraction peaks typically occur around time frames 3 and 10. Tests are performed using non-stationary DBNs since specific phenomena occurs in particular time instances. The experiments have the objective of testing the system behavior to inconsistent data.
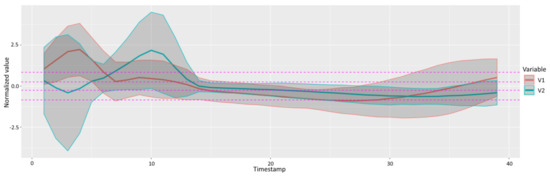
Figure 6.
Mean and standard deviation of normalized ECG variables along time using a SAX alphabet for .
Series are discretized with an alphabet of size 5 ( for all i) and modeled using a second-order DBN () with one inter-slice connectivity per node (). Score distributions are negatively skewed, advising the use of Tukey’s thresholds. An experiment, depicted in Figure 7, shows that METEOR has difficulty evaluating time slices with higher variance. To further test the aforementioned, 10% of the subjects are flipped horizontally and mixed together in the original set; therefore, the ventricular contraction peaks in these series occur in their last time frames. Results demonstrate the detection of such transitions present on subjects with higher id.
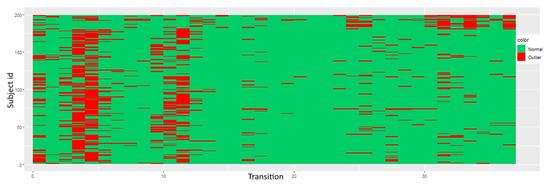
Figure 7.
ECG transitions arranged by subject. A non-stationary second-order tDBN () model with inter-slice connectivity () is used together with Tukey’s score-analysis. Flipped subjects are associated to the highest subject ids. Data is discretized using SAX with an alphabet of 5 symbols ( for all i). Transitions displayed in red are classified as abnormal while in green are classified as normal.
The system has the ability of detecting unusually behaved sections in ECGs which coincide with the high variance portions. The latter is due to not existing a predominant pattern in the location of the peaks, observable as vertical red stripes, since these vary intensively from subject to subject contrary to more advanced slices. SAX discretization offers low definition in such locations.
4.3. Mortality
An outlier detection scenario is studied in [44], where the suggested approach DetectDeviatingCells classifies cell-wise as well as row-wise anomalies in a data matrix. One of the tested experiments [44] refers to a dataset comprising male mortality in France from 19th century forward, extracted from [45]. The aim is to discover outlying years, representative of the main iconic events in France history.
Data is structured as a matrix. To adapt it to METEOR, age groups are regarded as variables, meaning that correlations among mortality rates of different ages can be modeled. Due to the excessive number of attributes, only a subset is selected. The normalized dataset can be seen in Figure 8, where each time series represent France’s male mortality rates from 1841 to 1987 in a specific age group. The years in which measurements were obtained are regarded as time instants t. With the assembling of longitudinal data, SAX pre-processing is applied to each series. Attributes are thus male mortality rates of specific age groups at particular years. It is worth noting that with all the transformations performed, the dataset is reduced to a single subject which portrays a MTS.
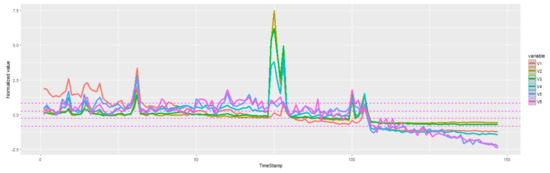
Figure 8.
Normalized values of variables representing France’s mortality rates of males with ages 10, 20, 30, 40, 60 and 80, respectively, from 1841 to 1987. Each time stamp represents a year. Data is discretized with a SAX alphabet for all i.
Two experiments are presented in Figure 9. In the first experiment, 5 variables are selected, being ages 20, 30, 40, 60 and 80. Each variable is discretized with an alphabet size of 5 ( for all i) and all tests employ Tukey’s strategy in the score analysis phase. The objective is to determine unusual events such as wars and epidemics. The trained model involves a stationary third-order tDBN. Nodes are allowed to have at most one parent from previous slices. The reasoning behind the parameter choice is purely experimental. The problem exhibits a preference of attributes establishing connections with previous nodes which are not consecutive with themselves. It is worth recalling that having an order of three does not mean that every or even any relation has such lag, it just offers such possibility. Results confirm major events which shaked France history. These are displayed in Figure 9, representing both world wars, the influenza pandemic, the Franco-Prussian War and the European revolutionary wave of 1848. France was a belligerent in several conflicts as well as colonization wars in the 1850s.
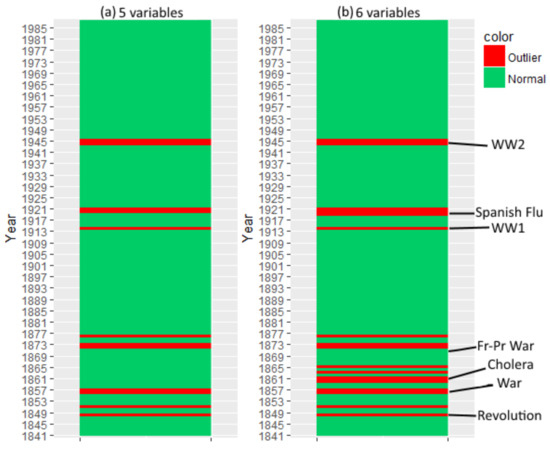
Figure 9.
Transition outlierness for mortality datasets of 5 (a) and 6 (b) variables using a third-order tDBN () with one inter-slice connectivity per node (). Dataset (a) is comprised by 5 variables () representing mortality rates of males with ages 20, 30, 40, 60 and 80. Dataset (b) includes the same variables as (a) with the addition of a variable representing the mortality rate of males aged 10 (). Transitions are arranged by year and classified as anomalous (red) and normal (green). Major wars and epidemics which affected France in the selected years are exhibited.
In the second experiment, a variable is added to the first set. The new age group represents the male mortality rate of children aged up to 10 years old. The aim is to capture the impact of youth mortality in the outputted years. Results are similar, being the differences observed in the 1860s and around the Spanish flu confirming that youth is more susceptible to epidemics.
4.4. Pen-Digits
A distinct application is the recognition of drawn digits. Measurements are taken along time from each drawing phase. Data is available at [46] and studied in [47]. Handwriting samples are captured using a sensitive tablet which outputs the x and y coordinates of the pen at fixed time intervals. The goal is to model the system to a certain character being simultaneously unwanted digits amid the data. A set comprising 1143 MTS () along 8 time frames () representing digit 1 is assembled from 44 different writers. The original MTS are discretized with an alphabet size of 8 ( for all i). The dataset is injected with 130 subjects () belonging to a different digit. The aim is to detect the aforementioned and subsequently understand similarities between digits.
Results are present in Table 4, where represents the anomaly digit i introduced. A first-order non-stationary tDBN is modeled, since a pair of coordinates is more easily explained by its immediate precedent. Every attribute can possess at most one parent from its preceding slice (). Thresholds are selected manually. The objective is not only to capture the performance of the outlier detection system but further understand which digits are more commonly resembled with digit 1. Results show that distinguishing digit 7 from 1 is difficult due to their similarity, proved by the low score obtained. Such reflects the blending of both class distributions. Digits 8 and 9 proved to be more easily discerned from 1.

Table 4.
Results of pen digits outlier detection experiments.
5. Conclusions
The presence of outliers can severely distort data analysis and, consequently, hamper statistical model identification. Outlier detection has become a very challenging task in many application fields. For example, in medical scans, outliers elicit abnormal or changed patterns, and therefore, their detection may help detect certain types of diseases. When following-up patients, detecting patient outliers governed by abnormal temporal patterns can advance pharmaceutical or medical research. Still, versatile and automatic outlier detection methods for MTS are almost inexistent, with scarce available algorithms and software.
The developed system, known as METEOR, utilizes a sliding window mechanism to uncover contextual anomalies with temporal and inter-variable dependencies arising from portions and entire MTS, oblivious in the existing literature. Observations are scored with respect to a modeled DBN, adjustable to both stationary and non-stationary scenarios. A widely available web application [20] is deployed to assist an analyst in their specific endeavour along with a user-friendly interface and tutorial. A diverse set of applications has benefited from the former, presenting an adaptable outlier detection system previously nonexistent, ranging from pre-processing to score-analysis.
METEOR showed promising results when employed in synthetic and real data in quite different domains: it detected unusually behaved sections in ECG; it detected abnormal youth mortality during Spanish flu epidemics; and recognized that digit 7 more commonly resembles digit 1 than digits 8 and 9. Moreover, a comparison with a PST technique that independently looks at each variable, as in the univariate case, showed that PST does not detect outliers discovered by METEOR due to relationships between subjects becoming identical.
Possible future research could consist in augmenting the tDBN algorithm with the employment of change-point mechanisms in the case of non-stationarity as well as the study of additional pre-processing and score-analysis mechanisms capable of better-capturing data’s underlying features. Application of METEOR to the analysis of clinical data is also a promising future development. Indeed, METEOR is perfectly suited for multivariate time series analysis stored in electronic medical records (with patients’ follow-up). This data is becoming increasingly common in chronic conditions such as rheumatic disorders and dementia, and also cancer.
Author Contributions
J.L.S. implemented the algorithms, performed the computational experiments and wrote the first draft of the manuscript (all authors made the required updates). A.M.C. and S.V. conceived the study, supervised the research, results and manuscript. All authors read and agreed the final version of this manuscript.
Funding
Supported by the Portuguese Foundation for Science and Technology (Fundação para a Ciência e a Tecnologia—FCT) through UIDB/50008/2020 (Instituto de Telecomunicações) and UIDB/50021/2020 (INESC-ID), and projects PREDICT (PTDC/CCI-CIF/29877/2017) and MATISSE (DSAIPA/DS/0026/2019). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 951970 (OLISSIPO project).
Data Availability Statement
All data used in this work is available at the METEOR Github project accessible via the webpage https://meteor.jorgeserras.com.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grubbs, F.E. Procedures for detecting outlying observations in samples. Technometrics 1969, 11, 1–21. [Google Scholar] [CrossRef]
- López-de Lacalle, J. tsoutliers: Detection of Outliers in Time Series; R Package Version 0.6-6; The Comprehensive R Archive Network (CRAN): Wien, Austria, 2017. [Google Scholar]
- Matt Dancho, D.V. anomalize: Tidy Anomaly Detection; R Package Version 0.1.1; The Comprehensive R Archive Network (CRAN): Wien, Austria, 2018. [Google Scholar]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. (CSUR) 2009, 41, 15. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Outlier Analysis; Springer: Berlin, Germany, 2017. [Google Scholar]
- Gupta, M.; Gao, J.; Aggarwal, C.C.; Han, J. Outlier Detection for Temporal Data: A Survey. IEEE Trans. Knowl. Data Eng. 2014, 26, 2250–2267. [Google Scholar] [CrossRef]
- Galeano, P.; Peña, D.; Tsay, R.S. Outlier detection in multivariate time series by projection pursuit. J. Am. Stat. Assoc. 2006, 101, 654–669. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly Detection for Discrete Sequences: A Survey. IEEE Trans. Knowl. Data Eng. 2012, 24, 823–839. [Google Scholar] [CrossRef]
- Ma, J.; Perkins, S. Time-Series Novelty Detection Using One-Class Support Vector Machines. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA, 20–24 July 2003; Volume 3, pp. 1741–1745. [Google Scholar]
- Koch, K.R. Robust estimation by expectation maximization algorithm. J. Geod. 2013, 87, 107–116. [Google Scholar] [CrossRef]
- Wang, X.; Lin, J.; Patel, N.; Braun, M. Exact variable-length anomaly detection algorithm for univariate and multivariate time series. Data Min. Knowl. Discov. 2018, 32, 1806–1844. [Google Scholar] [CrossRef]
- Ding, N.; Gao, H.; Bu, H.; Ma, H.; Si, H. Multivariate-Time-Series-Driven Real-time Anomaly Detection Based on Bayesian Network. Sensors 2018, 18, 3367. [Google Scholar] [CrossRef]
- He, Q.; Zheng, Y.J.; Zhang, C.; Wang, H.Y. MTAD-TF: Multivariate Time Series Anomaly Detection Using the Combination of Temporal Pattern and Feature Pattern. Complexity 2020, 2020, 8846608. [Google Scholar] [CrossRef]
- Monteiro, J.L.; Vinga, S.; Carvalho, A.M. Polynomial-Time Algorithm for Learning Optimal Tree-Augmented Dynamic Bayesian Networks. In Proceedings of the Polynomial-Time Algorithm for Learning Optimal Tree-Augmented Dynamic Bayesian Networks (UAI 2015), Amsterdam, The Netherlands, 12–16 July 2015; pp. 622–631. [Google Scholar]
- Hill, D.J.; Minsker, B.S.; Amir, E. Real-time Bayesian anomaly detection in streaming environmental data. Water Resour. Res. 2009, 45, W00D28. [Google Scholar] [CrossRef]
- Murphy, K.; Mian, S. Modelling Gene Expression Data Using Dynamic Bayesian Networks; Technical Report; Computer Science Division, University of California: Berkeley, CA, USA, 1999. [Google Scholar]
- Tukey, J.W. Exploratory Data Analysis; Pearson: Reading, MA, USA, 1977; Volume 2. [Google Scholar]
- Hoaglin, D.C.; John, W. Tukey and data analysis. Stat. Sci. 2003, 311–318. [Google Scholar] [CrossRef]
- McLachlan, G. Finite mixture models. Annu. Rev. Stat. Appl. 2019, 5, 355–378. [Google Scholar] [CrossRef]
- Serras, J.L.; Vinga, S.; Carvalho, A.M. METEOR—Dynamic Bayesian Outlier Detection. 2020. Available online: https://meteor.jorgeserras.com/ (accessed on 23 February 2021).
- Friedman, N. The Bayesian Structural EM Algorithm; Morgan Kaufmann: Burlington, MA, USA, 1998; pp. 129–138. [Google Scholar]
- Carvalho, A.M.; Roos, T.; Oliveira, A.L.; Myllymäki, P. Discriminative Learning of Bayesian Networks via Factorized Conditional Log-Likelihood. J. Mach. Learn. Res. 2011, 12, 2181–2210. [Google Scholar]
- Carvalho, A.M.; Adão, P.; Mateus, P. Efficient Approximation of the Conditional Relative Entropy with Applications to Discriminative Learning of Bayesian Network Classifiers. Entropy 2013, 15, 2176–2735. [Google Scholar] [CrossRef]
- Carvalho, A.M.; Adão, P.; Mateus, P. Hybrid learning of Bayesian multinets for binary classification. Pattern Recognit. 2014, 47, 3438–3450. [Google Scholar] [CrossRef]
- Carvalho, A.M. Scoring Functions for Learning Bayesian Networks; INESC-ID Tech. Rep.; INESC.ID: Lisbon, Portugal, 2009. [Google Scholar]
- Friedman, N.; Murphy, K.P.; Russell, S.J. Learning the Structure of Dynamic Probabilistic Networks; Morgan Kaufmann: Burlington, MA, USA, 1998; pp. 139–147. [Google Scholar]
- Chickering, D.; Geiger, D.; Heckerman, D. Learning Bayesian Networks: Search Methods and Experimental Results. In Proceedings of the Fifth Conference on Artificial Intelligence and Statistics, Montreal, QC, Canada, 20–25 August 1995; pp. 112–128. [Google Scholar]
- Dojer, N. Learning Bayesian Networks Does Not Have to Be NP-Hard; Springer: Berlin, Germany, 2006; pp. 305–314. [Google Scholar]
- Friedman, N.; Geiger, D.; Goldszmidt, M. Bayesian network classifiers. Mach. Learn. 1997, 29, 131–163. [Google Scholar] [CrossRef]
- Sousa, M.; Carvalho, A.M. Polynomial-Time Algorithm for Learning Optimal BFS-Consistent Dynamic Bayesian Networks. Entropy 2018, 20, 274. [Google Scholar] [CrossRef]
- Sousa, M.; Carvalho, A.M. Learning Consistent Tree-Augmented Dynamic Bayesian Networks. In Machine Learning, Optimization, and Data Science, Proceedings of the 4th International Conference, Volterra, Tuscany, Italy, 13–16 September 2018—Revised Selected Papers; Nicosia, G., Pardalos, P.M., Giuffrida, G., Umeton, R., Sciacca, V., Eds.; Springer: Berlin, Germany, 2019; Volume 11331, pp. 179–190. [Google Scholar]
- Lin, J.; Keogh, E.J.; Lonardi, S.; Chiu, B.Y. A Symbolic Representation of Time Series, with Implications for Streaming Algorithms. In Proceedings of the 8th ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery (DMKD 2003), San Diego, CA, USA, 13 June 2003; ACM: New York, NY, USA, 2003; pp. 2–11. [Google Scholar]
- Keogh, E.; Lin, J.; Fu, A. HOT SAX: Finding the Most Unusual Time Series Subsequence: Algorithms and Applications. In Proceedings of the Sixth International Conference on Data Mining (ICDM), Brighton, UK, 1–4 November 2004; pp. 440–449. [Google Scholar]
- Larsen, R.J.; Marx, M.L. An Introduction to Mathematical Statistics and Its Applications; Prentice-Hall: Englewood Cliffs, NJ, USA, 1986; Volume 2. [Google Scholar]
- Edmonds, J. Optimum branchings. J. Res. Natl. Bur. Stand. 1967, 71, 233–240. [Google Scholar] [CrossRef]
- Manning, C.D.; Raghavan, P.; Schütze, H. Introduction to Information Retrieval; Cambridge University Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Rousseeuw, P.J.; Croux, C. Alternatives to the median absolute deviation. J. Am. Stat. Assoc. 1993, 88, 1273–1283. [Google Scholar] [CrossRef]
- Jones, P.R. A note on detecting statistical outliers in psychophysical data. Atten. Percept. Psychophys. 2019, 81, 1189–1196. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Jain, A.K. Unsupervised learning of finite mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 381–396. [Google Scholar] [CrossRef]
- Fraley, C.; Raftery, A.; Scrucca, L.; Murphy, T.B.; Fop, M.; Scrucca, M.L. mclust: Gaussian Mixture Modelling for Model-Based Clustering, Classification, and Density Estimation; R Package Version 5; The Comprehensive R Archive Network (CRAN): Wien, Austria, 2017. [Google Scholar]
- Ron, D.; Singer, Y.; Tishby, N. The power of amnesia: Learning probabilistic automata with variable memory length. Mach. Learn. 1996, 25, 117–149. [Google Scholar] [CrossRef]
- Gabadinho, A.; Ritschard, G. Analyzing state sequences with probabilistic suffix trees: the PST R package. J. Stat. Softw. 2016, 72, 1–39. [Google Scholar] [CrossRef]
- Dau, H.A.; Keogh, E.; Kamgar, K.; Yeh, C.C.M.; Zhu, Y.; Gharghabi, S.; Ratanamahatana, C.A.; Hu, B.; Begum, N.; Bagnall, A.; et al. The UCR Time Series Classification Archive. 2018. Available online: https://www.cs.ucr.edu/~eamonn/time_series_data_2018/ (accessed on 18 September 2018).
- Rousseeuw, P.J.; Bossche, W.V.D. Detecting deviating data cells. Technometrics 2018, 60, 135–145. [Google Scholar] [CrossRef]
- University of California; Max Planck Institute for Demographic Research (Germany). Human Mortality Database. Available online: www.humanmortality.de (accessed on 18 September 2018).
- Dheeru, D.; Karra Taniskidou, E. UCI Machine Learning Repository. 2017. University of California, Irvine, School of Information and Computer Sciences. Available online: http://archive.ics.uci.edu/ml (accessed on 18 September 2018).
- Alimoglu, F.; Alpaydin, E. Methods of Combining Multiple Classifiers Based on Different Representations for Pen-based Handwritten Digit Recognition. In Proceedings of the Fifth Turkish Artificial Intelligence and Artificial Neural Networks Symposium (TAINN), Istanbul, Turkey, 27–28 June 1996. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).