Bifurcation Flight Dynamic Analysis of a Strake-Wing Micro Aerial Vehicle

Abstract

Non-linear phenomena are particularly important in -flight dynamics of micro-class unmanned aerial vehicles. Susceptibility to atmospheric turbulence and high manoeuvrability of such aircraft under critical flight conditions cover non-linear aerodynamics and inertia coupling. The theory of dynamical systems provides methodology for studying systems of non-linear ordinary differential equations. The bifurcation theory forms part of this theory and deals with stability changes leading to qualitatively different system responses. These changes are called bifurcations. There is a number of papers, the authors of which applied the bifurcation theory for analysing aircraft flight dynamics. This article analyses the dynamics of critical micro aerial vehicle flight regimes. The flight dynamics under such conditions is highly non-linear, therefore the bifurcation theory can be applied in the course of the analysis. The application of the theory of dynamical systems enabled predicting the nature of micro aerial vehicle motion instability caused by bifurcations and analysing the post-bifurcation microdrone motion. This article presents the application of bifurcation analysis, complemented with time-domain simulations, to understand the open-loop dynamics of strake-wing micro aerial vehicle model by identifying the attractors of the dynamic system that manages upset behaviour. A number of factors have been identified to cause potential critical states, including non-oscillating spirals and oscillatory spins. The analysis shows that these spirals and spins are connected in a one-parameter space and that due to improper operation of the autopilot on the spiral, it is possible to enter the oscillatory spin.

1. Introduction

Classic methods of testing dynamic aircraft stability enable analysing their dynamic properties in the framework of minor disturbances of a steady straight flight. However, Micro Aerial Vehicles (MAV) operating in open space, where instantaneous gusts of wind can exceed 10 m/s (which amounts for 25% of their cruising velocity) are exposed to sudden flight parameter changes, the angles of attack and slip, in particular. At strong gusts of wind, the disturbance velocity reaches values comparable to the flight velocity. This issue has been reviewed in, among others, the publications [1,2,3]. In average weather conditions, the changes of attack angle are sudden, and their amplitude amounts from +60° to −30°. The velocity changes from 20 to 130 km/h, and the altitude from 250 to 25 m [3]. This is why there was a need to analyse the dynamic properties of micro aerial vehicles over the entire operational range, including the range of near-critical and super-critical angles of attack. Due to the high non-linearity of the differential equations describing flight dynamics, well-developed and described methods of modal analysis cannot be applied in this case. There was a need to develop a new method for testing aircraft motion stability, which would enable studying its dynamic properties throughout the entire range of usable angles of attack and slip. In the second half of the 20th century, researchers suggested a continuation method based on the bifurcation theory that enabled analysing dynamic properties of an aircraft, over a wide range of flight states. Articles on this matter, published in the 1970s include: [4,5]. The cited research work concerned the analysis of a fast inertial barrel roll and spin. Numerous studies devoted to the bifurcation analysis of aircraft flight dynamics and aerodynamics appeared in the 1970s, 80s and 90s. These include the AGARD report from 1985 [6], and many papers on the issues of non-stationary aerodynamics and non-linear dynamics of flight in the perspective of the dynamical system theory and the bifurcation theory: [7,8,9,10,11,12,13,14].

The dynamical system theory enabled a global analysis of a system of strongly non-linear ordinary differential equations describing the state of a dynamical system, and in this aspect it is a generalization of the aforementioned dynamic stability analysis involving a steady straight flight of an aircraft. The first step in this method is the assessment of quasi-steady state stability. The quasi-steady state is determined by equating the derivatives of state vector to zero and solving a system of non-linear algebraic equations. The local stability of a dynamical system can be assessed based on the Hartman-Grobman [15] theorem. This stability is determined by the eigenvalues of a locally linearised equations of MAV flight dynamics. In our case, this system is linearized around the equilibrium position, [7,8,9,10,11,12,13,14]. If even one of eigenvalues has a positive real part, then the equilibrium position is unstable. It can be proved that if a linearized equation system is non-singular, then the steady state of a dynamical system is a continuous function of state parameters [15]. It can also be proved that steady states of differential equations describing an aircraft motion are continuous functions of rudder surface deflections [16]. Stability changes occur when at least one eigenvalue of a locally linearized differential equation system of aircraft motion changes its sign. The changes in the steady state stability lead to a qualitatively various system response and are called bifurcations. Stability limits can be determined through searching for eigenvalues with zero real zero part [17,18]. In the bifurcation theory, the stability of quasi-steady states is tested as a function of the so-called bifurcation parameters [15,19,20]. The usual assumption in the course of a flight dynamics bifurcation analysis is that such parameters are the rudder surface deflections within the range of change from the minimum to the maximum value of these angles. It enables obtaining an image of all steady states (or quasi-steady) of aircraft motion. The source literature often refers to this computation process as “global analysis” (cf. work [10,12,21,22,23,24,25,26,27,28,29]). This is why, this type of aircraft flight analysis will be called a “global analysis of equilibrium position stability”. Of course, classic states defining the stability of a steady and straight micro aerial vehicle flight are one of the points determined in the course of a global analysis of equilibrium position stability. In this perspective, this analysis is a generalization of the classical aircraft stability analysis.

This article presents the application of bifurcation analysis, complemented with time-domain simulations, to understand the open-loop dynamics of strake-wing micro aerial vehicle model by identifying the attractors of the dynamic system that manages upset behaviour. A number of factors have been identified to cause potential critical states, including non-oscillating spirals and oscillatory spins. The analysis shows that these spirals and spins are connected in a one-parameter space and that due to improper operation of the autopilot on the spiral, it is possible to enter the oscillatory spin.

The Cobra maneuver was also studied from the point of view of the bifurcation theory and the results of the time histories of the flight parameters during this maneuver were presented.

2. Bifurcation and Continuation Analysis

A bifurcation can be defined as a qualitative change in the system dynamics as a parameter is varied. In flight dynamics, a qualitative change is usually understood as a change in the stability of the aircraft. Bifurcation analysis and continuation methods are based on the principles of the dynamical system theory. The basis of the dynamical systems theory are described in many books (it can be mention here: [15,16,17,20,30,31]). These methods consist in finding and tracking solutions numerically, in a selected range of parameters, in order to generate bifurcation diagrams. Bifurcation diagrams allow to identify qualitative changes in the dynamic response of the system.

2.1. Bifurcation Theory and Bifurcation Types

In our case bifurcation analysis is applied to autonomous dynamical system of general form:

$$\dot{x}=f(x,\mu )$$

(1)

where $x\in {\Re }^n$ is vector of n state variables, $\mu \in {\Re }^m$ is vector of m control parameters, f is nonlinear vector field governing system dynamics. The bifurcation for Equation (1) is every qualitative change of the phase portrait occurring upon the passage of parameter µ through a certain point µ₀. Point µ₀ is called the bifurcation point for Equation (1). By establishing the set of parameters $\mu ={\mu }_0$ and selecting the initial conditions x(t = 0) = x₀, the system of differential Equation (1) can be integrated for the selected initial condition. In this way, one can study the evolution of vector field x over time. In order to thoroughly study the dynamics of the system, this process can be repeated an infinite number of times starting from different initial conditions and for an innumerable fixed combination of parameter values µ. This task is exhausting and tedious. The major problem in this exercise is the selection of initial conditions, which is a non-trivial task when dealing with systems that are nonlinear. An alternative and more efficient approach to the analysis of nonlinear dynamical systems described by Equation (1) is based on the asymptotic bifurcation and continuation method. The bifurcation and continuation method begins with the calculation of steady states of the equilibrium type of the Equation (1), which comes down to solving a system of nonlinear algebraic equations:

$$\dot{x}=0 \to f(x,\mu )=0$$

(2)

and computing the eigenvalues of the Jacobi matrix:

$$J=\frac{\partial f}{\partial x}$$

(3)

in each equilibrium state. The numerical scheme for solving both problems is called the continuation algorithm. It is an algorithm of the predictor-corrector type. A continuation algorithm is used to solve the system of Equation (2) as a function of a single parameter of the system $\mu \in \mu$. In other words, the task comes down to determining the zeros of family $f:{\Re }^n\to {\Re }^n$, namely, to determine the solutions to stationary, non-linear algebraic Equation (2). The dimension of the µ parameter vector is called the bifurcation dimension. For a one dimensional case µ ≡ µ∈ ℜ¹.

The bifurcation theory concerning non-linear ordinary differential equations deals with a system of first-order differential Equation (1), which is a mathematical model of a dynamical system in an n-dimensional Euclidean space ℜⁿ. If the system (1) has asymptotically stable stationary solutions x=0, then for all solutions x(0) belonging to this neighbourhood:

-

trajectory x(t) fulfils the condition: |x(t)| < ε for t > 0;

-

|x(t)| → 0 for t → ∞.

Solving the problem involves finding answers to the question of how a parameter change μ ∈ μ locally affects the neighbourhood of point x = x₀. Due to the fact that for all μ the Equation (2) is satisfied, and Equation (1) can be expressed as:

$$\dot{x}=Rx+\sigma \left(x,\mu \right)$$

(4)

where in R is a square characteristic matrix (Jacobian matrix) with elements provided by the equation:

$${\left[R\right]}_{ i,j}=\frac{\partial f_i\left(x_0,\mu \right)}{\partial x_j},$$

(5)

and non-linear vector function σ fulfils the conditions:

$$\sigma \left(x_0,\mu \right)=0,\frac{\partial {\sigma }_i\left(x_0,\mu \right)}{\partial x_j}=0.$$

(6)

and finally:

$$\dot{x}=Rx$$

(7)

The Hartman-Grobman theorem applies within the process of studying the stability of a stationary solutions to equation [15,16,19,20]. It states that if all eigenvalues of a Jacobian matrix R of a linearized system (1) lie in the left complex half-plane, i.e.,

$$\mathrm{Re}\left({\lambda }_j\right)<0,i=1,2,\dots ,n$$

(8)

then there is a certain continuous, homomorphic transformation of variables reducing a locally non-linear system of Equation (1) to a linear system. This means that if a stationary solution to a linearized system of equations is asymptotically stable, then also the solution to a non-linear system is stable. The Hartman-Grobman theorem also indicates that every qualitative change in the nature of solutions to a system of non-linear equations describing a dynamical system is indicated by the appearance of zero real parts of the eigenvalues of a linearized system characteristic matrix R.

In mathematical terms, bifurcation of equilibrium positions takes place, when a eigenvalue of Jacobi matrix (3), (5) of system (1), estimated in the state of equilibrium, intersects the imaginary axis. Similarly, in the case of an oscillating solution, bifurcation occurs when the Floquet multiplier intersects the unit circle. The results shown in this article discuss five bifurcation types; they all have a codification of one, which means that they are encountered when a single continuation parameter changes.

Basic bifurcation types are [32]:

A.

A saddle-node bifurcation, also called a saddle limit point, occurs when the real eigenvalue of a Jacobian matrix (5) estimated in a state of equilibrium, intersects the imaginary axis. There is no equilibrium on one side of the bifurcation point (locally), whereas there are two equilibrium branches on the other (e.g., one stable and one unstable) (Figure 1).

B.

Hopf bifurcation occurs, when a complex pair of Jacobian (5) eigenvalues, assessed at equilibrium, intersect the imaginary axis. In this case, the equilibrium changes stability and a periodic orbit is formed, which can be stable or unstable (Figure 1).

C.

The limit point or periodic orbit fold bifurcation occur when the real Floquet multiplier intersects the unit circle at 1; as for the states of equilibrium, then there are no periodic orbits on one side of the bifurcation (locally), whereas there are two periodic orbits on the other (Figure 1).

D.

A period-doubling bifurcation occurs when the real Floquet multiplier intersects the unit circle at −1. The periodic orbit loses stability when a new period orbit appears with a period (approximately) twice as long (Figure 1).

E.

The Neimark-Sacker bifurcation or torus bifurcation appears, when the periodic orbit becomes unstable, namely, when a pair of complex Floquet multipliers intersects the unit circle and an additional oscillation frequency is introduced. The outcome is a torus dynamic, which can be periodic (blocked) or quasi-periodic (Figure 1).

To sum up, it can be concluded that:

The bifurcation theory is a set of mathematical results aimed at analysing and explaining unexpected modifications in the asymptotic behaviour of non-linear systems of differential equations, when their parameters slowly change.

Starting from the asymptotic state approximation, for a set value of bifurcation parameters, the computer code, in the course of a continuation process, determines curves for the solution of x(μ), which constitute a set of solutions to non-linear algebraic equations (2). In the case of each of the points of the solutions to system (2) and (7), the stability of solutions is determined:

$$\{\begin{array}{l}\mathrm{Equilibrium} \mathrm{points}: f\left(x,\mathit{\mu }\right)=0\hfill \\ \begin{array}{l}\mathrm{Limit} \mathrm{points}: f\left(x,\mathit{\mu }\right)=0\\ \mathrm{and} \mathrm{at} \mathrm{least} \mathrm{one} \mathrm{of} \mathrm{eigenvalues}: \mathit{\lambda }=0 \end{array}\hfill \\ \begin{array}{l}\mathrm{Hopf} \mathrm{points} : f\left(x,\mathit{\mu }\right)=0\\ \mathrm{and} \mathrm{at} \mathrm{least} \mathrm{Re}\left({\mathit{\lambda }}_{ij}\right)=0 \mathrm{of} \mathrm{pair} \mathrm{of} \mathrm{complex} \mathrm{eigenvluwes}: {\mathit{\lambda }}_{ij}=\pm 2i\mathit{\pi }/T\end{array}\hfill \\ \mathrm{Periodic} \mathrm{orbits}: x\left(T\right)=x\left(0\right)+{\displaystyle {\int }_0^T\mathrm{f}\left(x,\mathit{\mu }\right)dt}\hfill \end{array}$$

(9)

The continuation process assumes that all functions of the system of Equation (2) are continuous and differentiable.

Summarising, the numerical continuation methods are a set of tools that enables obtaining information required to conduct bifurcation analyses. These methods utilize the predictor-corrector technique for finding, tracking and constructing equilibrium curves or periodic orbits of a differential Equation (1), as solutions of a properly defined system of algebraic Equation (2). Information on the stability is calculated based on analysing the J eigenvalues of Jacobian matrix (5) for equilibrium states, or based on Floquet multipliers (in the case of periodic orbits). Bifurcations can be detected, as well as tracked at various bifurcation parameter values.

2.2. Continuation Software

Numerical methods for solving bifurcation problems appeared relatively recently and complement the analytical achievements in this field. The following fundamental difficulties encountered when applying these methods can be distinguished:

-

numerical instabilities associated with calculations in close proximity to bifurcation points,

-

issues related to parametrization in close proximity to bifurcation points and limit points,

-

structures of bifurcation branches,

-

determination whether bifurcation actually takes place,

-

problems associated with the convergence of the Newton-Raphson method at singular points.

The system of Equation (2) can have numerous solutions. These can be isolated solutions and they may not exist at all. There is no theory, which could be used as a base to determine which case you are dealing with. Therefore, this issue is quite challenging, because when using numerical methods, the question whether all solutions have already been found still stands. Among the many methods, the ones applied the most when the f functions are smooth is the Newton-Raphson method.

At the time, there are several software packages available, which are designed to analyse non-linear dynamical systems, e.g., MatCont [33,34] or KRIT [35]. The most recognizable computer program designed for bifurcation analysis of non-linear dynamical systems is the one developed at the Canadian Concordia University, by a team led by Prof. Eusebius Doedel, the AOTO97 package—program developed in the FORTRAN language and AUTO2000—developed in the C language. The latest (as of 2021) version of these packages is the AUTO07P [36]. The description of subsequent versions of the AUTO package can be found in: [37,38,39]. AUTO07P was developed in the FORTRAN language, for the UNIX operating system environment. A team at the University of Pittsburgh in America, led by prof. Bard Ermentrout, developed XPPAUT [40], which is a version of the AUTO package compatible with the WINDOWS system. A comprehensive description of this package, together with a manual, can be found in the textbook by prof. Bard Ermentrout [41]. A MATLAB system toolbox—Dynamical System Toolbox [42] was also created based on the AUTO [43].

The best-known program designed for the bifurcation analysis of homogeneous ordinary differential equations is that developed by a team lead by Prof. Doedel from the Canadian Concordia University called AUTO. Differential equations describing MAV flight dynamics were analysed using an AUTO version implemented in MATLAB (Dynamical System Toolbox [42]).

3. Micro Aerial Vehicle Mathematical Model

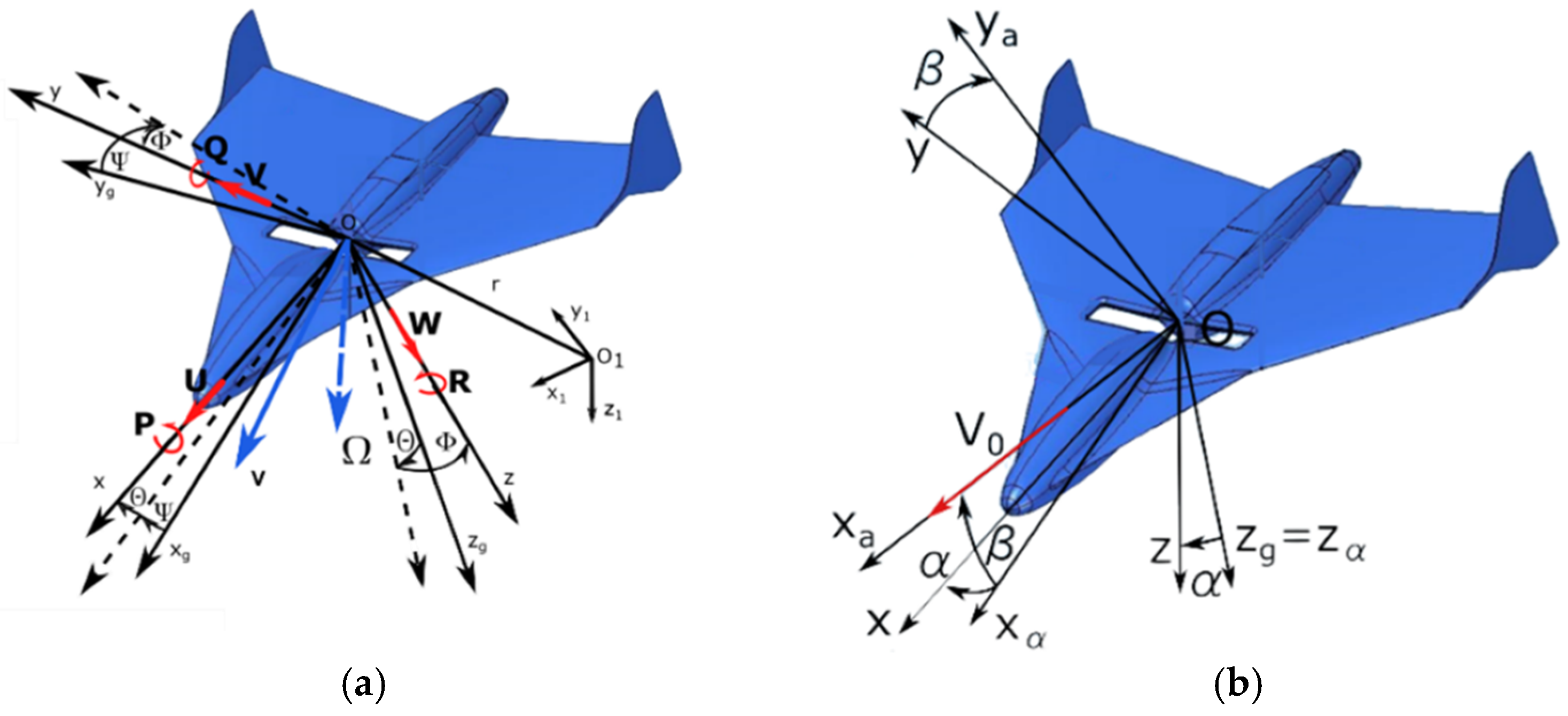
3.1. Reference Frames

Coordinate systems rigidly associated with the object (MAV for example) or associated with the inflow of air streams, and their combinations are usually selected to represent motion equations in aviation. Figure 2 shows coordinate systems, used to derive aircraft motion equations. Details of deriving aircraft motion equations can be found in numerous textbooks and monographs (e.g., [44,45,46,47,48,49]), which is why will not discuss them in this work. Below you can find micro aerial vehicle motion equations expressed in a so-called-semi constrained coordinate system. This means that centre of mass motion equations are written within a velocity system of coordinates (Figure 2b), while the equations of MAV spherical motion relative to the centre of mass are written within a system related to MAV axes of inertia.

3.2. Equations of Motion

In the course of implementing a mathematical dynamics model of an aircraft into MATLAB Dynamical System Toolbox, it is more convenient to present aircraft centre of mass motion equations in a velocity coordinate system Ox_ay_az_a (Figure 2) [49]. Furthermore, the equations omitted the aircraft yaw (heading) angle Ψ and the aircraft centre of mass position relative to the system related to the Earth, since these values do not influence the dynamic properties of an aircraft [25]. This enabled the state vector dimension to be reduced to eight components:

$$x={\left[V,\alpha ,\beta ,P,Q,R,\mathsf{\Theta },\mathsf{\Phi }\right]}^T$$

(10)

where:

V  flight velocity,

α  angle of attack

β  slip angle,

P  banking angular velocity,

Q  pitching angular velocity,

R  yawing angular velocity,

Θ  pitch angle,

Ф  bank angle.

In the general case of bifurcation analysis of aircraft flight dynamics, the components of the vector of bifurcation parameters m may be the control surface deflection angles (aileron, elevator, rudder, thrust) and other parameters such as the position of the center of gravity. In this particular case of bifurcation analysis of strake-wing microdrone flight dynamics, the bifurcation parameters vector has following form:

$$\mu ={\left[T,{\delta }_e,{\delta }_{elv}\right]}^T$$

(11)

where:

T  propeller thrust

δ_e  angle of symmetrical elevon deflection

δ_elv  angle of asymmetrical elevon deflection,

The general form of the micro-airplane motion equations takes the form of autonomous differential Equation (1). Components of vector f have the form [44,45,46,47,48]:

$$\begin{array}{cc}\hfill f_1& =\frac{1}{m}\left[T\cos \alpha -P_{X_a}\right]-g\left[\cos \Theta \sin \Phi \sin \beta -(\sin \Theta \cos \alpha -\cos \Theta \cos \Phi \sin \alpha )\cos \beta \right]\hfill \\ \hfill f_2& =Q-(P\cos \alpha +R\sin \alpha )\tan \beta +\hfill \\ & -\frac{1}{m{V}_0\cos \beta }\left[T\sin \alpha +P_{Z_a}-mg(\sin \Theta \sin \alpha +\cos \Theta \cos \Phi \cos \alpha )\right]\hfill \\ \hfill f_3& =P\sin \alpha -R\cos \alpha -\frac{1}{mV}\left[T\cos \alpha -mg(\sin \Theta \cos \alpha -\cos \Theta \cos \Phi \sin \alpha )\right]\sin \beta +\hfill \\ & -mg\cos \Theta \cos \Phi \cos \beta -P_{Y_a}\}\hfill \end{array}$$

(12)

$$\begin{array}{l}{f}_4=\left(\frac{J_X-J_Z}{J_X}-\frac{J^2{}_{XZ}}{J_X{J}_Z}\right)\frac{QR}{D}+\left(1-\frac{J_Y-J_X}{J_Z}\right)\frac{J_{XZ}PQ}{J_{X}D}+\\ +\frac{qSb}{J_{X}D}\left\{C_{l_0}\left(\alpha ,\beta \right)+\frac{\partial C_l}{\partial \overline{R}}\frac{\overline{R}b}{2V_0}+\frac{\partial C_l}{\partial {\delta }_{elv}}{\delta }_{elv}+\left[\frac{\partial C_l}{\partial \overline{P}}+\left(\frac{{\partial }^2{C}_l}{\partial \overline{P}\partial \beta }\beta +\frac{{\partial }^2{C}_l}{\partial {\overline{P}}^2}\frac{\overline{P}b}{2V_0}\right)\right]\frac{\overline{P}b}{2V_0}\right\}+\frac{L_T}{J_{x}D}+\\ +\frac{J_{XZ}qSb}{J_X{J}_{Z}D}\left\{C_{n_0}\left(\alpha ,\beta \right)+\frac{\partial C_n}{\partial \overline{R}}\frac{\overline{R}b}{2V_0}+\frac{\partial C_n}{\partial {\delta }_{elv}}{\delta }_{elv}+\left[\frac{\partial C_n}{\partial \overline{P}}+\left(\frac{{\partial }^2{C}_n}{\partial \overline{P}\beta }\beta +\frac{{\partial }^2{C}_n}{\partial \overline{P}\beta }\frac{\overline{P}b}{2V_0}\right)\right]\frac{\overline{P}b}{2V}\right\}+\frac{J_{xz}{N}_T}{J_x{J}_{z}D}\\ f_5=\frac{qS{c}_A}{J_Y}\left\{C_{m_0}\left(\alpha ,\beta \right)+\frac{\partial C_m}{\partial \dot{\alpha }}\frac{1}{V_0}+\frac{\partial C_m}{\partial \overline{Q}}\frac{\overline{Q}{c}_A}{2V_0}+\frac{\partial C_m}{\partial {\delta }_e}{\delta }_e\right\}+\frac{M_T}{J_Y}+\frac{J_Z-J_X}{J_Y}QP+\frac{J_{XZ}}{J_Y}\left(R^2-P^2\right)\\ f_6=\left(\frac{J^2{}_{XZ}}{J_X{J}_Z}-\frac{J_Y-J_X}{J_Z}\right)\frac{PQ}{D}+\left(\frac{J_Y-J_Z}{J_X}-1\right)\frac{J_{XZ}QR}{J_{Z}D}+\\ +\frac{J_{XZ}}{J_X{J}_Z}\left\{C_{l_0}\left(\alpha ,\beta \right)+\frac{\partial C_l}{\partial \overline{R}}\frac{\overline{R}b}{2V_0}+\frac{\partial C_l}{\partial {\delta }_{elv}}{\delta }_{elv}+\left[\frac{\partial C_l}{\partial \overline{P}}+\left(\frac{{\partial }^2{C}_l}{\partial \overline{P}\beta }\beta +\frac{{\partial }^2{C}_l}{\partial {\overline{P}}^2}\frac{\overline{P}b}{2V_0}\right)\right]\frac{\overline{P}b}{2V_0}\right\}+\frac{J_{XZ}{L}_T}{J_X{J}_Z}+\\ +\frac{qSb}{J_{Z}D}\left\{C_{n_0}\left(\alpha ,\beta \right)+\frac{\partial C_n}{\partial \overline{R}}\frac{\overline{R}b}{2V_0}+\frac{\partial C_n}{\partial {\delta }_{elv}}{\delta }_{elv}+\left[\frac{\partial C_n}{\partial \overline{P}}+\left(\frac{{\partial }^2{C}_n}{\partial \overline{P}\beta }\beta +\frac{{\partial }^2{C}_n}{\partial \overline{P}\beta }\frac{\overline{P}b}{2V_0}\right)\right]\frac{\overline{P}b}{2V}\right\}\end{array}$$

(13)

$$\begin{array}{l}{f}_7=P+Q\sin \Phi \tan \Theta +R\cos \Phi \tan \Theta \\ f_8=Q\cos \Phi -R\sin \Phi \end{array}$$

(14)

where:

$D=1-\frac{J^2{}_{XZ}}{J_X{J}_Z}$,

$q=\frac{1}{2}\rho V_0^2$ is the dynamic pressure,

$\overline{P}=\frac{bP}{2V_0}, \overline{Q}=\frac{c_{A}Q}{2V_0}, \overline{R}=\frac{bP}{2V_0}$ are dimensionless angular velocities.

The aerodynamic characteristics of the “Bee” MAV shown in Figure 3 were identified based on aerodynamic water tunnel testing. The static and dynamic aerodynamic loads were measured using a five-component aerodynamic balance. The testing was conducted over a wide range of angles of attack and slip. A wide description of these tests can be found in the works [49,50]. The identified aerodynamic characteristics presented in the work [Sibilski et al.] were shown in the form of graphs and were available in tabular form. Examples of aerodynamic derivative waveforms are shown in Figure 4.

The linear interpolation of aerodynamic data tables commonly used in simulation studies, due to the lack of derivative continuity, cannot be used in the case of continuation tests, since the continuation software of the AUTO type can misidentify bifurcation points. This is why a different method for interpolating aerodynamic data had to be used. Smooth, differentiable state parameter function were created as a result of interpolating aerodynamic characteristics. The pchip function interpolation in the MATLAB software was used for this purpose, while maintaining linear interpolation and a multi-variative orthogonal function. Block interpolation was also implemented using a 3rd-order spline function. Owing to the structure of the “Bee”, which only has elevons, the bifurcation parameters were the elevon deflection angles: δ_e and δ_elv.

4. Methodology of Bifurcation Tests in Aircraft Flight Dynamics

MAV motion is described through a system of highly non-linear ordinary differential equations. For a classical model of a non-deformable micro aerial vehicle with movable control surfaces, motion equations are presented by relationships (1), (12), (13), and (14).

The dynamical system theory enables analysing solutions to a system of highly non-linear ordinary differential equations describing aircraft motion, depending on slow parameter changes (so-called bifurcation parameters). When analysing aircraft flight dynamics, it is assumed that the bifurcation parameters are the control vector components (i.e., deflection angles of the elevator, rudder, ailerons, thrust vector, etc.). The first stage in the analysis of a non-linear system of differential equations in the dynamical system theory is assessing the stability of steady states of a system of differential equations describing aircraft flight dynamics (1), (12), (13), and (14). The steady state is determined by equating the derivatives to zero and solving a system of algebraic Equation (2).

Given the experience from numerous research (based on the bifurcation analysis and continuation technique), the following, three-stage test diagram for a non-linear aircraft motion was formulated [8,9,10,11,12,13,14,18,21,22,23,24,25,26,27,28,34,48,49,51,52,53,54,55,56]

• The first stage involves determining all parameters of a dynamical system. The fundamental task is to study all possible equilibrium states and periodic orbits, and the analysis of their local stability. This test should be very thorough. The outcome of the attempted test should be a determined global structure of the state space (e.g., phase portraits) of all discovered attractors (steady states and closed orbits). Approximated graphic representations of the calculations are crucial in this case, since they enable diagnosing the obtained results.
• The second stage involves, based on information on the evolution of phase portraits together with parameter changes, predicting dynamical system behaviour. Next, based on the knowledge on the type of present bifurcations and the current position of system parameters relative to stable areas, further aircraft behaviour is predicted. Information on the range of parameter changes is also important for these analyses and predictions. Rapid parameter changes and higher differences between steady and transient states are also observed.
• The third step involves a numerical simulation, which enables verification of the expected aircraft behaviour. Waveforms of transient system characteristics for significant state parameter changes upon a dynamical system parameter change are obtained.

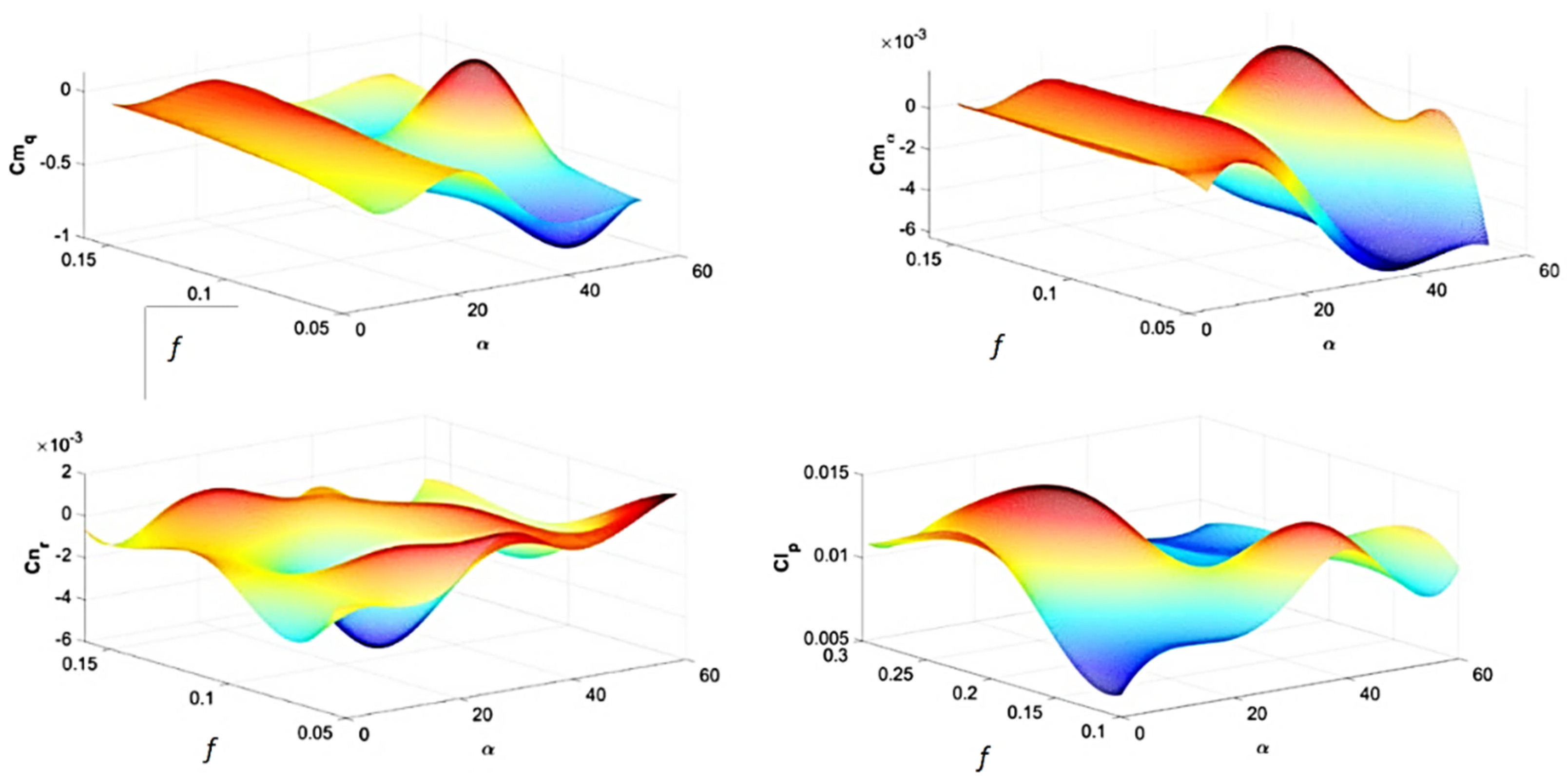
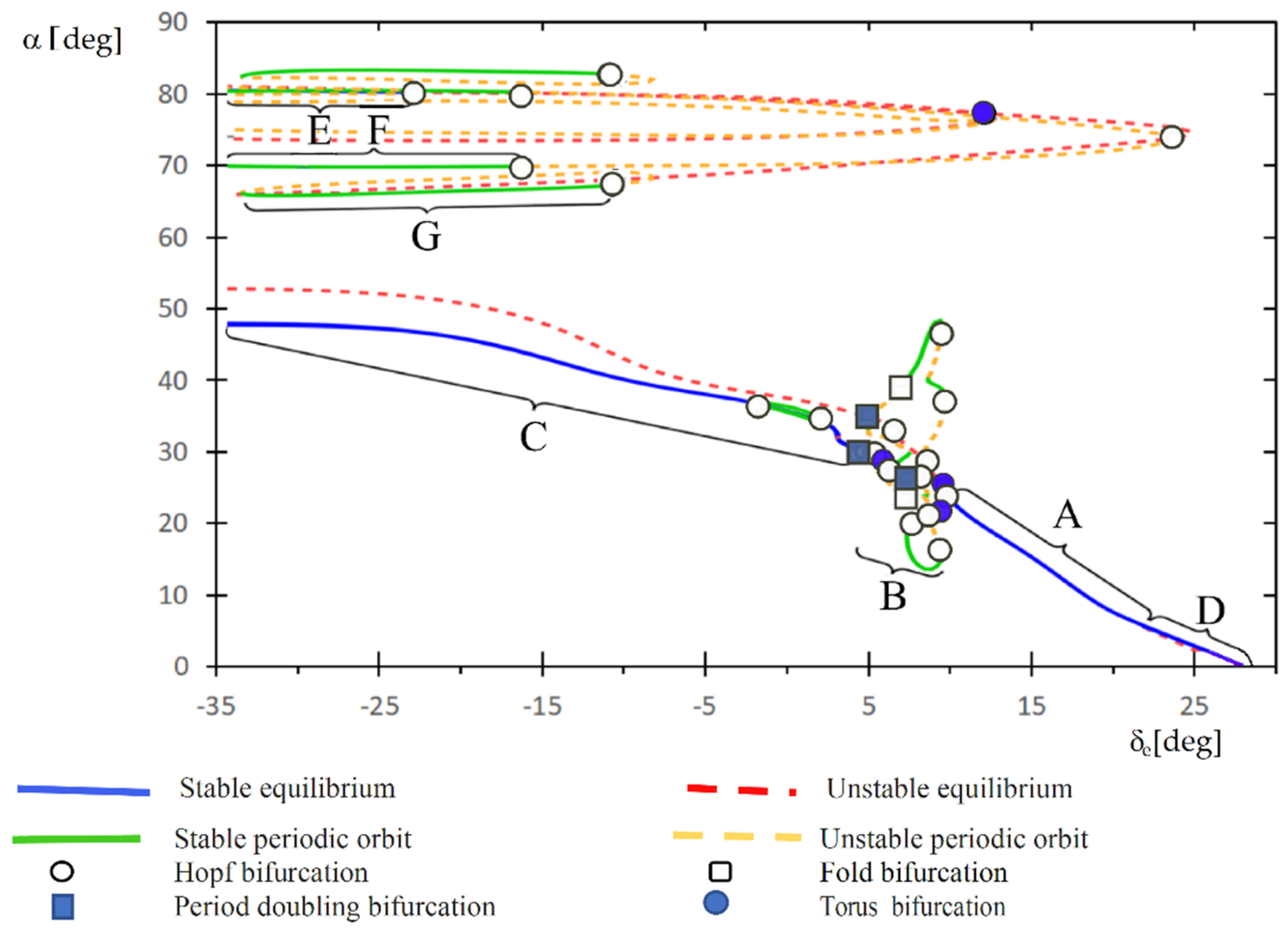
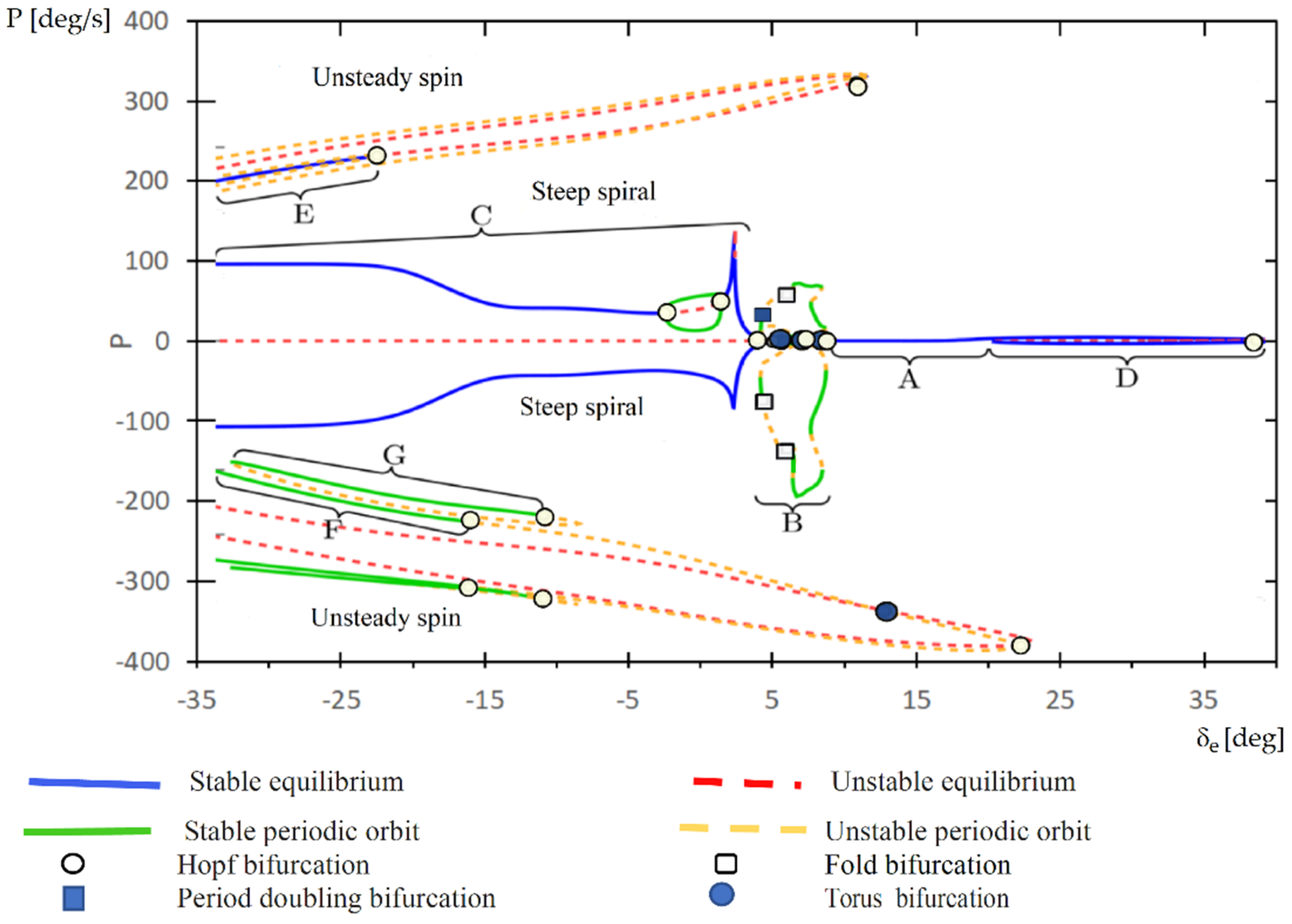
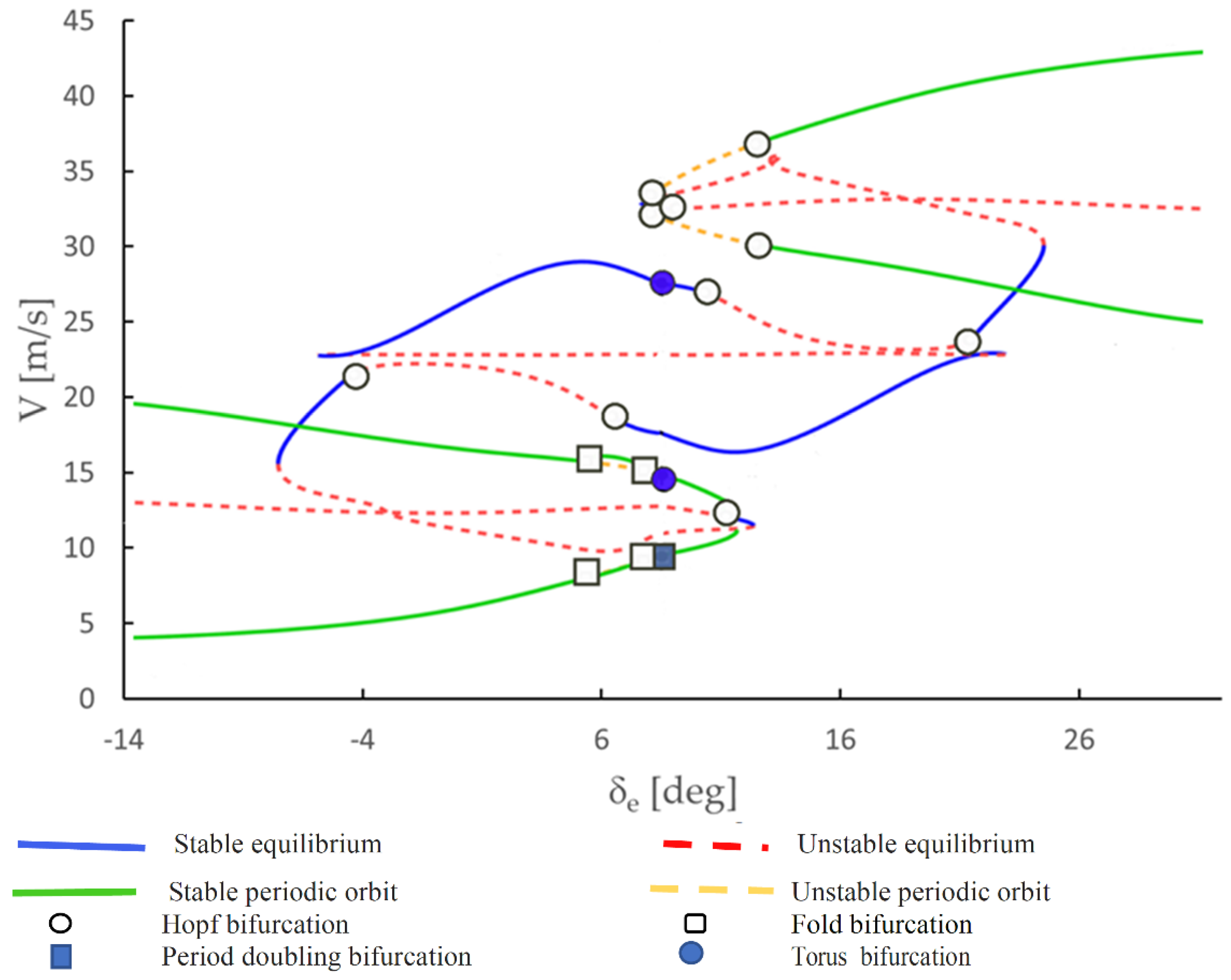
5. Bifurcation Flight Dynamic Analysis of a Micro Aerial Vehicle

Figure 5 and Figure 6 show single-parameter bifurcation diagrams for equilibrium positions: angles of attack α and angular velocity of banking P for different values of the bifurcation parameter, namely, elevator deflection angles δ_e from a range of δ_e ∈ (−35°, 30°) for angles of attack equilibrium position, δ_e ∈ (−35°, 40°) for banking angular velocity equilibrium positions. Figure 5 shows enlarged bifurcation diagrams for elevator deflections in the range of δ_e ∈ (3°, 10°), corresponding to steady states at low and moderate angles of attack for α ∈ (0°, 54°), the second area corresponds to a range of high angles of attack α ∈ (65°, 83°). Various types of micro aerial vehicle dynamics, corresponding to seven flight regimes, can be classified in these areas. These regimes are marked with the letters A to G. Regime A means steady symmetrical flight equilibrium states, for angles of attack in the range of α ∈ (2°, 23°). Area B, for angles of attack in the range of α ∈ (15°, 50°), corresponds to various motion states with stable and unstable orbits. Area C, for angles of attack in the range of α ∈ (35°, 55°), corresponds to deep steady spirals. Area D corresponds to inverted spirals. Area E corresponds to steady spins. Areas F and G correspond to transient spins.

The aircraft equilibrium positions in each of these two areas were analysed depending on the bifurcation parameter, namely elevator deflection angles (symmetrical elevon deflections) δ_e and asymmetrical elevon deflections δ_elv. During continuation tests, following the methodology described in Section 4, it was assumed that the propeller thrust does not change, and elevon deflections are only symmetrical (or δ_elv = 0). Continuation analyses were conducted for positive and negative changes in the bifurcation parameter (symmetrical elevon deflections δ_e), starting with δ_e = 20°. The calculations were conducted for the elevator deflection angle range of change of −35° ≤ δ_e ≤ 40°, so that it was possible to detect almost all solutions corresponding to the quasi-steady flight states.

At the starting point of the continuation analysis (δ_e = 20°, α = 3°), the aircraft was conducting a steady symmetrical flight. As the elevator deflection angle changed, the elevator angle of attack initially increased, and the deflection angular velocity remained at zero. This dynamic regime was denoted with the letter A. Its corresponding range of angles of attack is 2° < α < 25° (Figure 5 and Figure 7). The range of steady states denoted with the letter A corresponds to a symmetrical flight of the MAV (angular velocity P = 0). When the elevator deflection angle decreases below δ_e≈10 and the angle of attack α ≈ 28 degrees, the micro aerial vehicle enters the dynamics regime denoted with the letter B, with both anti-symmetrical, as well as symmetrical motions. They can be associated with unstable Dutch roll, wing-rock oscillations, spiral motion instabilities, as well as unstable phugoids. Ant-symmetrical oscillations result from Hopf bifurcations in B. In this area, when the elevator deflection angle continues to decrease, reaching a value of δ_e ≈ 4° and α ≈ 34°, the spiral mode loses stability, which leads to the bifurcation of the stable and almost symmetrical solution. Two asymmetrical equilibrium position branches appear. At higher angles of attack, the spiral model becomes unstable along the almost symmetrical solution branch.

Development of equilibrium position asymmetry can be observed at continued reduction in the elevator deflection angle, and at δ_e ≈ 4°, the micro aerial vehicle enters the range of equilibrium states marked with C, which corresponds to spiral motions with a high amplitude of bank angles (Figure 7). Stable position branches corresponding to spiral motions exist on both sides of the straight line defining unstable horizontal flight equilibrium positions. Due to the aerodynamic load asymmetry, the micro aerial vehicle banks to the left wing (with a negative banking angular velocity P), since the equilibrium branch representing the breaking away is connected with A (Figure 6). The equilibrium branch representing rightward MAV banking is practically detached from branch A. The bifurcations therein lead to the appearance of unstable equilibrium positions, where P ≈ 0 [°/s]. However, it should be noted that the spiral motion direction is determined in practice by the nature of the disturbance or the transient dynamics state of a micro aerial vehicle. As shown in Figure 5 and Figure 6, equilibrium branches of dynamics regime C (within the physical range of elevator deflections), do not converge on the straight line corresponding to the horizontal flight conditions. The MAV will remain at one of two spiral branches only up to a value of δ_e = −35°. Branch C, shown on the bifurcation diagrams (Figure 5 and Figure 6), also represents undesirable steep spirals. Steep spirals can be deemed undesirable flight conditions, therefore, it is important to determine a recovery strategy. Based on a bifurcation diagram (Figure 5), a micro aerial vehicle can be easily recovered from such a flight state by reducing the angle of attack to a level below which no spiral branches are formed. This can be achieved by increasing the elevator deflection angle. The ability to find and determine branches, such as steep spirals, stresses the advantage of continuation and bifurcation analyses over classical linear methods. Although classical linear methods for analysing flight stability can identify stability changes, they are unable to find stable and unstable branches of quasi-steady flight states (Figure 8).

The slight lateral instability is also present at low angles of attack (α ≤ 2°), (branch D in Figure 5 and Figure 6). In the case of the bifurcation analysis and continuation test pattern in question, which assumes constant thrust, flight velocity reaches the highest and not always realistic values at low, negative angles of attack, which entails an increase in the negative angle of MAV pitch, until inverted flight conditions. Thus, although regime D can be deemed an inverted spiral, it is not representative for realistic flight conditions and will not be discussed in more detail (Figure 8).

Equilibrium positions of quasi-steady flight states also appear at high angles of attack 65° < α < 85° (bifurcation diagrams shown in Figure 5 and Figure 6). There are unstable equilibrium position branches for negative deflection angular velocities and angles of attack within a range of 80° < α < 85°, and elevator deflections angles in the range of −35° < δ_e < 10°. There is a certain area of stable equilibrium positions for positive values of deflection angular velocity. The differences arise from the asymmetry of MAV loads. Left- and right-handed spins differ in terms of the state of equilibrium of inertial and aerodynamic forces, which undoubtedly impacts the local stability of spin branches (just as in the case of lower angles of attack α). Stable equilibrium positions, corresponding to spins executed at a constant angular velocity, are represented by branch E of the bifurcation diagrams. It can be seen that there is also a slight area of stable spins near the elevator deflection angle of ${\delta }_e\approx {12}^{\mathrm{o}}$. The waveform of flight parameters indicates that attractors are present within branch E, hence, this equilibrium branch does not play a significant role in the dynamics of disturbed spins [26,27].

For an angle of attack range of 65° < α < 85°, most equilibrium positions are unstable. There can be no steady spins on unstable branches, while one can expect solutions of deterministic chaos nature on these branches [13]. The spin dynamics is significantly impacted by two Hopf bifurcations present at δ_e = 23.4° and δ_e = −13.2° and a period-doubling bifurcation present at δ_e = 12.5°. All three bifurcations appear for angles of attack of α > 65°. In the case of an elevator deflection angle of δ_e = −13.2°, the periodic orbits created through the Hopf bifurcation are unstable throughout the entire range of bifurcation parameters. The period-doubling bifurcation appearing at δ_e = 12.5° can lead to a spin of chaotic nature [13]. The periodic orbit created through Hopf bifurcation at δ_e = 23.4° is more significant. It is initially unstable and then branches into a stable periodic orbit through the torus bifurcation at δ_e = −15.9°. The stable periodic orbit of branch F (Figure 5) is significant, since in this case, the average angle of attack is α ≈ 70°, with high values of deflection angular velocities. Therefore, it can be concluded that branch F corresponds to steep oscillation spin states. It can also be inferred that MAV oscillation spins occur at angles of attack of approximately 70°. Also, a second stable periodic orbit can be identified on branch G (Figure 6) within the range of high angles of attack. This solution is true for a closed curve that is not connected with other curves. It is the outcome of torus bifurcation present on branch F (for δ_e = −15.9°). Due to torus bifurcations, the periodic orbit becomes unstable, and MAV flight dynamics equation solutions are attracted by branch G periodic orbit. Solutions to micro aerial vehicle motion equations over branch G represent more rapid, oscillation spins, relative to branch F solutions [26,27].

6. Numerical Verification of Predicted MAV Behaviour

According to the bifurcation test methodology, the third step in continuation analysis involves numerical simulations, which enable verifying the predicted aircraft behaviour. Waveforms of transient system characteristics for significant state parameter changes upon a dynamical system parameter change are obtained. Examples of “wing rock” oscillation, unsteady spin and the “Cobra” manoeuvre simulations are shown below.

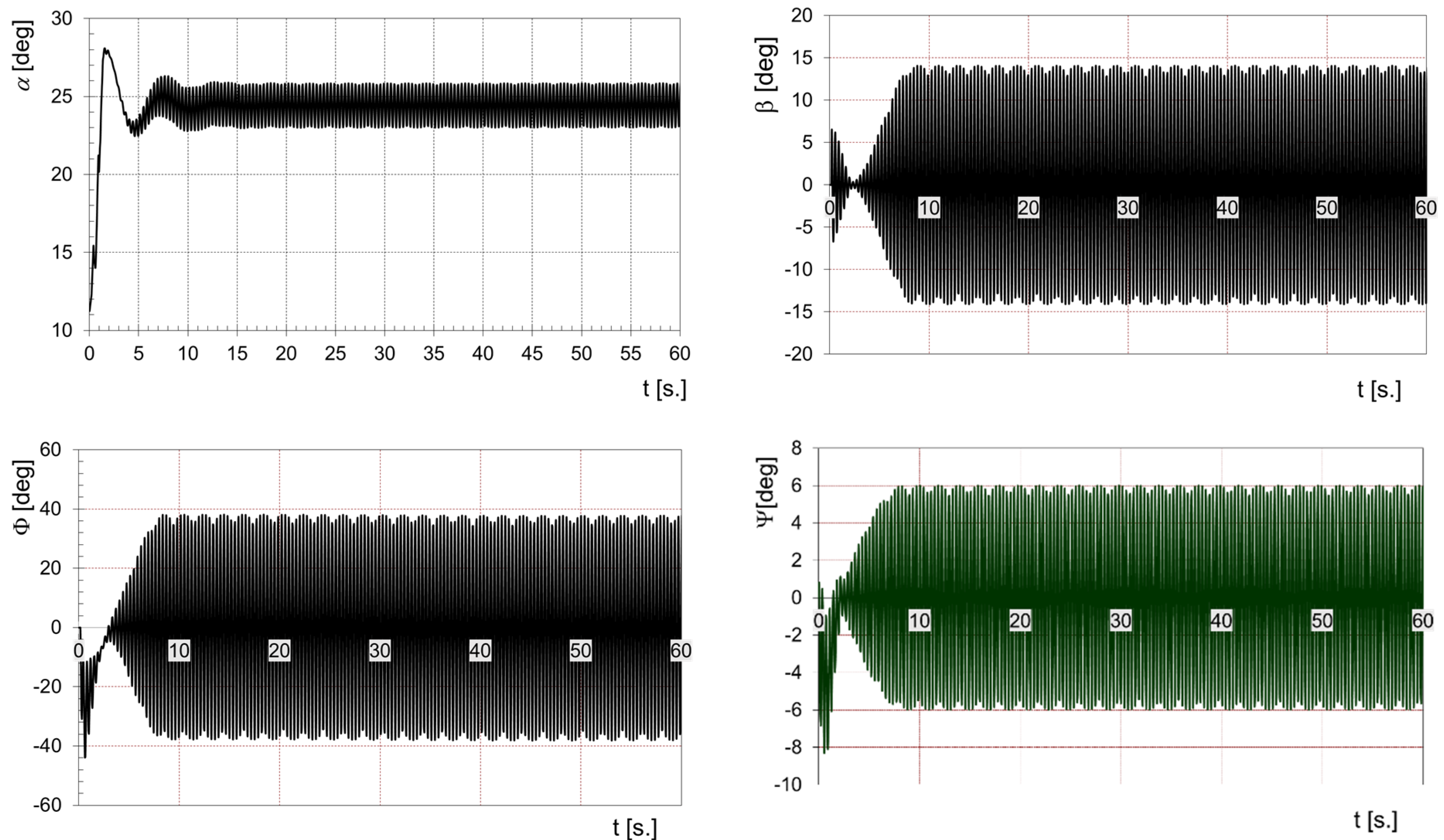
6.1. “Wing Rock” Oscillation Simulation

A typical phenomenon encountered when flying at large angles of attack is the so-called “wing rock”. It is a self-excited phenomenon, which occurs at subcritical and supercritical angles of attack. Despite “wing-rock” generally not being dangerous, it is advisable to examine it more thoroughly. Studying the dynamics of this motion was attempted in numerous research work (for example: [10,55,56,57,58,59,60]. All of the quoted work adopted quasi-static aerodynamic aircraft characteristics or presented different identification methods. However, due to the oscillatory changes in the angle of attack occurring at high, near-critical and supercritical angles of attack, the occurrence of phenomena associated with flow non-stationarity, including hysteresis, is obvious. “Wing rock” oscillation simulations were conducted based on aerodynamic derivatives obtained during water tunnel testing and identified through a pulse function.

Examples of simulation results are shown in Figure 9. The motion disturbance involved elevator displacement from 8° to 7.8°. This caused MAV displacement into an area of unstable steady states (Hopf bifurcation). The outcomes were gradually increasing oscillations, turning into a limit cycle, with a period of about 0.2 s.

Characteristic oscillations appeared as a result of the micro aerial vehicle moving into the area of unstable steady states. They primarily involve rocking of the MAV from wing to wing. That rocking has an amplitude of approximately 39° (for the banking angle), and 6° for the angle of attack and slip. The flight velocity is practically constant. Whereas the period of oscillations corresponding to MAV pitch angle change is equal to the period of phugoid motions. These oscillations are of limit cycle vibration character.

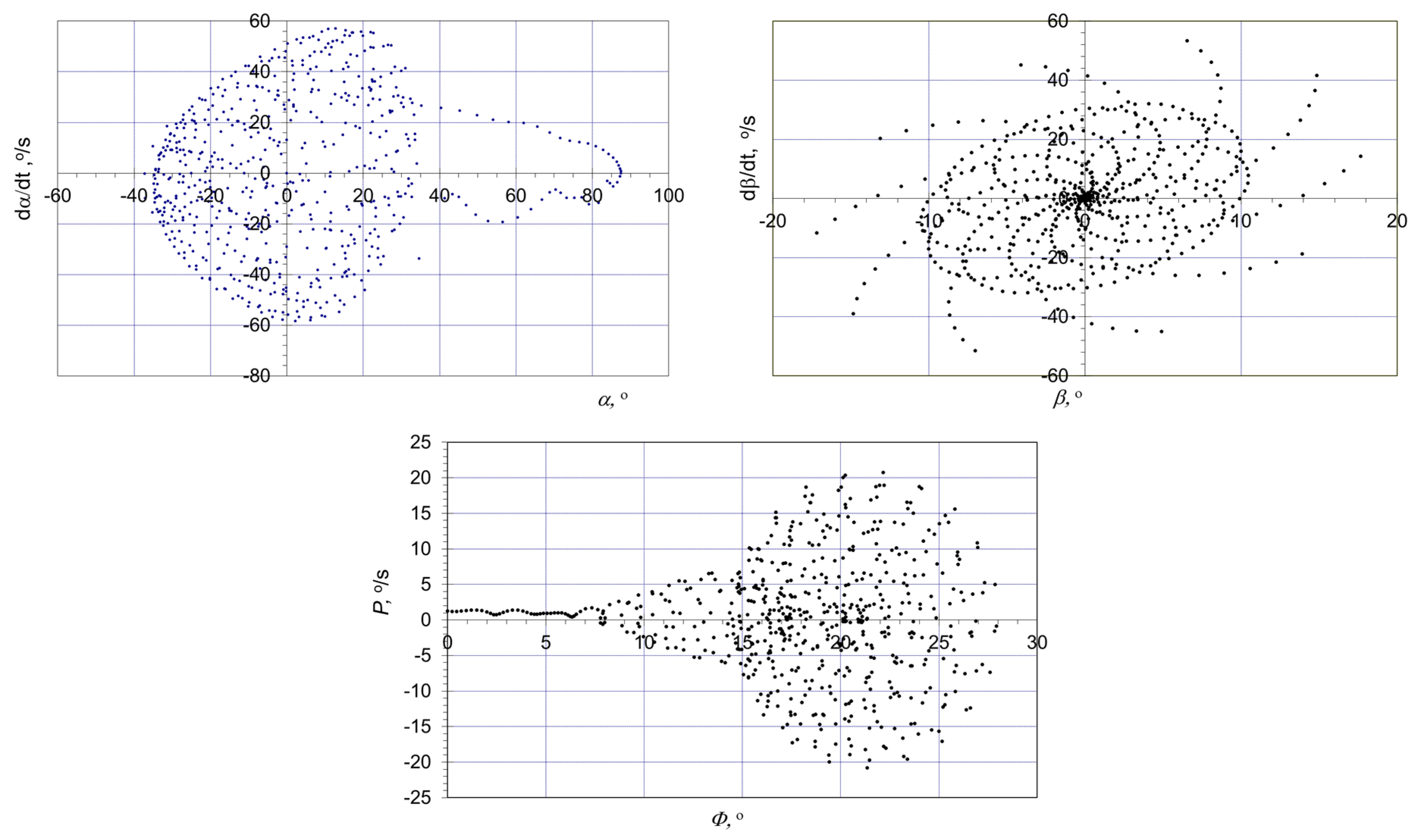
6.2. MAV Spin Simulation

The G and F branches of quasi-steady states (Figure 6 and Figure 7) correspond to states of steady spins. The bifurcation analysis enables “control matching”, which allows to recover from critical flight states. A sketch of a “bifurcation control matching” is shown in Figure 10. The equilibrium surface of banking angular velocities P and the bifurcation graph on the deflection plane of the elevator δ_e and elevons δ_elv show critical autorotation areas (excluding the spin and a rapid inertia barrel). Recovery trajectories encounter an “apex catastrophe”. Skipping through this singularity allows to “smoothly” achieve the desired point of zero banking rate.

Figure 11 show the results of a spin recovery simulation. The method of spin recovery was matched using the method shown in Figure 10 and involved displacement of control surface positions beyond the area of unstable equilibrium states and limit cycles. The analysis of simulation results shows the effectiveness of the “bifurcation control matching” method.

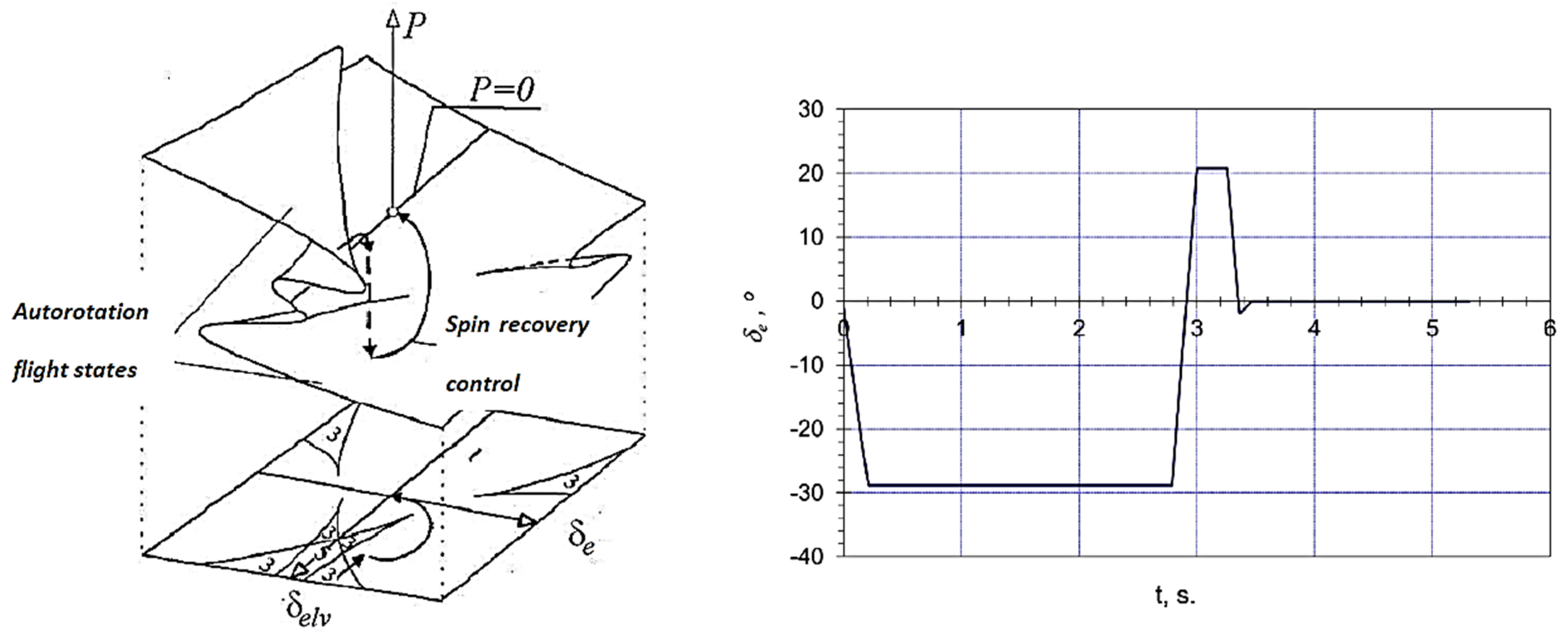
6.3. “Cobra” Manoeuvre Simulation

“Cobra” is one of aerobatic figures. The manoeuvre was first executed at the turn of the 1950s and 60s, by the pilots of the Swedish Air Force (Svenska Flygvapnet) flying J-35 Draken fighters. It has a Swedish name of “kort parad”—“short parade” and was part of standard short-range manoeuvring combat training for Swedish fighter pilots [48,49]. In the 1980s, the manoeuvre was executed by OKB Sukhoi test pilot, Igor Volk, during Su-27 spin tests. The Cobra was first demonstrated in public by Viktor Pugachev at the Le Bourget air show in 1989, on a MiG-29 fighter. This manoeuvre can be executed with an aircraft exhibiting excellent manoeuvrability and low thrust load or equipped with thrust vector control engines. Besides the spectacular impression it makes at air shows, enabling to demonstrate the manoeuvrability and turning abilities of modern combat aircraft, this manoeuvre, used in direct air combat, is primarily aimed at forcing the chasing foe to overtake through rapid deceleration, thus providing the chased aircraft with a convenient position to open fire. The effect of sudden deceleration is achieved owing to rapidly increasing aircraft drag resulting from vertical positioning of the aircraft body in the upward direction (perpendicular to the previous flight direction).

The “Cobra” is conducted at supercritical angles of attack, significantly exceeding the value under normal operating conditions. Figure 12 shows a diagram of the “Cobra”. This manoeuvre is divided into three basic stages:

• Transition from horizontal flight into the phase of increasing the aircraft pitch angle, due to very rapid increase in the elevator deflection angle (sudden pulling of the control stick to a maximum), while simultaneously throttling the engine or engines,
• manoeuvre phase in which, as a result of such action by the pilot, the aircraft nose rapidly rises up, until it reaches a very high angle of attack (even up to 120°),
• the exit phase, which involves increasing the thrust and releasing the control stick, leading to the aircraft rapidly increasing its pitch angle, while simultaneously accelerating and returning to horizontal flight, with a minor altitude loss.

The “Bee” MAV has a stake-wing and its dynamics is similar to the dynamics of modern high-manoeuvring combat aircraft. Based on in-flight tests, it was concluded that it was able to execute a “Cobra” manoeuvre (Figure 12) [61]. The “Cobra” manoeuvre simulations were conducted based on aerodynamic and mass data of the “Bee” micro aerial vehicle. Simple analyses show that executing the “Cobra” manoeuvre will be possible without changing the flight altitude, when the vertical projection of the sum of external forces acting on the MAV in the course of the manoeuvre should be equal to zero. However, due to the fact that the computational thrust force value was initially negative, it was assumed that the MAV starts the manoeuvre with the engine off (zero thrust). It was also assumed that, in the course of executing a manoeuvre, the thrust depends on the difference in the aircraft’s angles of pitch Θ and attack α, and the flight velocity V [62,63].

Due to the fact that aircraft equipped with strake wings are characterized by wing-rock instability and are not spirally stable, it was impossible to obtain a fully symmetrical flight parameter waveform. This is associated with the occurrence of Hopf bifurcation and torus creation bifurcation on G, E and F branches (Figure 5 and Figure 6). The “Cobra” manoeuvre is initiated with a sudden downward displacement of elevons (δ_e = −35°). This causes a rapid transition of the MAV through C, G, E and F branches of steady flight states (Figure 5 and Figure 6).

Figure 13 and Figure 14 show the results of a digital simulation of the “Cobra” manoeuvre, taking into account the occurrence of limit cycles. Based on the analysis of these graphs, it can be concluded that all flight parameters are significantly changed during a Cobra figure, increasing their values. Using the terminology of the Dynamical System Theory, it can be said that the “Cobra” is unstable due to the presence of Hopf bifurcation (at an elevator displacement angle of δ_e = −23.1°) and torus bifurcation (for δ_e = −16.5°). Figure 14 shows Poincarè maps for selected state parameters. It can be concluded when the non-stationarity (hysteresis) of aerodynamic coefficients were taken into account, MAV motion equation solution irregularities of quasi-harmonic nature were obtained. The digital simulation took into account the fact that at high angles of attack, the aircraft is spirally unstable (branch C, Figure 5 and Figure 6) and has a tendency to wing-rock oscillations (branch B, Figure 6 and Figure 7). In the course of a manoeuvre, the aircraft attack and pitch angles rapidly increase, reaching maximum values of approximately 84° (for an attack angle of α) and 100° (for a pitch angle of Θ). The MAV bank and yaw angle waveforms (Figure 13) indicate that these angles increase over time. This is associated with the present area of spiral instability (branch C in bifurcation diagrams—Figure 5 and Figure 6). The development of wing-rock oscillations is also visible. The period of these oscillations varies at approx. 0.2 s. It should be noted that the amplitude and frequency of these oscillations are irregular (quasi-harmonic).

7. Conclusions

The article presents application examples of the theory of dynamical systems relative to studying the flight dynamic specifics of a micro aerial vehicle, constructed as a fixed-wing aircraft with a strake-wing. Such microdrons are characterized by high manoeuvrability and can fly with high, supercritical angles of attack. The bifurcation analysis shown in the article enabled identifying some of the numerous factors impacting the behaviour of a strake-wing MAV. More specifically, this analysis allowed to discover a number of stable attractors, associated with disturbances to the states of equilibrium. Compared with purely simulational studies, which require long-term computations leading to the disappearance of motion history transitions on weak attractors, creating bifurcation diagrams is much less computation-demanding. Furthermore, bifurcation diagrams show the fundamental structure of a dynamical system, hence they suggest, where and when the time domain simulation should be conducted in order to better explain the behaviour of a dynamical system (in this case, a micro aerial vehicle). Time domain simulations were presented as supplementary to bifurcation diagrams, in order to gain more clarity in terms of the nature of various attractor dynamics regimes. It was shown that an MAV was susceptible to steep spiral motion disturbances, induced by loss of stability in this flight range. Bifurcation analysis was also able to identify that elevator displacement aimed at recovery from a steep spiral glide can lead to an oscillating spin. Bifurcation diagram analysis indicates that the correct reaction is to restore elevator position to the value corresponding to balancing conditions in straight flight.

The approach adopted in this article can be extended in several ways. Firstly, MAV behaviour in an open control loop can be further tested through expanding the parameter space in question; this can cover additional control signals, as well as combining the centre of gravity and various damage scenarios, which can be added to the model. Another potentially beneficial extension is the use of bifurcation methods to analyse micro aerial vehicle models expanded with closed control loops, including bifurcation matching that enables recovery from critical flight states.