PFDA-FMEA, an Integrated Method Improving FMEA Assessment in Product Design

Abstract

Product Design (PD) currently faces challenges in new product development, since the industry is in a rush to introduce new products into the market, with customers demanding products that are faster, cheaper, and free from failure. In addition, global companies are trying to improve their product design risk assessment process to gain advantages over competitors, using proven tools like Failure Mode and Effect Analysis (FMEA) and mixing risk assessment methods. However, with current risks assessment tools and a combination of other methods, there is the opportunity to improve risk analysis. This document aims to reveal a novel integrated method, where FMEA, Pythagorean Fuzzy Sets (PFS), and Dimensional Analysis (DA) are cohesive in one model. The proposed method provides an effective technique to identify risks and remove uncertainty and vagueness of human intervention during risk assessment using the Failure Mode and Effect Analysis method. A real-life problem was carried out to illustrate the proposed method. Finally, the study was substantiated by using a correlation and sensitivity analysis, demonstrating the presented integrated method’s usefulness in decision-making and problem-solving.

1. Introduction

Product Design (PD) maintains market dynamics and global economy progression simultaneously [1]. In addition, PD is a complex and long process, involving a cross-functional team trying to perform multiple activities [2]. Thus, the complexity of this process adds uncertainty to the different PD phases. Kahn [1] affirmed that it is important to continue the effort to improve the PD process. The revised literature lists hybrid methods to deal with risk analysis in the PD process; for example, recent investigations used Quality Function Deployment (QFD) and mix TRIZ, fuzzy sets, and DOE [3], with the intent to make the PD process robust. Wichmann et al. [4] used fuzzy sets to minimize uncertainty in the PD project schedule.

Failure Mode and Effect Analysis (FMEA) is a sustained tool that allows to analyze the risk of possible impact on any process; since its proposal, it has rapidly been adapted in different industries like automotives and electronics, and is continuously being improved. One of the main improvements in FMEA is Risk Priority Number (RPN), first introduced by Braband [5]. Usually, FMEA is ranked by experts on the basis of process under analysis; RPN is the product ranked on three values, from 1 to 10: Severity (S), Occurrence (O), and Detection (D), the final value of the RPN ranks the critical potential failure modes (PFMs) in the process analyzed, helping to take decisions based on possible risks. Next, based on the previous established range of the RPN value, contingency plans must be applied to avoid the risk of possible failure in the process under analysis.

Additionally, fuzzy sets introduced by Zadeh in 1965 [6] manipulated the uncertainty of a system under study, giving accurate output. Moreover, intuitionistic fuzzy sets presented by Atanassov in 1986 [7] handled the uncertainty using membership function and non-membership function. Later, Pythagorean fuzzy sets (PFS) proposed by Yager in 2014 [8] helped to manage the uncertainty on the input data of the system analyzed, eradicating ambiguity and bias because of an improved representation of the membership and non-membership functions, resulting in better output.

Different multi-criteria problems were faced by using Dimensional Analysis (DA) in a combination of PFS, as per Perez-Dominguez et al. [9]. Recently Mahoney and Yeralan [10] documented different examples of the use of DA. According to them, DA has advantages in solving multi-criteria problems used in combination with Fuzzy Logic. Shen et al. [11] analyzed the applications of DA over its statistics.

There are gaps identified in FMEA assessment [12]. As a summary of the main FMEA, the identified gaps are as per those based on Mzougui and Felsoufi [13], and Huang et al. [12]. First, the ambiguity when factors S, O, and D showed the same RPN value having different orders. Another gap mentioned by the authors is the difficulty to obtain a consensus for RPN because of ranking by multiple disciplines experts. Another gap is the uncertainty over FMEA inputs owing to the different judgments of experts assessing the FMEA. In addition, a gap mentioned in the literature is the vagueness due to crossed opinions of the cross-functional team assessing the FMEA. Another identified gap is that the decision to choose the risks impacting the PD process is polarized, when assuming that the risk is of high severity.

1.1. Failure Mode and Effect Analysis (FMEA) Literature Review

The FMEA is used in a broad variety of applications and different study areas. Some authors mix methodologies to improve it and make the FMEA application robust for their processes under study. Dezan et al. [14] used Bayesian Network and FMEA for the decision making logic, to improve safety in autonomous vehicles. Rastayesh et al. [15] used the FMEA methodology as a basis to analyze the failures in hybrid energy systems; they include the Failure Tree Analysis (FTA) to identify risks between the different electronic components, identifying the critical components in the hybrid energy system. Oliveira et al. [16] proposed the use of FMEA to analyze and prevent risks in Cyber-Physical Systems; the authors also proposed an alternative method to estimate the RPN in the FMEA using economic impact. Zandi et al. [17] suggested the use of FMEA for risks management in the agricultural sector; they add the use of the TOPSIS and Analytical Hierarchy Process (AHP) methodologies and add the ranking of severity, time, cost, and quality, summarizing that their method works to analyze the risks to investment projects considering those factors. Besides, Celiker et al. used AHP and FMEA to [18] solve production problems; later, Karatop et al. [19] added AHP, EDAS, Fuzzy, and FMEA methods in a renewable energy problem. Furthermore, Liu et al. [20] applied FMEA and Fuzzy FMEA and demonstrate the method in a practical case using sensors to obtain the data of the process and found good results in controlling the quality of the hot-pressing process. Another application of the FMEA is in the construction industry; Dahooie et al. [21] used the FMEA in a combination of Stepwise Weight Assessment Ratio Analysis (SWARA) for risk management in the construction industry. The authors based their proposed method on the FMEA method and used SWARA to calculate the weights of the risk factors, proposing a new adaptation of the FMEA process. In addition, in recent works, we found a fusion between neutrosophic logic and best worst method to improve Failure Mode and Effects Analysis (FMEA) [22]. In recent investigations, classical FMEA is still used to solve problems in the industry [23].

FMEA is a useful tool to identify risks in multicriteria problems; however, FMEA has a weakness identified in the literature [24,25,26,27]: the uncertainty when the RPN value is the same, and the factors S, O, and D have a different order. Besides the different opinions, FMEA is a popular tool used to identify product risks before, during, and after the PD process; moreover, applying new techniques to this tool is also common in improving the outputs, like FMEA and Multi-Criteria integrated by Lui et al. [28]. Many authors also combine methods to improve specific processes, like Pillay and Wang [29], who used FMEA with grey relational theory to correct the same FMEA flaw on the RPN. Zhou and Thai [30] use fuzzy and grey theories to predict failure with a practical example. Safari et al. [31] applied the fuzzy VIKOR technique to FMEA enterprise architecture’s risk evaluation. Pun et al. [32] applied Fuzzy Integrated FMEA to the NPD process in the flexible electronics field. The literature additionally includes combinations using FMEA and Fuzzy techniques [19,33,34,35,36,37]. Later, Khalilzadeh et al. [38] applied the Best Worst Method and GRA-VIKOR mixed with fuzzy logic methods for oil and gas projects; the authors concluded that the prioritization of risks is better compared to the conventional FMEA method. Thus, other hybrid methods are reported [39,40,41,42,43,44], for example rough best-worst method (R-BWM) and TOPSIS [45] help with analyzing judges’ weights and ranking in FMEA assessment. Carnero in [46] also uses a hybrid method applying IFS and Potentially All Pairwise Rankings of All Possible Alternatives (PAPRIKA) to FMEA for risk assessment on nuclear waste segregation. In addition, detailed research on FMEA using uncertainty theories and MCDM methods is presented in [47].

1.2. Risk Assessment in PD, a Literature Review

Product Design is a complex process that has multiple different problems to solve during different design phases [48]. Risk analysis is essential during the process, as mentioned in [49,50,51,52,53,54]. In the literature, there have been multiple efforts to improve the risk assessment for PD, where different tools are used for this purpose. Recent research [55] examined different methods used for risk analysis, where industry experts were interviewed to identify their points of view for risk assessment methods, like Failure Tree Analysis (FTA), Root Cause Analysis (RCA), Risk index, FMEA, Decision Tree, and more. Further investigations also sue multi-agent systems [56], proposing a risk assessment model in complex product design; the authors used venture evaluation and review technique (VERT) and probabilistic risk analysis (PRA) to propose a hierarchical risk assessment for complex design. Another study presents the use of development flexibility to mitigate risks during product launches [57]. The use of Monte-Carlo simulations and historical data to make a better-informed decision based on risks in product design is presented in [58]. Another recent research remarks on the use of Product Lifecycle Management and Computer-Aided Design (CAD) tools to identify product design risks during the design stage, considering changes to the CAD [59].

Currently there are diverse methodologies applied to the PD process for risk assessment as per the literature reviewed. However, there is no integral model that uses the Pythagorean Fuzzy Dimensional Analysis (PFDA) method [60] to eliminate the gaps brought about by FMEA’s uncertainty and vagueness.

This document aims to improve FMEA risk assessment for the PD process, covering these gaps, as well as helping to achieve a clear and enhanced risk ranking. Likewise, the proposed method offers a practical way to make decisions based on risks during the Product Design process. The PFDA-FMEA proposed method integrates PFDA and FMEA methods. This specific integration is intended to improve FMEA risk assessment and decision-making in the PD process. The PFDA-FMEA method intends to remove the uncertainty and vagueness of human ranking in conventional FMEA risk analysis. The proposed methodology is validated and demonstrated step by step using a real practical example.

This document is structured as follows: Section 2 contains the basic concepts of the different methodologies used in the proposed PFDA-FMEA method. Section 3 details the PFDA-FMEA methodology step-by-step with the help of a practical real example. Section 4 reveals the details of the calculus performed. The results and discussion are presented in Section 5, and finally, Section 6 concludes the document.

2. Basic Concepts

In this section, basic concepts are presented.

2.1. Failure Mode and Effect Analysis (FMEA)

FMEA is a well-known method used in different industries to detect possible risks in a process under study. The detailed FMEA methodology is described by the Automotive Industry Action Group (AIAG) [61]. FMEA assessment starts by identifying the potential failure modes in the process under analysis, then a team of experts evaluates three risk factors for potential failures modes: (i) severity (S); (ii) occurrence (O); and (iii) detection (D). Finally, the product of S, O, and D generates an RPN [5]. The FMEA assessment continues in rows while PFMs are identified, and the highest RPN values point to the highest risks in the analysis. Full details of the method are described by the Automotive Industry Action Group (AIAG) [61].

2.2. Pythagorean Fuzzy Sets

Yager introduced PFS [62], used in this document and defined as following:

Definition 1.

As per Zhang and Xu [63], Yang and Hussain [64];$X$represents the universe, then PFS$P$in$X$is given by:

$$P=\{\langle x,{\mu }_p\left(x\right),{\nu }_p\left(x\right)\rangle |x\in X\}.$$

(1)

where μ_p($x$): X → [0, 1] defines the degree of membership

Then ν_p($x$): X → [0, 1] defines the degree of non-membership of the element x, where x ∈ X to P.

Definition 2.

According to Zhang and Xu [63], for any PFS, p = (μ, $\nu$), p is defined as follows:

$$s\left(p\right)={\left(\mu \right)}^2-{\left(\nu \right)}^2$$

(2)

where$s\left(p\right)\in \left[-1,1\right]$.

Pythagorean Fuzzy Dimensional Analysis

Pythagorean Fuzzy Dimensional Analysis (PFDA) is used in a practical example before the FMEA assessment; an extra step to assess the FMEA based on linguistic values is also required, following which the results are ranked. This will help have a clear path to identify the main PFS affecting the PD process. PFDA is applied to normalize the inputs and allow to use mixed data, qualitative and quantitative, coming from the FMEA, enabling the information to be comparable, even if we have mixed data types in the FMEA inputs. Villa et al. [60], integrates PFS and DA using Equation (3); they used PFS and DA to solve a multicriteria decision problem.

$$PFI{S}_i\left({\mathsf{⍵}}_1^i,{\mathsf{⍵}}_2^i,\dots ,{\mathsf{⍵}}_m^i\right)=\left({\displaystyle \prod }_{k=1}^n{({\mu }_{{\xi }_j^i})}^{T_j},\sqrt{1-{\displaystyle \prod }_{k=1}^n(1-{({\nu }_{{\xi }_j^i}{)}^2)}^{T_j}}\right)$$

(3)

where, PFIS_i = Pythagorean fuzzy Index of Similarity, for i = 1, 2, …, m

⍵ = Pythagorean sets, μ = Membership values assigned, and ν = Values of S, O and D

Then: T_j = Weights assigned to the experts, for j $=1,2,\dots ,m$, K = 1, 2, …, n, and ξ = universe of considered elements

where, T_j ∈ [0, 1], index i defined by the PFS.

3. The PFDA-FMEA Approach

The proposed PFDA-FMEA method (Pythagorean Fuzzy Dimensional Analysis—Failure Mode and Effect Analysis), intends to minimize the uncertainty in the FMEA assessment and improve the way to make decisions based on the risks identified in the PD process. The method uses FMEA as a basis to collect and organize the main PFMs for the process to be analyzed by the SME group, following which the PFDA method is applied. The suggested method is generalized in the five steps given below and illustrated in Figure 1.

Step 1. Creation of SMEs group. Depending on the process to assess, a group of n experts on the matter to be assessed are required to identify, to perform the assessment.

Step 2. Assign weights to SME. Once the SME group is selected, a weight is assigned to each of the experts; the weight to each SME can be assigned depending on the grade of expertise on the matter under analysis.

Step 3. SME group identifies PFMs. The group of experts agrees and establishes the main internal and external characteristics that affect direct or indirect process under analysis.

Step 4. Assess FMEA using Linguistic Values. The list of PFMs is evaluated by each SME independently and based on their experience on the matter, using

Table 1. Linguistic Values for PFDA, Membership and Non-Membership Functions.

Linguistic Values	Membership Function (μξ)	Non-Membership Function (νξ)
Low affectation to quality (LQ)	0.15	0.95
Regular affectation to quality (RQ)	0.55	0.55
High affectation to quality (HQ)	0.80	0.20
Low affectation on time (LT)	0.35	0.85
Regular affectation to time (RT)	0.45	0.55
High affectation to time (HT)	0.95	0.10
Low affectation to budget (LB)	0.20	0.75
Regular affectation to budget (RB)	0.45	0.45
High affectation to budget (HB)	0.75	0.25
Low affectation to market (LM)	0.25	0.95
Regular affectation to market (RM)	0.50	0.50
High affectation to market (HM)	0.85	0.15

to assign the corresponding Linguistic Values. Table 1 collects the main areas of impact on the process, defined by the SMEs group. These areas are quality (Q), time (T), budget (B), and market (M); each of these areas is divided into levels of impact, low (L), regular (R), and high (H) impact; based on this, the SMEs group assigns the membership and non-membership functions according to the SMEs’ experience in each area of the process.

Step 5. Computing and obtain PFDA-FMEA. The results obtained in the previous step are used to apply PFDA per Equation (3); then using Equation (2) the values are de-fuzzified getting the PFDA-FMEA results for S, O, and D.

Step 6. Obtain the PFDA-FMEA index. The mathematical product of PFDA-FMEA S, O, and D, gives us the PFDA-FMEA index.

Step 7. Determine the PFM ranking. The results are ranked to identify the PFM risks and to support the decision to be taken.

4. Numerical Case

The industry currently identifies challenges to risk assessment during the PD process. The proposed integrated method PFDA-FMEA will bridges the identified gaps and help have a clear view to take decisions based on risks during the process.

A practical real case is presented in this document, to exemplify and validate the PFDA-FMEA methodology. The example is based on an electronic device new product design scenario, and the group of SMEs is engineering, closed connected with the electronic design product process. A risk assessment is required for Product Design to avoid failures in the product and to complete the design on time within customer specifications. This numerical case shows the PFDA-FMEA assessment at the very beginning of the first stage of the project. PFDA-FMEA helps in obtaining a clear view of the impact of the risks associated with the electronic device product design process and helps to take the right decisions on where to apply more resources to avoid the impact of the risks identified.

The proposed PFDA-FMEA method uses FMEA as a base for this methodology; FMEA helps to collect and organize the main PFMs in the PD process by the SMEs group for the practical example. Then, PFDA is applied with the intention to minimize the uncertainty in human decision taken on the ranking of S, O, and D. PFDA is as per Equation (1) by [8,9,64].

Step 1. Creation of the SMEs group. A group of three experts in electronic devices’ Product Design is created; they are numbered in a sequence as SME 1, SME 2, and SME 3.

Step 2. Assign weights to SMEs. Weights are assigned to each SME member depending on their experience. In this practical example, the values of the weights are assigned equally to each SME, giving 1/3 in accordance with the total value between 0 to 1, as per (3).

Step 3. The SME group identifies PFMs. The SMEs group on the electronic devices’ PD process suggests PFMs that directly or indirectly impact the performance of the PD in the first stages of the process. For this example, the SME group agree to use the 19 PFMs listed in

Table 2. Product Design main Potential Failure Modes identified by the SME group.

PFM ID	Potential Failure Mode
PFM1	Extremely limited time to launch
PFM2	Customer requirements change
PFM3	Lack of consideration for aesthetics
PFM4	Technical failures in the product
PFM5	Last minute design changes
PFM6	Product’s low performance
PFM7	Manufacturing not ready for launch
PFM8	Lack of manufacturing capacity
PFM9	Material’s long lead times
PFM10	Potential market saturated
PFM11	Pilot runs failures
PFM12	Failure in customer samples
PFM13	Lack of inventory for launch
PFM14	Wrong market analysis
PFM15	No tech available for development
PFM16	Environmental compliance not considered
PFM17	New tech in the manufacturing process
PFM18	Lack of experts to develop the product
PFM19	Bad quality of raw material

.

Step 4. Assess FMEA using Linguistic Values. The Linguistic Values in Table 1 were used to assess the FMEA. The SMEs group performs the FMEA assessment using Linguistic Values instead of the regular FMEA scale to assess the S, O, and D for each PFM. This step pretends to manipulate the uncertainty in the evaluation process with human judgment.

Table 3. FMEA assessment by SMEs using linguistic values.

PFM ID	SME1	S SME2	SME3	SME1	O SME2	SME3	SME1	D SME2	SME3
PFM1	HT	RT	RT	RT	RT	LT	HT	RT	RT
PFM2	RT	RT	LT	RT	RT	LT	HT	HT	RT
PFM3	RM	LM	RM	RM	RM	LM	HM	RM	RM
PFM4	HB	RB	HB	LB	LB	RB	LB	RB	LB
PFM5	RT	HT	HT	RT	RT	RT	RT	RT	RT
PFM6	HQ	RQ	HQ	RQ	RQ	LQ	HQ	RQ	RQ
PFM7	RT	RT	LT	RT	LT	LT	RT	RT	LT
PFM8	RM	LM	RM	RM	LM	LM	RM	LM	RM
PFM9	RT	RT	LT	RT	RT	LT	LT	LT	LT
PFM10	LM	LM	RM	HM	RM	RM	RM	LM	RM
PFM11	RT	LT	RT	LT	RT	LT	LT	RT	LT
PFM12	RQ	HQ	RQ	RQ	LQ	RQ	HQ	RQ	RQ
PFM13	LT	LT	LT	RT	LT	RT	RT	RT	RT
PFM14	HM	RM	HM	RM	RM	LM	HM	RM	HM
PFM15	LT	LT	RT	RT	RT	RT	RT	LT	LT
PFM16	LT	RT	LT	RT	LT	LT	LT	LT	RT
PFM17	HT	RT	RT	RT	RT	LT	RT	LT	RT
PFM18	RT	LT	RT	RT	RT	LT	LT	RT	RT
PFM19	LQ	RQ	LQ	LQ	LQ	RQ	RQ	LQ	LQ

collects linguistic values used to assess the PFDA-FMEA. To be practical, we used the acronym of the linguistic values to represent Table 3, i.e., “Low affectation to quality” = LQ, using “LQ” instead of the full sentence.

Step 5. Compute and obtain PFDA-FMEA. PFDA is applied to the assessment results by using Equation (3); later, Equation (2) is used to de-fuzzify the fuzzy numbers and obtain crisp values. The computation results are presented in

Table 4. PFDA-FMEA results for severity, occurrence, and detection.

S	O	D
0.0060	0.0353	0.0060
0.0353	0.0353	0.0017
0.0715	0.0715	0.0041
0.0015	0.0313	0.0313
0.0017	0.0114	0.0114
0.0023	0.0756	0.0064
0.0353	0.0633	0.0353
0.0715	0.1520	0.0715
0.0353	0.0353	0.0789
0.1520	0.0041	0.0715
0.0353	0.0633	0.0633
0.0064	0.0756	0.0064
0.0789	0.0353	0.0114
0.0013	0.0715	0.0013
0.0633	0.0114	0.0633
0.0633	0.0633	0.0633
0.0060	0.0353	0.0353
0.0353	0.0353	0.0353
0.1496	0.1496	0.1496

, obtaining values for S, O, and D using the PFDA-FMEA.

Step 6. Obtain the PFDA-FMEA index. Table 4’s values are blended in the mathematical product of PFDA-FMEA S, O, and D, subsequently resulting in the PFDA-FMEA index (i.e., S × O × D); the results are presented in

Table 5. PFDA-FMEA results and risks ranking.

PFM ID	PFDA-FMEA Index
PFM1	1.3 × 10−6
PFM2	2.1 × 10−6
PFM3	2.1 × 10−5
PFM4	1.4 × 10−6
PFM5	2.2 × 10−7
PFM6	1.1 × 10−6
PFM7	7.9 × 10−5
PFM8	7.8 × 10−4
PFM9	9.9 × 10−5
PFM10	4.4 × 10−5
PFM11	1.4 × 10−4
PFM12	3.1 × 10−6
PFM13	3.2 × 10−5
PFM14	1.2 × 10−7
PFM15	4.5 × 10−5
PFM16	2.5 × 10−4
PFM17	7.5 × 10−6
PFM18	4.4 × 10−5
PFM19	3.3 × 10−3

.

Step 7. Determine the PFM ranking. The results are ranked to identify the PFM risks and to support decisions to be taken.

Table 6. PFDA-FMEA results and risks ranking.

PFM ID	PFDA-FMEA Index	PFDA-FMEA PFM Ranking
PFM1	1.3 × 10−6	16
PFM2	2.1 × 10−6	14
PFM3	2.1 × 10−5	11
PFM4	1.4 × 10−6	15
PFM5	2.2 × 10−7	18
PFM6	1.1 × 10−6	17
PFM7	7.9 × 10−5	6
PFM8	7.8 × 10−4	2
PFM9	9.9 × 10−5	5
PFM10	4.4 × 10−5	8
PFM11	1.4 × 10−4	4
PFM12	3.1 × 10−6	13
PFM13	3.2 × 10−5	10
PFM14	1.2 × 10−7	19
PFM15	4.5 × 10−5	7
PFM16	2.5 × 10−4	3
PFM17	7.5 × 10−6	12
PFM18	4.4 × 10−5	9
PFM19	3.3 × 10−3	1

illustrates the PFDA-FMEA results, revealing the PFDA-FMEA index and the ranking, allowing to identify risk priority. This PFM ranking reveals the scenario of how the PD risk assessment will be considered. In this sense, PFM 19 depicts the biggest risk due to the highest number in the index.

5. Results and Discussion

This section explains the PFDA-FEMA method results obtained, and the experiments performed to validate it. Likewise, a discussion based on the current FMEA method gaps against the PFDA-FMEA method is provided; additionally, methods in [65,66], and the conventional FMEA method are compared, and advantages of the PFDA-FMEA method are highlighted.

Table 6 shows the PFM ranking, as part of the numerical case applied to an electronic devices’ PD process. The major risk of the PFM is represented by the lowest number on the PFM ranking, and the risk is less while the ranking is bigger.

Based on the revised literature in previous sections, it is observed that the FMEA method has been criticized, mostly because of the uncertainty in the risks ranking; therefore, the proposed PFDA-FMEA method has advantages against the current FMEA method, covering uncertainty gaps.

Although there are currently different hybrid methods proposed to improve the FMEA, some recent works use hybrid methods focused on the weights and RPN ranking like [67]; in contrast, the proposed PFDA-FMEA method blends the Pythagorean Fuzzy Sets, Dimensional Analysis, and FMEA, improving the current FMEA method. In other words, PFDA-FMEA removes the uncertainty of risk assessment.

Aiming to illustrate the validation of the PFDA-FMEA method, a comparison was made using a similar method found in the literature. This discussion used the Pythagorean Fuzzy MOORA method (PF-MOORA) by [65] and the Pythagorean Fuzzy Entropy (PF-Entropy) by [66].

Table 7. The proposed PFDA-FMEA method vs. other methods.

PFM	PF-MOORA Ranking [65]	PF-Entropy Ranking [66]	PFDA-FMEA Ranking (Proposed Method)
PFM1	15	18	16
PFM2	3	15	14
PFM3	6	9	11
PFM4	14	17	15
PFM5	19	19	18
PFM6	16	13	17
PFM7	10	10	6
PFM8	9	2	2
PFM9	12	5	5
PFM10	1	3	8
PFM11	11	6	4
PFM12	13	12	13
PFM13	4	7	10
PFM14	17	16	19
PFM15	8	8	7
PFM16	5	4	3
PFM17	18	14	12
PFM18	7	11	9
PFM19	2	1	1

shows the results.

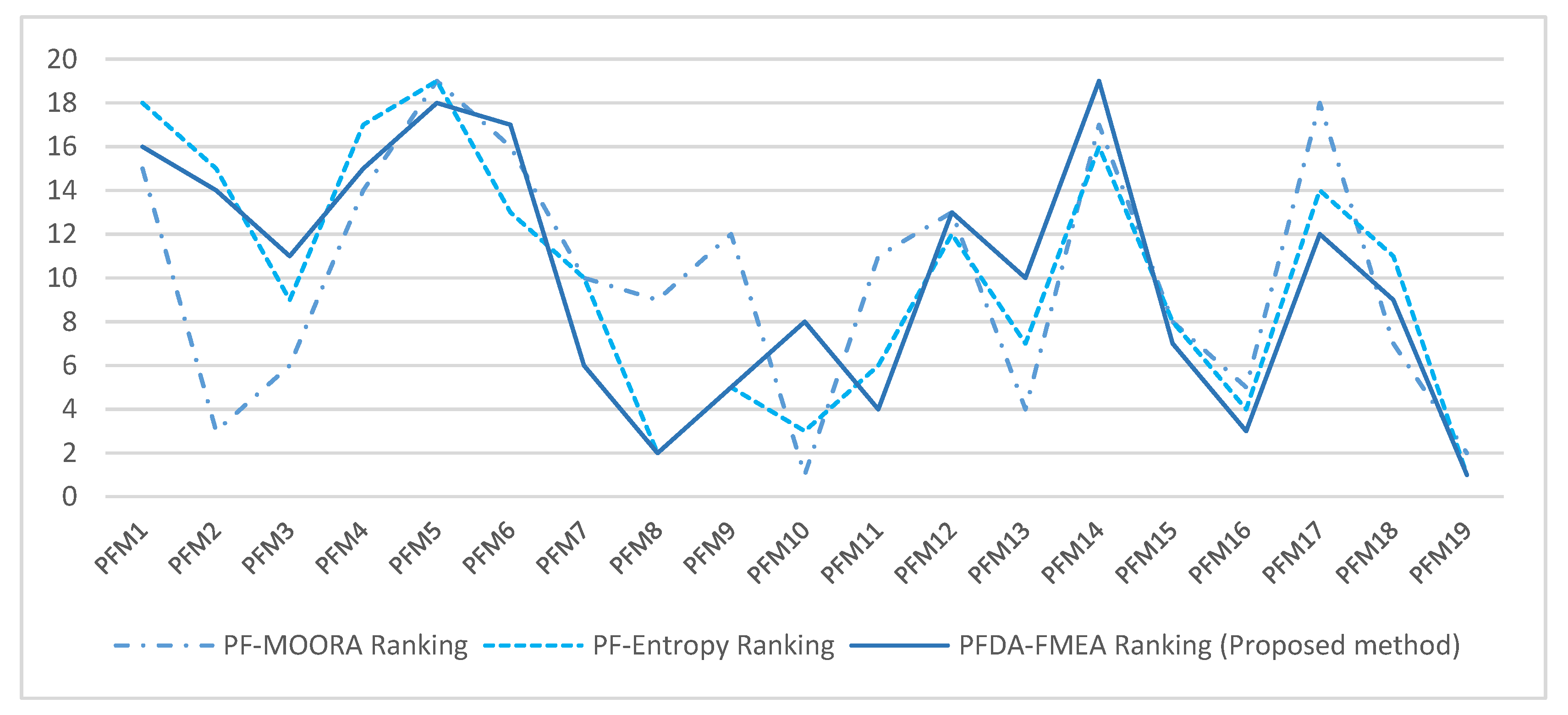
The similitude between the results while using fuzzy methods is solid, showing a close trend and pattern. Furthermore, the PFDA-FMEA method offers more accuracy than the rest of the compared methods, mainly because of the integration of PFS and DA, giving the advantage of solving problems where big accuracy is required.

In addition, the comparison between the methods reveals that PFM19 has the same ranking for PF-Entropy and PFDA-FMEA. In this sense, the main risk identified is PFM19 (bad quality of raw material) for the PD process analyzed in this paper.

In a graphical representation, Figure 2 shows the comparison between the three methods in Table 7. Based on this comparison, a similarity while using fuzzy techniques is observed, where the results are consistent in providing ranking of PFMs. In this mode, a risk assessment study can be addressed using the PFDA-FMEA method, offering high accuracy. Finally, the expectation in the PD process is to improve risk assessment of the electronic devices environment using the PFDA-FMEA proposed method.

Figure 3 depicts the correlation of the compared methods, PF-MOORA, Pythagorean Entropy, and the novel PFDA-FMEA method. A high similarity between rankings correlation is observed.

According to Cronbach’s study, the index is 0.8930; this result is significant in indicating that the PFDA-FMEA has a high reliability with regard to risk rankings.

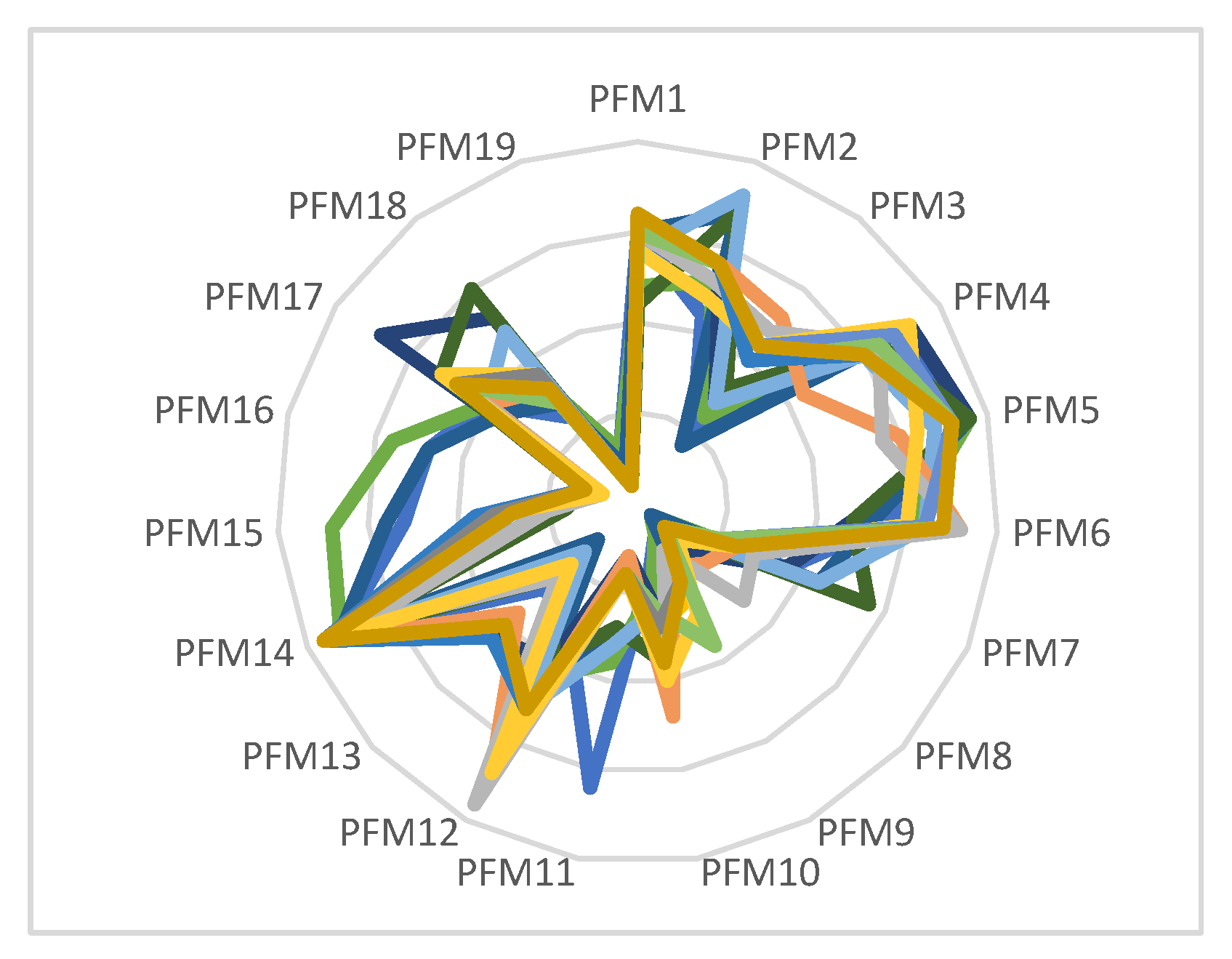
Additionally, as a validation of the PFDA-FMEA method, 22 random experiments were performed, modifying the weights on critical factors. Figure 4 shows the consistency and similar pattern of the PFM ranking during different experiments, where each color represents a different experiment changing the weights in the method (step 2), and the PFMs remain in the same order numbered. The similitude of the pattern confirms that even if the weights are modified in step 2, the PFDA-FMEA method is consistent.

Besides, to validate the PFDA-FMEA method, the same 22 random experiments were used to perform a correlation analysis. Correlation analysis results are given in

Table 8. Experiment iterating 22 runs using different weights; correlation analysis.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22
Exp. 1	1.0
Exp. 2	1.0	1.0
Exp. 3	1.0	1.0	1.0
Exp. 4	1.0	1.0	1.0	1.0
Exp. 5	0.6	0.7	0.7	0.6	1.0
Exp. 6	0.7	0.7	0.7	0.7	0.9	1.0
Exp. 7	0.7	0.7	0.7	0.7	0.9	0.9	1.0
Exp. 8	1.0	1.0	1.0	1.0	0.7	0.7	0.7	1.0
Exp. 9	1.0	1.0	1.0	1.0	0.7	0.7	0.7	1.0	1.0
Exp. 10	1.0	1.0	1.0	1.0	0.6	0.7	0.7	1.0	1.0	1.0
Exp. 11	0.9	0.9	0.9	0.9	0.6	0.6	0.7	0.9	0.9	0.9	1.0
Exp. 12	0.8	0.8	0.8	0.8	0.6	0.6	0.7	0.8	0.8	0.8	0.9	1.0
Exp. 13	0.9	0.9	0.8	0.9	0.6	0.7	0.8	0.8	0.9	0.9	0.8	0.9	1.0
Exp. 14	0.9	0.9	0.9	0.9	0.4	0.5	0.6	0.9	0.9	0.9	0.7	0.7	0.8	1.0
Exp. 15	0.9	0.9	0.9	0.9	0.4	0.5	0.6	0.9	0.9	0.8	0.7	0.7	0.8	0.9	1.0
Exp. 16	0.9	0.9	0.9	0.9	0.6	0.6	0.7	0.9	0.9	0.9	0.8	0.8	0.9	0.9	0.9	1.0
Exp. 17	1.0	1.0	1.0	1.0	0.6	0.7	0.7	1.0	1.0	1.0	0.9	0.8	0.9	0.9	0.8	0.9	1.0
Exp. 18	1.0	1.0	1.0	1.0	0.6	0.7	0.7	1.0	1.0	1.0	0.9	0.7	0.9	0.9	0.8	0.9	1.0	1.0
Exp. 19	1.0	1.0	1.0	1.0	0.7	0.7	0.7	1.0	1.0	1.0	0.9	0.8	0.8	0.9	0.9	0.9	1.0	1.0	1.0
Exp. 20	1.0	1.0	1.0	1.0	0.6	0.7	0.7	1.0	1.0	1.0	0.9	0.8	0.9	0.9	0.9	0.9	1.0	1.0	1.0	1.0
Exp. 21	1.0	1.0	1.0	1.0	0.7	0.7	0.7	1.0	1.0	1.0	0.9	0.8	0.9	0.9	0.9	0.9	1.0	1.0	1.0	1.0	1.0
Exp. 22	1.0	1.0	1.0	1.0	0.6	0.7	0.7	1.0	1.0	1.0	0.9	0.8	0.9	0.9	0.9	0.9	1.0	1.0	1.0	1.0	1.0	1.0

, where the 22 experiments in the rows show values close to 1, explaining the good ratio of correlation, even changing the weights described in the method (step 2).

In addition, Cronbach’s alpha was performed, giving a result of 0.9924, confirming that the obtained results are consistent, and the PFDA-FMEA method has a remarkable degree of confidence.

The PFDA-FMEA method offers more granularity for risk assessment, allowing to take better decisions based on risks, as well as guiding to assign just the right resources to mitigate identified risks.

6. Conclusions

Risk assessment for the PD process is a valuable step in developing products for any company, according to the literature reviewed. However, at the same time, the PD process still needs to be improved; therefore, global companies have a high interest in the process. Furthermore, the FMEA method is a recognized tool in the industry, frequently used in risk assessment for a broad variety of processes; however, as discussed in the introduction, the FMEA tool has some weaknesses, mainly because of the ambiguity and vagueness generated by human judgment.

PFDA-FMEA is a systematic and integrated method that removes one of the main limitations in the conventional FMEA method—the uncertainty in the cross-functional team judgment and assessment due to different points of view on risk assessment. At the same time, PFDA-FMEA improves the risk assessment in the PD process. Emphasizing on the advantages of the PFDA-FMEA method, it enhances the risk ranking compared to the conventional FMEA, while human judgment ambiguity is removed, since PFS is integrated. Furthermore, based on the integration of DA, a granular and accurate risk ranking is obtained. Successively, the PFDA-FMEA method has been proven and is demonstrated to be a harmonically integrated method enhancing the PD process. The PFDA-FMEA method was validated with a correlation and sensitivity analysis in the results section, where 22 random experiments were performed, confirming the consistency of the method. Lastly, the PFDA-FMEA method was also validated by Cronbach’s alpha, with a degree of confidence equal to 99.24%. Therefore, we carried out comparisons between other published methods, and finally, the results indicate that the PFDA-FMEA method is robust under a risk assessment environment. Consequently, the statistic study demonstrates the significance of this comparison study.

Nonetheless, as a limitation of this work, the PFDA-FEMA method was proved on the basis of an electronic devices’ PD process case study. However, the PFDA-FMEA method paves the way for future applications in different areas, expanding the possibilities to use it in any industry, including medical, pharmaceutical, and nanotechnology, where high accuracy is required for risk assessment.

Conclusively, the conventional FMEA is improved by the integrated PFDA-FMEA method, closing the current FMEA gap of vagueness; therefore, the PFDA-FMEA method is easier to be implemented in any industry, offering accurate and granular risk assessment, helping take decisions based on risk assessment.

Additionally, future work to create a programmed template using software is planned, to make the application of PFDA-FMEA in any process easier. Furthermore, upcoming work plans to make a comparison between the PFDA-FMEA method and other similar proposed methods.