Analysis of Polygonal Vortex Flows in a Cylinder with a Rotating Bottom
Abstract
:1. Introduction
1.1. Experimental Studies
1.2. Analytical Modeling
1.3. Numerical Modeling
2. Numerical Modeling
2.1. Choice of the Numerical Approach
2.2. Computational Details
3. Results and Discussion
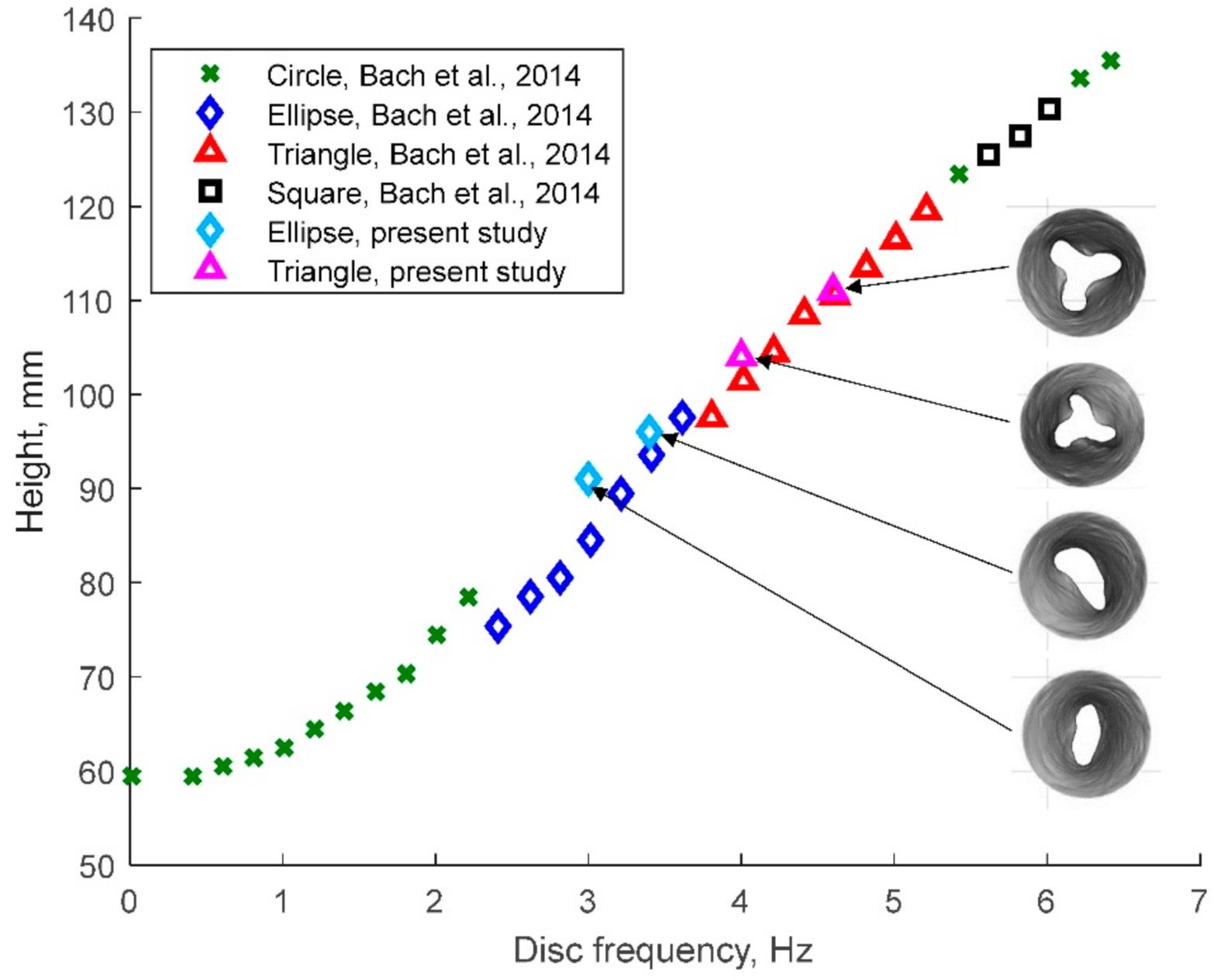
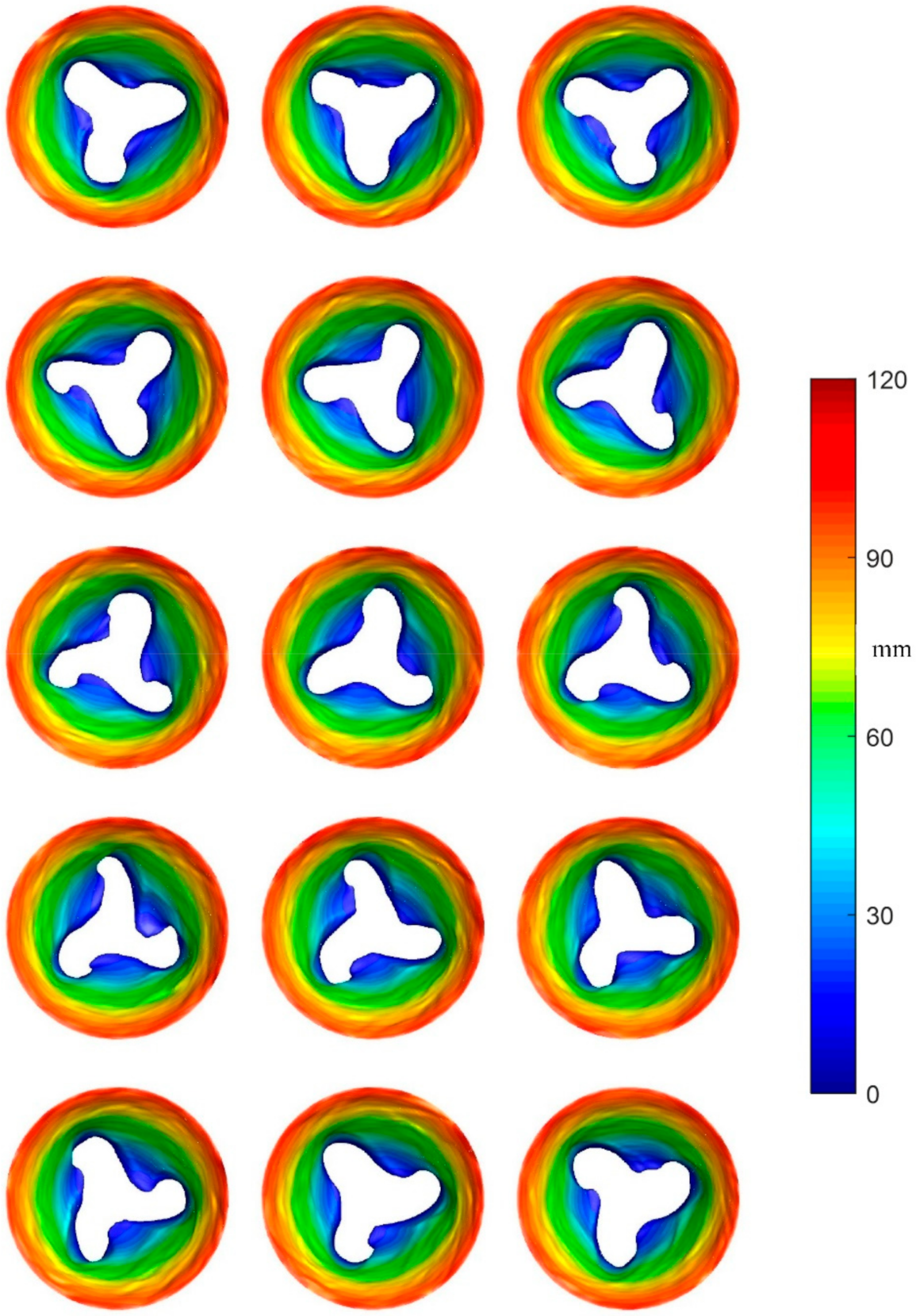
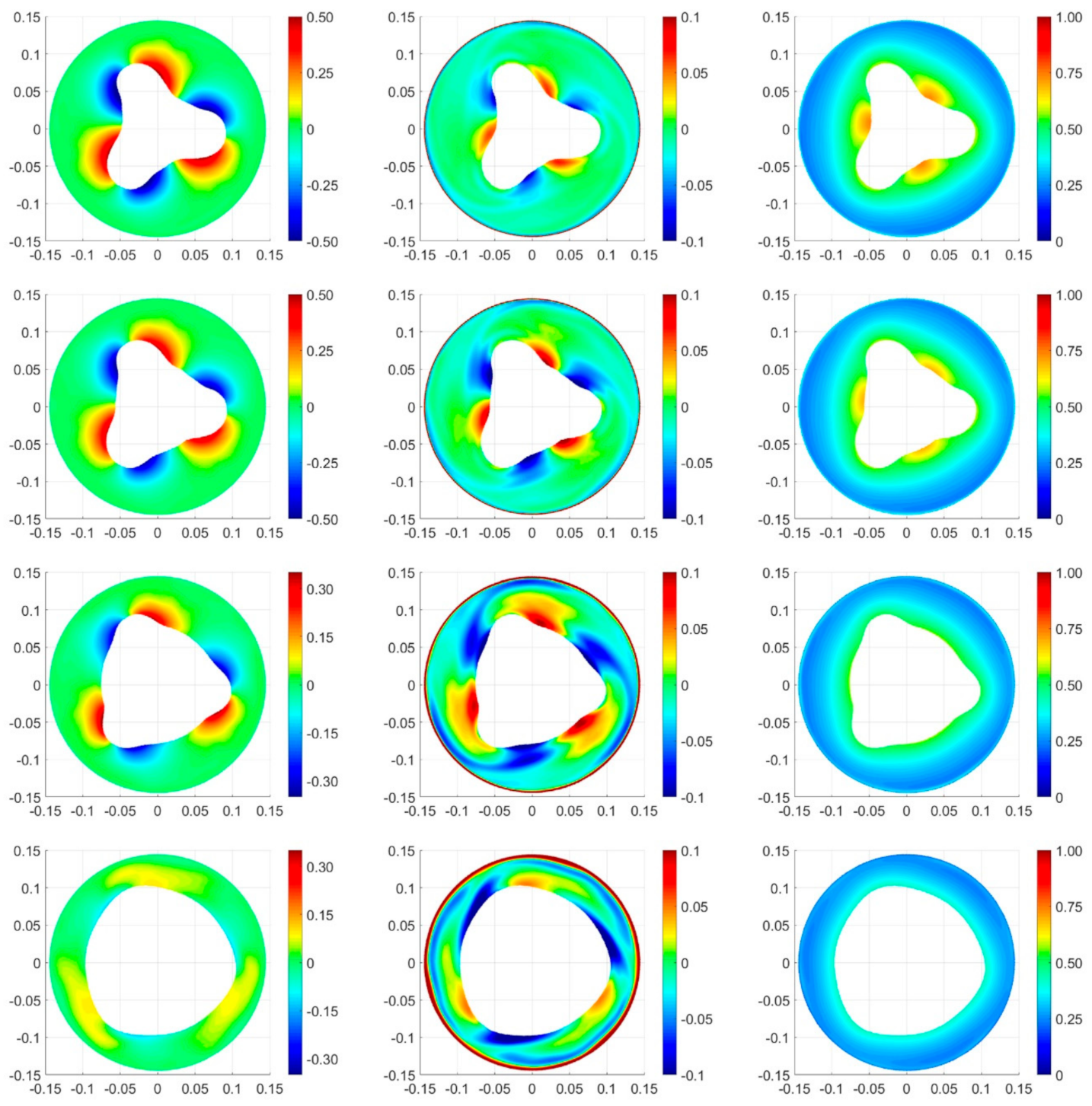
3.1. Flow Patterns
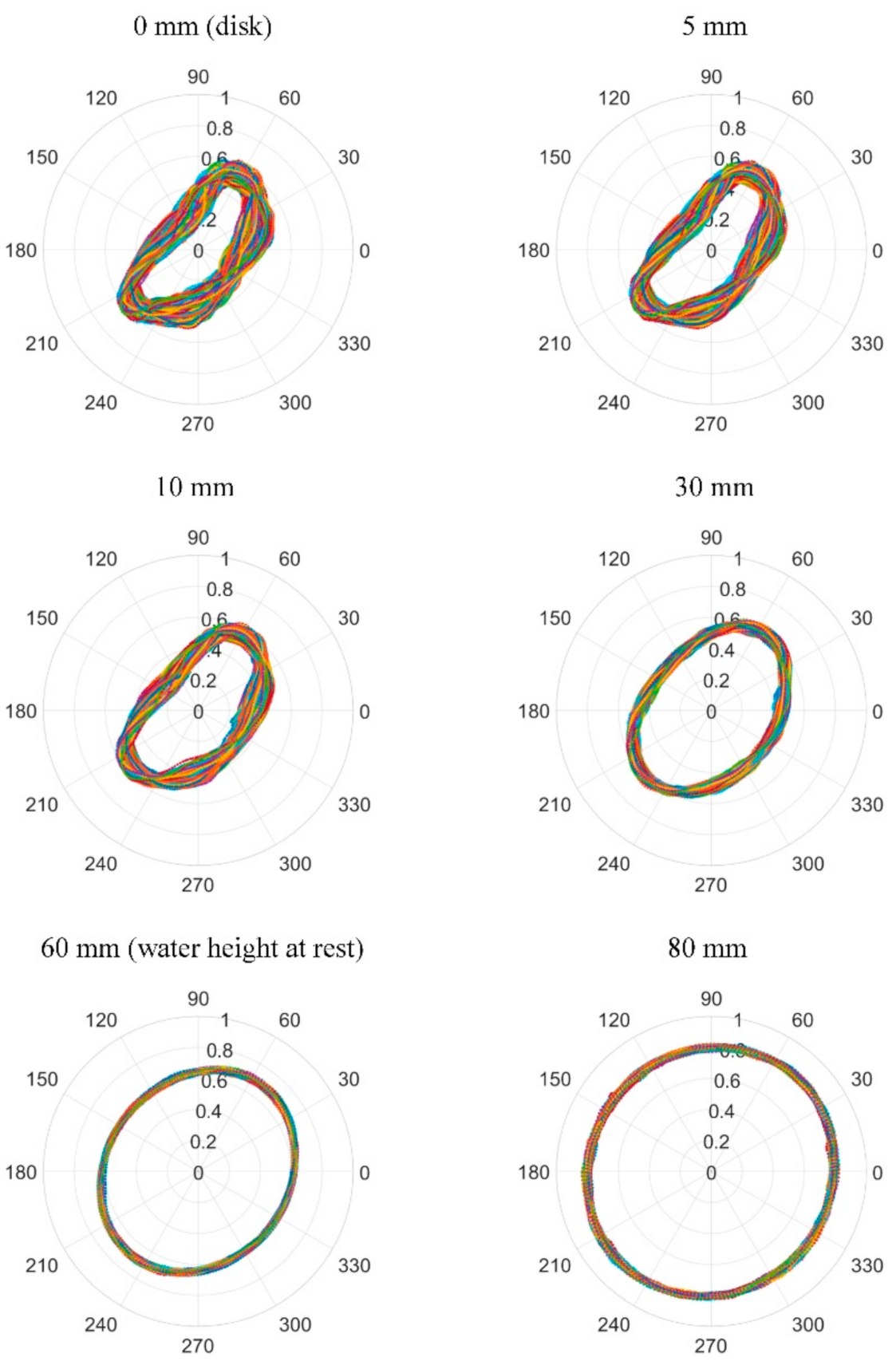
3.2. Pattern Stability
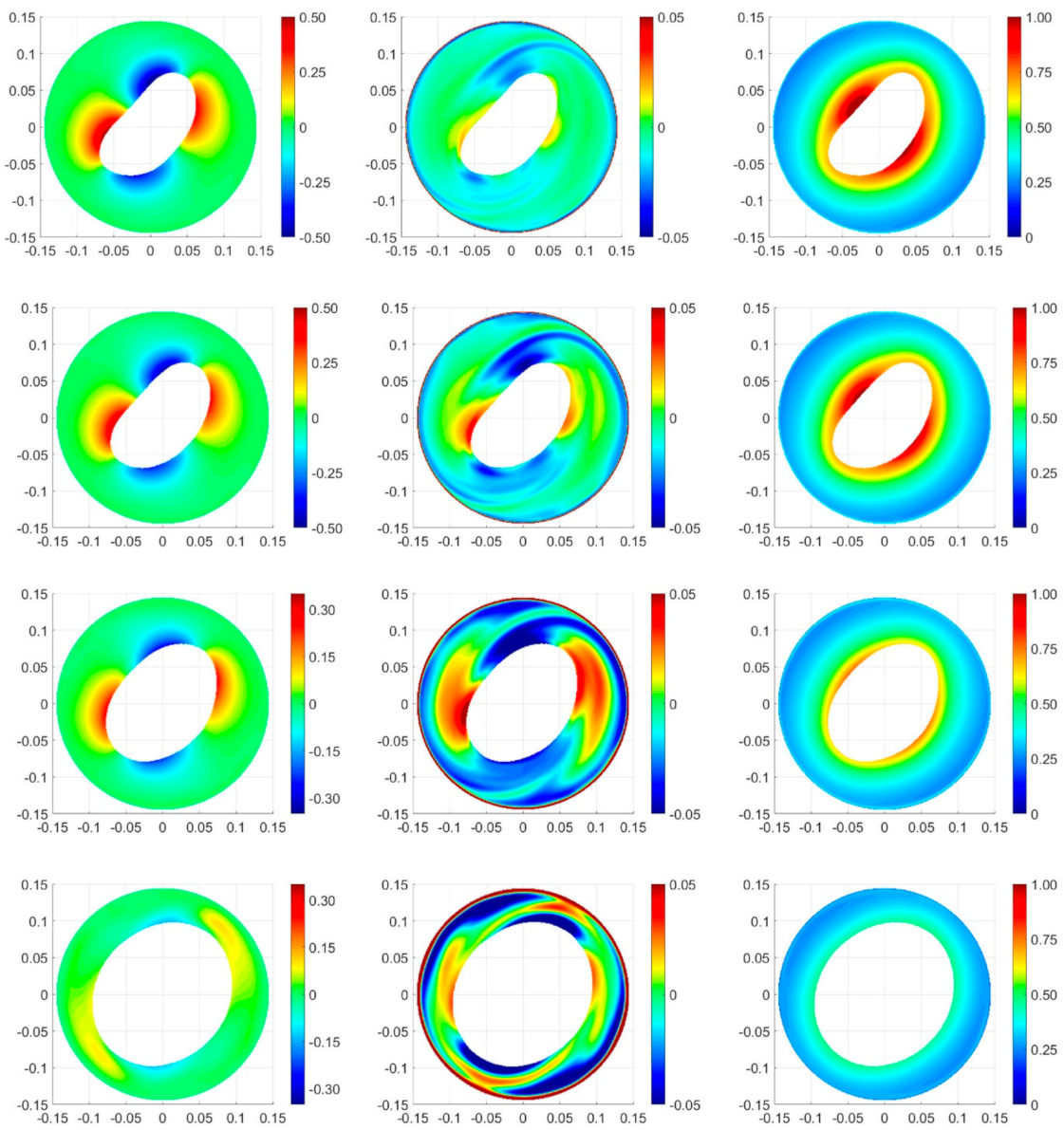
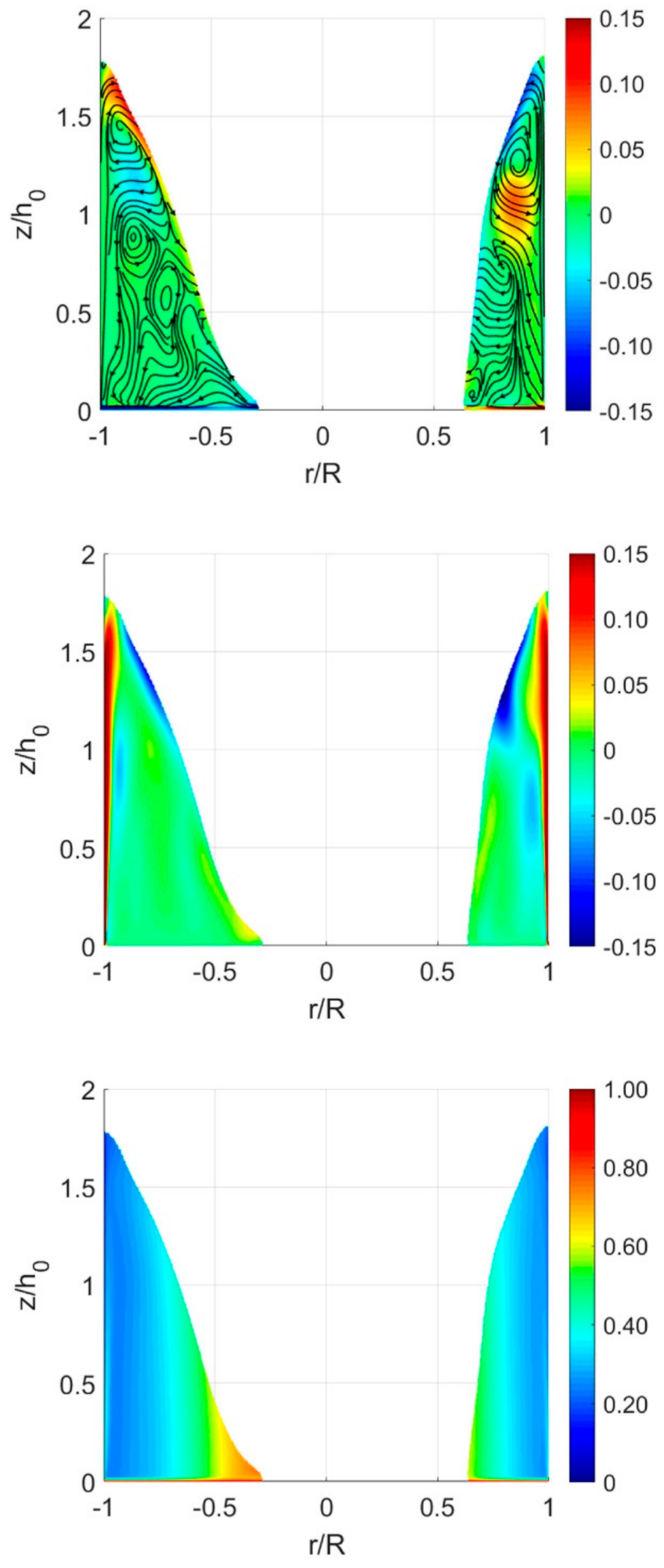
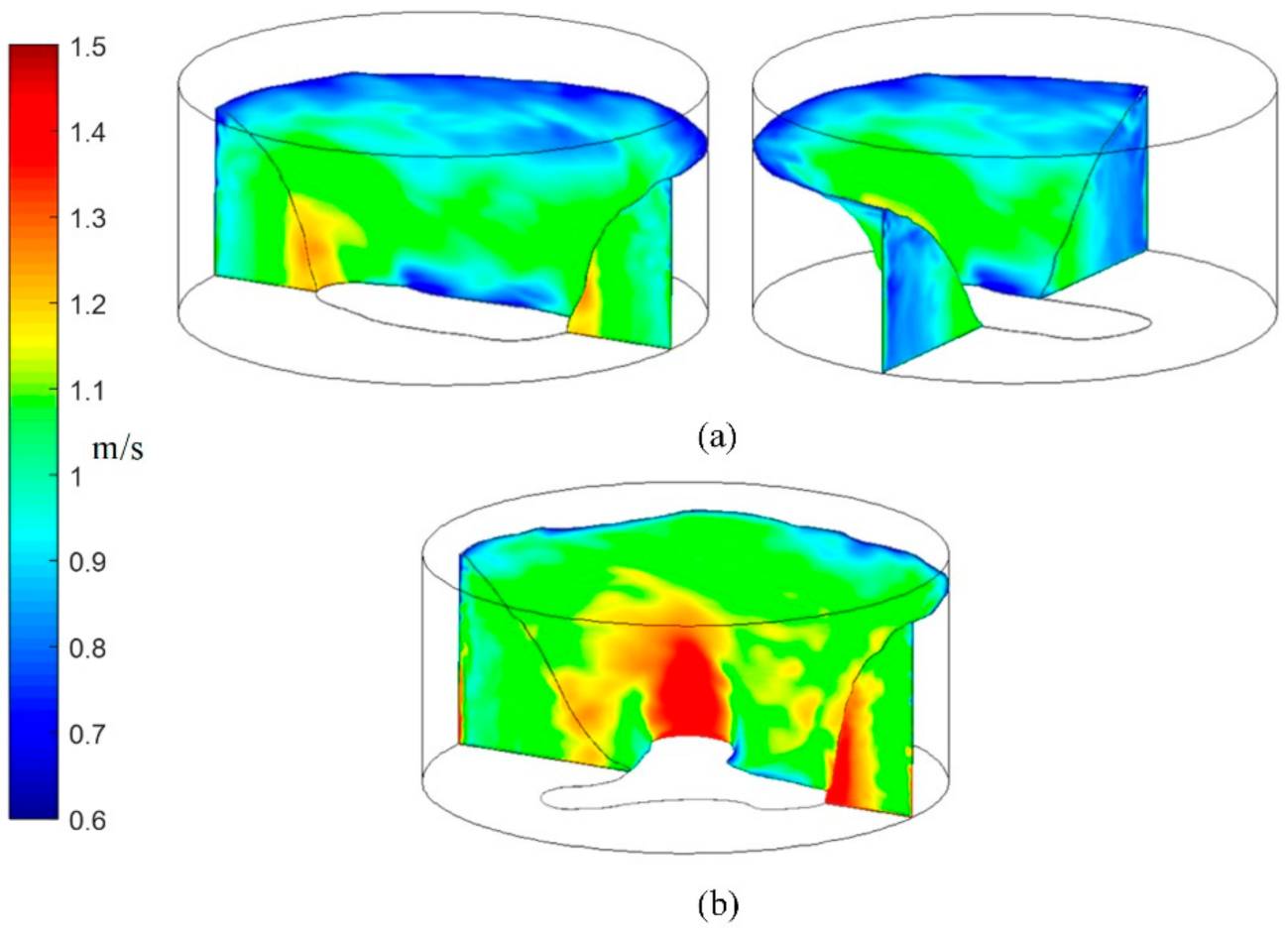
3.3. Velocity Field
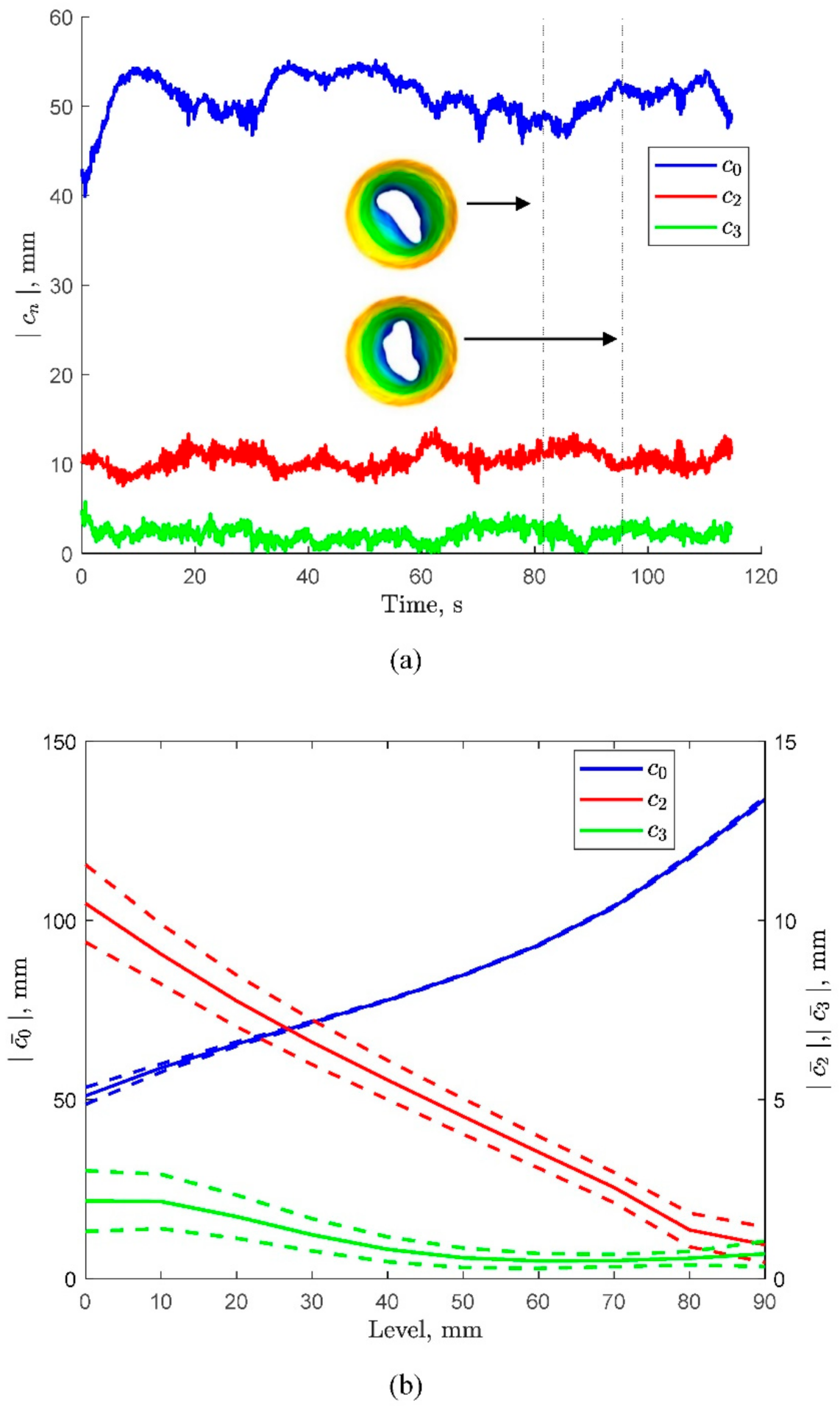
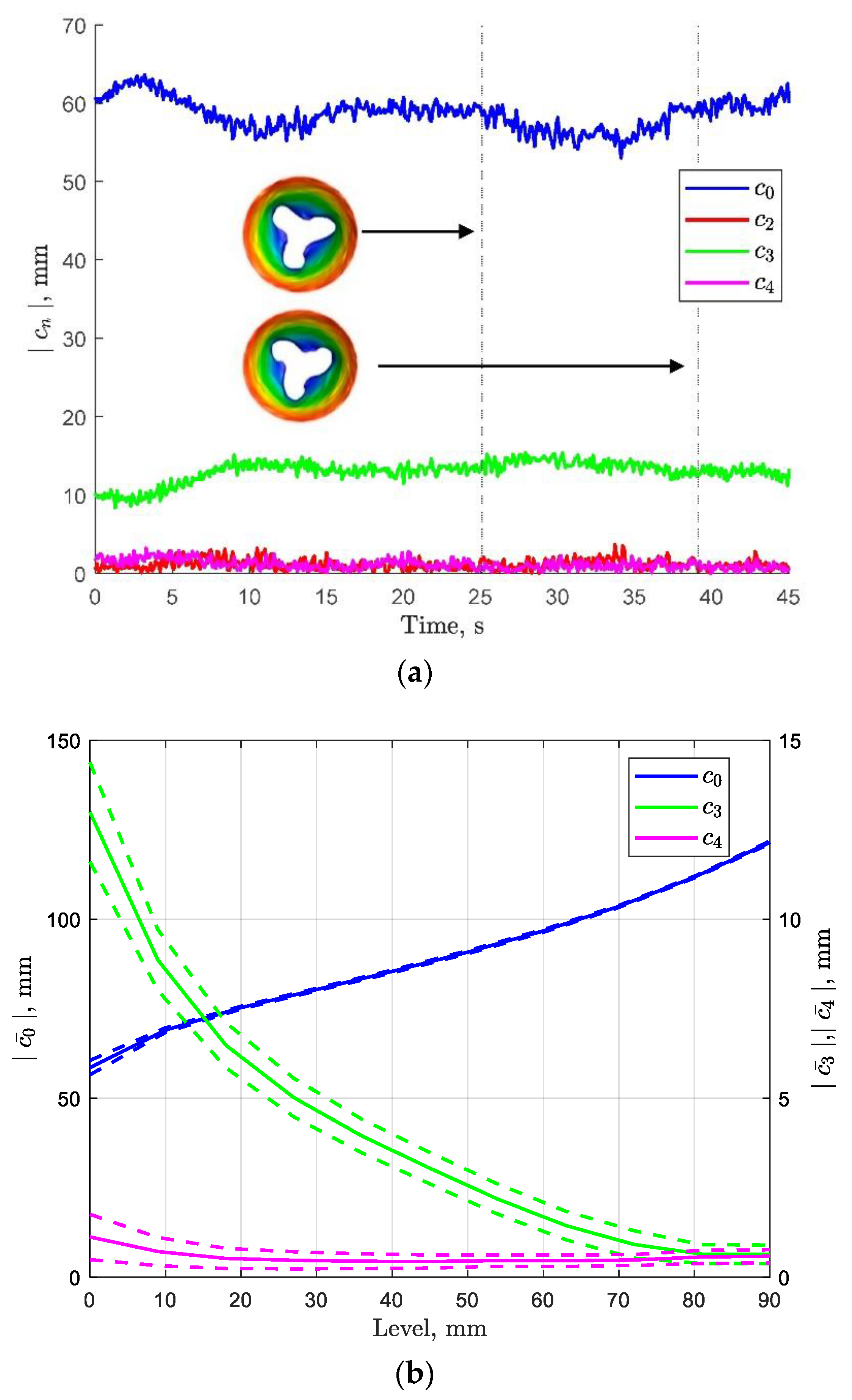
3.4. Fourier Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lugt, H.J. Introduction to Vortex Theory; Vortex Flow Press: Potomac, MD, USA, 1996. [Google Scholar]
- Childs, P.R.N. Rotating Flows; Butterworth-Heinemann (Elsevier): Oxford, UK, 2011. [Google Scholar]
- Andersen, A.; Bohr, T.; Stenum, B.; Rasmussen, J.J.; Lautrup, B. The bathtub vortex in a rotating container. J. Fluid Mech. 2006, 556, 121–146. [Google Scholar] [CrossRef] [Green Version]
- Vatistas, G.H. A note on liquid vortex sloshing and Kelvin’s equilibria. J. Fluid Mech. 1990, 217, 241–248. [Google Scholar] [CrossRef]
- Kelvin, L. Vibrations of a columnar vortex. Philos. Mag. 1880, 10, 155–168. [Google Scholar]
- Vatistas, G.H.; Wang, J.; Lin, S. Experiments on waves induced in the hollow core of vortices. Exp. Fluids 1992, 13, 377–385. [Google Scholar] [CrossRef]
- Jansson, T.R.N.; Haspang, M.P.; Jensen, K.H.; Hersen, P.; Bohr, T. Polygons on a rotating fluid surface. Phys. Rev. Lett. 2006, 96, 174502. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, T.; Iima, M.; Hayase, Y. Surface switching of rotating fluid in a cylinder. Phys. Fluids 2006, 18, 101701. [Google Scholar] [CrossRef]
- Poncet, S.; Chauve, M.P. Shear-layer instability in a rotating system. J. Flow Vis. Image Process. 2007, 14, 85–105. [Google Scholar] [CrossRef]
- Bach, B.; Linnartz, E.C.; Vested, M.H.; Andersen, A.; Bohr, T. From Newton’s bucket to rotating polygons: Experiments on surface instabilities in swirling flows. J. Fluid Mech. 2014, 759, 386–403. [Google Scholar] [CrossRef]
- Abderrahmane, H.A.; Fayed, M.; Ng, H.D.; Vatistas, G.H. Synchronization of traveling waves within a hollow-core vortex. IJMEM 2017, 11, 742–746. [Google Scholar]
- Vatistas, G.H. Comment on “Surface switching of rotating fluid in a cylinder” [Phys. Fluids 18, 101701 (2006)]. Phys. Fluids 2007, 19, 069101. [Google Scholar] [CrossRef] [Green Version]
- Tasaka, Y.; Ito, K.; Iima, M. Visualization of a rotating flow under large-deformed free surface using anisotropic flakes. J. Vis. 2008, 11, 163–172. [Google Scholar] [CrossRef]
- Tasaka, Y.; Iima, M. Flow transitions in the surface switching of rotating fluid. J. Fluid Mech. 2009, 636, 475–484. [Google Scholar] [CrossRef] [Green Version]
- Vatistas, G.H.; Abderrahmane, H.A.; Siddiqui, M.H.K. Experimental confirmation of Kelvin’s equilibria. Phys. Rev. Lett. 2008, 100, 174503. [Google Scholar] [CrossRef]
- Thomson, J.J. A Treatise on the Motion of Vortex Rings—An Essay to Which the Adams Prize Was Adjudged in 1882, in the University of Cambridge; Macmillan: London, UK, 1883. [Google Scholar]
- Havelock, T.H. LII. The stability of motion of rectilinear vortices in ring formation. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1931, 7, 617–633. [Google Scholar] [CrossRef]
- Abderrahamne, H.A.; Siddiqui, K.; Vatistas, G.H. Transition between Kelvin’s equilibria. Phys. Rev. E 2009, 80, 066305. [Google Scholar] [CrossRef]
- Abderrahmane, H.A.; Siddiqui, K.; Vatistas, G.H. Rotating waves within a hollow vortex core. Exp. Fluids 2011, 50, 677–688. [Google Scholar] [CrossRef]
- Abderrahmane, H.A.; Siddiqui, K.; Vatistas, G.H.; Fayed, M.; Ng, H.D. Symmetrization of a polygonal hollow-core vortex through beat-wave resonance. Phys. Rev. E 2011, 83, 056319. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bergmann, R.P.H.M.; Tophøj, L.; Homan, T.A.M.; Hersen, P.; Andersen, A.; Bohr, T. Polygon formation and surface flow on a rotating fluid surface. J. Fluid Mech. 2011, 679, 415, Erratum in 2012, 691, 605. [Google Scholar] [CrossRef] [Green Version]
- Abderrahmane, H.A.; Fayed, M.; Ng, H.D.; Vatistas, G.H. A note on relative equilibria in a rotating shallow water layer. J. Fluid Mech. 2013, 724, 695–703. [Google Scholar] [CrossRef] [Green Version]
- Iga, K.; Yokota, S.; Watanabe, S.; Ikeda, T.; Niino, H.; Misawa, N. Various phenomena on a water vortex in a cylindrical tank over a rotating bottom. Fluid Dyn. Res. 2014, 46, 031409. [Google Scholar] [CrossRef]
- Abderrahmane, H.A.; Fayed, M.; Ng, H.D.; Vatistas, G.H. New experimental confirmation of Kelvin’s equilibria. Eur. Phys. J. Plus 2018, 133, 339. [Google Scholar] [CrossRef]
- Jansson, T.R.N.; Haspang, M.P.; Jensen, K.H. Symmetry Breaking in the Free Surface of Rotating Fluids with High Reynolds Numbers. Bachelor’s Project, University of Copenhagen, Copenhagen, Denmark, December 2004. [Google Scholar]
- Vatistas, G.H.; Wang, J.; Lin, S. Recent findings on Kelvin’s equilibria. ACTA Mech. 1994, 103, 89–102. [Google Scholar] [CrossRef]
- Tophoj, L.; Mougel, J.; Bohr, T.; Fabre, D. Rotating polygon instability of a swirling free surface flow. Phys. Rev. Lett. 2013, 110, 194502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iima, M.; Tasaka, Y. Dynamics of flow structures and surface shapes in the surface switching of rotating fluid. J. Fluid Mech. 2016, 789, 402–424. [Google Scholar] [CrossRef] [Green Version]
- Fabre, D.; Mougel, J. Generation of three-dimensional patterns through wave interaction in a model of free surface swirling flow. Fluid Dyn. Res. 2014, 46, 061415. [Google Scholar] [CrossRef]
- Amaouche, M.; Abderrahmane, H.A.; Vatistas, G.H. Nonlinear modes in the hollow-cores of liquid vortices. Eur. J. Mech. B/Fluids 2013, 41, 133–137. [Google Scholar] [CrossRef]
- Yellin-Bergovoy, R.; Heifetz, E.; Umurhan, O.M. Physical mechanism of centrifugal-gravity wave resonant instability in azimuthally symmetric swirling flows. Phys. Rev. Fluids 2017, 2, 104801. [Google Scholar] [CrossRef]
- Mougel, J.; Fabre, D.; Lacaze, L.; Bohr, T. On the instabilities of a potential vortex with a free surface. J. Fluid Mech. 2017, 824, 230–264. [Google Scholar] [CrossRef] [Green Version]
- Spohn, A.; Mory, M.; Hopfinger, E.J. Observations of vortex breakdown in an open with a rotating bottom. Exp. Fluids 1993, 14, 70–77. [Google Scholar] [CrossRef]
- Brøns, M.; Voigt, L.K.; Sørensen, J.N. Topology of vortex breakdown bubbles in a cylinder with a rotating bottom and a free surface. J. Fluid Mech. 2001, 428, 133–148. [Google Scholar] [CrossRef]
- Bouffanais, R.; Jacono, D.L. Transitional cylindrical swirling flow in presence of a flat free surface. Comput. Fluids 2009, 38, 1651–1673. [Google Scholar] [CrossRef] [Green Version]
- Bouffanais, R.; Jacono, D.L. Unsteady transitional swirling flow in the presence of a moving free surface. Phys. Fluids 2009, 21, 64107. [Google Scholar] [CrossRef] [Green Version]
- Miraghaie, R.; Lopez, J.M.; Hirsa, A.H. Flow induced patterning at the air–water interface. Phys. Fluids 2003, 15, L45. [Google Scholar] [CrossRef] [Green Version]
- Lopez, J.M.; Marques, F.; Hirsa, A.H.; Miraghaie, R. Symmetry breaking in free-surface cylinder flows. J. Fluid Mech. 2004, 502, 99–126. [Google Scholar] [CrossRef] [Green Version]
- Valentine, D.T.; Jahnke, C.C. Flows induced in a cylinder with both end walls rotating. Phys. Fluids 1994, 6, 2702–2710. [Google Scholar] [CrossRef]
- Lopez, J.M. Unsteady swirling flow in an enclosed cylinder with reflectional symmetry. Phys. Fluids 1995, 7, 2700–2714. [Google Scholar] [CrossRef] [Green Version]
- Gelfgat, A.; Bar-Yoseph, P.Z.; Solan, A. Three-dimensional instability of axisymmetric flow in a rotating lid–cylinder enclosure. J. Fluid Mech. 2001, 438, 363–377. [Google Scholar] [CrossRef] [Green Version]
- Marques, F.; Lopez, J.M. Precessing vortex breakdown mode in an enclosed cylinder flow. Phys. Fluids 2001, 13, 1679–1682. [Google Scholar] [CrossRef] [Green Version]
- Poncet, S. The stability of a thin water layer over a rotating disk revisited. Eur. Phys. J. Plus 2014, 129, 167. [Google Scholar] [CrossRef]
- Kahouadji, L. Analyse de Stabilité Linéaire D’écoulements Tournants en Présence de Surface Libre. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2011. [Google Scholar]
- Niino, H.; Misawa, N. An Experimental and theoretical study of barotropic instability. J. Atmos. Sci. 1984, 41, 1992–2011. [Google Scholar] [CrossRef] [Green Version]
- Kahouadji, L.; Witkowski, L.M. Free surface due to a flow driven by a rotating disk inside a vertical cylindrical tank: Axisymmetric configuration. Phys. Fluids 2014, 26, 072105. [Google Scholar] [CrossRef] [Green Version]
- Piva, M.; Meiburg, E. Steady axisymmetric flow in an open cylindrical container with a partially rotating bottom wall. Phys. Fluids 2005, 17, 063603. [Google Scholar] [CrossRef]
- Yang, W.; Delbende, I.; Fraigneau, Y.; Witkowski, L.M. Axisymmetric rotating flow with free surface in a cylindrical tank. J. Fluid Mech. 2018, 861, 796–814. [Google Scholar] [CrossRef] [Green Version]
- Iga, K. Axisymmetric flow in a cylindrical tank over a rotating bottom. Part I. Analysis of boundary layers and vertical circulation. Fluid Dyn. Res. 2017, 49, 065502. [Google Scholar] [CrossRef]
- Iga, K.; Yokota, S.; Watanabe, S.-I.I.; Ikeda, T.; Niino, H.; Misawa, N. Axisymmetric flow in a cylindrical tank over a rotating bottom. Part II. Deformation of the water surface and experimental verification of the theory. Fluid Dyn. Res. 2017, 49, 065501. [Google Scholar] [CrossRef] [Green Version]
- Ansys® Fluent, Release 19.0.0; ANSYS Inc.: Canonsburg, PA, USA, 2019.
- Silva, M.F.; Campos, J.B.L.M.; Miranda, J.M.; Araújo, J.D.P. Numerical study of single Taylor bubble movement through a microchannel using different CFD packages. Processes 2020, 8, 1418. [Google Scholar] [CrossRef]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kim, W.W.; Menon, S. An unsteady incompressible Navier–Stokes solver for large eddy simulation of turbulent flows. Int. J. Numer. Methods Fluids 1999, 31, 983–1017. [Google Scholar] [CrossRef]
- Pallares, J.; Davidson, L. Large-eddy simulations of turbulent flow in a rotating square duct. Phys. Fluids 2000, 12, 2878. [Google Scholar] [CrossRef]
- McSherry, R.J.; Chua, K.V.; Stoesser, T. Large eddy simulation of free-surface flows. J. Hydrodyn. 2017, 29, 1–12. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef] [Green Version]
- Gopala, V.R.; van Wachem, B.G. Volume of fluid methods for immiscible-fluid and free-surface flows. Chem. Eng. J. 2008, 141, 204–221. [Google Scholar] [CrossRef]
- Sethian, J.A.; Smereka, P. Level set methods for fluid interfaces. Annu. Rev. Fluid Mech. 2003, 35, 341–372. [Google Scholar] [CrossRef] [Green Version]
- Yue, W.; Lin, C.-L.; Patel, V.C. Large eddy simulation of turbulent open-channel flow with free surface simulated by level set method. Phys. Fluids 2005, 17, 25108. [Google Scholar] [CrossRef]
- Suh, J.; Yang, J.; Stern, F. The effect of air–water interface on the vortex shedding from a vertical circular cylinder. J. Fluids Struct. 2011, 27, 1–22. [Google Scholar] [CrossRef]
- Sussman, M.; Puckett, E.G. A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows. J. Comput. Phys. 2000, 162, 301–337. [Google Scholar] [CrossRef] [Green Version]
- Zi, D.; Xuan, A.; Wang, F.; Shen, L. Numerical study of mechanisms of air-core vortex evolution in an intake flow. Int. J. Heat Fluid Flow 2020, 81, 108517. [Google Scholar] [CrossRef]
- Stachnik, M.; Jakubowski, M. Multiphase model of flow and separation phases in a whirlpool: Advanced simulation and phenomena visualization approach. J. Food Eng. 2020, 274, 109846. [Google Scholar] [CrossRef]
- McCraney, J.; Weislogel, M.; Steen, P. OpenFOAM Simulations of late stage container draining in microgravity. Fluids 2020, 5, 207. [Google Scholar] [CrossRef]
- Tembely, M.; Alameri, W.S.; Alsumaiti, A.M.; Jouini, M.S. Pore-scale modeling of the effect of wettability on two-phase flow properties for newtonian and non-newtonian fluids. Polymers 2020, 12, 2832. [Google Scholar] [CrossRef]
- Celik, I.B.; Cehreli, Z.N.; Yavuz, I. Index of resolution quality for large eddy simulations. J. Fluids Eng. 2005, 127, 949–958. [Google Scholar] [CrossRef]
- Klein, M.; Meyers, J.; Geurts, B.J. Assessment of LES quality measures using the error landscape approach. In Direct and Large-Eddy Simulation VII; Springer Nature: Berlin/Heidelberg, Germany, 2008; Volume 12, pp. 131–142. [Google Scholar]
- Pope, S.B. Turbulent Flows. Meas. Sci. Technol. 2001, 12, 2020–2021. [Google Scholar] [CrossRef]
- Mulligan, S.; De Cesare, G.; Casserly, J.; Sherlock, R. Understanding turbulent free-surface vortex flows using a Taylor-Couette flow analogy. Sci. Rep. 2018, 8, 824. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jakubowski, M.; Diakun, J. Simulation investigations of the effects of whirlpool dimensional ratios on the state of secondary whirls. J. Food Eng. 2007, 83, 106–110. [Google Scholar] [CrossRef]
- Jakubowski, M.; Wyczalkowski, W.; Poreda, A. Flow in a symmetrically filled whirlpool: CFD modelling and experimental study based on Particle Image Velocimetry (PIV). J. Food Eng. 2015, 145, 64–72. [Google Scholar] [CrossRef]







| r mm | R mm | h mm | ω rad/s | ν × 106 m2/s | Re = ωr2/ν | Fr = ωr/(gh)0.5 | h/R | r/R | Detectable Polygons—N | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vatistas [4] | 126 | 142.5 | 150 | 25.1 | 1 a | 3.99 × 105 | 2.61 | 1.05 | 0.88 | No, periodic sloshing without surface exposed |
| 126 | 142.5 | 293 | 81.7 | 1.30 × 106 | 6.07 | 2.06 | 0–2, periodic sloshing with surface exposed from circular to elliptical cross section | |||
| 101 a | 142.5 | 63 | 10.5–31.4 | 1.07 × 105–3.20 × 105 | 1.35–4.04 | 0.44 | 0.71 | 0–6 | ||
| 69 | 1.29–3.86 | 0.48 | 0–5 | |||||||
| Vatistas et al. [6] | 126 | 142 | 24, 27 | 5.2–25.1 | 1 | 8.31 × 104–4.16 × 105 | 1.28–6.80 | 0.17–0.19 | 0.89 | 0–6 |
| 5 | 18.8–31.4 | 56.7 | 5.28 × 103–8.80 × 103 | 10.72–17.87 | 0.04 | 5–11 | ||||
| 7 | 15.7–25.1 | 4.40 × 103–7.04 × 103 | 7.55–12.08 | 0.05 | 5–10 | |||||
| 10 | 19.9–30.4 | 5.57 × 103–8.50 × 103 | 8.00–12.22 | 0.07 | 4–8 | |||||
| 22 | 15.7–27.2 | 4.40 × 103–1.09 × 105 | 0.61–7.38 | 0.15 | 0–8 | |||||
| >100 | >83.8 | 640 | >2.08 × 103 | >10.66 | 0.70 | 0 | ||||
| Jansson et al. [7] | 144 b | 145b | 25–100 | 3.1–44.0 | 1 c | 6.51 × 104–9.12 × 105 | 0.46–12.79 | 0.17–0.69 | 0.99 | 0–6 |
| 15 | 4.34 × 103–6.08 × 104 | 0–3 | ||||||||
| 193 | 194 | 25–95 | 3.1–31.4 | 1 c | 1.17 × 105–1.17 × 106 | 0.61–12.24 | 0.13–0.52 | 0–5 | ||
| Suzuki et al. [8] | 42 | 42.5 | 40 | <146.4 | 1 | <2.58 × 105 | <9.82 | 0.94 | 0.99 | 0–2, surface exposed from circular to elliptical cross sections |
| Poncet and Chauve [9] | 140 | 140.85 ± 0.05 | 2.5–15 | 0–6.2 | 1 | ≤1.21 × 105 | 2.25–5.52 | ≤0.11 | 0.99 | 0–8 without 2 |
| Bach et al. [10] | 144 | 145 | 30-80 | 2.5–40.8 | 1 | 5.21 × 104 – 8.47 × 105 | 0.41–10.48 | 0.21–0.55 | 0.99 | 0-5 |
| Ait Abderrahmane et al. [11] | 140 | 142 | 20, 30, 40 | 7.9–28.0 | 1-22 d | 7.00 × 103–5.48 × 105 | 1.76–8.84 | 0.14–0.28 | 0.99 | 0–6 |
| Present study | 145 | 145 | 60 | 18.8, 21.4, 25.1, 28.9 | 1 | 3.96 × 105–6.08 × 105 | 3.56–5.46 | 0.41 | 1 | 0–3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashkovan, A.; Amar, S.D.; Bieder, U.; Ziskind, G. Analysis of Polygonal Vortex Flows in a Cylinder with a Rotating Bottom. Appl. Sci. 2021, 11, 1348. https://doi.org/10.3390/app11031348
Rashkovan A, Amar SD, Bieder U, Ziskind G. Analysis of Polygonal Vortex Flows in a Cylinder with a Rotating Bottom. Applied Sciences. 2021; 11(3):1348. https://doi.org/10.3390/app11031348
Chicago/Turabian StyleRashkovan, A., S.D. Amar, U. Bieder, and G. Ziskind. 2021. "Analysis of Polygonal Vortex Flows in a Cylinder with a Rotating Bottom" Applied Sciences 11, no. 3: 1348. https://doi.org/10.3390/app11031348
APA StyleRashkovan, A., Amar, S. D., Bieder, U., & Ziskind, G. (2021). Analysis of Polygonal Vortex Flows in a Cylinder with a Rotating Bottom. Applied Sciences, 11(3), 1348. https://doi.org/10.3390/app11031348





