Binary Spring Search Algorithm for Solving Various Optimization Problems
Abstract
1. Introduction
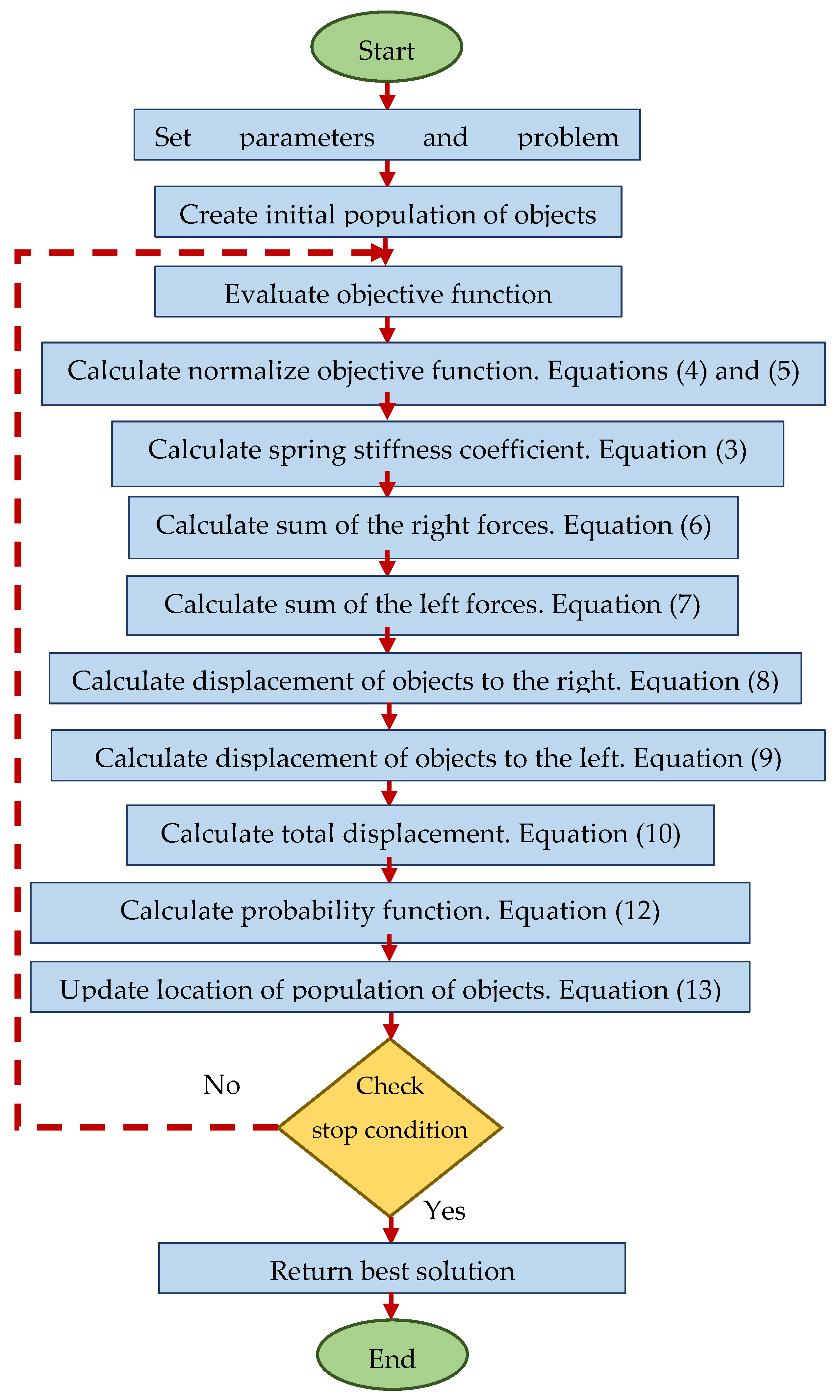
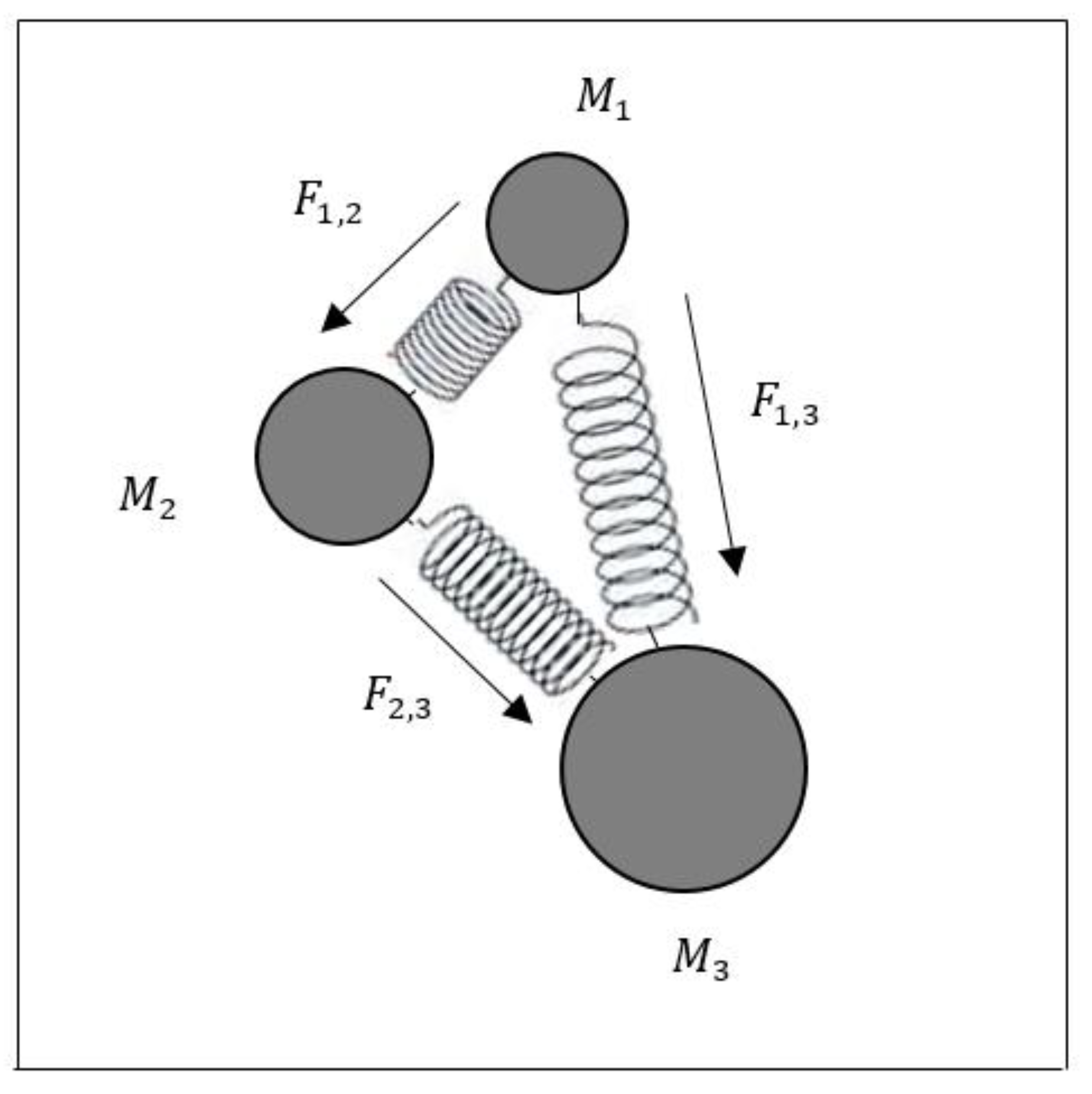
2. Spring Search Algorithm
2.1. BSSA Formulation
2.2. BSSA Implantation
3. Binary Spring Search Algorithm (BSSA)
4. Features of the BSSA
5. Computational Complexity
5.1. Time Complexity
5.2. Space Complexity
6. Exploration and Exploitation of the BSSA
7. Simulation Results
Statistical Testing
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dehghani, M.; Samet, H. Momentum search algorithm: A new meta-heuristic optimization algorithm inspired by momentum conservation law. SN Appl. Sci. 2020, 2, 1720. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Dehghani, A.; Samet, H.; Sotelo, C.; Sotelo, D.; Ehsanifar, A.; Malik, O.P.; Guerrero, J.M.; Dhiman, G.; et al. DM: Dehghani Method for Modifying Optimization Algorithms. Appl. Sci. 2020, 10, 7683. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Dhiman, G.; Malik, O.P.; Morales-Menendez, R.; Ramirez-Mendoza, R.A.; Dehghani, A.; Guerrero, J.M.; Parra-Arroyo, L. A Spring Search Algorithm Applied to Engineering Optimization Problems. Appl. Sci. 2020, 10, 6173. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Malik, O. Energy Commitment: A Planning of Energy Carrier Based on Energy Consumption. Electr. Eng. Electromech. 2019, 4, 69–72. [Google Scholar] [CrossRef]
- Dehghani, M.; Mardaneh, M.; Malik, O.P.; Guerrero, J.M.; Sotelo, C.; Sotelo, D.; Nazari-Heris, M.; Al-Haddad, K.; Ramirez-Mendoza, R.A. Genetic Algorithm for Energy Commitment in a Power System Supplied by Multiple Energy Carriers. Sustainability 2020, 12, 10053. [Google Scholar] [CrossRef]
- Ehsanifar, A.; Dehghani, M.; Allahbakhshi, M. Calculating the leakage inductance for transformer inter-turn fault detection using finite element method. In Proceedings of the 2017 Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2–4 May 2017; pp. 1372–1377. [Google Scholar]
- Dehghani, M.; Montazeri, Z.; Malik, O.P. Optimal Sizing and Placement of Capacitor Banks and Distributed Generation in Distribution Systems Using Spring Search Algorithm. Int. J. Emerg. Electr. Power Syst. 2020, 21. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Malik, O.P.; Al-Haddad, K.; Guerrero, J.M.; Dhiman, G. A New Methodology Called Dice Game Optimizer for Capacitor Placement in Distribution Systems. Electr. Eng. Electromech. 2020, 1, 61–64. [Google Scholar] [CrossRef]
- Dehbozorgi, S.; Ehsanifar, A.; Montazeri, Z.; Dehghani, M.; Seifi, A. Line loss reduction and voltage profile improvement in radial distribution networks using battery energy storage system. In Proceedings of the 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 22–22 December 2017; pp. 0215–0219. [Google Scholar]
- Montazeri, Z.; Niknam, T. Optimal Utilization of Electrical Energy from Power Plants Based on Final Energy Consumption Using Gravitational Search Algorithm. Electr. Eng. Electromech. 2018, 4, 70–73. [Google Scholar] [CrossRef]
- Dehghani, M.; Mardaneh, M.; Montazeri, Z.; Ehsanifar, A.; Ebadi, M.J.; Grechko, O. Spring Search Algorithm for Simultaneous Placement of Distributed Generation and Capacitors. Electr. Eng. Electromech. 2018, 6, 68–73. [Google Scholar] [CrossRef]
- Pelusi, D.; Mascella, R.; Tallini, L.G. A Fuzzy Gravitational Search Algorithm to Design Optimal IIR Filters. Energies 2018, 11, 736. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Ehsanifar, A.; Seifi, A.; Ebadi, M.; Grechko, O.M. Planning of Energy Carriers Based on Final Energy Consumption Using Dynamic Programming and Particle Swarm Optimization. Electr. Eng. Electromech. 2018, 5, 62–71. [Google Scholar] [CrossRef]
- Montazeri, Z.; Niknam, T. Energy carriers management based on energy consumption. In Proceedings of the 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 22–22 December 2017; pp. 0539–0543. [Google Scholar]
- Pelusi, D.; Mascella, R.; Tallini, L.G.; Nayak, J.; Naik, B.; Deng, Y. Improving exploration and exploitation via a Hyperbolic Gravitational Search Algorithm. Knowl. Based Syst. 2020, 193, 105404. [Google Scholar] [CrossRef]
- Pelusi, D.; Mascella, R.; Tallini, L.G.; Nayak, J.; Naik, B.; Deng, Y. An Improved Moth-Flame Optimization algorithm with hybrid search phase. Knowl. Based Syst. 2020, 191, 105277. [Google Scholar] [CrossRef]
- Pelusi, D.; Mascella, R.; Tallini, L.G.; Nayak, J.; Naik, B.; Abraham, A. Neural network and fuzzy system for the tuning of Gravitational Search Algorithm parameters. Expert Syst. Appl. 2018, 102, 234–244. [Google Scholar] [CrossRef]
- Gigerenzer, G.; Todd, P.M. Simple Heuristics that Make Us Smart; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Lazar, A. Heuristic knowledge discovery for archaeological data using genetic algorithms and rough sets. Heuristics Optim. Knowl. Discov. 2002, 263. [Google Scholar] [CrossRef]
- Gigerenzer, G.; Gaissmaier, W. Heuristic Decision Making. Annu. Rev. Psychol. 2011, 62, 451–482. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. A heuristic algorithm and simulation approach to relative location of facilities. Optim. Simulated Annealing 1983, 220, 671–680. [Google Scholar]
- Shah-Hosseini, H. Principal components analysis by the galaxy-based search algorithm: A novel metaheuristic for continuous optimisation. Int. J. Comput. Sci. Eng. 2011, 6, 132. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Moghaddam, F.F.; Moghaddam, R.F.; Cheriet, M. Curved space optimization: A random search based on general relativity theory. arXiv 2012, arXiv:1208.2214. [Google Scholar]
- Alatas, B. ACROA: Artificial Chemical Reaction Optimization Algorithm for global optimization. Expert Syst. Appl. 2011, 38, 13170–13180. [Google Scholar] [CrossRef]
- Kaveh, A.; Khayatazad, M. A new meta-heuristic method: Ray Optimization. Comput. Struct. 2012, 112, 283–294. [Google Scholar] [CrossRef]
- Du, H.; Wu, X.; Zhuang, J. Small-World Optimization Algorithm for Function Optimization. In Proceedings of the Second International Conference on Advances in Natural Computation; Springer: Berlin/Heidelberg, Germany, 2006; pp. 264–273. [Google Scholar]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Formato, R.A. Central force optimization: A new nature inspired computational framework for multidimensional search and optimization. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2007); Springer: Berlin/Heidelberg, Germany, 2008; pp. 221–238. [Google Scholar]
- Erol, O.K.; Eksin, I. A new optimization method: Big Bang–Big Crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE Service Center: Piscataway, NY, USA, 1942; Volume 1948. [Google Scholar]
- Yang, X.-S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Karaboga, D.; Basturk, B. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization, problems. In Proceedings of the 12th International Fuzzy Systems Association World Congress on Foundations of Fuzzy Logic and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Dehghani, M.; Mardaneh, M.; Guerrero, J.M.; Malik, O.P.; Ramirez-Mendoza, R.A.; Matas, J.; Vasquez, J.C.; Parra-Arroyo, L. A New “Doctor and Patient” Optimization Algorithm: An Application to Energy Commitment Problem. Appl. Sci. 2020, 10, 5791. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications. Adv. Eng. Softw. 2017, 114, 48–70. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Dehghani, A.; Mendoza, R.R.; Samet, H.; Guerrero, J.M.; Dhiman, G. MLO: Multi Leader Optimizer. Int. J. Intell. Eng. Syst. 2020, 13, 364–373. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Dehghani, A.; Malik, O.P. GO: Group Optimization. GAZI Univ. J. Sci. 2020, 33, 381–392. [Google Scholar] [CrossRef]
- Mucherino, A.; Seref, O. Monkey Search: A Novel Metaheuristic Search for Global Optimization. AIP Conf. Proc. 2007, 953, 162–173. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M.; Toosi, A.N. Artificial fish swarm algorithm: A survey of the state-of-the-art, hybridization, combinatorial and indicative applications. Artif. Intell. Rev. 2014, 42, 965–997. [Google Scholar] [CrossRef]
- Oftadeh, R.; Mahjoob, M.J.; Shariatpanahi, M. A novel meta-heuristic optimization algorithm inspired by group hunting of animals: Hunting search. Comput. Math. Appl. 2010, 60, 2087–2098. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Emperor penguin optimizer: A bio-inspired algorithm for engineering problems. Knowl. Based Syst. 2018, 159, 20–50. [Google Scholar] [CrossRef]
- Shiqin, Y.; Jianjun, J.; Guangxing, Y. A dolphin partner optimization. In Proceedings of the Global Congress on Intelligent Systems, Xiamen, China, 19–21 May 2009; pp. 124–128. [Google Scholar]
- Dehghani, M.; Mardaneh, M.; Malik, O.P.; NouraeiPour, S.M. DTO: Donkey Theorem Optimization. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019; pp. 1855–1859. [Google Scholar]
- Dhiman, G.; Garg, M.; Nagar, A.; Kumar, V.; Dehghani, M. A novel algorithm for global optimization: Rat Swarm Optimizer. J. Ambient. Intell. Humaniz. Comput. 2020. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Zhang, H.; Hui, Q. A Coupled Spring Forced Bat Searching Algorithm: Design, Analysis and Evaluation. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 5016–5021. [Google Scholar]
- Dehghani, M.; Mardaneh, M.; Malik, O. FOA: ‘Following’ Optimization Algorithm for solving power engineering optimization problems. J. Oper. Autom. Power Eng. 2020, 8, 57–64. [Google Scholar]
- Dehghani, M.; Mardaneh, M.; Guerrero, J.M.; Malik, O.P.; Kumar, V. Football Game Based Optimization: An Application to Solve Energy Commitment Problem. Int. J. Intell. Eng. Syst. 2020, 13, 514–523. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Malik, O.P.; Dhiman, G.; Kumar, V. BOSA: Binary Orientation Search Algorithm. Int. J. Innov. Technol. Explor. Eng. 2019, 9, 5306–5310. [Google Scholar]
- Dehghani, M.; Montazeri, Z.; Givi, H.; Guerrero, J.M.; Dhiman, G. Darts Game Optimizer: A New Optimization Technique Based on Darts Game. Int. J. Intell. Eng. Syst. 2020, 13, 286–294. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Malik, O.P.; Ehsanifar, A.; Dehghani, A. OSA: Orientation Search Algorithm. Int. J. Ind. Electron. Control Optim. 2019, 2, 99–112. [Google Scholar]
- Mohammad, D.; Zeinab, M.; Malik, O.P.; Givi, H.; Guerrero, J.M. Shell Game Optimization: A Novel Game-Based Algorithm. Int. J. Intell. Eng. Syst. 2020, 13, 246–255. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Malik, O.P. DGO: Dice Game Optimizer. GAZI Univ. J. Sci. 2019, 32, 871–882. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Saremi, S.; Dehghani, A.; Malik, O.P.; Al-Haddad, K.; Guerrero, J.M. HOGO: Hide Objects Game Optimization. Int. J. Intell. Eng. Syst. 2020, 13, 216–225. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Deng, W.; Liu, H.; Xu, J.; Zhao, H.; Song, Y. An Improved Quantum-Inspired Differential Evolution Algorithm for Deep Belief Network. IEEE Trans. Instrum. Meas. 2020, 69, 7319–7327. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Fogel, L.J.; Owens, A.J.; Walsh, M.J. Artificial Intelligence through Simulated Evolution; Wiley: NewYork, NY, USA, 1966. [Google Scholar]
- Beyer, H.-G.; Schwefel, H.-P. Evolution strategies—A comprehensive introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Mirjalili, S. Particle Swarm Optimisation. In Evolutionary Algorithms and Neural Networks; Springer: Berlin/Heidelberg, Germany, 2019; pp. 15–31. [Google Scholar]
- Tarasewich, P.; McMullen, P.R. Swarm intelligence: Power in numbers. Commun. ACM 2002, 45, 62–67. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organization and Associative Memory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 8. [Google Scholar]
- Dehghani, M.; Montazeri, Z.; Dehghani, A.; Nouri, N.; Seifi, A. BSSA: Binary spring search algorithm. In Proceedings of the 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 22–22 December 2017; pp. 220–224. [Google Scholar]
- Halliday, D.; Resnick, R.; Walker, J. Fundamentals of Physics; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Eiben, A.E.; Schippers, C.A. On Evolutionary Exploration and Exploitation. Fundam. Inform. 1998, 35, 35–50. [Google Scholar] [CrossRef]
- Lynn, N.; Suganthan, P.N. Heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation. Swarm Evol. Comput. 2015, 24, 11–24. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, Y.; Hua, C.; Guan, X. A new particle swarm optimization algorithm with adaptive inertia weight based on Bayesian techniques. Appl. Soft Comput. 2015, 28, 138–149. [Google Scholar] [CrossRef]
- Castillo, O.; Aguilar, L.T. Genetic Algorithms. In Type-2 Fuzzy Logic in Control of Nonsmooth Systems; Springer: Berlin/Heidelberg, Germany, 2019; pp. 23–39. [Google Scholar]
- Bala, I.; Yadav, A. Gravitational Search Algorithm: A State-of-the-Art Review. In Harmony Search and Nature Inspired Optimization Algorithms; Springer: Berlin/Heidelberg, Germany, 2019; pp. 27–37. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.-S. Binary bat algorithm. Neural Comput. Appl. 2014, 25, 663–681. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Eleyan, D.; Jaber, I.; Hammouri, A.; Mirjalili, S. Binary Dragonfly Algorithm for Feature Selection. In Proceedings of the 2017 International Conference on New Trends in Computing Sciences (ICTCS), Amman, Jordan, 11–13 October 2017; pp. 12–17. [Google Scholar]
- Mafarja, M.; Aljarah, I.; Faris, H.; Hammouri, A.I.; Ala’M, A.-Z.; Mirjalili, S. Binary grasshopper optimisation algorithm approaches for feature selection problems. Expert Syst. Appl. 2019, 117, 267–286. [Google Scholar] [CrossRef]
- Daniel, W.W. Friedman two-way analysis of variance by ranks. In Applied Nonparametric Statistics; PWS-Kent: Boston, MA, USA, 1990; pp. 262–274. [Google Scholar]
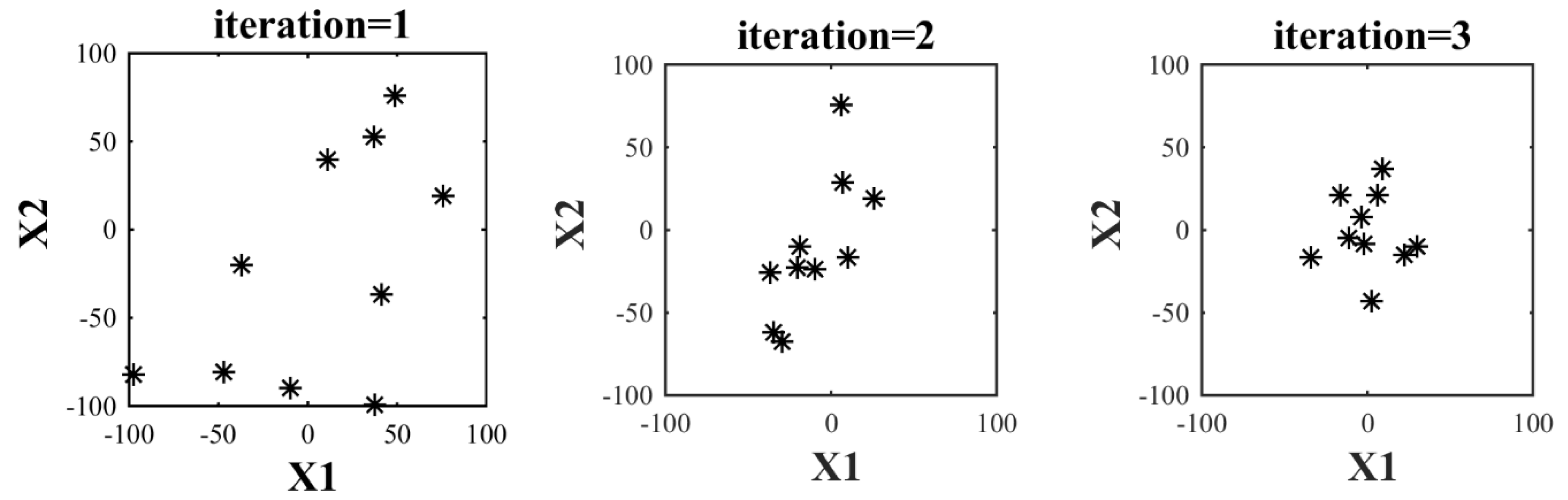
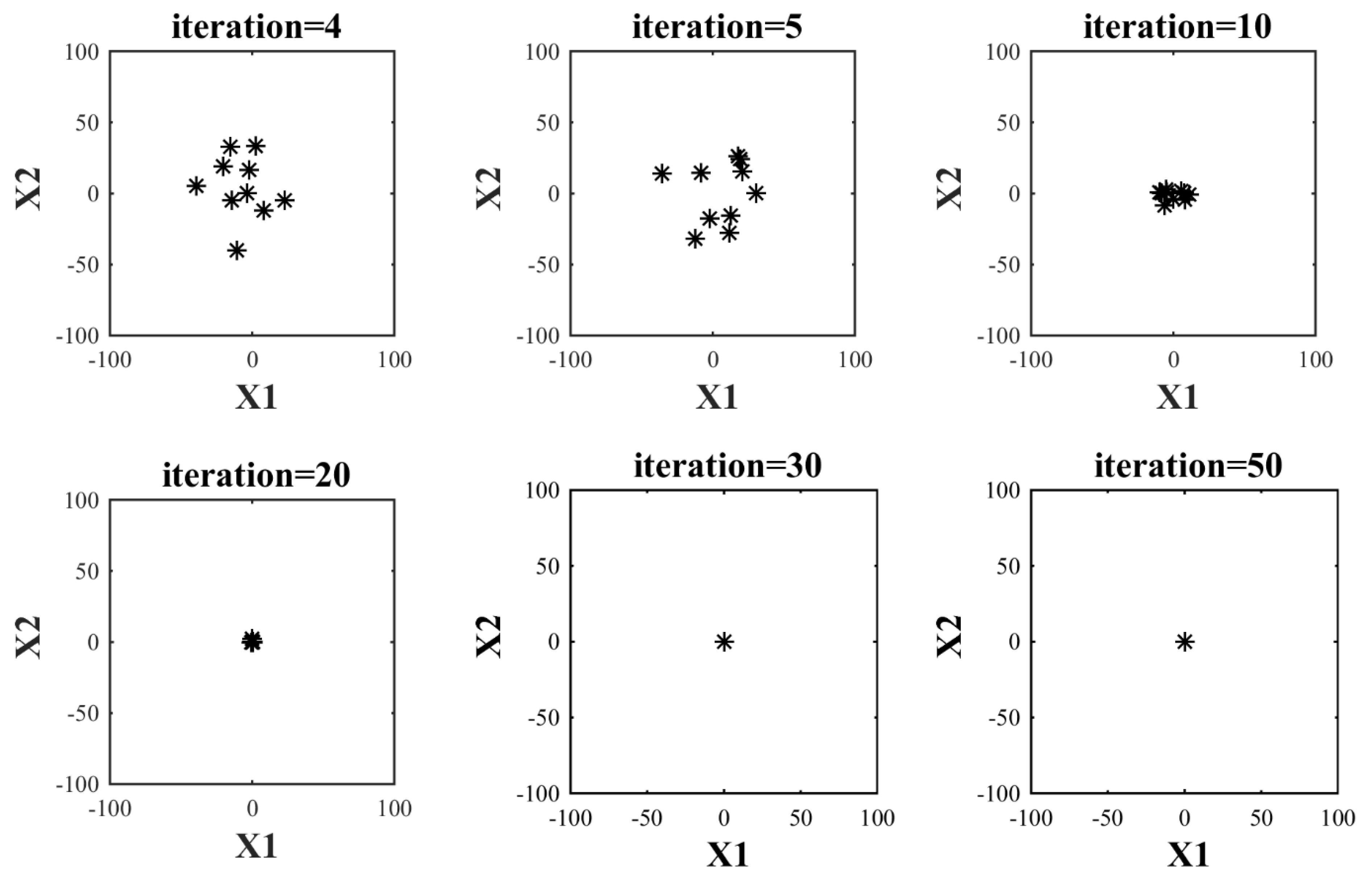
| Iteration = 1 | Iteration = 2 | Iteration = 3 | ||||||
|---|---|---|---|---|---|---|---|---|
| F(x) | F(x) | F(x) | ||||||
| 4.13E+01 | −3.70E+01 | 3.07E+03 | −1.90E+01 | −9.82E+00 | 4.59E+02 | 3.01E+01 | −9.82E+00 | 1.00E+03 |
| −4.72E+01 | −8.09E+01 | 8.77E+03 | −3.49E+01 | −6.17E+01 | 5.02E+03 | 2.47E+00 | −4.32E+01 | 1.87E+03 |
| 1.13E+01 | 3.96E+01 | 1.70E+03 | −3.69E+01 | −2.55E+01 | 2.01E+03 | −3.44E+01 | −1.65E+01 | 1.46E+03 |
| 7.58E+01 | 1.93E+01 | 6.11E+03 | 2.60E+01 | 1.93E+01 | 1.05E+03 | −3.62E+00 | 7.90E+00 | 7.55E+01 |
| −3.72E+01 | −2.03E+01 | 1.80E+03 | 9.97E+00 | −1.65E+01 | 3.73E+02 | −1.10E+01 | −4.78E+00 | 1.44E+02 |
| 4.90E+01 | 7.61E+01 | 8.20E+03 | 6.19E+00 | 7.57E+01 | 5.77E+03 | 6.19E+00 | 2.10E+01 | 4.78E+02 |
| 3.68E+01 | 5.27E+01 | 4.13E+03 | 7.16E+00 | 2.89E+01 | 8.85E+02 | −1.65E+01 | 2.13E+01 | 7.24E+02 |
| −9.73E+01 | −8.21E+01 | 1.62E+04 | −2.97E+01 | −6.76E+01 | 5.45E+03 | −2.16E+00 | −8.32E+00 | 7.39E+01 |
| −9.95E+00 | −8.96E+01 | 8.13E+03 | −9.95E+00 | −2.38E+01 | 6.63E+02 | 2.23E+01 | −1.52E+01 | 7.29E+02 |
| 3.74E+01 | −9.96E+01 | 1.13E+04 | −2.04E+01 | −2.28E+01 | 9.37E+02 | 9.06E+00 | 3.67E+01 | 1.43E+03 |
| Iteration = 4 | Iteration = 5 | Iteration = 10 | ||||||
| F(x) | F(x) | F(x) | ||||||
| 2.41E+00 | 3.35E+01 | 1.13E+03 | −3.54E+01 | 1.38E+01 | 1.45E+03 | −5.37E+00 | 2.83E+00 | 3.68E+01 |
| −1.08E+01 | −3.98E+01 | 1.70E+03 | 1.16E+01 | −2.78E+01 | 9.10E+02 | −8.39E+00 | 2.79E−01 | 7.05E+01 |
| −3.47E+00 | 1.06E−01 | 1.20E+01 | 3.05E+01 | 1.06E−01 | 9.32E+02 | 7.56E+00 | 1.06E−01 | 5.71E+01 |
| 7.98E+00 | −1.21E+01 | 2.11E+02 | −7.97E+00 | 1.45E+01 | 2.75E+02 | 1.13E+01 | −9.93E−01 | 1.29E+02 |
| 2.27E+01 | −4.78E+00 | 5.40E+02 | 2.06E+01 | 1.54E+01 | 6.64E+02 | −4.43E+00 | 7.19E−01 | 2.02E+01 |
| −2.05E+01 | 1.93E+01 | 7.89E+02 | 1.26E+01 | −1.54E+01 | 3.96E+02 | 5.68E+00 | 1.53E+00 | 3.46E+01 |
| −1.43E+01 | −4.64E+00 | 2.26E+02 | 1.77E+01 | 2.61E+01 | 9.96E+02 | 7.86E+00 | −4.35E+00 | 8.08E+01 |
| −2.16E+00 | 1.64E+01 | 2.73E+02 | −2.16E+00 | −1.74E+01 | 3.08E+02 | −5.92E+00 | −8.32E+00 | 1.04E+02 |
| −1.52E+01 | 3.26E+01 | 1.30E+03 | 1.92E+01 | 2.42E+01 | 9.55E+02 | 1.20E−01 | −3.89E+00 | 1.51E+01 |
| −3.94E+01 | 5.31E+00 | 1.58E+03 | −1.23E+01 | −3.17E+01 | 1.16E+03 | −9.92E+00 | 7.80E−01 | 9.89E+01 |
| Iteration = 20 | Iteration = 30 | Iteration = 50 | ||||||
| F(x) | F(x) | F(x) | ||||||
| −6.49E−01 | −2.71E−02 | 4.21E−01 | −7.88E−04 | 8.56E−03 | 7.39E−05 | −2.14E−06 | −1.58E−03 | 2.49E−06 |
| 3.51E−01 | −3.30E−01 | 2.32E−01 | −2.12E−02 | −1.86E−02 | 7.95E−04 | −3.02E−06 | 1.64E−05 | 2.79E−10 |
| 8.31E−03 | 3.10E−02 | 1.03E−03 | 6.29E−03 | −3.22E−03 | 4.99E−05 | −1.50E−06 | 9.95E−06 | 1.01E−10 |
| 2.81E−01 | 1.34E−01 | 9.70E−02 | −1.65E−02 | −1.36E−02 | 4.60E−04 | −7.90E−06 | −7.15E−06 | 1.14E−10 |
| −9.40E−02 | −4.12E−02 | 1.05E−02 | 1.36E−02 | −1.55E−02 | 4.25E−04 | 3.76E−06 | 1.10E−04 | 1.21E−08 |
| −2.46E−01 | 1.16E−01 | 7.39E−02 | 2.40E−03 | 1.02E−03 | 6.82E−06 | −3.30E−05 | −2.45E−06 | 1.09E−09 |
| −1.76E−01 | 2.19E+00 | 4.84E+00 | −1.56E−02 | 2.82E−01 | 8.00E−02 | −1.99E−03 | 2.34E−01 | 5.50E−02 |
| −6.43E−02 | 2.03E−01 | 4.52E−02 | −4.90E−04 | −4.00E−02 | 1.60E−03 | 8.19E−06 | −9.05E−06 | 1.49E−10 |
| 4.60E−01 | 7.55E−02 | 2.18E−01 | 1.66E−02 | 2.87E−03 | 2.82E−04 | 2.56E−05 | −1.30E−05 | 8.27E−10 |
| −8.30E−02 | 3.75E−01 | 1.47E−01 | −3.15E−02 | −8.20E−03 | 1.06E−03 | −7.89E−04 | −2.61E−06 | 6.22E−07 |
| [–5,10] [0,15] | |
| BSSA | BGOA | BMOA | BBA | BDA | BGSA | BPSO | BGA | ||
|---|---|---|---|---|---|---|---|---|---|
| F1 | Ave | 6.74E−35 | 5.71E−28 | 4.61E−23 | 7.86E−10 | 2.81E−01 | 1.16E−16 | 4.98E−09 | 1.95E−12 |
| std | 9.17E−36 | 8.31E−29 | 7.37E−23 | 8.11E−09 | 1.11E−01 | 6.10E−17 | 1.40E−08 | 2.01E−11 | |
| F2 | Ave | 7.78E−45 | 6.20E−40 | 1.20E−34 | 5.99E−20 | 3.96E−01 | 1.70E−01 | 7.29E−04 | 6.53E−18 |
| std | 3.48E−45 | 3.32E−40 | 1.30E−34 | 1.11E−17 | 1.41E−01 | 9.29E−01 | 1.84E−03 | 5.10E−17 | |
| F3 | Ave | 2.63E−25 | 2.05E−19 | 1.00E−14 | 9.19E−05 | 4.31E+01 | 4.16E+02 | 1.40E+01 | 7.70E−10 |
| std | 9.83E−27 | 9.17E−20 | 4.10E−14 | 6.16E−04 | 8.97E+00 | 1.56E+02 | 7.13E+00 | 7.36E−09 | |
| F4 | Ave | 4.65E−26 | 4.32E−18 | 2.02E−14 | 8.73E−01 | 8.80E−01 | 1.12E+00 | 6.00E−01 | 9.17E+01 |
| std | 4.68E−29 | 3.98E−19 | 2.43E−14 | 1.19E−01 | 2.50E−01 | 9.89E−01 | 1.72E−01 | 5.67E+01 | |
| F5 | Ave | 5.41E−01 | 5.07E+00 | 2.79E+01 | 8.91E+02 | 1.18E+02 | 3.85E+01 | 4.93E+01 | 5.57E+02 |
| std | 5.05E−02 | 4.90E−01 | 1.84E+00 | 2.97E+02 | 1.43E+02 | 3.47E+01 | 3.89E+01 | 4.16E+01 | |
| F6 | Ave | 8.03E−24 | 7.01E−19 | 6.58E−01 | 8.18E−17 | 3.15E−01 | 1.08E−16 | 9.23E−09 | 3.15E−01 |
| std | 5.22E−26 | 4.39E−20 | 3.38E−01 | 1.70E−18 | 9.98E−02 | 4.00E−17 | 1.78E−08 | 9.98E−02 | |
| F7 | Ave | 3.33E−08 | 2.71E−05 | 7.80E−04 | 5.37E−01 | 2.02E−02 | 7.68E−01 | 6.92E−02 | 6.79E−04 |
| std | 1.18E−06 | 9.26E−06 | 3.85E−04 | 1.89E−01 | 7.43E−03 | 2.77E+00 | 2.87E−02 | 3.29E−03 | |
| BSSA | BGOA | BMOA | BBA | BDA | BGSA | BPSO | BGA | ||
|---|---|---|---|---|---|---|---|---|---|
| F8 | Ave | −1.2E+04 | −8.76E+02 | −6.14E+02 | −4.69E+01 | −6.92E+02 | −2.75E+02 | −5.01E+02 | −5.11E+02 |
| std | 9.14E−12 | 5.92E+01 | 9.32E+01 | 3.94E+01 | 9.19EE+01 | 5.72E+01 | 4.28E+01 | 4.37E+01 | |
| F9 | Ave | 8.76E−04 | 6.90E−01 | 4.34E−01 | 4.85E−02 | 1.01E+02 | 3.35E+01 | 1.20E−01 | 1.23E−01 |
| std | 4.85E−02 | 4.81E−01 | 1.66E+00 | 3.91E+01 | 1.89E+01 | 1.19E+01 | 4.01E+01 | 4.11E+01 | |
| F10 | Ave | 8.04E−20 | 8.03E−16 | 1.63E−14 | 2.83E−08 | 1.15E+00 | 8.25E−09 | 5.20E−11 | 5.31E−11 |
| std | 3.34E−18 | 2.74E−14 | 3.14E−15 | 4.34E−07 | 7.87E−01 | 1.90E−09 | 1.08E−10 | 1.11E−10 | |
| F11 | Ave | 4.23E−10 | 4.20E−05 | 2.29E−03 | 2.49E−05 | 5.74E−01 | 8.19E+00 | 3.24E−06 | 3.31E−06 |
| std | 5.11E−07 | 4.73E−04 | 5.24E−03 | 1.34E−04 | 1.12E−01 | 3.70E+00 | 4.11E−05 | 4.23E−05 | |
| F12 | Ave | 6.33E−08 | 5.09E−03 | 3.93E−02 | 1.34E−05 | 1.27E+00 | 2.65E−01 | 8.93E−08 | 9.16E−08 |
| std | 4.71E−04 | 3.75E−03 | 2.42E−02 | 6.23E−04 | 1.02E+00 | 3.14E−01 | 4.77E−07 | 4.88E−07 | |
| F13 | Ave | 0.00E+00 | 1.25E−08 | 4.75E−01 | 9.94E−08 | 6.60E−02 | 5.73E−32 | 6.26E−02 | 6.39E−02 |
| std | 0.00E+00 | 2.61E−07 | 2.38E−01 | 2.61E−07 | 4.33E−02 | 8.95E−32 | 4.39E−02 | 4.49E−02 | |
| BSSA | BGOA | BMOA | BBA | BDA | BGSA | BPSO | BGA | ||
|---|---|---|---|---|---|---|---|---|---|
| F14 | Ave | 9.98E−01 | 1.08E+00 | 3.71E+00 | 1.26E+00 | 9.98E+01 | 3.61E+00 | 2.77E+00 | 4.39E+00 |
| std | 7.64E−12 | 4.11E−02 | 3.86E+00 | 6.86E−01 | 9.14E−1 | 2.96E+00 | 2.32E+00 | 4.41E−02 | |
| F15 | Ave | 3.3E−04 | 8.21E−03 | 3.66E−02 | 1.01E−02 | 7.15E−02 | 6.84E−02 | 9.09E−03 | 7.36E−02 |
| std | 1.25E−05 | 4.09E−03 | 7.60E−02 | 3.75E−03 | 1.26E−01 | 7.37E−02 | 2.38E−03 | 2.39E−03 | |
| F16 | Ave | −1.03E+00 | −1.02E+00 | −1.02E+00 | −1.02E+00 | −1.02E+00 | −1.02E+00 | −1.02E+00 | −1.02E+00 |
| std | 5.12E−10 | 9.80E−07 | 7.02E−09 | 3.23E−05 | 4.74E−08 | 0.00E+00 | 0.00E+00 | 4.19E−07 | |
| F17 | Ave | 3.98E−01 | 3.98E−01 | 3.98E−01 | 3.98E−01 | 3.98E−01 | 3.98E−01 | 3.98E−01 | 3.98E−01 |
| std | 4.56E−21 | 5.39E−05 | 7.00E−07 | 7.61E−04 | 1.15E−07 | 1.13E−16 | 9.03E−16 | 3.71E−17 | |
| F18 | Ave | 3.00E+00 | 3.00E+00 | 3.00E+00 | 3.00E+00 | 3.00E+00 | 3.00E+00 | 3.00E+00 | 3.00E+00 |
| std | 1.15E−18 | 1.15E−08 | 7.16E−06 | 2.25E−05 | 1.48E+01 | 3.24E−02 | 6.59E−05 | 6.33E−07 | |
| F19 | Ave | −3.86E+00 | −3.86E+00 | −3.84E+00 | −3.75E+00 | −3.77E+00 | −3.86E+00 | −3.80E+00 | −3.81E+00 |
| std | 5.61E−10 | 6.50E−07 | 1.57E−03 | 2.55E−03 | 3.53E−07 | 4.15E−01 | 3.37E−15 | 4.37E−10 | |
| F20 | Ave | −3.32E+00 | −2.81E+00 | −3.27E+00 | −2.84E+00 | −3.23E+00 | −1.47E+00 | −3.32E+00 | −2.39E+00 |
| std | 4.29E−05 | 7.11E−01 | 7.27E−02 | 3.71E−01 | 5.37E−02 | 5.32E−01 | 2.66E−01 | 4.37E−01 | |
| F21 | Ave | −10.15E+00 | −8.07E+00 | −9.65E+00 | −2.28E+00 | −7.38E+00 | −4.57E+00 | −7.54E+00 | −5.19E+00 |
| std | 1.25E−02 | 2.29E+00 | 1.54E+00 | 1.80E+00 | 2.91E+00 | 1.30E+00 | 2.77E+00 | 2.34E+00 | |
| F22 | Ave | −10.40E+00 | −10.01E+00 | −1.04E+00 | −3.99E+00 | −8.50E+00 | −6.58E+00 | −8.55E+00 | −2.97E+00 |
| std | 3.65E−07 | 3.97E−02 | 2.73E−04 | 1.99E+00 | 3.02E+00 | 2.64E+00 | 3.08E+00 | 1.37E−02 | |
| F23 | Ave | −10.53E+00 | −3.41E+00 | −1.05E+01 | −4.49E+00 | −8.41E+00 | −9.37E+00 | −9.19E+00 | −3.10E+00 |
| std | 5.26E−06 | 1.11E−02 | 1.81E−04 | 1.96E+00 | 3.13E+00 | 2.75E+00 | 2.52E+00 | 2.37E+00 | |
| Test Function | BGA | BPSO | BGSA | BDA | BBA | BMOA | BGOA | BSSA | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Unimodal (F1–F7) | Friedman value | 39 | 39 | 42 | 46 | 38 | 26 | 14 | 7 |
| Friedman rank | 5 | 5 | 6 | 7 | 4 | 3 | 2 | 1 | ||
| 2 | Multimodal (F8–F13) | Friedman value | 25 | 21 | 36 | 40 | 28 | 31 | 22 | 6 |
| Friedman rank | 4 | 2 | 7 | 8 | 5 | 6 | 3 | 1 | ||
| 3 | Multimodal with fixed dimensions (F14–F23) | Friedman value | 52 | 31 | 42 | 44 | 44 | 34 | 29 | 10 |
| Friedman rank | 7 | 3 | 5 | 6 | 6 | 4 | 2 | 1 | ||
| 4 | All 23 test functions | Friedman value | 116 | 91 | 120 | 130 | 110 | 91 | 65 | 23 |
| Friedman rank | 5 | 3 | 6 | 7 | 4 | 3 | 2 | 1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dehghani, M.; Montazeri, Z.; Dehghani, A.; Malik, O.P.; Morales-Menendez, R.; Dhiman, G.; Nouri, N.; Ehsanifar, A.; Guerrero, J.M.; Ramirez-Mendoza, R.A. Binary Spring Search Algorithm for Solving Various Optimization Problems. Appl. Sci. 2021, 11, 1286. https://doi.org/10.3390/app11031286
Dehghani M, Montazeri Z, Dehghani A, Malik OP, Morales-Menendez R, Dhiman G, Nouri N, Ehsanifar A, Guerrero JM, Ramirez-Mendoza RA. Binary Spring Search Algorithm for Solving Various Optimization Problems. Applied Sciences. 2021; 11(3):1286. https://doi.org/10.3390/app11031286
Chicago/Turabian StyleDehghani, Mohammad, Zeinab Montazeri, Ali Dehghani, Om P. Malik, Ruben Morales-Menendez, Gaurav Dhiman, Nima Nouri, Ali Ehsanifar, Josep M. Guerrero, and Ricardo A. Ramirez-Mendoza. 2021. "Binary Spring Search Algorithm for Solving Various Optimization Problems" Applied Sciences 11, no. 3: 1286. https://doi.org/10.3390/app11031286
APA StyleDehghani, M., Montazeri, Z., Dehghani, A., Malik, O. P., Morales-Menendez, R., Dhiman, G., Nouri, N., Ehsanifar, A., Guerrero, J. M., & Ramirez-Mendoza, R. A. (2021). Binary Spring Search Algorithm for Solving Various Optimization Problems. Applied Sciences, 11(3), 1286. https://doi.org/10.3390/app11031286









