Relationship between General Jump Types and Spike Jump Performance in Elite Female and Male Volleyball Players
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Study Design and Test Protocol
2.3. Data Collection and Processing
2.4. Variables and Definitions
2.5. Statistical Analyses
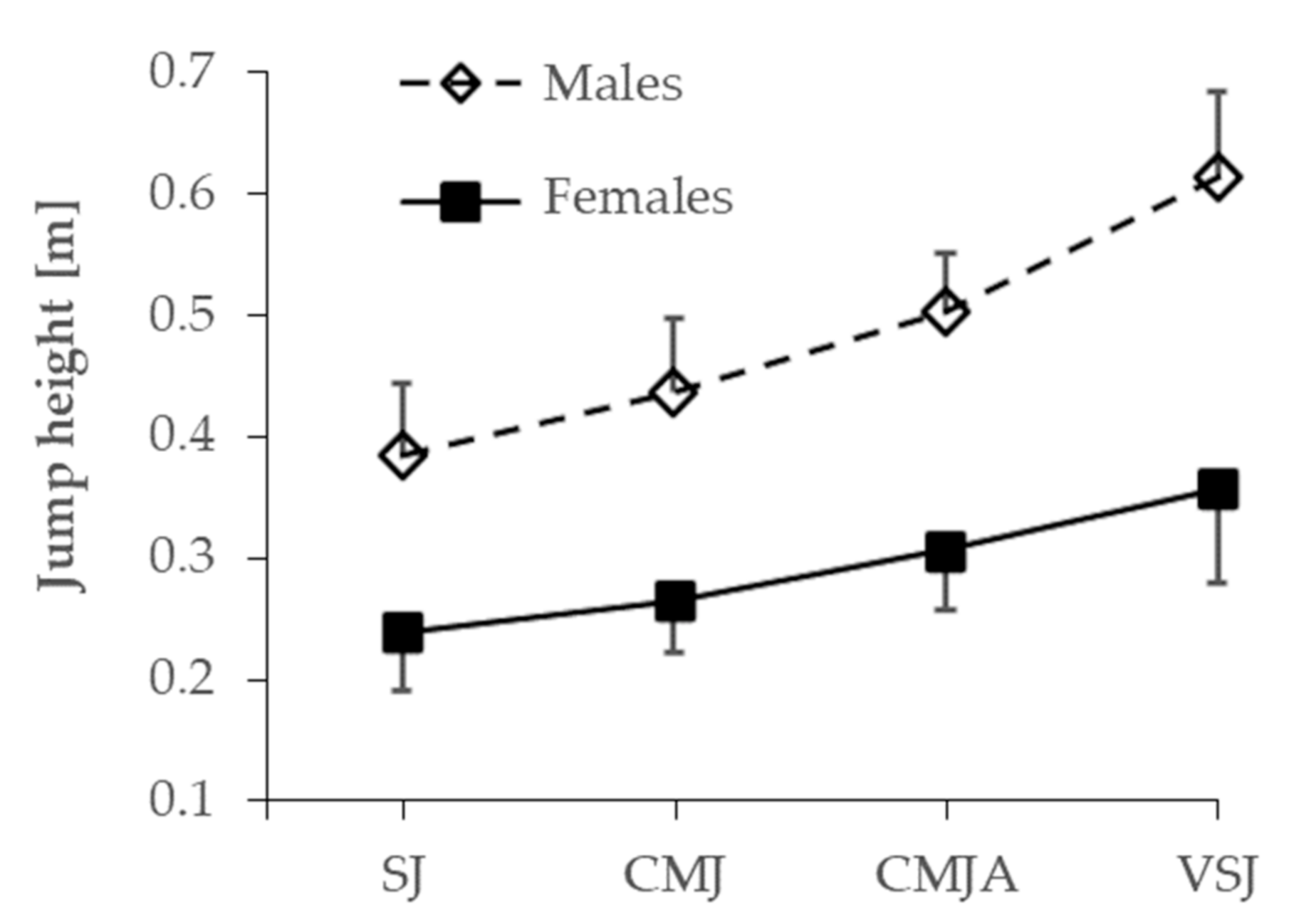
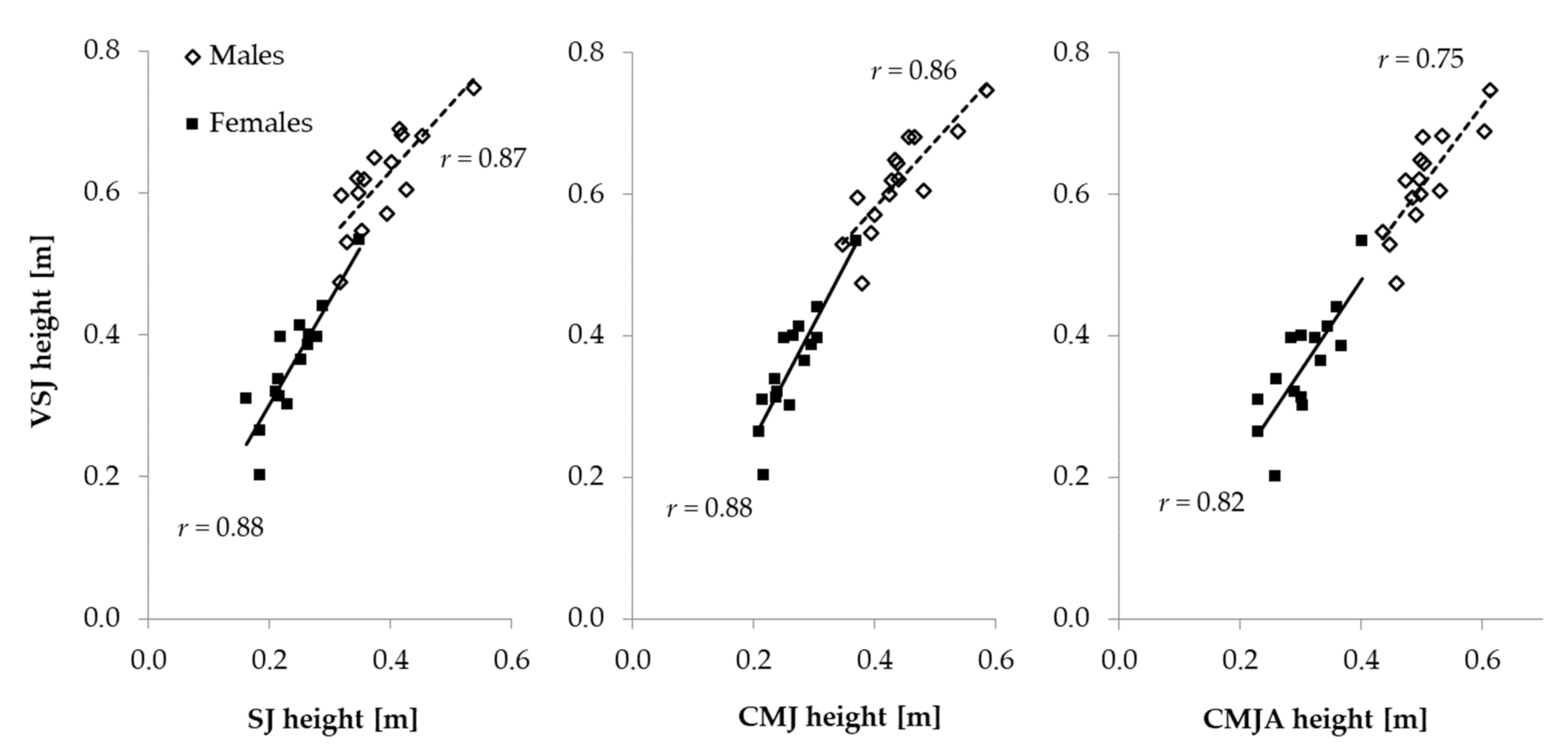
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Marcelino, R.; Mesquita, I. Associations between performance indicators and set’s result in male volleyball. In Kinesiology Research Trends and Applications; Milanović, D., Prot, F., Eds.; University of Zagreb: Zagreb, Croatia, 2008; pp. 955–957. [Google Scholar]
- Häyrinen, M.; Hoivala, T.; Blomqvist, M. Differences between winning and losing teams in men’s European top-level volleyball. In Proceedings of the 6th ISPAS World Congress, Belfast, Northern Ireland, January 2004. [Google Scholar]
- Reeser, J.C.; Bahr, R. Volleyball: Handbook of Sports Medicine and Science; John Wiley & Sons: Oxford, UK, 2017. [Google Scholar]
- Lidor, R.; Ziv, G. Physical and physiological attributes of female volleyball players—A review. J. Strength Cond. Res. 2010, 24, 1963–1973. [Google Scholar] [CrossRef]
- Forthomme, B.; Croisier, J.L.; Ciccarone, G. Factors correlated with volleyball spike velocity. Am. J. Sport Med. 2005, 33, 1513–1519. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, P.X.; Menzel, H.-J.; Guidotti, F.; Bell, J.; von Duvillard, S.P.; Wagner, H. Spike jump biomechanics in male versus female elite volleyball players. J. Sports Sci. 2019, 37, 2411–2419. [Google Scholar] [CrossRef] [PubMed]
- Lees, A.; Vanrenterghem, J.; De Clercq, D. Understanding how an arm swing enhances performance in the vertical jump. J. Biomech. 2004, 37, 1929–1940. [Google Scholar] [CrossRef] [PubMed]
- Ziv, G.; Lidor, R. Vertical jump in female and male volleyball players: A review of observational and experimental studies. Scand. J. Med. Sci. Sports 2010, 20, 556–567. [Google Scholar] [CrossRef]
- Powers, M.E. Vertical Jump Training for Volleyball. Strength Cond. J. 1996, 18, 18–23. [Google Scholar] [CrossRef]
- Markovic, G.; Dizdar, D.; Jukic, I.; Cardinale, M. Reliability and Factorial Vailidity of Squat and Countermovement Jump Tests. J. Strength Cond. Res. 2004, 18, 551–555. [Google Scholar]
- McLellan, C.P.; Lovell, D.I.; Gass, G.C. The Role of Rate of Force Development on Vertical Jump Performance. J. Strength Cond. Res. 2011, 25, 379–385. [Google Scholar] [CrossRef]
- Wagner, H.; Tilp, M.; von Duvillard, S.P.; Müller, E. Kinematic analysis of volleyball spike jump. Int. J. Sports Med. 2009, 30, 760–765. [Google Scholar] [CrossRef]
- Fuchs, P.X.; Fusco, A.; Bell, J.W.; von Duvillard, S.P.; Cortis, C.; Wagner, H. Movement characteristics of volleyball spike jump performance in females. J. Sci. Med. Sport 2019, 22, 833–837. [Google Scholar] [CrossRef]
- Hsieh, C.; Heise, G.D. Arm swing of volleyball spike jump performance between advanced and recreational female players. In Proceedings of the Fourth North American Congress on Biomechanics, Ann Arbor, MI, USA, 5–9 August 2008. [Google Scholar]
- Sarvestan, J.; Svoboda, Z.; de Oliveira Claudino, J.G. Force-time curve variables of countermovement jump as predictors of volleyball spike jump height. Ger. J. Exerc. Sport Res. 2020. [Google Scholar] [CrossRef]
- Hamill, J.; Selbie, W.S.; Kepple, T.M. Three-Dimensional Kinematics. In Research Methods in Biomechanics, 2nd ed.; Robertson, D.G.E., Caldwell, G.E., Hamill, J., Kamen, G., Whittlesey, S.N., Eds.; Human Kinetics: Champaign, IL, USA, 2014; pp. 35–59. [Google Scholar]
- Woltring, H.J. A Fortran package for generalized, cross-validatory spline smoothing and differentiation. Adv. Engl. Softw. 1986, 8, 104–113. [Google Scholar] [CrossRef]
- Cohen, J. A power primer. Psychol. Bull. 1992, 112, 155–159. [Google Scholar] [CrossRef] [PubMed]
- Riggs, M.P.; Sheppard, J.M. The relative importance of strength and power qualities to vertical jump height of elite beach volleyball players during the counter-movement and squat jump. J. Hum. Sport Exerc. 2009, 4, 221–236. [Google Scholar] [CrossRef]
- Cardinale, M.; Stone, M.H. Is testosterone influencing explosive performance? J. Strength Cond. Res. 2006, 20, 103–107. [Google Scholar]
- Häkkinen, K.; Pakarinen, A. Muscle strength and serum testosterone, cortisol and SHBG concentrations in middle-aged and elderly men and women. Acta Physiol. Scand. 1993, 148, 199–207. [Google Scholar] [CrossRef]
- Anderson, F.C.; Pandy, M.G. Storage and utilization of elastic strain energy during jumping. J. Biomech. 1993, 26, 1413–1427. [Google Scholar] [CrossRef]
- Van Hooren, B.; Zolotarjova, J. The Difference Between Countermovement and Squat Jump Performances: A Review of Underlying Mechanisms With Practical Applications. J. Strength Cond. Res. 2017, 31, 2011–2020. [Google Scholar] [CrossRef]
- Soundara rajan, R.; Pushparajan, A. Effects of plyometric training on the development of the vertical jump in volleyball players. J. Phys. Educ. Sport 2010, 28, 65–69. [Google Scholar]
- Newton, R.U.; Kraemer, W.J.; Häkkinen, K. Effects of ballistic training on preseason preparation of elite volleyball players. Med. Sci. Sports Exer. 1999, 31, 323–330. [Google Scholar] [CrossRef]
- Fry, A.C.; Kraemer, W.J.; Weseman, C.A.; Conroy, B.P.; Gordon, S.E.; Hoffman, J.R.; Maresh, C.M. The Effects of an Off-season Strength and Conditioning Program on Startes and Non-starters in Women’s Intercollegiate Volleyball. J. Strength Cond. Res. 1991, 5, 174–181. [Google Scholar]
- Sheppard, J.M.; Cronin, J.B.; Gabbett, T.J.; McGuigan, M.R.; Etxebarria, N.; Newton, R.U. Relative Importance of Strength, Power, and Anthropometric Measures to Jump Performance of Elite Volleyball Players. J. Strength Cond. Res. 2008, 22, 758–765. [Google Scholar] [CrossRef] [PubMed]
| Females | Males | ||||||
|---|---|---|---|---|---|---|---|
| SJ | CMJ | CMJA | SJ | CMJ | CMJA | ||
| Jump height | r= | 0.88 | 0.88 | 0.83 | 0.80 | 0.85 | 0.75 |
| p= | *** | *** | *** | *** | *** | ** | |
| Impulse | r= | 0.40 | 0.32 | 0.56 | 0.50 | 0.26 | −0.65 |
| p= | 0.07 | 0.13 | * | * | 0.17 | ** | |
| Minimal ND knee angle | r= | 0.26 | −0.52 | −0.28 | −0.15 | −0.08 | 0.04 |
| p= | 0.17 | * | 0.17 | 0.30 | 0.39 | 0.45 | |
| Minimal D knee angle | r= | 0.28 | −0.47 | −0.26 | −0.10 | −0.05 | 0.04 |
| p= | 0.16 | * | 0.18 | 0.37 | 0.43 | 0.45 | |
| CoM decrease | r= | −0.08 | 0.41 | 0.27 | 0.10 | 0.03 | 0.06 |
| p= | 0.40 | 0.07 | 0.18 | 0.37 | 0.46 | 0.43 | |
| Maximal RFD FP1+2 | r= | 0.75 | 0.05 | 0.12 | 0.65 | −0.13 | −0.39 |
| p= | ** | 0.44 | 0.34 | ** | 0.32 | 0.09 | |
| Maximal RFD FP1 | r= | 0.78 | 0.15 | 0.13 | −0.05 | −0.13 | −0.50 |
| p= | *** | 0.30 | 0.33 | 0.43 | 0.32 | * | |
| Maximal RFD PF2 | r= | 0.70 | −0.01 | 0.06 | 0.47 | −0.08 | −0.27 |
| p= | ** | 0.48 | 0.42 | * | 0.39 | 0.18 | |
| Torso incline | r= | −0.21 | −0.18 | −0.29 | 0.46 | −0.23 | 0.19 |
| p= | 0.23 | 0.26 | 0.16 | * | 0.21 | 0.26 | |
| Maximal angular velocity ND knee | r= | 0.70 | 0.69 | 0.60 | 0.53 | 0.54 | 0.21 |
| p= | ** | ** | * | * | * | 0.24 | |
| Maximal angular velocity D knee | r= | 0.75 | 0.80 | 0.72 | 0.73 | 0.55 | 0.37 |
| p= | ** | *** | ** | ** | * | 0.10 | |
| Maximal angular velocity ND shoulder | r= | 0.14 | 0.17 | ||||
| p= | 0.31 | 0.29 | |||||
| Maximal angular velocity D shoulder | r= | 0.06 | 0.05 | ||||
| p= | 0.41 | 0.43 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuchs, P.X.; Mitteregger, J.; Hoelbling, D.; Menzel, H.-J.K.; Bell, J.W.; von Duvillard, S.P.; Wagner, H. Relationship between General Jump Types and Spike Jump Performance in Elite Female and Male Volleyball Players. Appl. Sci. 2021, 11, 1105. https://doi.org/10.3390/app11031105
Fuchs PX, Mitteregger J, Hoelbling D, Menzel H-JK, Bell JW, von Duvillard SP, Wagner H. Relationship between General Jump Types and Spike Jump Performance in Elite Female and Male Volleyball Players. Applied Sciences. 2021; 11(3):1105. https://doi.org/10.3390/app11031105
Chicago/Turabian StyleFuchs, Philip X., Julia Mitteregger, Dominik Hoelbling, Hans-Joachim K. Menzel, Jeffrey W. Bell, Serge P. von Duvillard, and Herbert Wagner. 2021. "Relationship between General Jump Types and Spike Jump Performance in Elite Female and Male Volleyball Players" Applied Sciences 11, no. 3: 1105. https://doi.org/10.3390/app11031105
APA StyleFuchs, P. X., Mitteregger, J., Hoelbling, D., Menzel, H.-J. K., Bell, J. W., von Duvillard, S. P., & Wagner, H. (2021). Relationship between General Jump Types and Spike Jump Performance in Elite Female and Male Volleyball Players. Applied Sciences, 11(3), 1105. https://doi.org/10.3390/app11031105







