Rigidity through a Projective Lens
Abstract
Featured Application
Abstract
| Contents | ||
| 1. | Introduction | 3 |
| I | Projective Geometry in Core Rigidity Results | 5 |
| 2. | Introduction to Euclidean Rigidity Theory | 5 |
| 3. | Projective Rigidity | 8 |
| 3.1. | Plücker Coordinates and Extensors | 8 |
| 3.2. | Infinitesimal and Static Rigidity in Projective Space | 10 |
| 3.3. | Projective Invariance | 15 |
| 3.4. | Equivalence of Projective and Euclidean Rigidity Matrices | 16 |
| 4. | Projective Metrics: Euclidean; Spherical; Hyperbolic; and Minkowski. | 17 |
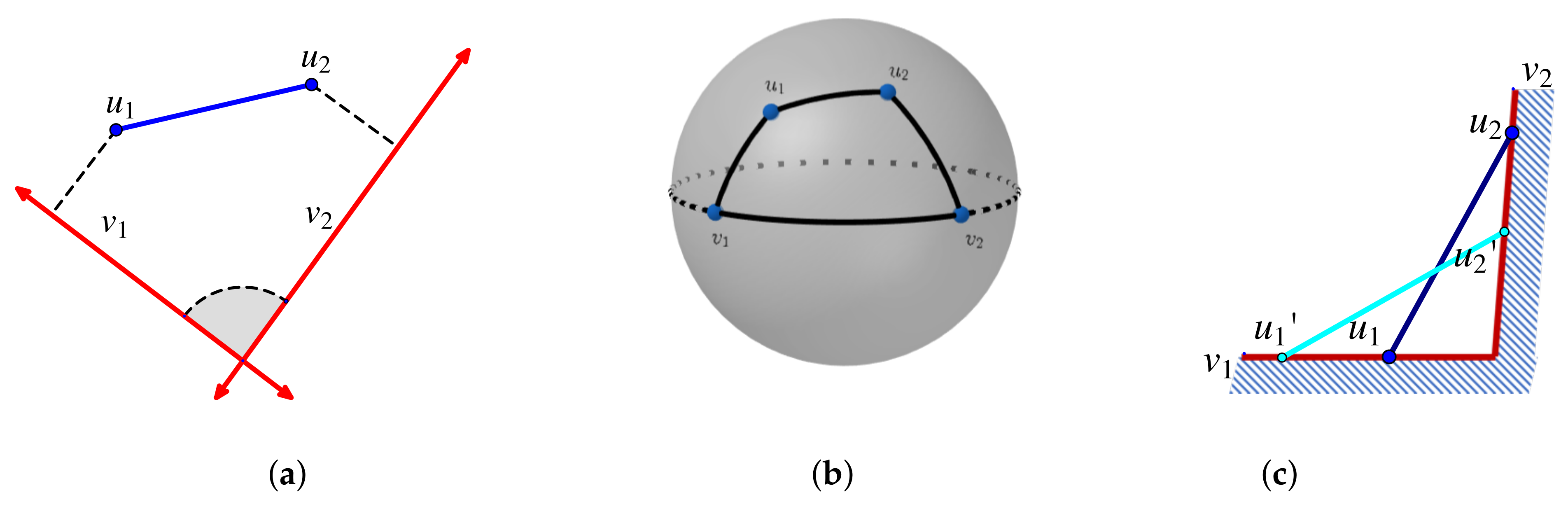
| 4.1. | Euclidean and Spherical Spaces | 18 |
| 4.2. | Minkowski Space | 20 |
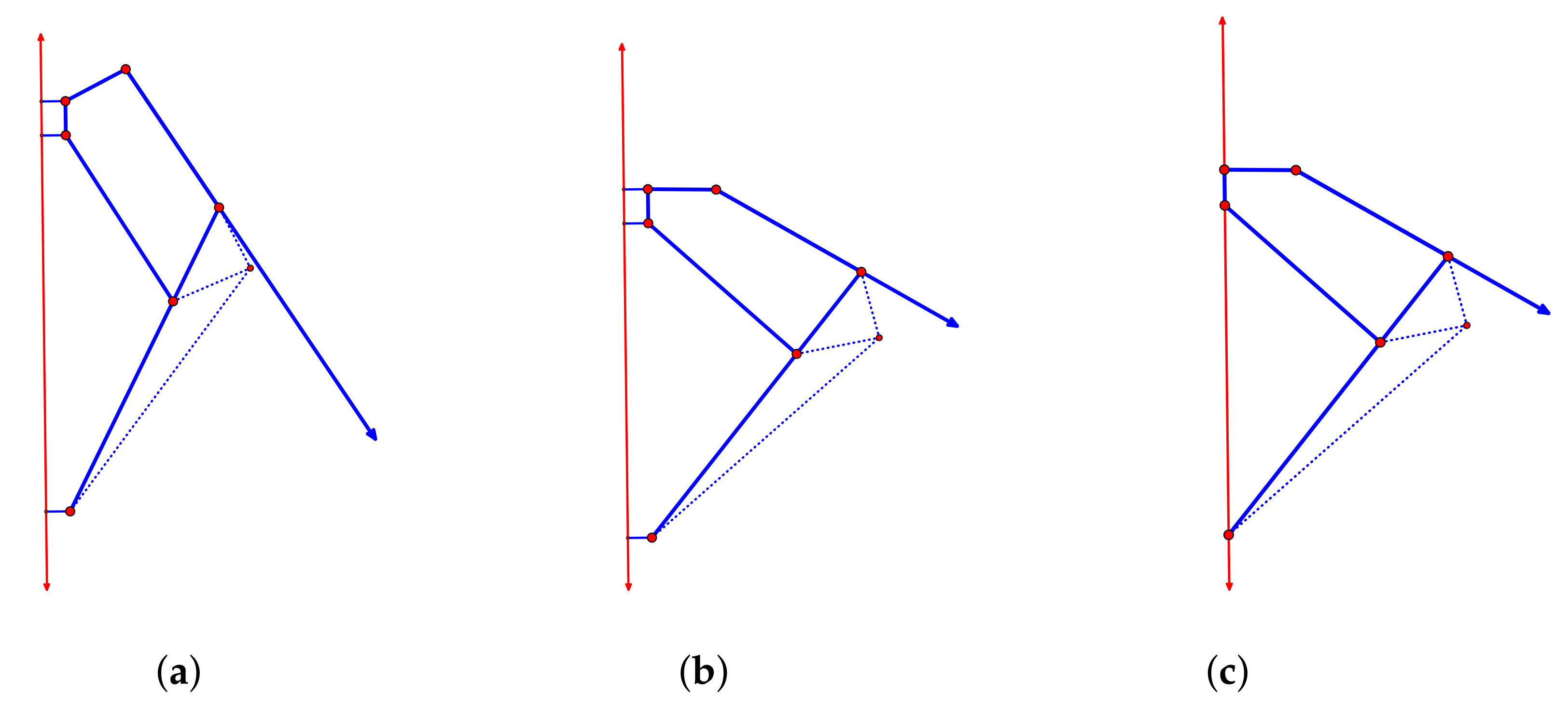
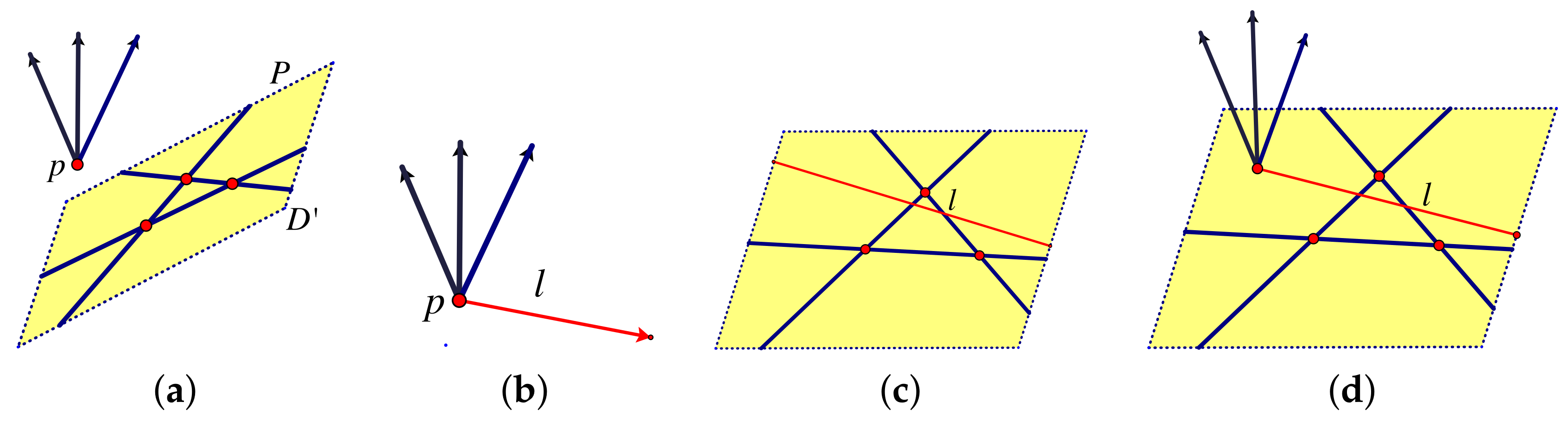
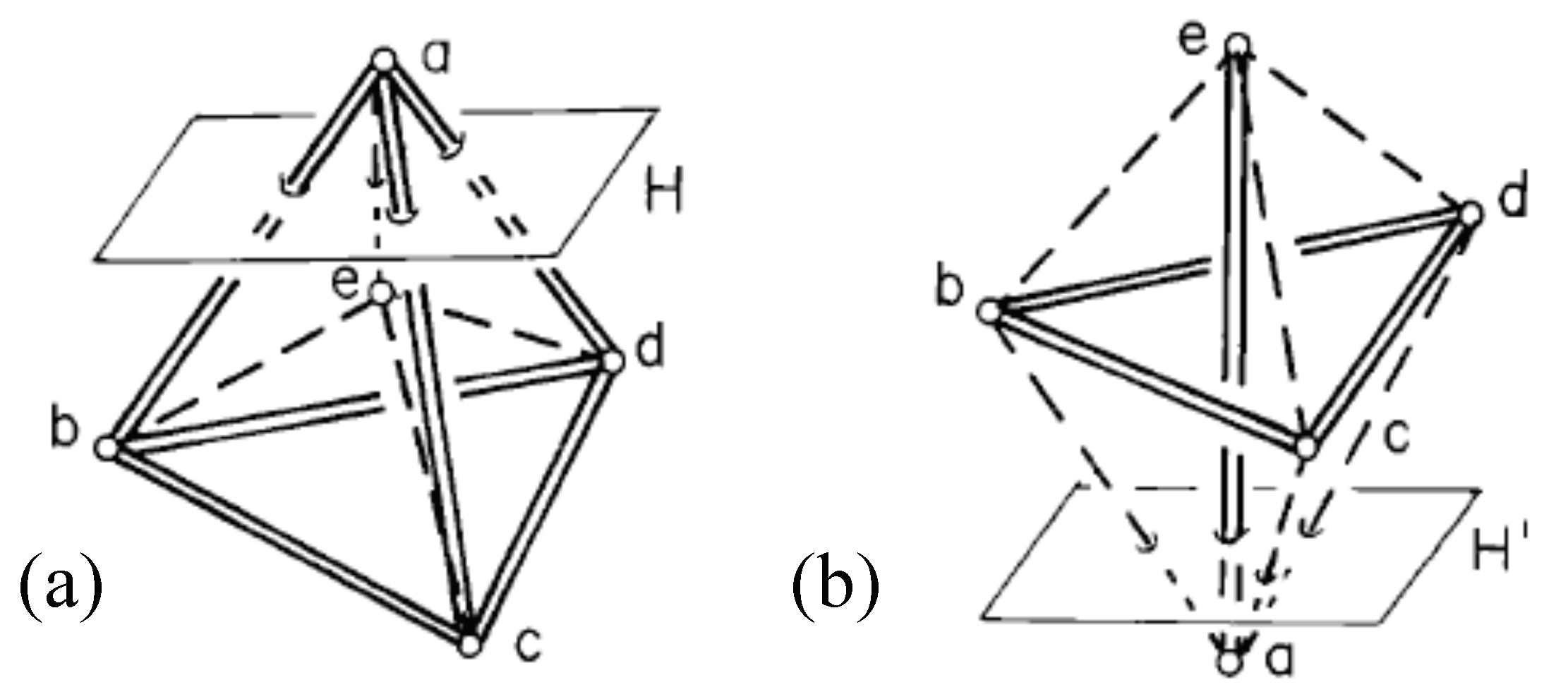
| 5. | Coning and Projecting | 21 |
| 5.1. | Coning a Framework from to | 21 |
| 5.2. | Coning and Projection for , , and | 24 |
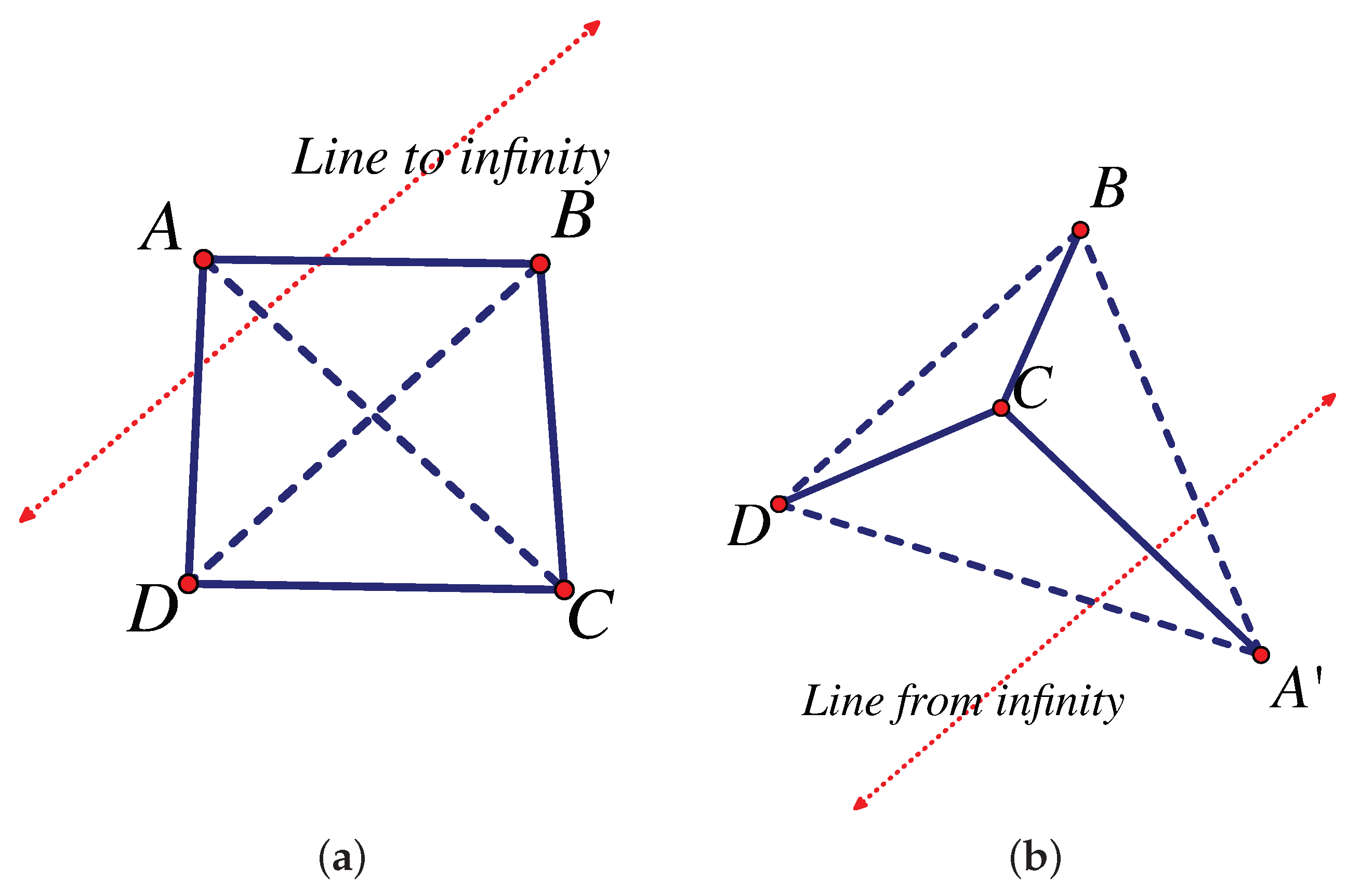
| 6. | Joints at Infinity and Sliders | 25 |
| 6.1. | Point-Hyperplane Frameworks | 27 |
| 6.2. | Point-Hyperplane Frameworks and Projections from Spherical Frameworks | 27 |
| 6.3. | Sliders: Free and Pinned | 29 |
| 6.4. | Linear Constraints as Sliders | 31 |
| 6.5. | Further Extensions to Include Infinity | 31 |
| 7. | Pure Conditions | 32 |
| 7.1. | Bracket Ring | 32 |
| 7.2. | Small Examples | 33 |
| 7.3. | Bipartite Frameworks and Quadratic Surfaces | 35 |
| 7.4. | Pure Conditions: Basic Theorems | 39 |
| 7.5. | Factoring and Rigid Components | 41 |
| 7.6. | Computing Pure Conditions: Pinned Frameworks, and d-Directed Graphs | 43 |
| 7.7. | Assur Graphs and Assur Decompositions | 46 |
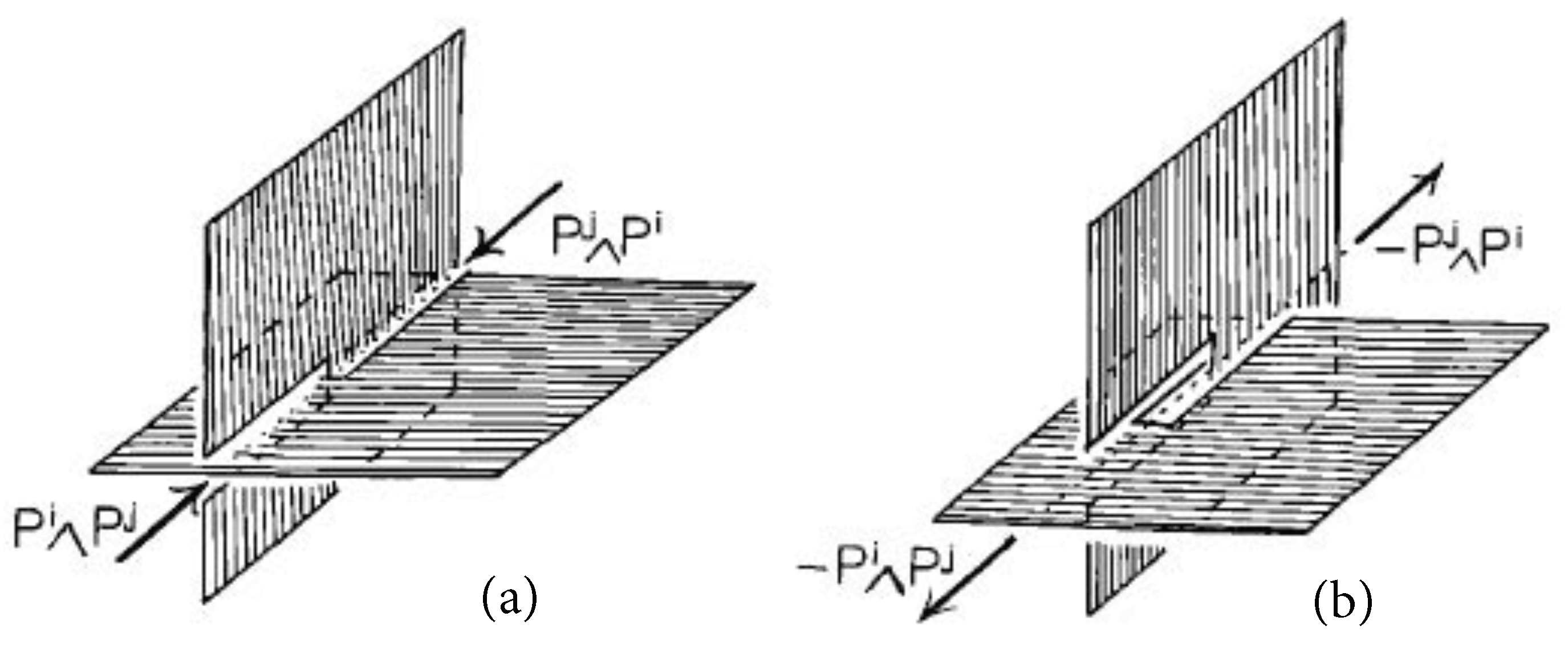
| 8. | Polarity for Rigidity . | 50 |
| 8.1. | Duality and Polarity for Projective Geometry | 51 |
| 8.2. | Sheet Structures and Polarity for Rigidity in | 51 |
| 8.3. | Substitution Principles | 56 |
| 8.4. | Cauchy, Alexandrov and Polarity | 57 |
| II | Projective Theory of Connected Body Frameworks | 58 |
| 9. | Body-Bar Frameworks | 58 |
| 9.1. | Body-Bar Combinatorics | 60 |
| 9.2. | Body-Bar Projective Conditions and Centers of Motion | 63 |
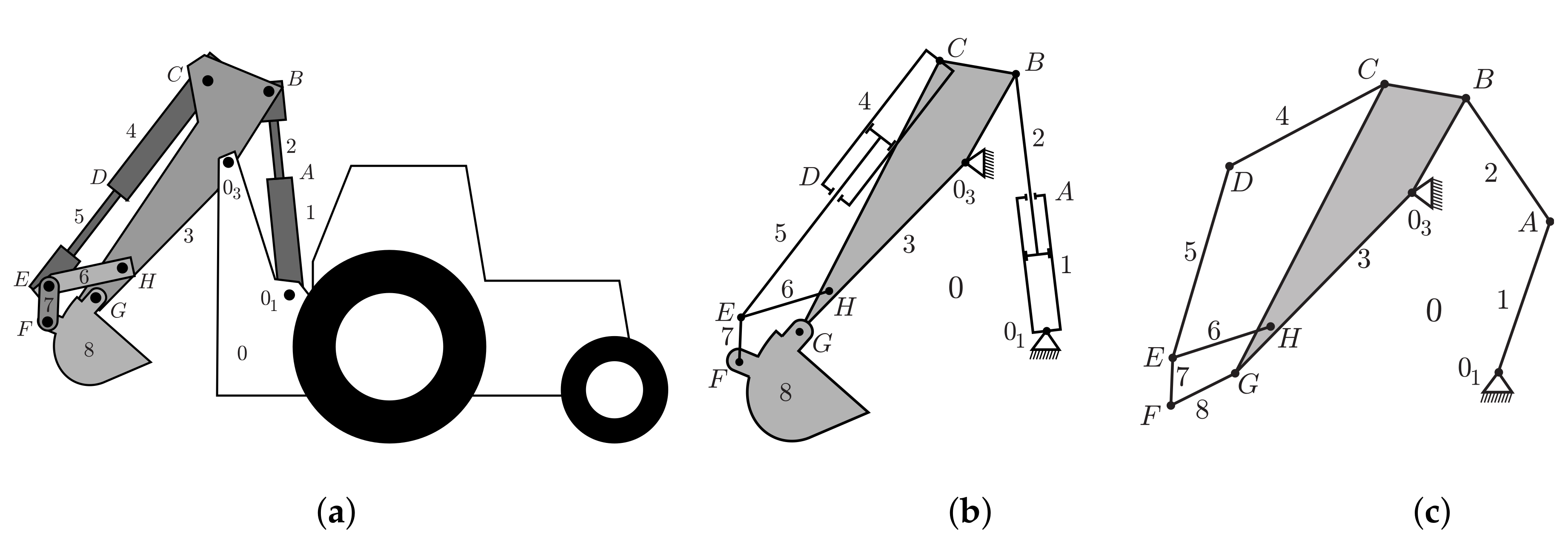
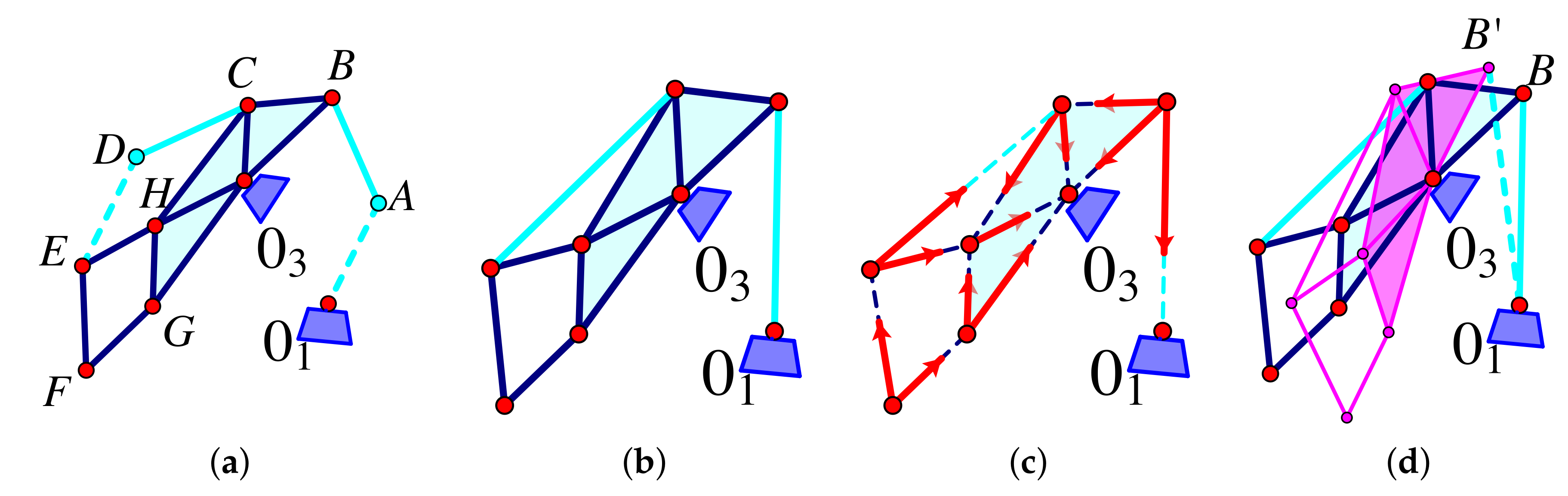
| 9.3. | Projective Line Dependences and the Stewart Platform | 65 |
| 9.4. | Static Rigidity and Stresses in Body-Bar Frameworks | 67 |
| 9.5. | Coning Body-Bar Frameworks | 70 |
| 9.6. | Rod and Bar Frameworks in 3-Dimensions | 70 |
| 10. | Body–Hinge Frameworks | 73 |
| 10.1. | Body–Hinge Basic Transfer | 73 |
| 10.2. | Body–Hinge Motion Assignments | 74 |
| 10.3. | Coning for Body–Hinge in | 75 |
| 10.4. | Molecular and Body-Plate Frameworks | 76 |
| 10.5. | Applications to Protein Structures | 77 |
| 10.6. | Block and Hole Polyhedra | 79 |
| 10.7. | Lower Dimensional Bodies: Pinned Rods in the Plane | 83 |
| 10.8. | Summary Table | 83 |
| III | Maximal Abstract Rigidity Matroids and Multivariate Splines | 84 |
| 11. | Multivariate Splines and Cofactor Matroids | 85 |
| 11.1. | Smoothing Cofactors for Splines and Compatibility Conditions | 85 |
| 11.2. | The -Cofactor Matroid on Plane Graphs: An Analogue of Rigidity in | 87 |
| 11.3. | Is the Maximal Abstract 3-Rigidity Matroid | 87 |
| 11.4. | Transferring Pure Conditions | 89 |
| 11.5. | Transferring Theorems to the -Cofactor Matroid | 92 |
| 11.6. | Coning Splines: Abstract 4-Dimensional Rigidity Matroids and Multivariate Splines | 93 |
| 11.7. | Using Projective Rigidity Style Techniques for | 93 |
| IV | Concluding Connections | 94 |
| 12. | Projective Tensegrities | 94 |
| 13. | Further Explorations | 97 |
| 13.1. | Skeletal Rigidity, Geometric Homology and f-Vectors | 97 |
| 13.2. | Global Rigidity, Universal Rigidity and Superstability | 97 |
| 13.3. | Interesting However, Not Projective: Finite Motions | 98 |
| 13.4. | Interesting However, Not Projective: CAD Constraints and Angles | 99 |
| 14. | Companion Paper: Projective Geometry of Scene Analysis, Parallel Drawing and Reciprocal Drawing | 99 |
| Backmatter | 100 | |
| References | 100 |
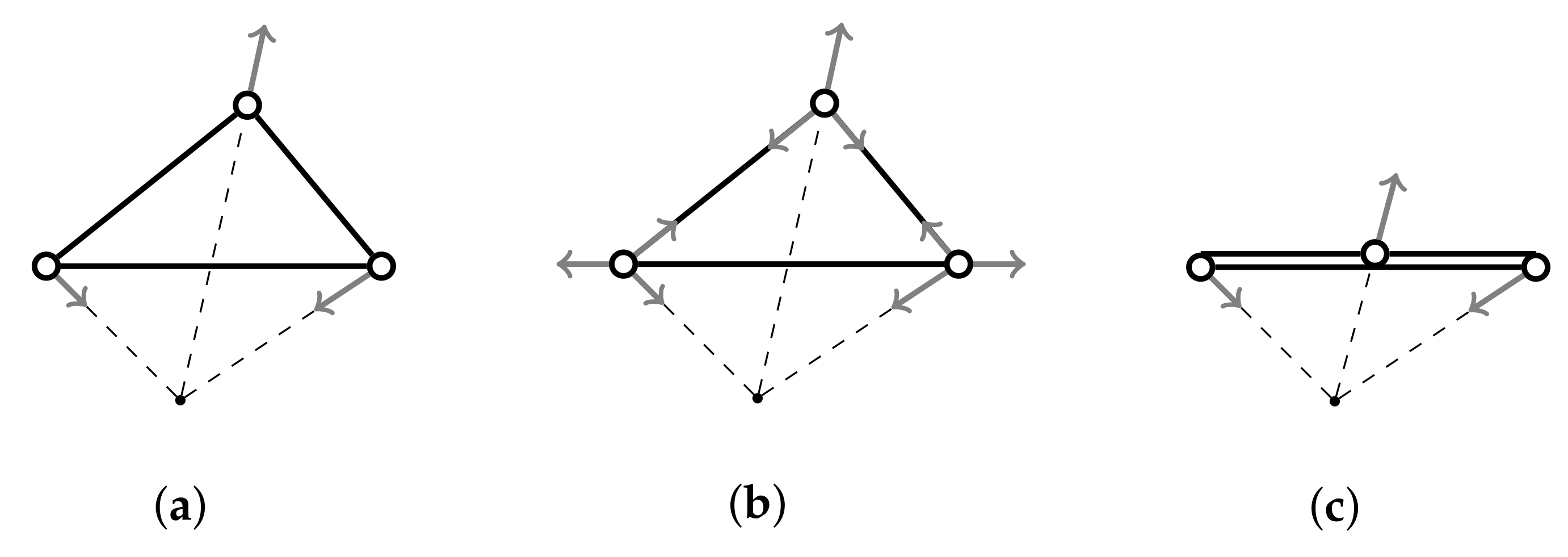
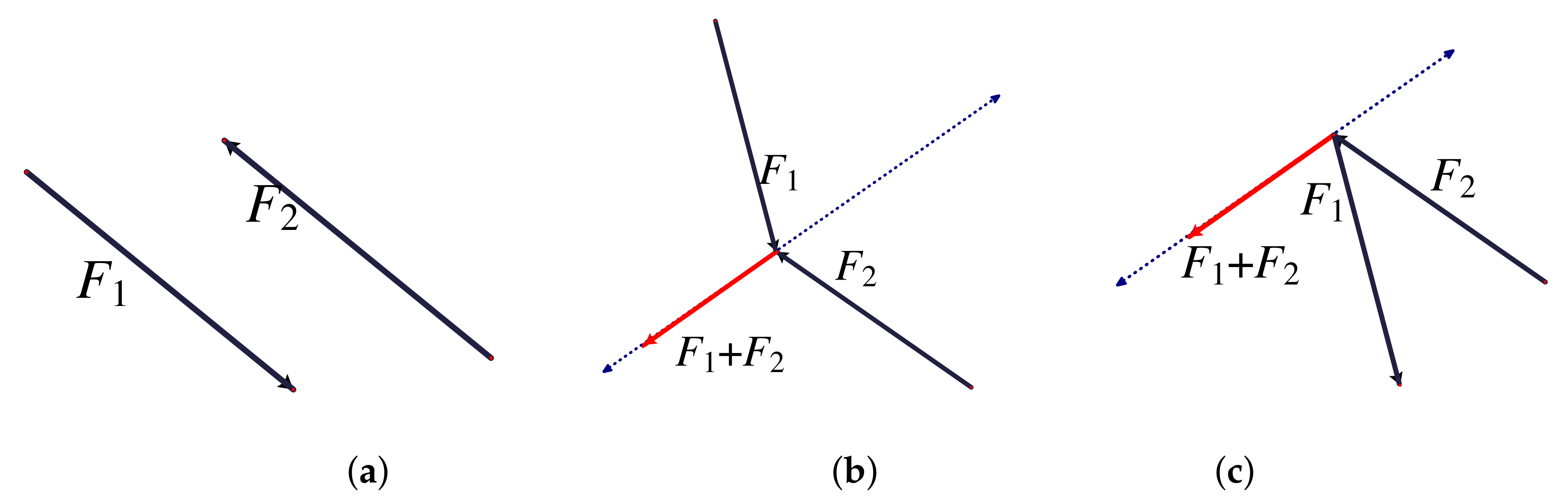
1. Introduction
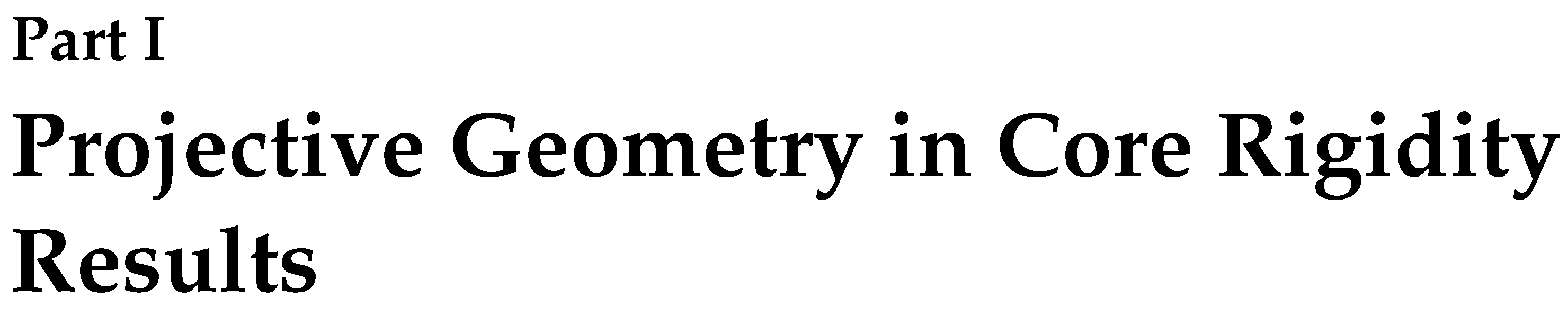
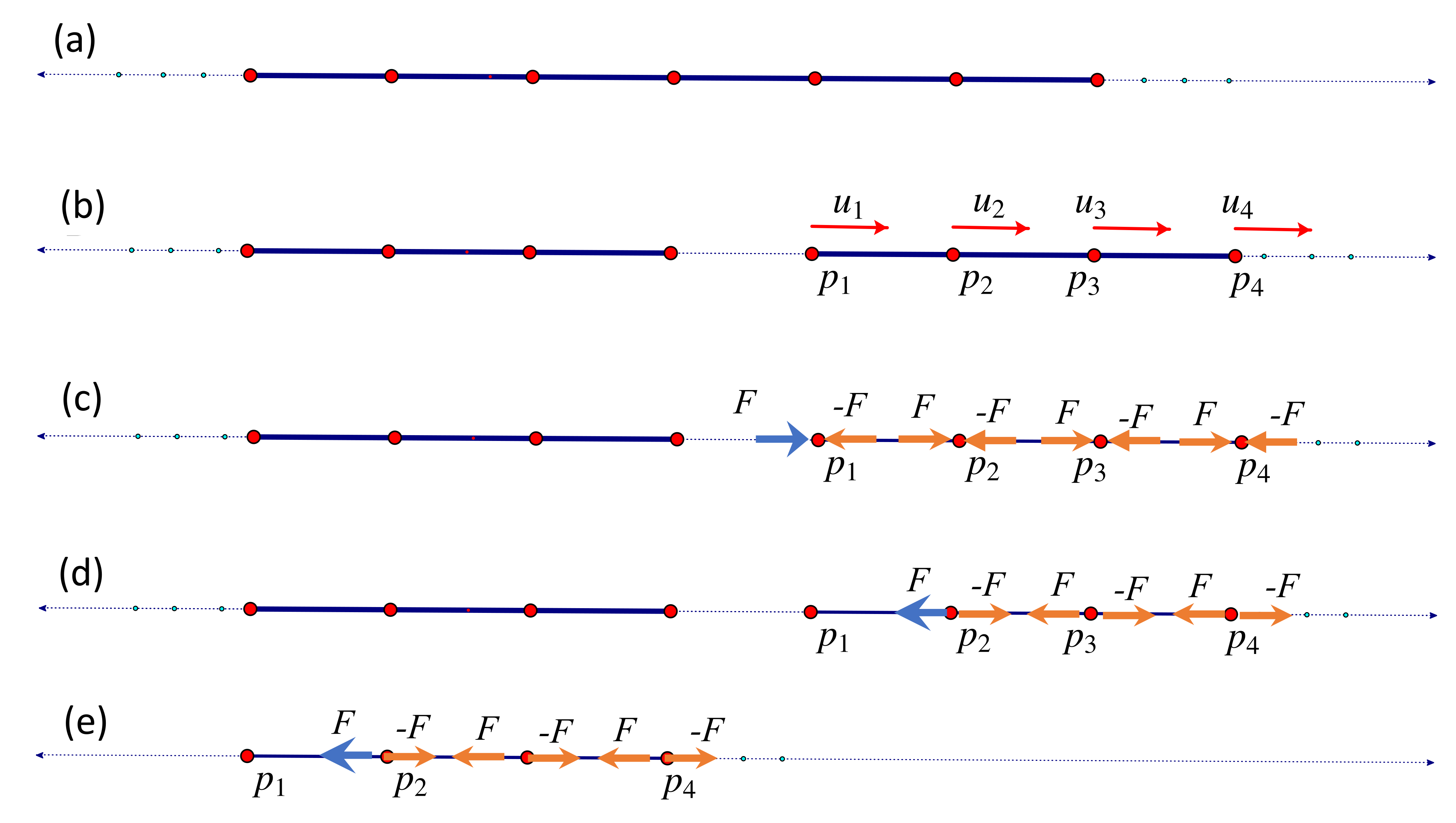
2. Introduction to Euclidean Rigidity Theory
3. Projective Rigidity
3.1. Plücker Coordinates and Extensors
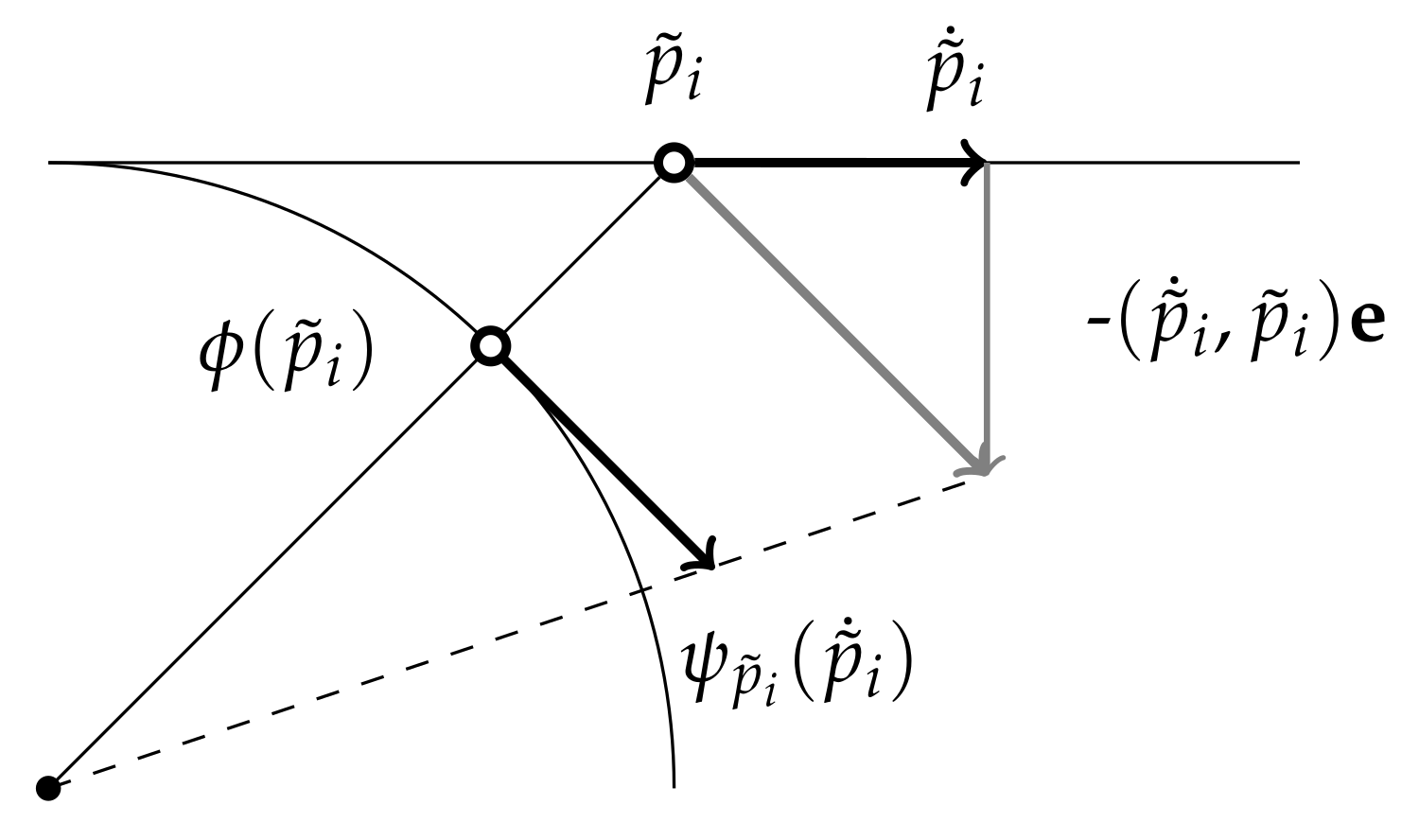
3.2. Infinitesimal and Static Rigidity in Projective Space
3.3. Projective Invariance
3.4. Equivalence of Projective and Euclidean Rigidity Matrices
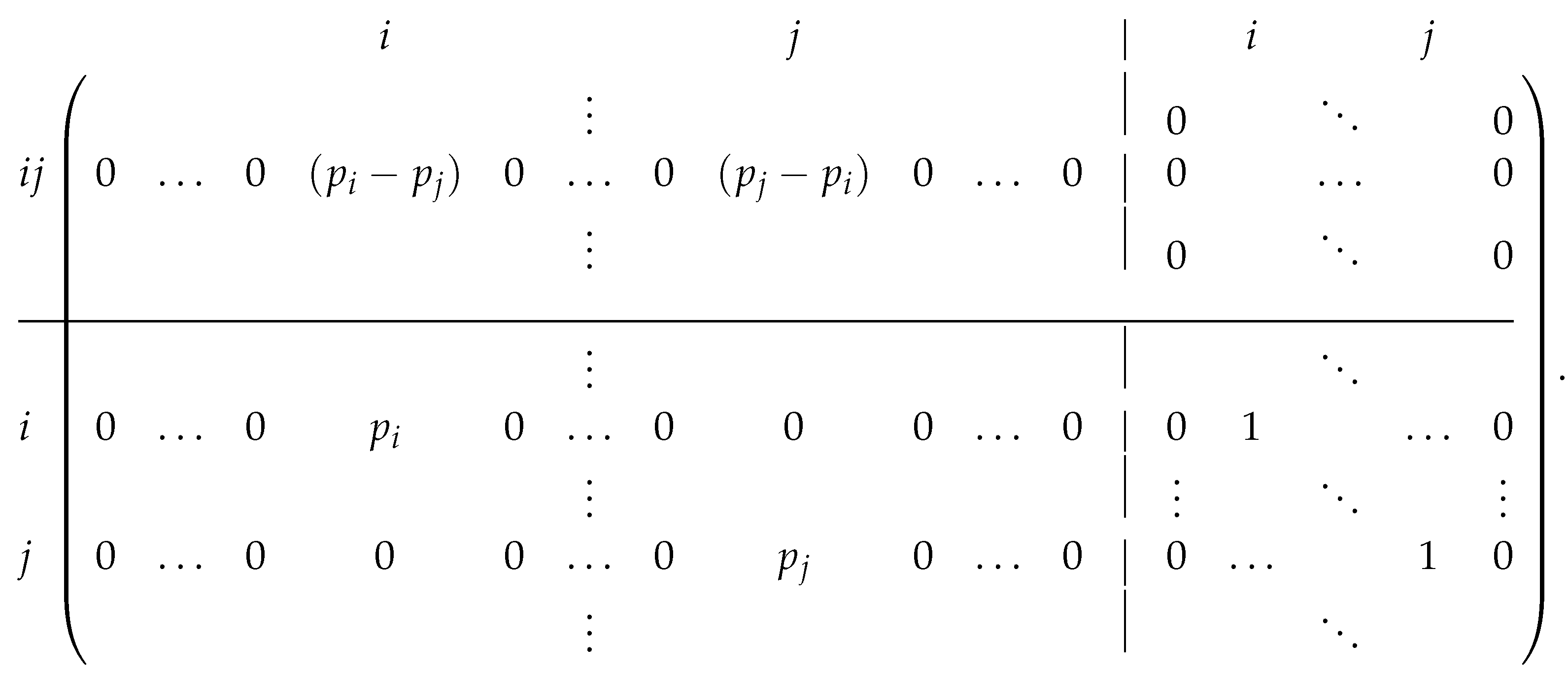 Note that the bottom right corner is essentially a identity matrix. This leaves the standard Euclidean rigidity matrix in the upper left, with the vertices in Euclidean d-space. These operations again preserve the dimensions of the kernel (the infinitesimal motions) and the cokernel (the equilibrium stresses). The equivalence of the projective and the Euclidean rigidity matrix follows.
Note that the bottom right corner is essentially a identity matrix. This leaves the standard Euclidean rigidity matrix in the upper left, with the vertices in Euclidean d-space. These operations again preserve the dimensions of the kernel (the infinitesimal motions) and the cokernel (the equilibrium stresses). The equivalence of the projective and the Euclidean rigidity matrix follows.4. Projective Metrics: Euclidean; Spherical; Hyperbolic; and Minkowski
4.1. Euclidean and Spherical Spaces
4.2. Minkowski Space
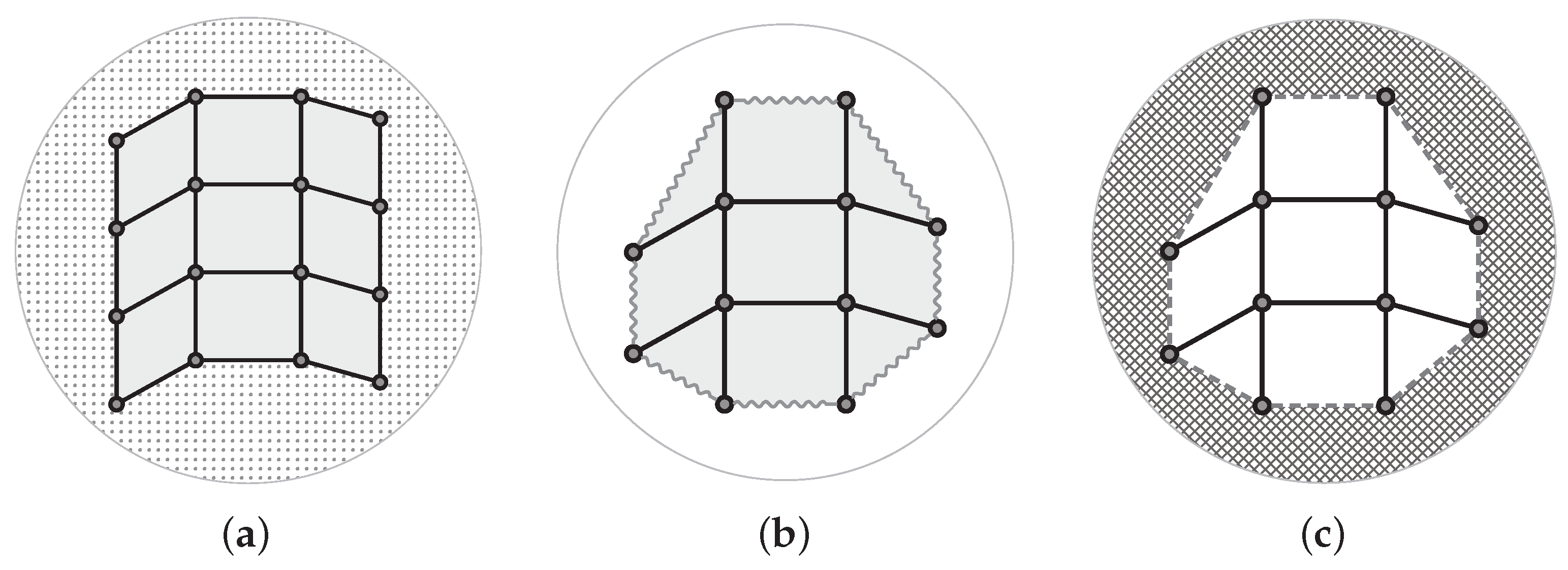
5. Coning and Projecting
5.1. Coning a Framework from to
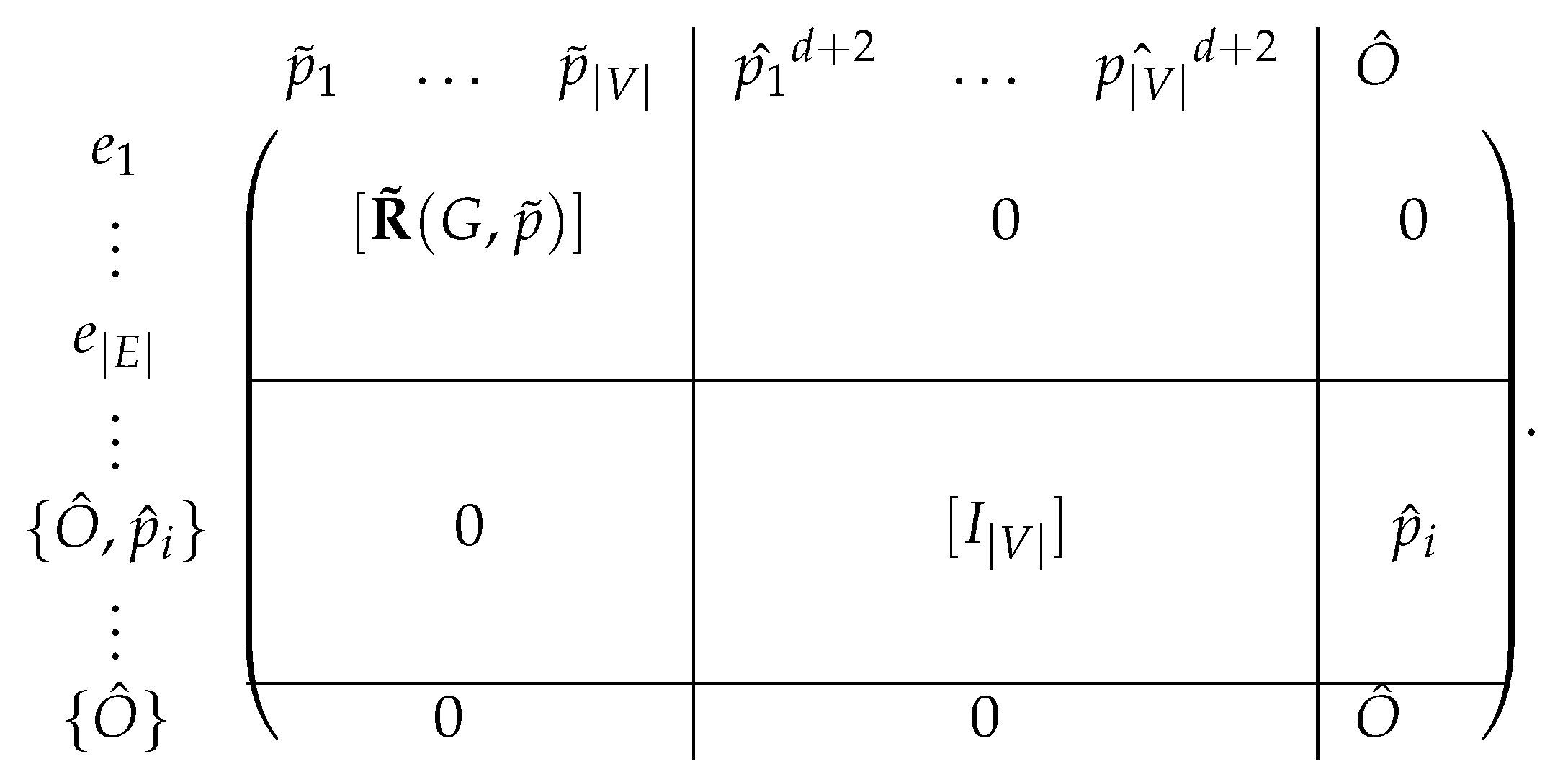 Now consider an equilibrium stress on the original framework. With added coefficients of 0 on all the added rows, it is still an equilibrium stress on the coned framework, that is, a row dependence for the extended matrix. Consider an equilibrium stress on the coned framework.
Now consider an equilibrium stress on the original framework. With added coefficients of 0 on all the added rows, it is still an equilibrium stress on the coned framework, that is, a row dependence for the extended matrix. Consider an equilibrium stress on the coned framework.
- Looking at the columns for … it must be an equilibrium stress on the original framework.
- Looking at the columns for , … the coefficients on the bars {} must all be zero.
- Looking at the residual column for , the coefficient on the row {} must also be 0.
5.2. Coning and Projection for , , and
6. Joints at Infinity and Sliders
6.1. Point-Hyperplane Frameworks
6.2. Point-Hyperplane Frameworks and Projections from Spherical Frameworks
- (a)
- G can be realised as an infinitesimally rigid point-hyperplane framework in such that each vertex in X is realised as a hyperplane and each vertex in is realised as a point.
- (b)
- G can be realised on the sphere with each vertex in X on the equator and each vertex in is realised in the open upper hemisphere.
- (c)
- G can be realised as an infinitesimally rigid bar–joint framework in such that the points assigned to X lie on a hyperplane.
- (a)
- G can be realised as an infinitesimally rigid bar–joint framework in such that the points assigned to X lie on a line.
- (b)
- G can be realised as an infinitesimally rigid point-line framework in such that each vertex in X is realised as a line and each vertex in is realised as a point.
- (c)
- G contains a spanning subgraph such that and, for all and all partitions of A,
6.3. Sliders: Free and Pinned
- free sliders, where the line can translate freely without changing the constraint, and, at least infinitesimally, rotate;
- fixed normal or fixed angle sliders, where the angles between the lines are constrained (these constraints correspond to edges along the line at infinity);
- fixed intercept sliders, where any line can rotate freely about a fixed point, but not translate;
- fixed or pinned sliders, where the lines cannot translate or (infinitesimally) rotate to change the normal.
- 1.
- and
- 2.
- for all subgraphs the following conditions hold:
- (i)
- if ,
- (ii)
- if , and
- (iii)
- if and .
6.4. Linear Constraints as Sliders
6.5. Further Extensions to Include Infinity
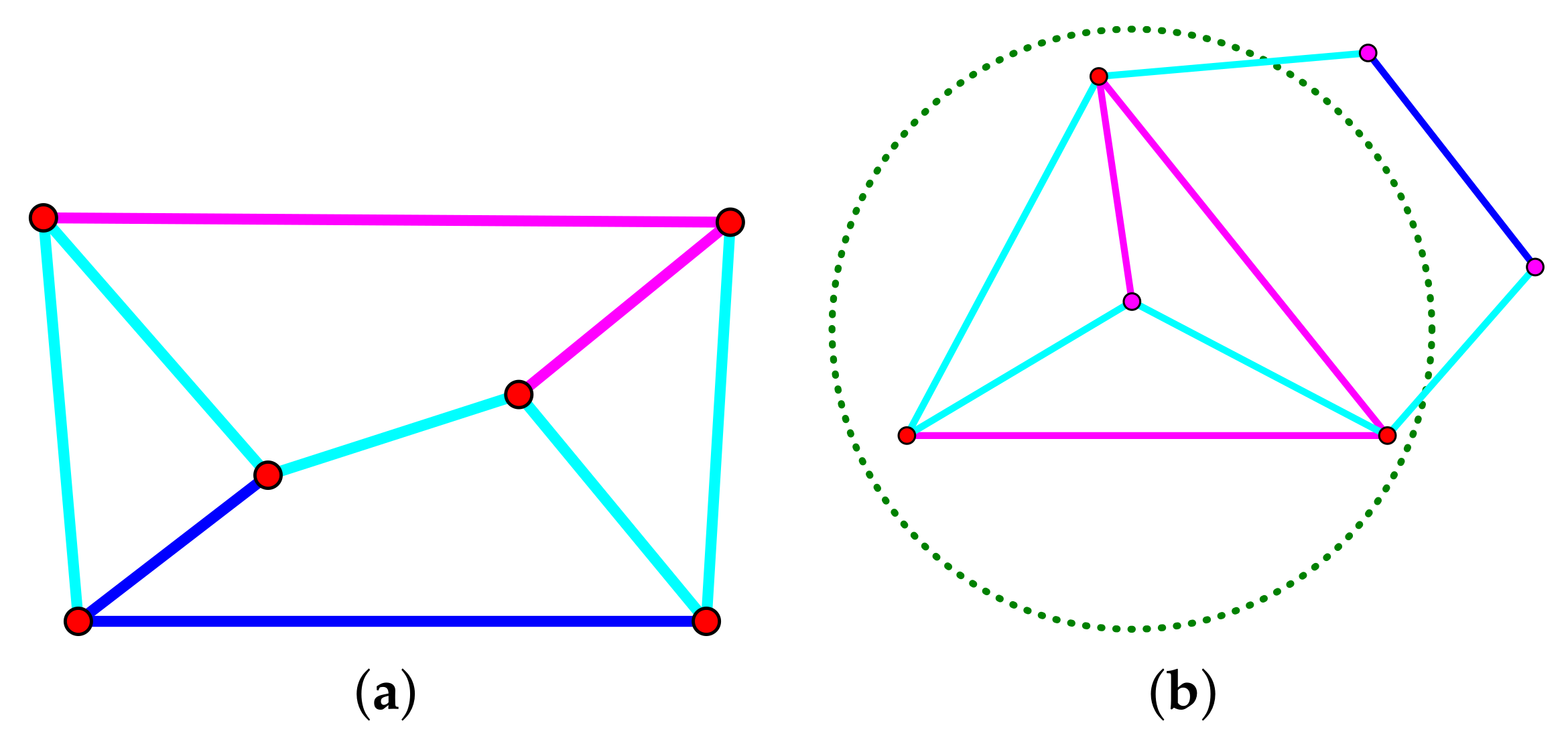
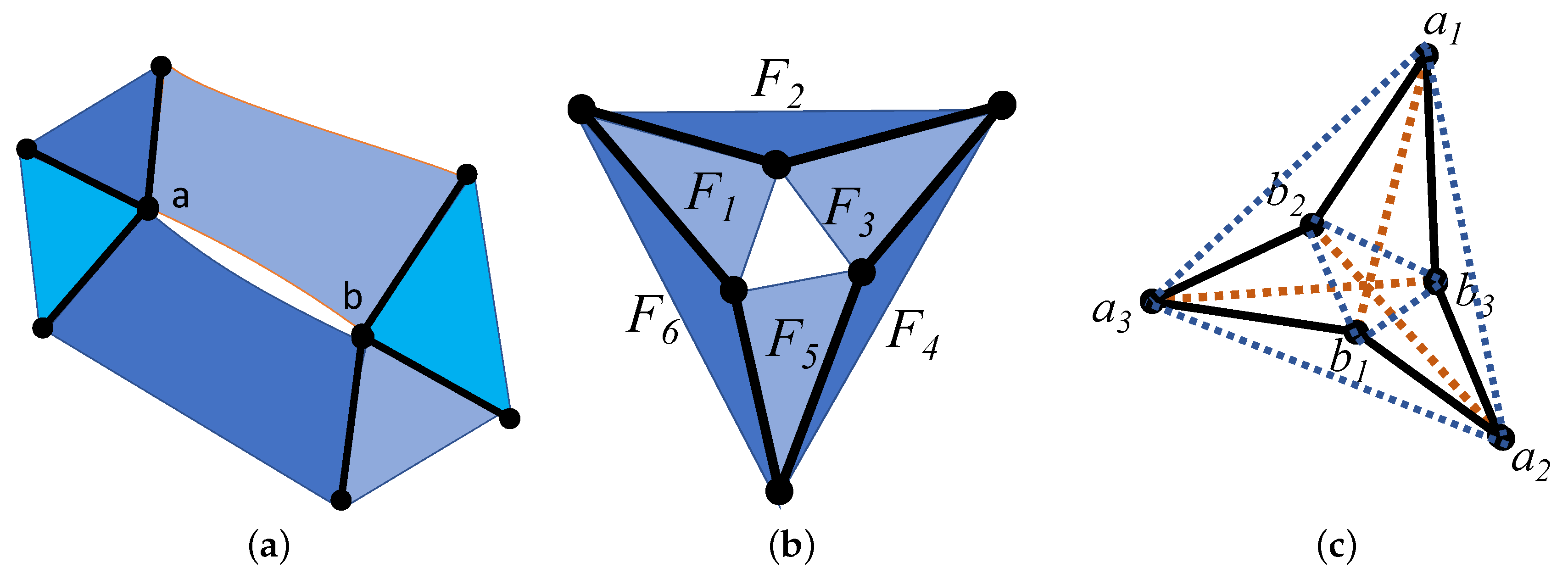
7. Pure Conditions
7.1. Bracket Ring
- Antisymmetry: for . Applied repeatedly, we havefor any permutation of . When we add the requirement that the brackets are linear in the entries, then if the vectors are projectively dependent.
- Basis Exchange:The flavour of basis exchange is that if is a standard basis, then this is the Laplace decomposition of the determinant with as the i-th minor and as the i-th coordinate of . (Note that for , the first term of the sum on the right hand side is .)
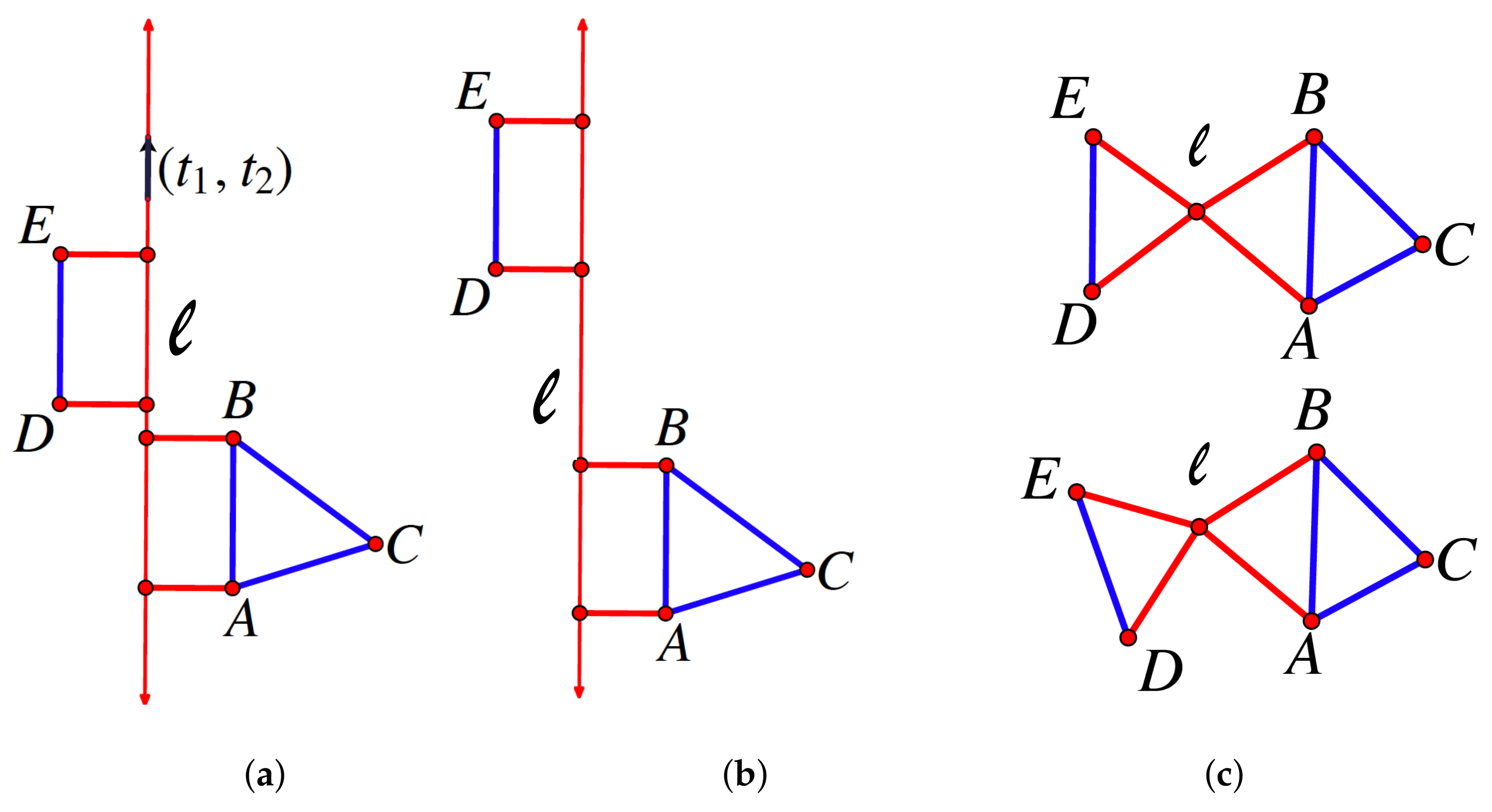
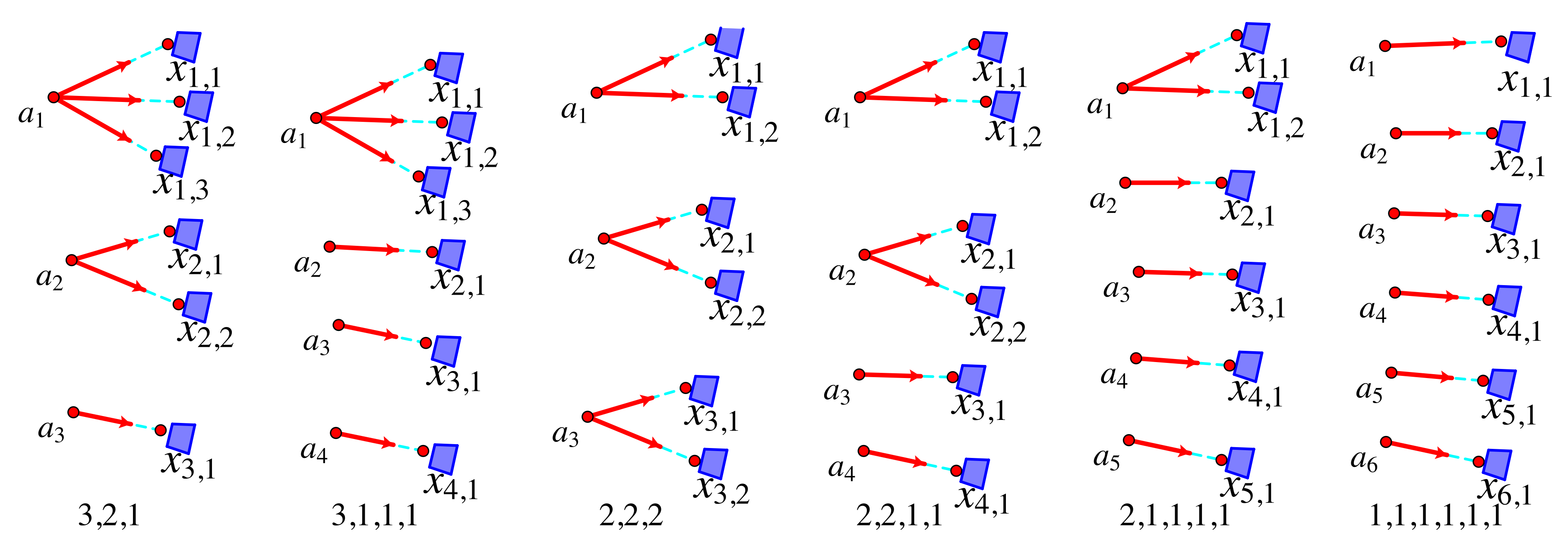
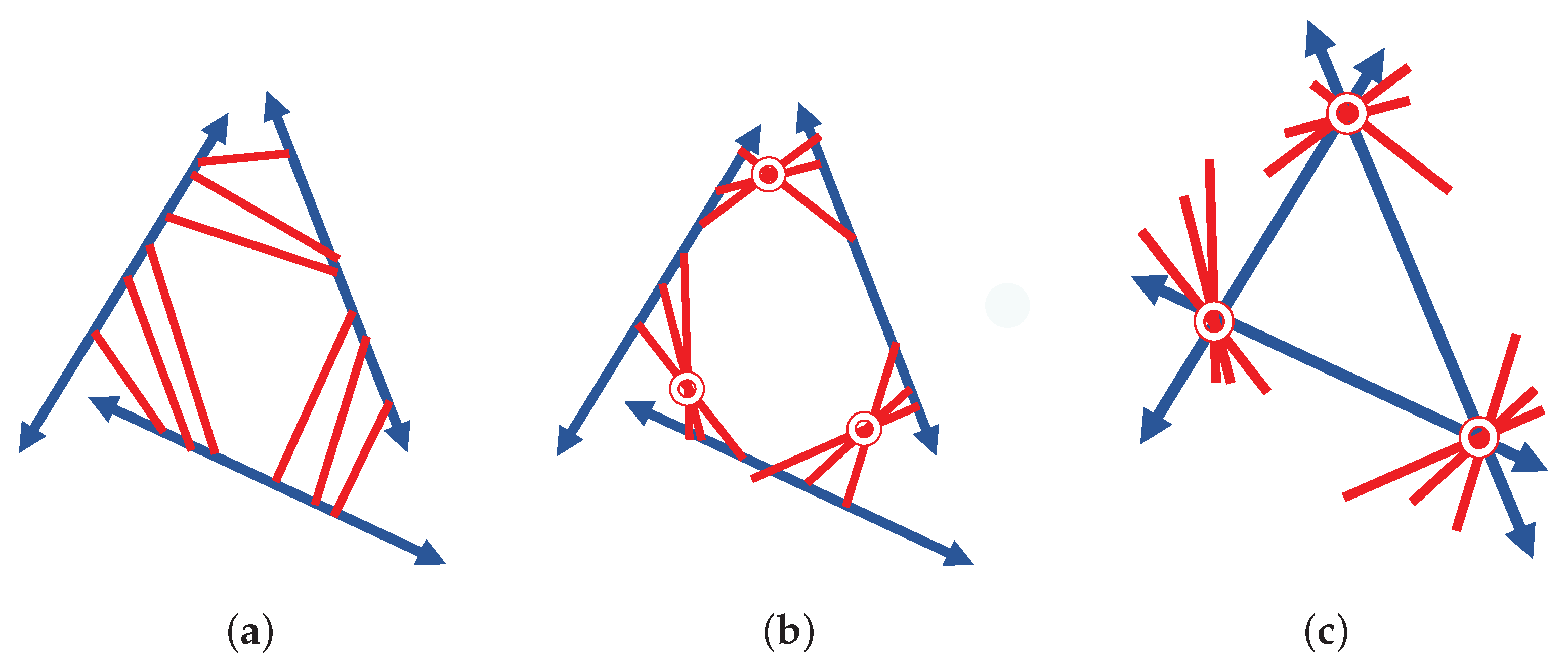
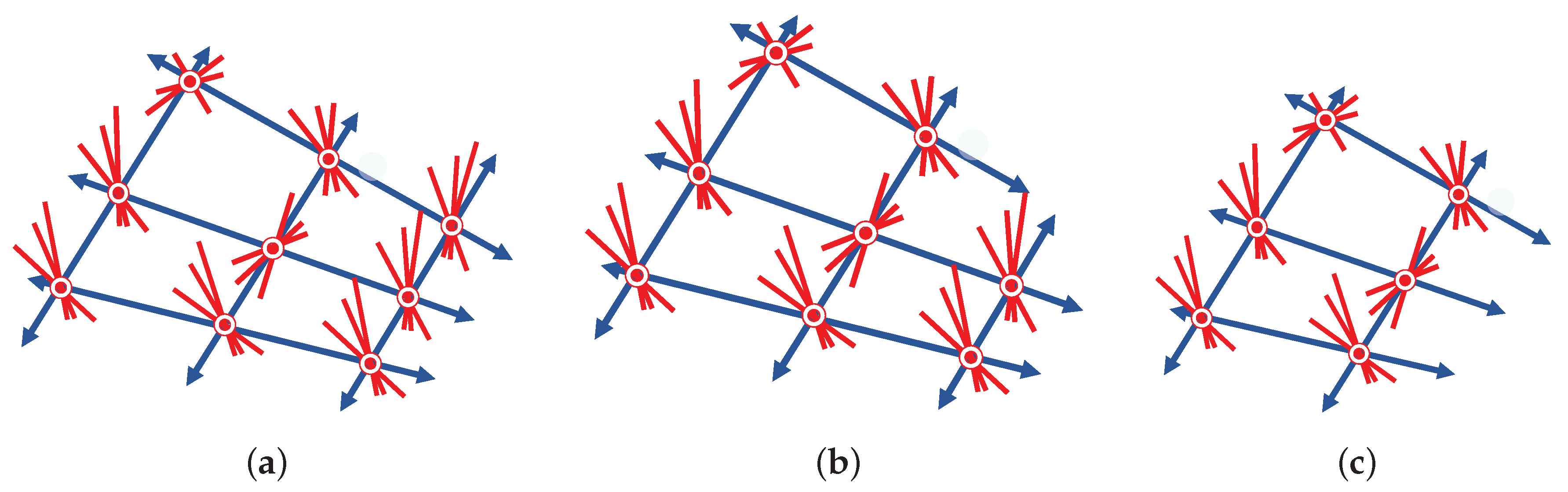
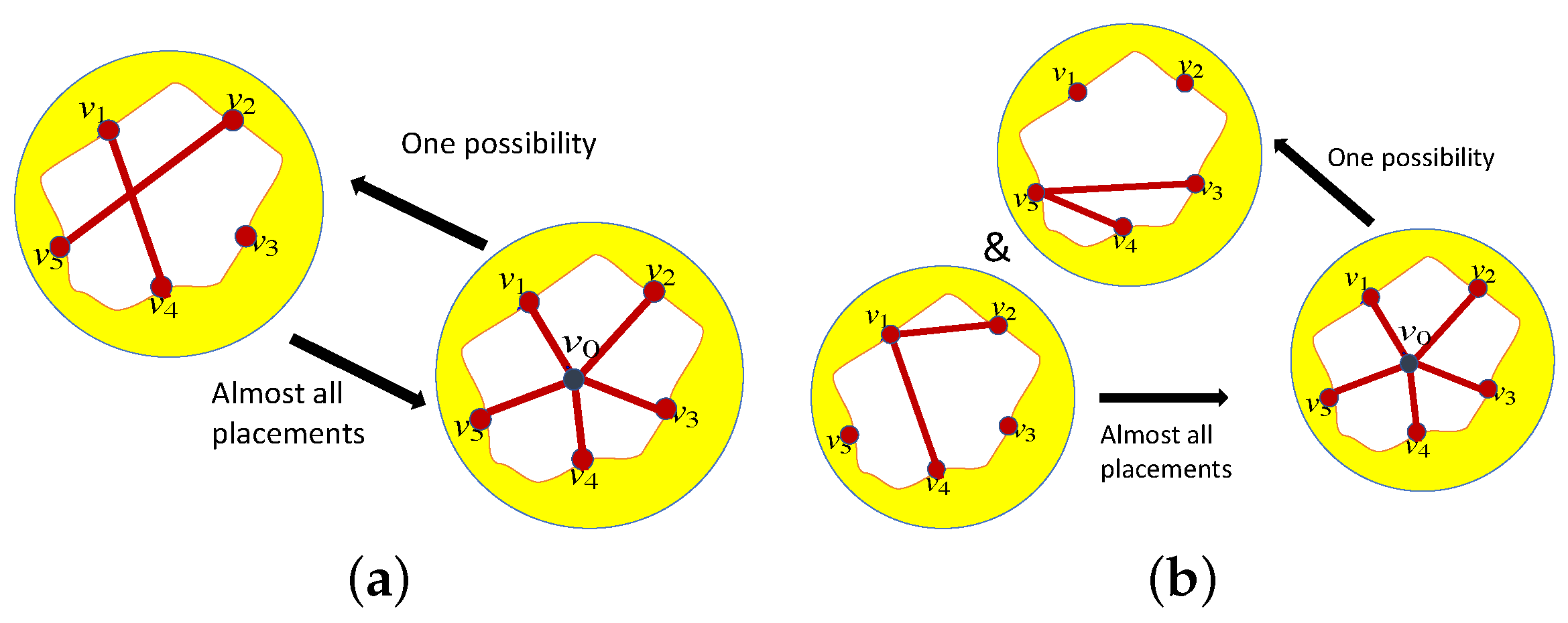
7.2. Small Examples
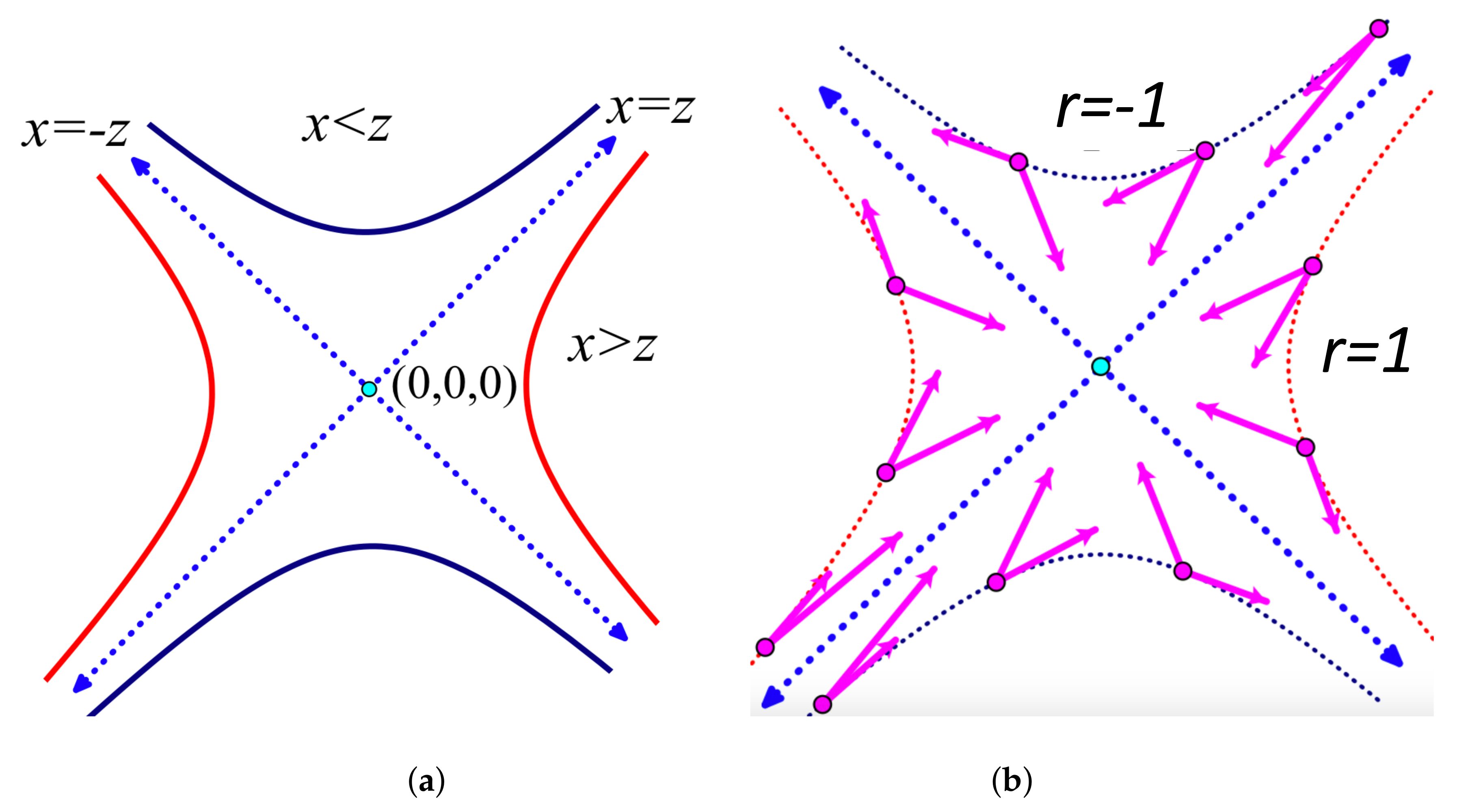
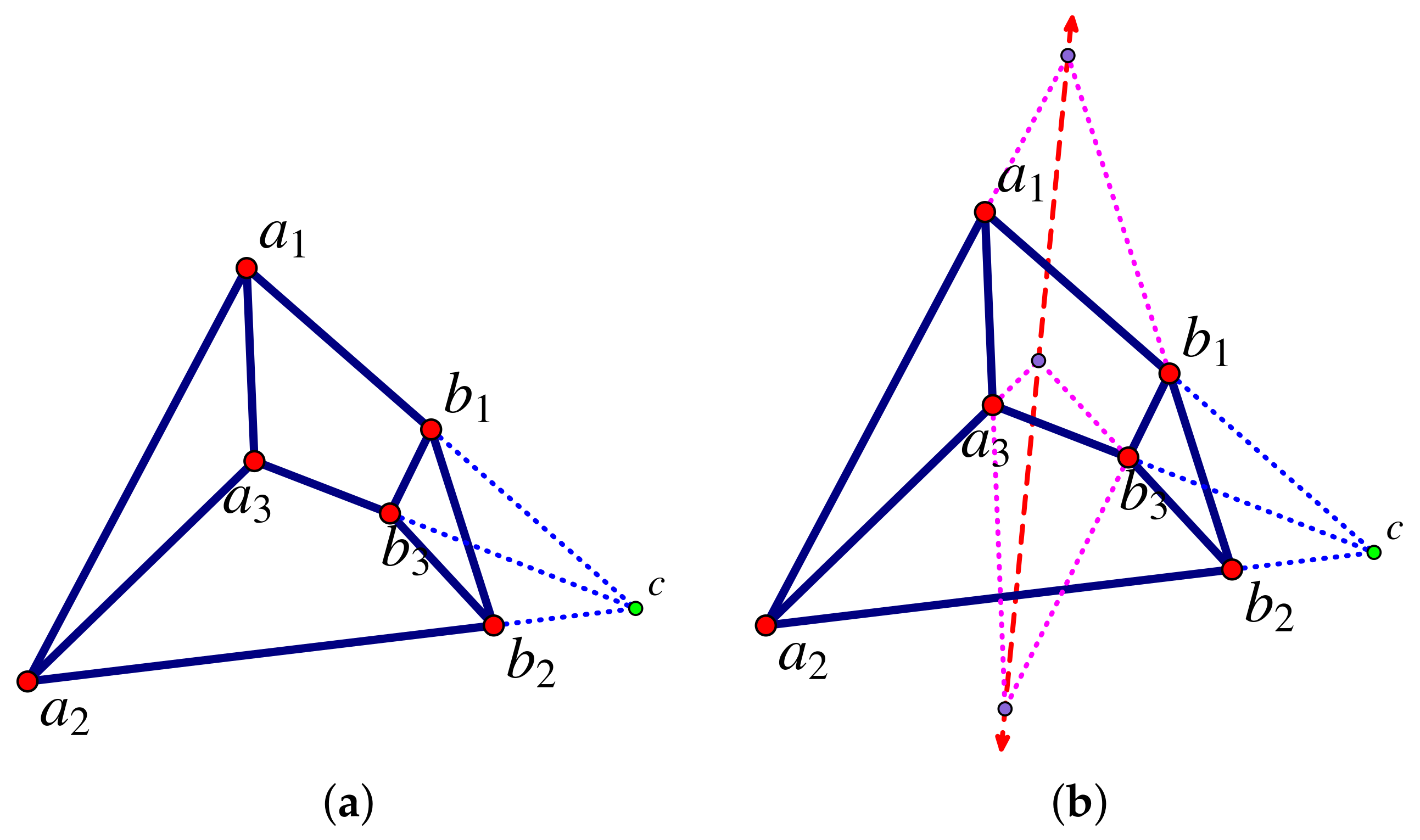
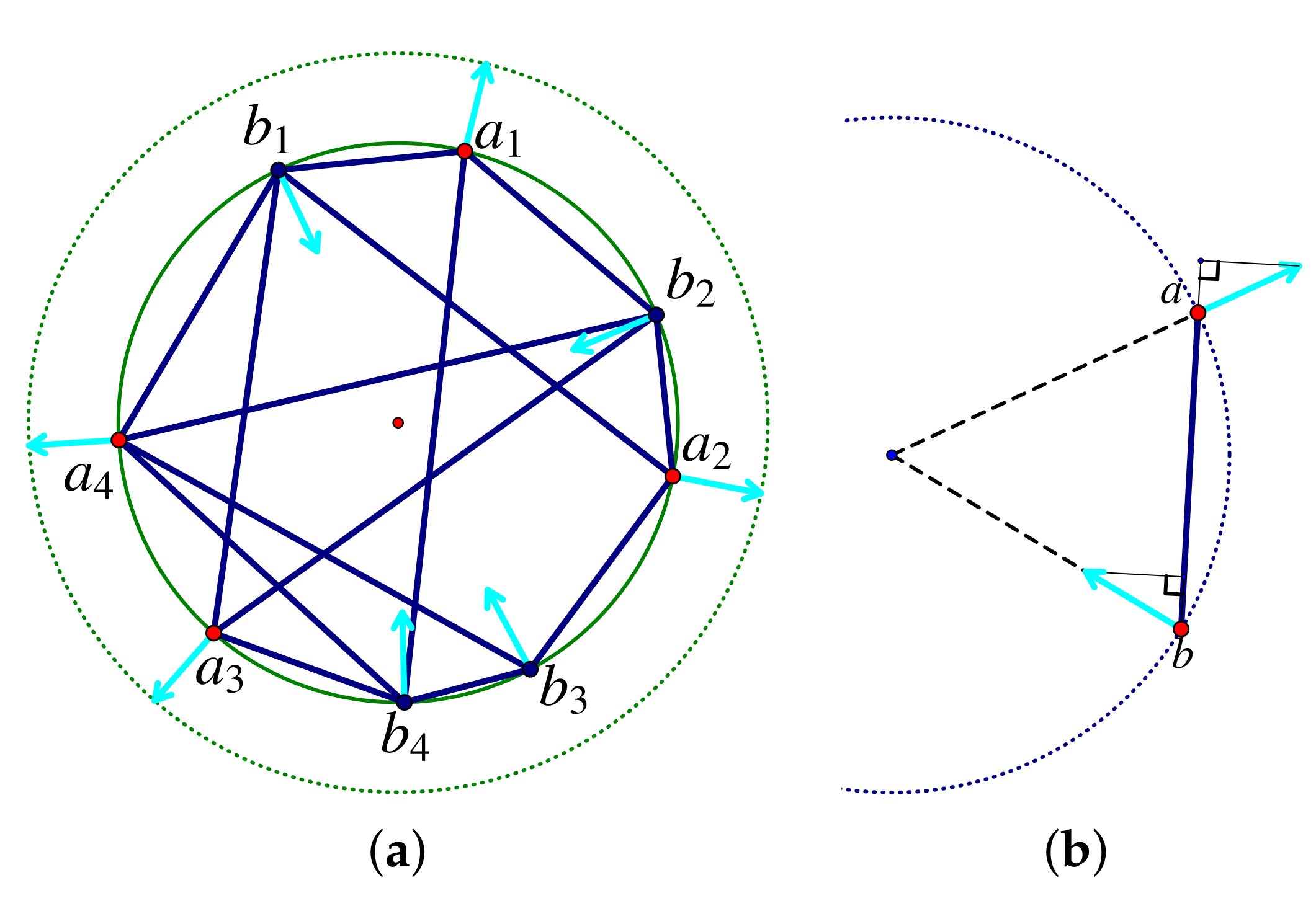
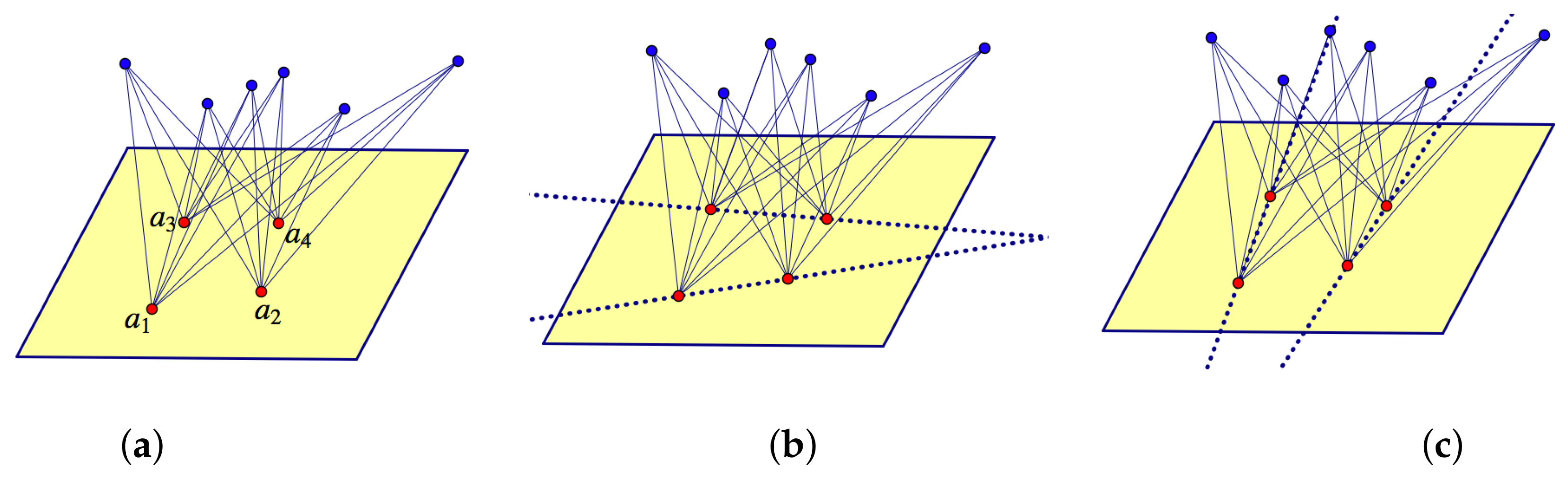
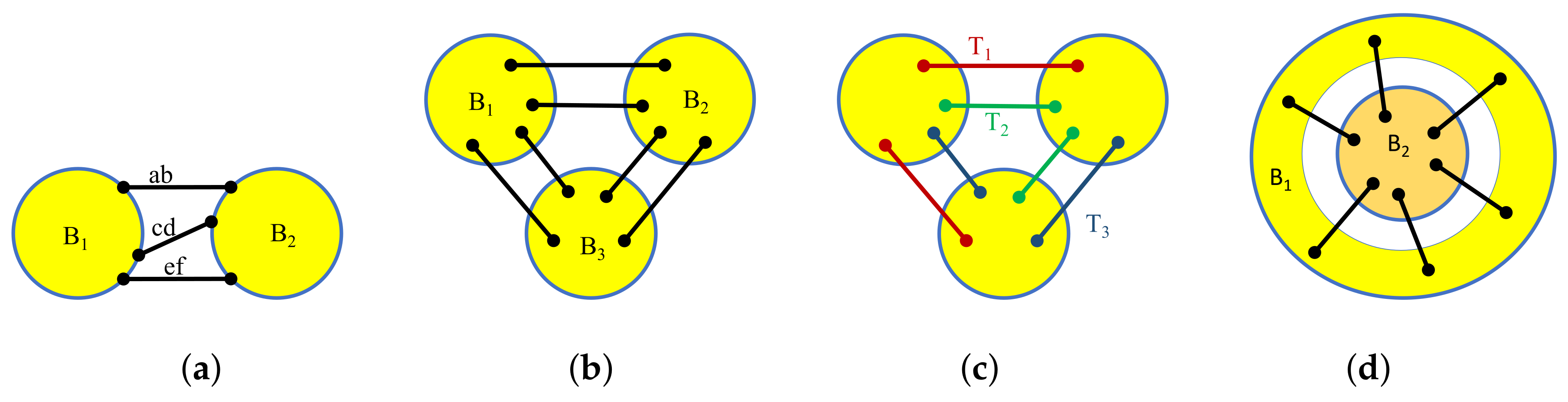
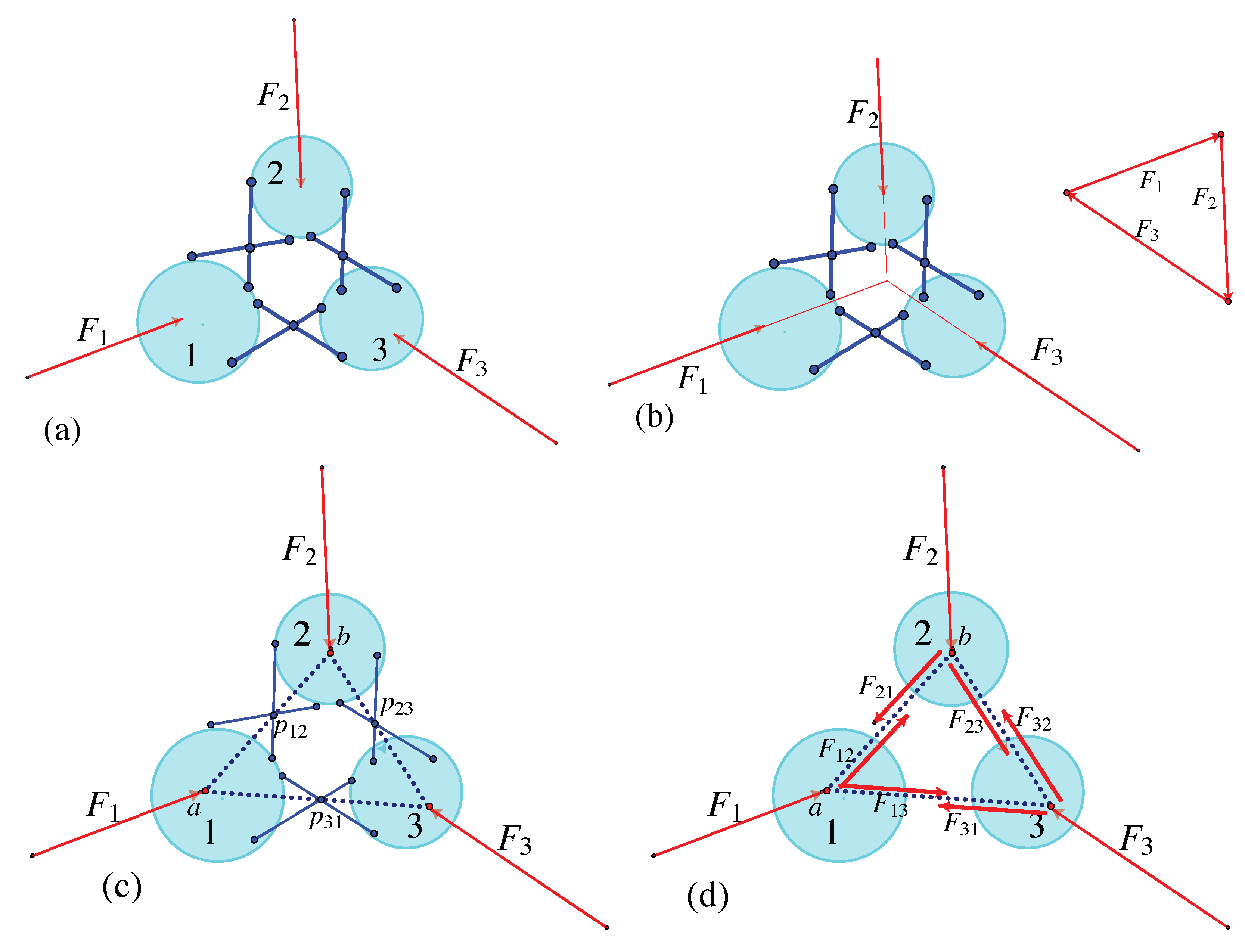
7.3. Bipartite Frameworks and Quadratic Surfaces
- 1.
- the joints of lie on a quadric surface,
- 2.
- one side (A or B) lies on a hyperplane along with at least one joint of the other side, or
- 3.
- one side (A or B) lies on a hyperplane H and lies on a quadric surface within the hyperplane.
- 1.
- the joints are contained on a quadric surface containing the line ;
- 2.
- the joints of A lie in a hyperplane containing some joint of B;
- 3.
- the joints of B line in a hyperplane containing both and or containing some other joint of A;
- 4.
- the joints of B lie on a hyperplane quadric and the line touches the quadric at 1 point;
- 5.
- the joints of A lie in a hyperplane quadric containing the line .
- 1.
- If A and B span the space, there is a non-trivial infinitesimal motion of if and only if there is a quadric surface containing all the joints and all the lines of bars in .
- 2.
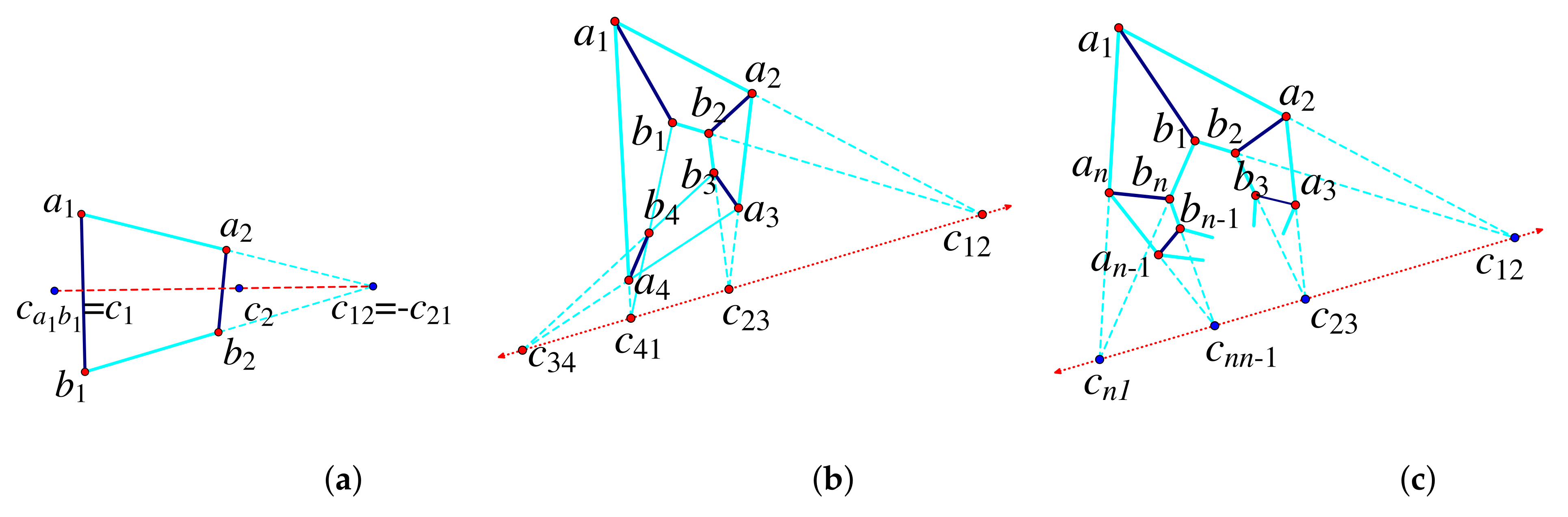
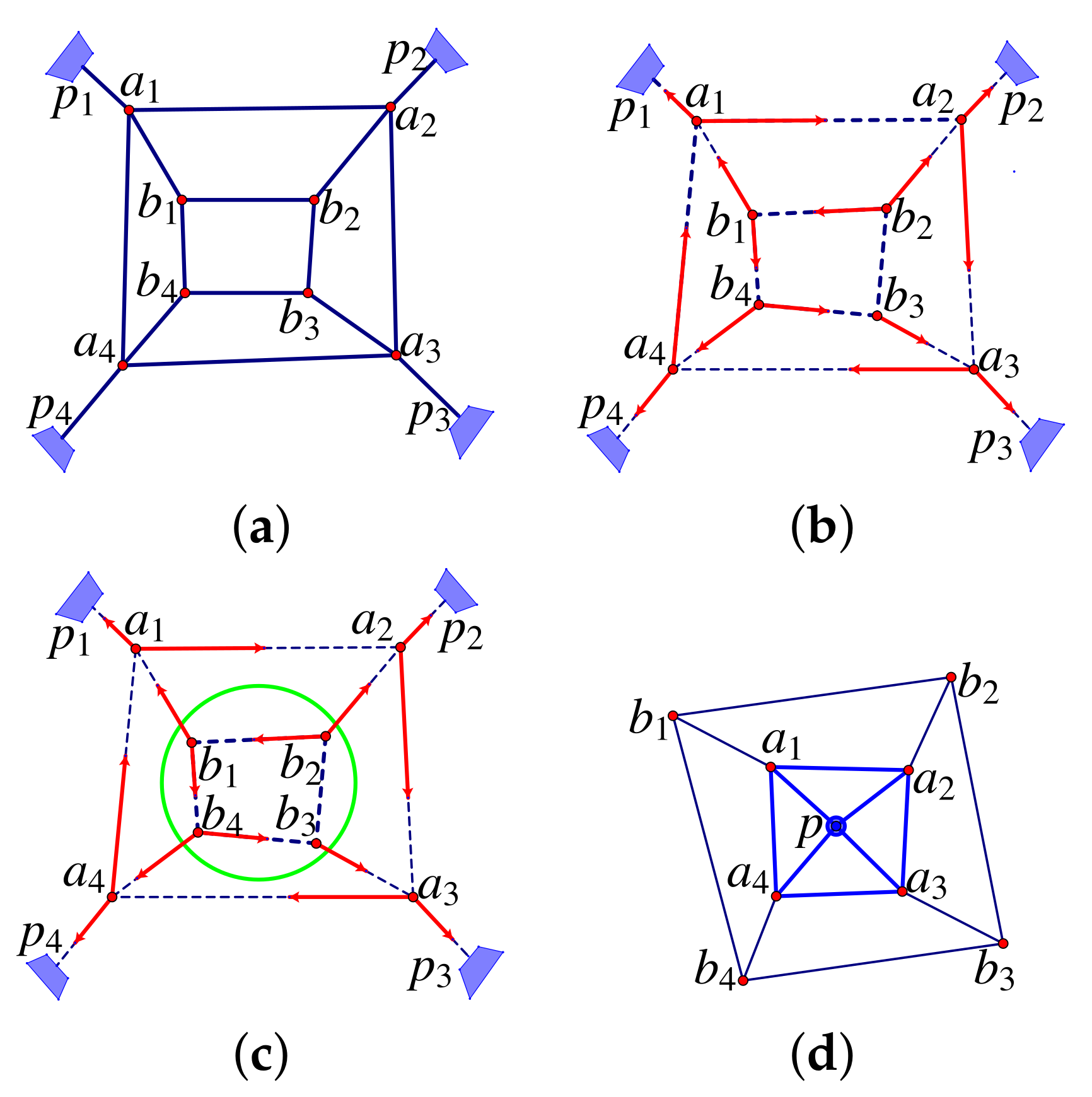
- If A spans a plane and B spans a plane , and no joints lie on the intersection of the two planes, then there is a non-trivial infinitesimal motion of if and only if there are two points p and q on the (projective) intersection of the two planes such that each line of a bar in passes through one of these points (Figure 24a).
- 3.
- If A spans a plane and B spans the space, with , then there is a non-trivial infinitesimal motion of if and only if there is a conic in the plane containing all joints of and all bars of as well as of C, and this conic touches the line of any other bar in D.
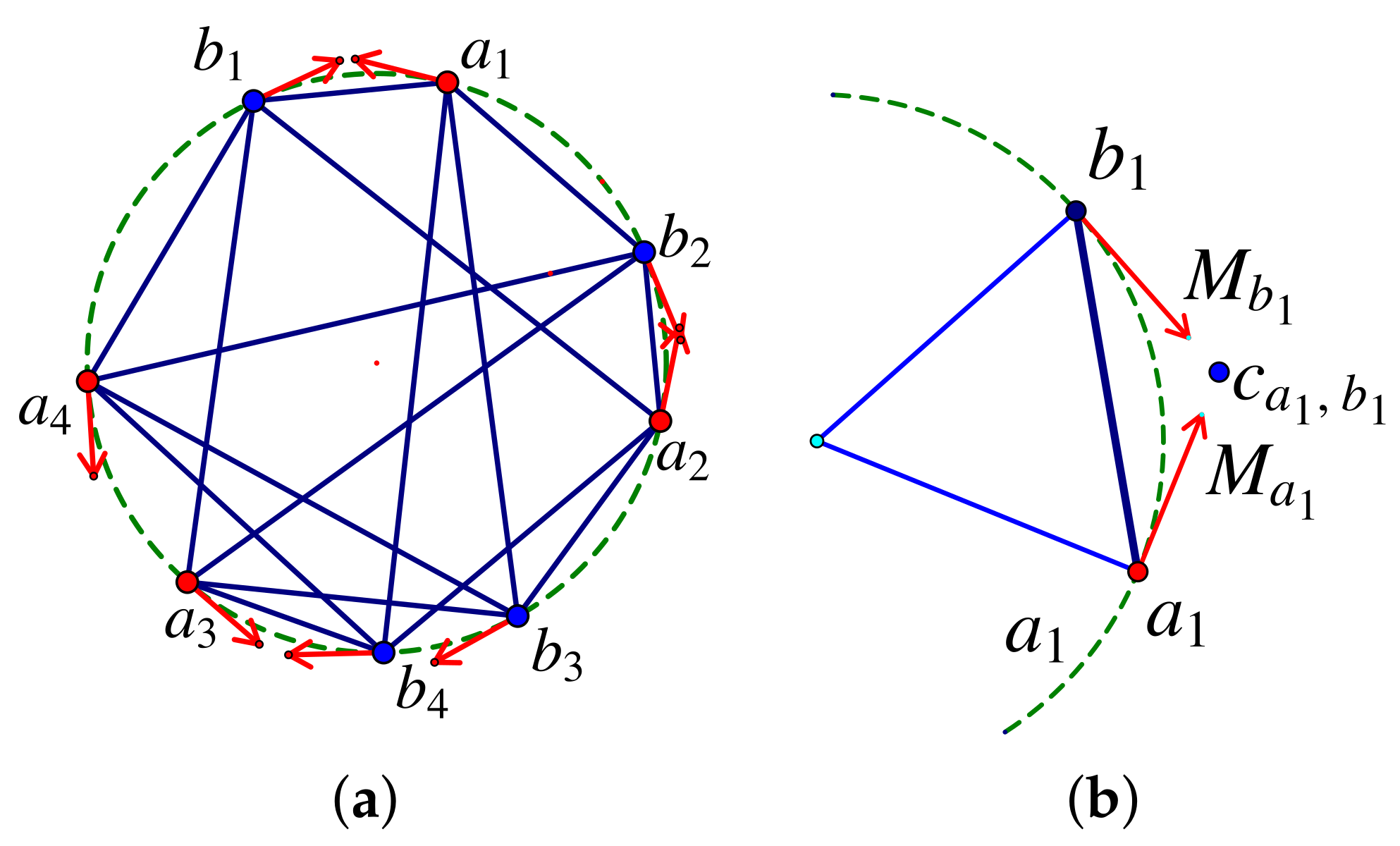
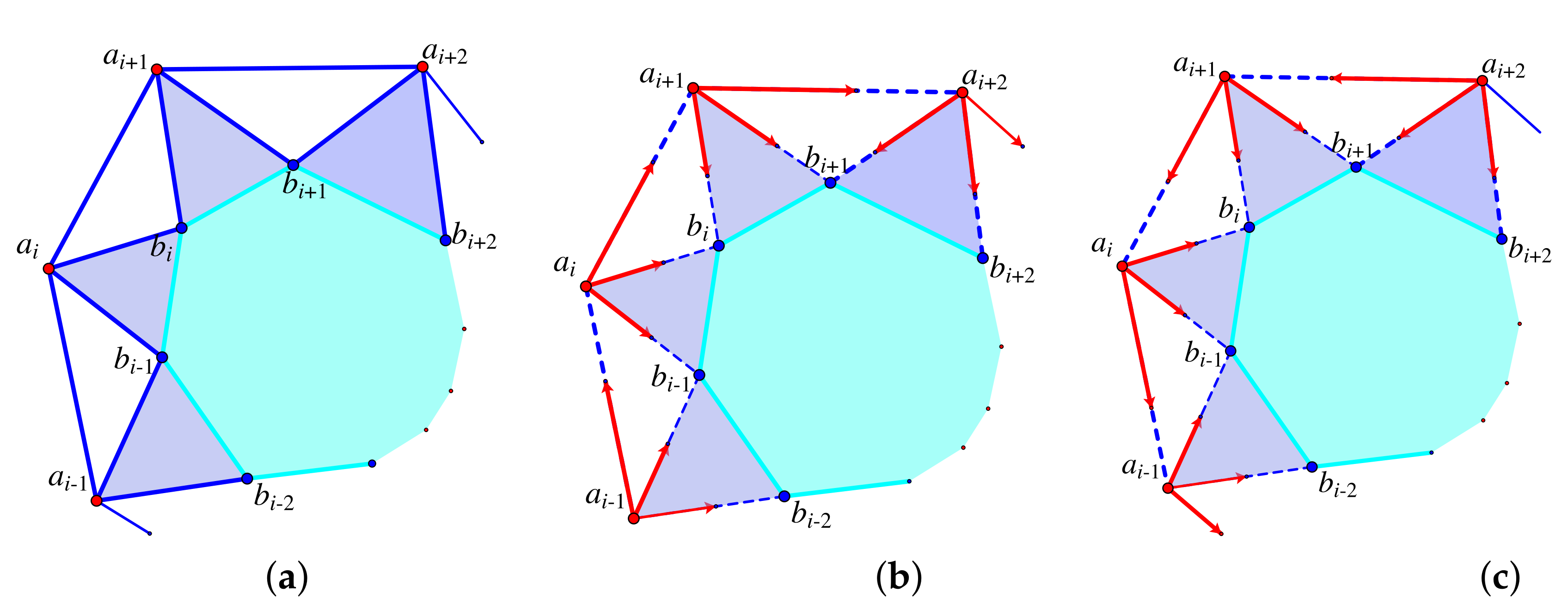
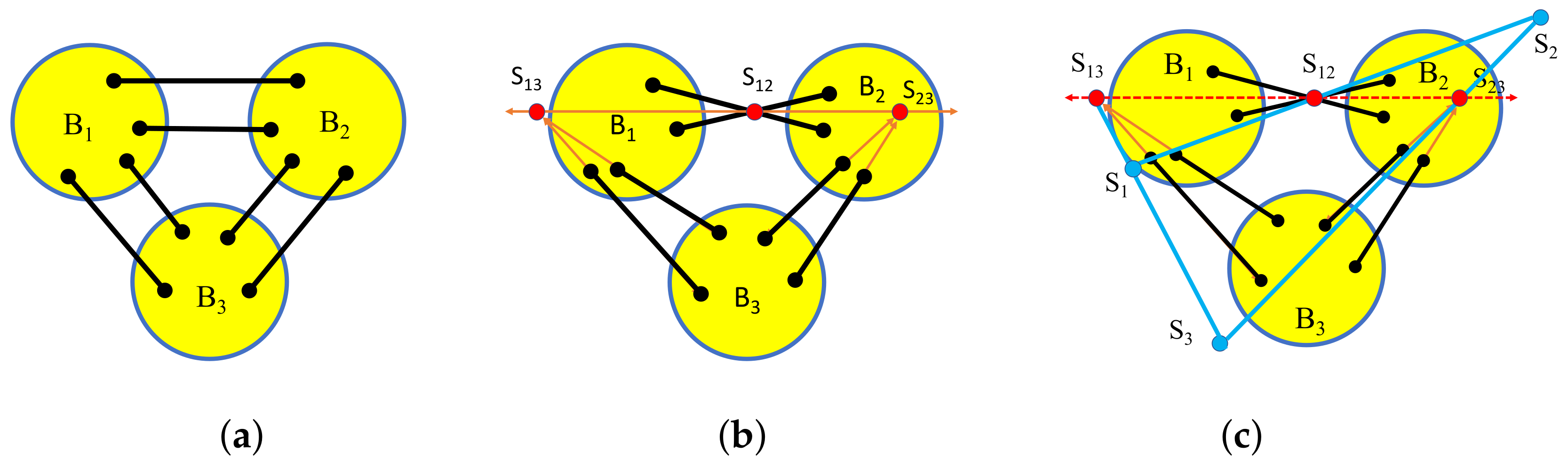
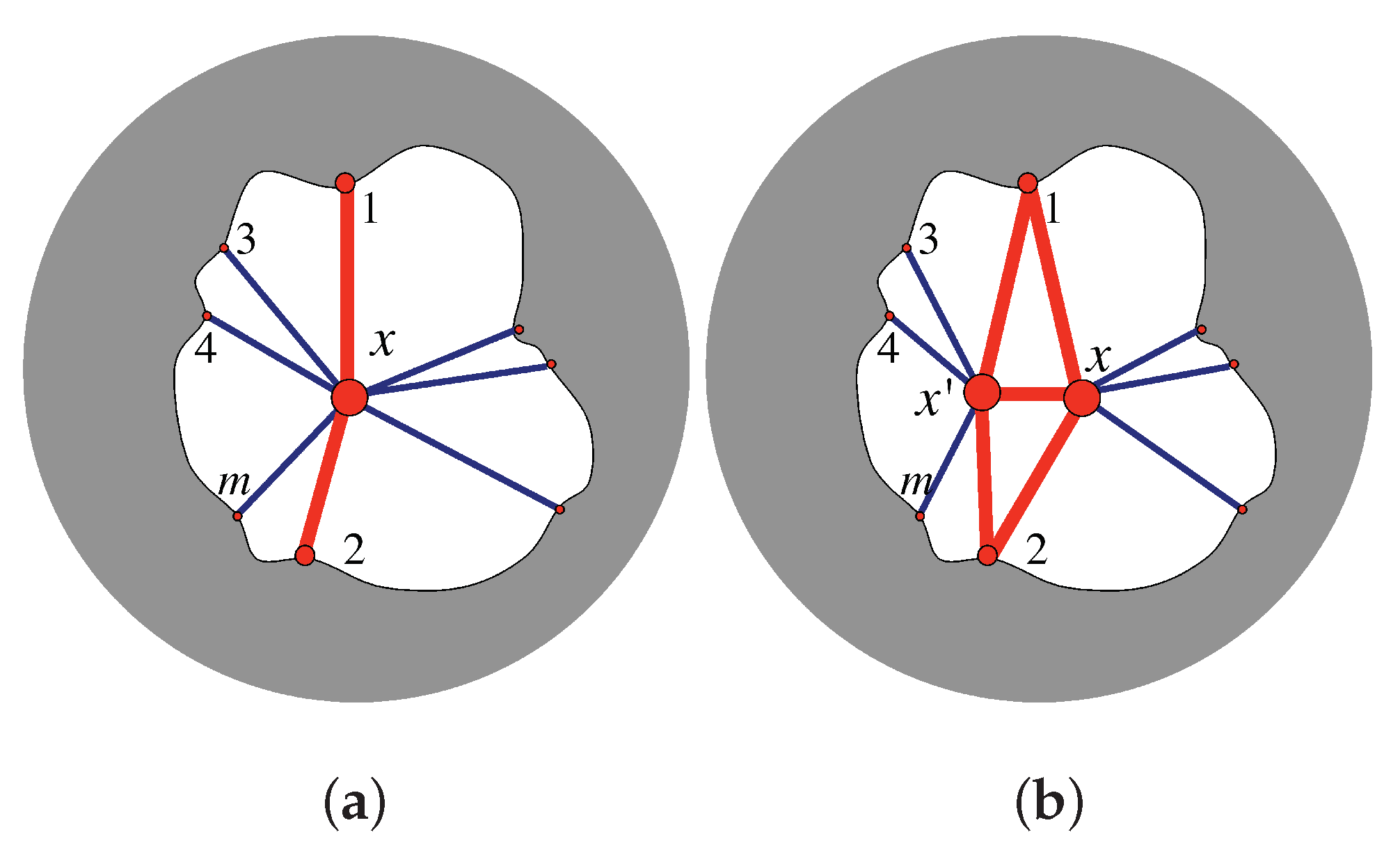
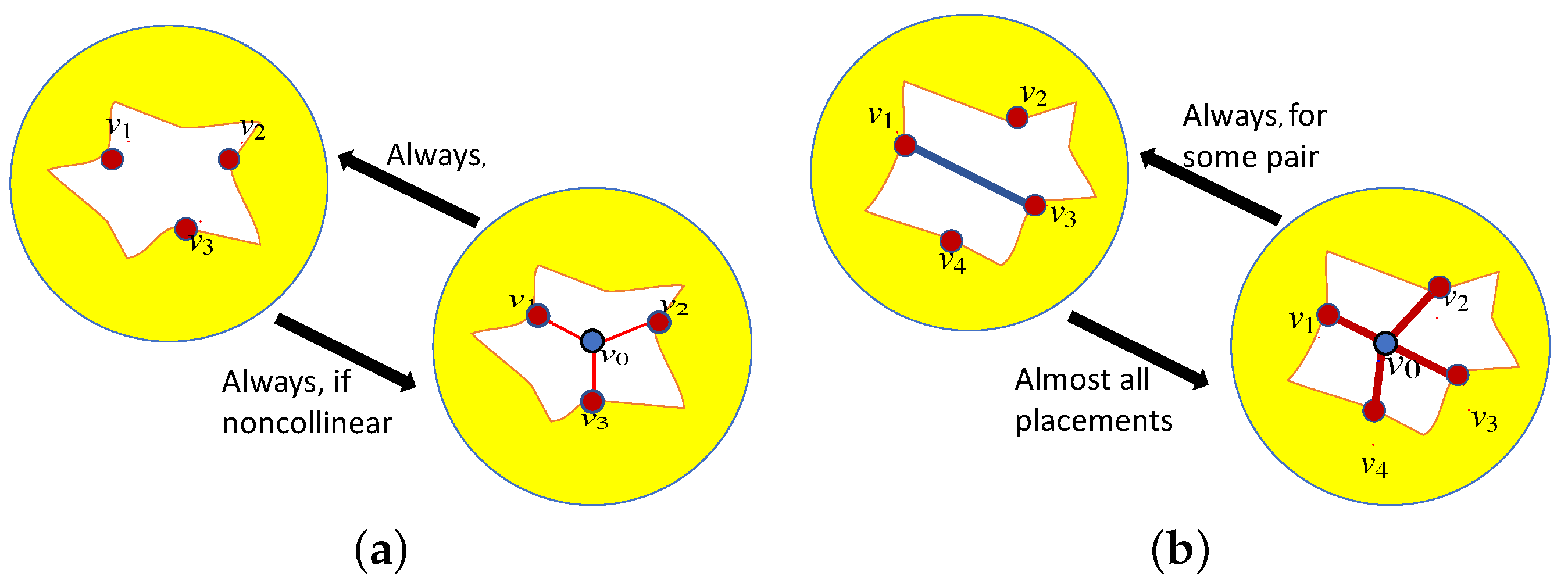
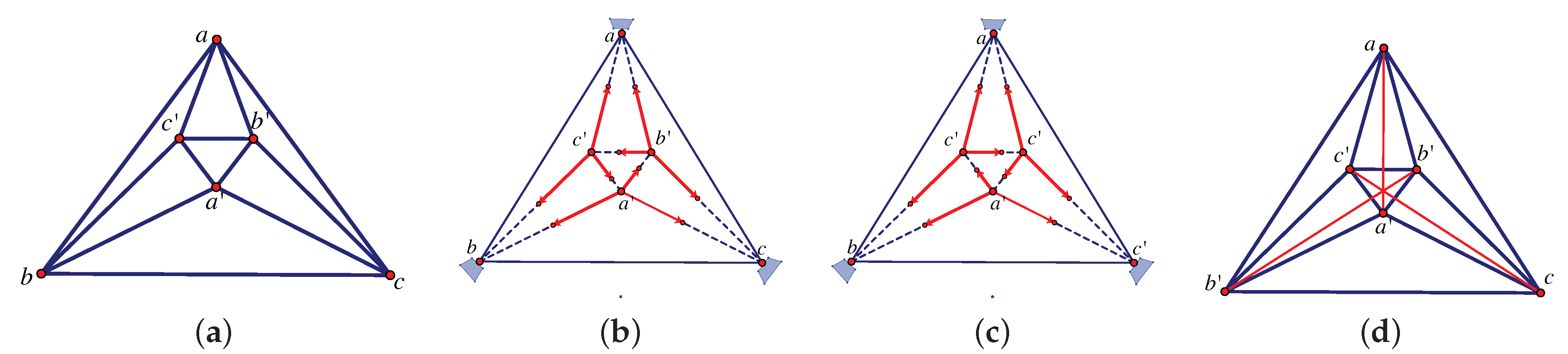
7.4. Pure Conditions: Basic Theorems
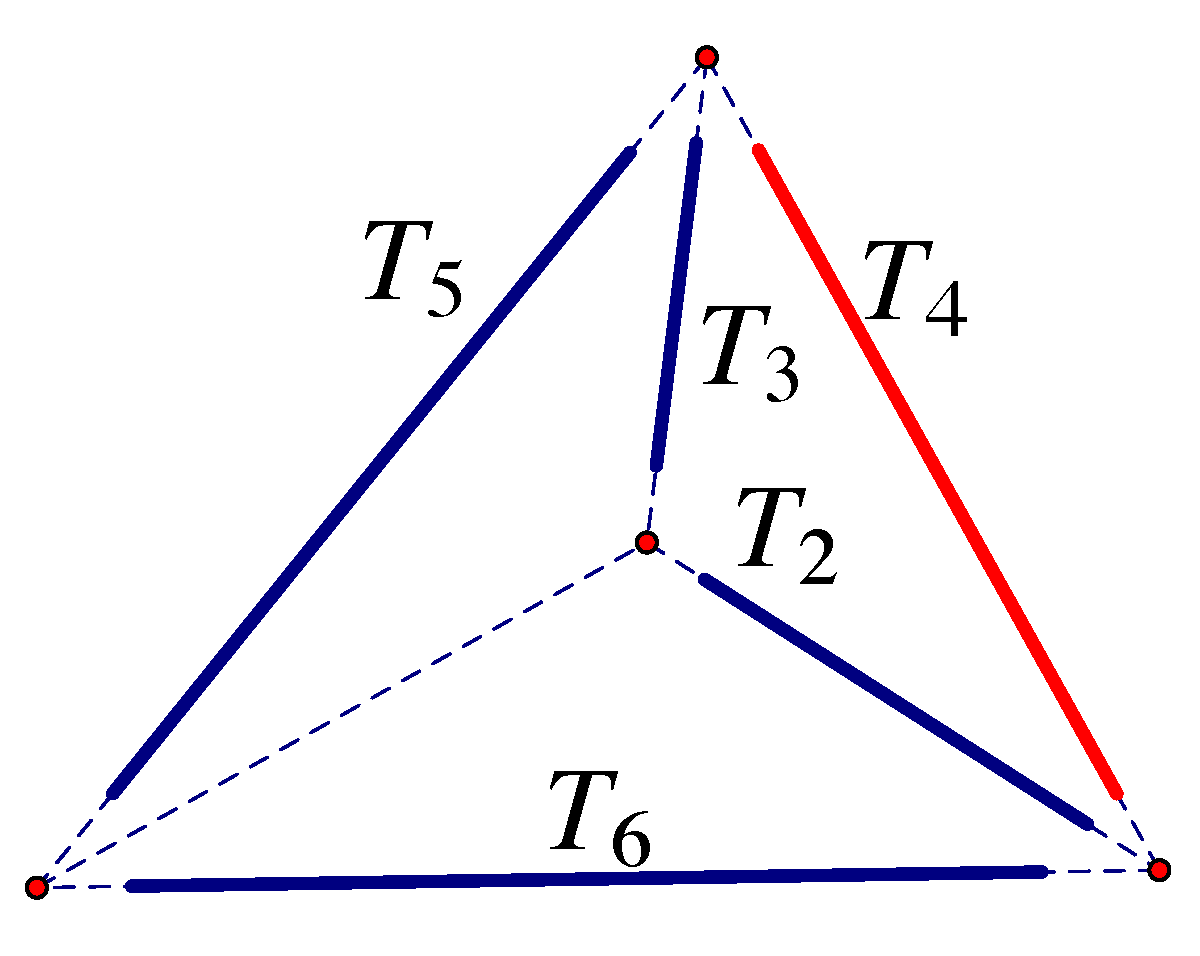
- The first step is a lemma from [85].Lemma 1.A framework in general position in is isostatic if and only if there exists a tie-down T which produces an invertible extended rigidity matrix .
- If we represent the tie-down bars of a framework by 2-extensors, we can construct a square matrix with determinant in the bracket algebra which is non-zero if and only if the tie-down will not support an equilibrium stress (the tie-down rows are independent). These are the non-degenerate tie-downs with .
- For , let be the number of tie-down bars incident to , and assume that we have reindexed so that . Then if and only if
- Suppose G is isostatic in and T is a non-degenerate tie-down. Then the determinant of the extended rigidity matrix equals an element of the bracket ring B on the set of vertices of [85].
- For a non-degenerate tie-down T, the polynomial is a factor of the larger determinant so that , for some bracket polynomial .
- For two non-degenerate tie-downs the residual factors , so there is a unique pure condition . This uses a lemma that moves one tie-down edge at a time along an edge of G, provided the moves preserve the non-degeneracy of the tie-down.
7.5. Factoring and Rigid Components
7.6. Computing Pure Conditions: Pinned Frameworks, and d-Directed Graphs
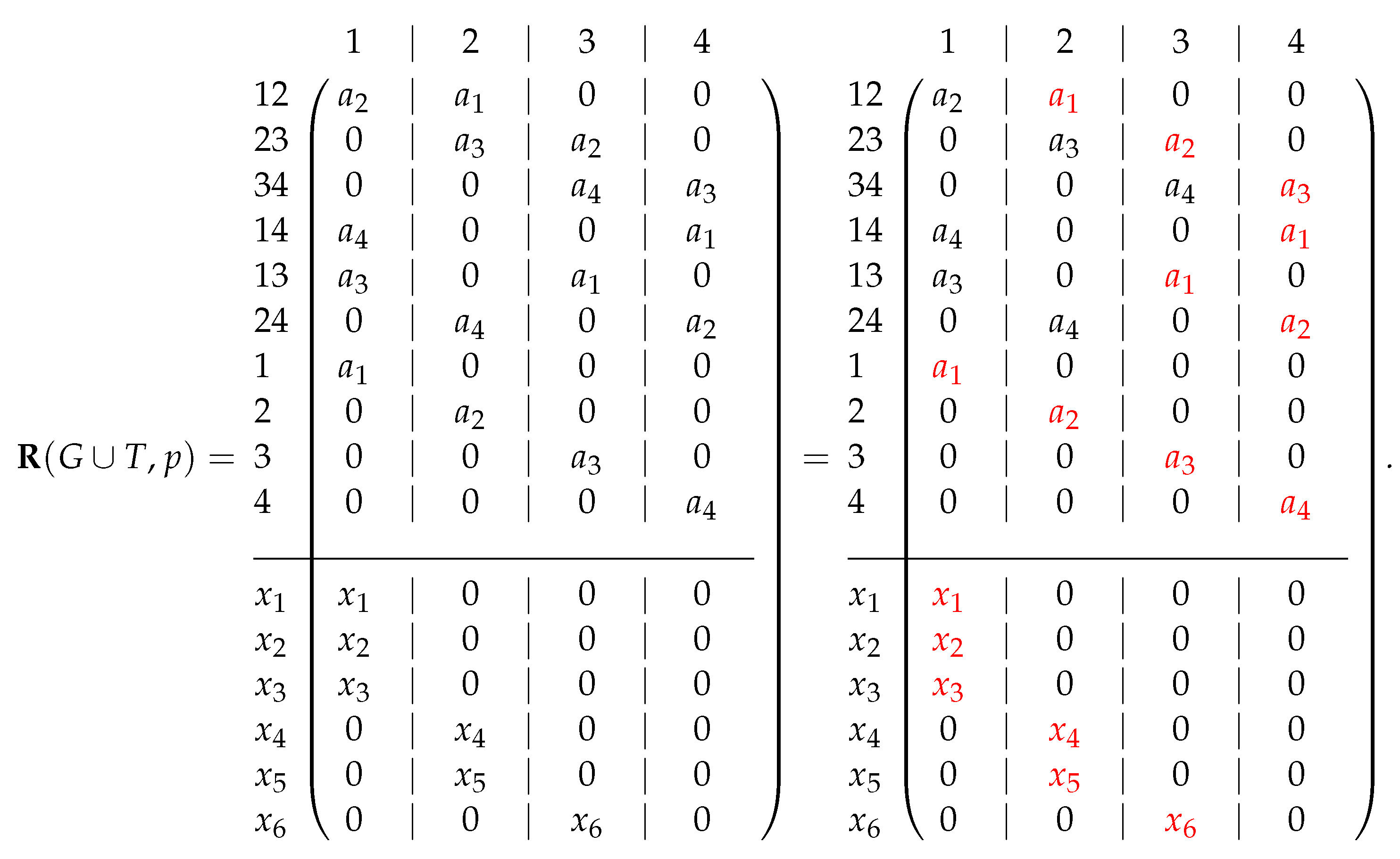
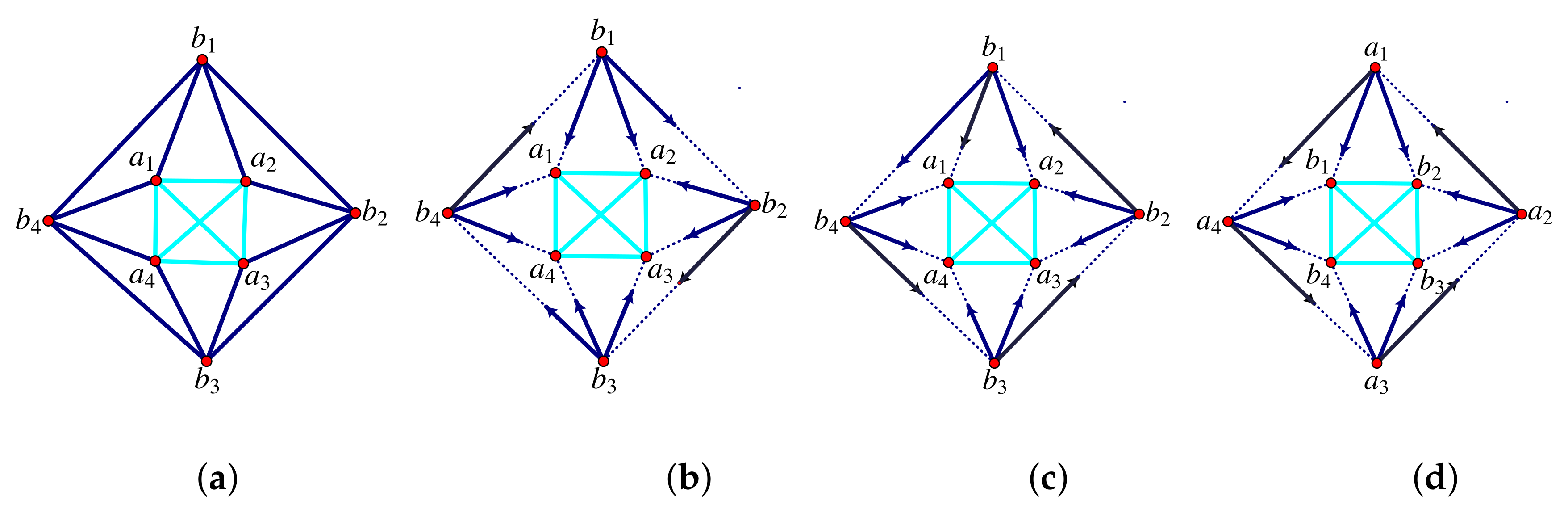
7.7. Assur Graphs and Assur Decompositions
- and
- for all subgraphs the following conditions hold for
- (i)
- if ,
- (ii)
- if , and
- (iii)
- if and .
- statically determinate graphs: graphs realizable as statically determinate (isostatic) structures for generic configurations.
- mechanisms: graphs which when realized in generic configurations give various positive degrees of freedom (DOF); such structures are called mobile. A linkage will be a mechanism with 1 DOF.
- independent graphs: graphs without redundance, so that removing any one edge results, for generic realizations, in a structure with an added DOF.
- redundant graphs: graphs that are not independent for any realizations. These may be rigid (kinematically determinate) or mobile at generic or special realizations.
- 1.
- is an Assur graph.
- 2.
- If the set P is contracted to a single vertex p, then the resulting contracted graph is a rigidity circuit.
- 3.
- Either the graph has a single inner vertex of degree 2 or each time we delete a vertex, the resulting pinned graph has a motion with non-zero velocity at all inner vertices (in generic position).
- 4.
- Deletion of any edge from G results in a pinned graph that has a motion with non-zero velocity at all inner vertices (in generic position).
- 5.
- Any 2-directed orientation of G is strongly connected.
- 1.
- has a unique (up to scalar) equilibrium stress which is non-zero on all edges; and
- 2.
- has a unique (up to scalar) infinitesimal motion, and this is non-zero on all inner vertices.
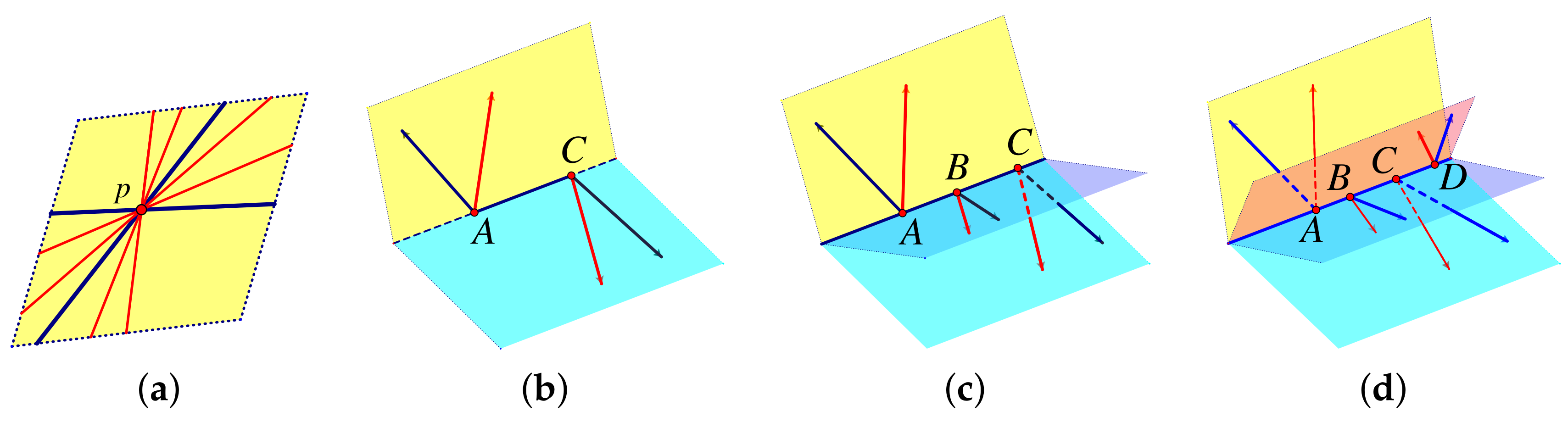
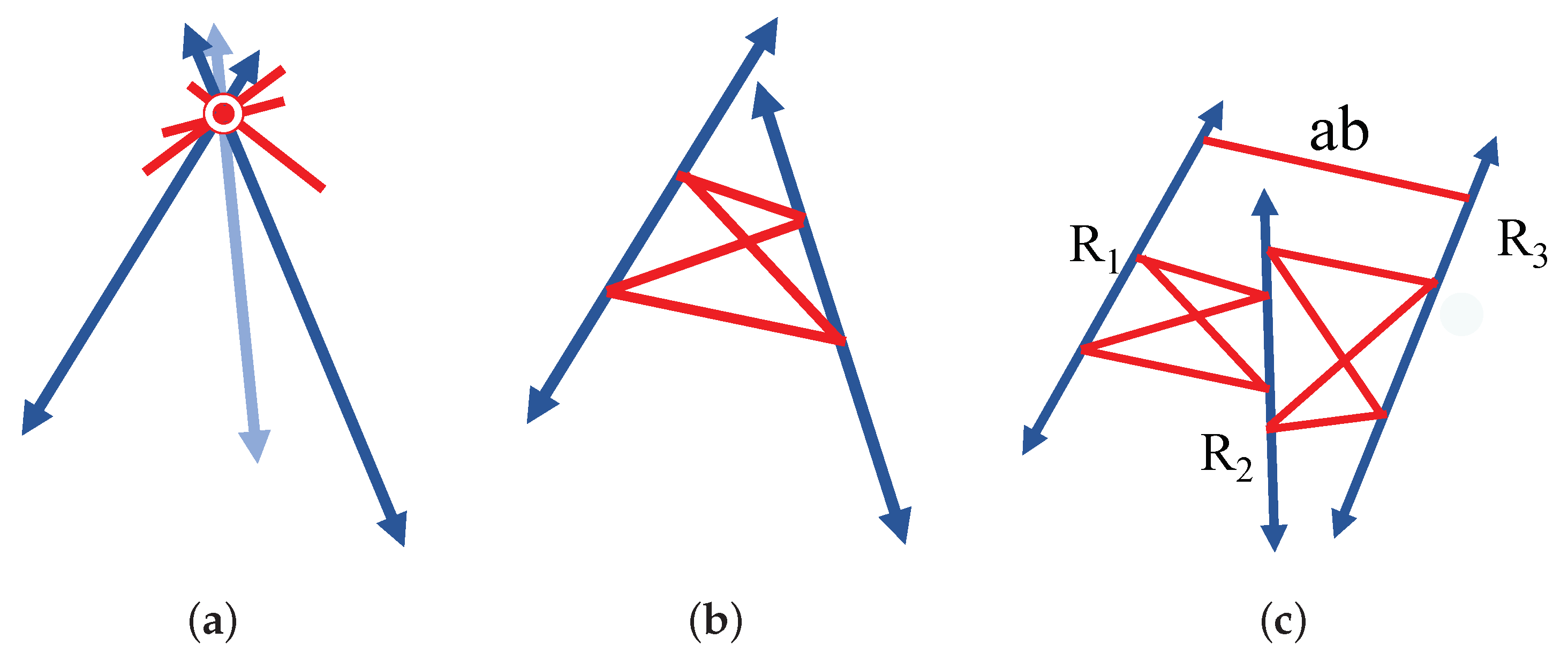
8. Polarity for Rigidity
8.1. Duality and Polarity for Projective Geometry
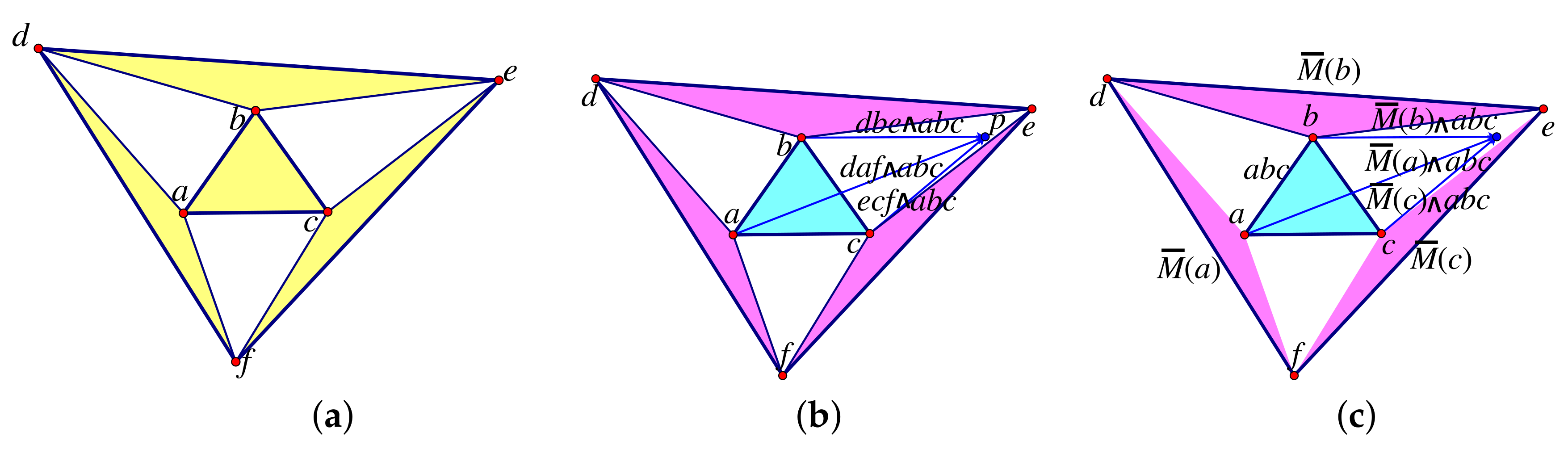
8.2. Sheet Structures and Polarity for Rigidity in
- 1.
- is statically rigid if and only if is statically rigid;
- 2.
- is independent if and only if is independent;
- 3.
- is isostatic if and only if is isostatic;
- 4.
- the spaces of equilibrium loads are isomorphic;
- 5.
- the spaces of resolved loads are isomorphic;
- 6.
- the spaces of stresses are isomorphic.
- 1.
- There is a complete geometric theory of infinitesimal motions of sheetworks with projective centers of motion. Each sheet has a point centre in the sheet, and the two centres on sheets at a shared edge satisfy a compatibility condition which is the polar of the condition for bar–joint frameworks. Does this offer additional insights?
- 2.
- What happens with points, lines and sheets at infinity?
- 3.
- What about four copunctual sheets—the polar of four coplanar points of a tetrahedron. The polar will be four sheets through a single point, but with six specified hinge lines through this point. What will the infinitesimal motions look like?
- 4.
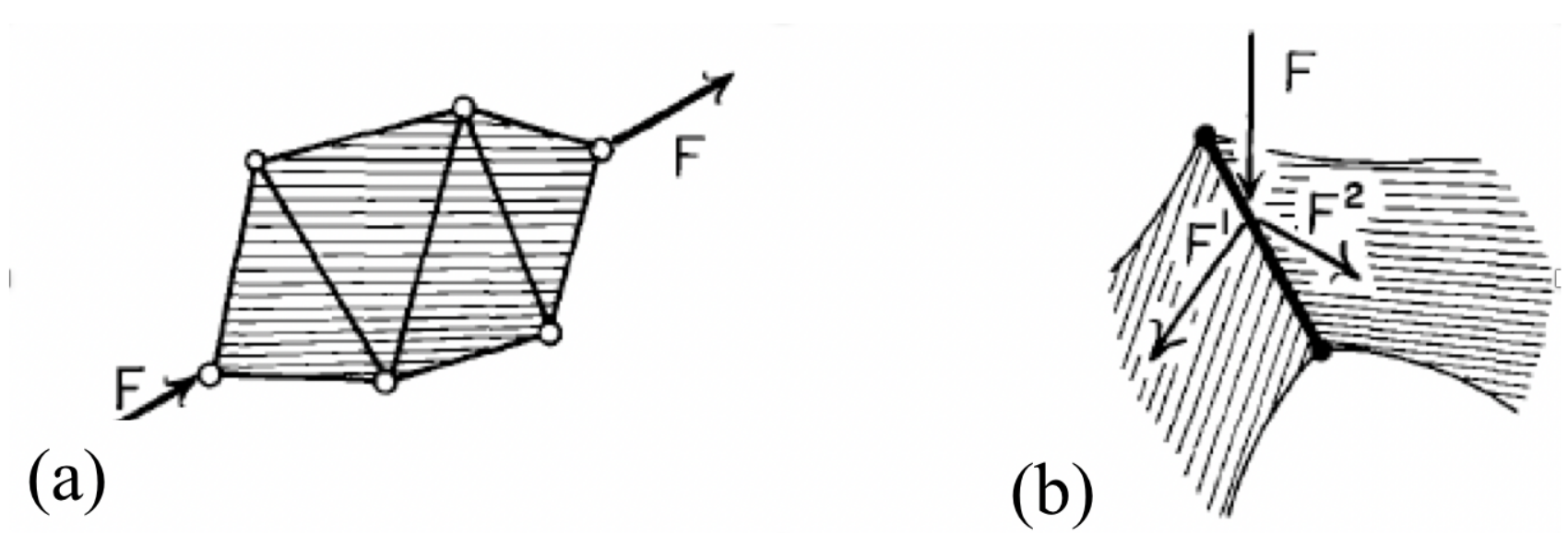
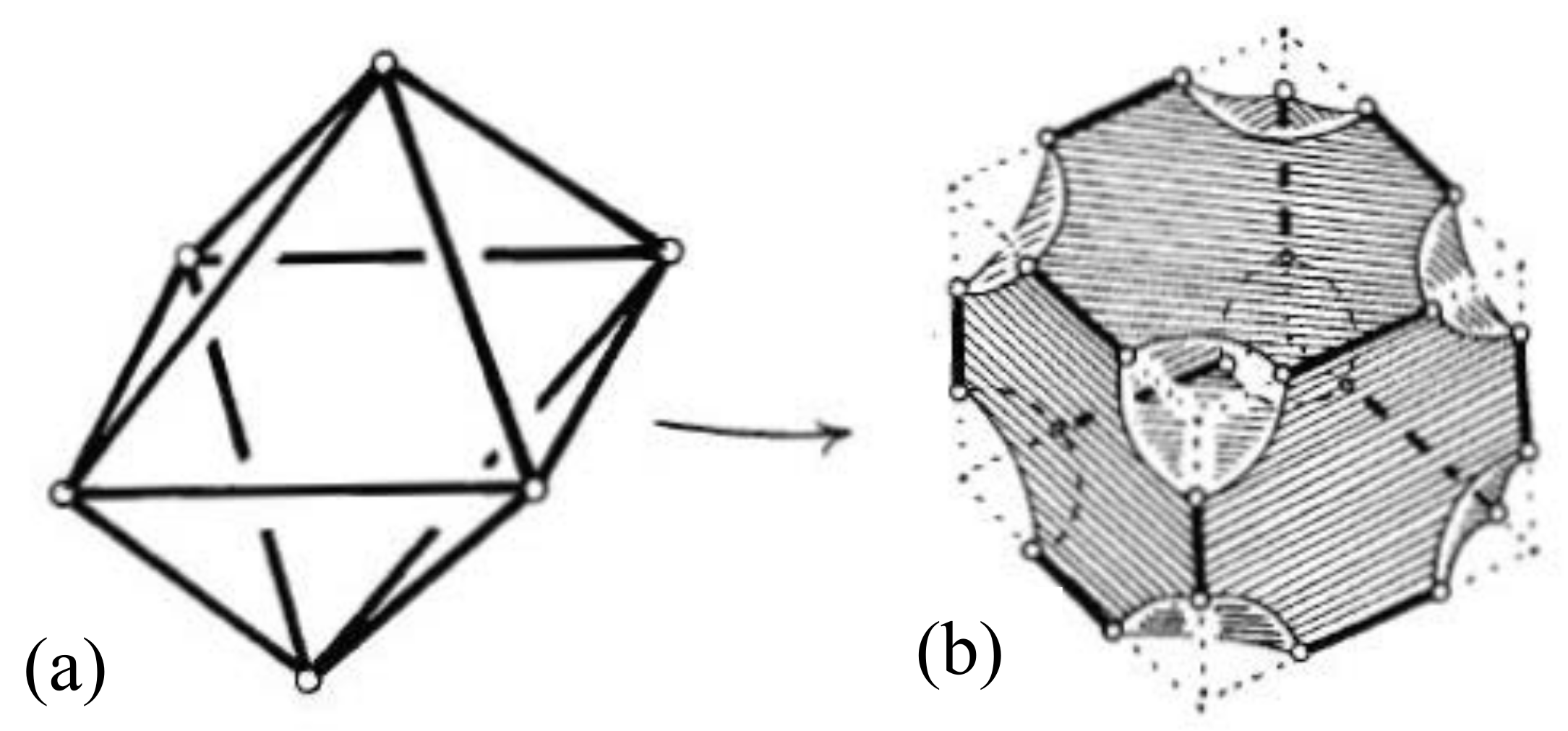
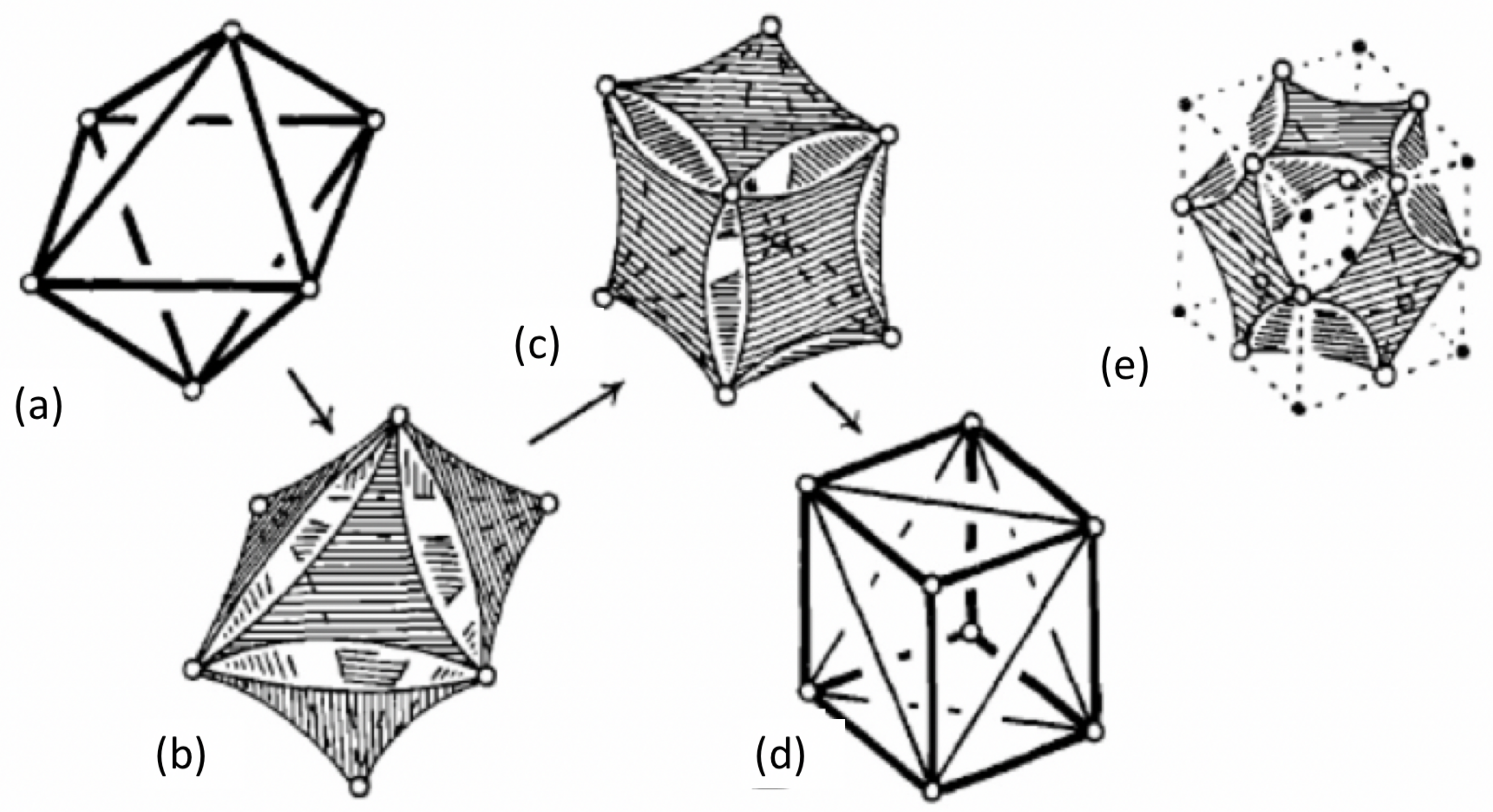
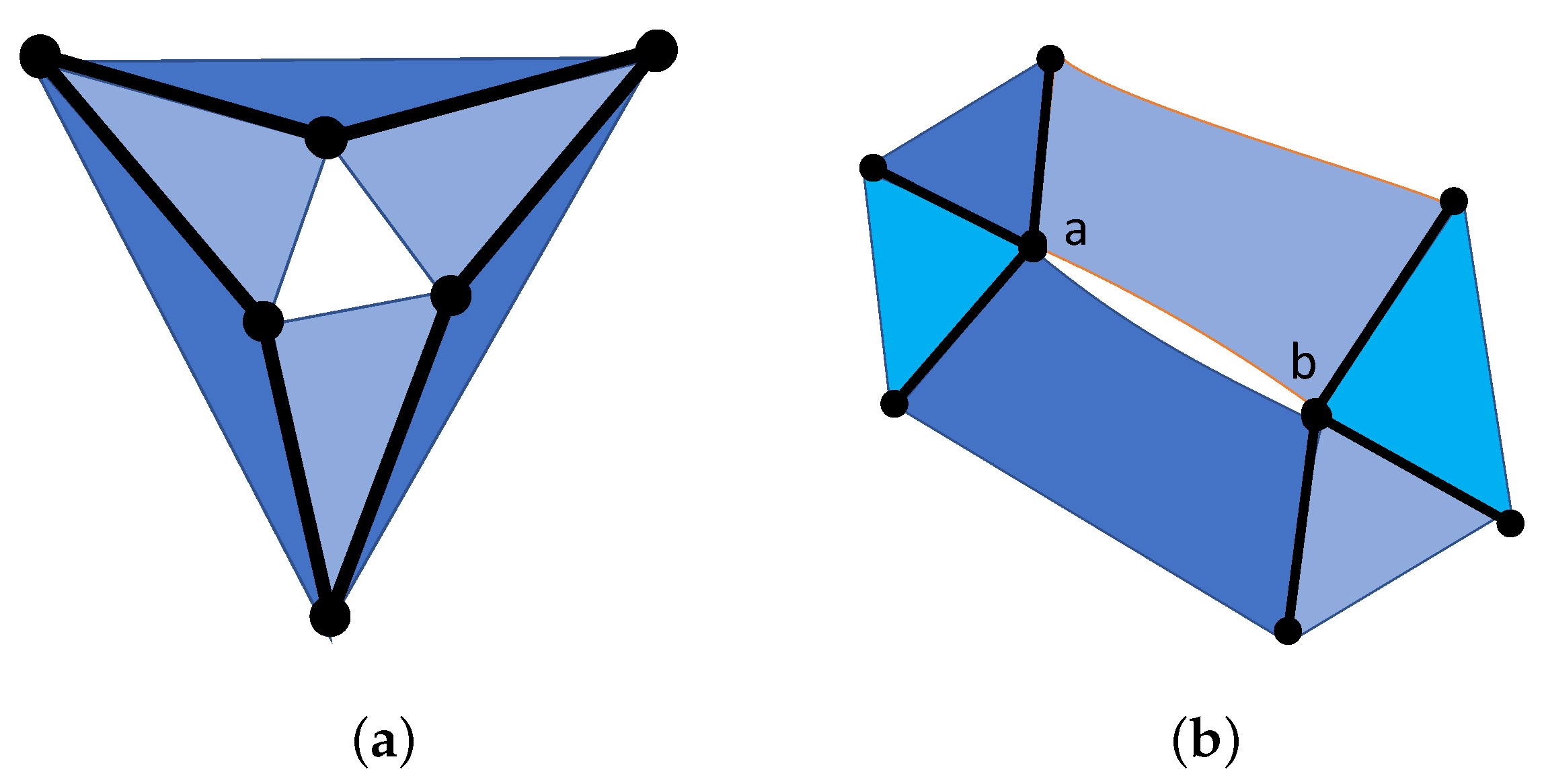
- Are there any examples of sheetworks with finite motions where sheets remain as coplanar sheets? Even the polar of the double banana—with two sheets joining two bodies—only has finite motions which warp these joining sheets. For example, the polar of the double banana shown in Figure 39b,c only has infinitesimal motions which bend the two sheets (d), though as a triangulated model it does have a finite motion.
- 5.
- Consider the polar of with the four points coplanar. The four points become four sheets which are co-punctual, with no hinges (edges) among them. As the polar of 6-valent vertices, these four sheets are hexagonal sheets. These sheets must meet in 6 four-valent sheets. This type of geometry has yet to be explored.
- 6.
- The analogue of tensegrity frameworks are slotted sheetworks. (We will formally introduce tensegrities in Section 12).
8.3. Substitution Principles
8.4. Cauchy, Alexandrov and Polarity
- 1.
- placing a joint at each vertex of a strictly convex polyhedron,
- 2.
- placing a bar along each edge of the polyhedron.
- 1.
- placing a joint at each vertex of the polytope,
- 2.
- placing a bar on each edge of the 4-polytope.

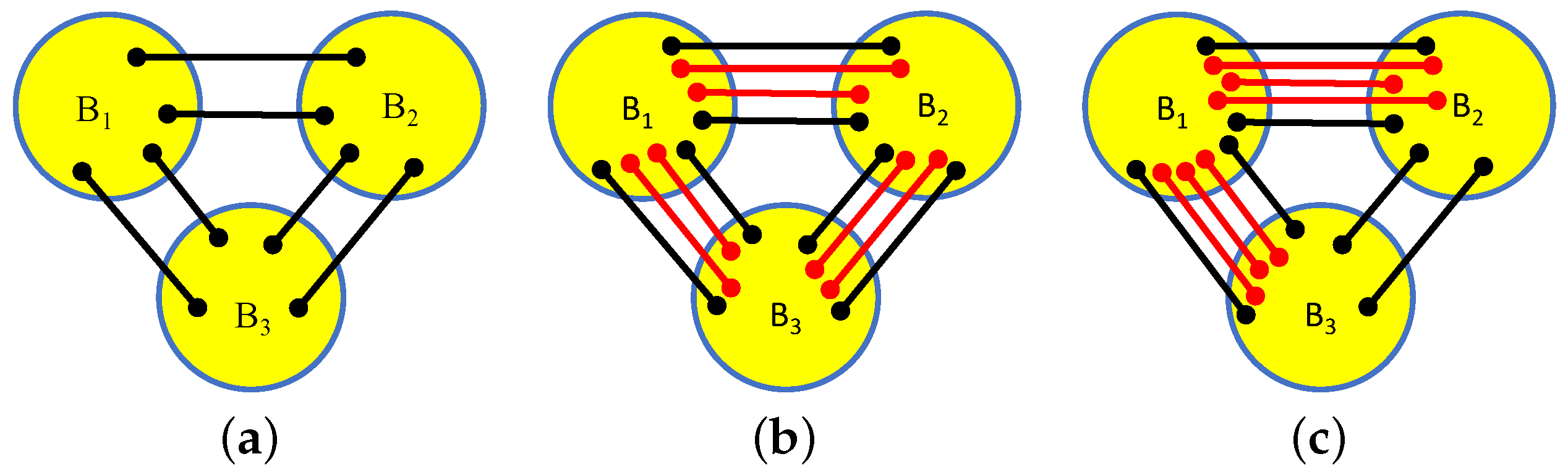
9. Body-Bar Frameworks
- 1.
- is infinitesimally rigid and independent as a body-bar framework;
- 2.
- and for all non-empty subsets of edges on bodies , we have ;
- 3.
- G can be partitioned into edge-disjoint spanning trees.
9.1. Body-Bar Combinatorics
 The determinant of any one of these diagonal blocks, which has rows which are multiples of rows of the graphic matroid on the edges is non-zero if and only if the edges form a spanning tree on the bodies [49,58,127]. Thus, these terms generate the desired decompositionof the edges into () spanning trees, partitioning the ()(m − 1) edges.
The determinant of any one of these diagonal blocks, which has rows which are multiples of rows of the graphic matroid on the edges is non-zero if and only if the edges form a spanning tree on the bodies [49,58,127]. Thus, these terms generate the desired decompositionof the edges into () spanning trees, partitioning the ()(m − 1) edges.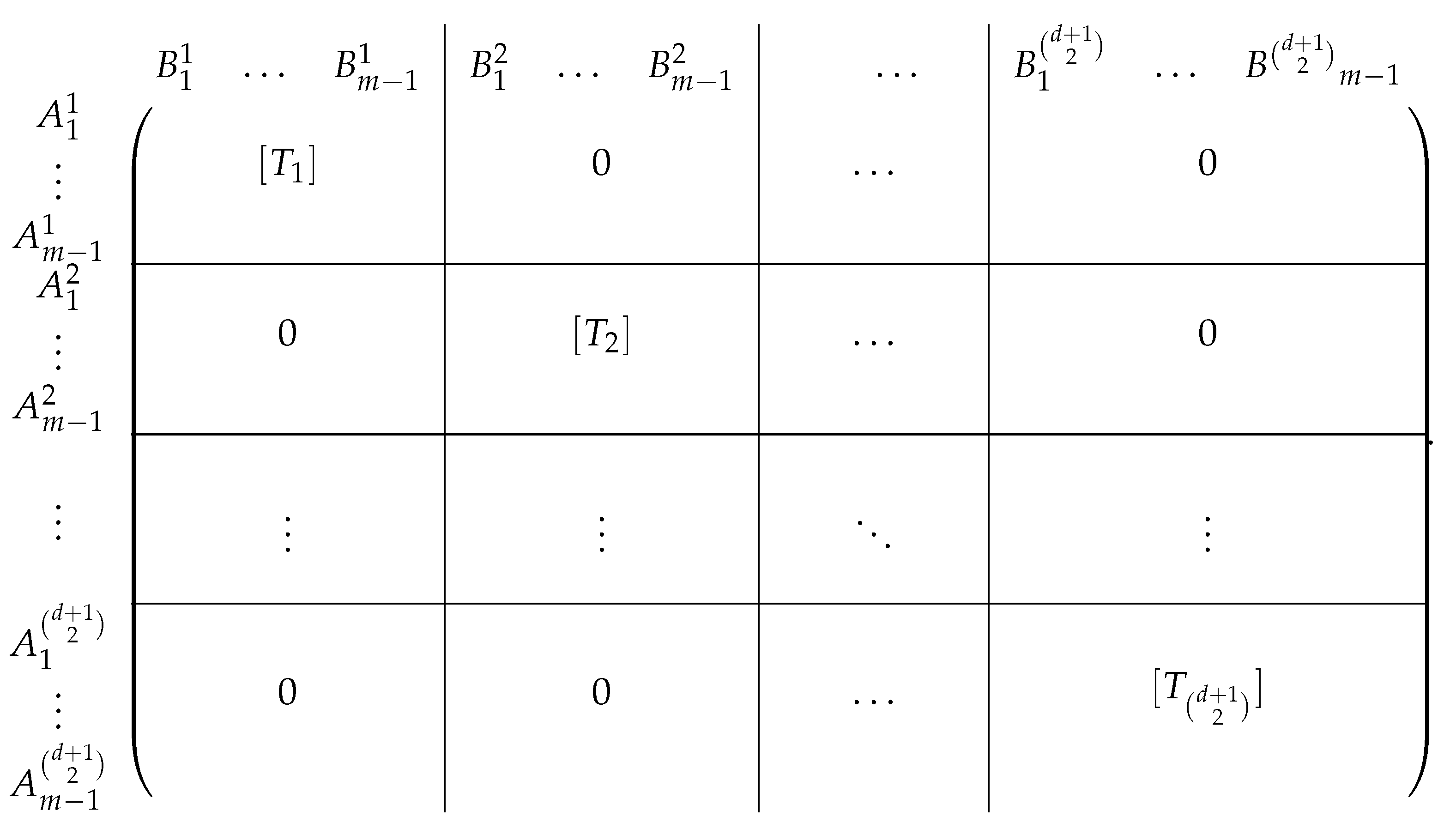
9.2. Body-Bar Projective Conditions and Centers of Motion
9.3. Projective Line Dependences and the Stewart Platform
9.4. Static Rigidity and Stresses in Body-Bar Frameworks
9.5. Coning Body-Bar Frameworks
9.6. Rod and Bar Frameworks in 3-Dimensions
- 1.
- the graph has isostatic realisations as a rod-bar framework in ;
- 2.
- the graph satisfies , and for all subgraphs with at least two rods we have ;
- 3.
- the graph has a 6Tree5 partition into 6 disjoint trees, 5 at each rod.
- 1.
- the graph has some isostatic realisations as a rod-bar framework in ;
- 2.
- the graph satisfies and for all subgraphs with at least two rods we have ;
- 3.
- the graph has a Tree partition into disjoint trees, at each rod.
10. Body–Hinge Frameworks
10.1. Body–Hinge Basic Transfer
- 1.
- G has realisations as an infinitesimally rigid body–hinge structure in .
- 2.
- G contains spanning trees which use any hinge edge at most times.
- 3.
- There is a subset of edges E with such that for any partition of the vertices the contracted subgraph , where is the set of edges induced by , satisfies .
10.2. Body–Hinge Motion Assignments
10.3. Coning for Body–Hinge in
10.4. Molecular and Body-Plate Frameworks
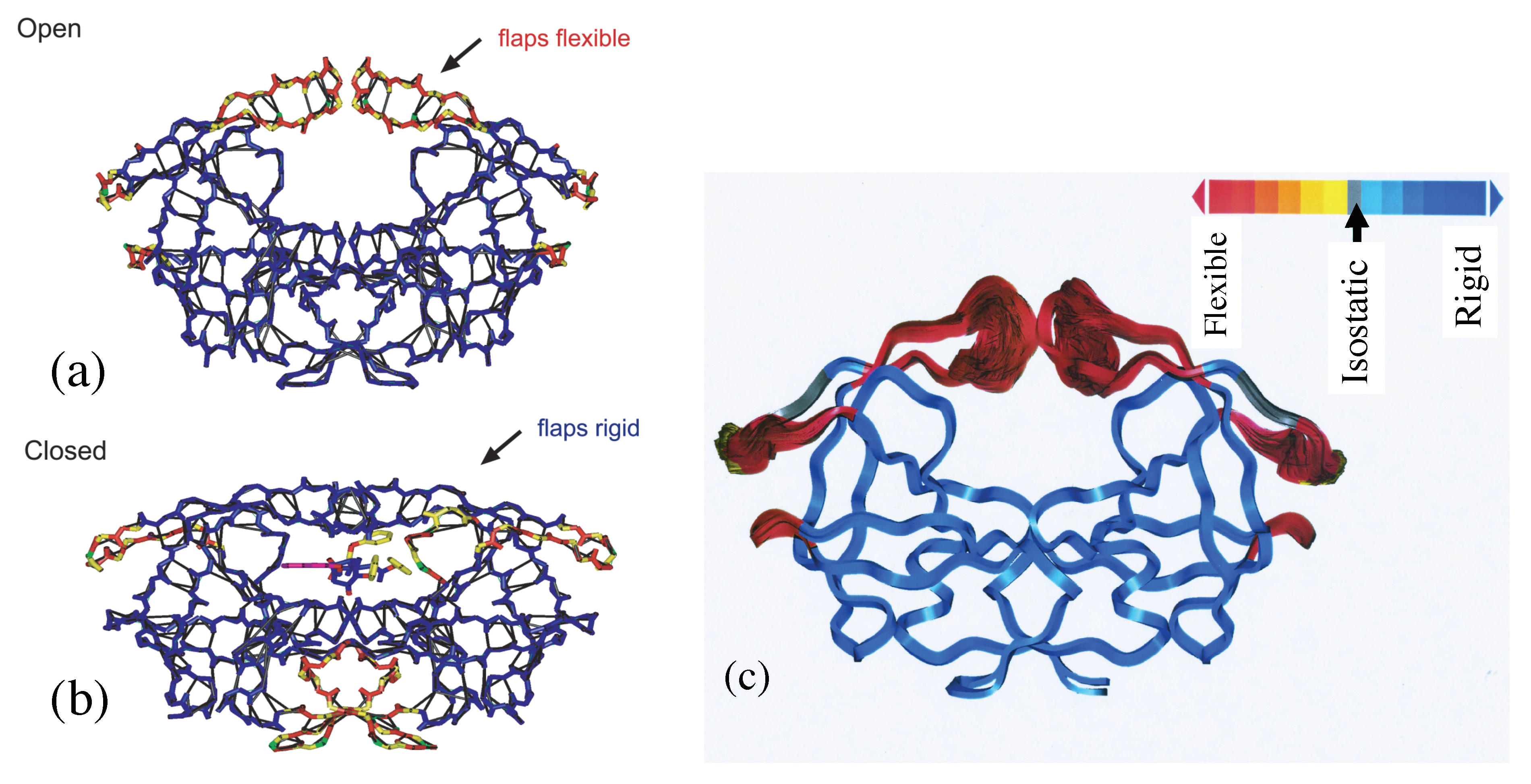
10.5. Applications to Protein Structures
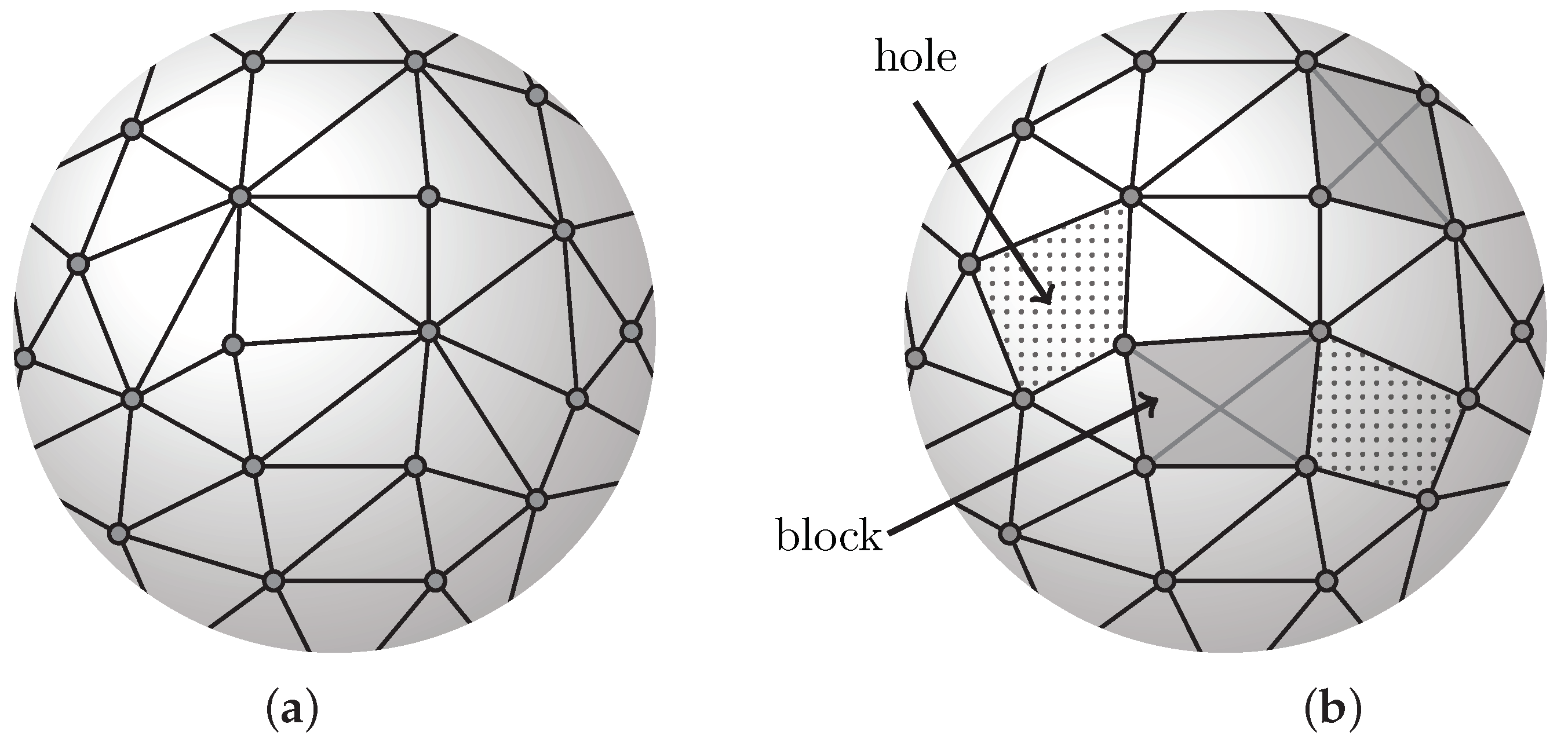
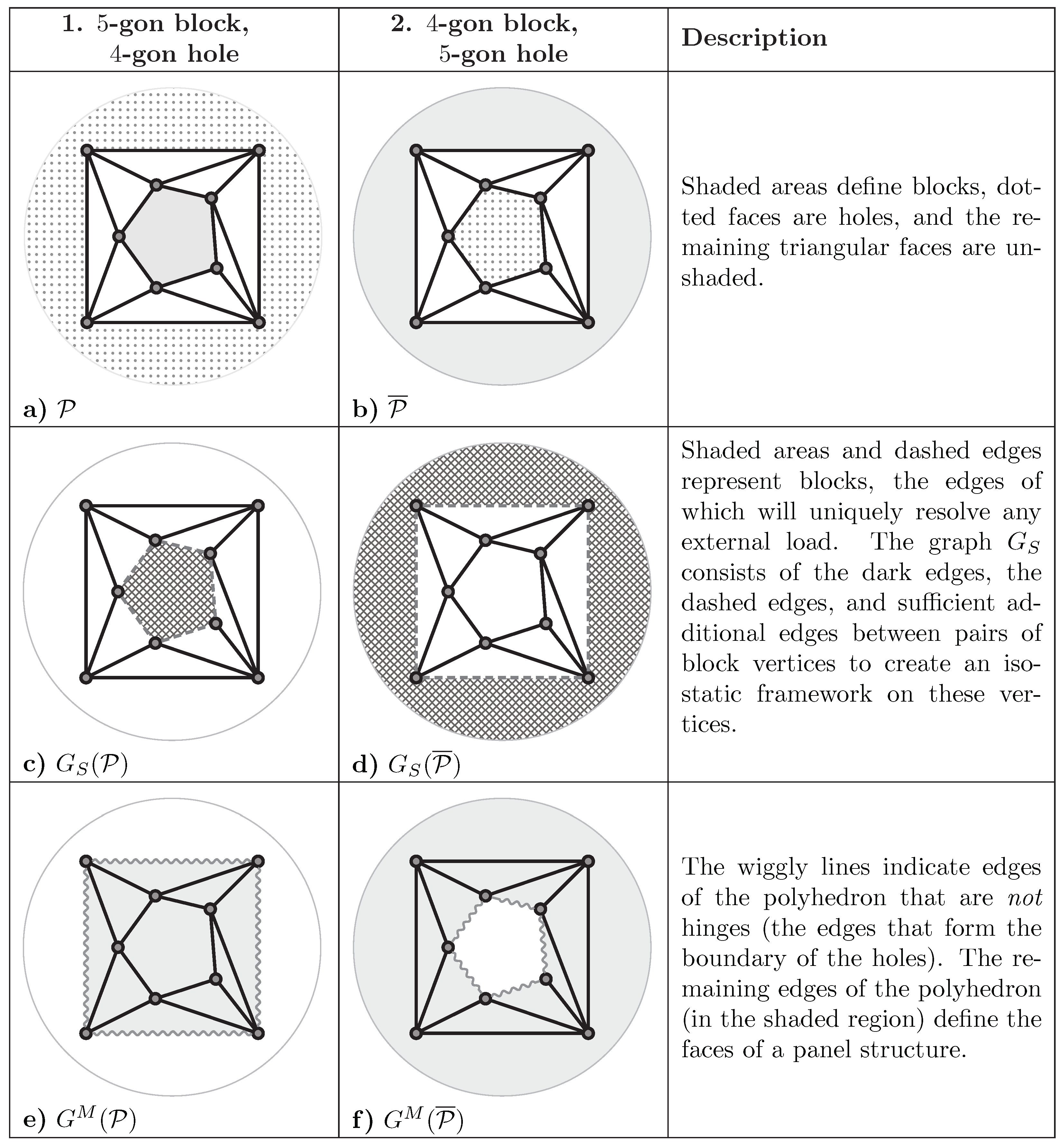
10.6. Block and Hole Polyhedra
- 1.
- If a block and hole polyhedral framework has a non-trivial infinitesimal motion as a panel–hinge structure, then the swapped block and hole structure has a static equilibrium stress in the same configuration;
- 2.
- If a block and hole polyhedral framework has a static equilibrium stress, then the swapped block and hole structure has a non-trivial infinitesimal motion in the same configuration;
- 3.
- is isostatic if and only if is isostatic.
- 1.
- is generically isostatic in ;
- 2.
- is -tight;
- 3.
- is constructible from by vertex splitting operations and isostatic block substitution.
10.7. Lower Dimensional Bodies: Pinned Rods in the Plane
10.8. Summary Table

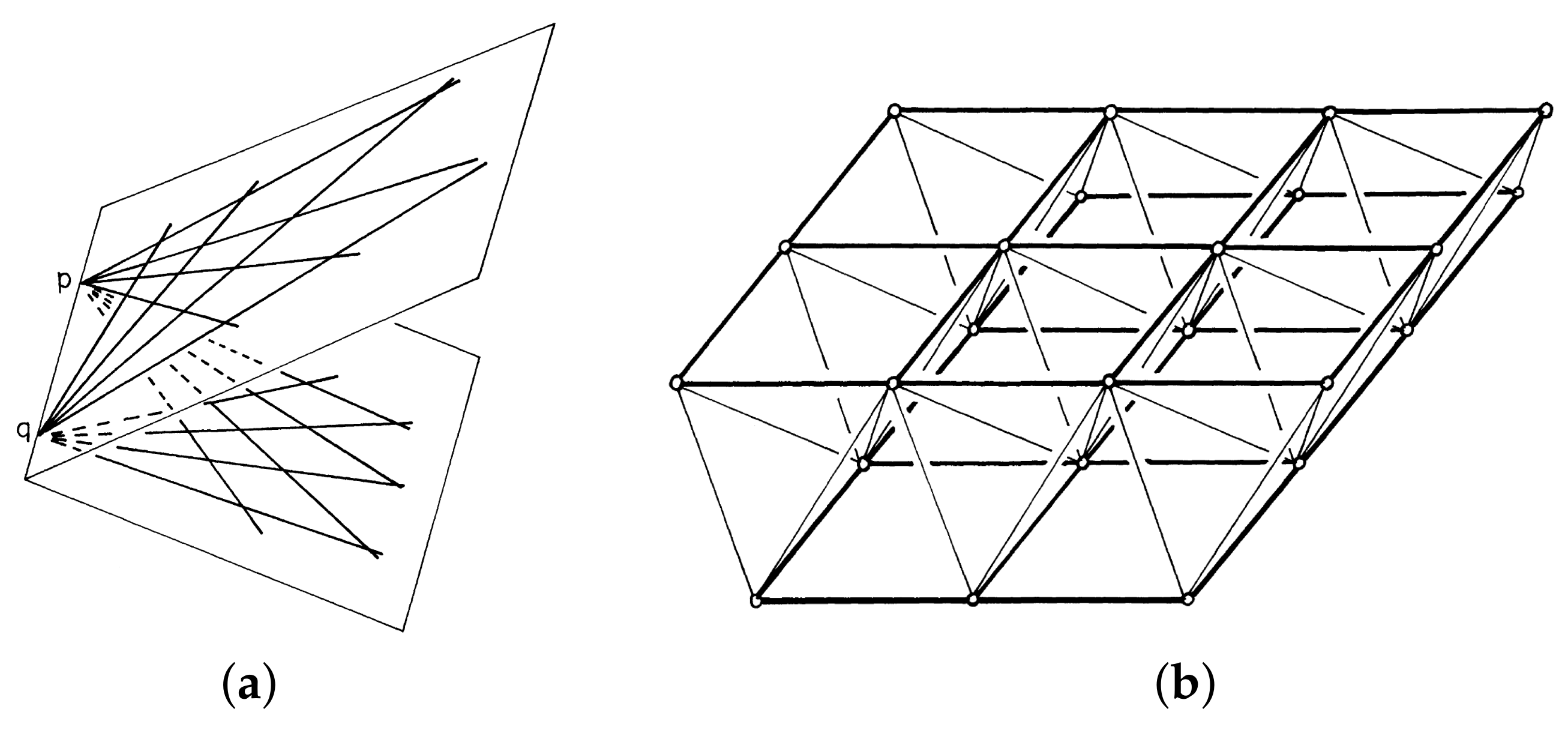
- the projective and combinatorial theory of frameworks, both bar–joint and panel–hinge in ; and
- bivariate splines for a polygonal decomposition of a disc in the plane, written in approximation theory [23]. This focuses on finding a piecewise degree 2 surface () for each polygonal cell so that they fit together over the edges with globally continuous first derivatives () across the whole surface. This space of splines is sometimes studied as the row dependencies (cofactors) of a rigidity type cofactor matrix based on the edges and vertices of the cell decomposition [22,24].
11. Multivariate Splines and Cofactor Matroids
11.1. Smoothing Cofactors for Splines and Compatibility Conditions
11.2. The -Cofactor Matroid on Plane Graphs: An Analogue of Rigidity in
11.3. Is the Maximal Abstract 3-Rigidity Matroid
- (R1)
- If with , then where ;
- (R2)
- If with where , where , and , then where .
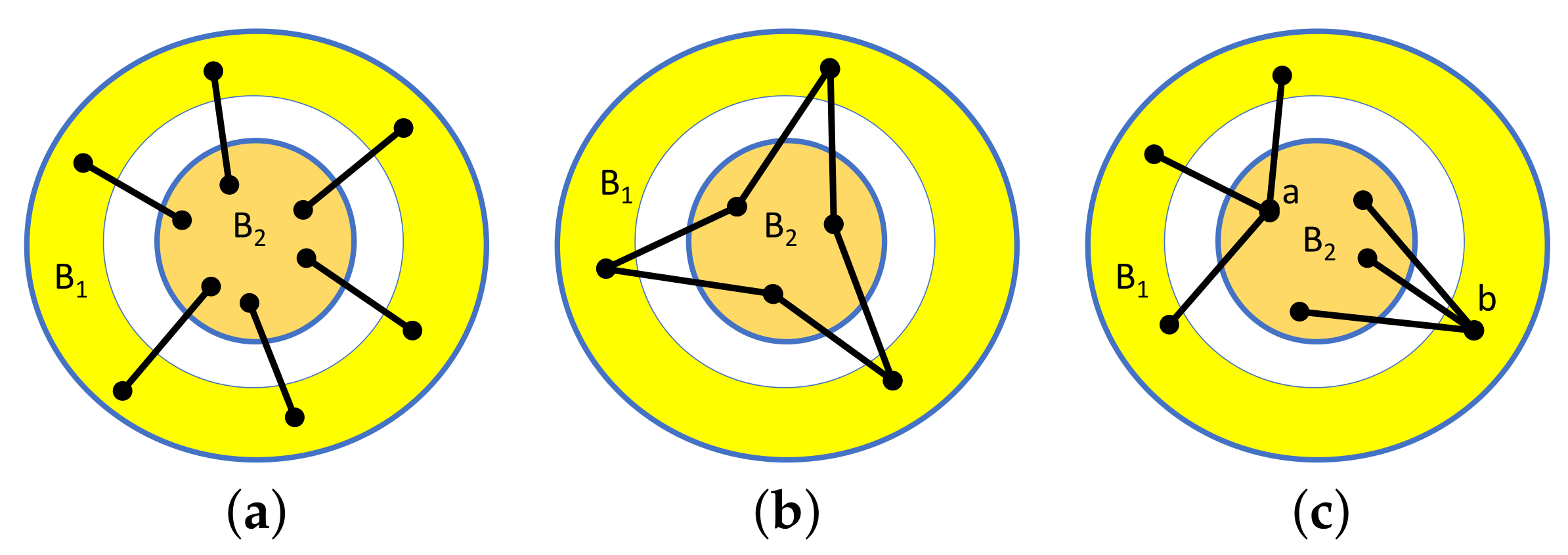
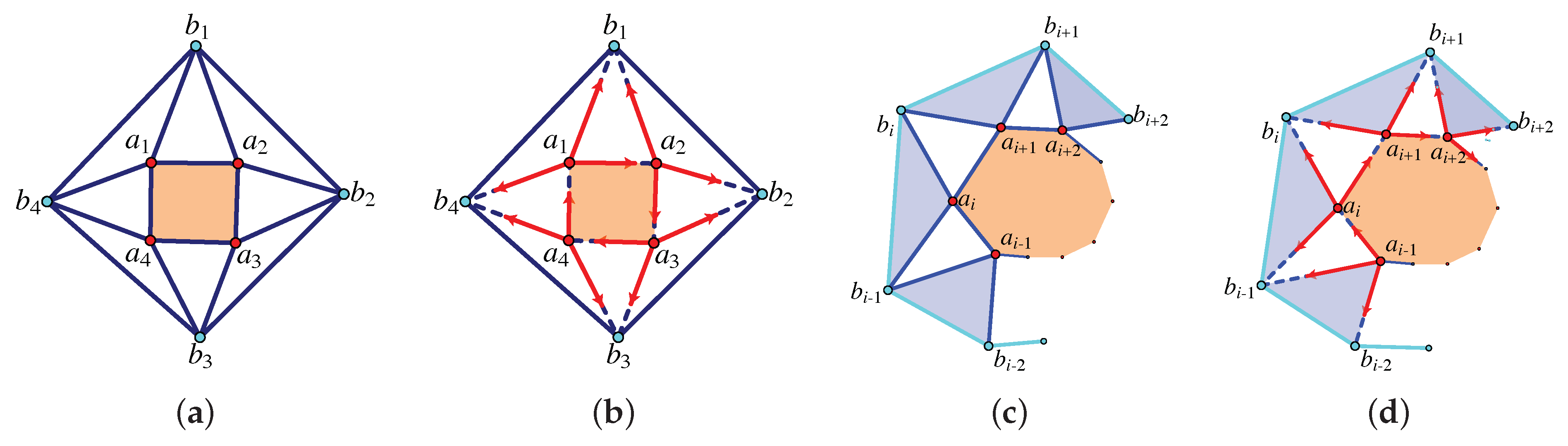
11.4. Transferring Pure Conditions
- Let G be a -cofactor graph. Represent the tie-down bars of a realisation of G, , in with the 6 coefficients of the squared lines . We can construct a square matrix with determinant in the bracket algebra which is non-zero if and only if the tie-down will not support a row dependence in these rows in the extended matrix (the tie-down rows are independent). These are the non-degenerate tie-downs with .
- The non-degenerate tie-downs include all 6 plane patterns from Figure 26 for generic points .
- Suppose G is -isostatic in and T is a non-degenerate tie-down. Then the determinant of the extended -cofactor matrix is an element of the bracket ring B on the set of vertices of . This follows because the terms in the Laplace decomposition by the columns of vertices are themselves bracket polynomials.
- For a non-degenerate tie-down the polynomial is a factor of the larger determinant so that for some .
- For two non-degenerate tie-downs the residual factors , so there is a unique pure condition . This again uses a lemma that moves one tie-down edge at a time along an edge of G, provided the moves preserve the non-degeneracy of the tie-down.
11.5. Transferring Theorems to the -Cofactor Matroid
11.6. Coning Splines: Abstract 4-Dimensional Rigidity Matroids and Multivariate Splines
11.7. Using Projective Rigidity Style Techniques for
12. Projective Tensegrities
- 1.
- for cables ;
- 2.
- for struts ;
- 3.
- for bars .
- 1.
- for cables ;
- 2.
- for struts ;
- 3.
- is arbitrary for bars .
13. Further Explorations
13.1. Skeletal Rigidity, Geometric Homology and f-Vectors
13.2. Global Rigidity, Universal Rigidity and Superstability
- Dimensional rigidity is projectively invariant [171].
- Coning: a graph G is generically globally rigid in if and only if the cone graph is generically globally rigid in [173].
- Open projective neighborhoods: if a framework is globally rigid, then within the projective images, an open neighborhood of projectively equivalent frameworks shares the global rigidity [173].
13.3. Interesting However, Not Projective: Finite Motions
13.4. Interesting However, Not Projective: CAD Constraints and Angles
14. Companion Paper: Projective Geometry of Scene Analysis, Parallel Drawing and Reciprocal Drawing
- scene analysis and liftings of pictures in to scenes in which project to these pictures;
- parallel drawings of configurations in ;
- reciprocal diagrams which entwine a configuration for a polyhedral graph with a configuration for the (spherical) dual polyhedral structure.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Möbius, A.F. Der Barycentrische Calcul; 1827 Reprint; Pranava Books: Charlestown, MA, USA, 2020. [Google Scholar]
- Möbius, A.F. Lehrbuch der Statik, Leipzig, Germany. 1837. Available online: https://archive.org/details/lehrbuchderstat04mbgoog (accessed on 14 October 2021).
- Maxwell, J.C. On Reciprocal Figures and Diagrams of Forces. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1864, 27, 250–261. [Google Scholar] [CrossRef]
- Rankine, W.J.M. On the Application of Barycentric Perspective to the Transformation of Structures. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1863, 4, 387–388. [Google Scholar] [CrossRef]
- Rankine, W.J.M. A Manual of Applied Mechanics, 8th ed.; C. Griffin: London, UK, 1876. [Google Scholar]
- Klein, F. Elementary Mathematics from an Advanced Standpoint: Geometry; English Translation; Dover: New York, NY, USA, 1939. [Google Scholar]
- Henneberg, L. Die Graphische Statik der Starren Systeme; Johnson Reprint: 1968; BG Teubner: Leipzig, Germany, 1911; Available online: https://archive.org/details/diegraphischest00henngoog/page/n6/mode/2up (accessed on 14 October 2021).
- Liebmann, H. Ausnahmefachwerke und ihre Determinante. Münch. Ber. 1920, 50, 197–227. [Google Scholar]
- Sauer, R. Infinitesimale Verbiegungen zueinander projektiver Flächen. Math. Ann. 1935, 111, 71–82. [Google Scholar] [CrossRef]
- Sauer, R. Projektive Sätze in der Statik des starren Körpers. Math. Ann. 1935, 110, 464–472. [Google Scholar] [CrossRef]
- Pogorelov, A. Extrinsic Geometry of Convex Surfaces; Translation of the 1969 Edition, Translations of Mathematical Monographs 35; AMS: Providence, RI, USA, 1973. [Google Scholar]
- Wunderlich, W. Projective invariance of shaky structures. Acta Mech. 1982, 42, 171–181. [Google Scholar] [CrossRef]
- Pollaczek-Geiringer, H. Über die Gliederung ebener Fachwerke. ZAMM-J. Appl. Math. Mech. Angew. Math. Mech. 1927, 7, 58–72. [Google Scholar] [CrossRef]
- Laman, G. On graphs and rigidity of plane skeletal structures. J. Engrg. Math. 1970, 4, 331–340. [Google Scholar] [CrossRef]
- Berg, A.; Jordán, T. Algorithms for graph rigidity and scene analysis. In Algorithms-ESA 2003, Volume 2832 of Lecture Notes in Computer Science; Springer: Berlin, Germany, 2003; pp. 78–89. [Google Scholar]
- Lee, A.; Streinu, I. Pebble game algorithms and sparse graphs. Discret. Math. 2008, 308, 1425–1437. [Google Scholar] [CrossRef]
- Jacobs, D.; Hendrickson, B. An Algorithm for Two-Dimensional Rigidity Percolation: The Pebble Game. J. Comput. Phys. 1997, 137, 346–365. [Google Scholar] [CrossRef]
- Eren, T.; Whiteley, W.; Anderson, B.D.O.; Morse, A.S.; Belhumeur, P.N. Information Structures to Secure Control of Rigid Formations with Leader-Follower Structure. In Proceedings of the American Control Conference 2005, Portland, OR, USA, 8–10 June 2005. [Google Scholar]
- Kuhn, L. Proflex Software. Available online: https://kuhnlab.natsci.msu.edu/software/proflex/ (accessed on 14 October 2021).
- Streinu, I. Kinari Software. Available online: http://kinari.cs.umass.edu/Site/index.html (accessed on 14 October 2021).
- Whiteley, W. An analogy in geometric homology: Rigidity and cofactors on geometric graphs. In Mathematical Essays in Honor of Gian-Carlo-Rota; Sagan, B., Stanley, R., Eds.; Birkhauser: Boston, MA, USA, 1998; pp. 413–437. [Google Scholar]
- Whiteley, W. Combinatorics of bivariate splines. In Applied Geometry and Discrete Mathematics-the Victor Klee Festschrift, DIMACS; AMS: Providence, RI, USA, 1991; Volume 4, pp. 587–608. [Google Scholar]
- Alfeld, P.; Schumaker, L.; Whiteley, W. The generic dimension of the space of C1 splines of degree d≥8 on tetrahedral decompositions. SIAM J. Numer. Anal. 1993, 30, 889–920. [Google Scholar] [CrossRef]
- Whiteley, W. The Geometry of Bivariate Splines; Researchgate: Berlin, Germany, 1987; Available online: https://www.researchgate.net/publication/271516580_The_Geometry_of_Bivariate_Ci-Splines (accessed on 14 October 2021). [CrossRef]
- Clinch, K.; Jackson, B.; Tanigawa, S. Abstract 3-Rigidity and Bivariate C21-Splines I: Whiteley’s Maximality Conjecture. arXiv 2021, arXiv:1911.00205. [Google Scholar]
- Clinch, K.; Jackson, B.; Tanigawa, S. Abstract 3-Rigidity and Bivariate C21-Splines II: Combinatorial Characterization. arXiv 2021, arXiv:1911.00207. [Google Scholar]
- Nixon, A.; Schulze, B.; Whiteley, W. Projective Geometry of Scene Analysis, Parallel Drawing and Reciprocal Drawings, Preprint, 2021.
- Whiteley, W. Introduction to Structural Geometry I: Infinitesimal Motions of Frameworks in Plane and Space. 1977. Available online: https://www.researchgate.net/publication/280805856_Introduction_to_Structural_Topology_I_Infinitesimal_Motions_and_Infinitesimal_Rigidity (accessed on 14 October 2021). [CrossRef]
- Whiteley, W. Introduction to Structural Geometry II: Statics and Stresses. 1978. Available online: https://www.researchgate.net/publication/280805920_Introduction_to_Structural_Topology_II_Statics_and_Stresses (accessed on 14 October 2021). [CrossRef]
- Asimov, L.; Roth, B. The Rigidity Of Graphs. Trans. AMS 1978, 245, 279–289. [Google Scholar] [CrossRef]
- Asimov, L.; Roth, B. The Rigidity Of Graphs II. J. Math Anal. Appl. 1979, 68, 171–190. [Google Scholar] [CrossRef]
- Graver, J. Counting on Frameworks. In MAA Dolciani Math. Explos; Mathematical Association of America: Washington, DC, USA, 2001; Volume 25. [Google Scholar]
- Schulze, B.; Whiteley, W. Rigidity and Scene Analysis. In Handbook of Discrete and Computational Geometry, 3rd ed.; Toth, C., Goodman, J., O’Rourke, J., Eds.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Whiteley, W. Some Matroids from Discrete Applied Geometry. In Contemporary Mathematics; AMS: Providence, RI, USA, 1996; Volume 197, pp. 171–311. [Google Scholar]
- Graver, J.; Servatius, B.; Servatius, H. Combinatorial Rigidity. In Graduate Studies in Mathematics; AMS: Providence, RI, USA, 1993. [Google Scholar]
- Roth, B.; Whiteley, W. Tensegrity Frameworks; AMS: Providence, RI, USA, 1981; Volume 266, pp. 419–446. [Google Scholar]
- Tay, T.-S.; Whiteley, W. Generating isostatic frameworks. Struct. Topol. 1985, 11, 31–38. Available online: http://www-iri.upc.es/people/ros/StructuralTopology/ST11/st11-07-a3-ocr.pdf (accessed on 14 October 2021).
- Lovász, L.; Yemini, Y. On generic rigidity in the plane. SIAM J. Algebr. Discret. Methods 1982, 3, 91–98. [Google Scholar] [CrossRef]
- Schulze, B. Symmetric versions of Laman’s Theorem. Discret. Comput. Geom. 2010, 44, 946–972. [Google Scholar] [CrossRef]
- Schulze, B. Symmetric Laman theorems for the groups C2 and Cs. Electron. J. Combin. 2010, 17, 1–61. [Google Scholar] [CrossRef]
- Schulze, B.; Tanigawa, S. Infinitesimal rigidity of symmetric bar–joint frameworks. SIAM J. Discret. Math. 2015, 29, 1259–1286. [Google Scholar] [CrossRef]
- Eftekhari, Y.; Jackson, B.; Nixon, A.; Schulze, B.; Tanigawa, S.; Whiteley, W. Point-hyperplane frameworks, slider joints, and rigidity preserving transformations. J. Combin. Theory Ser. B 2019, 135, 44–74. [Google Scholar] [CrossRef]
- Jackson, B.; Owen, J. A characterisation of the generic rigidity of 2-dimensional point-line frameworks. J. Comb. Theory Ser. B 2016, 119, 96–121. [Google Scholar] [CrossRef]
- John, A.L.; Sidman, J. Combinatorics and the rigidity of CAD systems. Comput.-Aided Des. 2013, 45, 473–482. [Google Scholar] [CrossRef]
- Nixon, A.; Owen, J.; Power, S. Rigidity of frameworks supported on surfaces. SIAM J. Discret. Math. 2012, 26, 1733–1757. [Google Scholar] [CrossRef]
- Streinu, I.; Theran, L. Slider-pinning rigidity: A Maxwell-Laman-type theorem. Discret. Comput. Geom. 2010, 44, 812–837. [Google Scholar] [CrossRef]
- Tay, T.-S. New Proof of Laman’s Theorem. Graphs Comb. 1993, 9, 365–370. [Google Scholar] [CrossRef]
- Tay, T.-S.; Whiteley, W. Recent progress in the rigidity of frameworks. Struct. Top. 1984, 9, 31–38. [Google Scholar]
- Whiteley, W. Matroid unions and rigidity. SIAM J. Discret. Math. 1988, 1, 237–255. [Google Scholar] [CrossRef]
- Katoh, N.; Tanigawa, S.-I. A Proof of the Molecular Conjecture. Discret. Comput. Geom. 2011, 45, 647–700. [Google Scholar] [CrossRef]
- Cremona, L. Graphical Statics; English Translation; Oxford University Press: London, UK, 1890. [Google Scholar]
- White, N. Geometric applications of the Grassmann-Cayley algebra. In Handbook of Discrete and Computational Geometry, 3rd ed.; Toth, C., Goodman, J., O’Rourke, J., Eds.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Crapo, H.; Whiteley, W. Statics of Frameworks and Motions of Panel Structures, a Projective Geometric Introduction. Struct. Top. 1982, 6, 43–82. Available online: http://www-iri.upc.es/people/ros/StructuralTopology/ST6/st6-10-a6-ocr.pdf (accessed on 14 October 2021).
- Jackson, B.; Jordán, T. The generic rank of body-bar-and-hinge frameworks. Eur. J. Comb. 2010, 31, 574–588. [Google Scholar] [CrossRef][Green Version]
- Sidman, J.; Traves, W. Special positions of frameworks and the Grassmann-Cayley algebra. In Handbook of Geometric Constraint Systems Principles; Sidman, J., Sitharam, M., John, A.S., Eds.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Staffetti, E.; Thomas, F. Kinestatic analysis of serial and parallel robot manipulators using Grassmann-Cayley algebra. In Advances in Robot Kinematics; Lenarcic, J., Stanisic, M.M., Eds.; Advances in Robot Kinematics; Springer: Dordrecht, The Netherlands, 2000. [Google Scholar] [CrossRef]
- White, N. Grassmann-Cayley algebra and robotics. J. Intell. Robot. Syst. 1994, 11, 91–107. [Google Scholar] [CrossRef]
- White, N.; Whiteley, W. The algebraic geometry of motions of bar-and-body frameworks. SIAM J. Algebr. Discret. Methods 1987, 8, 1–32. [Google Scholar] [CrossRef]
- Ball, R.S. Theory of Screws; Dublin, Ireland, Cambridge, UK. 1900. Available online: https://archive.org/details/cu31924059413389 (accessed on 14 October 2021).
- Penne, R.; Crapo, H. A general graphical procedure for finding motion centers of planar mechanisms. Adv. Appl. Math. 2007, 38, 419–444. [Google Scholar] [CrossRef]
- Perspective in Projective Geometry. Available online: https://en.wikipedia.org/wiki/Perspective_(geometry) (accessed on 14 October 2021).
- Crapo, H.; Whiteley, W. Plane stresses and projected polyhedra I: The basic pattern. Struct. Top. 1993, 20, 55–68. Available online: http://www-iri.upc.es/people/ros/StructuralTopology/ST20/st20-08-a4-ocr.pdf (accessed on 14 October 2021).
- Crapo, H.; Whiteley, W. Spaces of stresses, projections, and parallel drawings for spherical polyhedra. Beitraege Algebra Geom. Algebra Geom. 1994, 35, 259–281. [Google Scholar]
- Power, S. (Department of Mathematics and Statistics, Lancaster University, Lancaster, UK). Personal communication. 2020. [Google Scholar]
- Izmestiev, I. Projective background of the infinitesimal rigidity of frameworks. Geom. Dedicata 2009, 140, 183–203. [Google Scholar] [CrossRef]
- Sommerville, D.M.Y. Classification of Geometries with Projective Metric. Proc. Edinb. Math. Soc. 1910, 28, 25–41. [Google Scholar] [CrossRef]
- Yoglom, I.M. A Simple Non-Euclidean Geometry and Its Physical Basis; Translated by Abe Shentzer; Heidelberg Science Library: Heidelberg, Germany, 1979. [Google Scholar]
- Mullineux, G. Atlas of spherical four-bar mechanisms. Mech. Mach. Theory 2011, 46, 1811–1823. [Google Scholar] [CrossRef]
- Saliola, F.V.; Whiteley, W. Some notes on the equivalence of first-order rigidity in various geometries. arXiv 2007, arXiv:0709.3354. [Google Scholar]
- Nixon, A.; Whiteley, W. Change of Metrics in Rigidity Theory. In Handbook of Geometric Constraint Systems Principles; Sidman, J., Sitharam, M., John, A.S., Eds.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Schulze, B.; Whiteley, W. Coning, symmetry and spherical frameworks. Discret. Comput. Geom. 2012, 48, 622–657. [Google Scholar] [CrossRef]
- John, A.S. Generic Rigidity of Body-and-Cad Frameworks. In Handbook of Geometric Constraint Systems Principles; Sitharam, M., John, A.S., Sidman, J., Eds.; CRC Press: Boca Raton, FL, USA, 2018; pp. 505–524. [Google Scholar]
- Saliola, F.; Whiteley, W. Constraining Plane Configurations in CAD: Circles, Lines and Angles in the Plane. SIAM J. Disc. Math. 2005, 18, 246–271. [Google Scholar] [CrossRef]
- Pogorelov, A.V. A Study of Surfaces in an Elliptic Space, (English Translation of the Russian Title “Nekotor’e Vopros Teorii Poverkhnostei”); Hindustan Publishing Corporation (India) 6-U.B.: Jawahar Nagar, India, 1964; DELHI-6. [Google Scholar]
- Minkowski Space. Wikipedia. Available online: https://en.wikipedia.org/wiki/Minkowski_space (accessed on 14 October 2021).
- Whiteley, W. Cones, infinity and one-story buildings. Struct. Top. 1983, 8, 53–70. Available online: http://www-iri.upc.es/people/ros/StructuralTopology/ST8/st8-10-a7-ocr.pdf (accessed on 14 October 2021).
- Window Mechanism. Available online: https://www.youtube.com/watch?v=JSL-7kSk5K4 (accessed on 14 October 2021).
- Eftekhari, Y. Point-Hyperplane Frameworks, Slider Joints. Ph.D. Thesis, York University, Toronto, ON, Canada, 2018. [Google Scholar]
- Jackson, B.; Nixon, A.; Tanigawa, S. An Improved bound for the rigidity of linearly constrained frameworks. SIAM J. Discret. Math. 2021, 35, 928–933. [Google Scholar] [CrossRef]
- Shai, O.; Servatius, B.; Whiteley, W. Combinatorial Characterization of the Assur Graphs from Engineering. Eur. J. Combin. 2010, 31, 1091–1104. [Google Scholar]
- Cruickshank, J.; Guler, H.; Jackson, B.; Nixon, A. Rigidity of linearly constrained frameworks. Int. Math. Res. Not. IMRN 2020, 12, 3824–3840. [Google Scholar] [CrossRef]
- Katoh, N.; Tanigawa, S.-I. Rooted-tree decompositions with matroid constraints and the infinitesimal rigidity of frameworks with boundaries. SIAM J. Discret. Math. 2013, 27, 155–185. [Google Scholar] [CrossRef]
- Nixon, A.; Owen, J.; Power, S. A characterization of generically rigid frameworks on surfaces of revolution. SIAM J. Discret. Math. 2014, 28, 2008–2028. [Google Scholar] [CrossRef]
- Jackson, B.; Nixon, A. Global rigidity of generic frameworks on the cylinder. J. Comb. Theory Ser. B 2019, 139, 193–229. [Google Scholar] [CrossRef]
- White, N.; Whiteley, W. The algebraic geometry of stresses in frameworks. SIAM J. Algebr. Discret. Methods 1983, 4, 481–511. [Google Scholar] [CrossRef]
- White, N. The bracket ring of a combinatorial geometry I. Trans. Am. Math. Soc. 1975, 202, 79–95. [Google Scholar] [CrossRef]
- Lamb, H. Statics, 3rd ed.; Cambridge University Press: Cambridge, UK, 1928. [Google Scholar]
- Bennett, G. Deformable octahedra. Proc. Lond. Math. Soc. 1912, 2, 309–343. [Google Scholar] [CrossRef]
- Dowling, D.; Samuel, A.; Hunt, K. Identification of special configurations of the octahedral manipulator using the Pure Condition. Int. J. Robot. Res. 2002, 21, 147–159. [Google Scholar] [CrossRef]
- Bricard, R. Mémoire sur la théorie de l’octaèdre articulé. J. Math. Pures Appl. 1897, 5, 113–148. [Google Scholar]
- Connelly, R. A counterexample to the rigidity conjecture for polyhedra. Inst. Haut. Etud. Sci. Publ. Math. 1978, 47, 333–335. [Google Scholar] [CrossRef]
- Bolker, E.; Roth, B. When is a bipartite graph a rigid framework? Pac. J. Math. 1980, 90, 27–44. [Google Scholar] [CrossRef]
- Sang, S.E. On Cases of Instability in Open Structures. Trans. R. Sot. Edinb. 1888, 33, 321–333. [Google Scholar] [CrossRef][Green Version]
- Blaha, G. Investigations of Critical Configurations for Fundamental Range Networks; Dept. of Geodetic Science Report 150, Ohio State Univ.: Columbus, OH, USA, 1971. [Google Scholar]
- Whiteley, W. Motions of a bipartite framework. Struct. Topol. 1979, 3, 62–63. Available online: http://www-iri.upc.es/people/ros/StructuralTopology/ST3/st3-07-a3-ocr.pdf (accessed on 14 October 2021).
- Whiteley, W. Infinitesimal motions of a bipartite framework. Pac. J. Math. 1984, 110, 233–255. [Google Scholar] [CrossRef]
- Whiteley, W. Infinitesimally Rigid Polyhedra I. Statics of Frameworks. Trans. AMS 1984, 285, 431–465. [Google Scholar] [CrossRef]
- Fogelsanger, A. The Generic Rigidity of Minimal Cycles. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1988. [Google Scholar]
- Crapo, H. The tetrahedral/octahedral truss. Struct. Top. 1982, 7, 51–60. Available online: http://www-iri.upc.es/people/ros/StructuralTopology/ST7/st7-08-a5-ocr.pdf (accessed on 14 October 2021).
- Whiteley, W. Motions of trusses and bipartite frameworks. Struct. Top. 1982, 9, 61–69. Available online: http://www-iri.upc.es/people/ros/StructuralTopology/ST7/st7-09-a6-ocr.pdf (accessed on 14 October 2021).
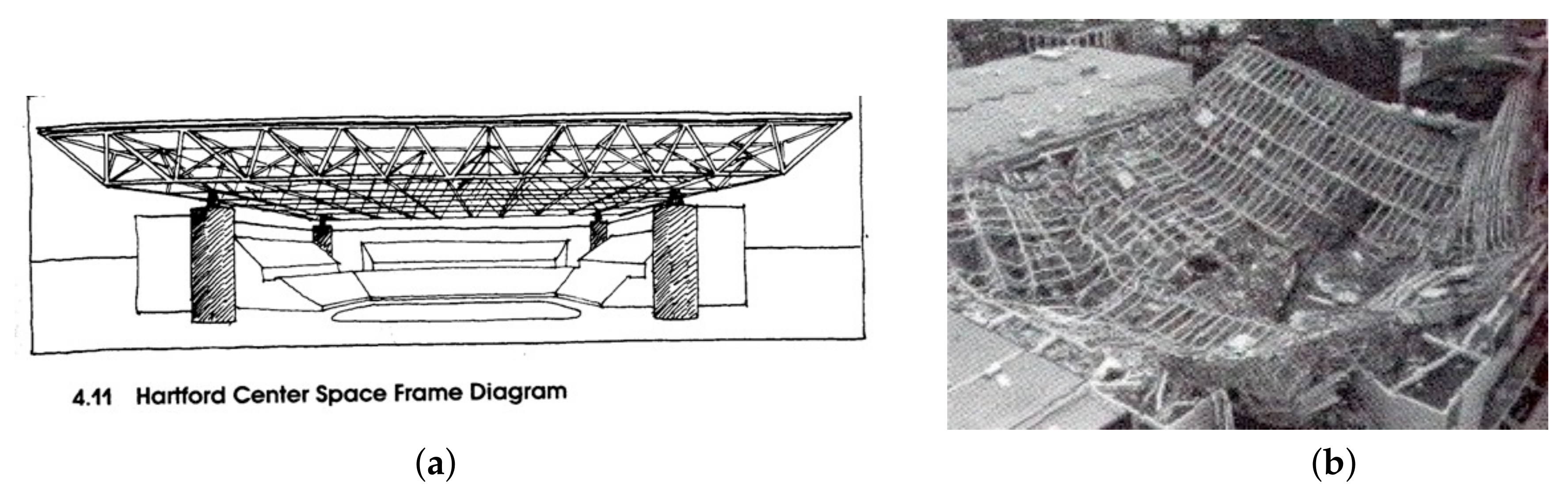
- Hartford Coliseum Roof Collapse: Case Study in Building Failure. Available online: https://eng-resources.uncc.edu/failurecasestudies/building-failure-cases/hartford-civic-center/ (accessed on 14 October 2021).
- Failures: A Downloadable Slide Presentation. Available online: https://slideplayer.com/slide/6648530/ (accessed on 14 October 2021).
- Sturmfels, B.; Whiteley, W. Synthetic factoring of invariant computations. J. Symb. Comput. 1991, 11, 439–453. [Google Scholar] [CrossRef][Green Version]
- Penne, R. Isostatic bar–joint frameworks in the plane with irreducible pure conditions. Discret. App. Math. 1994, 55, 37–57. [Google Scholar] [CrossRef]
- Shai, O.; Servatius, B.; Whiteley, W. Geometric Properties of Assur Graphs. Eur. J. Combin. 2010, 31, 1105–1120. [Google Scholar]
- Shai, O.; Sljoka, A.; Whiteley, W. Directed Graphs, Decompositions, and Spatial Linkages. Discret. Appl. Math. 2013, 161, 3028–3047. [Google Scholar] [CrossRef]
- Finbow-Singh, W.; Ross, E.; Whiteley, W. The Rigidity of Spherical Frameworks: Swapping Blocks and Holes. SIAM J. Discret. Math. 2012, 26, 280–304. [Google Scholar] [CrossRef][Green Version]
- Finbow-Singh, W.; Whiteley, W. Isostatic Almost Spherical Frameworks via Disc Decomposition. SIAM J. Discret. Math. 2013, 27, 991–1020. [Google Scholar] [CrossRef]
- Assur, L. Issledovanie Ploskih Steržnevyh Mehanizmov s Nizšimi Parami s Točki Zreniya ih Struktury i Klassifikacii; Artobolevskiùõ, I.I., Ed.; Izdatel’stvo Akademii Nauk: Moscow, Russia, 1952. [Google Scholar]
- Sljoka, A.; Shai, O.; Whiteley, W. Checking Mobitity and decomposition of Linkages via Pebble Game Algorithm. In Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference 2011, Washington, DC, USA, 28–31 August 2011; pp. 493–502. [Google Scholar]
- Yannou, B.; Vasiliu, A. Design platform for planar mechanisms based on a qualitative kinematics. In Proceedings of the Ninth International Workshop on Qualitative Reasoning 1995, Amsterdam, The Netherlands, 16–19 May 1995; pp. 191–200. [Google Scholar]
- Gogu, G. Chebychev-Grubler-Kutzbach’s criterion for mobility calculation of multi-loop mechanisms revisited via theory of linear transformations. Eur. J. Mech./A Solids 2005, 24, 427–441. [Google Scholar] [CrossRef]
- Whiteley, W. Rigidity and polarity II: Weaving lines and plane tensegrity frameworks. Geom. Dedicata 1989, 30, 255–279. [Google Scholar] [CrossRef]
- Whiteley, W. Rigidity and polarity I: Statics of sheetworks. Geom. Dedicata 1987, 22, 329–362. [Google Scholar] [CrossRef]
- DiPasquale, M.; Villamizar, N. A lower bound for splines on tetrahedral vertex stars. arXiv 2020, arXiv:2005.13043. [Google Scholar] [CrossRef]
- Konstantatou, M.; D’Acunto, P.; McRobie, A. Polarities in structural analysis and design: N-dimensional graphic statics and structural transformations. Int. J. Solids Struct. 2018, 152–153, 1–22. [Google Scholar] [CrossRef]
- Cauchy, A.L. Sur les polygons et les polyèdres. Oevres Complèt. d’Augustin Cauchy 2è Série Tom 1905, 1, 26–38. [Google Scholar]
- Dehn, M. Über die Starreit konvexer Polyeder. Math. Ann. 1916, 77, 466–473. [Google Scholar] [CrossRef]
- Kalai, G. Rigidity and the lower bound theorem. I. Invent. Math. 1987, 88, 125–151. [Google Scholar] [CrossRef]
- Whiteley, W. Vertex splitting in isostatic frameworks. Struct. Top. 1990, 16, 23–30. Available online: http://www-iri.upc.es/people/ros/StructuralTopology/ST16/st16-04-a2-ocr.pdf (accessed on 14 October 2021).
- Whiteley, W. A matrix for splines. In Progress in Approximation Theory; Nevai, P., Pinkus, A., Eds.; Academic Press: Cambridge, MA, USA, 1991; pp. 821–828. [Google Scholar]
- Alexandrov, A. Konvexe Polyeder; German Translation; Akademie-Verlag: Berlin, Germany, 1958. [Google Scholar]
- Darboux, G. Theorie General des Surfaces; 1894 historical reproduction; BiblioLife: Charleston, SC, USA, 2009. [Google Scholar]
- Kahn, E. Infinitesimally Rigidity of Almost Convex Oriented Polyhedra of Arbitrary Eucler Characteristic. Pac. J Math. 1990, 144, 71–103. [Google Scholar] [CrossRef][Green Version]
- Tay, T.-S. Linking (n-2)-Dimensional Panels in n-Space I: (k-1,k)-Graphs and (k-1,k)-Frames. Graphs Comb. 1991, 7, 289–304. [Google Scholar] [CrossRef]
- Whiteley, W. Counting Out to the Flexibility of Molecules. J. Phys. Biol. 2005, 2, 1–11. [Google Scholar] [CrossRef]
- Whiteley, W. Matroids and rigidity. In Applications of Matroid Theory; White, N., Ed.; Encyclopedia of Mathematics; Cambridge University Press: Cambridge, UK, 1992; pp. 1–53. [Google Scholar]
- Connelly, R.; Jordán, T.; Whiteley, W. Generic Global Rigidity of Body-Bar Frameworks. J. Comb. Theory Ser. B 2013, 103, 689–705. [Google Scholar] [CrossRef]
- Tay, T.-S. Linking (n-2)-Dimensional Panels in n-Space II: (n-2,2)-Frameworks and Body and Hinge Structures. Graphs Comb. 1989, 5, 245–273. [Google Scholar] [CrossRef]
- Tay, T.-S. Henneberg’s Method for Bar and Body Frameworks. Struct. Topol. 1991, 17, 53–58. [Google Scholar]
- Cheung, A.; Crapo, H. A combinatorial perspective on algebraic geometry. Adv. Math. 1976, 20, 388–414. [Google Scholar] [CrossRef][Green Version]
- Jessop, C.M. A Treatise on the Line Complex; Reprint of the 1903 Edition; Chelsea: New York, NY, USA, 1969. [Google Scholar]
- Wikepedia, Stewart Platform. Available online: https://en.wikipedia.org/wiki/Stewart_platform (accessed on 14 October 2021).
- Timeshenko, S.; Young, D.H. Theory of Structures, 2nd ed.; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Tanigawa, S. Generic Rigidity Matroids with Dilworth Truncations. SIAM J. Discret. Math. 2012, 26, 1412–1439. [Google Scholar] [CrossRef]
- Baracs, J. Rigidity of Articulated Panel Structures; Bull. International Association for Shell and Spatial Structures: Madrid, Spain, 1975; Volume 59. [Google Scholar]
- Thorpe, M.F.; Lei, M.; Rader, A.J.; Jacobs, D.J.; Kuhn, L. Protein Flexibility and Dynamics using Constraint Theory. Proteins Struct. Funct. Genet. 2001, 44, 150–165. [Google Scholar] [CrossRef]
- Schulze, B.; Sljoka, A.; Whiteley, W. How does symmetry impact the flexibility of proteins? Phil. Trans. R. Soc. A 2008, 372, 2014. [Google Scholar] [CrossRef]
- Thorpe, M.; Chubynsky, M.; Hespenheide, B.; Menor, S.; Day, A.; Jacobs, D.; Kuhn, L.; Zavodszky, M.; Lei, M.; Rader, A.; et al. Flexibility in Biomolecules. In Current Topics in Physics: The Sir Roger Elliott Festschrift; World Scientific: Singapore, 2005; pp. 97–112. [Google Scholar]
- Jacobs, D.; Rader, A.; Kuhn, L.; Thorpe, M. Protein Flexibility Predictions Using Graph Theory. Proteins Struct. Funct. Genet. 2001, 44, 150–165. [Google Scholar] [CrossRef] [PubMed]
- Fowler, N.J.; Sljoka, A.; Williamson, M.P. A method for validating the accuracy of NMR protein structures. Nat. Commun. 2020, 11, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Bobenko, A. Discrete Differential Geometry II. 2020. Available online: https://www3.math.tu-berlin.de/geometrie/Lehre/SS20/GeometryII/geometry2-sose2020.pdf (accessed on 14 October 2021).
- Cruickshank, J.; Kitson, D.; Power, S. The generic rigidity of triangulated spheres with blocks and holes. J. Combin. Theory Ser. B 2017, 122, 550–577. [Google Scholar] [CrossRef]
- Whiteley, W. Fragmentary and incidental behaviour of columns, slabs and crystals. Phil. Trans. R. Soc. A 2014, 372. [Google Scholar] [CrossRef]
- Jackson, B.; Jordán, T. Pin-collinear body-and-pin frameworks and the molecular conjecture. Discret. Comput. Geom. 2008, 40, 258–278. [Google Scholar] [CrossRef][Green Version]
- Whiteley, W. A Matroid on Hypergraphs, with Applications in Scene Analysis and Geometry. Discret. Comput. Geom. 1989, 4, 75–95. [Google Scholar] [CrossRef]
- Lundqvist, S.; Stokes, K.; Öhman, L.D. Exploring the infinitesimal rigidity of planar configurations of points and rods. arXiv 2021, arXiv:2110.07972. [Google Scholar]
- Lundqvist, S.; Stokes, K.; Öhman, L.D. When is a planar rod configuration infinitesimally rigid? arXiv 2021, arXiv:2112.01960. [Google Scholar]
- Crespo, L.; Santos, F. Bar-and-Joint Rigidity on the Moment Curve Coincides with Cofactor Rigidity on a Conic. arXiv 2021, arXiv:2106.08923. [Google Scholar]
- Chui, C.; Wang, R. On Smooth Multivariate Spline Functions. Math. Comp. 1983, 41, 131–142. [Google Scholar] [CrossRef]
- Morgan, J.; Scott, R. A nodal basis for C1 piecewise polynomials of degree n>5. Math. Comp. 1975, 29, 736–740. [Google Scholar]
- Schenck, H.; Stillman, M.; Yuan, B. A new bound for smooth spline spaces. arXiv 2019, arXiv:1909.13399. [Google Scholar] [CrossRef]
- Graver, J. Rigidity matroids. SIAM J. Discret. Math. 1991, 4, 355–368. [Google Scholar] [CrossRef]
- Nguyen, V.H. On abstract rigidity matroids. SIAM J. Discret. Math. 2010, 24, 363–369. [Google Scholar] [CrossRef]
- Grasegger, G.; Guler, H.; Jackson, B.; Nixon, A. Flexible circuits in the d-dimensional rigidity matroid. arXiv 2020, arXiv:2003.06648v1. [Google Scholar] [CrossRef]
- Alfeld, P.; Neamtu, M.; Schumaker, L.L. Dimension and Local Bases of Homogeneous Spline Spaces. SIAM J. Math. Anal. 1996, 27, 1482–1501. [Google Scholar] [CrossRef]
- Billera, L. Homology of smooth splines: Generic triangulations and a conjecture of Strang. Trans. Am. Math. Soc. 1988, 310, 325–340. [Google Scholar] [CrossRef]
- Connelly, R. Rigidity and Energy. Invent. Math. 1982, 66, 11–33. [Google Scholar] [CrossRef]
- Connelly, R.; Guest, S. Frameworks, Tensegrities and Symmetry; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Clinch, K.; Nixon, A.; Schulze, B.; Whiteley, W. Pairing symmetries for Euclidean and spherical frameworks. Discret. Comput. Geom. 2020, 64, 483–518. [Google Scholar] [CrossRef]
- Adiprasito, K. Combinatorial Lefschetz Theorems Beyond Positivity. arXiv 2018, arXiv:1812.10454. [Google Scholar]
- Tay, T.-S.; White, N.; Whiteley, W. Skeletal rigidity of simplicial complexes: I. Eur. J. Combin. 1995, 16, 381–403. [Google Scholar] [CrossRef]
- Tay, T.-S.; White, N.; Whiteley, W. Skeletal rigidity of simplicial complexes: II. Eur. J. Combin. 1995, 16, 503–523. [Google Scholar] [CrossRef]
- Tay, T.-S. A homological approach to skeletal rigidity. Adv. Appl. Math. 2000, 25, 102–151. [Google Scholar] [CrossRef]
- Gortler, S.; Healy, A.; Thurston, D. Characterizing generic global rigidity. Am. J. Math. 2010, 132, 897–939. [Google Scholar] [CrossRef]
- Hendrickson, B. Conditions for unique graph realizations. SIAM J. Comput. 1992, 21, 65–84. [Google Scholar] [CrossRef]
- Jackson, B.; Jordán, T. Connected Rigidity Matroids and Unique Realisations of Graphs. J. Combin. Theory Ser. B 2005, 94, 1–29. [Google Scholar] [CrossRef]
- Connelly, R. On generic global rigidity. In Applied Geometry and Discrete Mathematics. DIMACS Series in Discrete Mathematics and Theoretical Computer Science; AMS: Providence, RI, USA, 1991; Volume 4, pp. 147–155. [Google Scholar]
- Jordán, T.; Kiraly, C.; Tanigawa, S. Generic global rigidity of body–hinge frameworks. J. Comb. Theory Ser. B 2016, 117, 59–76. [Google Scholar] [CrossRef]
- Guler, H.; Jackson, B.; Nixon, A. Global Rigidity of 2D Linearly Constrained Frameworks. Int. Math. Res. Not. 2020. [Google Scholar] [CrossRef]
- Alfakih, A. On dimensional rigidity of bar-and-joint frameworks. Discret. Appl. Math. 2007, 155, 1244–1253. [Google Scholar] [CrossRef][Green Version]
- Jordán, T.; Whiteley, W. Global Rigidity. In Handbook of Discrete and Computational Geometry, 3rd ed.; Toth, C., Goodman, J., O’Rourke, J., Eds.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Connelly, R.; Whiteley, W. Global Rigidity and the Effects of Coning. Discret. Comput. Geom. 2010, 43, 717–735. [Google Scholar] [CrossRef]
- Connelly, R.; Gortler, S.; Theran, L. Affine Rigidity and Conics at Infinity. Int. Math. Res. Not. IMRN 2018, 13, 4084–4102. [Google Scholar] [CrossRef]
- Farre, J.; Kleinschmidt, H.; Sidman, J.; Johnn, A.S.; Stark, S.; Theran, L.; Yu, X. Algorithms for detecting dependencies and rigid subsystems for CAD. Comput. Aided Geom. Des. 2016, 47, 130–149. [Google Scholar] [CrossRef]

















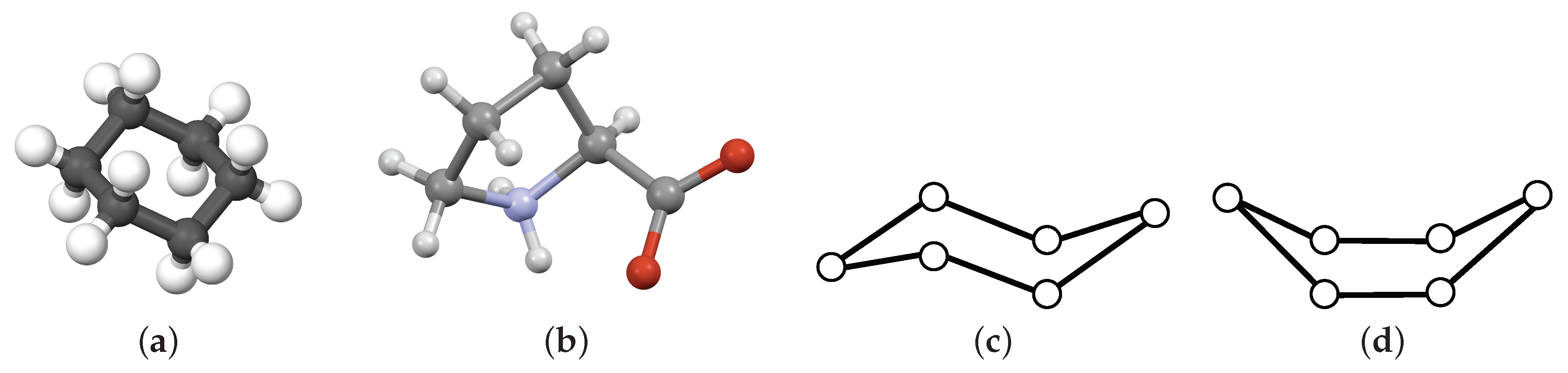

| Table of Geometric Structures and Distance Constraints: Euclidean, Minkowski | ||||
|---|---|---|---|---|
| Dim. | Geometric Objects | Necessary Counts | Suff. | Sect. |
| point line (bar–joint) | Yes (=) | |||
| line pin-rod | Yes (=) | |||
| point edge (bar–joint) | Yes (=) | [13,14] | ||
| bar face (body-bar) | Yes | Section 9.1 [58] | ||
| point face (body-pin) | Yes | Section 10 | ||
| pinned rods | Yes | Section 10.7 [145] | ||
| bar–joint | No | [34] | ||
| body-bar | Yes (=) | Section 9.1 [58] | ||
| rod and bar | Yes (=) | Section 9.6 [135] | ||
| body–hinge | Yes | Section 10 [58] | ||
| flat-body hinge | Yes | Section 10.4 [50] | ||
| molecular body hinge | Yes | Section 10.4 [50] | ||
| body-pin | No | |||
| clamped rods | No | Section 9.6 | ||
| edge-face (sheetworks) | No | Section 8.2 [114] | ||
| point-face (sheetworks) | No | Section 8.2 [114] | ||
| bar–joint | No | [34] | ||
| d | body-bar | Yes (=) | Section 9.2 [58] | |
| d | body–hinge | Yes | Section 10 [58] | |
| d | flat-body hinge | Yes | Section 10.4 [50] | |
| d | rod and bar | Yes | Section 9.6 [135] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nixon, A.; Schulze, B.; Whiteley, W. Rigidity through a Projective Lens. Appl. Sci. 2021, 11, 11946. https://doi.org/10.3390/app112411946
Nixon A, Schulze B, Whiteley W. Rigidity through a Projective Lens. Applied Sciences. 2021; 11(24):11946. https://doi.org/10.3390/app112411946
Chicago/Turabian StyleNixon, Anthony, Bernd Schulze, and Walter Whiteley. 2021. "Rigidity through a Projective Lens" Applied Sciences 11, no. 24: 11946. https://doi.org/10.3390/app112411946
APA StyleNixon, A., Schulze, B., & Whiteley, W. (2021). Rigidity through a Projective Lens. Applied Sciences, 11(24), 11946. https://doi.org/10.3390/app112411946





