Evaluation of Unfilled Sheath in Concrete Structures Using Response Waveform in Time Domain
Abstract
:1. Introduction
1.1. Non-Destructive Testing for Concrete Structures
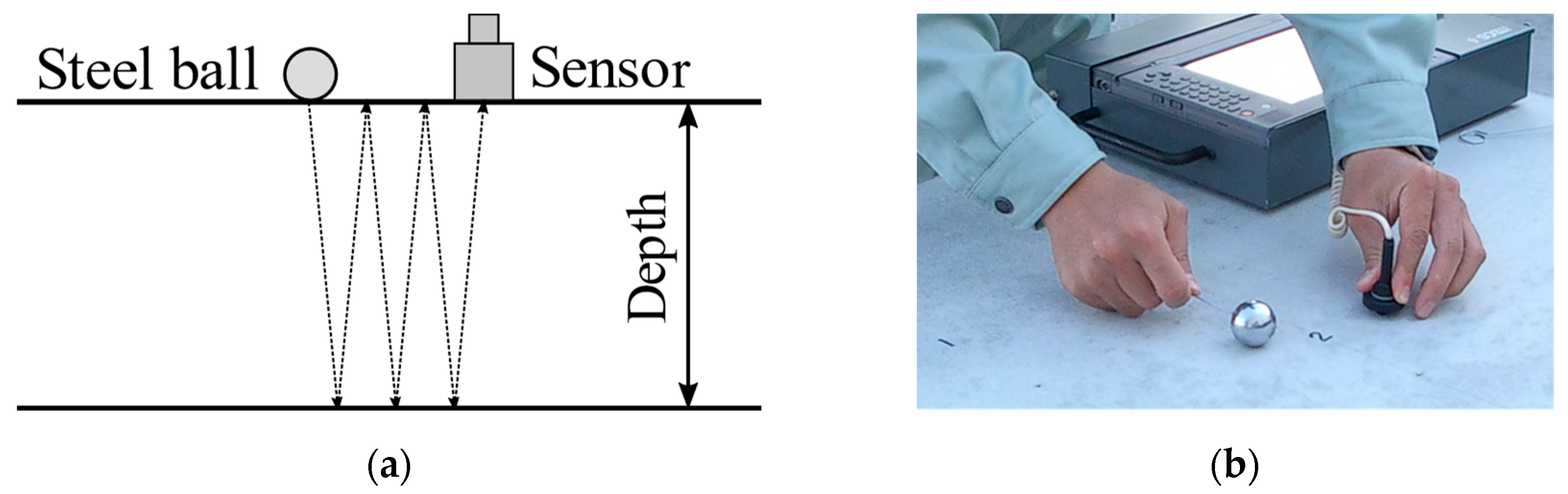
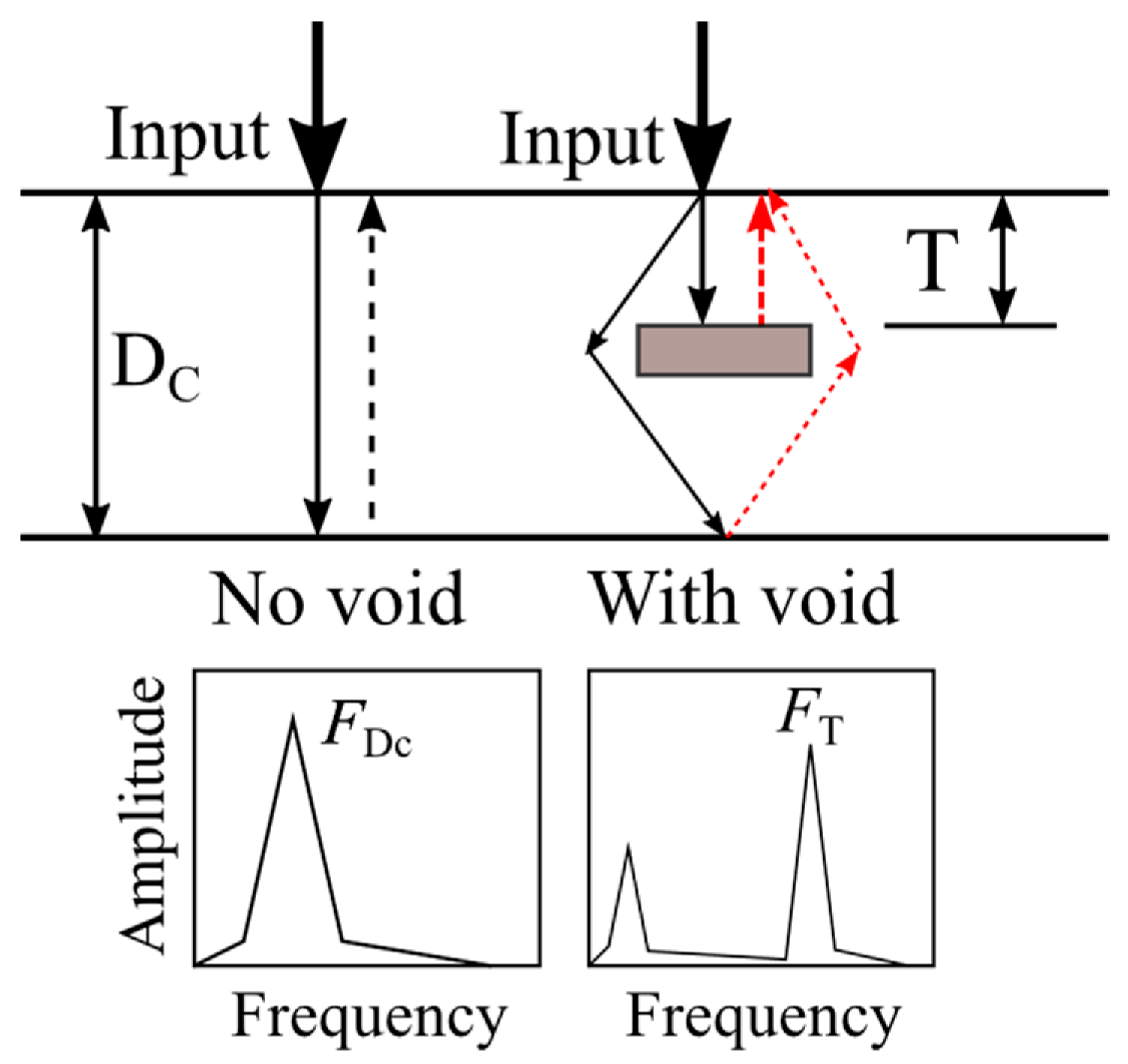
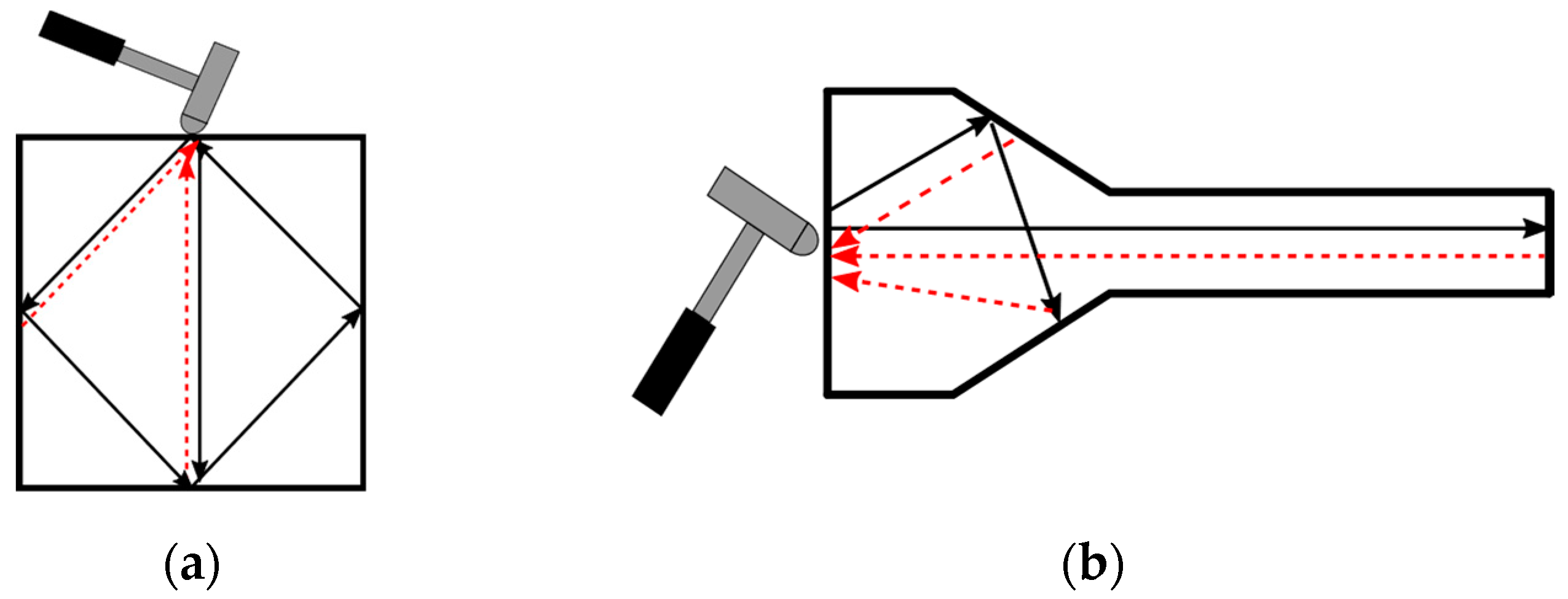
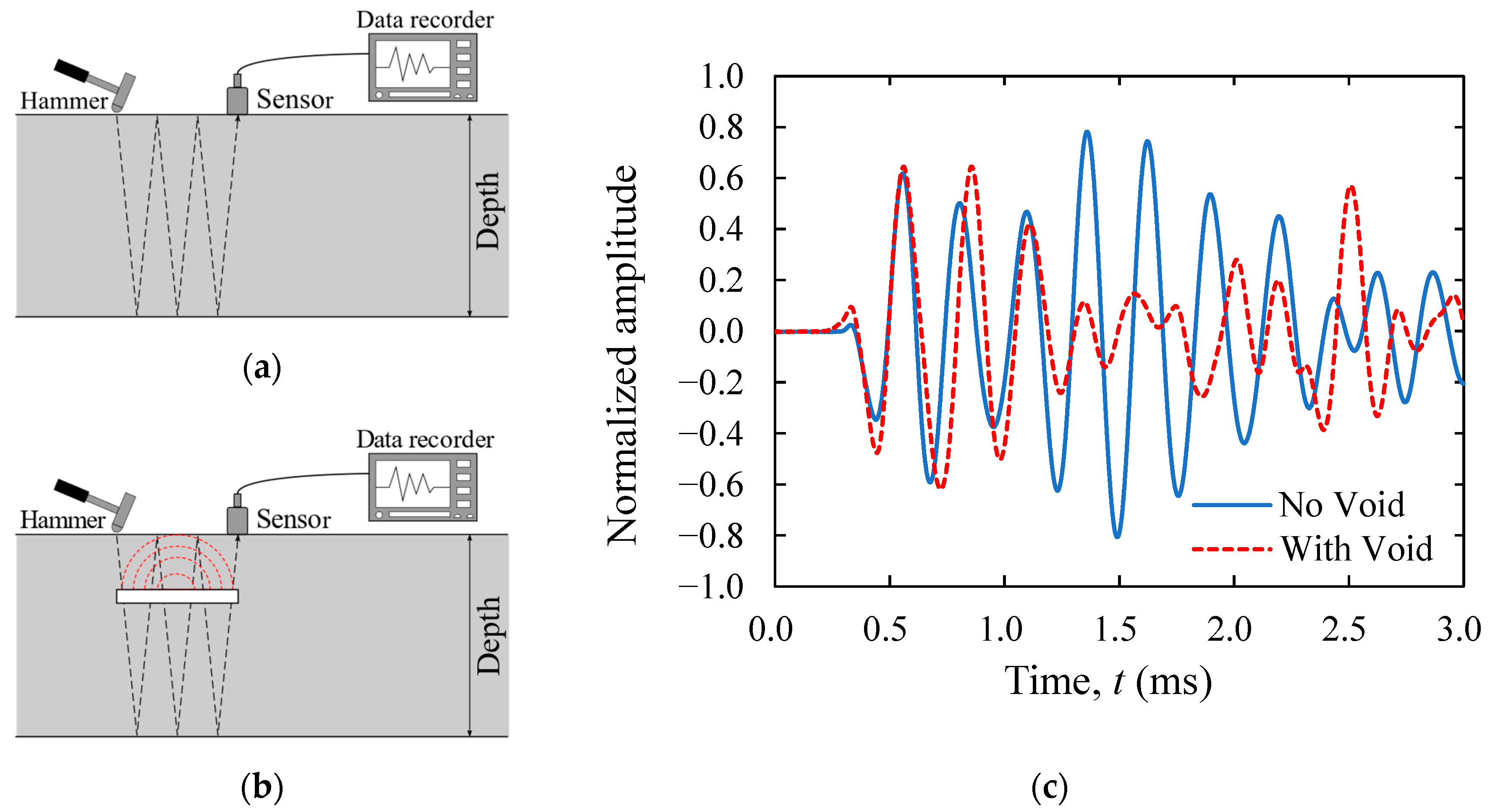
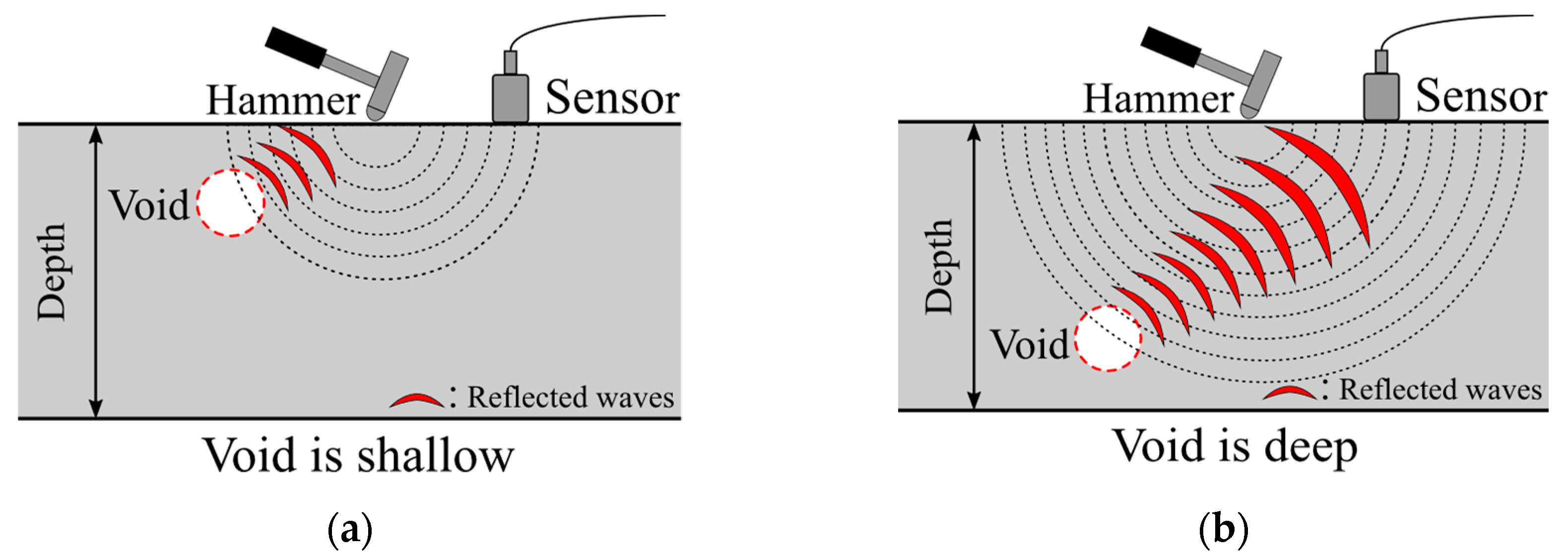
1.2. Impact Elastic Wave Method (IEW)
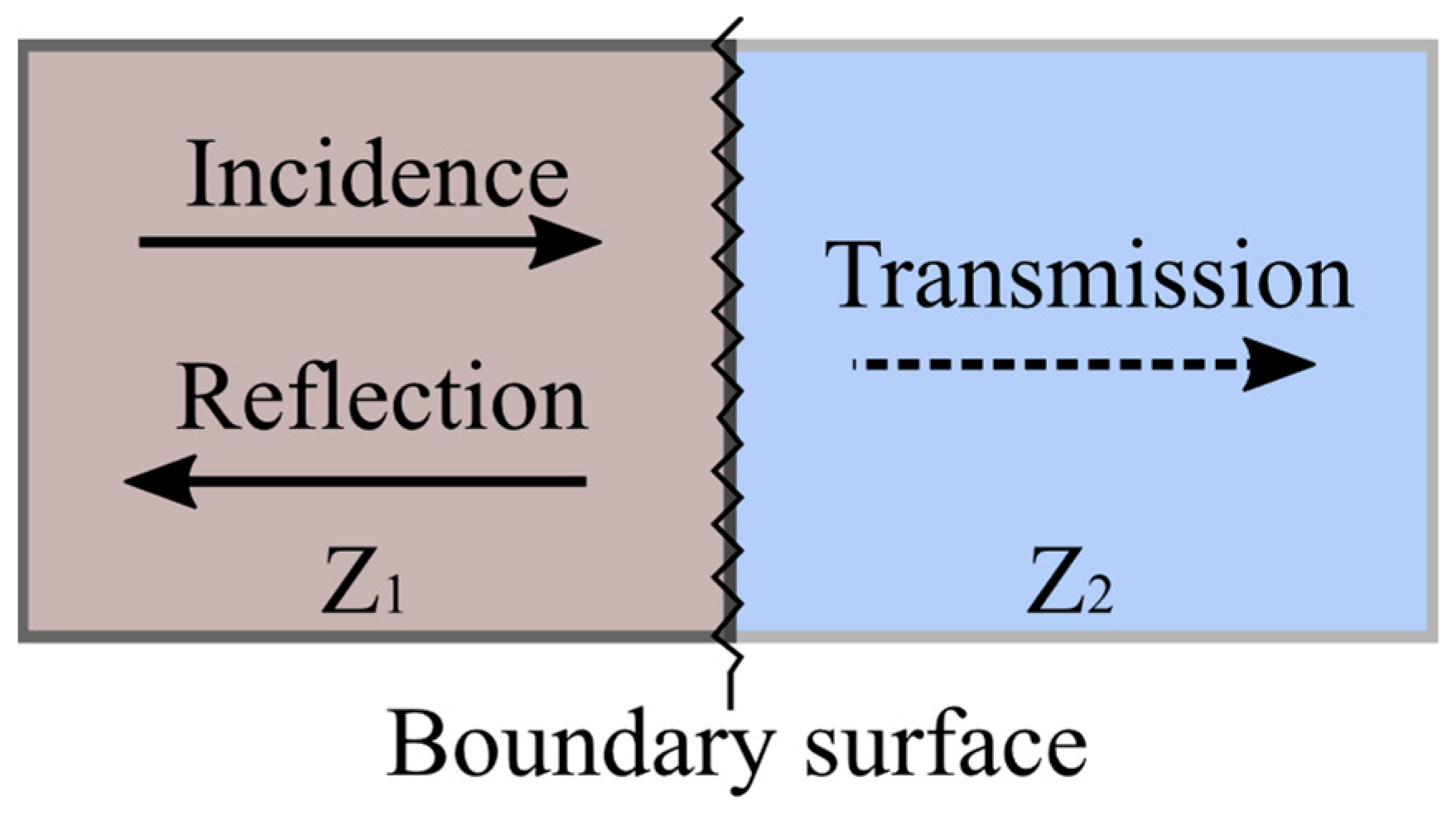
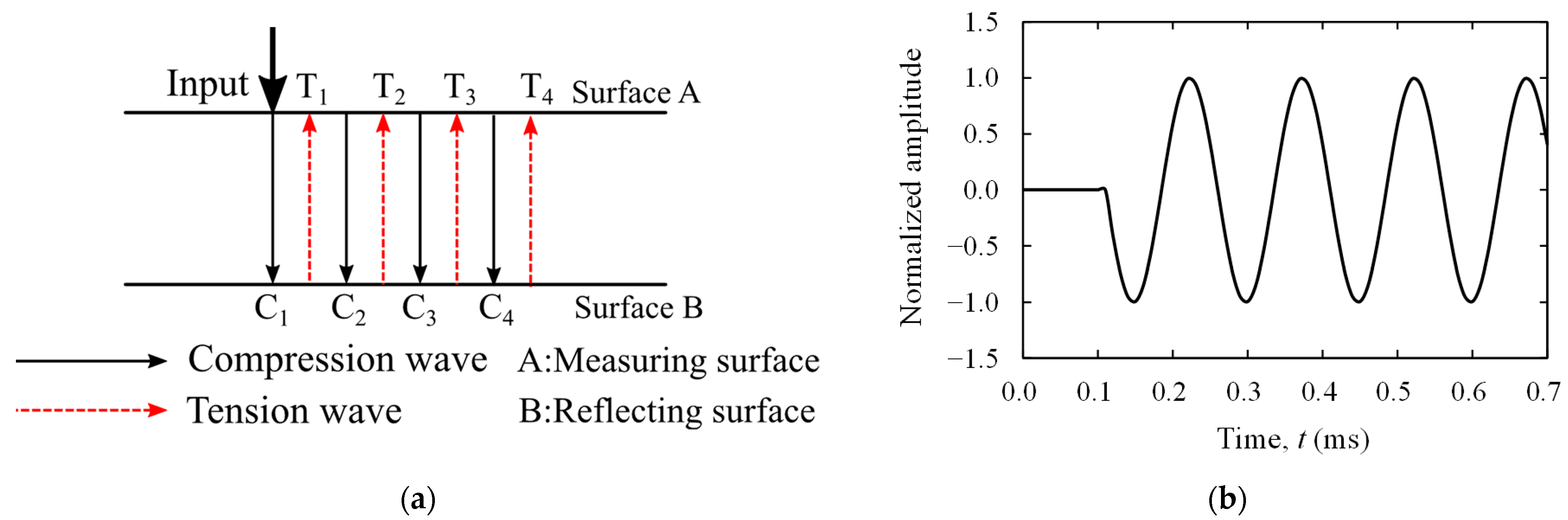
2. Difference Value Analysis (DVA)
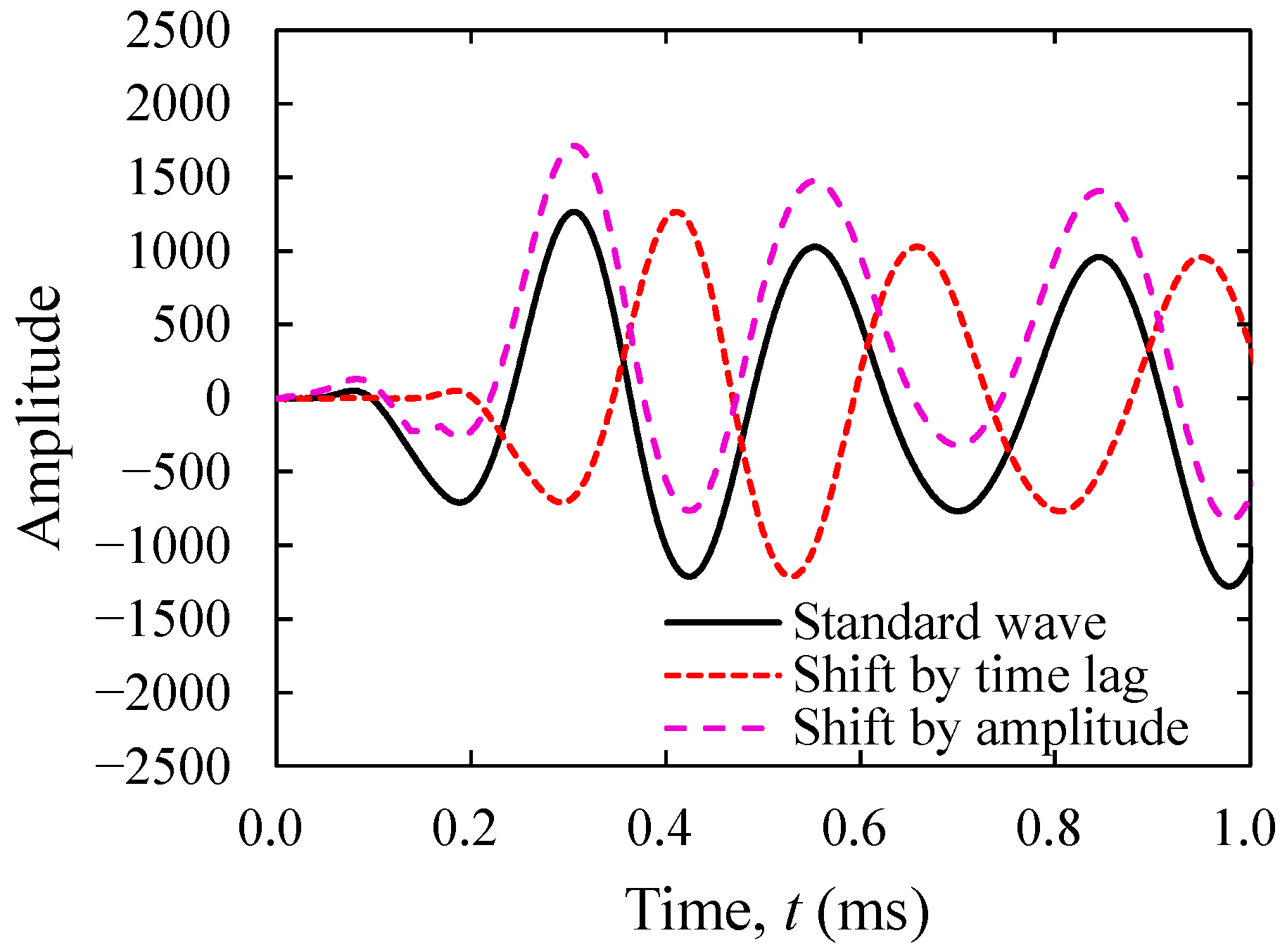
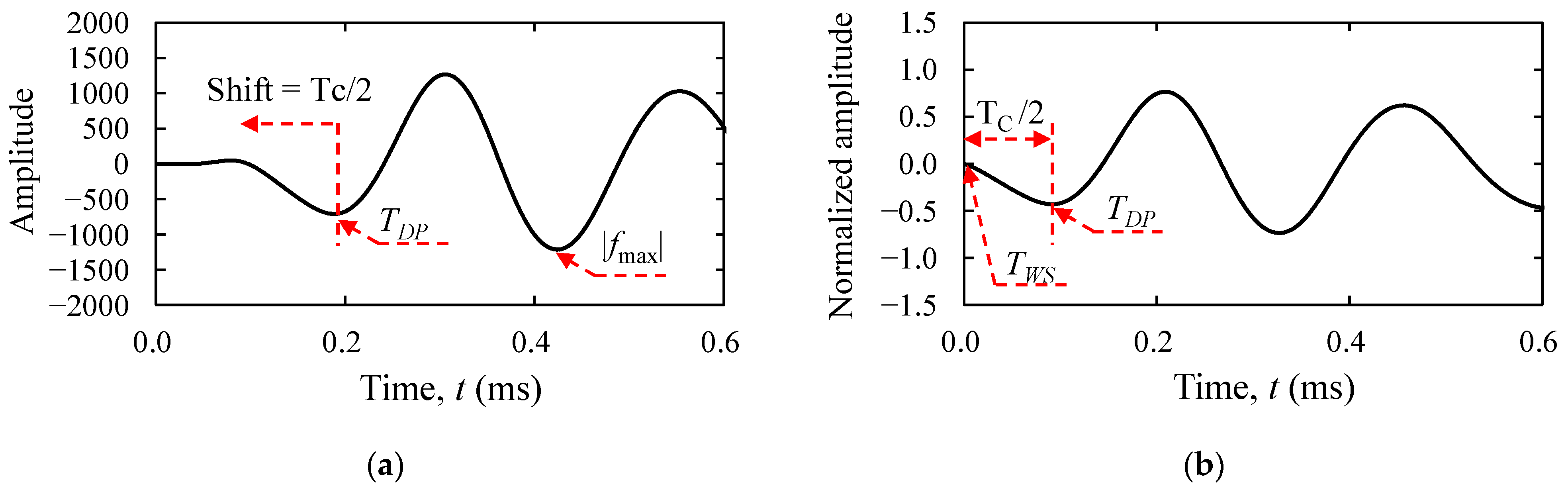
2.1. Difference Value
2.2. Normalization of Measured Waveform
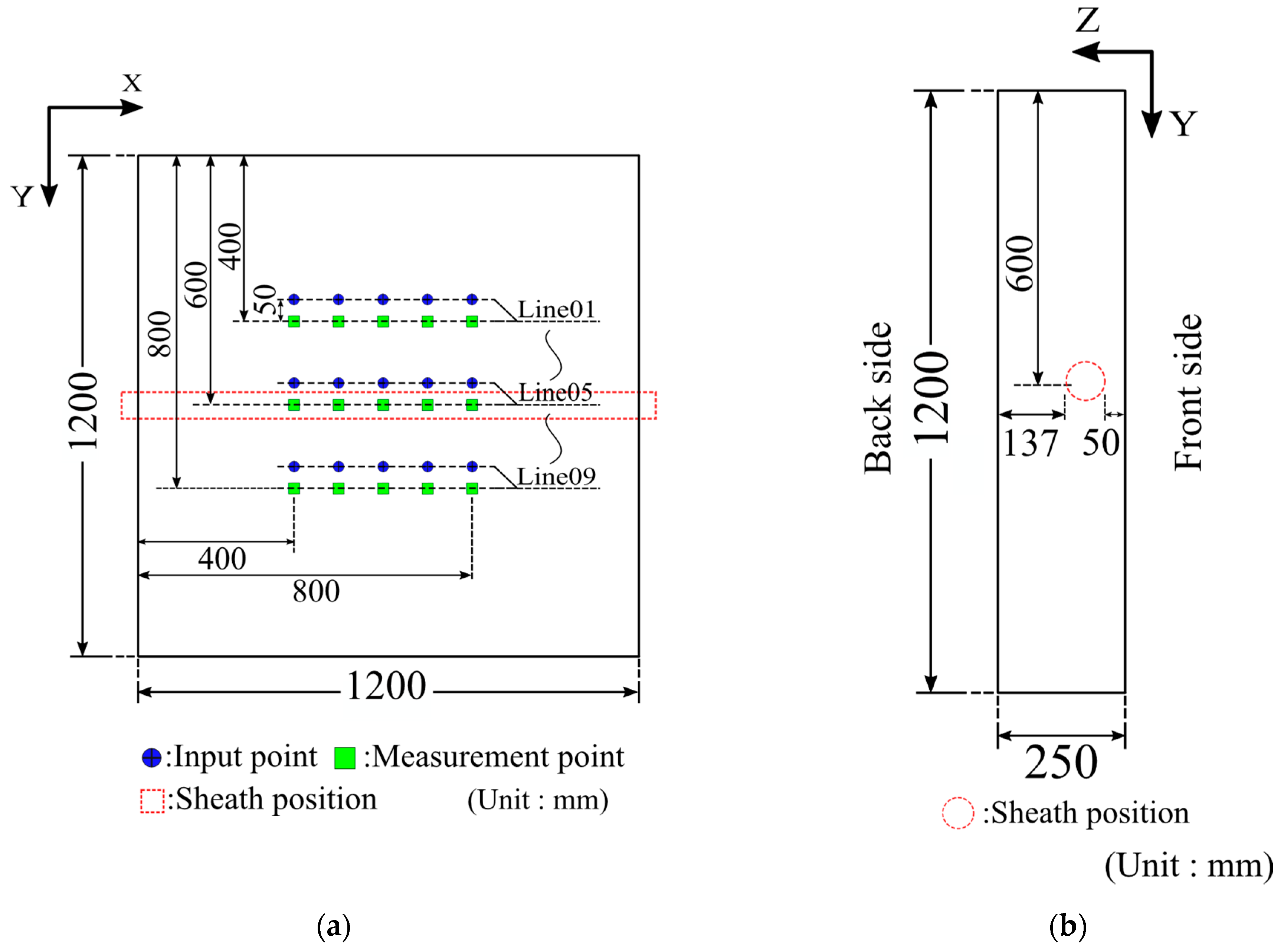
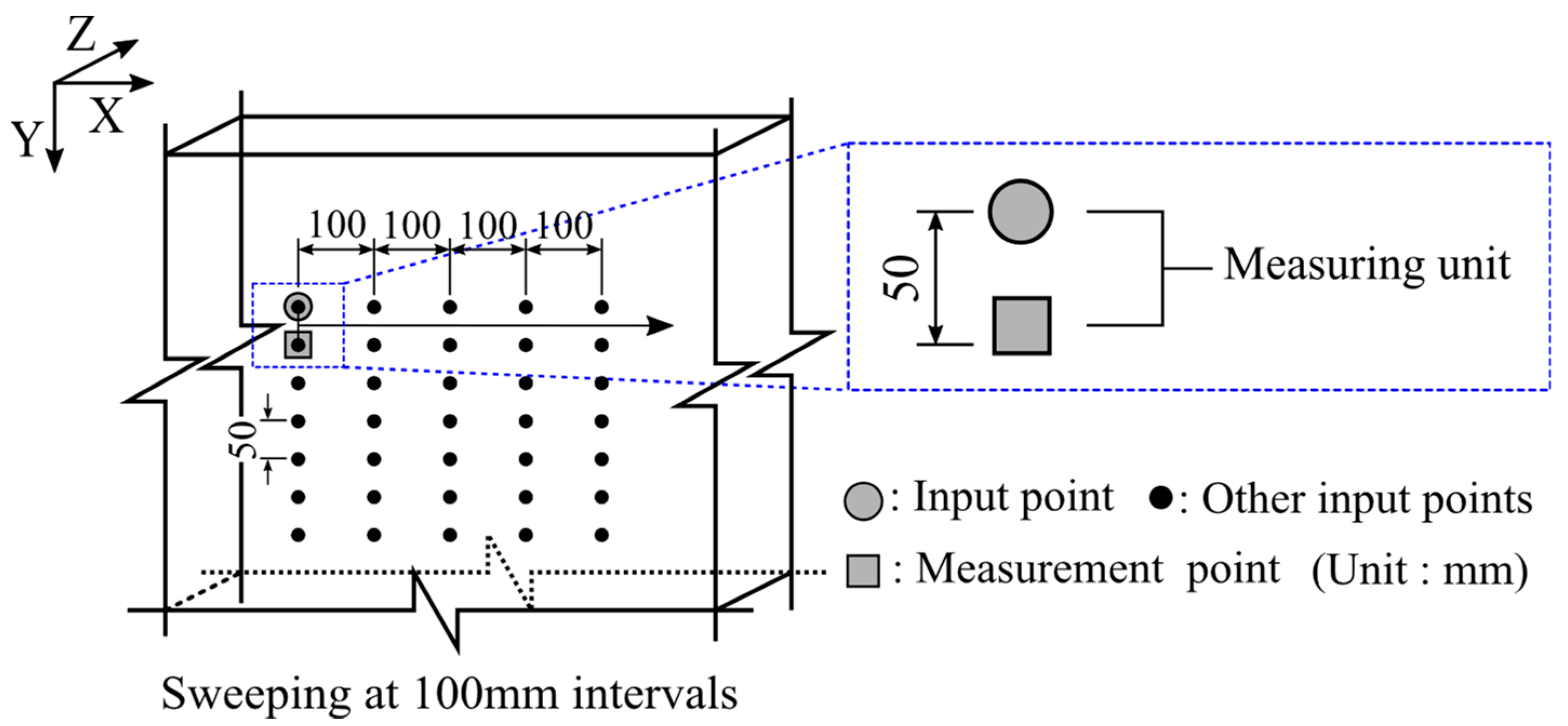
3. Experiment Conditions
4. Results
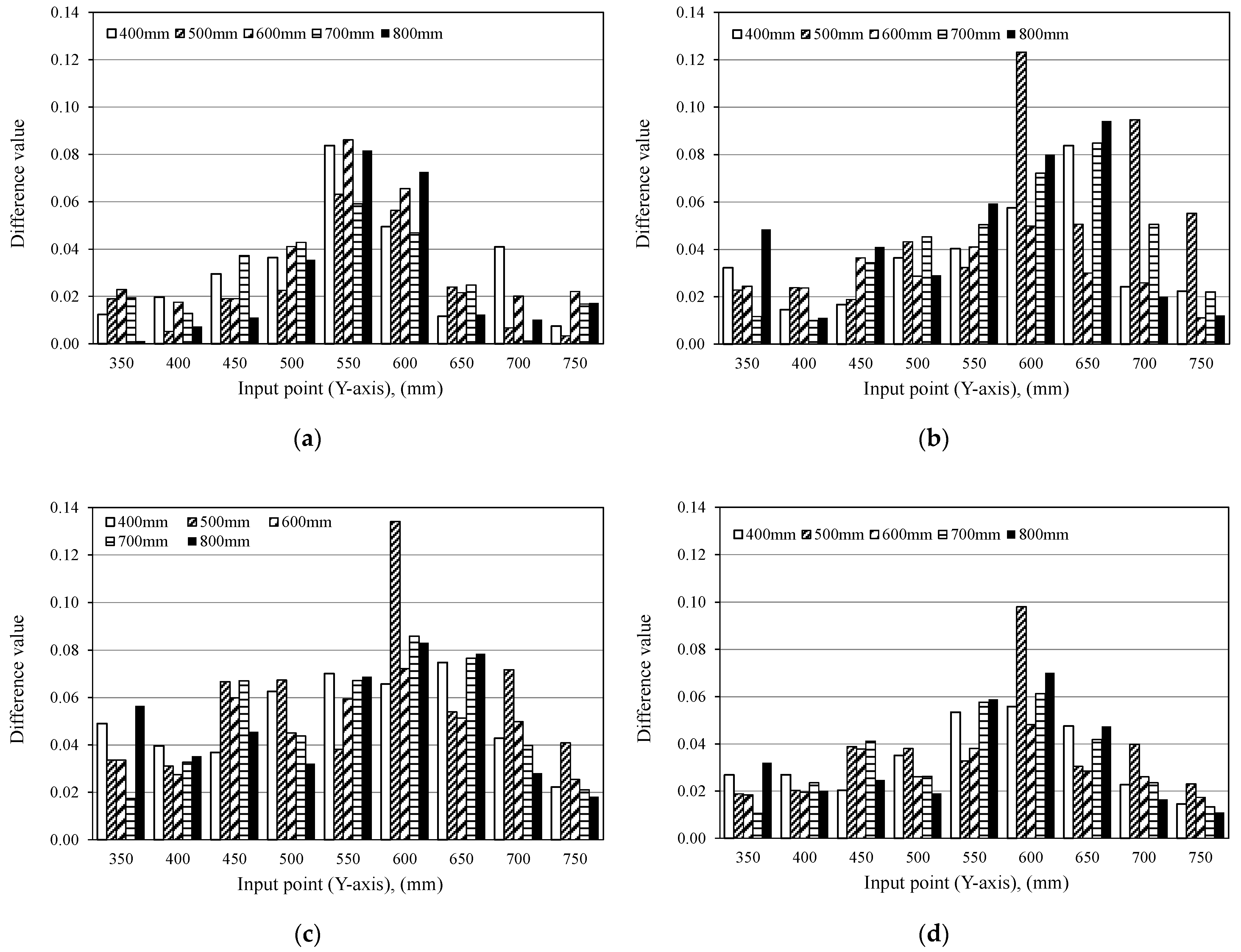
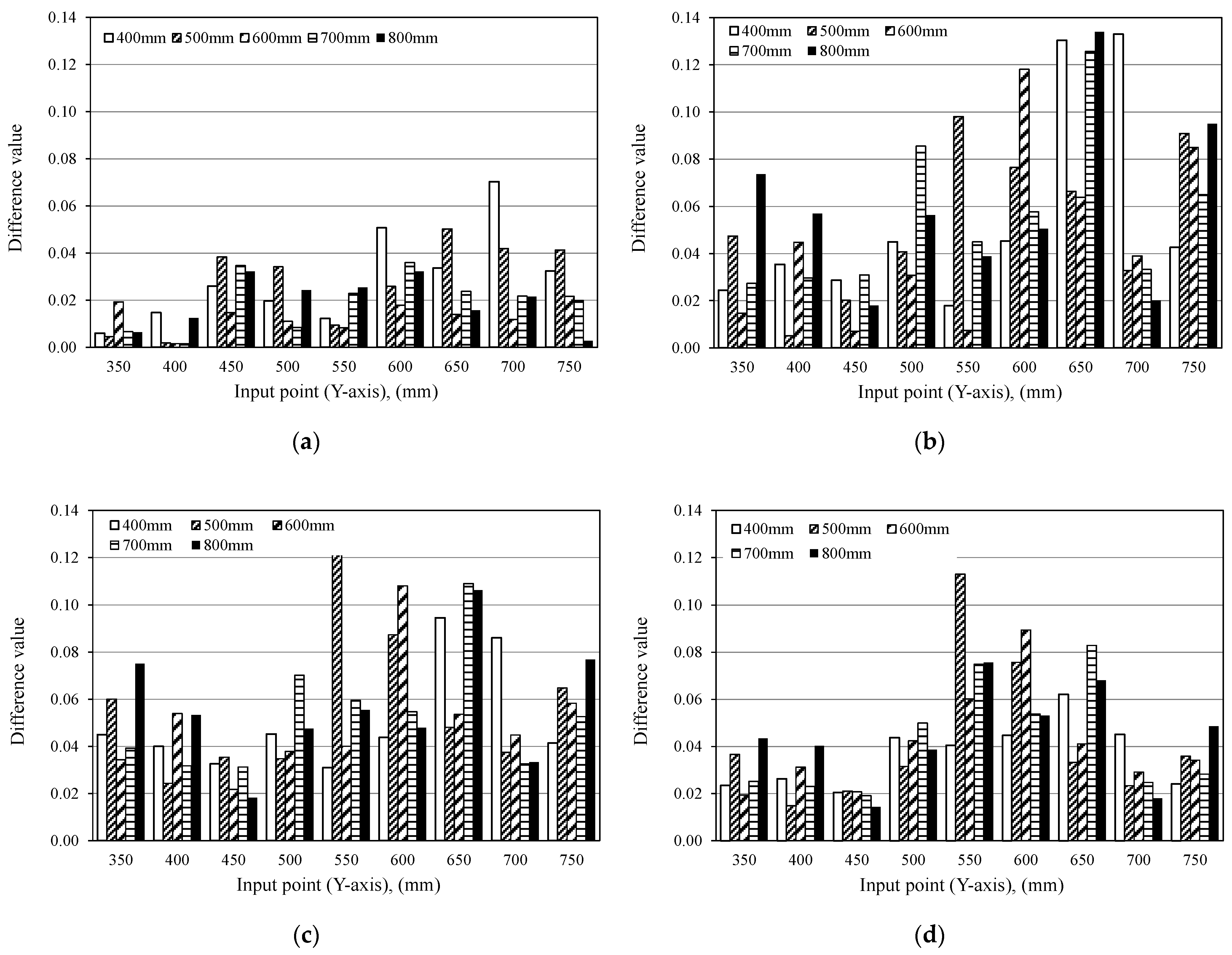
4.1. Influence of the Number of Data on the Calculation of Difference Value
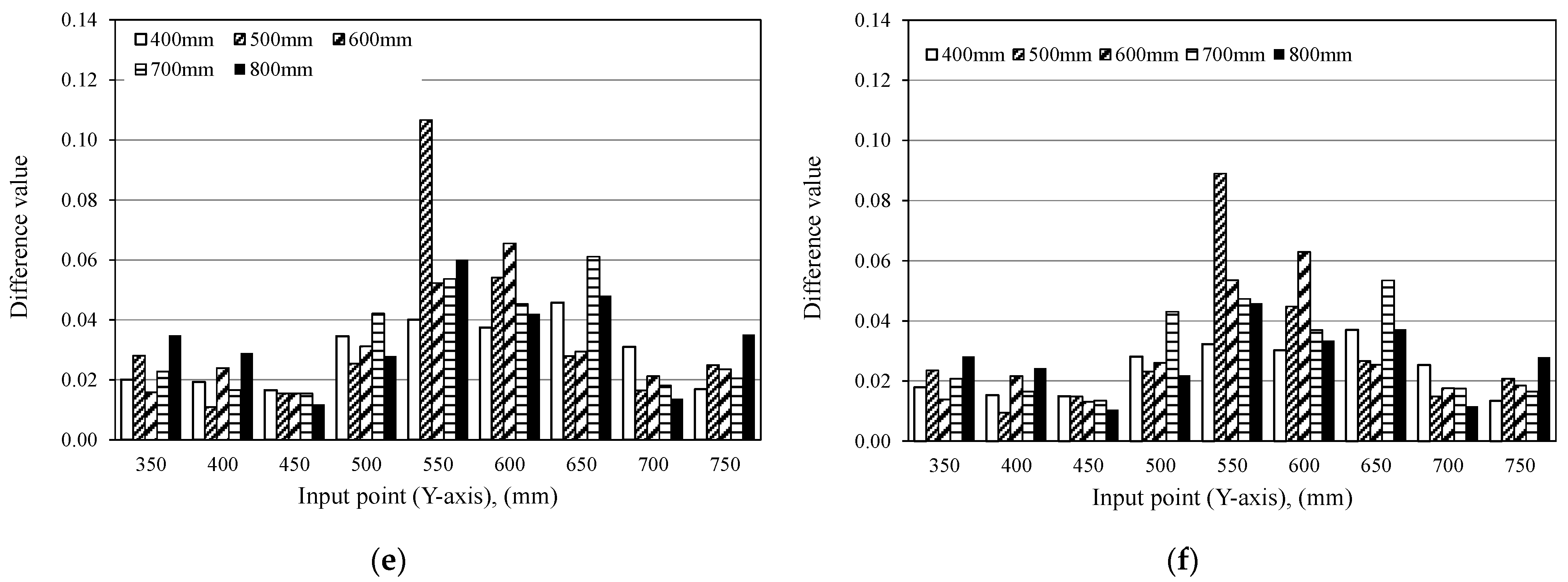
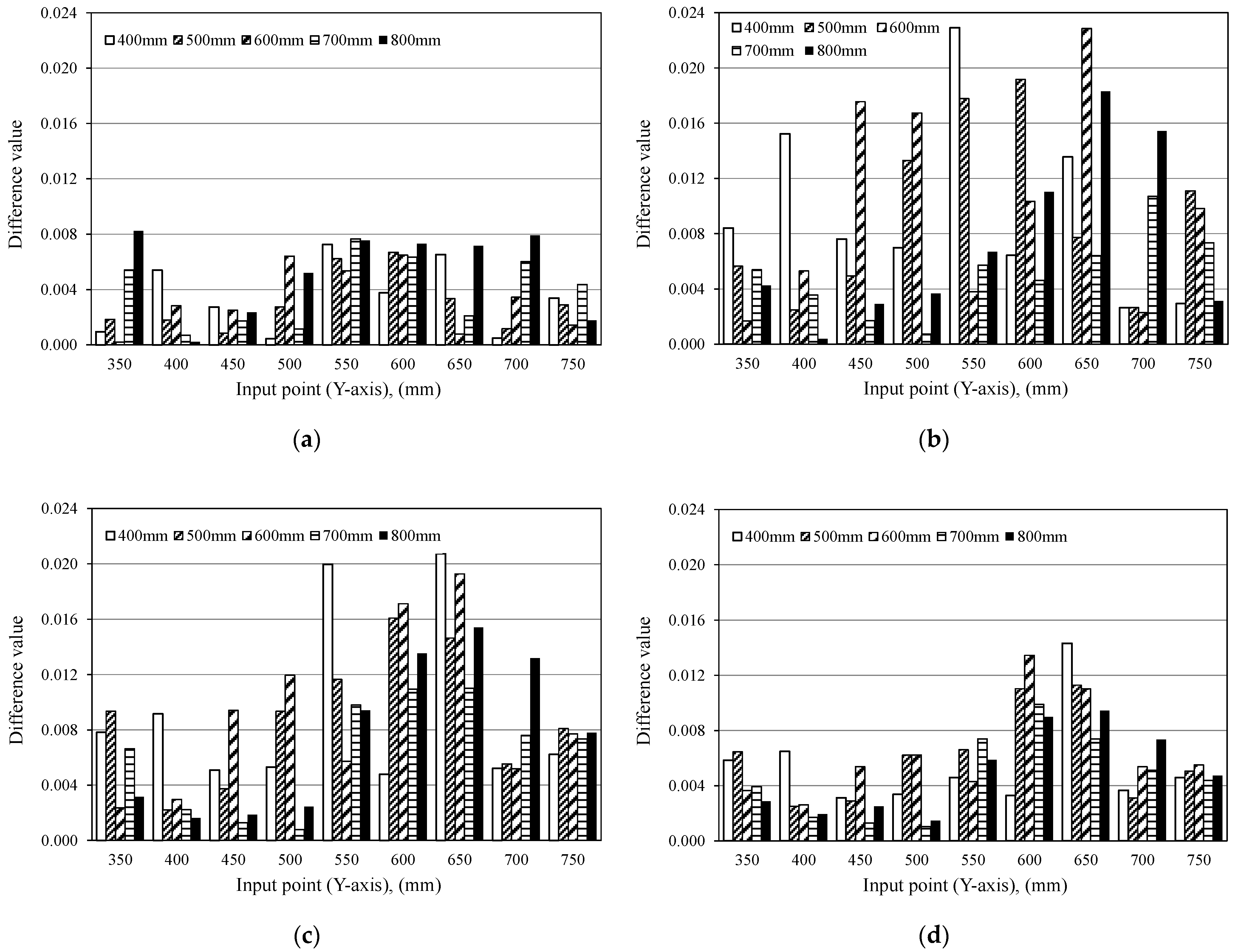
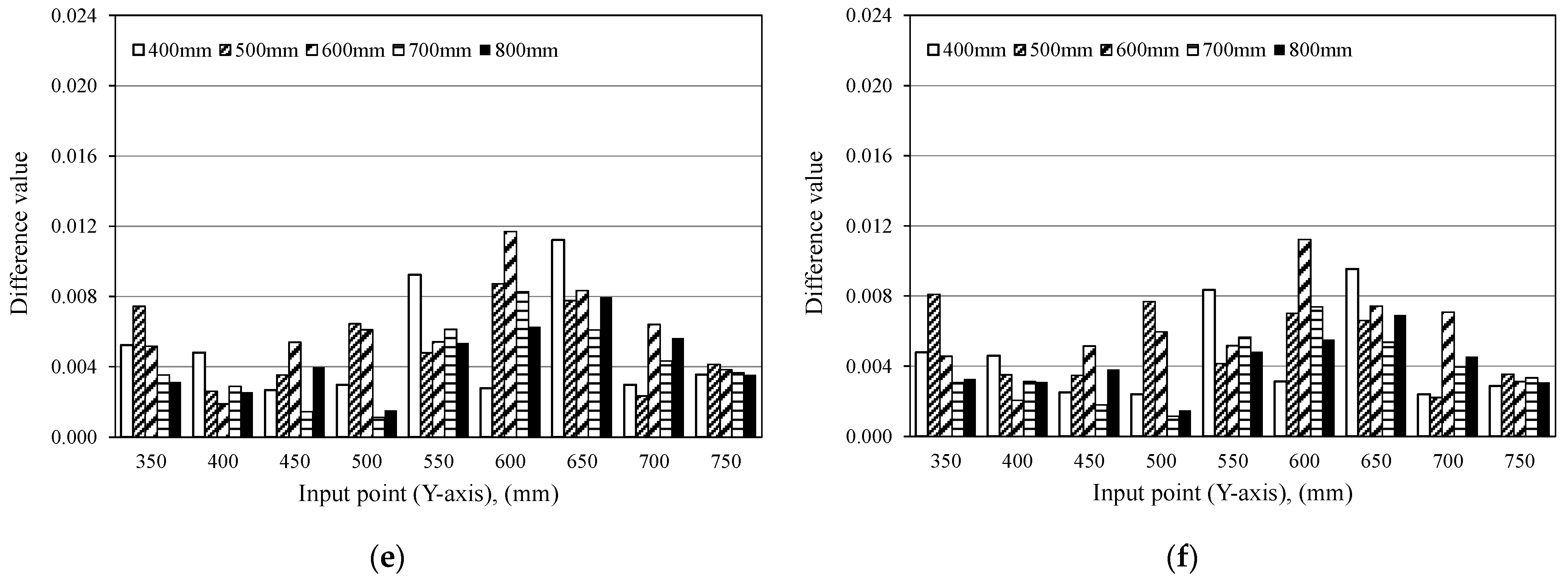
4.1.1. Magnitude of Difference Value
4.1.2. Distribution of the Difference Value
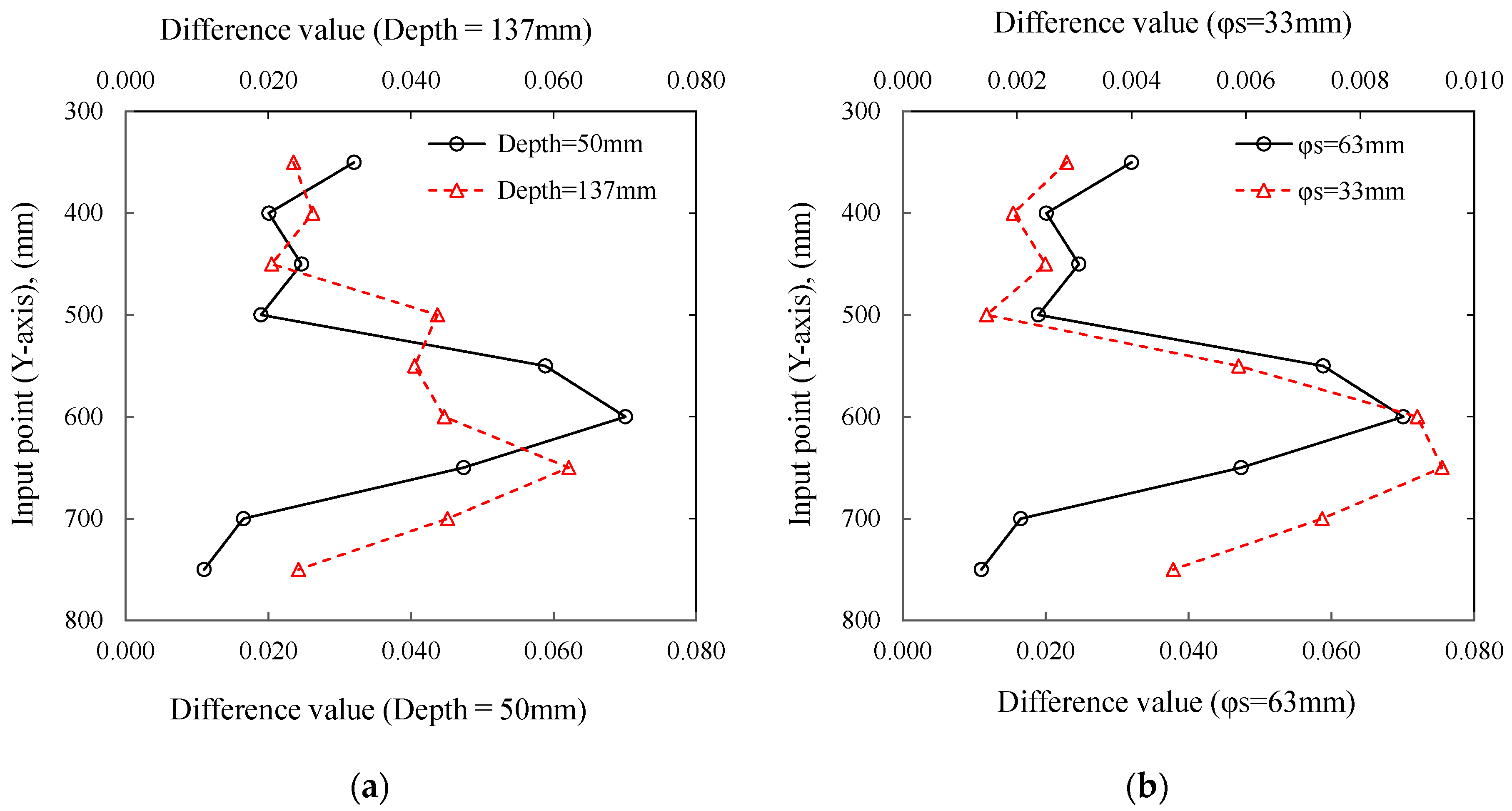
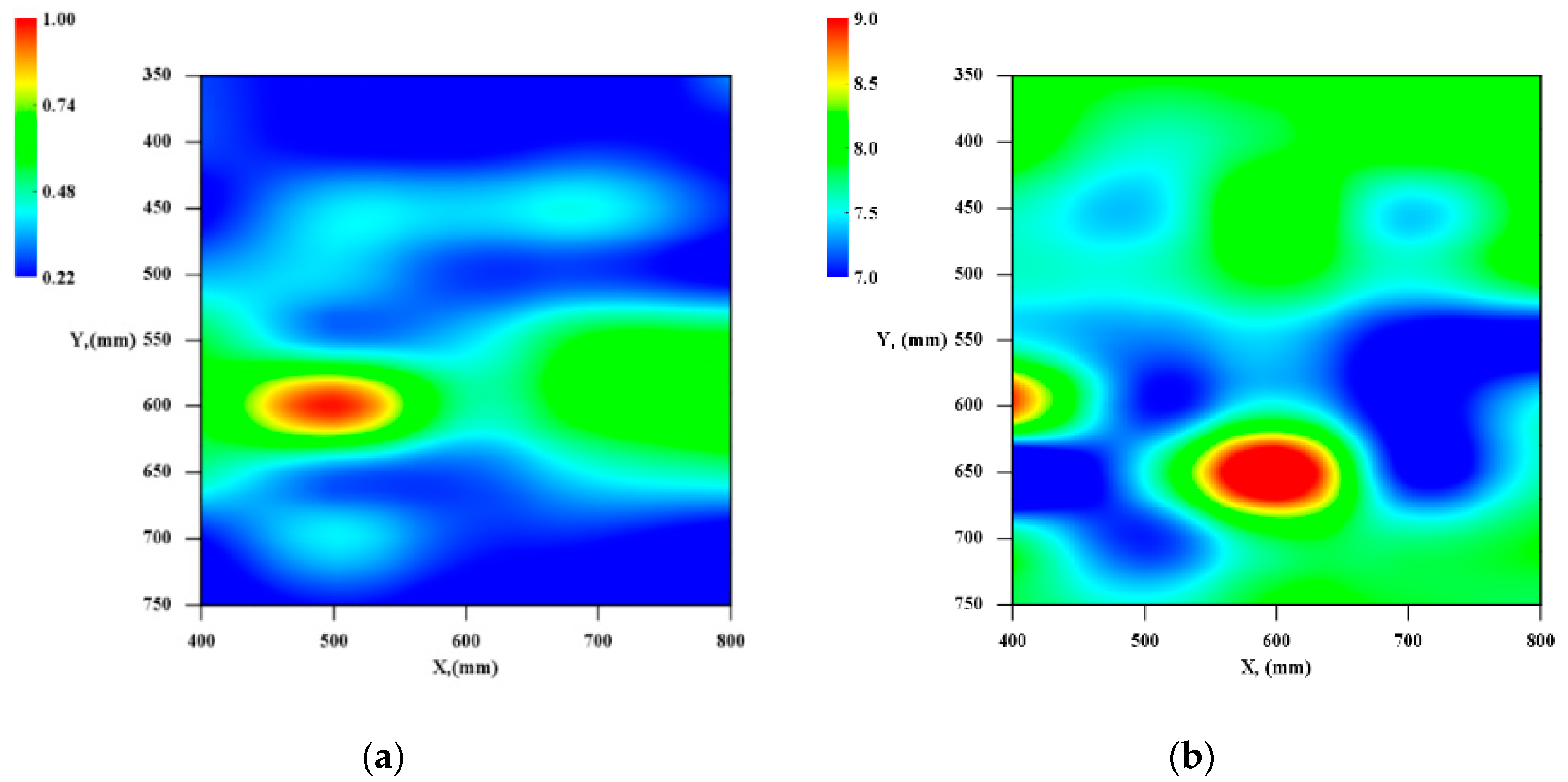
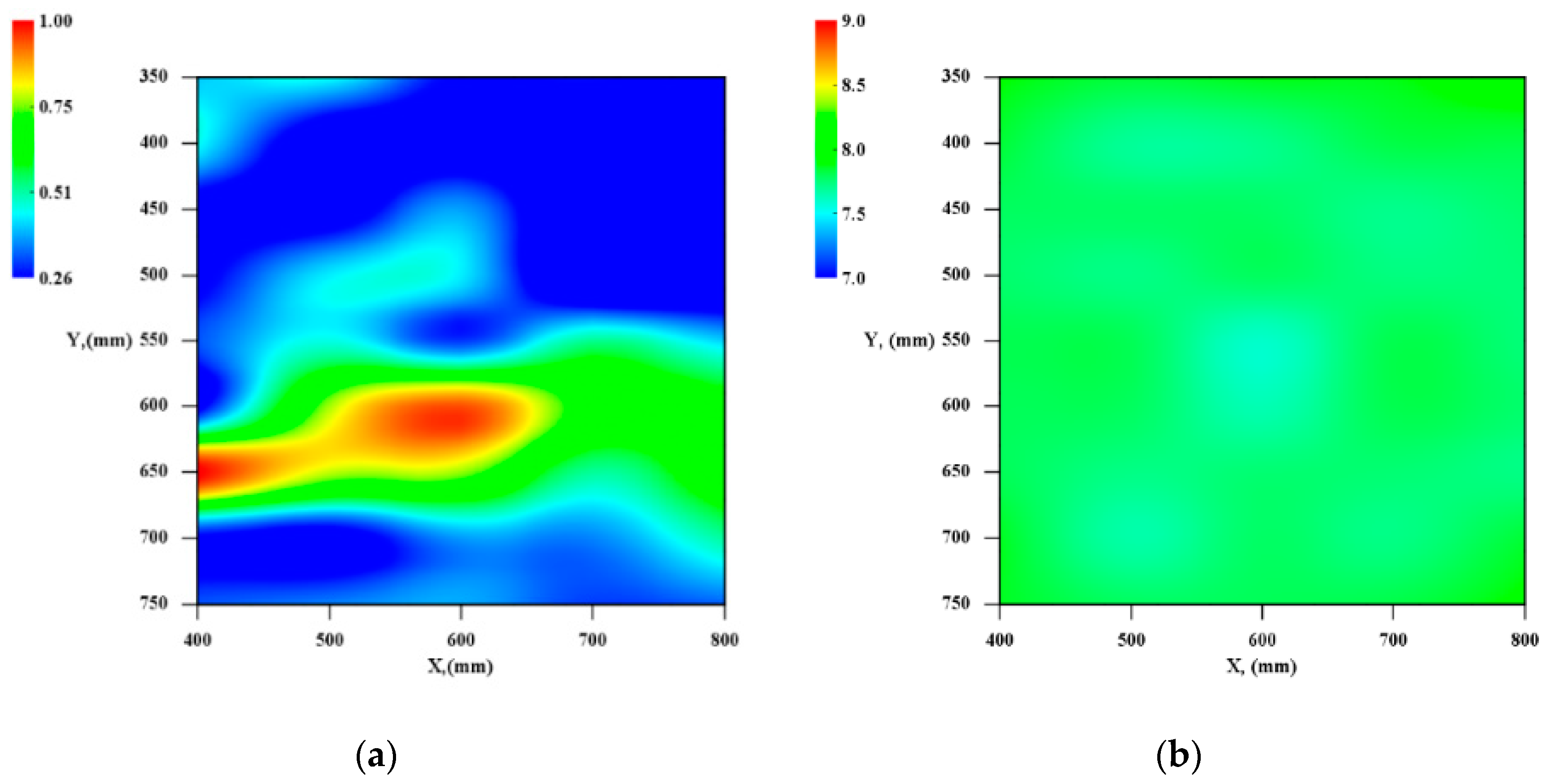
4.2. Distribution and Magnitude of Difference Values
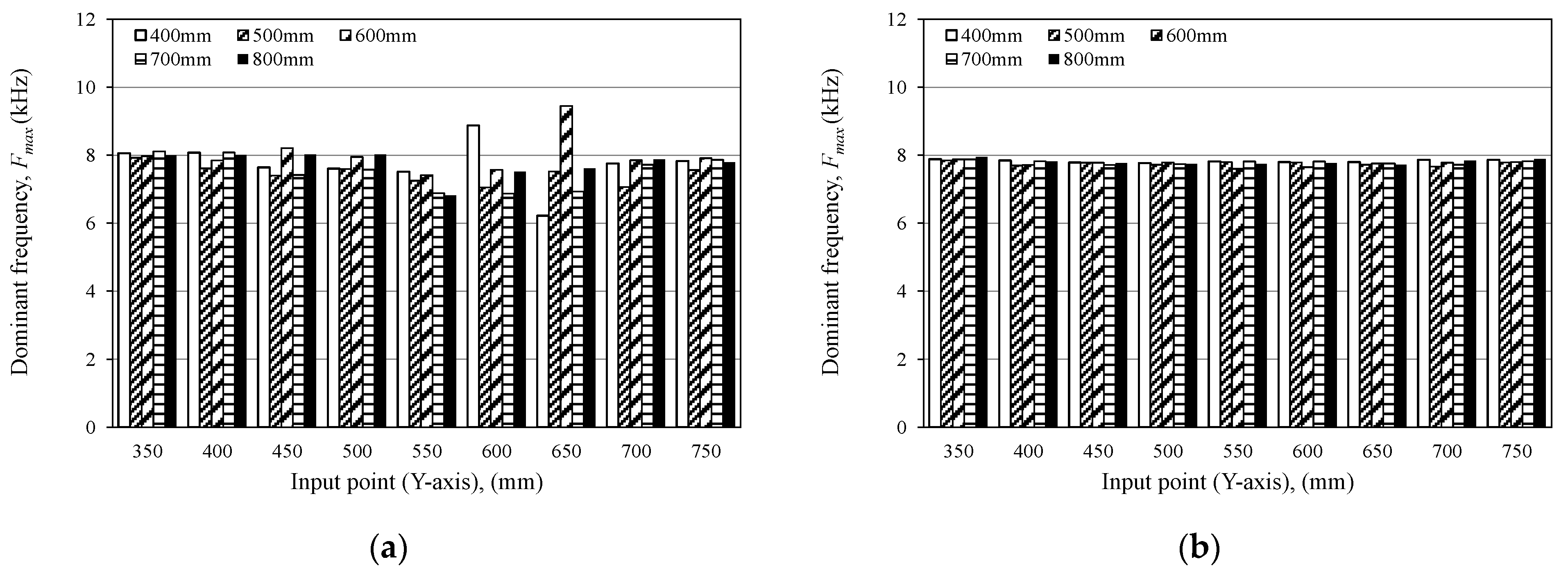
4.3. Comparison of DVA and Dominant Frequency Evaluation Results
5. Conclusions
- It is confirmed that the magnitude and distribution of Difference value depend on the number of data N. This arises from the influence of the input decays in the later part of the time history, and Difference value decreases if N is large because the influence of the input is averaged. Conversely, the Difference value is larger if the N is adequately small since the influence of the input is emphasized. On the other hand, if the number of data does not satisfy the contact time of the steel ball, the Difference value decreases because the reflected wave has no interference with the time history and the input condition and surface do not change. Further, if the number of data is not sufficient to cover the target thickness, of the defects depth and contact time, it is difficult to properly evaluate the internal defect. In addition, even if the thickness condition is complied with, the evaluation of internal defects becomes difficult because the difference value of the defects area is not characteristically increased with a small number of data. In contrast, as the number of data increases, the change of Difference value at the location of the defect is emphasized by the change of the reflected wave between the measurement surface and the defect and the change in the propagation path. From these results, it is revealed that DVA evaluates the position of the sheath correctly by choosing the appropriate N.
- The depth of the internal defect has the small influence for the magnitude of the difference value, and it is difficult to evaluate the depth of the defect of the same size from the magnitude of the difference value. However, it is confirmed that the difference value increases area if the defect is deep. This result suggests that the depth of the defect is possibly evaluated from the distribution of the difference values.
- It is confirmed that the size of the defect has a great influence of the difference value, and it is suggested that the size of the internal defect can be evaluated by difference values.
- Finally, comparing the evaluation results of the conventional method and DVA, it is found that DVA has the equivalent capability, and furthermore, it has the potential to evaluate relatively small defects that are not detected by the conventional method
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Portland Cement Association. 2016 U.S. Cement Industry Annual Yearbook; Construction Facts, Industry Trends and Domestic & International Coverage: Old Orchard Road Skokie, IL, USA, 2016. [Google Scholar]
- Omar, T.; Nehdi, M.L. Condition Assessment of Reinforced Concrete Bridges: Current Practice and Research Challenges. Infrastructures 2018, 3, 36. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.J.; Kim, A.-R.; Lee, S.-W. Artificial Neural Network-Based Automated Crack Detection and Analysis for the Inspection of Concrete Structures. Appl. Sci. 2020, 10, 8105. [Google Scholar] [CrossRef]
- Sansalone, M.; Streett, W.B. Impact-Echo: Nondestructive Testing of Concrete and Masonry; Bullbrier Press: Ithaca, NY, USA, 1997. [Google Scholar]
- Sansalone, M. Impact-Echo: The Complete Story. ACI J. 1997, 94, 777–786. [Google Scholar]
- Sansalone, M.; Carino, N.J. Impact-Echo: A Method for Flaw Detection in Concrete Using Transient Stress Waves, NBSIR 86-3452. 1986. Available from NTIS, Springfield, VA, 22161, PB #87-104444/AS. Available online: https://www.rjlg.com/materials-insights/nondestructive-evaluation-nde-of-concrete-with-impact-echo/ (accessed on 5 May 2021).
- Carino, N.J. Training: Often the Missing Link in Using NDT Methods. Constr. Build. Mater. 2013, 38, 1316–1329. [Google Scholar] [CrossRef]
- Carino, N.J. The Impact-Echo Method: An Overview1. NIST 2001, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Carino, N.J. Impact Echo: The Fundamentals. In Proceedings of the International Symposium Non-Destructive Testing in Civil Engineering (NDT-CE), Berlin, Germany, 15–17 September 2015. [Google Scholar]
- Carino, N.J.; Sansalone, M. Flaw Detection in Concrete Using the Impact-Echo Method. Bridge Eval. Repair Rehabil. 1990, 187, 101–118. [Google Scholar]
- Jaeger, B.J.; Sansalone, M.J.; Poston, R.W. Detecting Voids in Grouted Tendon Ducts of Post-Tensioned Concrete Structures Using the Impact-Echo Method. ACI J. 1996, 93, 462–473. [Google Scholar]
- Abraham, O.; Cote, P. Impact-echo thickness frequency profiles for detection of voids in tendon ducts. ACI J. 2002, 99, 239–247. [Google Scholar]
- Zou, C.; Chen, Z.; Dong, P.; Chen, C.; Cheng, Y. Experimental and Numerical Studies on Nondestructive Evaluation of Grout Quality in Tendon Ducts Using Impact-Echo Method. J. Bridge Eng. 2014, 21, 04015040. [Google Scholar] [CrossRef]
- Yoon, Y.-G.; Lee, J.-Y.; Choi, H.; Oh, T.-K. A Study on the Detection of Internal Defect Types for Duct Depth of Prestressed Concrete Structures Using Electromagnetic and Elastic Waves. Materials 2021, 14, 3931. [Google Scholar] [CrossRef]
- Ohtsu, M.; Watanabe, T. Stack Imaging of Spectral Amplitudes based on Impact-Echo for Flaw Detection. NDT E Int. 2002, 35, 189–196. [Google Scholar] [CrossRef]
- Muldoon, R.; Chalker, A.; Forde, M.C.; Ohtsu, M.; Kunisue, F. Identifying voids in plastic ducts in post-tensioning prestressed concrete members by resonant frequency of impact-echo, SIBIE and tomography. CBM 2007, 21, 527–537. [Google Scholar]
- Hashimoto, K.; Shiotani, T.; Ohtsu, M. Application of Impact-Echo Method to 3D SIBIE Procedure for Damage Detection in Concrete. Appl. Sci. 2020, 10, 2729. [Google Scholar] [CrossRef] [Green Version]
- Ma, M.; Cao, R.; Niu, C.; Zhang, H.; Liu, W. Influence of Soil Parameters on Detecting Voids behind a Tunnel Lining Using an Impact Echo Method. Appl. Sci. 2019, 9, 5403. [Google Scholar] [CrossRef] [Green Version]
- Kentaro, Y.; Tomoaki, S.; Kunio, G. Detection of internal defects of concrete structures by analyzing wave speed scattering. S F R Proc. 2012, 14. [Google Scholar]
- Shinya, U.; Oshiro, K.; Oshiki, I.; Satoshi, I.; Heung, L. A Study on Frequency Analysis Methods for Concrete Thickness Estimation by Impact Elastic-Wave Method. SCMT3 Proc. 2013, 3. [Google Scholar]
- Abraham, O.; Léonard, C.; Côte, P.; Piwakowski, B. Time Frequency Analysis of Impact-Echo Signals: Numerical Modeling and Experimental Validation. ACI J. 2000, 97, 645–657. [Google Scholar]
- Lin, Y.; Sansalone, M. Transient Response of Thick Circular and Square Bars Subjected to Transverse Elastic Impact. J. ASA 1992, 91, 885–893. [Google Scholar] [CrossRef]
- Lin, Y.; Sansalone, M. Detecting Flaws in Concrete Beams and Columns Using the Impact-Echo Method. ACI J. 1992, 89, 394–405. [Google Scholar]
- Popovics, S.J. Effect of Poisson’s Ratio on Impact-Echo Method Analysis. J. Eng. Mech. 1997, 123, 843–851. [Google Scholar] [CrossRef]
- Hsiao, C.; Cheng, C.C.; Liou, T.; Juang, Y. Detecting flaws in concrete blocks using the impact-echo method. NDT E Int. 2008, 41, 98–107. [Google Scholar] [CrossRef]
- ASTM C1383-04. Test Method for Measuring the P-Wave Speed and the Thickness of Concrete Plates Using the Impact-Echo Method; ASTM Standards: West Conshohocken, PA, USA, 2010. [Google Scholar]
- Ospitia, N.; Aggelis, D.G.; Lefever, G. Sensor Size Effect on Rayleigh Wave Velocity on Cementitious Surfaces. Sensors 2021, 21, 6483. [Google Scholar] [CrossRef] [PubMed]
- Krautkrämer, J.; Krautkrämer, H. Ultrasonic Testing of Materials, 4th ed.; Springer: New York, NY, USA, 1990; pp. 15–18. [Google Scholar]
- Toshiro, K.; Shinya, U. Theory and practice of NDT of concrete: No.3 Theory and practice of elastic wave method (ultrasonic method/impact elastic wave method). J. JCI 2013, 51, 340–347. (In Japanese) [Google Scholar]
- Goldsmith, W. Impact: The Theory and Physical Behavior of Colliding Solids; Edward Arnold Press, Ltd.: London, UK, 1965; pp. 24–50. [Google Scholar]






| Medium | ρ (kg/m3) | V (m/s) | Z (kg/s·m2) |
|---|---|---|---|
| 1: Concrete | 2400 | 4000 | 9.60 × 107 |
| 2: Air | 1.29 | 332 | 4.28 × 103 |
| Specimen_No. | Sheath Size: φS | Filling Ratio |
|---|---|---|
| Specimen_1 | 63 mm | 100% |
| Specimen_2 | 0% | |
| Specimen_3 | 33 mm | 100% |
| Specimen_4 | 0% |
| Line_No. | X (mm) | Input Point_No, (IP_No) | |||||
|---|---|---|---|---|---|---|---|
| Y (mm) | 400 | 500 | 600 | 700 | 800 | ||
| Line_01 | 350 | IP_01 | IP_02 | IP_03 | IP_04 | IP_05 | |
| Line_02 | 400 | IP_06 | IP_07 | IP_08 | IP_09 | IP_10 | |
| Line_03 | 450 | IP_11 | IP_12 | IP_13 | IP_14 | IP_15 | |
| Line_04 | 500 | IP_16 | IP_17 | IP_18 | IP_19 | IP_20 | |
| Line_05 | 550 | IP_21 | IP_22 | IP_23 | IP_24 | IP_25 | |
| Line_06 | 600 | IP_26 | IP_27 | IP_28 | IP_29 | IP_30 | |
| Line_07 | 650 | IP_31 | IP_32 | IP_33 | IP_34 | IP_35 | |
| Line_08 | 700 | IP_36 | IP_37 | IP_38 | IP_39 | IP_40 | |
| Line_09 | 750 | IP_41 | IP_42 | IP_43 | IP_44 | IP_45 | |
| Case _No | Sheath Size: φS | Depth |
|---|---|---|
| Case_1 | 63 mm | 50 mm |
| Case_2 | 63 mm | 137 mm |
| Case_3 | 33 mm | 50 mm |
| Diameter of steel ball | dS | 20 mm |
| Contact time | Tc | 0.086 ms |
| Input frequency | Finp | 11.6 kHz |
| Measurement time | t | 2.00 ms |
| Sampling time | Δt | 0.50 μs |
| Measurement data | 4000 | |
| Acceleration sensor | 100 mV/G |
| Number of Data: N | Propagation Time (μs) | Propagation Distance (mm) |
|---|---|---|
| 100 | 50 | 200 |
| 250 | 125 | 500 |
| 500 | 250 | 1000 |
| 1000 | 500 | 2000 |
| 1500 | 750 | 3000 |
| 2000 | 1000 | 4000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ikebata, K.; Kobayashi, Y.; Oda, K.; Nakamura, K. Evaluation of Unfilled Sheath in Concrete Structures Using Response Waveform in Time Domain. Appl. Sci. 2021, 11, 11402. https://doi.org/10.3390/app112311402
Ikebata K, Kobayashi Y, Oda K, Nakamura K. Evaluation of Unfilled Sheath in Concrete Structures Using Response Waveform in Time Domain. Applied Sciences. 2021; 11(23):11402. https://doi.org/10.3390/app112311402
Chicago/Turabian StyleIkebata, Kota, Yoshikazu Kobayashi, Kenichi Oda, and Katsuya Nakamura. 2021. "Evaluation of Unfilled Sheath in Concrete Structures Using Response Waveform in Time Domain" Applied Sciences 11, no. 23: 11402. https://doi.org/10.3390/app112311402
APA StyleIkebata, K., Kobayashi, Y., Oda, K., & Nakamura, K. (2021). Evaluation of Unfilled Sheath in Concrete Structures Using Response Waveform in Time Domain. Applied Sciences, 11(23), 11402. https://doi.org/10.3390/app112311402






