Fiducial Lower Confidence Limit of Reliability for a Power Distribution System

Abstract

Reliability performance, especially the lower confidence limit of reliability, plays an important role in system risk and safety assessment. A good estimator of the lower confidence limit of system reliability can help engineers to make the right decisions. Based on the lifetime of the key component in a typical satellite intelligent power distribution system, the generalized fiducial method is adopted to estimate the lower confidence limit of the system reliability in this paper. First, the generalized pivotal quantity and the lower confidence limit of reliability for the key component are derived for the lifetimes of the exponential-type and Weibull-type components. Simulations show that the sample median is more appropriate than the sample mean when the lower confidence limit of reliability is estimated. Moreover, the lower confidence limit of reliability is obtained for the typical satellite intelligent power distribution system through the pseudo-lifetime data of the metallic oxide semiconductor field effect transistor. The lower confidence limit of reliability for this power distribution system at 15 years is 0.998, which meets the factory’s reliability requirement. Finally, through the comparison, a hot standby subsystem can be substituted with a cold standby subsystem to increase the lower confidence limit of the system reliability.

1. Introduction

A power distribution system (PDS) is a power network system consisting of a variety of power distribution equipment (or components), and it carries electricity from the transmission system to individual consumers. The basic function of a PDS is to supply customers with electrical energy as reliably as possible [1]. The reliability and maintainability of a PDS have attracted some scholars’ interests. For example, the authors of [2] discussed the protection devices for the aircraft power distribution system. The authors in [3] evaluated the reliability of a PDS subjected to hurricanes. A framework for the optimal maintenance of a PDS subjected to non-stationary hurricane hazard and decay is presented in [4]. The authors of [5] reviewed the technological perspective of cyber secure smart inverters used in PDS. The authors of [6] analyzed the reliability of a 20-KV electric PDS, while those in [7] and [8] calculated the reliability of two Nigeria PDSs, one of which was aging. The authors in [9] evaluated an Indian PDS and gave some suggestions to minimize the outages which can improve reliability. The authors of [10] presented an inverse reliability evaluation where some components’ reliability parameters were unknown in a specific PDS.

In general, there is a key subsystem named the solid state power controller (SSPC) in a PDS. The SSPC is a system protection device which provides protections for the electric installations from short circuits and overloads [11]. Based on the importance of SSPC, several researchers studied the structure and applications of the SSPC. The authors of [12] summarized the advantages of an SSPC, such as high reliability, small size and accessible remote control. The authors in [13] presented an optimizing scheme for behavioral modeling of an SSPC, while those in [14] proposed some models for some special SSPCs. The authors in [15] analyzed the reliability of a kind of SSPC from an engineering standpoint, and those in [16] proposed two fault detection methods with the analysis of only the half cycle data.

Due to the characteristics of a long lifetime and high reliability, it is particularly important to analyze the reliability of the PDS and SSPC. Technically, the reliability is often defined as the probability that a system will perform its intended function under operating conditions for a specified period of time [17]. In system reliability assessment, the estimator of reliability is a major concern. The authors of [18] estimated the reliability of the multicomponent stress–strength based on a two-parameter exponentiated Weibull distribution. The authors in [19] compared different least squares methods for reliability of the Weibull distribution based on the right censored data, and those in [20] and [21] analyzed the reliability of Weibull distribution with zero-failure data and very little failure data, respectively. However, a point estimator makes little sense if the variance of the estimator is too high. Consequently, it is necessary to give the lower confidence limit (LCL) of reliability [22]. How to get the LCL of system reliability through the lifetimes of components is an important issue. Many scholars have conducted a lot of research on this. An effective reliability confidence bound for a multi-state system with binary-capacitated components is suggested in [23]. This is only applied for a series or parallel system. In addition, the authors of [24] considered the LCL of reliability under a nonparametric assumption, but the parametric method is often more accurate than the nonparametric method when the distribution type is known. The authors in [25] provided the maximum likelihood estimate (MLE) and a more accurate lower confidence limit for the SoS reliability, but the MLE method is more appropriate for a large sample size. Based on the small sample size, the authors of [26] applied the WCF approach to analyze the reliability of a special complicated system based on accelerated degradation data, but the WCF method is complicated for mathematical formula derivation. Based on records data, the authors of [27] calculated the interval estimation of quantiles and reliability in a two-parameter exponential distribution. In practice, some electronic components, such as the key components of a PDS, have a long lifetime and high reliability [28,29]. The sample size of these lifetime data is usually very small. To overcome the shortcoming of a large sample, some references adopted the Bayesian method to estimate the LCL of reliability. For example, the authors of [30] and [31] used the Bayesian method to study the reliability for binomial systems, while those in [32] used Bayesian networks to present developments for traditional series and parallel systems. The authors in [33] and [34] applied the Bayesian approach to analyze the reliability of the degradation data. Although the Bayesian approach is suitable for a small sample of lifetime data, the selection of the prior distribution is difficult.

To avoid the difficulty of choosing a proper prior distribution, the fiducial method is adopted to estimate the LCL of reliability for a PDS in this paper. The fiducial method considers the parameter as a random variable whose distribution is decided by the observation instead of the prior distribution. The authors of [35] developed the fiducial method by defining a functional model, and those in [36] proved that the LCL derived by the fiducial method is the same as the LCL obtained by the traditional method under some conditions. Recently, some optimal inferences [37] and generalizations of the fiducial method [38] have been developed based on [38,39,40], giving the generalized fiducial inference for generalized exponential and Lomax distribution.

It can be seen that the generalized fiducial method is an effective method to estimate the reliability of a long-life product. Based on the high reliability of the PDS, this paper estimates the LCLs of the reliability of the PDS by using the generalized fiducial method. For a typical satellite intelligent PDS, the lifetime distribution of the key components in the satellite intelligent PDS are assumed to follow an exponential distribution and Weibull distribution according to the experience of the engineers. In this situation, two algorithm procedures are presented to estimate the LCL of the reliability for an exponential-type component and a Weibull-type component. Then, the LCLs of reliability for the satellite intelligent PDS are established by the relationship between the key components and the system. Compared with the Bayesian method, the generalized fiducial method of this paper is more flexible to avoid the selection of the prior distribution.

2. Materials and Methods

2.1. Power Distribution System Reliability Model

In the design of the satellite intelligent PDS, the Beijing Satellites Casting Factory divided the PDS into three subsystems according to different functions of the components. These three subsystems were the direct current to direct current power supply (DC/DC), solid state power controller (SSPC) and telemetry and telecontrol unit (TM/TC). The DC/DC is responsible for converting the bus bar voltage into the voltage which is required by the analog circuit and digital circuit in the system. The SSPC can play a protective role, including limiting the current protection and short circuit protection and collecting current voltage. The TM/TC can not only save current voltage data but also check the various SSPCs and monitor the historical data.

In order to improve the reliability of the PDS, standby systems are often adopted in system design. There are two traditional types of standby redundancy: hot standby and cold standby. In hot standby redundancy, components which are in standby mode operate in synchrony with the main unit and are ready to take over at any time, while in cold standby redundancy, components in standby mode are unpowered and thus do not operate until needed to replace a faulty main unit [41,42]. In the satellite intelligent PDS, the hot standby systems are used for the DC/DC and SSPC, and the cold standby systems are used for the TM/TC. These three subsystems are in arranged in a series way. The reliability block diagram of this PDS is shown in Figure 1.

Here, the SSPC is composed of six components, which are a metallic oxide semiconductor field effect transistor (MOSFET), short circuit protector, voltage detector, current detector, sense resistor and drive circuit. These components are connected in a series structure. The reliability block diagram of the SSPC is shown in Figure 2.

In this paper, we focus on the reliability estimation for the SSPC and PDS. The SSPC is a key subsystem in a PDS, and thus the reliability of the SSPC plays an important role in reliability assessment of the PDS. In the SSPC, the MOSFET is generally the most critical component, which is a switching device [43]. The failure of the MOSFET may lead to a short circuit with a significant increase in temperature. This failure is not acceptable for the SSPC or PDS. Therefore, the reliability of the SSPC needs to be estimated by analyzing the lifetime of the MOSFET, which can further evaluate the reliability of a PDS. Due to the different lifetime distributions for different components in the typical satellite intelligent PDS, some assumptions are given from the experience of engineers as follows for convenience:

Assumption 1.

A PDS has independent components, and the switching mechanism from the main subsystem to the standby subsystem is considered to be completely reliable.

Assumption 2.

In an SSPC, the lifetime of the MOSFET follows a Weibull distribution, and the lifetimes of the others follow exponential distributions with different failure rates.

Assumption 3.

The failure rates of the voltage detector, current detector, sense resistor and drive circuit are known from experience, but the short circuit protector’s is unknown.

Assumption 4.

The lifetimes of the DC/DC and TM/TC follow exponential distributions with known failure rates.

Based on these assumptions, in the following subsections, the fiducial method was adopted to derive the LCLs of reliability for a single component: an SSPC and a PDS.

2.2. Fiducial LCL of Reliability for an Exponential-Type Component

In this subsection, we discuss the LCL of reliability based on a typical component whose lifetime follows the exponential distribution commonly used in a PDS.

Except for the MOSFET, the lifetimes of the other components in an SSPC were assumed to be exponentially distributed. Thus, we derived the LCL of reliability for an exponential-type component first.

Let T be a random variable which follows an exponential distribution with an unknown parameter λ. The cumulative distribution function of T is

$$F(t)=1-e^{-\lambda t},\hspace{1em}t>0.$$

(1)

Suppose T₁, T₂, ⋯, T_n is a random sample from the population T, where n is the sample size. Then, the total test time T_sum = T₁ + T₂ + ⋯ + T_n follows a Gamma distribution with parameters n and λ. Therefore, 2λT_sum follows an χ² distribution with 2n degrees of freedom. Then, parameter λ can be represented as

$$\lambda =\frac{E}{2T_{sum}},\hspace{1em}E~{\chi }^2(2n),$$

(2)

where E is the pivotal quantity which follows a completely known distribution.

We can derive the estimator and the confidence interval (CI) of parameter λ by solving the expectation and the quantile of χ² distribution, respectively, or by generating a random number. The CI for λ with the confidence level is given by

$$\left[{\chi }_{\alpha /2}^2(2n)/2T_{sum},{\chi }_{1-\alpha /2}^2(2n)/2T_{sum}\right],$$

(3)

where ${\chi }_{\alpha /2}^2(2n)$ is the α/2 quantile of a Chi-square distribution with 2n degrees of freedom. Equation (3) is the same as the result of the traditional method.

However, the quantity of interest is the reliability, which is a function of parameter λ. The reliability of the component whose lifetime follows an exponential distribution at time t can be expressed as

$$R(t)=\exp \left\{-\frac{t}{2T_{sum}}E\right\},\hspace{1em}E~{\chi }^2(2n).$$

(4)

Then, the LCL of reliability with the confidence level 1 − α is

$$R_L(t)=\exp \left\{-\frac{t}{2T_{sum}}{\chi }_{1-\alpha }^2(2n)\right\}.$$

(5)

The fiducial algorithm for the CI of parameter λ and the LCL of reliability based on an exponential distribution is shown in Algorithm 1.

Algorithm 1. Fiducial algorithm procedure for exponential distribution.

Input: x: the lifetime of the exponential-type component;    1-α: the confidence level;    t: time;    M: the sample size of simulated pivotal quantity;    rep: the number of simulation trials. Output: The CI of parameter λ and the LCL of reliability. for i← 1 to rep do    for j ← 1 to M do     λij ← a random number follows χ2(2n), in which n is the sample size of x.     Rij (t) ← exp{−λijt}.    end    Sort (λi1, λi2, …, λiM) from small to large: (λi (1), λi (2), …, λi (M)).    Sort (Ri1 (t), Ri2 (t), …, RiM (t)) from small to large: (Ri (1) (t), Ri (2) (t), …, Ri (M)(t)).    The ith LCL of reliability is RLi (t) ←Ri (M(1-α)) (t).    The ith CI of parameter λ is λCIi ← (λi (Mα/2), λi (M(1-α/2))). end The LCL of reliability is RL (t) ← mean of (RL1(t), RL2(t), …, RLrep(t)). The CI of parameter λ is (λL, λU) ← mean of (λCI1, λCI2, …, λCI,rep).

Next, we use a simulated example to show how to derive the LCL of reliability for an exponential-type component.

Example 1.

In the satellite intelligent PDS, the failure rate of the voltage detector, current detector and sense resistor are approximately 0.2 × 10⁻⁹, 0.5 × 10⁻⁹ and 0.4 × 10⁻⁹, respectively. The simulated lifetime data are listed in

Table 1. Simulated lifetime datasets of the voltage detector, current detector and sense resistor.

Components	Datasets (h)
Voltage Detector	749,318,825, 249,122,143, 3,041,561,966, 1,290,709,269, 9,207,672,141, 346,452,730, 898,416,864, 1,921,665,561, 832,302,119, 22,978,273,342
Current Detector	2,976,355,068, 1,614,412,014, 1,596,199,429, 4,385,031,242, 343,767,602, 1,394,727,033, 1,699,963,564, 1,395,646,527, 4,092,186,674, 303,092,873
Sense Resistor	3,249,590,569, 2,144,799,183, 4,865,614,194, 1,061,070,057, 2,052,784,459, 946,101,390, 5,840,861,755, 3,188,572,801, 955,939,901, 260,937,877

. In practice, these data are usually obtained by an accelerated lifetime test.

For the voltage detector, current detector and sense resistor, the simulated pivotal quantity, whose sample size was 2000, was generated by Monte Carlo simulation. Simulations were conducted in statistical software R. Through Equations (2) and (3), the estimators and the CIs of parameter λ were obtained after generating 2000 random numbers which followed χ² distribution with 20 degrees of freedom. However, the estimate changed if another 2000 Chi-square random numbers were generated. To avoid this change, the estimates were averaged by 1000 simulation trials. The results are listed in

Table 2. Estimators and CIs of the parameters for the exponential-type components.

Components	Estimators	Confidence Intervals
Voltage Detector	$0.241\hspace{0.33em}\times \hspace{0.33em}{10}^{-9}$	$(0.215\hspace{0.33em}\times \hspace{0.33em}{10}^{-9},0.252\hspace{0.33em}\times \hspace{0.33em}{10}^{-9})$
Current Detector	$0.505\hspace{0.33em}\times \hspace{0.33em}{10}^{-9}$	$(0.450\hspace{0.33em}\times \hspace{0.33em}{10}^{-9},0.529\hspace{0.33em}\times \hspace{0.33em}{10}^{-9})$
Sense Resistor	$0.407\hspace{0.33em}\times \hspace{0.33em}{10}^{-9}$	$(0.362\hspace{0.33em}\times \hspace{0.33em}{10}^{-9},0.426\hspace{0.33em}\times \hspace{0.33em}{10}^{-9})$

.

In Table 2, the estimators of the parameters for the voltage detector, current detector and sense resistor lifetime distributions were 0.241 × 10⁻⁹, 0.505 × 10⁻⁹, and 0.407 × 10⁻⁹, respectively. It is shown that the fiducial estimators were close to the true value. In the same way, with Equations (4) and (5), the estimators and the LCLs of reliability at t₀ = 87,600 h (10 years) with a confidence level 0.8 are listed in

Table 3. Estimators and LCLs of reliability for the exponential-type components (t₀ = 87,600 h).

Components	Estimators	Lower Confidence Limits
Voltage Detector	0.9999789	0.9999736
Current Detector	0.9999558	0.9999446
Sense Resistor	0.9999644	0.9999553

.

From Table 3, we find that the estimator and the LCL of reliability for the voltage detector were 0.9999789 and 0.9999736 at 10 years, respectively. These two numbers were both very close to one since the failure rate was very small. In fact, if t₀ is taken as 8.76 × 10⁷ h, the reliability is approximately 0.97, which is still very high. The analyses of the current detector and sense resistor were similar. We could treat them as “non-failed” components.

2.3. Fiducial LCL of Reliability for a Weibull-Type Component

In this subsection, we use the fiducial method to derive the LCL of reliability for a Weibull-type component.

Let T₁, T₂, ⋯, T_n be a random sample from the Weibull distribution. The cumulative distribution function of the Weibull distribution is

$$F_T(t)=1-\exp \left\{-{\left(t/\eta \right)}^m\right\},\hspace{1em}t>0,$$

(6)

where η > 0 and m > 0 are called the scale parameter and shape parameter, respectively. It is difficult to derive the estimators of η and m directly.

In general, T_j is transformed to X_j by X_j = ln T_j, and then X_j follows an extreme value distribution with σ = 1/m and μ = ln η, j = 1, 2, ⋯, n. The common cumulative distribution function of X_j, j = 1, 2, ⋯, n is

$$F_{X_j}(x_j)=1-\exp \left\{-e^{\frac{x_j-\mu }{\sigma }}\right\}.$$

(7)

Let the following be true:

$$W_j=\frac{X_j-\mu }{\sigma }=m\left(\ln T_j-\ln \eta \right),\hspace{1em}j=1,2,\cdots ,n.$$

(8)

Then, W_j follows a common standard extreme value distribution which is completely known, and the distribution of their function is also completely known. Thus, we treat the function of W_j as the pivotal quantity.

Denote the following:

$$\overline{X}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{X}_i},\hspace{1em}{S}^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n{(X_i-\overline{X})}^2},\overline{W}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{W}_i},\hspace{1em}{V}^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n{(W_i-\overline{W})}^2}.$$

(9)

These statistics have relations as follows:

$$\mu =\overline{X}-\frac{\overline{W}}{V}S,\sigma =\frac{S}{V},\eta =\exp \left\{\overline{X}-\frac{\overline{W}}{V}S\right\},m=\frac{V}{S}.$$

(10)

Then, parameters η and m can be expressed as

$$\eta =\exp \left\{\overline{X}-\frac{E_1}{E_2}S\right\},\hspace{1em}m=\frac{E_2}{S},$$

(11)

where E₁ and E₂ are pivotal quantities which have the same distributions as $\overline{W}$ and V, respectively. However, it is difficult to derive the explicit formula of the probability density for these two distributions. Instead, the random numbers which follow a standard extreme value distribution are easily generated by Monte Carlo simulation. Then, we treated the sample mean and the sample standard deviation as E₁ and E₂. The simulated values of parameters η and m were derived by Equation (11). By repeating this sampling method, we could get many pairs of η and m. By averaging the sample, the estimators of the parameters were derived. The CIs were obtained by finding the sample quantiles of the simulated parameters.

Here, the quantity of interest is the reliability, which can be expressed as

$$R(t)=\exp \left\{-{\left(t/\eta \right)}^m\right\}=\exp \left\{-{\left(t\exp \left\{\frac{E_1}{E_2}S-\overline{X}\right\}\right)}^{\frac{E_2}{S}}\right\}.$$

(12)

Then, the estimator and the LCL of reliability with a confidence level could be derived.

The fiducial algorithm for the CIs of parameters η and m and the LCL of reliability based on a Weibull distribution is shown in Algorithm 2.

Algorithm 2. Fiducial algorithm procedure for Weibull distribution.

Input: tw: the lifetime of the Weibull-type component;    1-α: the confidence level;    t: time;    M: the sample size of simulated pivotal quantity;    rep: the number of simulation trials. Output: The CIs of parameters η and m and the LCL of reliability. n ← sample size of tw. x ←logarithm of tw. xbar ← mean of x. s← standard deviation of x. for i ← 1 to rep do    for j← 1 to M do     for k ← 1 to n do      wijk ← a random number which follows standard extreme value distribution.     end     wbarij ← mean of (wij1, wij2, …, wijn).     vij ← standard deviation of (wij1, wij2, …, wijn).     ηij ← exp(xbar − wbarij/vij*s).     mij ← vij/s.     R ij (t) ← exp(−(tij/η)mij)    end    Sort (ηi1, ηi2, …, ηiM) from small to large: (ηi (1), ηi (2), …, ηi (M)).    Sort (mi1, mi2, …, miM) from small to large: (mi (1), mi (2), …, mi (M)).    Sort (Ri1 (t), Ri2 (t),…, RiM (t)) from small to large: (Ri (1) (t), Ri (2) (t),…, Ri (M)(t)).    The ith LCL of reliability is RLi (t) ←Ri (M(1-α))(t).    The ith CI of parameter η is ηCIi← (ηi (Mα/2),ηi (M(1-α/2))).    The ith CI of parameter m is mCIi← (mi (Mα/2),mi (M(1-α/2))). end The LCL of reliability is RL (t) ← mean of (RL1(t), RL2(t),…, RLrep(t)). The CI of parameter η is (ηL,ηU) ← mean of (ηCI1,ηCI2,…, ηCI,rep). The CI of parameter m is (mL,mU) ←mean of (mCI1,mCI2,…, mCI,rep).

Next, we also used a simulated example to show how to derive the LCL of reliability for a Weibull-type component.

Example 2.

Consider a MOSFET in an SSPC whose lifetime is assumed to be Weibull-distributed with the scale parameter η = 950,000 and the shape parameter m = 5. The simulated and logarithmic transformed data are listed in

Table 4. Simulated lifetime dataset of the MOSFET.

MOSFET	Datasets (h)
Original Data	1,168,880.9, 1,048,819.6, 1,094,062.7, 995,454.8, 951,788.8, 923,084.9,427,006.4, 812,771.7, 619,423.7, 862,760.0
Logarithmic Transformed Data	13.97156, 13.86318, 13.90541, 13.81095, 13.76610, 13.73548, 12.96455, 13.60821, 13.33654, 13.66789

.

The simulated pivotal dataset, whose sample size was 2000, was generated by Monte Carlo simulation. The estimates were averaged by 1000 simulation trials. The estimators and CIs of the parameters are shown in Figure 3.

From Figure 3, the estimators of η and m were 990,335.1 and 4.04566, respectively. It is shown that the fiducial estimators of the parameters were close to the true value. The estimator and the LCL of reliability at t₀ = 131,400 h (15 years) with a confidence level of 0.8 are shown in Figure 4.

From Figure 4, we found that the estimator and the LCL of reliability at 15 years were 0.9995892 and 0.9975223, respectively. Here, we used the median to estimate the reliability instead of the mean. In fact, the LCL was sometimes larger than the mean, because the reliability was close to 1 at 15 years. In the Monte Carlo simulations, several simulated values may have been much smaller than the others, and these small values could be treated as the outliers. The outliers made the mean smaller than the LCL. In this case, the median was better than the mean. In other words, the sample median was more robust than the sample mean. Therefore, we used the sample median and the sample mean to estimate the reliability in the subsequent analysis.

2.4. LCL Analysis of Reliability for a Typical PDS

In Section 2.2 and Section 2.3, the pivotal quantities were derived for the lifetime of an exponential-type component and a Weibull-type component. In this subsection, we analyze the LCL of reliability for a typical satellite intelligent PDS. The structure of this PDS is shown in Figure 1. The SSPC is a key subsystem in this PDS. Thus, we analyzed the LCL of reliability for the SSPC first.

The lifetime of the MOSFET was assumed to be Weibull-distributed with unknown parameters η and m, and the lifetime of the short circuit protector was assumed to be exponentially distributed with an unknown failure rate λ_S2. The lifetimes of the voltage detector, current detector, sense resistor and drive circuit in the SSPC were assumed to be exponentially distributed with known failure rates λ_S3, λ_S4, λ_S5 and λ_S6, respectively.

Let R_S(t) be the reliability of the SSPC at time t. R_S1(t), R_S2(t), R_S3(t), R_S4(t), R_S5(t) and R_S6(t) represent the reliability of the MOSFET, short circuit protector, voltage detector, current detector, sense resistor and drive circuit, respectively. Thus, R_S(t) can be expressed as follows:

$$\begin{array}{c}{R}_S(t)=R_{S1}(t)R_{S2}(t)R_{S3}(t)R_{S4}(t)R_{S5}(t)R_{S6}(t)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\exp \left\{-{\left(t/\eta \right)}^m-{\lambda }_{S2}t-{\lambda }_{S3}t-{\lambda }_{S4}t-{\lambda }_{S5}t-{\lambda }_{S6}t\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\exp \left\{-{\left(t\exp \left\{\frac{E_1}{E_2}S-\overline{X}\right\}\right)}^{\frac{E_2}{S}}-\frac{t}{2T}E-{\displaystyle \sum _{i=3}^6{\lambda }_{Si}}t\right\},\end{array}$$

(13)

where $\overline{X}$ and S are the logarithm mean and the logarithm standard deviation of the sample lifetime for the MOSFET, respectively. E, E₁ and E₂ are independent random variables. E follows an χ² distribution with 2n₂ (n₂ is the sample size of the short circuit protector) degrees of freedom. E₁ and E₂ have the same distribution as the sample mean and standard deviation of W₁, ⋯, W_n1 (W₁, ⋯, W_n1 follow the standard extreme value distribution, and n₁ is the sample size of the MOSFET). By simulating χ² random numbers and standard extreme value random numbers, the simulations of the pivotal quantities E, E₁ and E₂ were derived. Then, the simulated R_S(t) was computed by Equation (13). The estimator and the LCL of R_S(t) for a single SSPC were taken as the sample mean (or sample median) and the sample quantile of the simulations.

In order to improve the reliability of an SSPC, a standby system is usually adopted, especially a hot standby system, which is in parallel with the main subsystem. The main subsystem and the standby subsystem were independent and identically distributed. The structure of the SSPC is shown in Figure 5.

Similar to Equation (13), let R_SS(t) represent the reliability of the SSPC subsystem, which is shown in Figure 5. R_SS(t) is a function of E, E₁ and E₂:

$$\begin{array}{l}{R}_{SS}(t)=1-{\left[1-R_S(t)\right]}^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=1-{\left[1-\exp \left\{-{\left(t\exp \left\{\frac{E_1}{E_2}S-\overline{X}\right\}\right)}^{\frac{E_2}{S}}-\frac{t}{2T}E-{\displaystyle \sum _{i=3}^6{\lambda }_{Si}}t\right\}\right]}^2.\end{array}$$

(14)

Then, we analyzed the LCL of reliability for a satellite intelligent PDS, which is shown in Figure 1. The cold standby subsystem was adopted for the TM/TC, whose lifetime was assumed to be exponentially distributed with a failure rate λ_T = 338.58 × 10⁻⁹. This constant could be used directly when the reliability was calculated. Then the reliability of the TM/TC subsystem with one cold standby subsystem at time t can be expressed as

$$R_{TT}(t)=e^{-{\lambda }_T{t}_0}(1+{\lambda }_{T}t).$$

(15)

For the DC/DC, a hot standby system was adopted. The lifetime of the DC/DC was assumed to follow an exponential distribution with a failure rate λ_D = 96.3 × 10⁻⁹. The reliability of this subsystem with a hot standby subsystem at time t is

$$R_{DD}(t)=1-{\left(1-e^{-{\lambda }_{D}t}\right)}^2.$$

(16)

In general, there are a DC/DC, TM/TC and at least one SSPC in an intelligent PDS. First, one SSPC was considered for simplicity. Therefore, the reliability of the PDS with one SSPC subsystem at time t is

$$\begin{array}{l}R(t)=R_{DD}(t)R_{TT}(t)R_{SS}(t)\\ =\left[1-{\left(1-e^{-{\lambda }_{D}t}\right)}^2\right]e^{-{\lambda }_{T}t}(1+{\lambda }_{T}t)\\ \cdot \left\{1-{\left[1-\exp \left\{-{\left(t\exp \left\{\frac{E_1}{E_2}S-\overline{X}\right\}\right)}^{\frac{E_2}{S}}-\frac{t}{2T}E-{\displaystyle \sum _{i=3}^6{\lambda }_{Si}}t\right\}\right]}^2\right\}.\end{array}$$

(17)

The reliability of the entire PDS with N SSPC subsystems at time t is

$$\begin{array}{l}{R}_N(t)=R_{DD}(t)R_{TT}(t){\left[R_{SS}(t)\right]}^N\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left[1-{\left(1-e^{-{\lambda }_{D}t}\right)}^2\right]e^{-{\lambda }_{T}t}(1+{\lambda }_{T}t)\\ \hspace{1em} \cdot {\left\{1-{\left[1-\exp \left\{-{\left(t\exp \left\{\frac{E_1}{E_2}S-\overline{X}\right\}\right)}^{\frac{E_2}{S}}-\frac{t}{2T}E-{\displaystyle \sum _{i=3}^6{\lambda }_{Si}}t\right\}\right]}^2\right\}}^N.\end{array}$$

(18)

In this subsection, the LCLs of reliability for the SSPC and PDS were formulized. The detailed calculation process is given in the next section.

3. Results

This section uses the datasets of the MOSFET and short circuit protector, which are the key components in a typical satellite intelligent PDS made by the Beijing Satellites Casting Factory, to illustrate the proposed method. The lifetimes of the MOSFET came from the accelerated lifetime test, and the lifetimes of the short circuit protector came from the simulated data. The datasets of the MOSFET and short circuit protector are shown in

Table 5. Datasets of the MOSFET and short circuit protector.

Components	Datasets (h)
MOSFET	913,440.6, 919,580.9, 415,447.5, 754,872.8, 592,204.5, 1,101,658.4, 993,999.6, 1,006,450.1, 570,526.9, 993,583.7
Short Circuit Protector	5,871,090,193, 5,989,641,035, 1,108,022,425, 182,198,277, 191,327,415, 1,037,844,580, 23,220,248,016, 2,069,706,535

. The failure rates of the voltage detector, current detector, sense resistor and drive circuit were 0.2 × 10⁻⁹, 0.5 × 10⁻⁹, 0.4 × 10⁻⁹ and 0.6 × 10⁻⁹, respectively, which were known from experience.

From Equation (13), the simulated reliability with 2000 repetitions was obtained. The estimates were averaged by 1000 simulation trials. The estimator of reliability at 131,400 h (15 years) was taken as the sample mean or the sample median of simulations. Then, we ranked the reliability values in order from small to large. The LCL of reliability at 15 years was the reliability of the ordered simulations. The results are shown in

Table 6. Estimators and LCL of reliability for the SSPC (t₀ = 131,400 h).

Reliability	Estimator (Mean)	Estimator (Median)	Lower Confidence Limit
$R(t_0)$	0.9960092	0.9989452	0.9952635

.

From Table 6, we found that the mean of simulated reliability was 0.9960092, which was close to the LCL (0.9952635). Therefore, it was more appropriate to take the median (0.9989452) as the estimator of reliability. It is illustrated that the LCL of reliability at 15 years with a confidence level of 0.8 was 0.9952635.

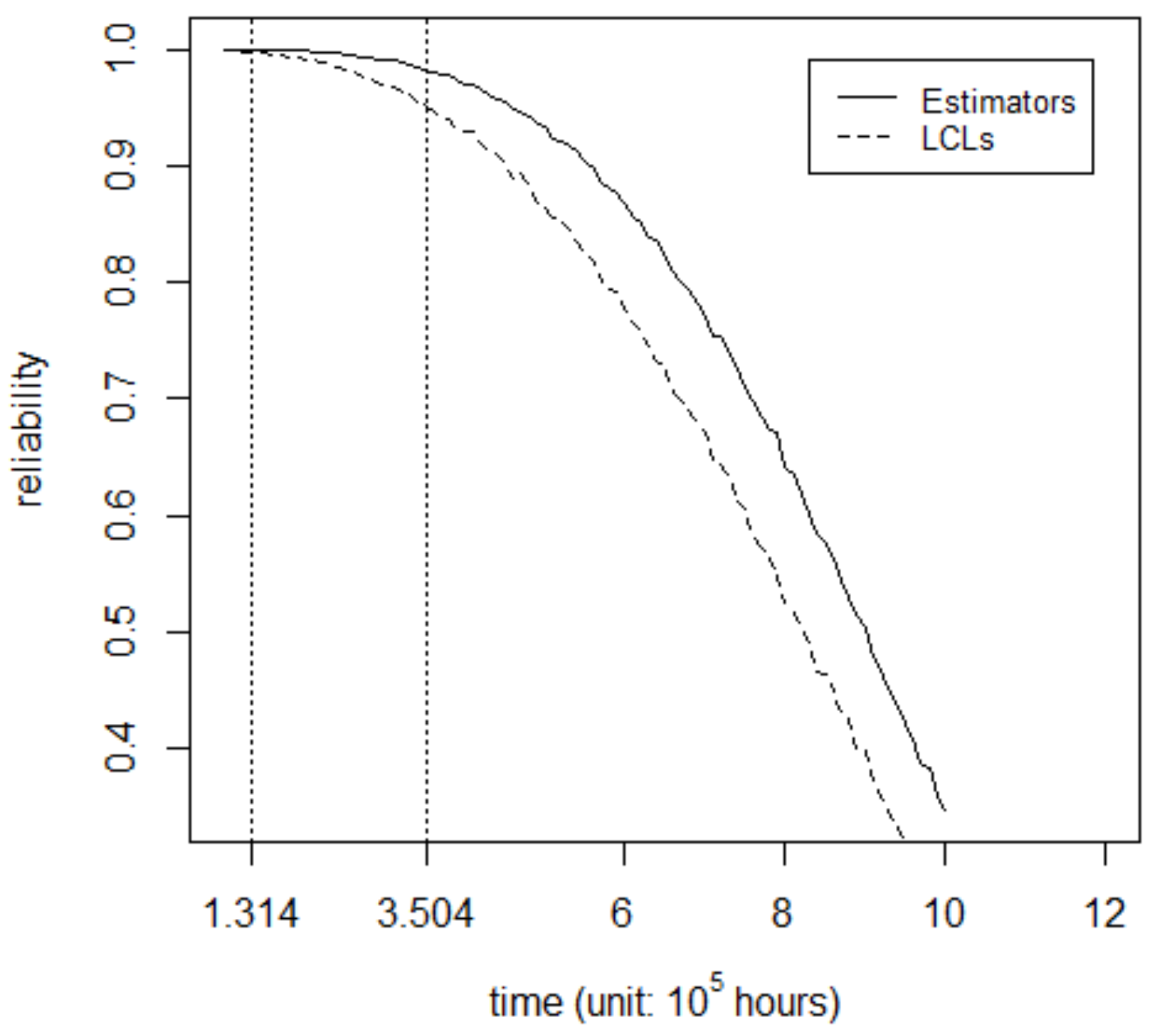
Figure 6 gives a plot of the estimator and the LCL of reliability for the SSPC. The real line represents the estimator of reliability for the SSPC. We took the median of the simulated sample as the estimator instead of the mean. The dashed line represents the LCL of reliability for the SSPC.

From Figure 6, we can see the rate of decline was slow when t ranged from 131,400 h (15 years) to 350,400 h (40 years). The LCLs of reliability for the SSPC at 15 years and 40 years with a confidence level of 0.8 were 0.995 and 0.930, respectively. Both the estimator and the LCL of reliability for the SSPC were very high, which could meet the factory’s requirement for reliability.

Next, the reliability for the SSPC with hot standby equipment was calculated. The structure is shown in Figure 5. The estimators and the LCL of reliability for the SSPC with hot standby equipment could also be obtained by Monte Carlo simulation from Equation (14). The results are shown in

Table 7. Estimators and LCL of reliability for an SSPC with hot standby equipment (t₀ = 131,400 h).

Reliability	Estimator (Mean)	Estimator (Median)	Lower Confidence Limit
$R(t_0)$	0.9998993	0.9999989	0.9999775

.

Table 7 illustrates that the estimator and the LCL of reliability at 15 years were 0.9999989 and 0.9999775, respectively. When comparing Table 6 with Table 7, it is shown that the reliability and the LCL were improved when the hot standby systems were adopted. In fact, if the cold or warm standby systems were adopted, the reliability was also improved similarly.

Next, the reliability of the whole PDS with at least one SSPC was calculated. The estimators and the LCL of the whole PDS reliability with one SSPC subsystem were obtained by Equation (17) and are shown in

Table 8. Estimators and LCL of reliability for the PDS with one SSPC (t₀ = 131,400 h).

Reliability	Estimator (Mean)	Estimator (Median)	Lower Confidence Limit
$R(t_0)$	0.9987806	0.9988801	0.9988588

.

From Table 8, it is shown that the estimators and the LCL of reliability were 0.9988801 and 0.9988588, respectively. In the same way, we could calculate the LCL of reliability for a PDS with more than one SSPC. For example,

Table 9. Estimators and LCL of reliability for a PDS with 20 SSPCs (t₀ = 131,400 h).

Reliability	Estimator (Mean)	Estimator (Median)	Lower Confidence Limit
$R(t_0)$	0.9970009	0.998859	0.9984319

calculates the estimators and the LCL of PDS reliability at 15 years with 20 SSPCs.

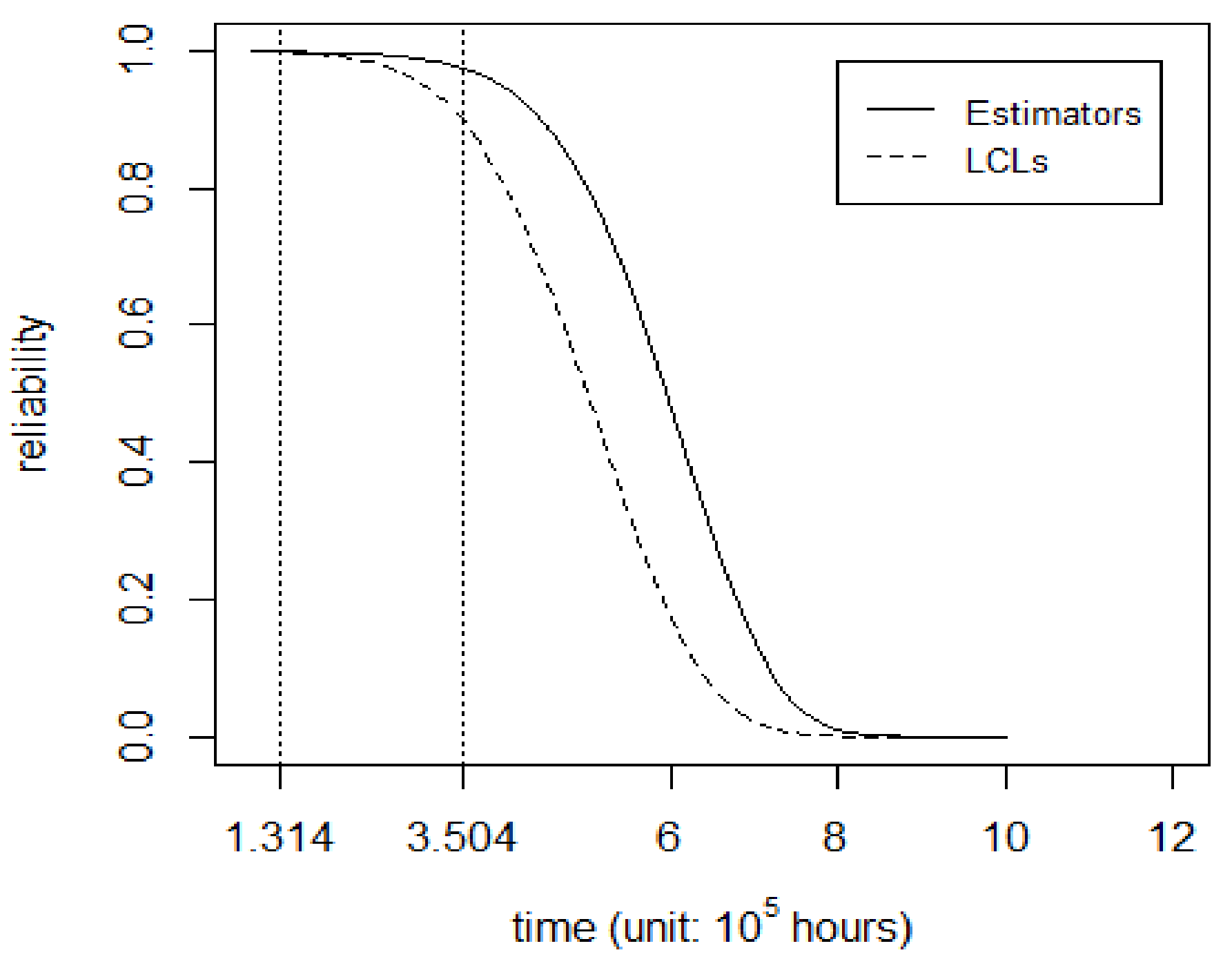
Figure 7 gives two curves of the estimator and the LCL of reliability for the PDS. The real line and dashed line represent the estimator and the LCL of reliability for the PDS, respectively.

As shown in Figure 7, the rate of decline was slow when t ranged from 131,400 h (15 years) to 350,400 h (40 years). The LCL of reliability for the PDS at 15 years and 40 years with a confidence level of 0.8 were 0.998 and 0.899, respectively. Compared with Figure 6, the decline rate of reliability for the PDS was faster than that for the SSPC when t ranged from 350,400 h (40 years) to 788,400 h (90 years). The reason for this was that there were 20 SSPCs in the PDS. When the reliability of the SSPC was reduced, the reliability of the PDS decreased faster.

According to the factory’s requirement, the LCL of the reliability for this typical satellite intelligent PDS at 15 years should be greater than 0.980 with a confidence level of 0.8. From Table 9, the LCL of reliability at 15 years was 0.998, which was greater than 0.980 (i.e., the reliability met the factory’s requirement).

4. Discussion

Cold standby systems, hot standby systems and k-out-of-n systems are the most commonly used redundancy systems in reliability. Specifically, the hot standby system is a particular case of a k-out-of-n system where k = 1 and n = 2. For comparison, the authors of [25] derived the LCL of reliability for a k-out-of-n system. In this paper, a reliability model was developed for a typical satellite intelligent PDS, which used hot standby systems (one-out-of-two systems) in the DC/DC and SSPC subsystems. Experienced engineers recommend using a cold standby TM/TC as a redundancy of the main TM/TC. According to the results obtained in Section 3, the LCL of reliability for this typical satellite intelligent PDS was 0.998. When the TM/TC cold standby subsystem was replaced by a hot standby subsystem, the reliability of the TM/TC subsystem could be calculated from Equation (16) instead of Equation (15) such that

$$R_{TT}(t)=1-{\left(1-e^{-{\lambda }_{T}t}\right)}^2.$$

(19)

The reliability of the entire satellite intelligent PDS with 20 SSPC subsystems at time t was

$$\begin{array}{l}{R}_{20}(t)=R_{DD}(t)R_{TT}(t){\left[R_{SS}(t)\right]}^{20}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left[1-{\left(1-e^{-{\lambda }_{D}t}\right)}^2\right]\left[1-{\left(1-e^{-{\lambda }_{T}t}\right)}^2\right]\\ \hspace{1em}\hspace{1em} \cdot {\left\{1-{\left[1-\exp \left\{-{\left(t\exp \left\{\frac{E_1}{E_2}S-\overline{X}\right\}\right)}^{\frac{E_2}{S}}-\frac{t}{2T}E-{\displaystyle \sum _{i=3}^6{\lambda }_{Si}}t\right\}\right]}^2\right\}}^{20}.\end{array}$$

(20)

By using the generalized fiducial method, the LCL of the reliability would fall to 0.997, which was less than 0.998.

It is widely known that the reliability of a cold standby system is always higher than that of a hot standby system. After calculation and analysis, the same conclusion applies the LCL of the reliability. It is suggested that engineers can substitute a cold standby subsystem for a hot standby subsystem (one-out-of-two system), which can increase the LCL of the reliability for the whole system.

5. Conclusions

In this paper, the LCL of the reliability for a typical satellite intelligent PDS was obtained by using the generalized fiducial method. First, the LCL of the reliability for an exponential-type component and a Weibull-type component were provided by two algorithm procedures. The simulation results showed that the sample median was more appropriate than the sample mean when the LCL of the reliability was estimated. In addition, the LCL of the reliability for a typical satellite intelligent PDS was formulated based on the structure of the complicated system. The results showed that the LCL of the reliability for the typical satellite intelligent PDS at 15 years was 0.998, which was greater than 0.980. The obtained reliability of the system met the factory’s requirement. Finally, the LCLs of the reliability for a cold standby system and a hot standby system were calculated. Analysis showed that a cold standby system outperformed a hot standby system when we were interested in the LCL of the system reliability. The research results of this paper will provide a theoretical basis to make the right decisions for reliability engineers.

6. Future Works

Some questions warrant further study. The first question is whether the generalized fiducial method of the reliability can be used not only for the reliability of the components but also for some other reliability characteristic quantities which are functions of the sample and pivotal quantities, such as the availability and failure rate of the component. The next question concerns the reliability structure of the typical satellite intelligent PDS. The evaluation method proposed in this paper can be also applied to the LCLs of some other complicated reliability structures of a PDS. Finally, because the PDS has the characteristics of a long lifetime and high reliability, the validation experiment is very difficult. How to conduct the validation experiment is our future work.