A Performance–Consumption Balanced Scheme of Multi-Hop Quantum Networks for Teleportation
Abstract
1. Introduction
- This paper proposes a new scheme of a multi-hop quantum network based on bipartite communication with fusion states. It improves the noise immunity of the network while avoiding the huge consumption.
- A purification algorithm is proposed to ensure the robustness of the system, providing a solution for future quantum communication.
- The fidelity for multi-particle entanglement purification is calculated.
2. Preliminary
2.1. Entangled State
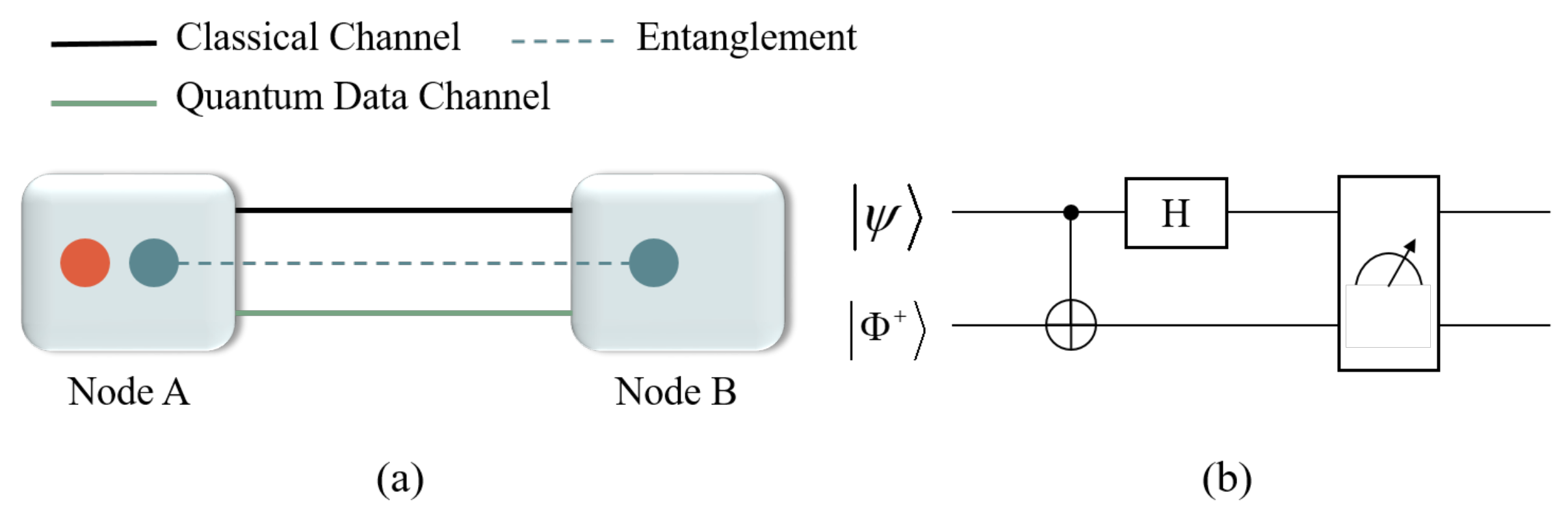
2.2. Teleportation
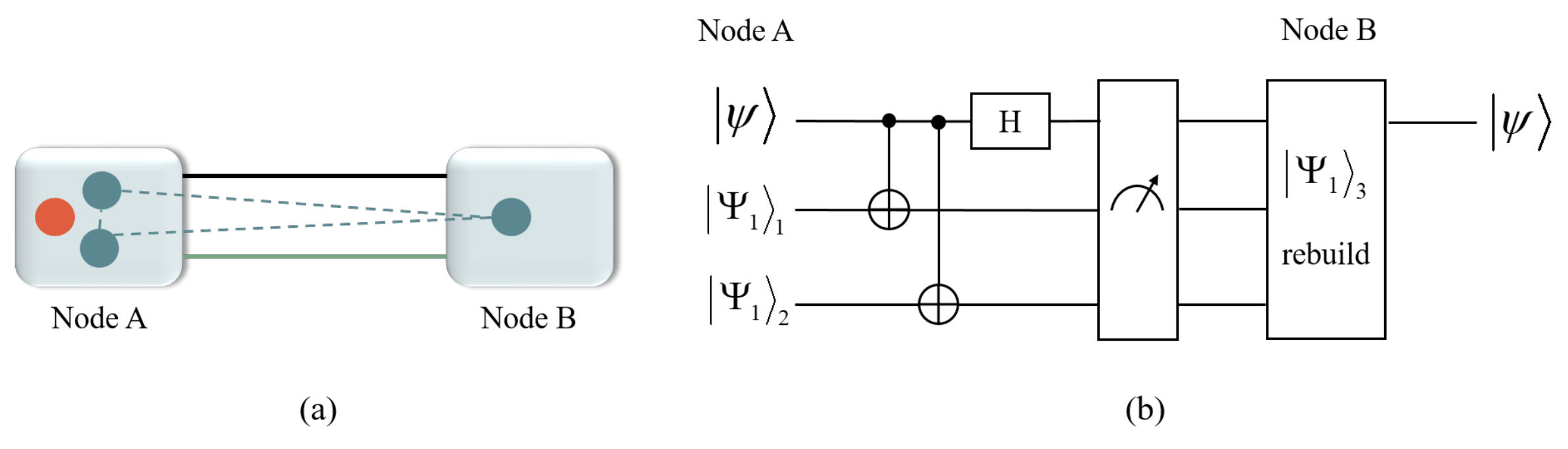
2.3. Entanglement Swapping
2.4. Fidelity
2.5. Noisy Channel
3. The Scheme of Network Architecture and Purification
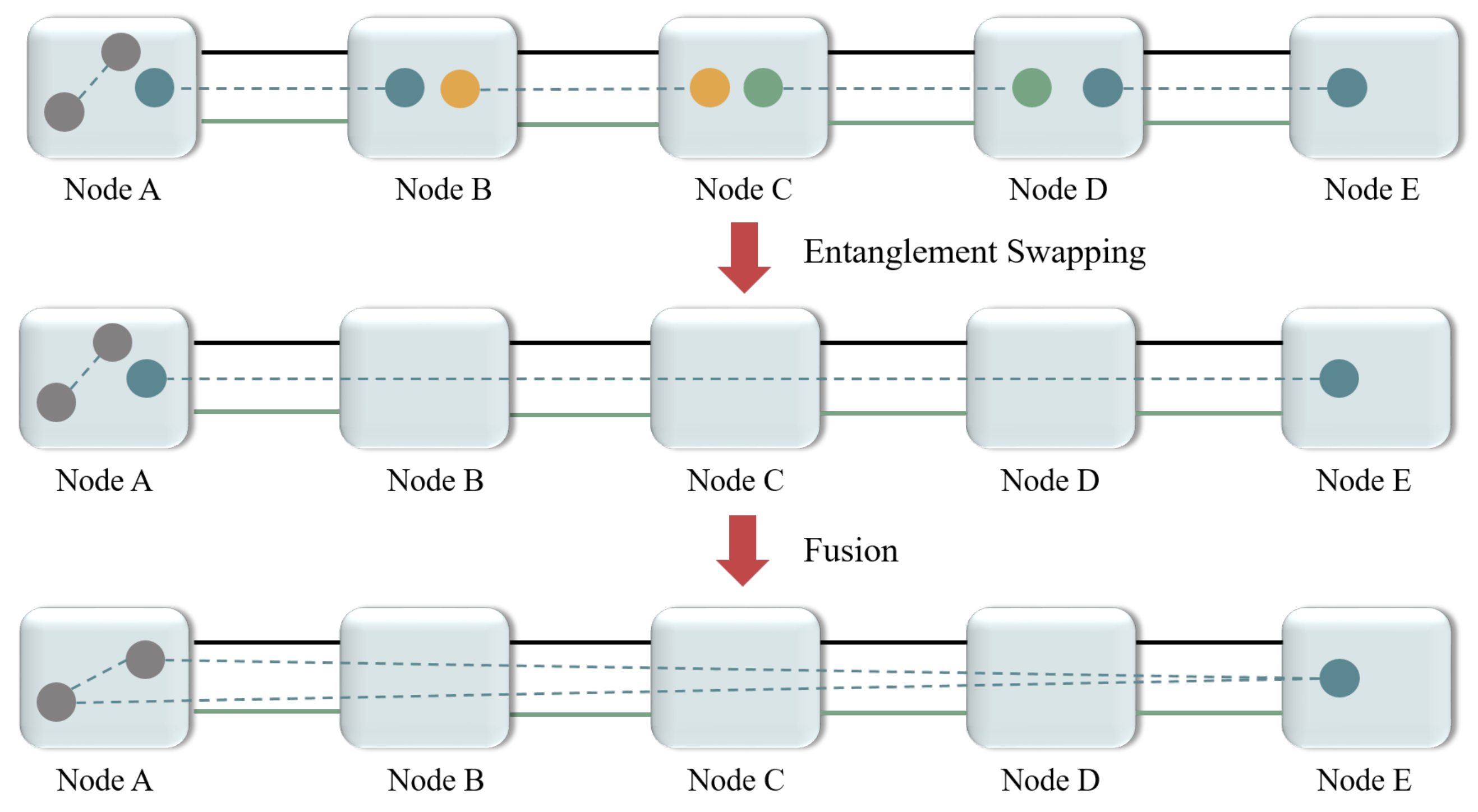
3.1. Network Architecture Based on Bipartite Communication
3.2. Purification Circuit for Different States
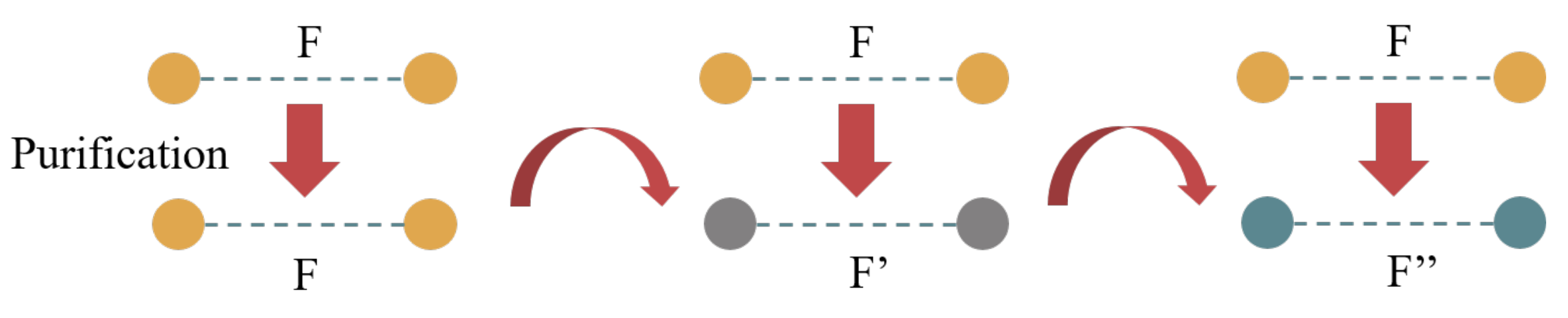
3.2.1. Purification of Bell Pairs
3.2.2. Purification of GHZ States
4. Design of Purification Algorithm and Simulation Results
4.1. Purification Algorithm
| Algorithm 1 Purification Algorithm |
|
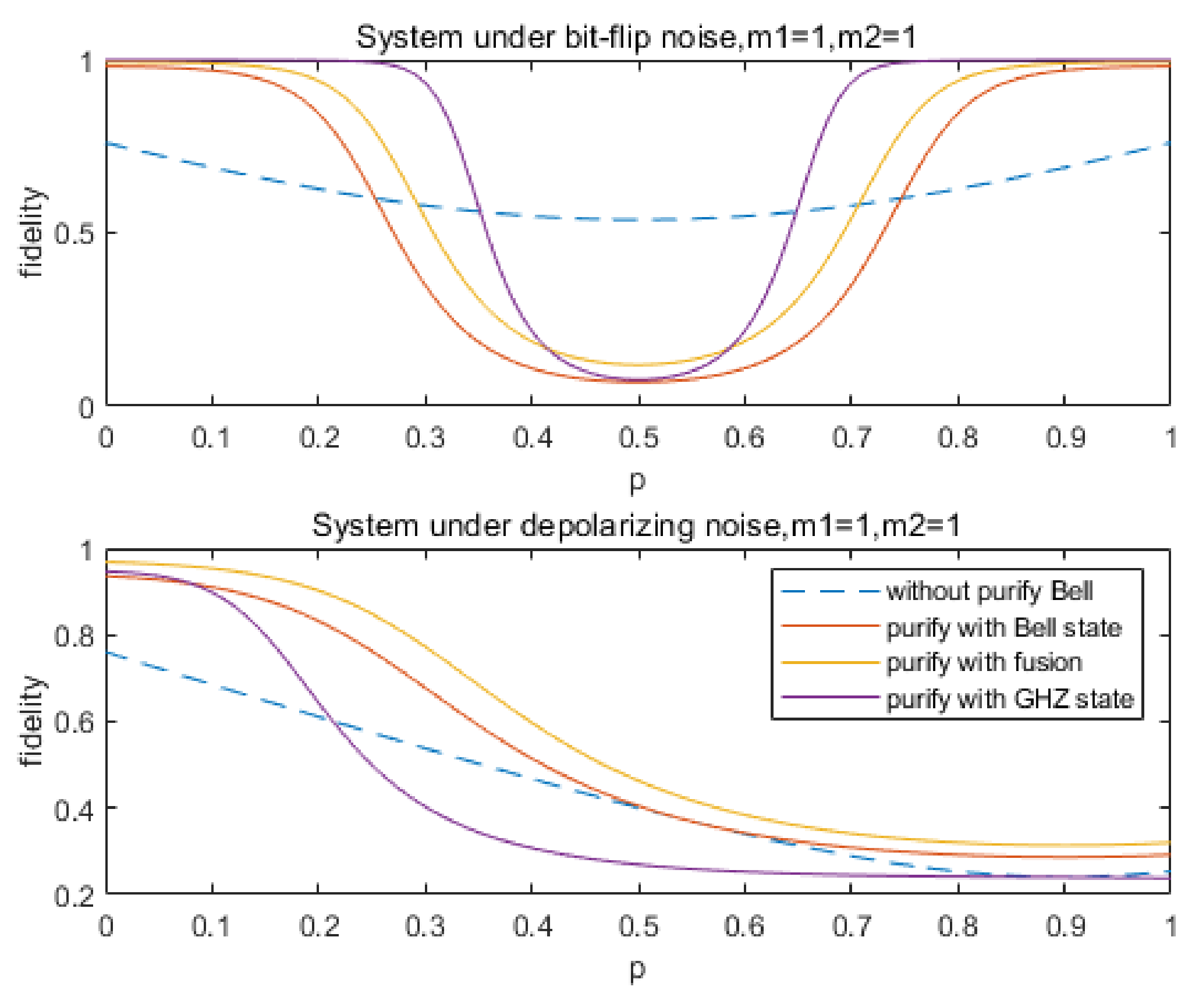
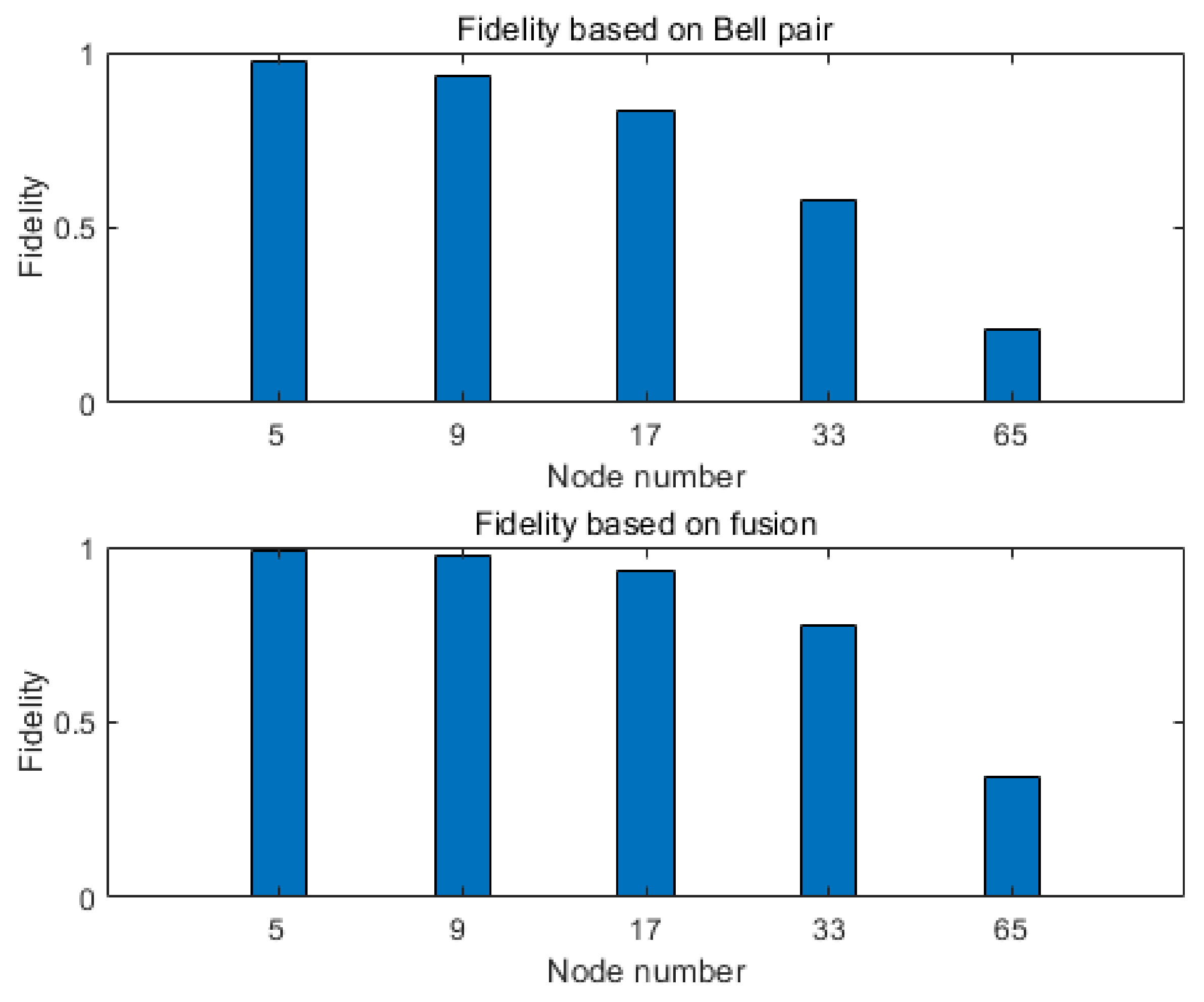
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| States in A | State in B | Operation in B |
|---|---|---|
| / | ||
| X gate | ||
| Z gate | ||
| ZX gate | ||
| / | ||
| X gate | ||
| Z gate | ||
| ZX gate |
Appendix B
| States in B | Shared States in A&C | Operation in C |
|---|---|---|
| / | ||
| X gate | ||
| Z gate | ||
| ZX gate |
References
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Pati, A.K. Assisted cloning and orthogonal complementing of an unknown state. Phys. Rev. A 2000, 61, 022308. [Google Scholar] [CrossRef]
- Agrawal, P.; Pati, A. Perfect teleportation and superdense coding with W states. Phys. Rev. A 2006, 74, 062320. [Google Scholar] [CrossRef]
- Adhikari, S.; Majumdar, A.S.; Roy, S.; Ghosh, B.; Nayak, N. Teleportation via Maximally and Non-Maximally Entangled Mixed States. Quantum Inf. Comput. 2010, 10, 398–419. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, C.; Tao, M. Quantum communication for wireless wide-area networks. IEEE Trans. Signal Process. 2005, 23, 1424–1432. [Google Scholar]
- Chen, N.; Quan, D.; Pei, C.; Yang, H. Quantum communication for satellite-to-ground networks with partially entangled states. Chin. Phys. B 2015, 24, 020304. [Google Scholar] [CrossRef][Green Version]
- Shi, L.; Yu, X.; Cai, X.; Gong, Y.; Zhang, Z. Quantum information transmission in the quantum wireless multihop network based on werner state. Chin. Phys. B 2015, 24, 050308. [Google Scholar] [CrossRef]
- Chen, N.; Shuai, S.; Yan, B.; Xu, N.; Pei, C. Multi-Hop Quantum Communication Based on Greenberger-Horne-Zeilinger States and Teleportation. IEEE Access 2020, 8, 52052–52061. [Google Scholar] [CrossRef]
- de Riedmatten, H.; Marcikic, I.; Tittel, W.; Zbinden, H.; Collins, D.; Gisin, N. Long Distance Quantum Teleportation in a Quantum Relay Configuration. Phys. Rev. Lett. 2004, 92, 047904. [Google Scholar] [CrossRef]
- Scherer, A.; Howard, R.B.; Sanders, B.C.; Tittel, W. Quantum states prepared by realistic entanglement swapping. Phys. Rev. A 2009, 80, 062310. [Google Scholar] [CrossRef]
- Xu, P.; Yong, H.L.; Chen, L.K.; Liu, C.; Xiang, T.; Yao, X.C.; Lu, H.; Li, Z.D.; Liu, N.L.; Li, L.; et al. Two-Hierarchy Entanglement Swapping for a Linear Optical Quantum Repeater. Phys. Rev. Lett. 2017, 119, 170502. [Google Scholar] [CrossRef]
- Dias, J.; Winnel, M.S.; Hosseinidehaj, N.; Ralph, T.C. Quantum repeater for continuous-variable entanglement distribution. Phys. Rev. A 2020, 102, 052425. [Google Scholar] [CrossRef]
- Pan, J.W.; Bouwmeester, D.; Weinfurter, H.; Zeilinger, A. Experimental Entanglement Swapping: Entangling Photons That Never Interacted. Phys. Rev. Lett. 1998, 80, 3891–3894. [Google Scholar] [CrossRef]
- Bernien, H.; Hensen, B.; Pfaff, W.; Koolstra, G.; Blok, M.S.; Robledo, L.; Taminiau, T.H.; Markham, M.; Twitchen, D.J.; Childress, L.; et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 2013, 497, 86–90. [Google Scholar] [CrossRef]
- Rosenfeld, W.; Burchardt, D.; Garthoff, R.; Redeker, K.; Ortegel, N.; Rau, M.; Weinfurter, H. Event-Ready Bell Test Using Entangled Atoms Simultaneously Closing Detection and Locality Loopholes. Phys. Rev. Lett. 2017, 119, 010402. [Google Scholar] [CrossRef] [PubMed]
- Tsujimoto, Y.; Tanaka, M.; Iwasaki, N.; Ikuta, R.; Miki, S.; Yamashita, T.; Terai, H.; Yamamoto, T.; Koashi, M.; Imoto, N. High-fidelity entanglement swapping and generation of three-qubit GHZ state using asynchronous telecom photon pair sources. Sci. Rep. 2018, 8, 1446. [Google Scholar] [CrossRef]
- Basso Basset, F.; Rota, M.B.; Schimpf, C.; Tedeschi, D.; Zeuner, K.D.; Covre da Silva, S.F.; Reindl, M.; Zwiller, V.; Jöns, K.D.; Rastelli, A.; et al. Entanglement Swapping with Photons Generated on Demand by a Quantum Dot. Phys. Rev. Lett. 2019, 123, 160501. [Google Scholar] [CrossRef] [PubMed]
- Pirker, A.; Wallnöfer, J.; Dür, W. Modular architectures for quantum networks. New J. Phys. 2018, 20, 053054. [Google Scholar] [CrossRef]
- Hahn, F.; Pappa, A.; Eisert, J. Quantum network routing and local complementation. NPJ Quantum Inf. 2019, 5, 76. [Google Scholar] [CrossRef]
- Bratzik, S.; Abruzzo, S.; Kampermann, H.; Bruß, D. Quantum repeaters and quantum key distribution: The impact of entanglement distillation on the secret key rate. Phys. Rev. A 2013, 87, 062335. [Google Scholar] [CrossRef]
- Dür, W.; Briegel, H.J. Entanglement purification and quantum error correction. Rep. Prog. Phys. 2007, 70, 1381–1424. [Google Scholar] [CrossRef]
- Fujii, K.; Yamamoto, K. Entanglement purification with double selection. Phys. Rev. A 2009, 80, 042308. [Google Scholar] [CrossRef]
- Kalb, N.; Reiserer, A.A.; Humphreys, P.C.; Bakermans, J.W.; Kamerling, S.J.; Nickerson, N.H.; Benjamin, S.C.; Twitchen, D.J.; Markham, M.; Hanson, R. Entanglement distillation between solid-state quantum network nodes. Science 2017, 356, 928–932. [Google Scholar] [CrossRef] [PubMed]
- Bone, S.; Ouyang, R.; Goodenough, K.; Elkouss, D. Protocols for creating and distilling multipartite GHZ states with Bell pairs. arXiv 2020, arXiv:2010.12259. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.K. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2012; pp. 409–415. [Google Scholar]
- Yan, F.; Yan, T. Probabilistic teleportation via a non-maximally entangled GHZ state. Chin. Sci. Bull. 2010, 55, 902–906. [Google Scholar] [CrossRef]
- Ozaeta, A.; McMahon, P.L. Decoherence of up to 8-qubit entangled states in a 16-qubit superconducting quantum processor. Quantum Sci. Technol. 2019, 4, 025015. [Google Scholar] [CrossRef]
- Deutsch, D.; Ekert, A.; Jozsa, R.; Macchiavello, C.; Popescu, S.; Sanpera, A. Erratum: Quantum Privacy Amplification and the Security of Quantum Cryptography over Noisy Channels. Phys. Rev. Lett. 1996, 77, 2818–2821. [Google Scholar] [CrossRef]
- Djordjevic, I. Quantum Information Processing and Quantum Error Correction; Academic Press: Cambridge, MA, USA, 2012; pp. 91–96. [Google Scholar]
- Qiu, P.; Chen, X.; Shi, Y. Solving Quantum Channel Discrimination Problem With Quantum Networks and Quantum Neural Networks. IEEE Access 2019, 7, 50214–50222. [Google Scholar] [CrossRef]







| One Shared Pair | Probability | Two Shared Pairs | Probability |
|---|---|---|---|
| Shared States | Probability |
|---|---|
| Node Number | Bell States Scheme | Fusion Scheme | GHZ States Scheme |
|---|---|---|---|
| 3 | 16/14 | 20/17 | 36/33 |
| 5 | 64/62 | 68/65 | 216/213 |
| 9 | 256/254 | 260/257 | 1296/1293 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Chen, X.; Xiao, H.; Wang, P.; Ma, M. A Performance–Consumption Balanced Scheme of Multi-Hop Quantum Networks for Teleportation. Appl. Sci. 2021, 11, 10869. https://doi.org/10.3390/app112210869
Xu J, Chen X, Xiao H, Wang P, Ma M. A Performance–Consumption Balanced Scheme of Multi-Hop Quantum Networks for Teleportation. Applied Sciences. 2021; 11(22):10869. https://doi.org/10.3390/app112210869
Chicago/Turabian StyleXu, Jin, Xiaoguang Chen, Hanwei Xiao, Pingxun Wang, and Mingzi Ma. 2021. "A Performance–Consumption Balanced Scheme of Multi-Hop Quantum Networks for Teleportation" Applied Sciences 11, no. 22: 10869. https://doi.org/10.3390/app112210869
APA StyleXu, J., Chen, X., Xiao, H., Wang, P., & Ma, M. (2021). A Performance–Consumption Balanced Scheme of Multi-Hop Quantum Networks for Teleportation. Applied Sciences, 11(22), 10869. https://doi.org/10.3390/app112210869






