Vector Optical Beam with Controllable Variation of Polarization during Propagation in Free Space: A Review
Abstract
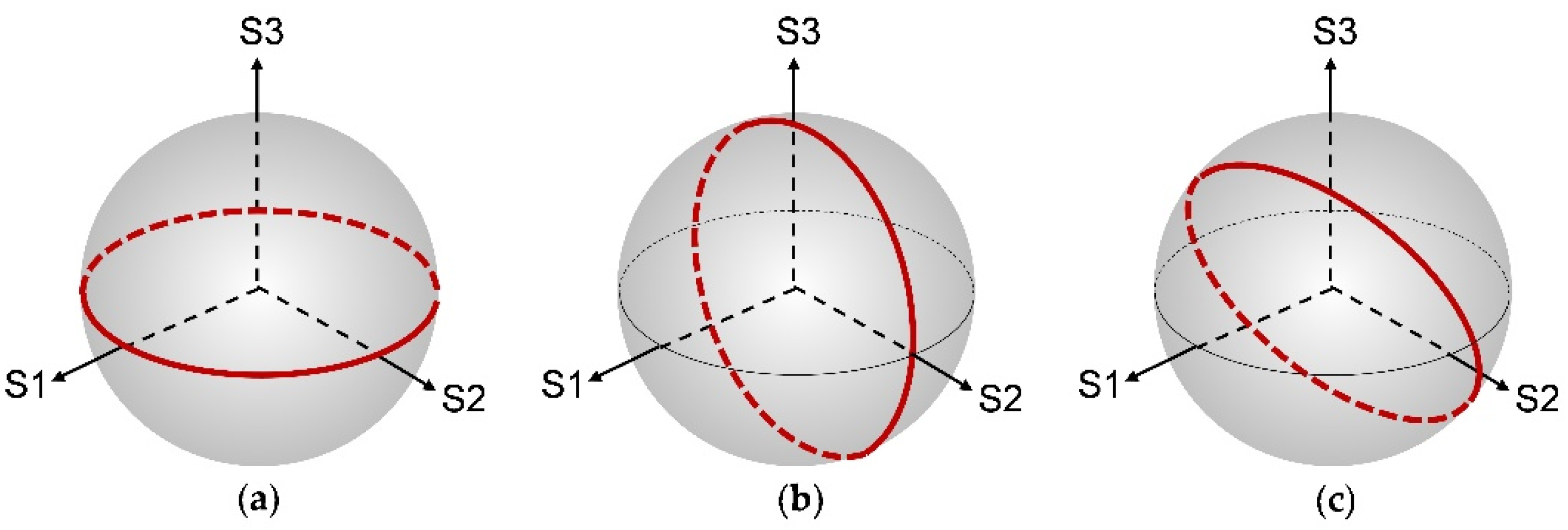
:1. Introduction
2. The Principle of Generating Vector Optical Beams with Polarization Varying along a Longitudinal Direction in Free Space
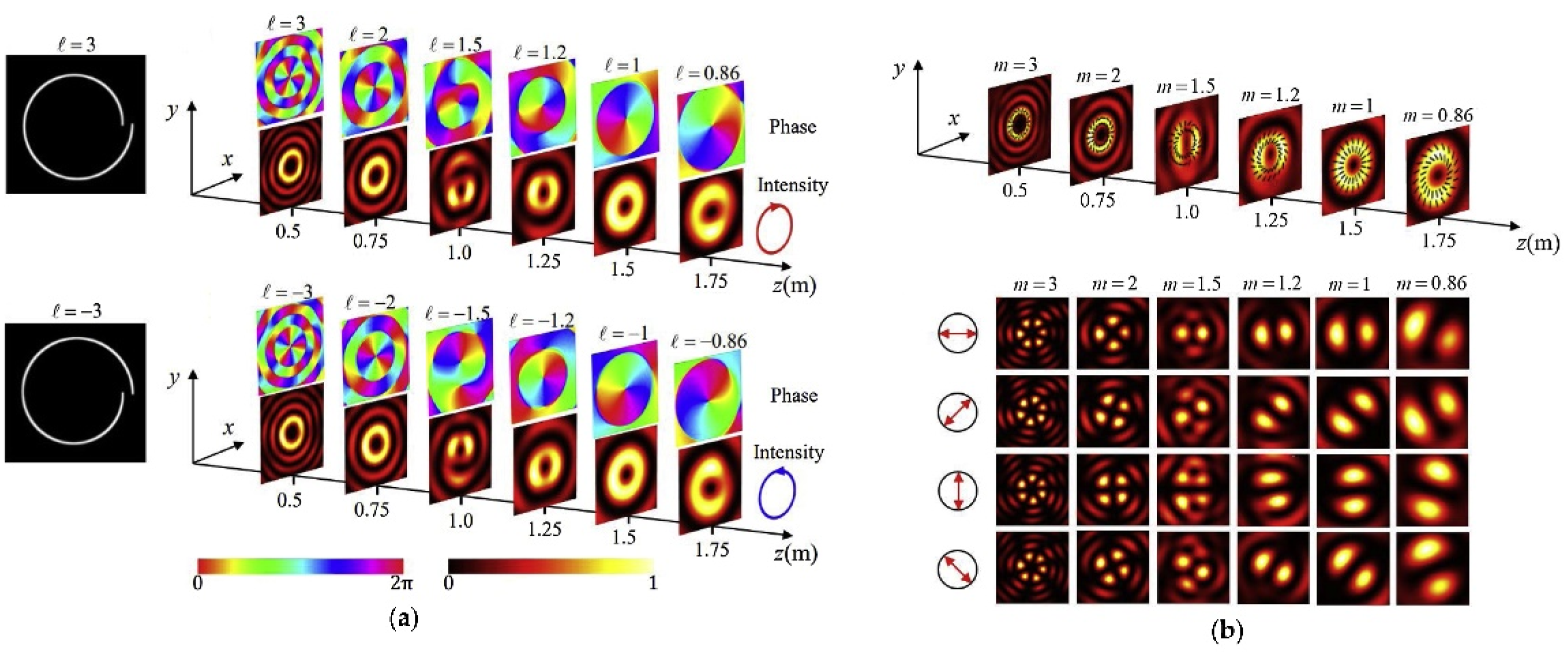
2.1. Construction of Varying Phase Difference in the Longitudinal Direction
2.2. Construction of Varying Amplitude Difference in the Longitudinal Direction
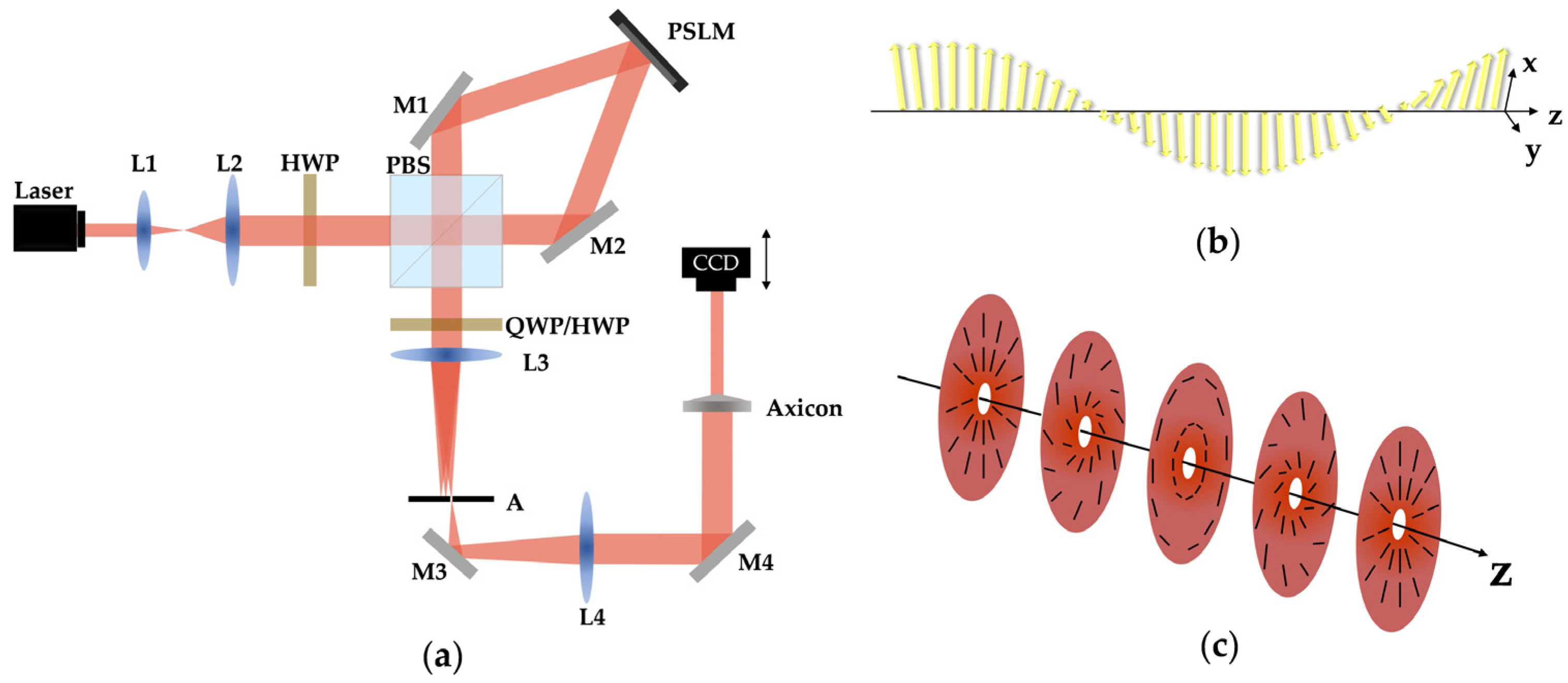
3. The Experimental Generation of Vector Optical Beams with Longitudinally Varying Polarization in Free Space
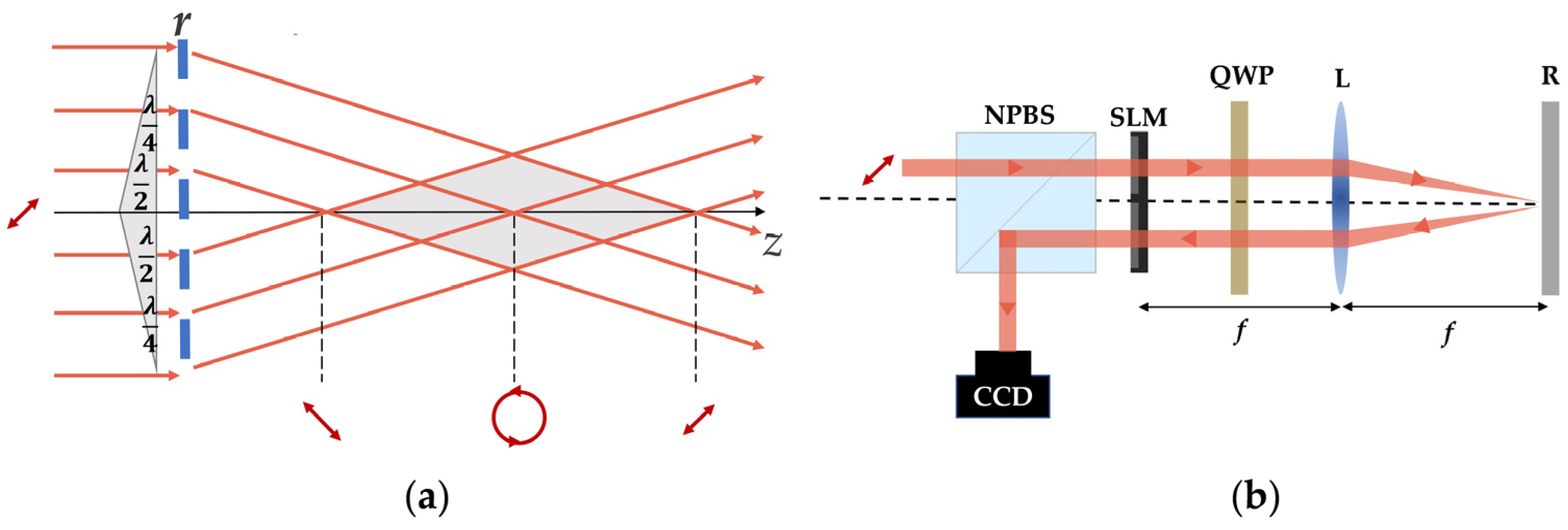
3.1. Modulation on the Complex Amplitude in Real Space
3.1.1. Single-Path Generation Method Based on Phase Mask
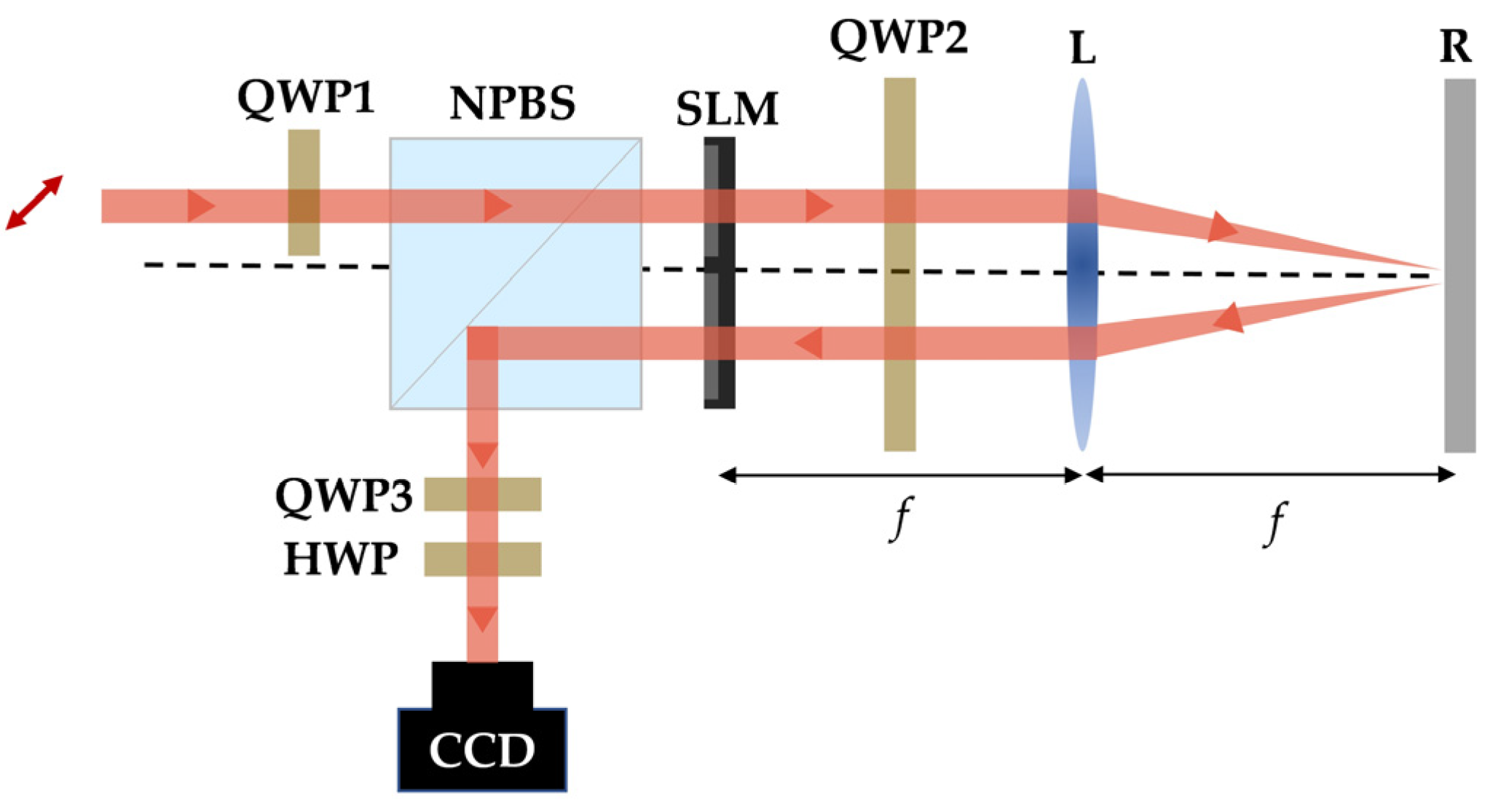
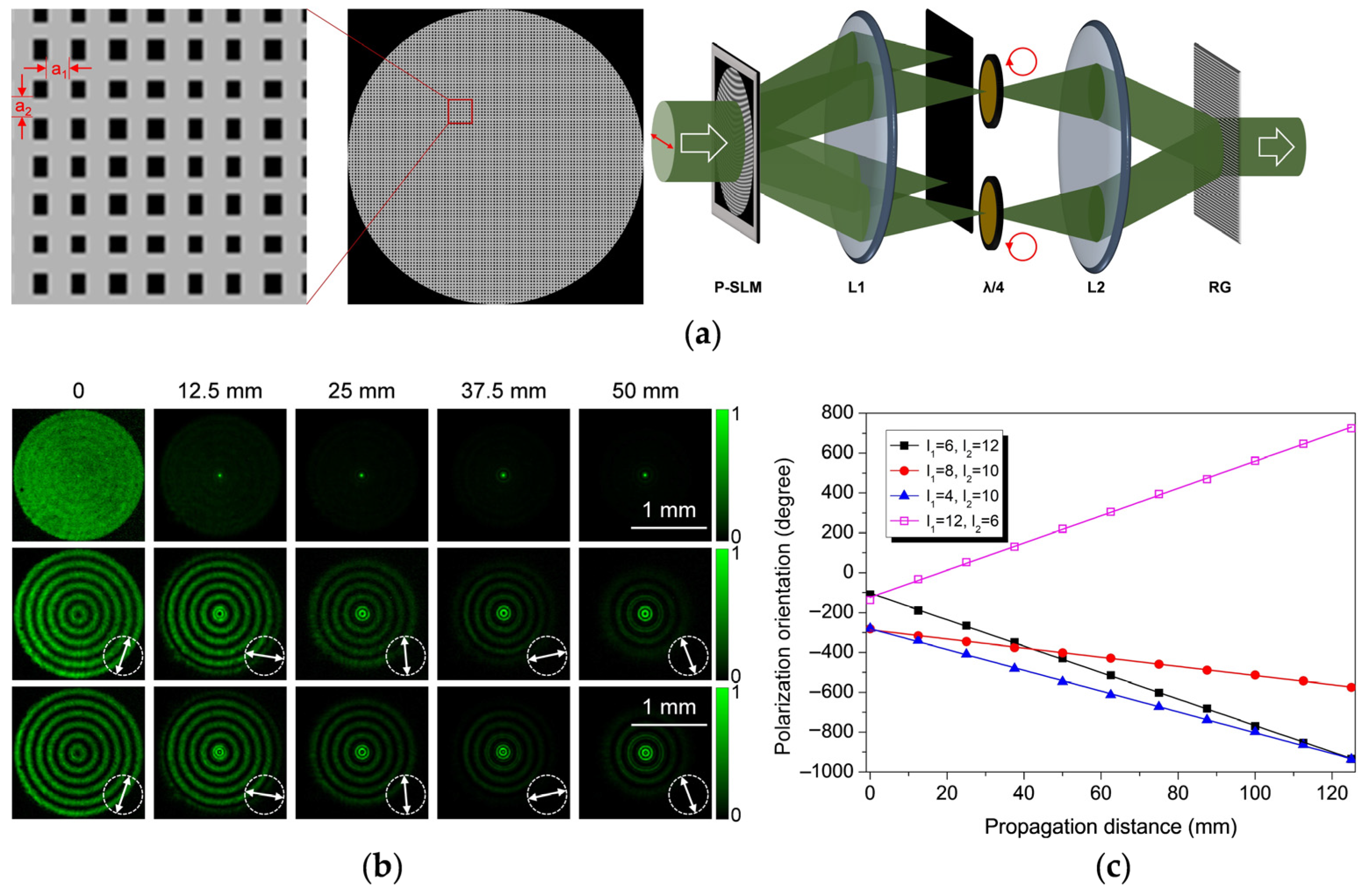
3.1.2. Double-Path Generation Method Based on Holographic Gratings
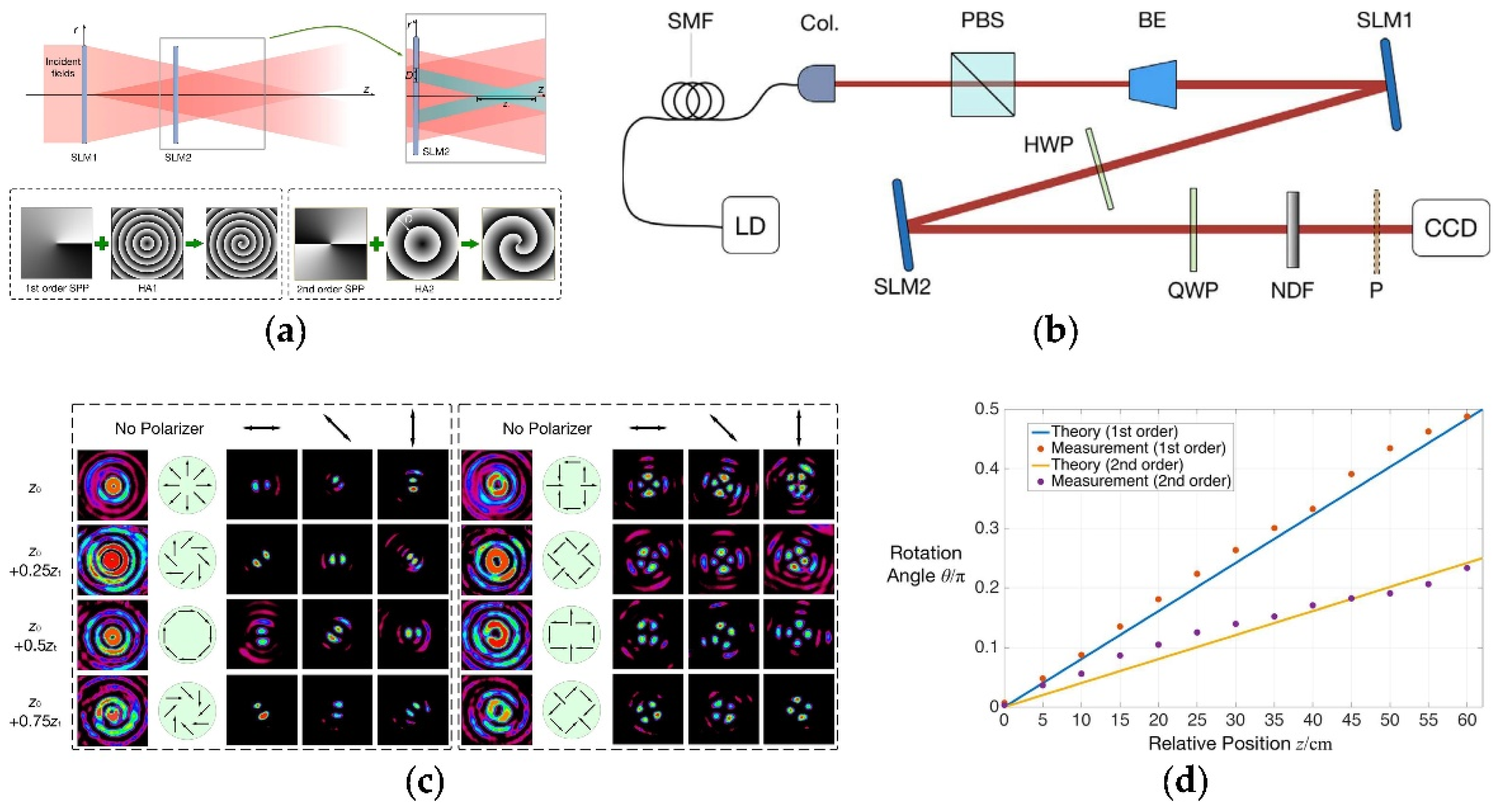
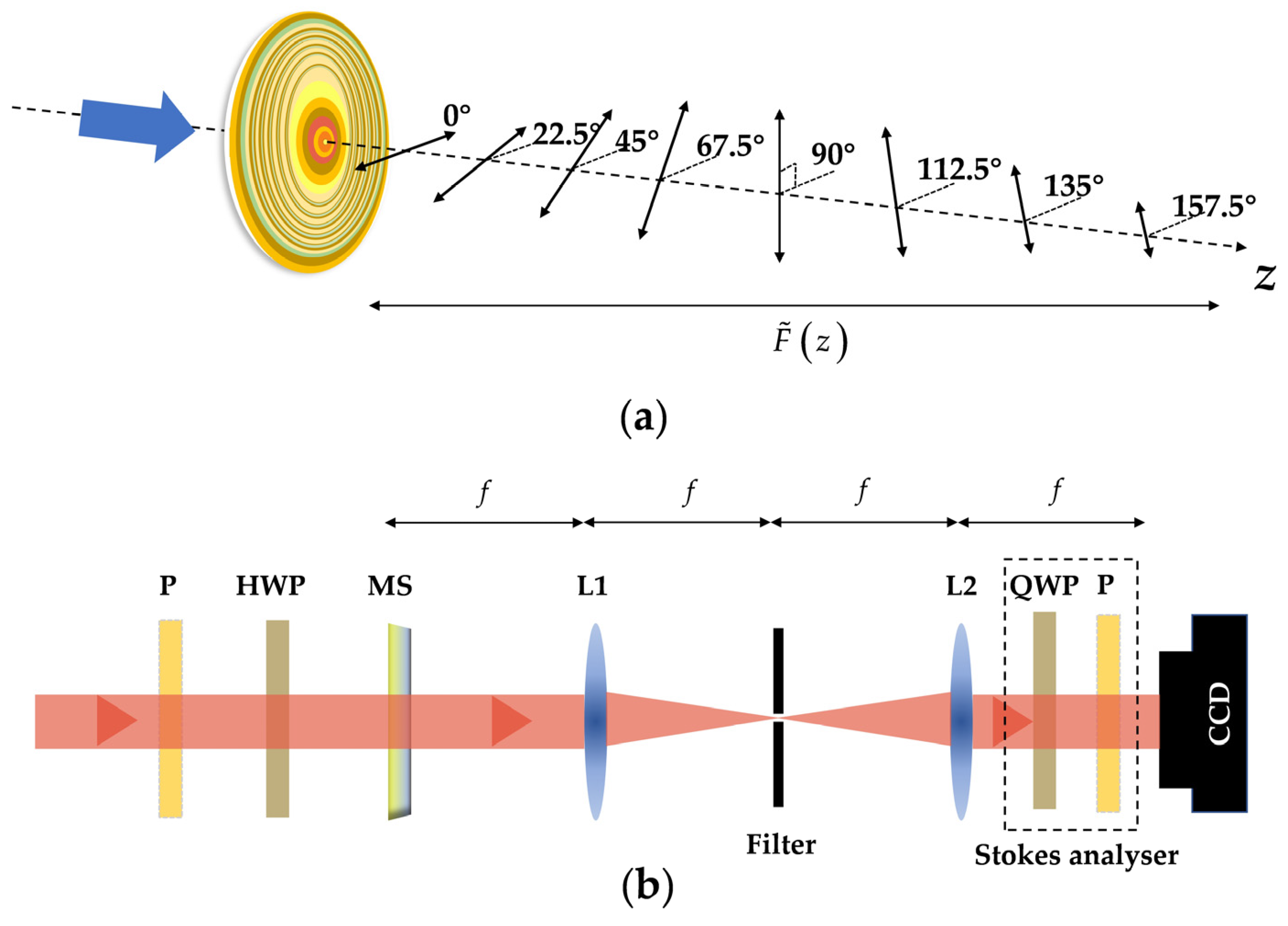
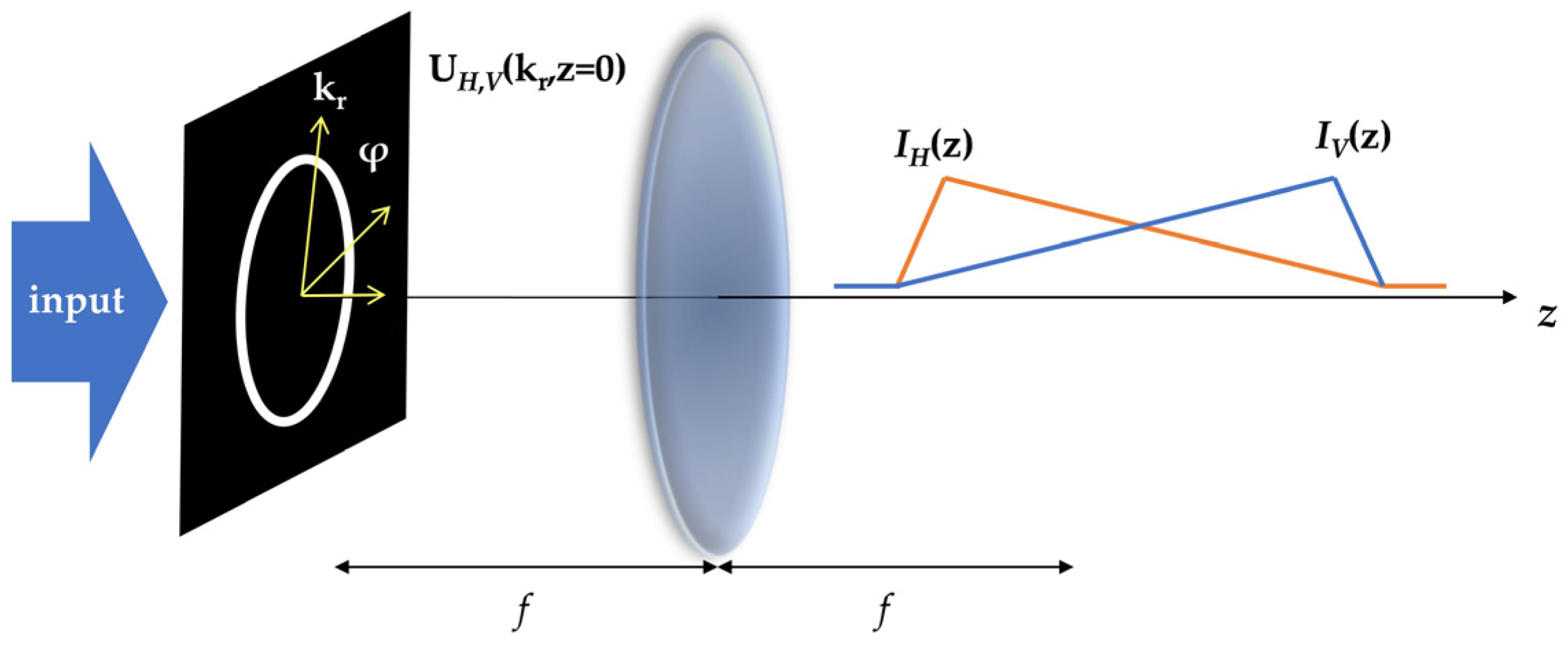
3.2. Filtering of Spatial Spectrum
4. Discussion
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Youngworth, K.S.; Brown, T.G. Focusing of high numerical aperture cylindrical-vector beams. Opt. Express 2000, 7, 77–87. [Google Scholar] [CrossRef]
- Dorn, R.; Quabis, S.; Leuchs, G. Sharper focus for a radially polarized light beam. Phys. Rev. Lett. 2003, 91, 233901. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wan, C.; Zhan, Q. Vectorial optical fields: Recent advances and future prospects. Sci. Bull. 2018, 63, 54–74. [Google Scholar] [CrossRef] [Green Version]
- Li, S.M.; Li, Y.; Wang, X.L.; Kong, L.J.; Lou, K.; Tu, C.; Tian, Y.; Wang, H.T. Taming the collapse of optical fields. Sci. Rep. 2012, 2, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Bouchard, F.; Larocque, H.; Yao, A.M.; Travis, C.; De Leon, I.; Rubano, A.; Karimi, E.; Oppo, G.-L.; Boyd, R.W. Polarization shaping for control of nonlinear propagation. Phys. Rev. Lett. 2016, 117, 233903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Shi, L.; Lukyanchuk, B.; Sheppard, C.; Chong, C.T. Creation of a needle of longitudinally polarized light in vacuum using binary optics. Nat. Photonics 2008, 2, 501–505. [Google Scholar] [CrossRef]
- Sederberg, S.; Kong, F.; Corkum, P.B. Tesla-scale terahertz magnetic impulses. Phys. Rev. X 2020, 10, 011063. [Google Scholar] [CrossRef] [Green Version]
- Gabriel, C.; Aiello, A.; Zhong, W.; Euser, T.; Joly, N.; Banzer, P.; Förtsch, M.; Elser, D.; Andersen, U.L.; Marquardt, C. Entangling different degrees of freedom by quadrature squeezing cylindrically polarized modes. Phys. Rev. Lett. 2011, 106, 060502. [Google Scholar] [CrossRef] [PubMed]
- Novotny, L.; Beversluis, M.; Youngworth, K.; Brown, T. Longitudinal field modes probed by single molecules. Phys. Rev. Lett. 2001, 86, 5251. [Google Scholar] [CrossRef] [Green Version]
- Varin, C.; Piché, M. Acceleration of ultra-relativistic electrons using high-intensity TM01 laser beams. Appl. Phys. B 2002, 74, s83–s88. [Google Scholar] [CrossRef]
- Bouhelier, A.; Beversluis, M.; Hartschuh, A.; Novotny, L. Near-field second-harmonic generation induced by local field enhancement. Phys. Rev. Lett. 2003, 90, 013903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lou, K.; Qian, S.X.; Wang, X.L.; Li, Y.; Gu, B.; Tu, C.; Wang, H.T. Two-dimensional microstructures induced by femtosecond vector light fields on silicon. Opt. Express 2012, 20, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Kawauchi, H.; Yonezawa, K.; Kozawa, Y.; Sato, S. Calculation of optical trapping forces on a dielectric sphere in the ray optics regime produced by a radially polarized laser beam. Opt. Lett. 2007, 32, 1839–1841. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Q. Trapping metallic Rayleigh particles with radial polarization. Opt. Express 2004, 12, 3377–3382. [Google Scholar] [CrossRef]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T. Roadmap on structured light. J. Opt. 2016, 19, 013001. [Google Scholar] [CrossRef]
- Maurer, C.; Jesacher, A.; Fürhapter, S.; Bernet, S.; Ritsch-Marte, M. Tailoring of arbitrary optical vector beams. New J. Phys. 2007, 9, 78. [Google Scholar] [CrossRef]
- Wang, X.L.; Ding, J.; Ni, W.J.; Guo, C.S.; Wang, H.T. Generation of arbitrary vector beams with a spatial light modulator and a common path interferometric arrangement. Opt. Lett. 2007, 32, 3549–3551. [Google Scholar] [CrossRef]
- Liu, S.; Li, P.; Peng, T.; Zhao, J. Generation of arbitrary spatially variant polarization beams with a trapezoid Sagnac interferometer. Opt. Express 2012, 20, 21715–21721. [Google Scholar] [CrossRef]
- Han, W.; Yang, Y.; Cheng, W.; Zhan, Q. Vectorial optical field generator for the creation of arbitrarily complex fields. Opt. Express 2013, 21, 20692–20706. [Google Scholar] [CrossRef]
- Rong, Z.Y.; Han, Y.J.; Wang, S.Z.; Guo, C.S. Generation of arbitrary vector beams with cascaded liquid crystal spatial light modulators. Opt. Express 2014, 22, 1636–1644. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zeng, T.; Qian, B.; Ding, J. Complete shaping of optical vector beams. Opt. Express 2015, 23, 17701–17710. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Gu, B.; Rui, G.; Zhan, Q.; Cui, Y. Generation of arbitrary vector fields based on a pair of orthogonal elliptically polarized base vectors. Opt. Express 2016, 24, 4177–4186. [Google Scholar] [CrossRef] [PubMed]
- Fu, S.; Gao, C.; Wang, T.; Zhai, Y.; Yin, C. Anisotropic polarization modulation for the production of arbitrary Poincaré beams. JOSA B 2018, 35, 1–7. [Google Scholar] [CrossRef]
- Pohl, D. Operation of a ruby laser in the purely transverse electric mode TE01. Appl. Phys. Lett. 1972, 20, 266–267. [Google Scholar] [CrossRef]
- Pan, Y.; Li, Y.; Li, S.-M.; Ren, Z.C.; Si, Y.; Tu, C.; Wang, H.T. Vector optical fields with bipolar symmetry of linear polarization. Opt. Lett. 2013, 38, 3700–3703. [Google Scholar] [CrossRef]
- Pan, Y.; Li, Y.; Ren, Z.C.; Si, Y.; Tu, C.; Wang, H.T. Parabolic-symmetry vector optical fields and their tightly focusing properties. Phys. Rev. A 2014, 89, 035801. [Google Scholar] [CrossRef]
- Pan, Y.; Li, Y.; Li, S.M.; Ren, Z.C.; Kong, L.J.; Tu, C.; Wang, H.T. Elliptic-symmetry vector optical fields. Opt. Express 2014, 22, 19302–19313. [Google Scholar] [CrossRef]
- Pan, Y.; Gao, X.Z.; Cai, M.Q.; Zhang, G.L.; Li, Y.; Tu, C.; Wang, H.T. Fractal vector optical fields. Opt. Lett. 2016, 41, 3161–3164. [Google Scholar] [CrossRef]
- Moreno, I.; Davis, J.A.; Sánchez-López, M.M.; Badham, K.; Cottrell, D.M. Nondiffracting Bessel beams with polarization state that varies with propagation distance. Opt. Lett. 2015, 40, 5451–5454. [Google Scholar] [CrossRef]
- Alberucci, A.; Jisha, C.P.; Marrucci, L.; Assanto, G. Electromagnetic confinement via spin–orbit interaction in anisotropic dielectrics. ACS Photonics 2016, 3, 2249–2254. [Google Scholar] [CrossRef] [Green Version]
- Slussarenko, S.; Alberucci, A.; Jisha, C.P.; Piccirillo, B.; Santamato, E.; Assanto, G.; Marrucci, L. Guiding light via geometric phases. Nat. Photonics 2016, 10, 571–575. [Google Scholar] [CrossRef] [Green Version]
- Jisha, C.P.; Alberucci, A.; Marrucci, L.; Assanto, G. Interplay between diffraction and the Pancharatnam-Berry phase in inhomogeneously twisted anisotropic media. Phys. Rev. A 2017, 95, 023823. [Google Scholar] [CrossRef] [Green Version]
- Karpierz, M.A.; Sierakowski, M.; Świłło, M.; Woliński, T. Self focusing in liquid crystalline waveguides. Molecular Crystals and Liquid Crystals Science and Technology. Section A. Mol. Cryst. Liq. Cryst. 1998, 320, 157–163. [Google Scholar] [CrossRef]
- Assanto, G.; Smyth, N.F. Spin-optical solitons in liquid crystals. Phys. Rev. A 2020, 102, 033501. [Google Scholar] [CrossRef]
- Assanto, G.; Wang, Z.; Hagan, D.; VanStryland, E. All-optical modulation via nonlinear cascading in type II second-harmonic generation. Appl. Phys. Lett. 1995, 67, 2120–2122. [Google Scholar] [CrossRef] [Green Version]
- Assanto, G. Transistor action through nonlinear cascading in Type II interactions. Opt. Lett. 1995, 20, 1595–1597. [Google Scholar] [CrossRef] [PubMed]
- Kolesik, M.; Moloney, J.; Wright, E. Polarization dynamics of femtosecond pulses propagating in air. Phys. Rev. E 2001, 64, 046607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scott, G.; McArdle, N. Efficient generation of nearly diffraction-free beams using an axicon. Opt. Eng. 1992, 31, 2640–2643. [Google Scholar] [CrossRef]
- Burvall, A.; Kołacz, K.; Jaroszewicz, Z.; Friberg, A.T. Simple lens axicon. Appl. Opt. 2004, 43, 4838–4844. [Google Scholar] [CrossRef]
- Suresh, P.; Mariyal, C.; Rajesh, K.; Pillai, T.; Jaroszewicz, Z. Generation of a strong uniform transversely polarized nondiffracting beam using a high-numerical-aperture lens axicon with a binary phase mask. Appl. Opt. 2013, 52, 849–853. [Google Scholar] [CrossRef] [PubMed]
- Vasara, A.; Turunen, J.; Friberg, A.T. Realization of general nondiffracting beams with computer-generated holograms. JOSA A 1989, 6, 1748–1754. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.A.; Guertin, J.; Cottrell, D.M. Diffraction-free beams generated with programmable spatial light modulators. Appl. Opt. 1993, 32, 6368–6370. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.A.; Carcole, E.; Cottrell, D.M. Nondiffracting interference patterns generated with programmable spatial light modulators. Appl. Opt. 1996, 35, 599–602. [Google Scholar] [CrossRef] [Green Version]
- Jaroszewicz, Z.; Climent, V.; Duran, V.; Lancis, J.; Kolodziejczyk, A.; Burvall, A.; Friberg, A.T. Programmable axicon for variable inclination of the focal segment. J. Mod. Opt. 2004, 51, 2185–2190. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Y.; Liu, S.; Han, L.; Cheng, H.; Yu, F.; Zhao, J. Quasi-Bessel beams with longitudinally varying polarization state generated by employing spectrum engineering. Opt. Lett. 2016, 41, 4811–4814. [Google Scholar] [CrossRef]
- Čižmár, T.; Dholakia, K. Tunable Bessel light modes: Engineering the axial propagation. Opt. Express 2009, 17, 15558–15570. [Google Scholar] [CrossRef]
- Li, L.; Lee, W.M.; Xie, X.; Krolikowski, W.; Rode, A.V.; Zhou, J. Shaping self-imaging bottle beams with modified quasi-Bessel beams. Opt. Lett. 2014, 39, 2278–2281. [Google Scholar] [CrossRef] [Green Version]
- Davis, J.A.; Moreno, I.; Badham, K.; Sánchez-López, M.M.; Cottrell, D.M. Nondiffracting vector beams where the charge and the polarization state vary with propagation distance. Opt. Lett. 2016, 41, 2270–2273. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, S.; Gao, C. Bessel beams with spatial oscillating polarization. Sci. Rep. 2016, 6, 1–7. [Google Scholar]
- Li, P.; Wu, D.; Liu, S.; Zhang, Y.; Guo, X.; Qi, S.; Li, Y.; Zhao, J. Three-dimensional modulations on the states of polarization of light fields. Chin. Phys. B 2018, 27, 114201. [Google Scholar] [CrossRef]
- Dorrah, A.H.; Rubin, N.A.; Zaidi, A.; Tamagnone, M.; Capasso, F. Metasurface optics for on-demand polarization transformations along the optical path. Nat. Photonics 2021, 15, 287–296. [Google Scholar] [CrossRef]
- Intaravanne, Y.; Chen, X. Recent advances in optical metasurfaces for polarization detection and engineered polarization profiles. Nanophotonics 2020, 9, 1003–1014. [Google Scholar] [CrossRef]
- Rubin, N.A.; D’Aversa, G.; Chevalier, P.; Shi, Z.; Chen, W.T.; Capasso, F. Matrix Fourier optics enables a compact full-Stokes polarization camera. Science 2019, 365, 6448. [Google Scholar] [CrossRef] [PubMed]
- Hsueh, C.-K.; Sawchuk, A.A. Computer-generated double-phase holograms. Appl. Opt. 1978, 17, 3874–3883. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Zhang, Y.; Liu, S.; Cheng, H.; Han, L.; Wu, D.; Zhao, J. Generation and self-healing of vector Bessel-Gauss beams with variant state of polarizations upon propagation. Opt. Express 2017, 25, 5821–5831. [Google Scholar] [CrossRef]
- Bhandari, R. Polarization of light and topological phases. Phys. Rep. 1997, 281, 1–64. [Google Scholar] [CrossRef]
- Gorodetski, Y.; Biener, G.; Niv, A.; Kleiner, V.; Hasman, E. Optical properties of polarization-dependent geometric phase elements with partially polarized light. Opt. Commun. 2006, 266, 365–375. [Google Scholar] [CrossRef]
- Karimi, E.; Slussarenko, S.; Piccirillo, B.; Marrucci, L.; Santamato, E. Polarization-controlled evolution of light transverse modes and associated Pancharatnam geometric phase in orbital angular momentum. Phys. Rev. A 2010, 81, 053813. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Li, P.; Zhang, Y.; Gan, X.; Wang, M.; Zhao, J. Longitudinal spin separation of light and its performance in three-dimensionally controllable spin-dependent focal shift. Sci. Rep. 2016, 6, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Wang, M.; Li, P.; Zhang, P.; Zhao, J. Abrupt polarization transition of vector autofocusing Airy beams. Opt. Lett. 2013, 38, 2416–2418. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Y.; Liu, S.; Ma, C.; Han, L.; Cheng, H.; Zhao, J. Generation of perfect vectorial vortex beams. Opt. Lett. 2016, 41, 2205–2208. [Google Scholar] [CrossRef] [PubMed]
- Lü, J.-Q.; Wang, X.-L.; Zhang, G.-L.; Tu, C.; Li, Y.; Wang, H.-T. Bessel-like beams with controllable rotating local linear polarization during propagation. Opt. Lett. 2020, 45, 1738–1741. [Google Scholar] [CrossRef] [PubMed]
- Paterson, C.; Smith, R. Higher-order Bessel waves produced by axicon-type computer-generated holograms. Opt. Commun. 1996, 124, 121–130. [Google Scholar] [CrossRef]
- Yang, B.; Su, M.; Lu, L.; Liu, J.; Chai, G. Generation of anomalous vector Bessel beams with varying polarization order along the propagation direction. Optik 2021, 232, 166578. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, X.; Zeng, J.; Lu, X.; Zhao, C.; Cai, Y. Anomalous Bessel vortex beam: Modulating orbital angular momentum with propagation. Nanophotonics 2018, 7, 677–682. [Google Scholar] [CrossRef]
- Tsai, W.Y.; Huang, J.S.; Huang, C.-B. Selective trapping or rotation of isotropic dielectric microparticles by optical near field in a plasmonic archimedes spiral. Nano Lett. 2014, 14, 547–552. [Google Scholar] [CrossRef]
- McGloin, D.; Dholakia, K. Bessel beams: Diffraction in a new light. Contemp. Phys. 2005, 46, 15–28. [Google Scholar] [CrossRef]
- Li, S.-M.; Ren, Z.C.; Kong, L.J.; Qian, S.X.; Tu, C.; Li, Y.; Wang, H.-T. Unveiling stability of multiple filamentation caused by axial symmetry breaking of polarization. Photonics Res. 2016, 4, B29–B34. [Google Scholar] [CrossRef]
- Wang, D.; Pan, Y.; Lü, J.Q.; Li, P.P.; Liu, G.G.; Cai, M.Q.; Li, Y.; Tu, C.; Wang, H.T. Controlling optical field collapse by elliptical symmetry hybrid polarization structure. JOSA B 2018, 35, 2373–2381. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Liang, S.; Li, F.; Ning, S.; Li, Y.; Malpuech, G.; Zhang, Y.; Xiao, M.; Solnyshkov, D. Spin–orbit coupling in photonic graphene. Optica 2020, 7, 455–462. [Google Scholar] [CrossRef]
- Zhang, Y.; Nie, Z.; Zhao, Y.; Li, C.; Wang, R.; Si, J.; Xiao, M. Modulated vortex solitons of four-wave mixing. Opt. Express 2010, 18, 10963–10972. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Liu, X.; Yang, L.; Li, X.; Zhang, Z.; Zhang, Y. Modulated vortex six-wave mixing. Opt. Lett. 2017, 42, 3097–3100. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Li, F.; Malpuech, G.; Zhang, Y.; Bleu, O.; Koniakhin, S.; Li, C.; Zhang, Y.; Xiao, M.; Solnyshkov, D. Particle like behavior of topological defects in linear wave packets in photonic graphene. Phys. Rev. Lett. 2019, 122, 233905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bryant, D.M.; Mostov, K.E. From cells to organs: Building polarized tissue. Nat. Rev. Mol. Cell Biol. 2008, 9, 887–901. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.-Y.; Cheng, T.-Y.; Bai, Z.-X.; Liu, S.; Lü, J.-Q. Vector Optical Beam with Controllable Variation of Polarization during Propagation in Free Space: A Review. Appl. Sci. 2021, 11, 10664. https://doi.org/10.3390/app112210664
Wang W-Y, Cheng T-Y, Bai Z-X, Liu S, Lü J-Q. Vector Optical Beam with Controllable Variation of Polarization during Propagation in Free Space: A Review. Applied Sciences. 2021; 11(22):10664. https://doi.org/10.3390/app112210664
Chicago/Turabian StyleWang, Wen-Yue, Tian-Yu Cheng, Zhen-Xu Bai, Shuo Liu, and Jia-Qi Lü. 2021. "Vector Optical Beam with Controllable Variation of Polarization during Propagation in Free Space: A Review" Applied Sciences 11, no. 22: 10664. https://doi.org/10.3390/app112210664
APA StyleWang, W.-Y., Cheng, T.-Y., Bai, Z.-X., Liu, S., & Lü, J.-Q. (2021). Vector Optical Beam with Controllable Variation of Polarization during Propagation in Free Space: A Review. Applied Sciences, 11(22), 10664. https://doi.org/10.3390/app112210664






