Modular Model Composition for Rapid Implementations of Embedded Economic Model Predictive Control in Microgrids
Abstract
:1. Introduction
2. Materials and Methods
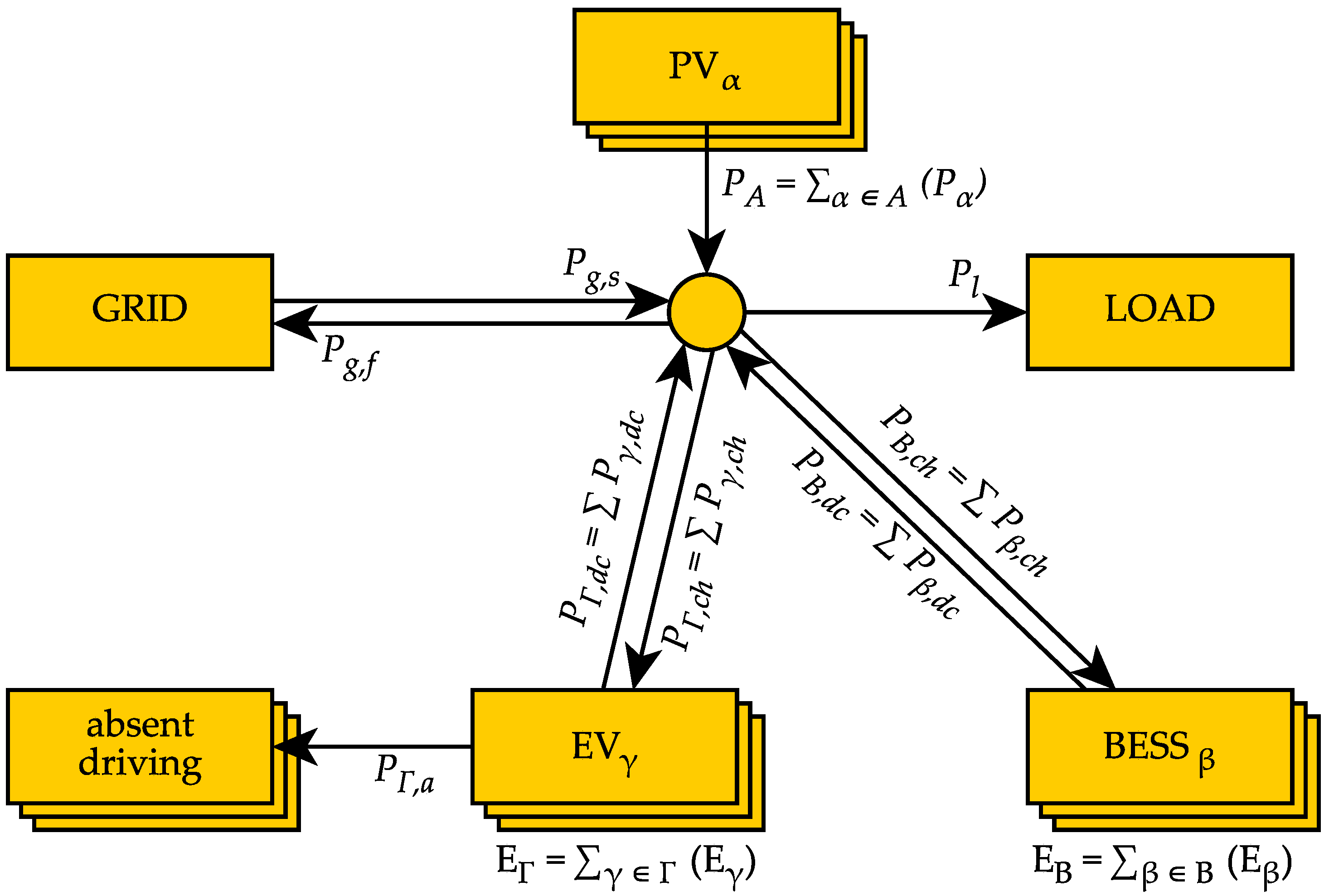
2.1. Generalised Dynamic System Model
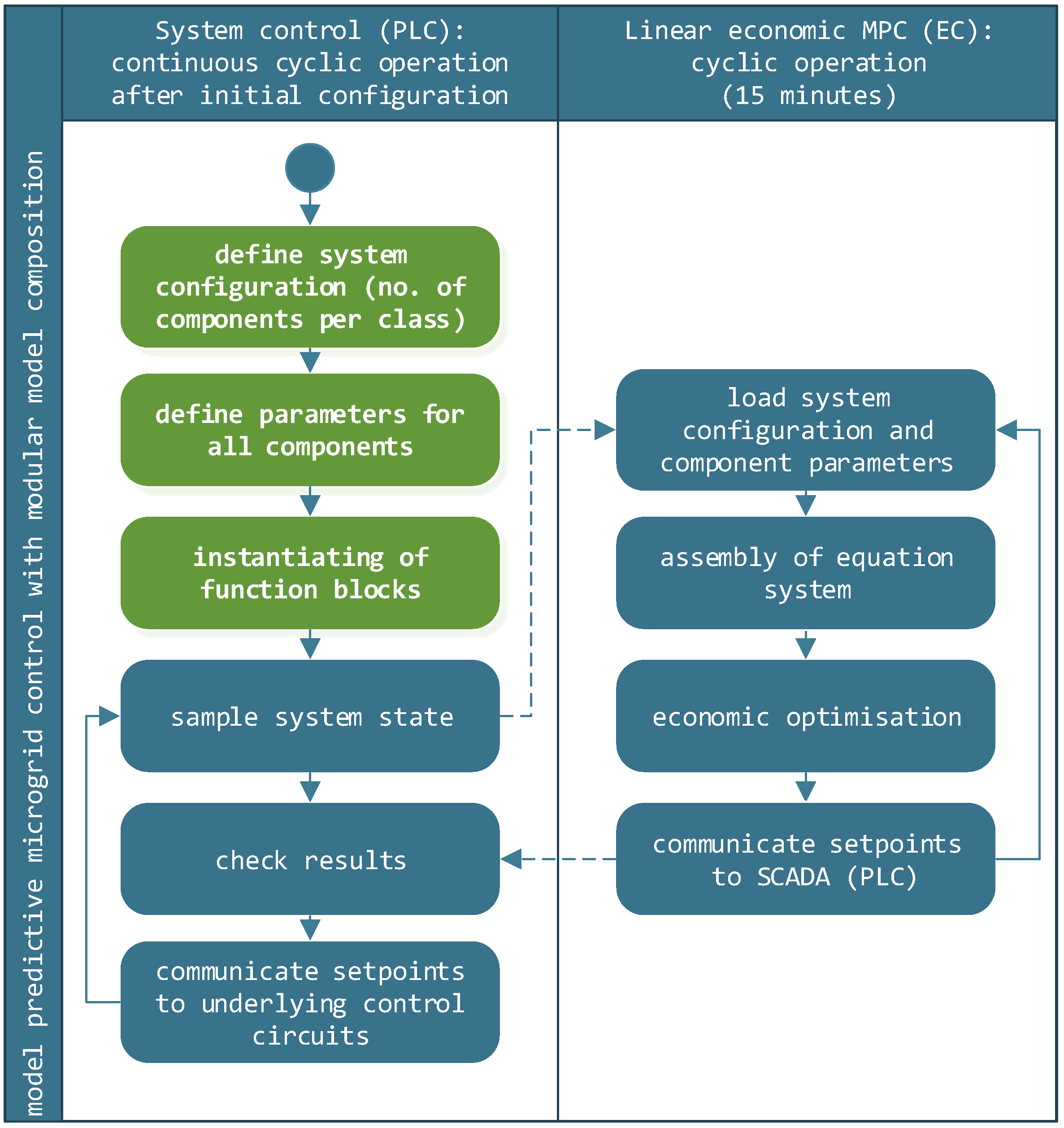
2.2. Control Hardware Structure and Commissioning Process
- A measurement of all configured devices is conducted by the PLC and its connected input and output modules.
- The system configuration, the component parameters, and the component measurements are communicated to the EC via field bus (PLC to EC).
- The dynamic system model, depending on the transmitted configuration, is automatically composed in the EC.
- An economic optimisation is conducted based on PV and power demand predictions and the recently sampled system state (EC).
- The optimal device setpoints are communicated via field bus (PLC to EC).
- The device setpoints are applied in the energy system (simulation) by the PLC.
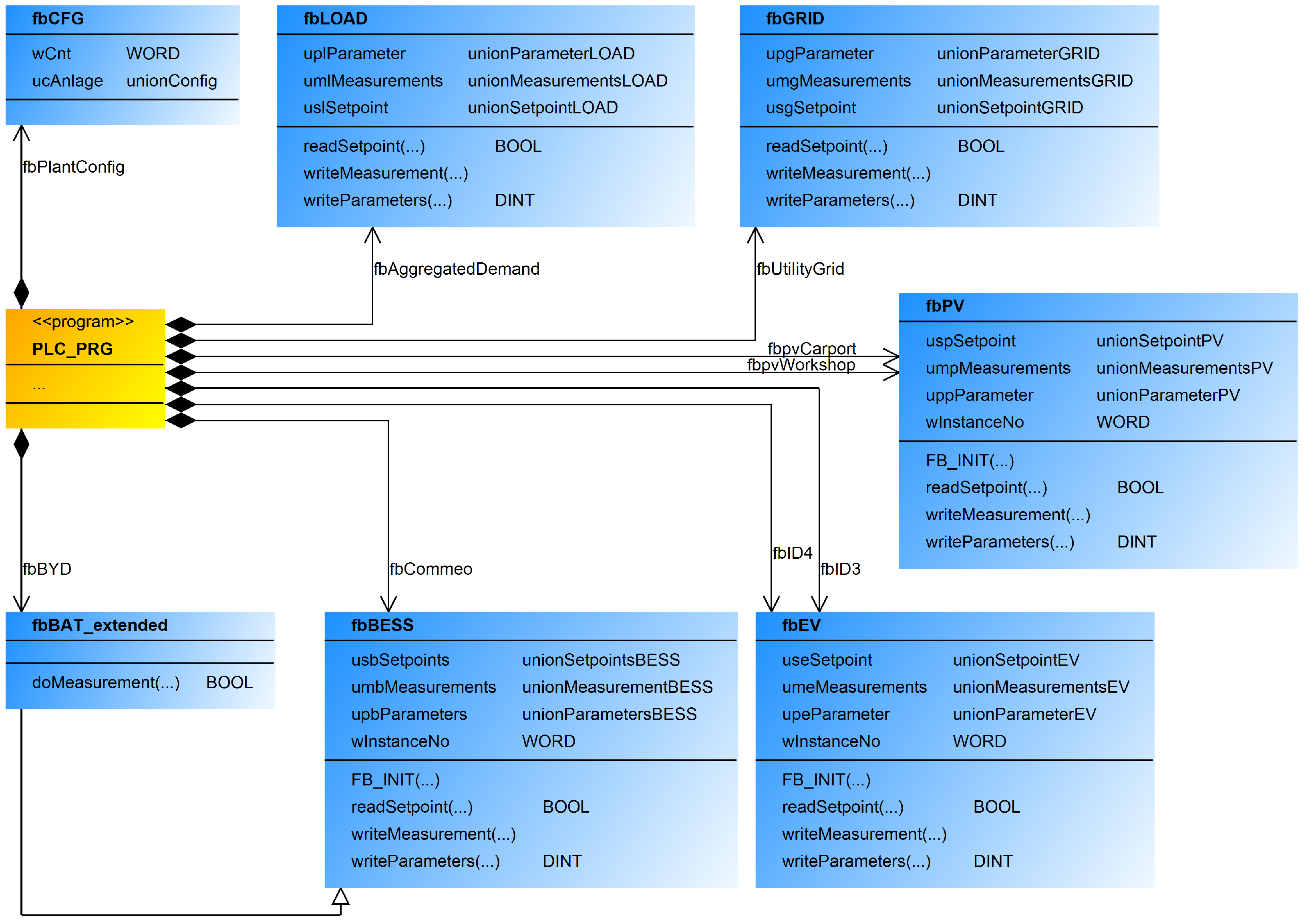
2.3. Programming Implementation of the Configuration and Measurements (PLC)
2.4. Programming Implementation of the Modular Model Composition (Edge Computer)
2.5. Extension on Mixed Integer and Nonlinear Problem Formulation
2.6. System Test Conditions of the MPC Controller
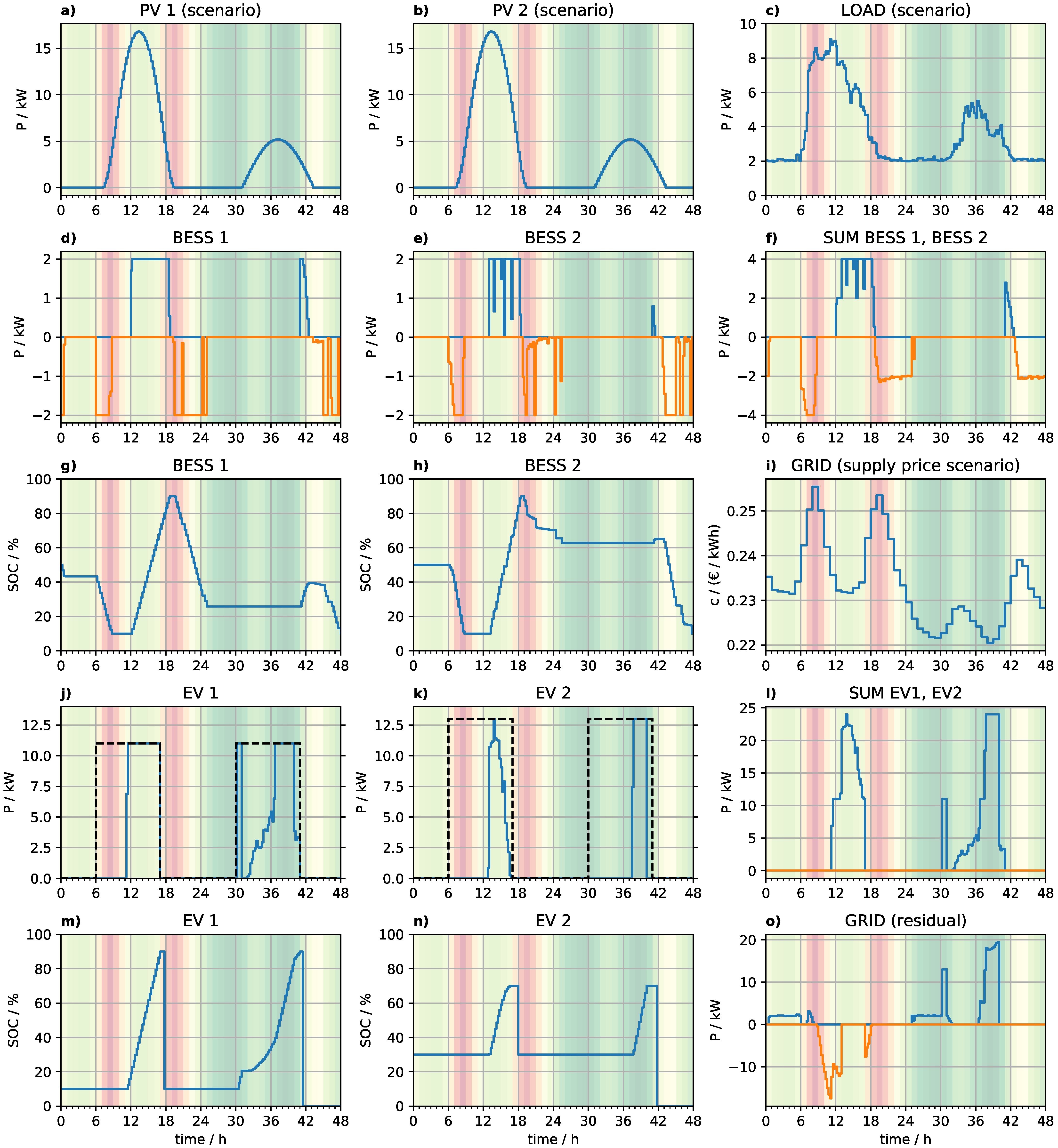
3. Results
4. Discussion
- Giving privilege to early charging when excess renewable power is available by adding a cost term to the objective function that penalises the charging power of storage devices and that increases over time. The cost per Watt must be small enough not to significantly alter the objective function value. This privilege can be given under the assumption that the forecast quality decreases over time. Thus, it is intuitive to use surplus renewable generation earlier rather than later, as later surplus generation may not be available anymore if the forecast is wrong. Privileging earlier charging does not have negative influences in case the forecast is right; therefore, there is no trade-off to be taken, as long as the original objective is not substantially changed by the added costs.
- Giving privilege to selected storage devices by adding a device-specific charging cost to the objective function that penalises the charging of storage devices more/less than others. Again, the cost per Watt must be small enough to not significantly alter the objective function value. A privilege sequence can be established by gradually offsetting the cost terms of the storage units.
- The commissioner has the possibility to ignore the device specific charging and discharging of the BESSs. He can use the summary charging and discharging power and share it among the two units. This can be conducted either equally or weighted with the SOCs, capacities, etc. of the storage units. Of course, the equality and inequality constraints have to be met. Nevertheless, this is the case anyway, as the PLC must continuously meet the constraints, because the economic optimisation is conducted only every 15 min and the real PV or load power can differ from the assumed prediction scenarios. This approach, however, is not suitable for the EVs, as their presence and SOC thresholds are device specific, and a summarised power approach is not possible.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A | Set of PV power plants |
| B | Set of BESSs |
| Set of EVs | |
| PV index | |
| BESS index | |
| EV index | |
| Grid supply power | |
| Grid feed-in power | |
| Supply power of PV power plant | |
| Summarised supply power of all PV plants | |
| Charge power of BESS | |
| Discharge power of BESS | |
| Energy content of BESS | |
| Summarised energy content of all BESSs | |
| Charge power of EV | |
| Discharge power of EV | |
| Discharge power of EV by driving | |
| Summarised charge power of all EVs | |
| Summarised discharge power of all EVs | |
| Energy content of EV | |
| Summarised energy content of all EVs | |
| k | Discretisation timestep |
| Time at step k | |
| i | Generalised index of the components |
| Sampling interval | |
| N | Number of timesteps |
| Charging efficiency of BESS | |
| Charging efficiency of EV | |
| Discharging efficiency of BESS | |
| Discharging efficiency of EV | |
| Power forecast of PV plant | |
| Power forecast of load | |
| Maximum power of general component i | |
| Power of general component i at timestep k | |
| Energy content of general component i at timestep k | |
| State of charge of BESS | |
| State of charge of EV | |
| Capacity of BESS | |
| Capacity of EV | |
| Feed-in tariff | |
| Dynamic electricity tariff at timestep k | |
| Feed-in tariff of PV plant | |
| Installed power of PV plant | |
| Installed power of all PV plants | |
| Power vector of general component i | |
| Energy vector of general component i | |
| State vector | |
| Cost vector | |
| Equality constraint matrix | |
| Upper bound inequality constraint matrix | |
| Equality constraint vector | |
| Upper bound inequality constraint vector | |
| Lower bounds | |
| Upper bounds | |
| BESS | Battery electric storage system |
| EC | Edge computer |
| EV | Electric vehicle |
| FB | Functional block |
| FBD | Functional block diagram language |
| ICT | Information and communication technology |
| MPC | Model predictive control |
| PLC | Programmable logic controller |
| PV | Photovoltaic |
| SME | Small and medium enterprise |
| SOC | State of charge |
| UML | Unified modeling language |
References
- Garcia-Torres, F.; Zafra-Cabeza, A.; Silva, C.; Grieu, S.; Darure, T.; Estanqueiro, A. Model Predictive Control for Microgrid Functionalities: Review and Future Challenges. Energies 2021, 14, 1296. [Google Scholar] [CrossRef]
- Ferreau, H.; Almér, S.; Verschueren, R.; Diehl, M.; Frick, D.; Domahidi, A.; Jerez, J.; Stathopoulos, G.; Jones, C. Embedded Optimization Methods for Industrial Automatic Control. IFAC-PapersOnLine 2017, 50, 13194–13209. [Google Scholar] [CrossRef]
- Krupa, P.; Limon, D.; Alamo, T. Implementation of Model Predictive Control in Programmable Logic Controllers. IEEE Trans. Control Syst. Technol. 2021, 29, 1117–1130. [Google Scholar] [CrossRef]
- Johansen, T.A. Toward Dependable Embedded Model Predictive Control. IEEE Syst. J. 2017, 11, 1208–1219. [Google Scholar] [CrossRef] [Green Version]
- Thieblemont, H.; Haghighat, F.; Ooka, R.; Moreau, A. Predictive control strategies based on weather forecast in buildings with energy storage system: A review of the state-of-the art. Energy Build. 2017, 153, 485–500. [Google Scholar] [CrossRef] [Green Version]
- Drgoňa, J.; Arroyo, J.; Figueroa, I.C.; Blum, D.; Arendt, K.; Kim, D.; Ollé, E.P.; Oravec, J.; Wetter, M.; Vrabie, D.L.; et al. All you need to know about model predictive control for buildings. Annu. Rev. Control 2020, 50, 190–232. [Google Scholar] [CrossRef]
- Forbes, M.G.; Patwardhan, R.S.; Hamadah, H.; Gopaluni, R.B. Model Predictive Control in Industry: Challenges and Opportunities. IFAC-PapersOnLine 2015, 48, 531–538. [Google Scholar] [CrossRef]
- Lucia, S.; Tătulea-Codrean, A.; Schoppmeyer, C.; Engell, S. Rapid development of modular and sustainable nonlinear model predictive control solutions. Control Eng. Pract. 2017, 60, 51–62. [Google Scholar] [CrossRef]
- Verschueren, R.; Frison, G.; Kouzoupis, D.; van Duijkeren, N.; Zanelli, A.; Quirynen, R.; Diehl, M. Towards a modular software package for embedded optimization. IFAC-PapersOnLine 2018, 51, 374–380. [Google Scholar] [CrossRef]
- Kathirgamanathan, A.; Rosa, M.D.; Mangina, E.; Finn, D.P. Data-driven predictive control for unlocking building energy flexibility: A review. Renew. Sustain. Energy Rev. 2021, 135, 110120. [Google Scholar] [CrossRef]
- IEC 61131-3:2013. Programmable Controllers—Part 3: Programming Languages; Standard, International Organisation for Standardization: Geneva, Switzerland, 2013. [Google Scholar]
- Sehr, M.A.; Lohstroh, M.; Weber, M.; Ugalde, I.; Witte, M.; Neidig, J.; Hoeme, S.; Niknami, M.; Lee, E.A. Programmable Logic Controllers in the Context of Industry 4.0. IEEE Trans. Ind. Inform. 2021, 17, 3523–3533. [Google Scholar] [CrossRef]
- Kull, T.; Zeilmann, B.; Fischerauer, G. Field-Ready Implementation of Linear Economic Model Predictive Control for Microgrid Dispatch in Small and Medium Enterprises. Energies 2021, 14, 3921. [Google Scholar] [CrossRef]
- VDE-AR-N 4100. Technische Anschlussregeln Niederspannung; Standard, VDE Verlag: Berlin, Germany, 2019. [Google Scholar]
- Commission Regulation (EU) 2016/631. Establishing a network code on requirements for grid connection of generators. Off. J. Eur. Union 2016, 631, 1–68. [Google Scholar]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Jin, X.; Vora, A.; Hoshing, V.; Saha, T.; Shaver, G.; Wasynczuk, O.; Varigonda, S. Applicability of available Li-ion battery degradation models for system and control algorithm design. Control. Eng. Pract. 2018, 71, 1–9. [Google Scholar] [CrossRef]
- WAGO. 750-8212 Controller PFC200, 2nd Generation; Datasheet; WAGO Kontakttechnik GmbH & Co. KG: Minden, Germany, 2021; Available online: https://www.wago.com/global/plcs-%E2%80%93-controllers/controller-pfc200/p/750-8212 (accessed on 25 October 2021).
- WAGO. 752-9400 Edge Computer; Datasheet; WAGO Kontakttechnik GmbH & Co. KG: Minden, Germany, 2021; Available online: https://www.wago.com/global/plcs-%E2%80%93-controllers/edge-computer/p/752-9400 (accessed on 25 October 2021).
- Python Software Foundation. Python Language Reference, Version 3.8.8. Available online: https://docs.python.org (accessed on 5 August 2021).
- Mitchell, S.; Peschiera, F.; Duquesne, C.M.; O’Neil, R.J.; Usher, W.; Hsueh, F.Y.; Prypin, O.; Detha, U.; Feng, J.; Marvin, A.; et al. Coin-or/Pulp: Version 2.4. 2020. Available online: https://zenodo.org/record/4326970#.YYy4froxVjU (accessed on 25 October 2021).
- Forrest, J.; Vigerske, S.; Ralphs, T.; Hafer, L.; Fasano, J.; Santos, H.G.; Saltzman, M.; Gassmann, H.; Kristjansson, B.; King, A. Coin-or/Clp: Version 1.17.6. 2020. Available online: https://zenodo.org/record/3748677#.YYy4k7oxVjU (accessed on 25 October 2021).
- Forrest, J.; Vigerske, S.; Santos, H.G.; Ralphs, T.; Hafer, L.; Kristjansson, B.; Fasano, J.; Straver, E.; Lubin, M.; Lougee, R.; et al. Coin-or/Cbc: Version 2.10.5. 2020. Available online: https://zenodo.org/record/3700700#.YYy4rroxVjU (accessed on 25 October 2021).
- Littlewood, B. Complexity is the enemy of dependability—Can diversity provide a defence? In Proceedings of the Eighth IEEE International Conference on Engineering of Complex Computer Systems, Greenbelt, MD, USA, 2–4 December 2002. [Google Scholar]
- Sangi, R.; Kümpel, A.; Müller, D. Real-life implementation of a linear model predictive control in a building energy system. J. Build. Eng. 2019, 22, 451–463. [Google Scholar] [CrossRef]
- Bolzoni, A.; Parisio, A.; Todd, R.; Forsyth, A. Model Predictive Control for optimizing the flexibility of sustainable energy assets: An experimental case study. Int. J. Electr. Power Energy Syst. 2021, 129, 106822. [Google Scholar] [CrossRef]


| Device Parameter | Unit | EV1 | EV2 | BESS1 | BESS2 |
|---|---|---|---|---|---|
| kW | 11 | 13 | 2 | 2 | |
| kW | 0 | 0 | 2 | 2 | |
| C | kWh | 77 | 77 | 16 | 11.04 |
| % | 99 | 99 | 98 | 95 | |
| % | 10 | 30 | n/a | n/a | |
| % | 90 | 70 | n/a | n/a | |
| % | n/a | n/a | 10 | 90 | |
| % | n/a | n/a | 10 | 90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kull, T.; Zeilmann, B.; Fischerauer, G. Modular Model Composition for Rapid Implementations of Embedded Economic Model Predictive Control in Microgrids. Appl. Sci. 2021, 11, 10602. https://doi.org/10.3390/app112210602
Kull T, Zeilmann B, Fischerauer G. Modular Model Composition for Rapid Implementations of Embedded Economic Model Predictive Control in Microgrids. Applied Sciences. 2021; 11(22):10602. https://doi.org/10.3390/app112210602
Chicago/Turabian StyleKull, Tobias, Bernd Zeilmann, and Gerhard Fischerauer. 2021. "Modular Model Composition for Rapid Implementations of Embedded Economic Model Predictive Control in Microgrids" Applied Sciences 11, no. 22: 10602. https://doi.org/10.3390/app112210602
APA StyleKull, T., Zeilmann, B., & Fischerauer, G. (2021). Modular Model Composition for Rapid Implementations of Embedded Economic Model Predictive Control in Microgrids. Applied Sciences, 11(22), 10602. https://doi.org/10.3390/app112210602






