Abstract
The article is devoted to estimating the intensifying efficiency of methane-air ignition by adding a small amount of hydrogen and/or ethylene. It presents features of the experimental determination of the ignition delay period for fuel-air mixtures using shock installation and methods of processing empirical data. The testing of the known ignition kinetic models for methane, hydrogen, and ethylene with air was carried out. The results of test calculations were compared with those previously published, as well as original experiments. The kinetic model was chosen to provide the minimum discrepancy between the calculated and experimental data. The regularities of the effect of hydrogen and ethylene additives on the ignition dynamics of the methane-air mixture for the range of initial pressures from 1 to 8 bar at temperatures from 900 to 1100 K were obtained with the use of non-stationary numerical modeling. Methane-air mixtures with the mass fraction of additives not exceeding 10% were studied. The quantitative indicators of possible reduction in the ignition delay period of methane-air mixtures were detected.
1. Introduction
The use of methane and natural gas as fuel is widespread in the energy and transport industries. The main reasons are the high energy intensity and manufacturability of methane, its relatively low cost, the presence of a large number of raw materials, and the ability to minimize environmental pollution compared to other hydrocarbon fuels in power plants. It is important to mention that the high ratio of the mass fraction of water vapor to the mass fraction of carbon dioxide gH2O/gCO2 is realized in the products of methane combustion. This factor/feature reduces the formation of soot on the elements of power plants compared to the use of other hydrocarbons as fuel.
Along with the advantages of methane, some difficulties can be highlighted in its effective application in practice. These disadvantages include a relatively low rate of oxidative chemical reactions and a narrow concentration range of stable combustion with air. Therefore, the energy-efficient use of methane is associated with the necessity of intensifying combustion by physical or chemical methods.
One of the promising chemical methods for methane combustion intensifying is adding a small amount of highly active components to the main fuel, which makes it possible to accelerate chemical reactions and reduce the concentration of pollutants in the combustion products. To improve the methane combustion characteristics in air, substances such as hydrogen and ethylene can be used. The choice of these additives is based on high combustion temperatures, short times of ignition delay, and wide temperature and pressure ranges for stable ignition and combustion of the fuel-air mixture. However, the addition of hydrogen or ethylene increases the explosiveness of the mixture. Therefore, in order to predict the reactivity, combustion efficiency, and explosiveness of mixtures of methane with hydrogen and ethylene, it is extremely important to determine the dynamic characteristics of ignition. One of the most important dynamic characteristics is the time of ignition delay, which depends on component concentration, temperature, and pressure.
Some fundamental features of methane and air combustion with the addition of hydrogen are presented in [1,2,3,4], where the flame of burning methane was studied with the addition of hydrogen into the fuel.
The analysis [1] was carried out using high-resolution photographs and registration of OH radicals. The addition of hydrogen (up to 29% by volume) reduced the height of the flame and increased the intensity of combustion at the base of the flame due to an increase in the burning rate. An increase in the proportion of hydrogen led to an increase in the concentration of OH radicals and a decrease in CO and NOx radicals in the combustion products. At the same time, the amount of soot in the burner flame was significantly reduced.
The presence of hydrogen may have beneficial effects by increasing laminar burning velocity [2]. Different blend compositions were researched at 300 K and 1 atm. The results showed that the values of the laminar burning velocity are always smaller than those obtained by averaging the corresponding values of the pure fuels in molar proportions. The authors found these results are also true for mixtures at pressure up to 10 atm and temperatures up to 400 K [2].
Hydrogen enrichment is also beneficial in increasing the resistance of the flame to strain-induced extinction [3,4]. The authors [3] investigated lean mixtures with the hydrogen mole fraction in the fuel varying from 0 to 0.5. They found that the intensity of the flame vortex interaction increased when the hydrogen mole fraction in the fuel increased. The addition of hydrogen to methane leads to a more dynamic regime where the continuity of the front is broken locally by the vortex, and it creates the separation of small flame pockets from the main front (H2 > 20% mole).
In article [4], the authors found that the non-equidiffusive effects play a negligible role in this process because the characteristic time of hydrogen diffusion is one order of magnitude higher than the characteristic time of flame roll-up around the vortex.
These data, as well as the concomitant effect of the increase in the flame temperature, were confirmed by calculations [5,6] based on numerical simulation of turbulent combustion of H2/CH4 mixture in the oxygen-containing flow. It was shown by calculation that the addition of ~40% hydrogen (by volume) increased the methane combustion efficiency from 0.78 to 0.96. This is due to the lower activation energies of hydrogen combustion reactions compared to methane combustion reactions. Combustion of a small amount of hydrogen at the beginning of the flame locally increased the flame temperature and intensified the methane combustion.
Combustion of depleted methane-hydrogen mixtures in air was studied in [7]. In this work, the volume fraction of hydrogen in the mixture was 20% and 30%. The work was based on calculated and experimental data of turbulent flame combustion at various pressures. The authors asserted that molecular diffusion and the Lewis number play an important role in the shape of the flame front in the depleted air-fuel mixture. It is supposed that the Lewis number, which characterizes molecular processes of transport, defines the shape of laminar flame to a significant extent. While if turbulent flow prevails, the molecular effects that occur are insignificant against the background of intensive commingling via vortexes. However, the authors assert that even in turbulent flow, this factor can also have a great influence. To prove this statement, the references to the experimental data and results of numerical modeling with the use of the DNS method (Direct Numerical Simulation) are presented. The present work mainly focuses on kinetic processes; however, it is worth mentioning that the addition of hydrogen, which possesses a strong diffusion ability, besides the intensification of kinetic processes, enables the spreading of the flame front even in a turbulent flow.
In some combustion modes [8], using a high-speed chamber and the PLIF method, the effect of destabilization of the flame front and the occurrence of high-frequency pulsations caused by diffusion-thermal instability and flow turbulization during hydrogen combustion were detected. It should be noted that, according to [9,10], flow turbulization increases the average speed of flame spreading in a multicomponent medium. The effects of diffusion-thermal instability occurrence, as well as the increase in the mixture reactivity when hydrogen is added to the turbulent flow, are also confirmed by numerical simulation [11].
In [12], the problems of turbulent flame stability in the model combustion chamber of a gas turbine, in which the burner with low swirl was used, were studied experimentally and numerically. In the experiment, depleted premixed mixtures of methane with hydrogen and air were used at flow velocities of 12–18 m/s. Flame fluctuations were recorded generally in the area of the outer shear layer at the burner rim. The flame with the addition of hydrogen was characterized by the prevalence of dissipating vortices. The authors paid particular attention to the flame base, where there was an intensive exchange of oxidizer and fuel. Based on these results and the results of [13,14,15], it can be assumed that the main mechanisms for excitation of oscillations are Kelvin–Helmholtz instability and the spreading of acoustic waves, which are common for a burner. Expansion of research on combustion of methane with hydrogen is presented in [16]. The change of the shape of a laminar flame of depleted methane-air mixture via the addition of hydrogen additive was studied. It was shown that the addition of hydrogen expands the ranges of the flame breakdown rate. In particular, adding 20% hydrogen increased the blowout rate by 7%, and 40% hydrogen increased the blowout rate by 35%. It was also noted that the addition of hydrogen significantly reduced the radius of curvature of the flame surface.
The particular influence of the hydrogen effect on the diffusion flame shape is presented in [17]. When adding hydrogen to methane, the concentration gradients of reactive particles in front of the flame increase, though the flame length decreases. This factor indicates the intensification of chemical reactions through the addition of hydrogen. The intensification of the ignition and combustion of methane upon the addition of hydrogen was also confirmed by the results of [18], where quantitative data were obtained on the spreading rate of deflagration flame in air + methane + hydrogen mixtures with different contents of H2.
When burning fuel-air mixtures in constant cross-section channels, it should be noted that the addition of hydrogen to methane leads not only to an increase in the spreading velocity of the flame front but also to a change in its shape [19,20,21]. Due to the rapid oxidative reactions of hydrogen, combustion is stabilized in the boundary layer near the channel wall. In this case, the shape of the flame passes from the V-shaped, characteristic of methane combustion, to the M-shaped. The stabilization effect of the M-shaped flame is enhanced along with an increase in the proportion of hydrogen and an increase in the wall temperature.
The practical use of methane and hydrogen mixtures as a fuel for internal combustion engines is considered in [22,23,24,25,26] and in [27,28,29] for power plants based on boiler and turbine devices. In these works, it was shown that the addition of hydrogen (less than 10%) made it possible to reduce NOx emissions and improve the characteristics of power plants due to an increase in the flame spreading rate and homogenization of the mixture in the working zone due to high diffusion of hydrogen.
In addition to hydrogen, other additives to methane are currently being considered to increase its flammability [30] and combustion efficiency. One of these additives is ethylene, which is less explosive and denser than hydrogen. Considering these advantages, as well as its high manufacturability and widespread use in industry, the use of C2H4 as a combustion-intensifying additive for methane can be considered for different power plants. These factors initiated additional studies of the combustion of mixtures CH4 + C2H4 + air.
For example, the study of the combustion rate of a mixture CH4 + C2H4 + air is given in [31]. In this work, the detonation of mixtures with an excess fuel ratio in the range from 0.72 to 1.3 and with a volume fraction of ethylene from 0% to 100% at ambient temperature and pressure in a closed chamber was experimentally investigated. The results showed that ethylene increases the maximum chamber pressure, and the derivative of pressure changes over time. This is due to the reduction in the ignition induction time and the increase in the relative time interval, which is characterized by so-called ‘fast combustion’. To describe the combustion of the fuel mixture, three characteristic modes are chosen, depending on the ethylene content:
- (I)
- combustion mode with a predominance of methane (volumetric ethylene content less than 30%);
- (II)
- transient mode (volumetric ethylene content from 30% to 70%);
- (III)
- combustion mode with a predominance of ethylene (volumetric ethylene content more than 70%).
Some experimental data on the ignition delay of methane, ethylene, propylene and their mixtures at high pressures are presented in [32]. As shown in this work, the presence of ethylene makes it possible to accelerate the methane combustion reactions.
It should be emphasized that the variety of experimental settings and methods for processing empirical data do not allow direct comparison with quantitative results presented by different authors. The example of this difference will be discussed below. Using scattered data requires their normalization and generalization on the basis of a physical model, as well as taking into account the specifics of the experimental determination of the ignition delay period.
Despite this, a preliminary complex analysis of known studies makes it possible to predict the achievement of high ignition efficiency of composite fuel consisting of methane with a small addition of hydrogen and/or ethylene. It is important to mention that the substitution of ethylene for some of the hydrogen can increase the operational efficiency of the mixed gaseous fuel and ensure the high reactivity of the CH4 + H2 + C2H4 mixture with air. The concomitant factor is the increase in the velocity of flame front spreading and the increase in the detonation ability of the mixture.
The use of gaseous fuels based on methane with the addition of hydrogen and ethylene for various heat engines gives a positive effect; however, the feasibility of using this additive requires an understanding of the physical and chemical processes. This requires an estimation of the main indicator, the ignition delay period. At present, there are no studies on the ignition and combustion of such mixed gaseous fuels. Therefore, this work is devoted to the computational-parametric study of the effect of the mixture composition and initial physical conditions on the ignition delay period of CH4 + H2 + C2H4 with air. The work’s tasks were:
- -
- selection and testing of the most suitable kinetic models of mixture ignition for methane, hydrogen, and ethylene with air;
- -
- identification of the features of the calculated and experimental determination of the ignition delay period of fuel-air mixtures using various percussion mechanisms and methods of processing empirical data;
- -
- comparison of test calculation results with the results of previously published and original experiments;
- -
- formation of the calculation database and regularity identification for the influence of the mixture composition and initial conditions on the ignition delay period of CH4 + H2 + C2H4 with air.
The novelty of this work is in researching the kinetic processes of ignition of the fuel mixture, which consists of three elements: methane, ethylene, and hydrogen. The expectation of this effect is improving fuel combustion processes via replacing some amount of hydrogen, which possesses low density, with ethylene. Some private data about the intensification of ignition processes of mixtures in a wide range of temperatures (900–1400 K) and pressures (1–8 bar) were obtained. An estimation of the delay of the ignition period, which is supposed to be the main factor, was made to accomplish this research. There are no researches on ignition and combustion of such commingled gaseous fuels except this work.
2. Features of the Experimental and Calculated Determination of the Ignition Delay Period
To begin with, let us describe the general regularity of most experiments carried out by means of shock installations. Determination of the ignition delay period on shock installations consists of determining the time interval between the passage of direct or reflected shock waves and the beginning of ignition of the fuel-air mixture. To determine the moment the shock wave passes through the fuel-air mixture, piezoelectric pressure sensors can be used in the experiment. By the difference in response time of several sensors located at some distance from each other, the shock wave velocity can be determined. The ignition of the mixture in the experiment can be recorded with emission spectroscopy (ESD), which signals an increase in the concentration of OH radicals. By means of special calibration, the linear correlation between the signal from ESD and the concentration of OH radicals is usually achieved. Typical results of measuring the parameters are shown in Figure 1. There are the filtered oscillograms of the relative values of the recorded signals from the I/Imax sensors in the ignition zone in time t, namely: the signal from the pressure sensor (1) and the emission spectroscopy device (2) here.
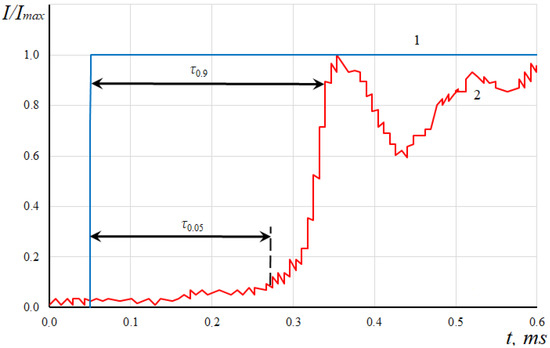
Figure 1.
Oscillogram of readings of the pressure sensor (1) and ESD (2).
It is vital to mention that in practice, two approaches are used to determine the ignition delay period. The first approach determines the time interval from the passage of the shock wave in the investigated region to the appearance of OH radicals there in the amount of about 5% of their maximum value. This time interval is designated by τ0.05. It is considered that at the moment of time τ0.05 the mixture was ignited because the reactions began. However, in a number of cases, further fading of the reactions and the corresponding relaxation of the ESD readings are noted. Therefore, it is assumed that stable ignition of the mixture is realized when the OH concentration reaches about 95% of the maximum value. The time interval corresponding to this value of radical concentration will be denoted by τ0.95.
Taking into account some differences in experimental processing techniques by different authors, to generalize the results, it is often required to normalize the values of the ignition delay period. However, literary sources often lack primary data on the registered I/Imax values, and the authors limit themselves to the final data on the ignition delay period. Therefore, for a complex analysis and generalization of the results, it is required to establish the relationship between the time intervals τ0.05 and τ0.95.
The approach proposed in our work is the analysis of the equation for changing the fuel concentration:
where Cf—fuel concentration, K—chemical reaction rate constant. According to the Arrhenius equation, the constant K depends on chemical properties (preexponential factor and activation energy), as well as on the temperature of the reacting medium. The temperature of the medium is a function of the number of combustible substances that have reacted. These dependencies can be taken into account in the numerical simulation of reactions; however, for primary estimates in the calculations, it is allowed to take the temperature constant and equal to the time-averaged temperature of the reacting medium.
Considering that the difference in concentrations Cf-Cf* is proportional to the expression (COH*-COH)/Y, after integrating Equation (1), it can be obtained that (COH*-COH)/Y = −e−K·t. Here Cf* maximum fuel concentration, COH—current concentration of OH radicals, COH*—maximum concentration of OH radicals, Y—relative stoichiometric coefficient. Thus, the system can be recorded for τ0.05 and τ0.95 time intervals:
Solving system (2), can be obtained an equation for τ0.95:
It should be noted that the coefficient K in Equation (3) can be determined through mathematical or physical modeling.
Considering the above, for further analysis, we will use the values of τ0.95 intervals. To calculate the true value of the ignition delay period Δτ, it is necessary to take into account the velocity of shock wave spreading D and the velocity of the gas behind the front of the shock wave V2. For this, the following dependency can be applied:
The calculated determination of the ignition delay period is usually determined by non-stationary simulation of ignition in a zero-dimensional closed reactor of constant volume with adiabatic walls or in a digital twin of the shock tube. In this case, the initial conditions (pressure and temperature) are set for the reactor volume, and the equations of chemical kinetics are solved using the selected reaction mechanisms. The shock tube digital twin requires a conjugate solution to the equations of gas dynamics and chemical kinetics. Based on the simulation results, the law of change in the calculated range of physical parameters (pressure and temperature), as well as the concentration of OH radicals, is determined.
Simulation in a zero-dimensional reactor allows obtaining directly the value of Δτ as the difference between the start of the calculation and the moment corresponding to τ0.95. In this case, to analyze the calculation results using the digital twin of the shock tube, a technique similar to that of processing a physical experiment is used.
3. Analysis of Existing Kinetic Mechanisms
A detailed kinetic mechanism of ignition and combustion of hydrocarbons with air was proposed in [33] and subsequently developed in other works. Today, detailed mechanisms can contain a few hundred to several thousand components. The number of forward and reverse reactions can exceed 104. Such a large number of components and reactions complicates the practical use of detailed kinetic mechanisms in modern calculations of the flow fields of combustion chambers of propulsion and power plants, taking into account the spatial configuration and turbulent nature of the flow [34]. In addition, the validation of detailed kinetic mechanisms remains an important task and has not yet been fully resolved.
In practice, the most popular and validated are reduced kinetic mechanisms, which make it possible to describe fuel combustion in a selected range of conditions without a significant loss of modeling accuracy in comparison with the original detailed mechanism. At the moment, there are a large number of reduced kinetic mechanisms describing the ignition and combustion of hydrocarbons. We will conduct some preliminary analyses of them based on research by other authors. The most common reduced kinetic mechanisms are [35]: GRI-Mech 3.0, USC Mech II, ARAMCO, FFCM, as well as their modifications. Less common are the author’s reduced mechanisms, which can give a higher agreement with experiments for special problems.
Since in our work, the ignition delay period of methane-air mixtures with additions of ethylene and hydrogen is investigated, the analysis of the reduced kinetic mechanisms describing the combustion of these gases is carried out. It should be emphasized that there are no experimental data on the ignition of CH4 + H2 + C2H4 mixture with air; therefore, a preliminary selection of the kinetic model and comparison of the results with the experiment was carried out for the process of ignition of individual substances (CH4 and H2), as well as a mixture of CH4 + H2 with air.
Let us consider the process of methane ignition. Work [36] is based on measuring the laminar flame velocity and the ignition delay period of methane–air mixtures at elevated pressures and temperatures in a constant volume bomb and shock tube. In this work, three kinetic mechanisms are compared with experimental data: GRI-Mech 3.0, USC Mech II, Aramco Mech 1.3. As a result of the analysis of the data obtained, the authors proposed a formula describing the dependence of the ignition delay period on the main characteristics of the mixture before ignition. However, the presented calculation method gives discrepancies with experimental data at high pressures.
Good agreement of the calculation results with experiments on the ignition of mixtures of hydrogen with air, methane with air, and natural gas with air were obtained for the kinetic models ARAMCO and FFCM. The results are presented in papers [37,38,39].
A special place is occupied by the results of [40], in which a noticeable discrepancy with other works with similar experimental conditions occurs. The measurement of the ignition delay period for methane–air mixtures was carried out behind reflected shock waves. The experiments were conducted at a fixed pressure of 1.8 MPa and fuel excess ratios of 0.5 and 1.0 in the temperature range of 800–1000 K. In this work, calculations were also performed using four well-known kinetic mechanisms: UBC Mech 2.1, GRI-Mech 3.0, Aramco Mech 2.0, and USC Mech 2.0. The results of calculations fulfilled using the UBC Mech 2.1 model coincided most closely with the experiment. As an explanation, the author suggests that at high temperatures, the ignition of a near-stoichiometric mixture of methane with air occurs in four stages:
- - induction of deflagration;
- - stable deflagration;
- - transformation between deflagration and detonation;
- - detonation.
In [41], the delay time, excitation, and ignition times for CH4-air mixtures are given, which were simulated using the kinetic mechanisms GRI-Mesh3.0 and developed by the authors Mesh_56.54. The created kinetic mechanism showed satisfactory agreement with GRI-Mesh3.0 and experiments. The authors focused on the key reactions affecting the ignition period of the mixture, which made the Mesh_56.54 mechanism suitable for three-dimensional numerical simulation of the engine. It should be noted that the work used experimental data which were taken from the published literature.
As for the ignition and combustion of hydrogen, according to [42,43], the ignition of hydrogen can be described with high reliability by the mechanisms GRI-Mesh 3.0 and Keromnes-2013 at pressures up to 16 bar and hydrogen content below 40%.
Attempts to improve the coincidence in the dynamics of hydrogen ignition are outlined in [44,45,46], where the author’s kinetic mechanism, the Konnov mechanism, is presented. The results of [47] showed that this mechanism could be extended for an approximate description of the ignition of ethylene, and the Konnov mechanism gives the best quality coincidence in the size of the detonation cell [48]. According to [49], the USC Mesh II model gives good agreement between the calculated ignition delay period and experiment in a wide range of parameters, while the SERDP PAH model 0.1-only at rich fuel mixtures and low pressures.
Let us consider the state of the problem in terms of ignition modeling of mixed fuels with air. The work [50] represents the particular interest, where the study of the ignition delay period of CH4 + H2 with air was carried out under the conditions realized in internal combustion engines. The assessment results were based on numerical simulations using the kinetic mechanisms GRI-Mesh 3.0, AramcoMech 1.3, and USC Mech 2.0. The most consistent with the experimental data was the USC Mech 2.0 mechanism. According to [50,51], the USC Mech 2.0 model gives the best agreement with the experiment. With increasing pressure and temperature, better agreement with the experiment was obtained using the AramcoMech 1.3 model [52].
The results of the study showed that the increase in the proportion of hydrogen reduces the ignition delay period by two orders of magnitude. Analysis of chemical reactions showed that the limiting factors of the ignition rate are the concentrations of CH4 and O2. The leading role at low temperatures is played by the reaction with the participation of H and O2 and at high temperatures by HO2 and H2O2.
The aim of the study [53] was to obtain a simplified kinetic combustion mechanism for the mixture of H2 + CH4 in air to reduce computational costs when simulating the processes of ignition and combustion in internal combustion engines. The proposed kinetic mechanism, partially ignoring the reverse reactions, showed satisfactory agreement with the experimental data. It should be noted that the laminar flame velocity of stoichiometric methane-hydrogen-air mixtures were studied using numerical simulations in the range of initial temperatures of 300–600 K. It is shown that modern kinetic models allow to accurately descript the combustion of such mixtures, and at low hydrogen concentrations (H2 < 50%), a simple global mechanism is sufficient. In the investigated range of initial temperatures, hydrogen weakly affects the laminar flame velocity when its concentration in the mixture is less than 50%. Only a more significant proportion of hydrogen in the fuel gives the beginning of a rapid increase in the investigated value; however, as the initial temperature increases, the effect of the hydrogen content on the combustion rate decreases.
The work [54] considers the rate of laminar combustion of the mixture H2 + CH4 + air. The proportion of hydrogen in the fuel mixture varied from 0 to 1 at φ = 0.8, 1.0, and 1.2. The authors argue that the flame spreading rate increased nonlinearly with an increase in the proportion of hydrogen. The Markstein number changed monotonically with the increase in the hydrogen fraction at φ > 1. With the decrease in φ, the monotony disappeared. The flame front instability was traced at φ < 1 and depended on the hydrogen fraction.
It should be emphasized that a detailed study of methane-ethylene mixture ignition has not been carried out. An example of work related to the combustion of methane and ethylene in a model burner is the study [55]. Experimental and numerical studies of natural gas turbulent flame, ethylene, and mixtures of these fuels in parallel streams with temperatures of 1250–1385 K and oxygen concentrations of 3–11% (vol.), as well as in hot streams, are described here for a better understanding of the turbulent flame structure and the effects of mixing gaseous fuels. In contrast to CH4 and fuel mixtures, in the case of C2H4, a unique collapse of ignition delays was observed at the temperature of about 1100 K due to the competition between the H/H2 and C2H4 ignition paths. Mixing CH4 and C2H4 had only a slight effect on the distribution of OH in a flame stabilized by hot streams but led to a significant decrease in the rate of heat release compared to C2H4.
Analysis of the literature has shown that the kinetic mechanisms of GRI-Mesh 3.0, NUIGMesh 1.1, and AramcoMech 3.0 can be considered to describe the mixture ignition of methane with hydrogen and ethylene in air.
4. Selection and Validation of the Kinetic Ignition Model
Since in this work, the period of the ignition delay of methane with additions of ethylene and hydrogen is considered, the analysis of studies related to the combustion of these gases is carried out. It was compared to 29 studies connected with combustion kinetic mechanisms. The combustion of pure gas in air gives the limiting case for the mixtures under consideration.
Checking of combustion kinetic mechanisms allows estimating possible discrepancies between calculations and experimental data. The calculations were carried out for the closed reactor of constant volume with adiabatic walls. The kinetic mechanisms for modeling the combustion process were considered in the work selected on the basis of analysis of the literature data GRI-Mesh 3.0, NUIGMesh 1.1, and AramcoMech 3.0.
All the experimental data presented have some differences related to the accuracy of assessing the onset of ignition (based on pressure sensors, sensors for the concentration of an additive in a gas, a laser or optical recording system), the locations of the detector system, the geometric features of the tube, the purity of the mixture, and a sufficient holding time to obtain a homogeneous mixture. However, the accumulated experimental data allows us to determine the approximate ignition delay time for each mixture in Table 1. Table 1 summarizes the experimental data for validating kinetic mechanisms.

Table 1.
Experimental data.
From the obtained analysis, it can be seen that the vast majority of works are devoted to the study of the ignition delay time of pure gases. This suggests that supplementation research is poorly understood and promising for the future.
In the overwhelming majority of works, including the data of the article’s authors, stoichiometric ratios of fuel to air were considered, so outside these conditions, there is great potential for research.
The practical impact of this work is that these results allow estimating possible discrepancies between calculations and experimental data. Also, it lets researchers see new fields for their investigations, such as new mixtures of fuel or new research conditions.
A comparison of the experimental data on the ignition delay period given in the literature and the ignition delay period calculated in this work is shown in Figure 2, Figure 3 and Figure 4 for the ignition delays of methane, hydrogen, ethylene, and methane-hydrogen mixture, respectively. The figures show close experimental points for characteristic pressures; lines in the graph indicate the results of calculations based on kinetic mechanisms.
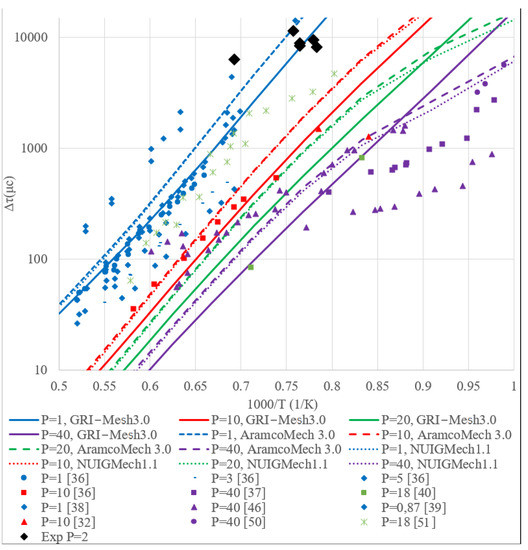
Figure 2.
A summary graph of the ignition delay period dependence on temperature for stoichiometric mixture of CH4 + air.
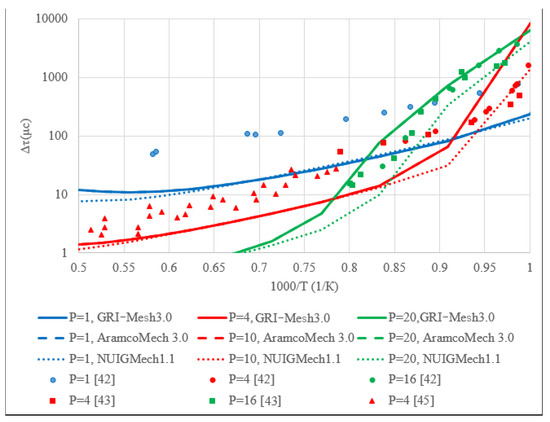
Figure 3.
The summary graph of the ignition delay time dependence on temperature for the stoichiometric mixture H2 + air.
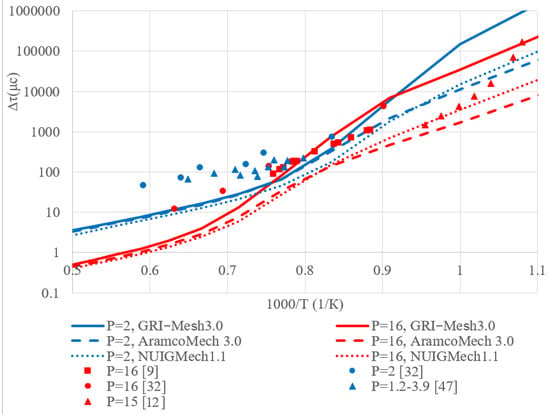
Figure 4.
The summary graph of the ignition delay time dependence on temperature for the stoichiometric mixture C2H4 + air.
In Figure 2, it is clearly explained that numerical modeling of kinetic models AramcoMech3.0 and NUIGMech1.1 differs from the results of GRI-Mesh3.0. Such differences could be explained by the discrepancy in the number of including reactions. This also is the reason for some incline of the curves with the temperature below 1200 K for AramcoMech3.0 и NUIGMech1.1. There is a sufficient coincidence between experimental data and results of numerical calculations with the pressure 1 and 10 bar. Experimental results of the ignition delay period with pressure 18 bar are presented in [40,51] and significantly differ from each other. So it should be emphasized that the variety of experimental settings and methods for processing empirical data do not allow direct comparison with quantitative results presented by different authors.
The results obtained using numerical modeling are between the experimental ones. The range of the experimental data is possibly related to the peculiarities of the experimental design and the method of processing the results. The ignition delay period calculated at a pressure of 40 bar, on average, turns out to be higher than the experimental results, which is possibly due to insufficient debugging of the kinetic models at these pressure levels.
Figure 3 shows that the GRI-Mesh3.0 and AramcoMech3.0 models describe the ignition delay period of hydrogen in air in the same way, which suggests that the hydrogen combustion processes in the two models are based on identical reactions with the same coefficients. The experimental values obtained from various works are also in good agreement with each other.
Comparison of the calculated and experimental data for the ignition delay time of the ethylene-air mixture, presented in Figure 4, shows good agreement at a pressure of P = 16 bar. At a pressure of 2 bar, the experimental values differ visibly from the calculated ones, while the values obtained using various kinetic models are in good agreement with each other.
When comparing the results of limiting the ignition delay period, the NUIGMesh1.1 mechanism turned out to be as close as possible, and it was proposed to use it in further calculations.
5. Influence of Mixture Composition and Initial Conditions on the Ignition Delay Period
The article presents the set of calculations and defines the regularities of changing the ignition delay period τ of methane and additives mixture depending on the mass fractions of combustible components at pressures P = 1–8 bar and at initial temperatures T = 900–1100 K. The following ignition conditions are considered for the most characteristic modes:
- -
- mode № 1–P = 1 bar, Т = 1100 K;
- -
- mode № 2–P = 2 bar, Т = 1000 K;
- -
- mode № 3–P = 2 bar, Т = 1100 K;
- -
- mode № 4–P = 2 bar, Т = 1200 K;
- -
- mode № 5–P = 4 bar, Т = 900 K;
- -
- mode № 6–P = 8 bar, Т = 900 K.
The results obtained by the ignition of methane + hydrogen + ethylene mixture with air at the oxidizer excess coefficients α = 0.5–2 are presented in Table 2, Table 3 and Table 4. Note that when processing the results, it is assumed that the ignition delay period should not exceed 0.5 s. In the case of calculated excess of this value, it is considered that the mixture is difficult to ignite and is excluded from further consideration.

Table 2.
The period of the ignition delay for the mixture of methane + hydrogen + ethylene with air for different modes at α = 0.5.

Table 3.
The period of the ignition delay for the mixture of methane + hydrogen + ethylene with air for different modes at α = 1.0.

Table 4.
The period of the ignition delay for the mixture of methane + hydrogen + ethylene with air for different modes at α = 2.0.
From Table 2, Table 3 and Table 4, it can be seen that the value of the ignition delay period in the air of the fuel based on methane with the addition of hydrogen and ethylene can be reduced up to 3 times relative to the ignition delay period of pure methane with air. It is shown that the minimum values of the ignition delay period were obtained for a mixture of methane with hydrogen. Replacing the hydrogen additive with ethylene slightly increases the ignition delay period (up to 15%), but it is still significantly lower than the ignition delay period of pure methane in air. At the same time, the addition of methane or ethylene significantly expands the temperature and pressure ranges of ignition. The greatest effect of a relative increase in the reactivity of the mixture is observed at low pressures (1–2 bar) and temperatures (<1000 K). Figure 5 shows a graph of the dependence of the ignition delay period for an air–methane–hydrogen mixture. Anything above the blue line is the area of “bad” ignition conditions; below the blue line is the area of conditions for “good” ignition (in the direction of the red arrow).
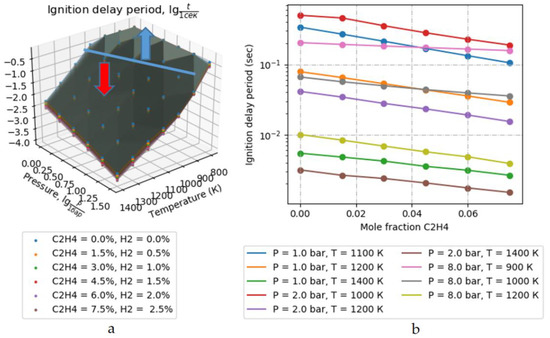
Figure 5.
Graphs of dependence of the air-methane-hydrogen mixture ignition delay period: (a) Summary graph of data; (b) Cut of specific points.
Similar calculations were also carried out for mixtures of methane + hydrogen + ethylene with oxygen (Table 5, Table 6 and Table 7).

Table 5.
The period of the ignition delay of a mixture of methane + hydrogen + ethylene with oxygen for different modes at α = 0.5.

Table 6.
The period of the ignition delay of a mixture of methane + hydrogen + ethylene with oxygen for different modes at α = 1.0.

Table 7.
The period of the ignition delay of a mixture of methane + hydrogen + ethylene with oxygen for different modes at α = 2.0.
In the case of mixture ignition of methane + hydrogen + ethylene in oxygen, chemical reactions are accelerated relative to ignition in air by almost an order of magnitude. In this case, the effect of the use of hydrogen and ethylene additives is somewhat enhanced at low pressures (up to 4%).
6. Conclusions
Based on the comparison of the calculated and experimental data, it is shown that the most satisfactory coincidence of ignition delay period values for mixtures of methane + hydrogen + ethylene with air or oxygen at initial pressures P = 1–8 bar and temperatures T = 900–1100 K can be achieved in the case of using kinetic model NUIGMesh 1.1, which includes 493 components and 2716 reactions.
It is shown that the values of the ignition delay period for the mixtures under consideration are in the range from 0.004 to 0.5 s. According to the data obtained, the ignition delay period of a fuel based on methane with additions of hydrogen and ethylene (up to 10 % in total by mass) can be reduced by up to 3 times relative to the ignition delay period of pure methane in air. It is shown that the minimum values of the ignition delay period were obtained for a mixture of methane with hydrogen. Replacing the hydrogen additive with ethylene slightly increases the ignition delay period (up to 15%), but it is still significantly lower than the ignition delay period for pure methane in air. The greatest effect of a relative increase in the reactivity of the mixture is observed at low pressures (1–2 bar) and temperatures (<1000 K). In the case of ignition of mixtures of methane + hydrogen + ethylene in oxygen, chemical reactions are accelerated relative to ignition in air by almost an order of magnitude. In this case, the effect of hydrogen and ethylene additives is somewhat enhanced at low pressures (up to 4%).
The practical impact of the results obtained in this work is that it is found to correlate and validate different experimental data. The results of the work make it possible to estimate the ignition delay time for fuel on a methane–hydrogen–ethylene gas mixture in air.
This work represents a first step in the direction of investigating the ignition delay time for mixtures. The data produced will be used for future experimental work with new conditions and compositions of the mixture. Further research into the ignition delay time of the methane-based fuel-air mixture suggests:
- -
- reinforcement of the results of kinetic mechanisms by experimental data in some modes;
- -
- the use of other additives to reduce the ignition delay time of the fuel-air mixture;
- -
- the development of its own kinetic mechanism based on the obtained results, which allows the satisfactory description of the generalized data.
Author Contributions
Conceptualization, V.S.Z.; Formal analysis, A.Y.V.; Writing—original draft, S.V.G., A.V.N., and V.M.E.; Writing—review & editing, L.S.Y. and K.Y.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Ministry of Science and Higher Education of the Russian Federation Agreement No 075-15-2020-806 dated 29 September 2020.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schefer, R.; Wicksall, D.; Agrawal, A. Combustion of hydrogen-enriched methane in a lean premixed swirl-stabilized burner. Proc. Combust. Inst. 2002, 29, 843–851. [Google Scholar] [CrossRef]
- Di Sarli, V.; Di Benedetto, A. Laminar burning velocity of hydrogen–methane/air premixed flames. Int. J. Hydrogen Energy 2007, 32, 637–646. [Google Scholar] [CrossRef]
- Di Sarli, V.; Di Benedetto, A.; Long, E.; Hargrave, G. Time-Resolved Particle Image Velocimetry of dynamic interactions between hydrogen-enriched methane/air premixed flames and toroidal vortex structures. Int. J. Hydrogen Energy 2012, 37, 16201–16213. [Google Scholar] [CrossRef] [Green Version]
- Di Sarli, V.; Di Benedetto, A. Effects of Non-Equidiffusion on unsteady propagation of hydrogen-enriched methane/air premixed flames. Int. J. Hydrogen Energy 2013, 38, 7510–7518. [Google Scholar] [CrossRef]
- Afarin, Y.; Tabejamaat, S. Effect of hydrogen on H2/CH4 flame structure of MILD combustion using the LES method. Int. J. Hydrogen Energy 2013, 38, 3447–3458. [Google Scholar] [CrossRef]
- Hernández-Pérez, F.E.; Groth, C.P.; Gulder, O. Large-eddy simulation of lean hydrogen–methane turbulent premixed flames in the methane-dominated regime. Int. J. Hydrogen Energy 2014, 39, 7147–7157. [Google Scholar] [CrossRef] [Green Version]
- Dinkelacker, F.; Manickam, B.; Muppala, S. Modelling and simulation of lean premixed turbulent methane/hydrogen/air flames with an effective Lewis number approach. Combust. Flame 2011, 158, 1742–1749. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, J.; Xie, Y.; Jin, W.; Wei, Z.; Huang, Z.; Kobayashi, H. Flame front structure and burning velocity of turbulent premixed CH4/H2/air flames. Int. J. Hydrogen Energy 2013, 38, 11421–11428. [Google Scholar] [CrossRef]
- Sun, Z.-Y.; Li, G.-X. Turbulence influence on explosion characteristics of stoichiometric and rich hydrogen/air mixtures in a spherical closed vessel. Energy Convers. Manag. 2017, 149, 526–535. [Google Scholar] [CrossRef]
- Sun, Z.-Y. Experimental studies on the explosion indices in turbulent stoichiometric H2/CH4/air mixtures. Int. J. Hydrogen Energy 2019, 44, 469–476. [Google Scholar] [CrossRef]
- Day, M.S.; Gao, X.; Bell, J.B. Properties of lean turbulent methane-air flames with significant hydrogen addition. Proc. Combust. Inst. 2011, 33, 1601–1608. [Google Scholar] [CrossRef]
- Therkelsen, P.L.; Portillo, J.E.; Littlejohn, D.; Martin, S.M.; Cheng, R.K. Self-induced unstable behaviors of CH4 and H2/CH4 flames in a model combustor with a low-swirl injector. Combust. Flame 2013, 160, 307–321. [Google Scholar] [CrossRef]
- Arefyev, K.Y.; Krikunova, A.; Panov, V.A. Experimental study of premixed methane–air flame coupled with an external acoustic field. J. Phys. Conf. Ser. 2019, 1147, 012050. [Google Scholar] [CrossRef] [Green Version]
- Arefyev, K.Y.; Krikunova, A.; Panov, V.A. Complex Effect of Electric and Acoustic Fields on Air-methane Flame Blow-off Characteristics. High Temp. 2019, 57, 909–915. [Google Scholar] [CrossRef]
- Krikunova, A.I.; Arefyev, K.Y.; Saveliev, A.S.; Kossov, G.A.; Cheshko, A.D. Inverted conical methane/air flame shape transformation under acoustic excitation. Phys. Fluids 2021, 33, 053610. [Google Scholar] [CrossRef]
- Emadi, M.; Karkow, D.; Salameh, T.; Gohil, A.; Ratner, A. Flame structure changes resulting from hydrogen-enrichment and pressurization for low-swirl premixed methane–air flames. Int. J. Hydrogen Energy 2012, 37, 10397–10404. [Google Scholar] [CrossRef]
- Li, D.; Wang, R.; Yang, G.; Wan, J. Effect of hydrogen addition on the structure and stabilization of a micro-jet methane diffusion flame. Int. J. Hydrogen Energy 2021, 46, 5790–5798. [Google Scholar] [CrossRef]
- Shoshin, Y.; de Goey, L. Experimental study of lean flammability limits of methane/hydrogen/air mixtures in tubes of different diameters. Exp. Therm. Fluid Sci. 2010, 34, 373–380. [Google Scholar] [CrossRef]
- Guiberti, T.; Durox, D.; Scouflaire, P.; Schuller, T. Impact of heat loss and hydrogen enrichment on the shape of confined swirling flames. Proc. Combust. Inst. 2015, 35, 1385–1392. [Google Scholar] [CrossRef]
- Gao, J.; Hossain, A.; Nakamura, Y. Flame base structures of micro-jet hydrogen/methane diffusion flames. Proc. Combust. Inst. 2017, 36, 4209–4216. [Google Scholar] [CrossRef]
- Yu, M.; Zheng, K.; Zheng, L.; Chu, T.; Guo, P. Effects of hydrogen addition on propagation characteristics of premixed methane/air flames. J. Loss Prev. Process. Ind. 2015, 34, 1–9. [Google Scholar] [CrossRef]
- Lim, G.; Lee, S.; Park, C.; Choi, Y.; Kim, C. Effect of ignition timing retard strategy on NOx reduction in hydrogen-compressed natural gas blend engine with increased compression ratio. Int. J. Hydrogen Energy 2014, 39, 2399–2408. [Google Scholar] [CrossRef]
- Zhao, J.; Ma, F.; Xiong, X.; Deng, J.; Wang, L.; Naeve, N.; Zhao, S. Effects of compression ratio on the combustion and emission of a hydrogen enriched natural gas engine under different excess air ratio. Energy 2013, 59, 658–665. [Google Scholar] [CrossRef]
- Di Iorio, S.; Sementa, P.; Vaglieco, B.M. Experimental investigation on the combustion process in a spark ignition optically accessible engine fueled with methane/hydrogen blends. Int. J. Hydrogen Energy 2014, 39, 9809–9823. [Google Scholar] [CrossRef]
- Kriaučiūnas, D.; Pukalskas, S.; Rimkus, A.; Barta, D. Analysis of the Influence of CO2 Concentration on a Spark Ignition Engine Fueled with Biogas. Appl. Sci. 2021, 11, 6379. [Google Scholar] [CrossRef]
- Mariani, A.; Unich, A.; Minale, M. Combustion of Hydrogen Enriched Methane and Biogases Containing Hydrogen in a Controlled Auto-Ignition Engine. Appl. Sci. 2018, 8, 2667. [Google Scholar] [CrossRef] [Green Version]
- He, D.; Yu, Y.; Kuang, Y.; Wang, C. Model Comparisons of Flow and Chemical Kinetic Mechanisms for Methane–Air Combustion for Engineering Applications. Appl. Sci. 2021, 11, 4107. [Google Scholar] [CrossRef]
- Diaz, G.J.A.; Montoya, J.P.G.; Martinez, L.A.C.; Olsen, D.B.; Navarro, A.S. Influence of engine operating conditions on combustion parameters in a spark ignited internal combustion engine fueled with blends of methane and hydrogen. Energy Convers. Manag. 2019, 181, 414–424. [Google Scholar] [CrossRef]
- Shih, H.-Y.; Liu, C.-R. A computational study on the combustion of hydrogen/methane blended fuels for a micro gas turbines. Int. J. Hydrogen Energy 2014, 39, 15103–15115. [Google Scholar] [CrossRef]
- Boulahlib, M.S.; Medaerts, F.; Boukhalfa, M.A. Experimental study of a domestic boiler using hydrogen methane blend and fuel-rich staged combustion. Int. J. Hydrogen Energy 2021, 46, 37628–37640. [Google Scholar] [CrossRef]
- Liu, W.; Kelley, A.; Law, C. Flame propagation and counterflow nonpremixed ignition of mixtures of methane and ethylene. Combust. Flame 2010, 157, 1027–1036. [Google Scholar] [CrossRef]
- Wang, T.; Luo, Z.; Wen, H.; Cheng, F.; Liu, L.; Su, Y.; Liu, C.; Zhao, J.; Deng, J.; Yu, M. The explosion enhancement of methane-air mixtures by ethylene in a confined chamber. Energy 2021, 214, 119042. [Google Scholar] [CrossRef]
- Shao, J.; Davidson, D.F.; Hanson, R.K. A shock tube study of ignition delay times in diluted methane, ethylene, propene and their blends at elevated pressures. Fuel 2018, 225, 370–380. [Google Scholar] [CrossRef]
- Westbrook, C.K.; Dryer, F.L. Simplified Reaction Mechanisms for the Oxidation of Hydrocarbon Fuels in Flames. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- Zettervall, N.; Fureby, C.; Nilsson, E. Evaluation of Chemical Kinetic Mechanisms for Methane Combustion: A Review from a CFD Perspective. Fuels 2021, 2, 210–240. [Google Scholar] [CrossRef]
- Hu, E.; Li, X.; Meng, X.; Chen, Y.; Cheng, Y.; Xie, Y.; Huang, Z. Laminar flame speeds and ignition delay times of methane–air mixtures at elevated temperatures and pressures. Fuel 2015, 158, 1–10. [Google Scholar] [CrossRef]
- Huang, J.; Hill, P.; Bushe, W.; Munshi, S. Shock-tube study of methane ignition under engine-relevant conditions: Experiments and modeling. Combust. Flame 2004, 136, 25–42. [Google Scholar] [CrossRef]
- Shao, J.; Choudhary, R.; Davidson, D.F.; Hanson, R.K.; Barak, S.; Vasu, S. Ignition delay times of methane and hydrogen highly diluted in carbon dioxide at high pressures up to 300 atm. Proc. Combust. Inst. 2019, 37, 4555–4562. [Google Scholar] [CrossRef]
- Koroglu, B.; Pryor, O.M.; Lopez, J.; Nash, L.; Vasu, S.S. Shock tube ignition delay times and methane time-histories measurements during excess CO2 diluted oxy-methane combustion. Combust. Flame 2016, 164, 152–163. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Sun, W.; Huang, W.; Qin, X.; Liu, J.; Dong, B.; Quan, Y.; Huang, Z. Multistage Auto-ignition of Undiluted Me-thane/Air Mixtures under Engine-relevant Condition. J. Chem. Res. Appl. 2019, 2, 898. [Google Scholar] [CrossRef]
- Bates, L.; Bradley, D.; Gorbatenko, I.; Tomlin, A.S. Computation of methane/air ignition delay and excitation times, using comprehensive and reduced chemical mechanisms and their relevance in engine autoignition. Combust. Flame 2017, 185, 105–116. [Google Scholar] [CrossRef]
- Herzler, J.; Naumann, C. Shock-tube study of the ignition of methane/ethane/hydrogen mixtures with hydrogen contents from 0% to 100% at different pressures. Proc. Combust. Inst. 2009, 32, 213–220. [Google Scholar] [CrossRef] [Green Version]
- Hu, E.; Pan, L.; Gao, Z.; Lu, X.; Meng, X.; Huang, Z. Shock tube study on ignition delay of hydrogen and evaluation of various kinetic models. Int. J. Hydrogen Energy 2016, 41, 13261–13280. [Google Scholar] [CrossRef]
- Alekseev, V.A.; Christensen, M.; Konnov, A.A. The effect of temperature on the adiabatic burning velocities of diluted hydrogen flames: A kinetic study using an updated mechanism. Combust. Flame 2015, 162, 1884–1898. [Google Scholar] [CrossRef]
- Konnov, A.A. Remaining uncertainties in the kinetic mechanism of hydrogen combustion. Combust. Flame 2008, 152, 507–528. [Google Scholar] [CrossRef]
- Konnov, A.A. On the role of excited species in hydrogen combustion. Combust. Flame 2015, 162, 3755–3772. [Google Scholar] [CrossRef]
- Xu, C.; Konnov, A. Validation and analysis of detailed kinetic models for ethylene combustion. Energy 2012, 43, 19–29. [Google Scholar] [CrossRef]
- Mével, R.; Javoy, S.; Coudoro, K.; Dupré, G.; Paillard, C.-E. Assessment of H2-CH4-air mixtures oxidation kinetic models used in combustion. Int. J. Hydrogen Energy 2012, 37, 698–714. [Google Scholar] [CrossRef]
- Saxena, S.; Kahandawala, M.; Sidhu, S.S. A shock tube study of ignition delay in the combustion of ethylene. Combust. Flame 2011, 158, 1019–1031. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, J.; Shu, J.; Xie, M.; Liu, J.; Jiang, T.; Peng, Z.; Deng, B. Numerical study on auto-ignition characteristics of hydrogen-enriched methane under engine-relevant conditions. Energy Convers. Manag. 2019, 200, 112092. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, X.; Wei, L.; Zhang, J.; Tang, C.; Huang, Z. Experimental and modeling study on auto-ignition characteristics of methane/hydrogen blends under engine relevant pressure. Int. J. Hydrogen Energy 2012, 37, 19168–19176. [Google Scholar] [CrossRef]
- Donohoe, N.; Heufer, A.; Metcalfe, W.K.; Curran, H.J.; Davis, M.L.; Mathieu, O.; Plichta, D.; Morones, A.; Petersen, E.L.; Güthe, F. Ignition delay times, laminar flame speeds, and mechanism validation for natural gas/hydrogen blends at elevated pressures. Combust. Flame 2014, 161, 1432–1443. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; del Alamo, G.; Gruber, A.; Bothien, M.R.; Seshadri, K.; Williams, F.A. A skeletal mechanism for prediction of ignition delay times and laminar premixed flame velocities of hydrogen-methane mixtures under gas turbine conditions. Int. J. Hydrogen Energy 2019, 44, 18573–18585. [Google Scholar] [CrossRef]
- Okafor, E.C.; Hayakawa, A.; Nagano, Y.; Kitagawa, T. Effects of hydrogen concentration on premixed laminar flames of hydrogen–methane–air. Int. J. Hydrogen Energy 2014, 39, 2409–2417. [Google Scholar] [CrossRef]
- Evans, M.; Chinnici, A.; Medwell, P.; Ye, J. Ignition features of methane and ethylene fuel-blends in hot and diluted coflows. Fuel 2017, 203, 279–289. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).