Abstract
Rotation search and point cloud registration are two fundamental problems in robotics, geometric vision, and remote sensing, which aim to estimate the rotation and transformation between the 3D vector sets and point clouds, respectively. Due to the presence of outliers (probably in very large numbers) among the putative vector or point correspondences in real-world applications, robust estimation is of great importance. In this paper, we present Inlier searching using COmpatible Structures (ICOS), a novel, efficient, and highly robust solver for both the correspondence-based rotation search and point cloud registration problems. Specifically, we (i) propose and construct a series of compatible structures for the two problems, based on which various invariants can be established, and (ii) design time-efficient frameworks to filter out outliers and seek inliers from the invariant-constrained random sampling based on the compatible structures proposed. In this manner, even with extreme outlier ratios, inliers can be effectively sifted out and collected for solving the optimal rotation and transformation, leading to our robust solver ICOS. Through plentiful experiments over standard datasets, we demonstrated that: (i) our solver ICOS is fast, accurate, and robust against over 95% outliers with nearly a 100% recall ratio of inliers for rotation search and both known-scale and unknown-scale registration, outperforming other state-of-the-art methods, and (ii) ICOS is practical for use in real-world application problems including 2D image stitching and 3D object localization.
1. Introduction
Rotation search and point cloud registration are two cornerstones in computer vision, robotics, remote sensing, and photogrammetry. The former has found broad applications in satellite attitude estimation [1], image stitching [2], etc., while the latter has been widely applied in 3D scene reconstruction and modeling [3,4,5,6], object localization and recognition [7,8,9], medical imaging [10], Simultaneous Localization and Mapping (SLAM) [11], archeology [12], etc.
1.1. Problems Formulation
Rotation search aims to find the best rotation that aligns two 3D vector sets in different coordinate frames, which can be formulated as follows.
Given two 3D vector sets and where we consider tuple as a vector correspondence, the following relation is satisfied:
where (the explicit properties and constraints of can be found in [13,14]) denotes the rotation matrix and represents the measurement of Gaussian noise with isotropic covariance ( is the standard deviation and is the identity matrix) and mean w.r.t. the vector correspondence. Thus, the rotation search problem can be mathematically defined as follows:
Problem 1
(Rotation search). The rotation search problem under the perturbance of noise can be equivalently formulated as a minimization problem such that:
where globally optimal solution is the best rotation desired.
Point cloud registration consists of estimating the transformation (including scale, rotation, and translation) between two given 3D point clouds. Now, we introduce the correspondence-based point cloud registration problem.
With two 3D point clouds and , where tuple represents a point correspondence, we can have the following relation:
where is the scale, is the rotation matrix, is the translation vector, and represents the measurement of Gaussian noise similar to that in Problem 1. The generalized point cloud registration problem can be defined as follows.
Problem 2
(Generalized point cloud registration). Solving the generalized point cloud registration problem under the perturbance of noise is equivalent to the following minimization problem:
where global minimizers are the optimal solutions to this registration problem.
When the scale aligning the two point clouds is fixed, which means scale , we can directly omit in Problem 2, called the known-scale registration problem. However, the scale could vary, which, for instance, exists in the cross-source point cloud registration problems. In this case, the scale needs to be estimated additionally, and such problems are called unknown-scale point cloud registration.
Our work seeks to solve both the known-scale and the unknown-scale registration problems in the presence of both noise and a great number of outliers among the putative correspondences, providing a highly robust backend for real applications.
1.2. Motivation and Contributions
Motivation: The correspondence-based rotation search and point cloud registration approaches are often confronted with one difficulty: in many real-world scenes, the input correspondences are very likely to be corrupted by outliers; for example, the feature matchers (e.g., SIFT [15] and SURF [16] for 2D images and FPFH [17] for 3D point clouds) may generate mismatched or spurious results owing to noise, repetitive patterns, low-textured scenes, etc. Therefore, in real applications, robust estimation solvers should be of paramount significance.
When it comes to robust estimation, RANSAC [18] is a common robust heuristic [19], but it has a critical disadvantage: its runtime increases exponentially with the outlier ratio. Thus, RANSAC could be impractical for use when encountering extreme outlier ratios (e.g., more than 90%). Branch-and-Bound (BnB) is able to search in the rotation () or transformation () group to globally optimize the objective function, whereas its computational cost grows exponentially with the input correspondence number; hence, it may be too slow for large-sized problems.
In addition, the outlier removal method GORE [20,21], as well as the nonminimal solvers FGR [22], QUASAR [23], and TEASER/TEASER++ [24,25] have been proposed to deal with the two problems with over 90% outliers. However, for point cloud registration, these solvers can only succeed when the scale between the two point clouds is known and fixed. When the scale varies (e.g., between point clouds formed with different sources), none of these methods could tolerate more than 90% outliers, which indeed necessitates a general solver capable of solving not only the known-scale problems, but also the unknown-scale ones.
To handle rotation search problems with high outlier ratios, though GORE [21] is efficient when the problem size is small, it requires more time to remove outliers as the correspondence number increases. Hence, proposing a high-outlier-ratio-tolerant solver that can be efficient regardless of the correspondence number seems rather imperative.
Contributions: Motivated by these facts, in this paper, we propose a novel highly robust paradigm, named Inlier searching with COmpatible Structures (ICOS), for addressing rotation search and generalized point cloud registration with extreme outlier ratios, as exemplified in Figure 1.
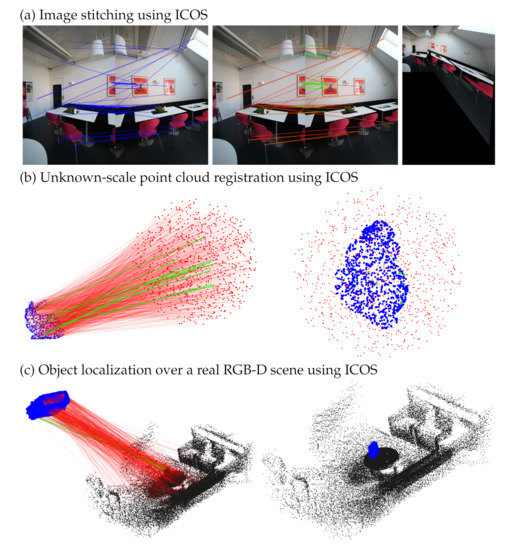
Figure 1.
Rotation search and point cloud registration using ICOS. (a) Image stitching. Left: correspondences matched by SURF [16]. Middle: inliers found by ICOS (green lines). Right: stitched images with the rotation estimated by ICOS. The outlier ratio is over 74%, and ICOS can correctly find the inliers. (b) Unknown-scale point cloud registration. Left: among the 1000 putative correspondences, there exist 990 outliers (red lines) and merely 10 inliers (green lines). Right: ICOS can still estimate the scale, rotation, and translation robustly and precisely. (c) Object localization with an unknown scale in a realistic RGB-D scene [26]. Left: correspondences are built between the object and the scene with over 95% outliers. Right: ICOS can accurately reproject the object back to the scene with the transformation it estimated.
To be specific, ICOS aims to seek the correct inliers through the random sample flow (rather than pruning outliers as performed in the previous works [20,27]), but significantly different from the RANSAC family (e.g., [18,28,29]), the sampling and filtering process of ICOS is built upon and also facilitated by the constraints derived from the compatible structures that we define based on the theory of invariance.
First, we introduced and constructed a series of compatible structures for the rotation search and generalized point cloud registration problems, with which we were able to “customize” special invariant-based constraints that can be used for effectively differentiating inliers from outliers only with simple Boolean conditions (Section 4).
Moreover, we designed sampling-based frameworks that can fit with the compatible structures to seek and preserve eligible inliers out of the putative correspondences for the two problems, in which peculiar constraint-based sampling strategies were employed to optimize time efficiency for the proposed algorithms (Section 5).
Finally, we validated ICOS in a variety of experiments over different datasets and demonstrated that: (i) ICOS is precise and robust even when over 95% of the correspondences are outliers in the rotation search, as well as both the known-scale and unknown-scale registration problems (it can be even robust against up to 99% outliers when correspondences are relatively sufficient); (ii) ICOS runs fast, yields accurate estimates, and recalls approximately 100% of the inliers; (iii) ICOS is also applicable to practical application problems over real datasets (Section 6).
2. Related Work
In this section, we provide reviews on: (i) methods for naive and robust rotation search, (ii) methods for naive and robust point cloud registration, and (iii) heuristics for robust outlier rejection.
Rotation search: The rotation search (also called “Wahba”) problem was first proposed by Wahba in [1], in order to estimate the attitude of satellites from the observation of vectors. It can be solved in closed form based on either a rotation matrix [30,31,32,33] or the quaternion-based parametrization [34,35], although these methods usually fail in the existence of outliers.
It is known to all that in the process of building vector correspondences using the feature descriptors [16,17] based on 2D or 3D keypoints, it is likely to obtain false results and mismatches, that is the so-called outliers. Thus, robust solvers are required.
The BnB framework is effective at finding the optimal rotation from the outlier-corrupted corresponding vectors, and the typical examples include the first globally optimal method searching over the rotation space [36], the L2-distance-based approach [37], and the speeded up angular-distance-based solution [38]. In addition to BnB, guaranteed outlier removal [21] is another way to estimate the rotation robustly and is generally faster than the BnB solvers. Some other robust rotation search solvers are also the subroutines for point cloud registration problems (e.g., [20,22,25]), which will be later discussed in the review on point cloud registration.
Point cloud registration: To solve the point cloud registration problem, the Iterative Closest Point (ICP) [39] is a common local-minimum approach, but it is too dependent on the initial guess of the transformation, thus prone to fail without a good initialization. Therefore, an initialization-free way to address the registration problem —to build correspondences between point clouds from 3D keypoints [40] using feature descriptors (e.g., FPFH [17], ISS [41], and FCGF [42]), has grown increasingly popular. Many correspondence-based methods have been proposed to address the registration problem in the presence of noise. For example, it can be solved using closed-form solutions [32,34] by decoupling the estimation of rotation, scale, and translation. BnB has also been applied to solve the registration problem [43] in a globally optimal way. More recently, the Lagrangian dual relaxation was developed to produce a globally optimal generalized registration solver [14] for handling point-to-point, point-to-line, and point-to-plane registration with optimality guarantees.
However, the 3D feature descriptors generally have lower accuracy and robustness compared with 2D ones [15,16], which could result in relatively higher or even extreme outlier ratios in some real-world scenes, as was discussed in [20]. The above-mentioned solutions are fairly sensitive and can be fragile once there exist outliers among the correspondences, which consequently demands the following robust registration methods.
The minimal closed-form solutions [32,34] can be fit into the RANSAC family frameworks [18,28,29] to deal with outliers, though they may be slow when the outlier ratio is high. Another idea to be robust is that: if as many outliers can be guaranteed to be removed or eliminated as possible, then what remains should be mostly inliers. GORE [20] is such a preprocessing outlier removal approach that guarantees that the correspondences removed must not be inliers. In terms of the nonminimal robust solvers, FGR [22] is the first method using Graduated Nonconvexity (GNC) to reject outliers, which estimates the rigid transformation matrix with a Gauss–Newton method. Though not globally optimal, FGR is efficient for known-scale registration. Currently, TEASER/TEASER++ [24,25] are the more robust nonminimal certifiably globally optimal solvers that can tolerate 99% outliers in known-scale situations. Another recent solution [44] utilizes RANSAC for scale and translation estimation and also adopts GNC to solve the rotation. Unfortunately, all these solvers are either incapable of estimating the scale or unable to tolerate over 90% outliers for unknown-scale point cloud registration (as will be shown in Section 6).
Robust estimators. Apart from the classic hypothesize-and-test framework RANSAC, M-estimation is useful for outlier rejection [22,45,46,47]. When the naive solver is nonminimal, the special M-estimator GNC [48] is a general-purpose estimator operated by alternating optimization and adopts robust cost functions such as Geman–McClure (GM) or Truncated Least Squares (TLS), which can handle 70–80% outliers in robotics or vision problems. In addition, invariants can be applied for robust estimation. This paper is an improved and extended version of our prior work RANSIC [49]. The main differences are as follows: (i) this paper introduces the concept of compatible structures for the first time, which can enable faster termination with extreme outlier ratios (this is shown in experiments); (ii) though both use invariants, RANSIC keeps searching for compatible three-point sets, while ICOS only seeks single correspondences based on an eligible compatible structure, so that novel robust algorithm frameworks are proposed in this paper; (iii) the method’s presentation is more extensive, and the experiments are also enriched in this paper.
3. Notation and Preliminaries
3.1. Invariants
We first define the concept of invariants by borrowing the notation and definition in [27].
Definition 1
(Invariants). In one geometric problem, assume that we obtain N putative correspondences whose indices are in set . Let denote a subset of with a fixed size, denote the vector stacking all variables, denote the measurements w.r.t. subset , denote the corresponding noise measurements independent of , and denote the mathematical model that is used to define the relation between and , given by .
If we find a function where is always satisfied and also independent of no matter which is selected, we can consider as an invariant function, also abbreviated as an invariant.
3.2. Naive and Nonminimal Solvers
In our solver ICOS, the computation of the scale, rotation, and translation without outliers is realized by introducing the fast nonminimal naive solvers below.
Assume that we have M correspondences (inliers); we first need to acquire the corresponding 3D vectors, which, in rotation search, are just the original vector correspondences such that:
while in point cloud registration, this can be represented with the centroid-based translation-free technique [32] such that:
where and are the centroids in the two frames, respectively, given by:
The optimal rotation can be computed in closed-form using Singular-Value Decomposition (SVD) [32] such that:
In point cloud registration, the best scale can be computed by the weighted representation as in [25] such that:
where . With the rotation and the scale obtained, the translation can be recovered using the centroids as:
4. Compatible Structures in the Point Cloud Registration Problem
In this section, we define the Compatible Structures (COSs) for the two problems and then fully explore the potential invariants among them to establish the constraints for the sampling process.
4.1. COS in Rotation Search
The basic structure in rotation search for constrained random sampling is the COS that consists of a pair of correspondences as introduced below.
Definition 2
(2-COS and length-based invariants). Assume we have 2 vector correspondences such that , defined as a 2-COS. We first normalize them all to unit length such that:
Then, we derive the following pairwise length-based invariants as:
where represents the length-based invariant w.r.t. this pair of correspondences and denotes the noise measurement (perturbance) on this invariant.
Intuitively, invariant represents the length difference between the third sides of the two triangles formed by the corresponding vector pairs over the two frames. Without noise perturbance, should be strictly equal to 0 as long as the correspondences pf this pair are both inliers. However, with noise, we can still impose a constraint on to examine whether this correspondence pair might contain outliers.
Proposition 1
(Constraints on ). For the pairwise invariant in the 2-COS defined above, we can derive that:
where L denotes the bound w.r.t. noise satisfying the inequality such that , in which .
Proof.
Based on the triangular inequality and the fact that norm is invariant of , we can always have:
where the length-based inequality (13) can be proven. □
If we have obtained an eligible 2-COS, we can compute the rotation w.r.t. this pair of correspondences using Horn’s triad-based matrix transformation [34] such that:
where “” maps the size-3 noise measurement (vector) to the rotation (for explicit derivations, please refer to Section 7.1.3 in [50]), and denotes the ground truth rotation.
Then, we further try to build a 3-COS by adding a new correspondence with this 2-COS, based on which new constraints can be imposed.
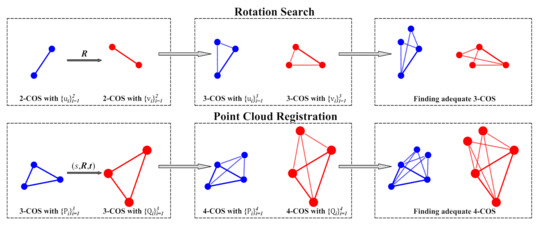
Proposition 2
(3-COS, invariants and constraints). Assume that now we obtain a new correspondence, say the correspondence, in addition to the 2-COS we have, as illustrated in Figure 2 we are able to construct a 3-COS with two more invariants such that:
and two additional length-based constraints are satisfied:
where . Apart from simply constraining the length-based rigidity, we also supplement a residual-based constraint on such that:
where G is the bound for the residual error w.r.t. the correspondence. Besides, for every single 2-COS in this 3-COS, we can compute a raw rotation, represented as with the correspondence tuple . In this fashion, we can impose new constraints on the mutual compatibility between the raw rotations w.r.t. different correspondence tuples selected from this 3-COS such that:
where “∠” is the geodesic distance (error) [51] between two rotations, written as:
where F is the bound of noise for the geodesic error satisfying that and denotes the identity matrix.

Figure 2.
Overview of the inlier searching process of ICOS. We start by finding eligible a-COS across the two point sets, then seek new correspondences that can establish b-COS with the existing a-COS and eventually stop sampling when we collect a sufficient number of eligible b-COS ().
Proof.
Up to now, in rotation search, the constraints over the 2-COS and 3-COS have been established, which will be later converted as a series of Boolean conditions for the sampling and filtering frameworks of ICOS in Section 5.
4.2. COS in Point Cloud Registration
The basic structure in point cloud registration lies in the COS with 3 correspondences.
Definition 3
(3-COS and pairwise scale-based invariants). Assume that we obtain 3 noncollinear point correspondences , defined as one 3-COS. We can derive the following pairwise scale-based invariants:
where , represents the scale-based invariant w.r.t. the and the jth correspondences, denotes the ground truth scale, and denotes the noise measurement on the scale.
Then, we can endow each pair of scale-based invariants with constraints given as follows:
Proposition 3
(Constraints on ). For any two invariants in the 3-COS, we can derive that:
where (here, and denote the same invariant) and A is the noise bound, satisfying that . In addition, when the scale is known (), we can further have that:
Proof.
It is easy to have that:
where , , and .
Subsequently, we calculate the raw scale as:
where and the raw rotation using Horn’s 3-point minimal solver [34], similar to (15). With the raw scale and rotation solved, we can define the translation-based invariants as follows:
Definition 4
(Translation-based invariants). In addition to (22), we can derive the translation-based invariants:
where , represents the translation-based invariant w.r.t. the correspondences and describes its noise measurement. In known-scale cases, we directly set .
To create constraints on any two invariants from this 3-COS, we can derive the following:
Proposition 4
(Constraints on ). For invariants in the 3-COS above, we can derive that:
where and B is the noise bound, satisfying that .
Proof.
The proof here is trivial. □
On the basis of this 3-COS, whenever we obtain a new (the ) correspondence, defined as a 4-COS, additional invariants can be established as follows.
Proposition 5
(4-COS, invariants and constraints). If we have the correspondence in addition to the 3-COS we have, we can first build 3 more scale-based invariants such that:
where , with the following constraints:
where . Similar to Proposition 2, we also supplement a residual-based constraint on such that:
where can be computed from the 3-COS as:
and C is the bound for this residual error. Moreover, for each 3-COS in this 4-COS, we can compute a raw rotation, represented as with the correspondence tuple . Thus, new constraints on the mutual compatibility of rotations can be established as:
where “∠” is also the geodesic error between two rotations, expressed as:
where and D is the noise bound satisfying .
Proof.
So far, we have derived the invariant-based constraints from both the 3-COS and 4-COS for the registration problem, leading to the resulting robust solver ICOS.
5. Our Solver: ICOS
In this section, we formulate our solver ICOS for rotation search and both the known-scale and the unknown-scale point cloud registration problems.
We first provide the insights and overview of the proposed solver. As intuitively illustrated in Figure 2, we begin with finding eligible a-COS across the two point sets by roughly checking the first layer of invariant-based constraints, where for rotation search and for point cloud registration, as discussed in Section 4.
Once an a-COS satisfies the required constraints, we solve the raw solutions (rotation, scale, or translation) with it, which is for further examining whether the second layer of constraints can be satisfied. Holding one eligible a-COS, we then pick random correspondences one after another with testing both their residual-based and invariant-based constraints simultaneously, in order to construct an eligible b-COS, where , on the basis of this a-COS.
The process of finding b-COS continues until we are able to obtain a sufficient number of such b-COS within reasonable times of the single-correspondence random sampling, which also serves as a hidden condition aiming to determine whether the a-COS and its corresponding b-COS can be all true inliers.
The following subsections provide more details on formulating the pseudocode of ICOS for specific problems.
5.1. ICOS for Rotation Search
For addressing the rotation search problem, we render the pseudocode of ICOS in Algorithm 1 and the description for each part as follows.
| Algorithm 1: ICOS for rotation search |
 |
Lines 2–10: ICOS initiates with random sampling. However, different from ordinary random sampling procedures, we impose constraints on each random sample selected. When picking one random subset of 2 correspondences, we immediately check the length-based invariant (13). If it can be satisfied, we solve the raw rotation with this 2-COS and then allow it to proceed to the next step, which is operated by setting ; if not, we start over from the sampling process.
Lines 11–25: If we manage to obtain an eligible 2-COS, say , we can then seek new correspondences to build a 3-COS, also by constrained sampling, where we select and test the correspondence samples one at a time. If one correspondence can satisfy Constraints (17)–(19), indicating that it can form an eligible 3-COS with , we add it to the inlier set and make increase by 1. Once we collect enough 3-COS (), we stop sampling and return the X + 2 inliers in total.
During this process, we supplement an important subroutine: checkSampling, in order to boost time efficiency, which is designed to timely break from the sampling if the obtained 2-COS () does not seem to be inliers, and this operation could be realized by regularly checking the number of 4-COS formed according to the iteration number, as demonstrated in Algorithm 2. To be specific, as long as the correspondences in set are both inliers, at least one inlier correspondence ought to be sampled after a sufficient number of iterations that can be computed from (37) by setting a high confidence; conversely, if the latter condition cannot be satisfied, we have every reason to suppose that set contains at least one outlier.
| Algorithm 2:checkSampling (subroutine of ICOS) |
 |
Lines 26–28: We first compute the rotation with the X+2 inliers and then consider all correspondences whose residual errors satisfy as the ultimate inliers. Finally, we can solve the optimal rotation with all the inliers found among the putative correspondences using the nonminimal estimator (8).
5.2. ICOS for Known-Scale Registration
The pseudocode of ICOS for point cloud registration with a known scale () is given in Algorithm 3.
Lines 2–14: We design a decoupled sampling method for the known-scale registration. First, we select a random subset of 2 correspondences, rather than 3, and check if their scale-based invariant is close enough to 1 using constraint (24). If it is, we then proceed to select random samples for the remaining one correspondence, during which we try forming an eligible 3-COS that satisfies the constraints (24) based on ; if not, we go back to the sampling process to seek .
Lines 15–32: Once an eligible 3-COS (set ) is obtained, we check their constraints (23). If satisfied, we then solve the raw rotation with and determine whether the constraints (30) are fulfilled in . If yes, we then move on to sampling once again, for building one 4-COS based on set . We take random correspondences one at a time and feed them sequentially to to check Constraints (32)–(35). After collecting enough correspondences (X) that can construct qualified 4-COS with , we jump out and return the inliers.
5.3. ICOS for Unknown-Scale Registration
When the scale is unknown, we design a different framework for ICOS, and its pseudocode is shown in Algorithm 4.
Algorithm 4 employs a methodology similar to lines 15–35 of Algorithm 3. The differences lie in that: (i) we are unable to impose the constraints (24) on the 3-COS using the decoupled sampling method as operated in Lines 3–14, since the scale is not fixed, which may result in more runtime than the known-scale problems generally; (ii) the raw scale and the scale-based invariants are not set to 1, but need to be computed as in (22) and (31) instead.
| Algorithm 4: ICOS for unknown-scale registration |
 |
5.4. Discussion on the Maximum Iteration Numbers
Note that in Algorithms 1 and 2, a series of maximum iteration numbers is involved during the sampling process, so now we discuss the proper choice of their values.
Generally, the maximum iteration we set can be given by the following formulation:
where x is the number of eligible inlier subsets desired, p is the confidence for the fact that all the correspondences selected are inliers (typically we choose ), usually the outlier ratio should be within 0–99% (typically, 99% is chosen unless we can know in advance that the outlier ratio is below a certain level), and n is the number of correspondences we select for each random sample (subset).
Therefore, for , we adopted , choosing two correspondences at one time, while for , and , we set all for single-correspondence sampling.
5.5. Discussion on the Performance of ICOS
Since the main body of our solver ICOS consists of simply judging a series of Boolean conditions (true or false) according to the constraints over the invariants w.r.t. different variables, it can be fast to implement. Besides, ICOS abandons the strategy of making an estimate for every random sample selected (as operated in RANSAC) and smartly solves the transformation only when the scale-based constraints (23) and (24) allow it to do so. Furthermore, the residual errors w.r.t. all the correspondences only require being solved once (just for finding the whole inlier set), saving much time for a realistic implementation, especially when the point cloud correspondences are in huge numbers, which is not uncommon in practice.
6. Experiments
In this section, we conduct a series of experiments based on multiple datasets to evaluate the proposed solver ICOS for rotation search and generalized point cloud registration, also in comparison with the existing state-of-the-art solvers. All the experiments were implemented in MATLAB on a laptop with an i7-7700HQ CPU and 16 GB RAM, and no parallelism programming was ever used. The explicit parameter setup for ICOS is given in Table 1.

Table 1.
Parameter setup of ICOS for the rotation search and point cloud registration problems.
6.1. Benchmarking of Rotation Search on Synthetic Data
Experimental setup: We tested our solver ICOS for rotation search over synthetic datasets, where our environmental setup was similar to that in [23]. We first randomly generated vectors with unit-norm, and rotated with a random rotation to obtain a new vector set in another coordinate frame. We then added random zero-mean Gaussian noise with and to all vectors in . After that, a portion of the vectors in (from 0% up to 99%) were substituted by randomly generated unit-norm vectors to generate outliers among the correspondences. All the experimental results were obtained over 50 Monte Carlo runs in the same environment.
To quantitatively represent the errors of rotation, we adopted the geodesic errors such that:
where “∠” is the geodesic error (21) [51] and the subscript “” denotes the ground truth value.
For benchmarking, we tested our solver ICOS (Algorithm 1) against FGR [22], GORE [21], RANSAC, BnB [38], and RANSIC [49]. For FGR, we merely solved the rotation rather than the whole transformation using the Gauss–Newton method. For RANSAC, we adopted Horn’s minimal method [34] to solve the rotation with the confidence set to 0.995, where we designed two stop conditions: (i) RANSAC with at most 100 iterations, named RANSAC (100), and (ii) RANSAC with at most 1000 iterations, named RANSAC (1000). When , we excluded BnB as it took tens of minutes per run. QUASAR [23] was also not adopted due to its very long runtime.
Results:Figure 3 displays the benchmarking results on both accuracy and runtime. It is not hard to observe that: (i) both FGR and RANSAC (100) failed at 90% and RANSAC (1000) broke at 98%, while RANSIC and our ICOS were robust against 95% with , 98% with , and 99% with ; (ii) ICOS was (one of) the most accurate solvers for all times since it constantly demonstrated the lowest rotation errors; (iii) with , ICOS was faster than the other solvers excluding RANSIC when the outlier ratio was below 95%, and with , it had a similar speed as GORE when the outlier ratio was no greater than 60%; (iv) though ICOS was slightly slower than RANSIC at 90–98% outliers, it became more time efficient at 99%.
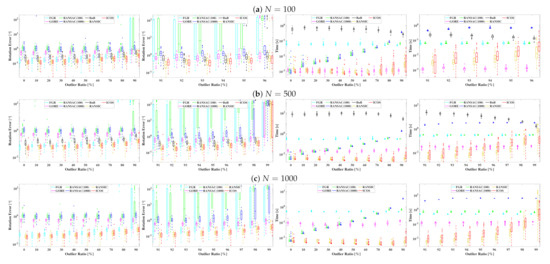
Figure 3.
Benchmarking of rotation search over the synthetic data. (a) Results with correspondences w.r.t. an increasing outlier ratio (0–99%). (b) Results with correspondences w.r.t. an increasing outlier ratio (0–99%). (c) Results with correspondences w.r.t. an increasing outlier ratio (0–99%).
6.2. Benchmarking of Point Cloud Registration on Real Data
Experimental setup: We evaluated ICOS against other state-of-the-art methods over the “bunny” and the “Armadillo” point clouds from the Stanford 3D Scanning Repository [52], and the environmental setup was inspired by [24,25]. We first randomly downsampled the point cloud to 1000 points and resized it to be placed in a cube of meters, which can be regarded as the initial point set . Then, we generated a random rigid transformation: (), in which scale , rotation , and translation m, to transform point set . We added random Gaussian noise with and to the transformed point set, as the point set . To create outliers in clutter, a portion of the points in were substituted by random points inside a sphere of diameter m according to the outlier ratio (from 0% up to 99%), as exemplified in Figure 4. All the experimental results were obtained over 50 Monte Carlo runs in the same environment.
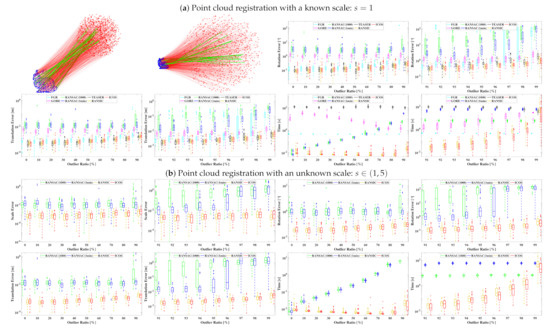
Figure 4.
Benchmarking of point cloud registration over the “bunny” point cloud [52]. Top left: examples of a known-scale and an unknown-scale point cloud registration problem with 98% outliers. (a) Known-scale registration results w.r.t. an increasing outlier ratio (0–99%). (b) Unknown-scale registration results w.r.t. an increasing outlier ratio (0–99%).
The estimation errors in all experiments were computed as:
and is the same as (38), where subscripts “” indicate the ground truth.
Known-scale problems: We adopted FGR, GORE, RANSAC, TEASER, RANSIC, and ICOS for the known-scale point cloud registration problems. As for RANSAC, we used Horn’s minimal (3-point) method [34] to solve the rigid transformation, and the confidence was set to 0.995. There were two stop conditions for RANSAC: (i) RANSAC with at most 1000 iterations, named RANSAC (1000), and (ii) RANSAC with at most 1 min of runtime, named RANSAC (1 min). In terms of TEASER, we adopted the GNC heuristic version as in [25], which uses GNC-TLS to solve the large robust SDP problem, rather than using convex relaxation, but differently: (i) we did not apply parallelism programming in order to ensure the fairness in the runtime evaluation for all the tested solvers; (ii) TEASER was completely implemented in MATLAB, not in C++, using the fast maximum clique solver [53].
Unknown-scale problems: For unknown-scale registration, we only compared ICOS with RANSAC and RANSIC because: (i) FGR and GORE were not designed for scale estimation originally; (ii) the scale estimator Adaptive Voting in TEASER was too slow for handling 1000 correspondences (requiring tens of minutes per run) and was also unable to tolerate over 90% outliers, thus no need to be compared.
Results: The main benchmarking results are shown in Figure 4 (over the “bunny” point cloud) and Figure 5 (over the “Armadillo” point cloud). We can observe that: (i) in the known-scale registration problem, GORE, TEASER, RANSIC, and our ICOS were all robust against 99% outliers, but GORE was hardly accurate; (ii) RANSAC (1000) failed at 90%, while FGR and RANSAC (1 min) failed at over 95%, not as robust as ICOS; (iii) in the unknown-scale registration problems, ICOS could still address 99% outliers highly robustly; (iv) ICOS was the fastest solver when the outlier ratio was below 98% (note that though FGR seemed faster at over 96%, it already became no longer robust) and was constantly faster than RANSIC when the outlier ratio was high (e.g., 90–99%).
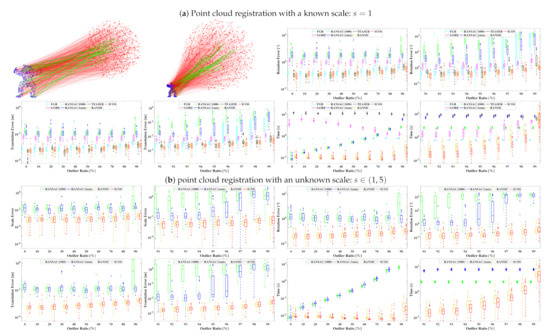
Figure 5.
Benchmarking of point cloud registration over the “Armadillo” point cloud [52]. Top left: Examples of a known-scale and an unknown-scale point cloud registration problem with 98% outliers. (a) Known-scale registration results w.r.t. an increasing outlier ratio (0–99%). (b) Unknown-scale registration results w.r.t. an increasing outlier ratio (0–99%).
6.3. Evaluation on the Inlier Recall Ratio
We tested the capability of ICOS for recalling correct inliers from the outlier-corrupted putative correspondence set in the rotation search and known-scale and unknown-scale registration with the same experimental setup as in Section 6.1 and Section 6.2, setting for all the problems, and the results are shown in Figure 6. The recall ratio is defined as the ratio of the number of true inliers found by ICOS to the ground truth number of inliers among the original correspondences. We can observe that ICOS was able to recall approximately 100% (no less than 99%) of the inliers from the correspondences with outlier ratio ranging from 0% to 99%, which underlies its high estimation accuracy against noise in the benchmarking above.
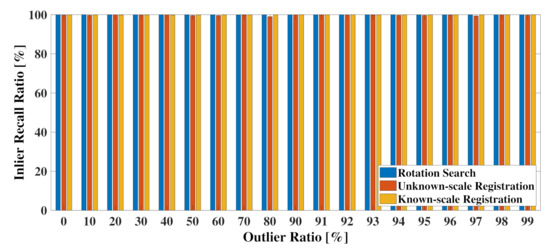
Figure 6.
Inlier recall ratio of ICOS in the rotation search and both known-scale and unknown-scale point cloud registration w.r.t. an increasing outlier ratio (0–99%).
6.4. Benchmarking on Scale Estimation in Registration
We benchmarked ICOS for scale estimation alone, compared with the Adaptive Voting in TEASER/TEASER++ and the 1-point RANSAC in [44]. Following the setup in Section 6.2, we further downsampled the “bunny” to only 100 points because the solver Adaptive Voting would run in tens of minutes with 1000 correspondences. In each run, the scale was randomly generated within m. Figure 7 shows the scale errors and the runtime w.r.t. an increasing outlier ratio. We can see that both Adaptive Voting and 1-point RANSAC broke at 90% outliers, while ICOS could stably tolerate 90% outliers and was faster than the other two competitors. In fact, ICOS could be robust against up to 99% outliers, as shown in Section 6.2.
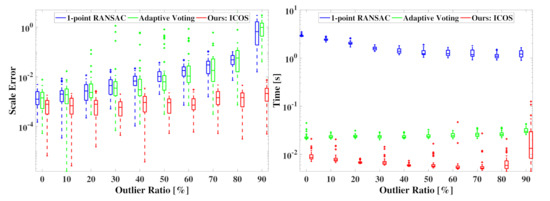
Figure 7.
Benchmarking of point cloud registration on scale estimation. Left: scale errors w.r.t. an increasing outlier ratio (0−99%). Right: runtime w.r.t. an increasing outlier ratio (0−99%).
6.5. Qualitative Registration Results over Real Datasets
In addition to the quantitative point cloud registration results rendered above, we provide qualitative results of the registration problems over multiple real point clouds, including the “bunny” and “Armadillo” from [52], the “Mario” and “Squirrel” from the SHOT dataset (http://vision.deis.unibo.it/list-all-categories/78-cvlab/80-shot, accessed on 30 July 2021), and the “city” and “castle” from the RGB-D Scans dataset [26], for concrete evaluation.
The experiments were set up as follows: (i) we transformed a certain point cloud with a random transformation (with both a known scale and unknown scale); (ii) we adopted the FPFH 3D feature descriptor [54] to match and build putative correspondences between the transformed point cloud (colored in magenta) and the initial one (colored in blue), where outliers are bound to exist; (iii) we applied ICOS to solve the transformation and then used it to reproject the transformed point cloud back to its initial place. The qualitative results are shown in Figure 8. After reprojection, the better the magenta point cloud overlaps with the blue one, the better the registration can be.
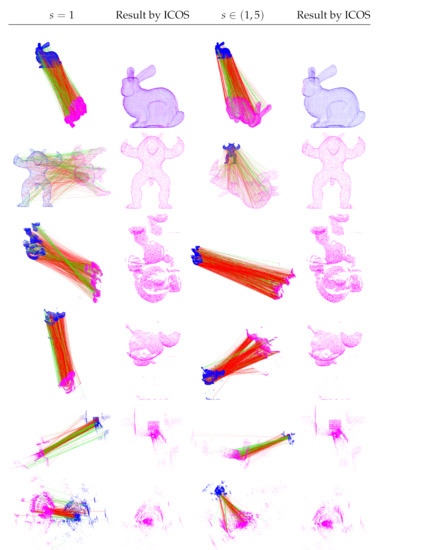
Figure 8.
Qualitative registration results on multiple real datasets. From Rows 1–6, the point clouds are: “bunny”, “Armadillo”, “Mario”, “Squirrel”, “city”, and “castle”, respectively. Left half: known-scale registration. Right half: unknown-scale registration. In each half, from Columns 1–2, we show the correspondences (inliers are in green lines, and outliers are in red lines) and registration (reprojection) results with ICOS.
From Figure 8, we see that ICOS yielded rather satisfactory robust registration results.
6.6. Additional Benchmarking on High Noise
We conducted more experiments on rotation search and unknown-scale point cloud registration with high noise. As the “bunny” point cloud is in a box, adding noise with is extreme, as shown in Figure 9, where the shape of the “bunny” is hardly seen. We tested ICOS against other solvers with (rotation search) and with (registration). The results are shown in Figure 9 (in registration, the translation errors were similar to the rotation errors, thus omitted).
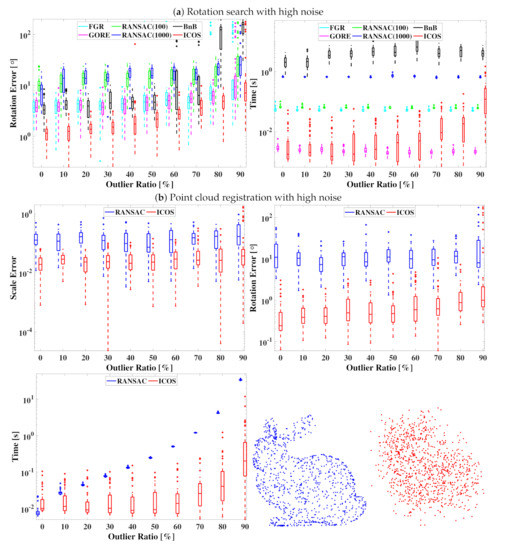
Figure 9.
Results with high noise. (a) Rotation search. (b) Unknown−scale registration. Right bottom: the left image is the “bunny” without noise, and the right one is that with noise .
We can observe that ICOS was still robust against at least 80% outliers in both of the tested problems with such high noise, while remaining time efficient, outperforming other competitors.
6.7. Application 1: Image Stitching
To validate ICOS in the real-world application of rotation search, we adopted ICOS to solve the image stitching problem over the LunchRoom image sequence from the PASSTA dataset [55], with an experimental setup similar to [23]. We first used the 2D feature descriptor SURF [16] to detect and match the 2D keypoints across a pair of images with overlapping scenes. Then, we applied the inverse of the camera intrinsic matrix to create the vector correspondences and over the two frames. Eventually, we used Algorithm 1 (with ) to solve the rotation between the two images and then obtained the homography matrix using matrix transformation: to stitch them together. The correspondences and experimental results are shown in Figure 10. We found that ICOS always found the correct inliers among the correspondences and stitched the images successfully.

Figure 10.
Image stitching results over the LunchRoom dataset [55]. Columns 1–3 display the raw correspondences matched by SURF [16] with the image indices and outlier ratios given on top, the inliers found by ICOS (the inliers found are labeled in green; the others are outliers, labeled in red), and the image stitching results using the rotation estimated by ICOS, respectively.
6.8. Application 2: 3D Object Localization
We tested ICOS over RGB-D scenes datasets [56] for tackling the 3D object localization (pose estimation) problems, as operated in [24,25]. We first extracted the 3D point cloud of the target object (cereal box, cap, and table in this case) from the scene according to the labels and imposed a random rigid transformation (with both a known scale and unknown scale), as well as random noise with and on the target object. We utilized FPFH to build putative correspondences between the scene and the transformed object. We found that the correspondences constructed by FPFH contained over 80% outliers in all the scenes tested; even worse, the outlier ratios even exceeded 90% in most scenes.
For each object-scene, we applied ICOS, RANSAC (1000), and RANSAC (1 min) to estimate the transformation (relative pose) of the object w.r.t. the scene and then reprojected the object back to the scene with the transformation estimated by each solver, respectively. The qualitative results are demonstrated in Figure 11 and Figure 12, and the quantitative results are specified in Table 2 and Table 3, in which the unit for is degrees () and the unit for is meters, computed as in (39). In each table, the best results are labeled in bold font.

Figure 11.
Qualitative results of object localization (cereal box) using ICOS, RANSAC (1000), and RANSAC (1 min). From left to right, we show the correspondences matched by FPFH (inliers are in green lines, and outliers are in red lines) and the registration (reprojection) results with ICOS, RANSAC (1000), and RANSAC (1 min), respectively.
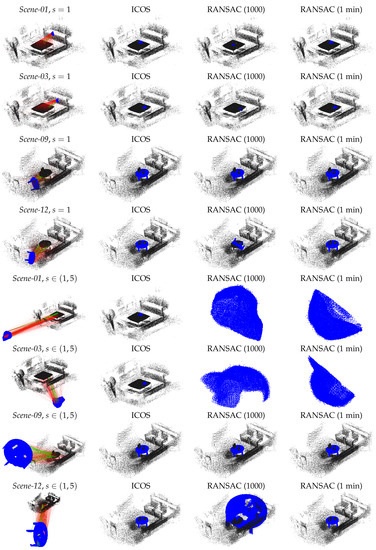
Figure 12.
Qualitative results of object localization (cap, table) using ICOS, RANSAC (1000), and RANSAC (1 min). From left to right, we show the correspondences matched by FPFH (inliers are in green lines and outliers are in red lines) and the registration (reprojection) results with ICOS, RANSAC (1000), and RANSAC (1 min), respectively.

Table 2.
Quantitative object localization results on cereal box.

Table 3.
Quantitative object localization results on cap and table.
From the results, ICOS was able to estimate the object poses robustly and accurately even with over 95% outliers among the 548 correspondences (e.g., the last scene in Table 2); however, the two RANSAC solvers failed in nearly half of the cases. Thus, in addition to its superior performance in standard benchmarking, ICOS manifested strong practicality for real problems.
7. Conclusions
In this paper, a novel, fast, and highly robust paradigm, ICOS, applicable to the correspondence-based rotation search and both the known-scale and unknown-scale point cloud registration problems was presented. We defined special compatible structures for the two problems above to generate invariants with mathematical constraints. Then, we rendered a sequence of well-designed invariant-constrained random sampling and inlier-seeking frameworks for these problems, which can eliminate outliers by means of fast Boolean conditions and search for qualified a-COS and b-COS as the inliers, giving birth to our solver ICOS. Generally, ICOS can automatically stop sampling and eventually return nearly 100% of the inliers from the putative correspondences.
We benchmarked ICOS against other state-of-the-art solvers in multiple experiments. We showed that: (i) ICOS is the most state-of-the-art, or at least one of the most stat-of-the-art, solvers for the two problems, since it was robust against over 95% outliers (at most up to 99%), had the best estimation accuracy, and ran fastest in most cases; (ii) ICOS demonstrated a similar robustness (robust against 99% outliers) and accuracy regardless of the scale situation, suitable for generalized point cloud registration; (iii) ICOS is practical for real-world applications. The MATLAB source code of ICOS can be found at: https://github.com/LeiSun-98/ICOS, (accessed on 1 August 2021).
Author Contributions
Conceptualization, L.S.; methodology, L.S.; source code, L.S.; validation, L.S.; formal analysis, L.S.; investigation, L.S.; resources, L.S.; data curation, L.S.; writing—original draft preparation, L.S.; writing—review and editing, L.S.; visualization, L.S.; supervision, L.S., Z.D.; project administration, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The demo in MATLAB can be found here: https://github.com/LeiSun-98/ICOS, (accessed on 1 August 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wahba, G. A least squares estimate of satellite attitude. SIAM Rev. 1965, 7, 409. [Google Scholar] [CrossRef]
- Bazin, J.C.; Seo, Y.; Hartley, R.; Pollefeys, M. Globally Optimal Inlier Set Maximization with Unknown Rotation and Focal Length; European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014; pp. 803–817. [Google Scholar]
- Heo, J.; Jeong, S.; Park, H.K.; Jung, J.; Han, S.; Hong, S.; Sohn, H.G. Productive high-complexity 3D city modeling with point clouds collected from terrestrial LiDAR. Comput. Environ. Urban Syst. 2013, 41, 26–38. [Google Scholar] [CrossRef]
- Blais, G.; Levine, M.D. Registering multiview range data to create 3D computer objects. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 820–824. [Google Scholar] [CrossRef] [Green Version]
- Henry, P.; Krainin, M.; Herbst, E.; Ren, X.; Fox, D. RGB-D mapping: Using Kinect-style depth cameras for dense 3D modeling of indoor environments. Int. J. Robot. Res. 2012, 31, 647–663. [Google Scholar] [CrossRef] [Green Version]
- Choi, S.; Zhou, Q.Y.; Koltun, V. Robust reconstruction of indoor scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Santiago, Chile, 13–16 December 2015; pp. 5556–5565. [Google Scholar]
- Drost, B.; Ulrich, M.; Navab, N.; Ilic, S. Model globally, match locally: Efficient and robust 3D object recognition. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 998–1005. [Google Scholar]
- Papazov, C.; Haddadin, S.; Parusel, S.; Krieger, K.; Burschka, D. Rigid 3D geometry matching for grasping of known objects in cluttered scenes. Int. J. Robot. Res. 2012, 31, 538–553. [Google Scholar] [CrossRef]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J. 3D object recognition in cluttered scenes with local surface features: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2270–2287. [Google Scholar] [CrossRef]
- Audette, M.A.; Ferrie, F.P.; Peters, T.M. An algorithmic overview of surface registration techniques for medical imaging. Med. Image Anal. 2000, 4, 201–217. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-Time. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014; Volume 2. [Google Scholar]
- Chase, A.F.; Chase, D.Z.; Fisher, C.T.; Leisz, S.J.; Weishampel, J.F. Geospatial revolution and remote sensing LiDAR in Mesoamerican archeology. Proc. Natl. Acad. Sci. USA 2012, 109, 12916–12921. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tron, R.; Rosen, D.M.; Carlone, L. On the inclusion of determinant constraints in lagrangian duality for 3D SLAM. In Proceedings of the Robotics: Science and Systems (RSS), Workshop the Problem of Mobile Sensors: Setting Future Goals and Indicators of Progress for SLAM, Rome, Italy, 13–17 July 2015; Volume 4. [Google Scholar]
- Briales, J.; Gonzalez-Jimenez, J. Convex global 3d registration with lagrangian duality. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 22–25 July 2017; pp. 4960–4969. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bustos, A.P.; Chin, T.J. Guaranteed outlier removal for point cloud registration with correspondences. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 2868–2882. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parra Bustos, A.; Chin, T.J. Guaranteed outlier removal for rotation search. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2165–2173. [Google Scholar]
- Zhou, Q.Y.; Park, J.; Koltun, V. Fast Global Registration; European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 766–782. [Google Scholar]
- Yang, H.; Carlone, L. A quaternion-based certifiably optimal solution to the Wahba problem with outliers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 1665–1674. [Google Scholar]
- Yang, H.; Carlone, L. A Polynomial-time Solution for Robust Registration with Extreme Outlier Rates. In Proceedings of the Robotics: Science and Systems, Freiburg im Breisgau, Germany, 22–26 June 2019. [Google Scholar]
- Yang, H.; Shi, J.; Carlone, L. Teaser: Fast and certifiable point cloud registration. IEEE Trans. Robot. 2020, 37, 1665–1674. [Google Scholar]
- Zeisl, B.; Koser, K.; Pollefeys, M. Automatic registration of RGB-D scans via salient directions. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 3–6 December 2013; pp. 2808–2815. [Google Scholar]
- Shi, J.; Yang, H.; Carlone, L. ROBIN: A Graph-Theoretic Approach to Reject Outliers in Robust Estimation using Invariants. arXiv 2020, arXiv:2011.03659. [Google Scholar]
- Chum, O.; Matas, J.; Kittler, J. Locally optimized RANSAC. In Joint Pattern Recognition Symposium; Springer: Berlin/Heidelberg, Germany, 2003; pp. 236–243. [Google Scholar]
- Lebeda, K.; Matas, J.; Chum, O. Fixing the Locally Optimized Ransac–Full Experimental Evaluation. In Proceedings of the British Machine Vision Conference, Surrey, UK, 3–7 September 2012; Volume 2. [Google Scholar]
- Horn, B.K.; Hilden, H.M.; Negahdaripour, S. Closed-form solution of absolute orientation using orthonormal matrices. JOSA A 1988, 5, 1127–1135. [Google Scholar] [CrossRef] [Green Version]
- Markley, F.L. Attitude determination using vector observations and the singular value decomposition. J. Astronaut. Sci. 1988, 36, 245–258. [Google Scholar]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-squares fitting of two 3-D point sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 698–700. [Google Scholar] [CrossRef] [Green Version]
- Forbes, J.R.; de Ruiter, A.H. Linear-matrix-inequality-based solution to wahbas problem. J. Guid. Control. Dyn. 2015, 38, 147–151. [Google Scholar] [CrossRef] [Green Version]
- Horn, B.K. Closed-form solution of absolute orientation using unit quaternions. JOSA A 1987, 4, 629–642. [Google Scholar] [CrossRef]
- Markley, F.L.; Crassidis, J.L. Fundamentals of Spacecraft Attitude Determination and Control; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Hartley, R.I.; Kahl, F. Global optimization through rotation space search. Int. J. Comput. Vis. 2009, 82, 64–79. [Google Scholar] [CrossRef] [Green Version]
- Bazin, J.C.; Seo, Y.; Pollefeys, M. Globally optimal consensus set maximization through rotation search. In Proceedings of the Asian Conference on Computer Vision, Daejeon, Korea, 5–9 November 2012; pp. 539–551. [Google Scholar]
- Parra Bustos, A.; Chin, T.J.; Suter, D. Fast rotation search with stereographic projections for 3d registration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3930–3937. [Google Scholar]
- Besl, P.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Tam, G.K.; Cheng, Z.Q.; Lai, Y.K.; Langbein, F.C.; Liu, Y.; Marshall, D.; Martin, R.R.; Sun, X.F.; Rosin, P.L. Registration of 3D point clouds and meshes: A survey from rigid to nonrigid. IEEE Trans. Vis. Comput. Graph. 2012, 19, 1199–1217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhong, Y. Intrinsic shape signatures: A shape descriptor for 3d object recognition. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 29 September–2 October 2009; pp. 689–696. [Google Scholar]
- Choy, C.; Park, J.; Koltun, V. Fully convolutional geometric features. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 8958–8966. [Google Scholar]
- Olsson, C.; Kahl, F.; Oskarsson, M. Branch-and-bound methods for euclidean registration problems. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 783–794. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Hu, Q.; Ai, M. Point Cloud Registration Based on One-Point RANSAC and Scale-Annealing Biweight Estimation. IEEE Trans. Geosci. Remote. Sens. 2021. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 523. [Google Scholar]
- Meer, P. Robust techniques for computer vision. Emerg. Top. Comput. Vis. 2004, 107–190. [Google Scholar]
- Mittal, S.; Anand, S.; Meer, P. Generalized projection-based M-estimator. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2351–2364. [Google Scholar] [CrossRef]
- Yang, H.; Antonante, P.; Tzoumas, V.; Carlone, L. Graduated non-convexity for robust spatial perception: From nonminimal solvers to global outlier rejection. IEEE Robot. Autom. Lett. 2020, 5, 1127–1134. [Google Scholar] [CrossRef] [Green Version]
- Sun, L. RANSIC: Fast and Highly Robust Estimation for Rotation Search and Point Cloud Registration using Invariant Compatibility. arXiv 2021, arXiv:2104.09133. [Google Scholar]
- Barfoot, T.D. State Estimation for Robotics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Hartley, R.; Trumpf, J.; Dai, Y.; Li, H. Rotation averaging. Int. J. Comput. Vis. 2013, 103, 267–305. [Google Scholar] [CrossRef]
- Curless, B.; Levoy, M. A volumetric method for building complex models from range images. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 4–9 August 1996; pp. 303–312. [Google Scholar]
- Eppstein, D.; Löffler, M.; Strash, D. Listing all maximal cliques in sparse graphs in near-optimal time. In International Symposium on Algorithms and Computation; Springer: Berlin/Heidelberg, Germany, 2010; pp. 403–414. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–19 May 2009; pp. 3212–3217. [Google Scholar]
- Meneghetti, G.; Danelljan, M.; Felsberg, M.; Nordberg, K. Image alignment for panorama stitching in sparsely structured environments. In Proceedings of the Scandinavian Conference on Image Analysis, Copenhagen, Denmark, 15–17 June 2015; pp. 428–439. [Google Scholar]
- Lai, K.; Bo, L.; Ren, X.; Fox, D. A large-scale hierarchical multi-view rgb-d object dataset. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1817–1824. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
