A Bayesian Modeling Approach to Situated Design of Personalized Soundscaping Algorithms
Abstract
:1. Introduction
2. Methods
2.1. Problem Statement and Proposed Solution Framework
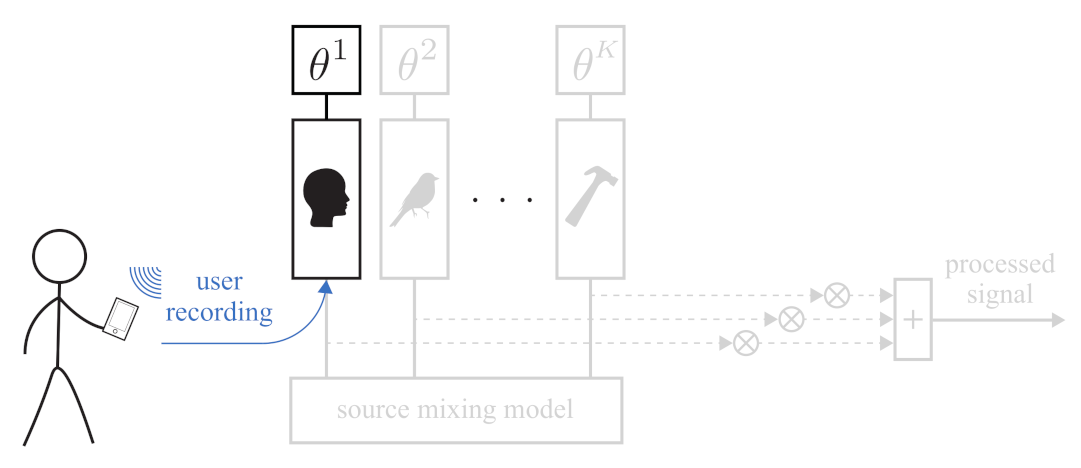
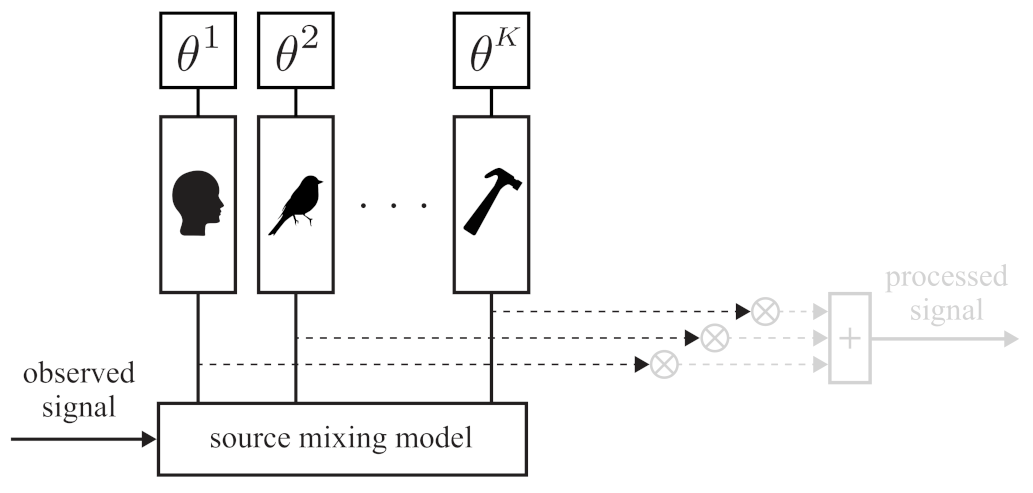
2.1.1. Source Modeling
2.1.2. Source Separation
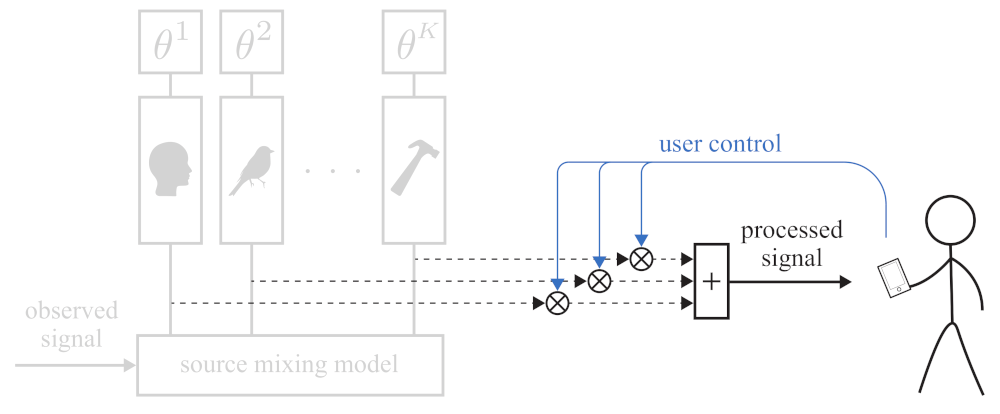
2.1.3. Soundscaping
2.2. Model Specification
2.2.1. Source Mixing Model 1: Algonquin Model
2.2.2. Source Mixing Model 2: Gaussian Scale Sum Model
2.2.3. Source Model: Gaussian Mixture Model
2.3. Factor Graphs and Message Passing-Based Inference
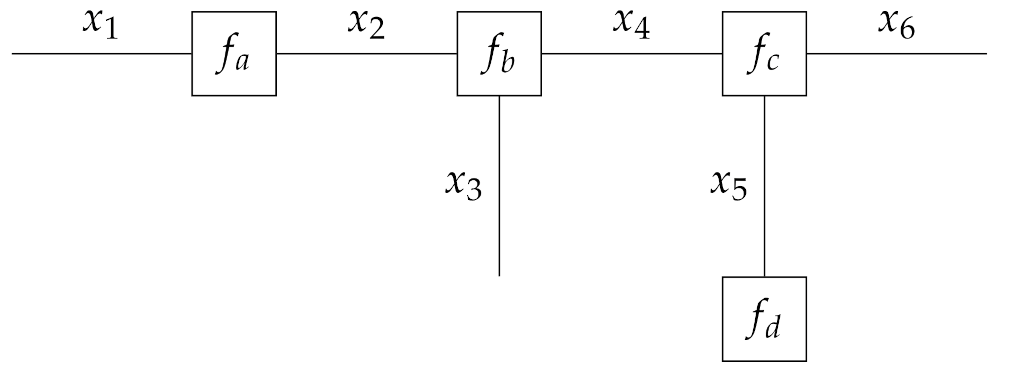
2.3.1. Forney-Style Factor Graphs
2.3.2. Sum-Product Message Passing
2.3.3. Variational Message Passing
2.3.4. Automating Inference and Variational Free Energy Evaluation
2.3.5. Message Passing-Based Inference in the Algonquin Model
2.3.6. Message Passing-Based Inference in the Gaussian Scale Sum Model
2.3.7. Implementation Details
3. Experimental Validation
3.1. Experimental Overview
3.2. Data Selection
- The LibriSpeech data set (the LibriSpeech data set is available at https://www.openslr.org/12, accessed on 31 March 2021) [51], which is a corpus of approximately 1000 h of 16 kHz read English speech.
- The FSDnoisy18k data set (the FSDnoisy18k data set is available at https://www.eduardofonseca.net/FSDnoisy18k, accessed on 13 April 2021) [52], is an audio data set, which has been collected with the aim of fostering the investigation of label noise in sound event classification. It contains 42.5 h of audio samples across 20 sound classes, including a small amount of manually-labeled data and a larger quantity of real-world noise data.
3.3. Preprocessing
3.4. Performance Evaluation
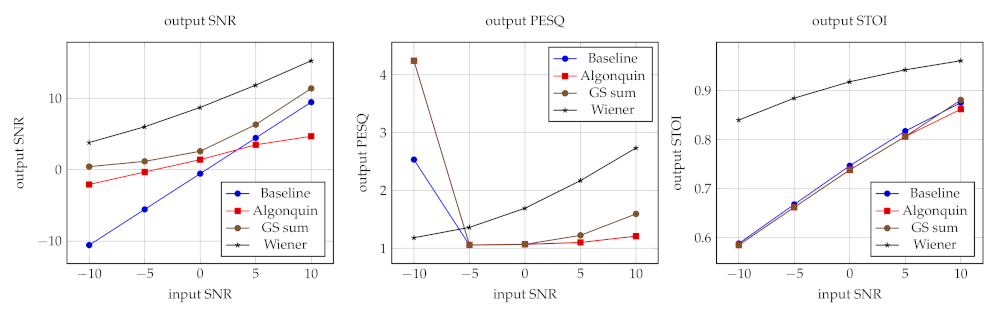
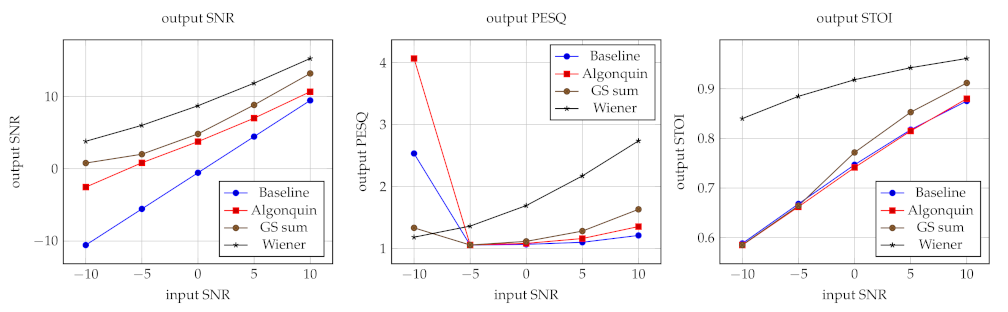
3.5. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Inference for Learning and Signal Processing
Appendix A.1. Source Modeling
Appendix A.2. Source Separation
Appendix A.3. Soundscaping
References
- Reddy, C.K.A.; Shankar, N.; Bhat, G.S.; Charan, R.; Panahi, I. An Individualized Super-Gaussian Single Microphone Speech Enhancement for Hearing Aid Users With Smartphone as an Assistive Device. IEEE Signal Process. Lett. 2017, 24, 1601–1605. [Google Scholar] [CrossRef]
- Comon, P. Independent Component Analysis, a new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Hong, L.; Rosca, J.; Balan, R. Bayesian single channel speech enhancement exploiting sparseness in the ICA domain. In Proceedings of the 12th European Signal Processing Conference, Vienna, Austria, 6–10 September 2004; pp. 1713–1716. [Google Scholar]
- Fevotte, C.; Godsill, S.J. A Bayesian Approach for Blind Separation of Sparse Sources. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 2174–2188. [Google Scholar] [CrossRef] [Green Version]
- Erdogan, A.T. Adaptive algorithm for the blind separation of sources with finite support. In Proceedings of the 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2008; pp. 1–5. [Google Scholar]
- Knuth, K.H. Informed Source Separation: A Bayesian Tutorial. arXiv 2013, arXiv:1311.3001. [Google Scholar]
- Rennie, S.; Kristjansson, T.; Olsen, P.; Gopinath, R. Dynamic noise adaptation. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 May 2006; Volume 1. [Google Scholar]
- Rennie, S.; Hershey, J.; Olsen, P. Single-channel speech separation and recognition using loopy belief propagation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 3845–3848. [Google Scholar] [CrossRef]
- Frey, B.J.; Deng, L.; Acero, A.; Kristjansson, T. ALGONQUIN: Iterating Laplace’s Method to Remove Multiple Types of Acoustic Distortion for Robust Speech Recognition. In Proceedings of the Eurospeech Conference, Aalborg, Denmark, 3–7 September 2001; pp. 901–904. [Google Scholar]
- Hershey, J.R.; Olsen, P.; Rennie, S.J. Signal Interaction and the Devil Function. In Proceedings of the Interspeech 2010, Makuhari, Japan, 26–30 September 2010; pp. 334–337. [Google Scholar]
- Radfar, M.; Banihashemi, A.; Dansereau, R.; Sayadiyan, A. Nonlinear minimum mean square error estimator for mixture-maximisation approximation. Electron. Lett. 2006, 42, 724–725. [Google Scholar] [CrossRef]
- Rennie, S.; Hershey, J.; Olsen, P. Single-Channel Multitalker Speech Recognition. IEEE Signal Process. Mag. 2010, 27, 66–80. [Google Scholar] [CrossRef]
- Chien, J.T.; Yang, P.K. Bayesian Factorization and Learning for Monaural Source Separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 185–195. [Google Scholar] [CrossRef]
- Magron, P.; Virtanen, T. Complex ISNMF: A Phase-Aware Model for Monaural Audio Source Separation. arXiv 2018, arXiv:1802.03156. [Google Scholar] [CrossRef]
- Wilkinson, W.J.; Andersen, M.R.; Reiss, J.D.; Stowell, D.; Solin, A. End-to-End Probabilistic Inference for Nonstationary Audio Analysis. arXiv 2019, arXiv:1901.11436. [Google Scholar]
- Zalmai, N.; Keusch, R.; Malmberg, H.; Loeliger, H.A. Unsupervised feature extraction, signal labeling, and blind signal separation in a state space world. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 838–842. [Google Scholar] [CrossRef] [Green Version]
- Bruderer, L.; Malmberg, H.; Loeliger, H. Deconvolution of weakly-sparse signals and dynamical-system identification by Gaussian message passing. In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 326–330. [Google Scholar] [CrossRef]
- Bruderer, L. Input Estimation and Dynamical System Identification: New Algorithms and Results. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2015. [Google Scholar]
- Loeliger, H.; Bruderer, L.; Malmberg, H.; Wadehn, F.; Zalmai, N. On sparsity by NUV-EM, Gaussian message passing, and Kalman smoothing. In Proceedings of the 2016 Information Theory and Applications Workshop (ITA), La Jolla, CA, USA, 31 January–5 February 2016; pp. 1–10. [Google Scholar] [CrossRef] [Green Version]
- Oord, A.V.D.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. WaveNet: A Generative Model for Raw Audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Vasquez, S.; Lewis, M. MelNet: A Generative Model for Audio in the Frequency Domain. arXiv 2019, arXiv:1906.01083. [Google Scholar]
- Engel, J.; Hantrakul, L.; Gu, C.; Roberts, A. DDSP: Differentiable Digital Signal Processing. arXiv 2020, arXiv:2001.04643. [Google Scholar]
- Dhariwal, P.; Jun, H.; Payne, C.; Kim, J.W.; Radford, A.; Sutskever, I. Jukebox: A Generative Model for Music. arXiv 2020, arXiv:2005.00341. [Google Scholar]
- Razavi, A.; Oord, A.V.D.; Vinyals, O. Generating Diverse High-Fidelity Images with VQ-VAE-2. arXiv 2019, arXiv:1906.00446. [Google Scholar]
- Cox, M.; van de Laar, T.; de Vries, B. A Factor Graph Approach to Automated Design of Bayesian Signal Processing Algorithms. Int. J. Approx. Reason. 2019, 104, 185–204. [Google Scholar] [CrossRef] [Green Version]
- Beal, M.J. Variational Algorithms for Approximate Bayesian Inference. Ph.D. Thesis, University College London, London, UK, 2003. [Google Scholar]
- Minka, T.P. A Family of Algorithms for Approximate Bayesian Inference. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Hao, J.; Lee, T.W.; Sejnowski, T.J. Speech Enhancement Using Gaussian Scale Mixture Models. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 1127–1136. [Google Scholar] [CrossRef] [Green Version]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Loeliger, H.A.; Dauwels, J.; Hu, J.; Korl, S.; Ping, L.; Kschischang, F.R. The Factor Graph Approach to Model-Based Signal Processing. Proc. IEEE 2007, 95, 1295–1322. [Google Scholar] [CrossRef] [Green Version]
- Gallager, R.G. Circularly-Symmetric Gaussian Random Vectors. Preprint. 2008. Available online: https://www.rle.mit.edu/rgallager/documents/CircSymGauss.pdf (accessed on 31 August 2020).
- Allen, J.B. Articulation and Intelligibility, 1st ed.; Synthesis Lectures on Speech and Audio Processing; Morgan & Claypool: San Rafael, CA, USA, 2005. [Google Scholar]
- Forney, G. Codes on graphs: Normal realizations. IEEE Trans. Inf. Theory 2001, 47, 520–548. [Google Scholar] [CrossRef] [Green Version]
- Loeliger, H.A. An introduction to factor graphs. IEEE Signal Process. Mag. 2004, 21, 28–41. [Google Scholar] [CrossRef] [Green Version]
- van de Laar, T. Automated Design of Bayesian Signal Processing Algorithms. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2019. [Google Scholar]
- Kschischang, F.; Frey, B.; Loeliger, H.A. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef] [Green Version]
- Murphy, K.; Weiss, Y.; Jordan, M.I. Loopy Belief Propagation for Approximate Inference: An Empirical Study. In Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence, Stockholm, Sweden, 30 July–1 August 1999. [Google Scholar]
- Winn, J.; Bishop, C.M. Variational Message Passing. J. Mach. Learn. Res. 2005, 661–694. [Google Scholar]
- Dauwels, J. On Variational Message Passing on Factor Graphs. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 2546–2550. [Google Scholar] [CrossRef] [Green Version]
- Akbayrak, S.; Bocharov, I.; de Vries, B. Extended Variational Message Passing for Automated Approximate Bayesian Inference. Entropy 2021, 23, 815. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; Adaptive Computation and Machine Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian Model Averaging: A Tutorial. Stat. Sci. 1999, 14, 382–401. [Google Scholar]
- Monteith, K.; Carroll, J.L.; Seppi, K.; Martinez, T. Turning Bayesian model averaging into Bayesian model combination. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 2657–2663. [Google Scholar] [CrossRef]
- Yedidia, J.S.; Freeman, W.T.; Weiss, Y. Bethe free energy, Kikuchi approximations, and belief propagation algorithms. Adv. Neural Inf. Process. Syst. 2001, 13, 689. [Google Scholar]
- Şenöz, I.; van de Laar, T.; Bagaev, D.; de Vries, B. Variational Message Passing and Local Constraint Manipulation in Factor Graphs. Entropy 2021, 23, 807. [Google Scholar] [CrossRef] [PubMed]
- Blei, D.M.; Lafferty, J.D. Correlated Topic Models. In Proceedings of the 18th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; pp. 147–154. [Google Scholar]
- Braun, M.; McAuliffe, J. Variational Inference for Large-Scale Models of Discrete Choice. J. Am. Stat. Assoc. 2007, 105. [Google Scholar] [CrossRef] [Green Version]
- Depraetere, N.; Vandebroek, M. A comparison of variational approximations for fast inference in mixed logit models. Comput. Stat. 2017, 32, 93–125. [Google Scholar] [CrossRef] [Green Version]
- Panayotov, V.; Chen, G.; Povey, D.; Khudanpur, S. Librispeech: An ASR corpus based on public domain audio books. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 5206–5210. [Google Scholar] [CrossRef]
- Fonseca, E.; Plakal, M.; Ellis, D.P.W.; Font, F.; Favory, X.; Serra, X. Learning Sound Event Classifiers from Web Audio with Noisy Labels. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 21–25. [Google Scholar] [CrossRef] [Green Version]
- Kates, J.M.; Arehart, K.H. Multichannel Dynamic-Range Compression Using Digital Frequency Warping. EURASIP J. Adv. Signal Process. 2005, 2005, 483486. [Google Scholar] [CrossRef] [Green Version]
- Zwicker, E. Subdivision of the Audible Frequency Range into Critical Bands (Frequenzgruppen). J. Acoust. Soc. Am. 1961, 33, 248. [Google Scholar] [CrossRef]
- Smith, J.; Abel, J. Bark and ERB bilinear transforms. IEEE Trans. Speech Audio Process. 1999, 7, 697–708. [Google Scholar] [CrossRef] [Green Version]
- Proakis, J.G.; Manolakis, D.G. Linear Prediction and Optimum Linear Filters. In Digital Signal Processing, 4th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2014. [Google Scholar]
- Rix, A.; Beerends, J.; Hollier, M.; Hekstra, A. Perceptual evaluation of speech quality (PESQ)-a new method for speech quality assessment of telephone networks and codecs. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings (Cat. No.01CH37221), Salt Lake City, UT, USA, 7–11 May 2001; Volume 2, pp. 749–752. [Google Scholar] [CrossRef]
- Taal, C.H.; Hendriks, R.C.; Heusdens, R.; Jensen, J. An Algorithm for Intelligibility Prediction of Time–Frequency Weighted Noisy Speech. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 2125–2136. [Google Scholar] [CrossRef]
- Friston, K.; FitzGerald, T.; Rigoli, F.; Schwartenbeck, P.; O’Doherty, J.; Pezzulo, G. Active inference and learning. Neurosci. Biobehav. Rev. 2016, 68, 862–879. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friston, K.; Penny, W. Post hoc Bayesian model selection. NeuroImage 2011, 56, 2089–2099. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friston, K.; Parr, T.; Zeidman, P. Bayesian model reduction. arXiv 2019, arXiv:1805.07092. [Google Scholar]
- van Erp, B.; Şenöz, I.; de Vries, B. Variational Log-Power Spectral Tracking for Acoustic Signals. In Proceedings of the 2021 IEEE Statistical Signal Processing Workshop (SSP), Rio de Janeiro, Brazil, 11–14 July 2021; pp. 311–315. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, L.; Ran, X. Online incremental EM training of GMM and its application to speech processing applications. In Proceedings of the IEEE 10th International Conference on Signal Processing Proceedings, Beijing, China, 24–28 October 2010; pp. 1309–1312. [Google Scholar] [CrossRef]
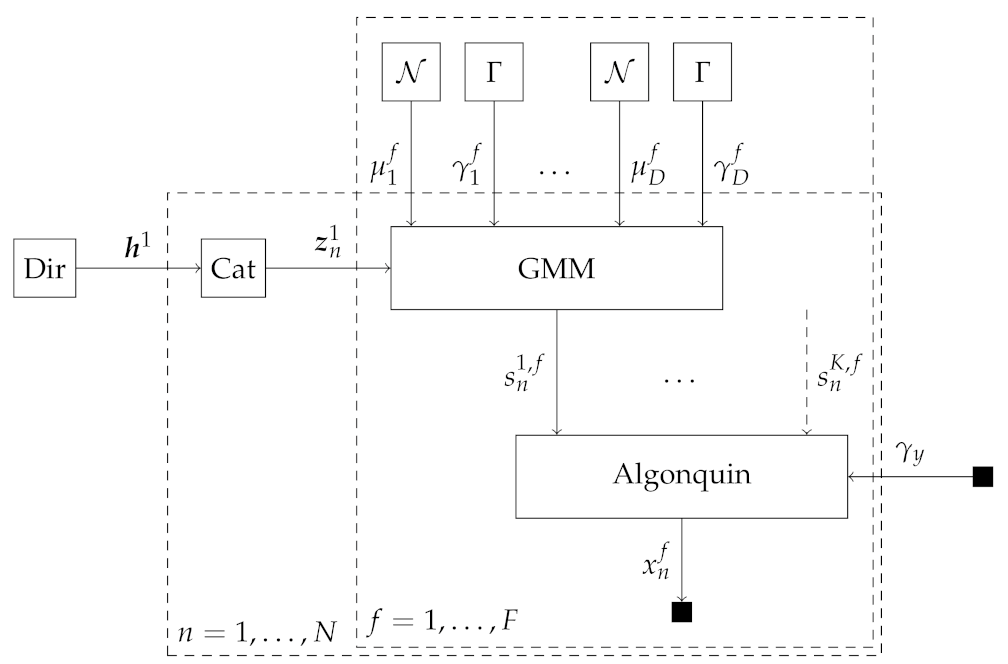
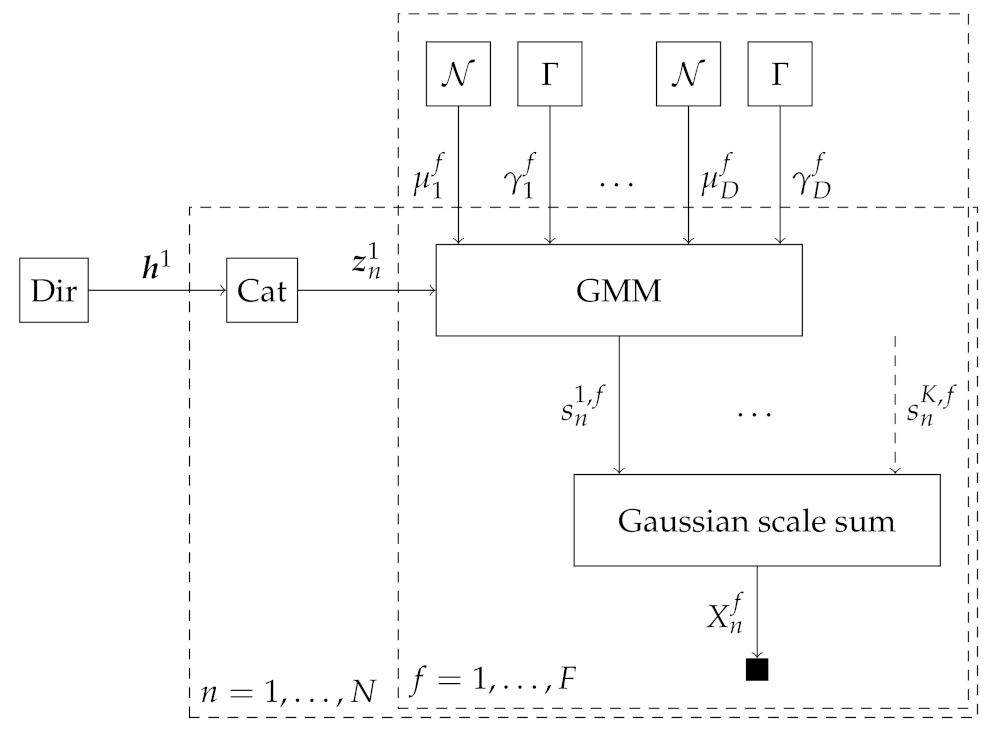
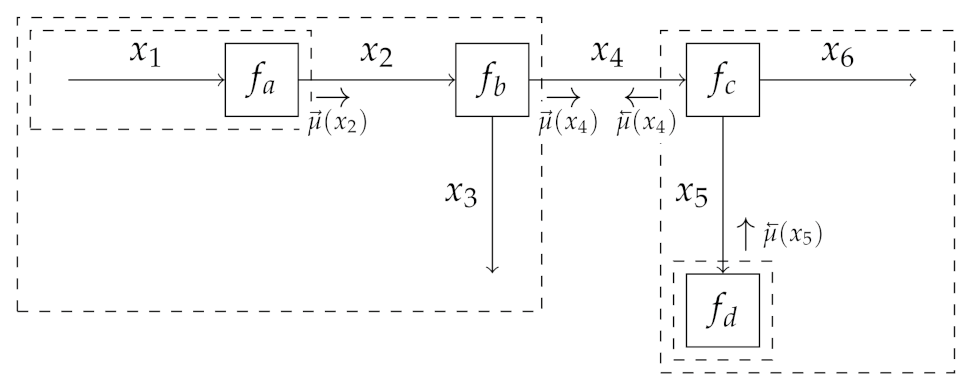
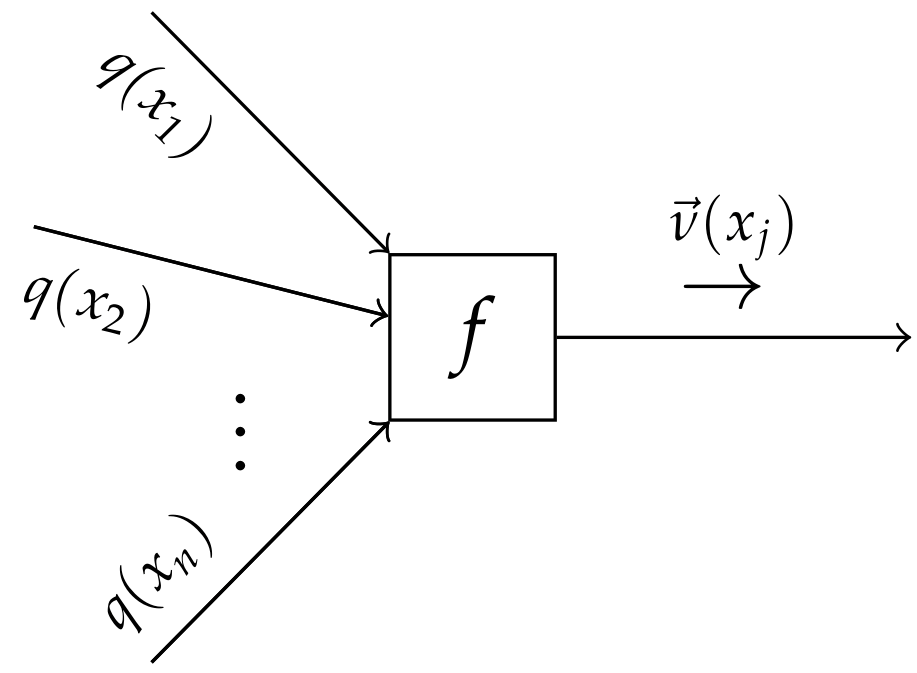
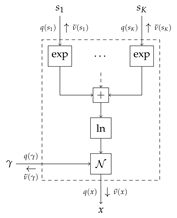
| Factor graph for the Algonquin node | |
|---|---|
 | |
| Node function | |
| Marginals | Functional form |
| Messages | Functional form |
| Local variational free energy | |
| Factor graph for the Gaussian scale sum node | |
|---|---|
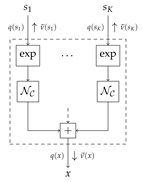 | |
| Node function | |
| Marginals | Functional form |
| Messages | Functional form |
| Local variational free energy | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Erp, B.; Podusenko, A.; Ignatenko, T.; de Vries, B. A Bayesian Modeling Approach to Situated Design of Personalized Soundscaping Algorithms. Appl. Sci. 2021, 11, 9535. https://doi.org/10.3390/app11209535
van Erp B, Podusenko A, Ignatenko T, de Vries B. A Bayesian Modeling Approach to Situated Design of Personalized Soundscaping Algorithms. Applied Sciences. 2021; 11(20):9535. https://doi.org/10.3390/app11209535
Chicago/Turabian Stylevan Erp, Bart, Albert Podusenko, Tanya Ignatenko, and Bert de Vries. 2021. "A Bayesian Modeling Approach to Situated Design of Personalized Soundscaping Algorithms" Applied Sciences 11, no. 20: 9535. https://doi.org/10.3390/app11209535
APA Stylevan Erp, B., Podusenko, A., Ignatenko, T., & de Vries, B. (2021). A Bayesian Modeling Approach to Situated Design of Personalized Soundscaping Algorithms. Applied Sciences, 11(20), 9535. https://doi.org/10.3390/app11209535







