A Block Arnoldi Algorithm Based Reduced-Order Model Applied to Large-Scale Algebraic Equations of a 3-D Field Problem
Abstract
Featured Application
Abstract
1. Introduction
2. Proposed Order Reduction Methodology
2.1. Three-Dimensional Transient Temperature Field Problems
2.2. Moment Matching Method for 3-D Transient Field Problems
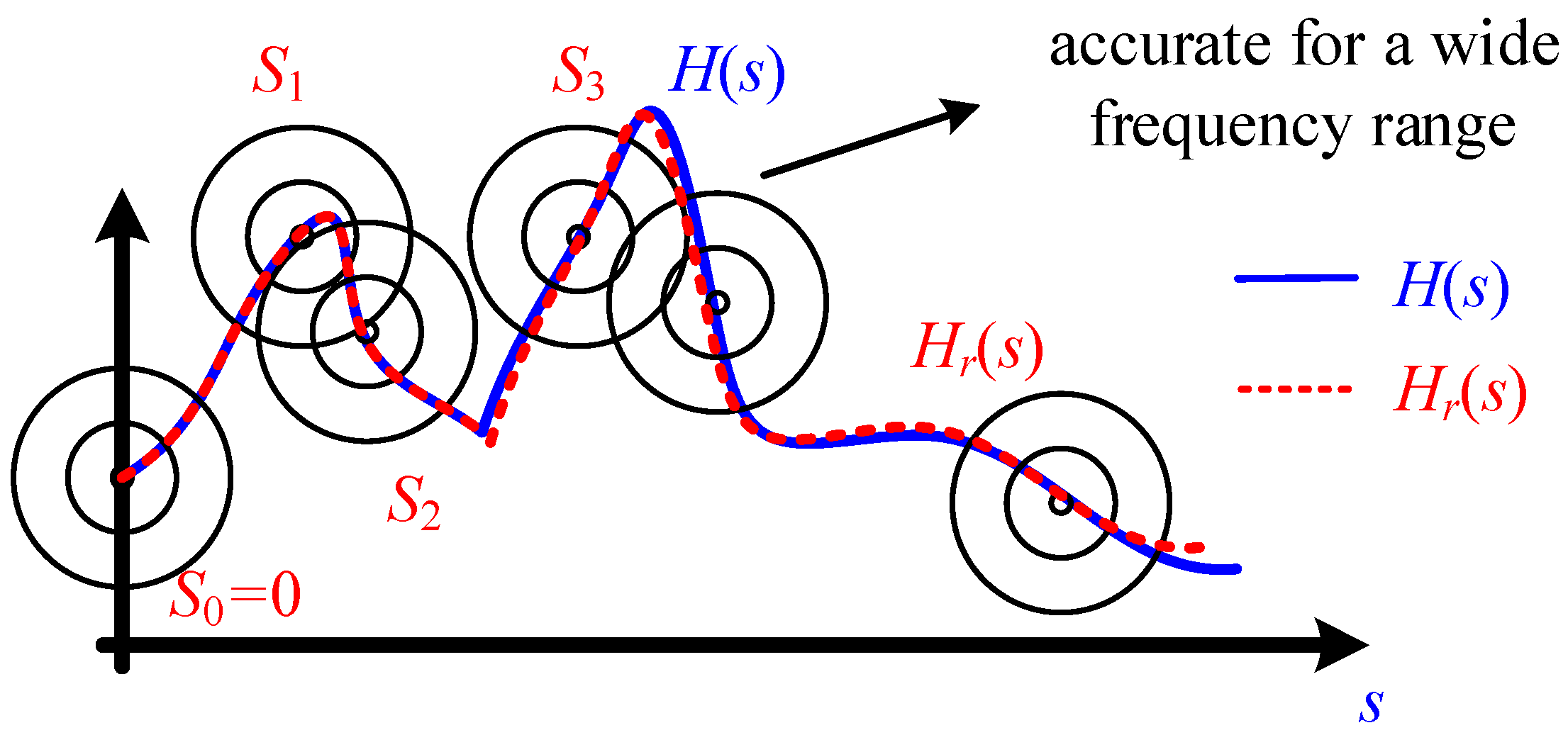
2.3. Multipoint Expansion
2.4. Adaptive Scheme
| Algorithm 1. Main loop of the proposed scheme for 3-D transient field problems |
| Input: The range of the broadband frequency (,), coefficient matrices of NTM model (,,), global error tolerance tolg and local error tolerance toll. |
| 1. 2. [] = S-POINT (, toll) 3. 4. while do [] = S-POINT (, toll) 5. end while 6. ,, Output: The coefficient matrices of a reduced system(,,) |
| Algorithm 2. S-POINT: Block Arnoldi-based moment matching at a single frequency point |
| Input: The current expansion point , local error tolerance toll and coefficient matrices of the high-fidelity model (,,) |
| 1. 2. 3. while do = EST-ERROR (,,A,B,P) 4. end while Output: |
| Algorithm 3. EST-ERROR: Error estimator |
| Input: ,, ,, local error: the single frequency point , global error, the range of the broadband frequency (,) |
| 1. ,, 2. Local error: Get from Equation (1) under , , Get from Equation (3) under , , 3. Global error: Get from Equation (1) under , , Get from Equation (3) under , , 4. Output: error |
3. Numerical Application
4. Conclusions
- (1)
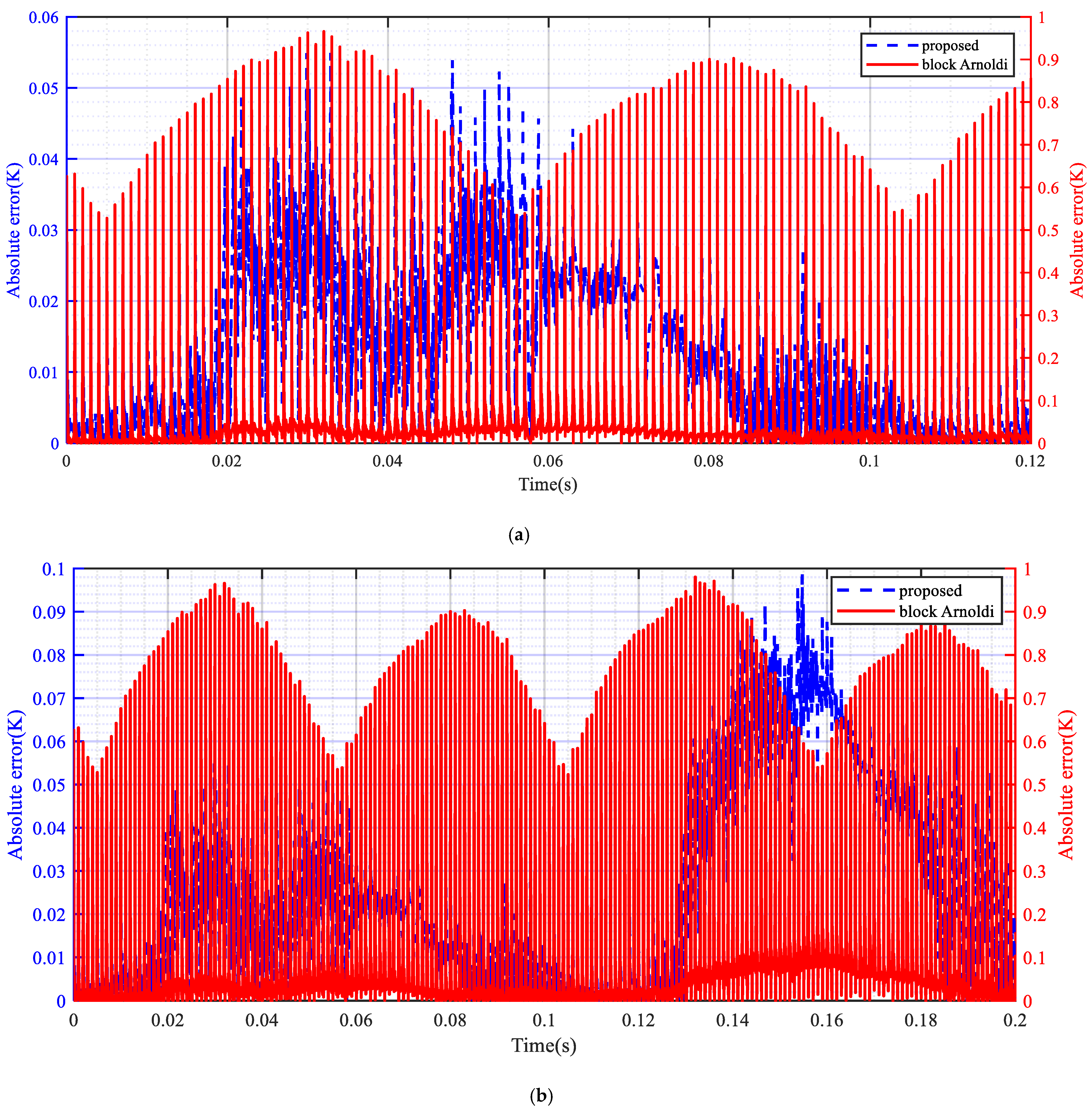
- The model reduced from the proposed methodology could achieve a higher accuracy compared to one reduced from conventional block Arnoldi in a wideband frequency. For point 1, the maximum error of the proposed model was 0.3603, whereas that of the conventional reduced model can reach 3.2275. For point 2, the maximum error of the proposed approach is 0.0986, whereas that of the conventional reduced model can reach 0.9803. For point 3, the maximum error of the proposed model is 0.1459, whereas that of the conventional reduced model can reach 6.3752.
- (2)
- The ROM obtained using the proposed scheme can accurately replicate the transient temperature fields of the NTM high-fidelity model through a wide frequency range, while the computational time of the reduced-order model is less than 13% of the original one.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Necoara, I.; Ionescu, T.C. H2 Model Reduction of Linear Network Systems by Moment Matching and Optimization. IEEE Trans. Autom. Control 2020, 65, 5328–5335. [Google Scholar] [CrossRef]
- Mohamed, K. Model Order Reduction Method for Large-Scale RC Interconnect and Implementation of Adaptive Digital PI Controller. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2019, 27, 2447–2458. [Google Scholar] [CrossRef]
- Farhan, M.A.; Nakhla, M.S. Parametric Order Reduction of Nonuniform Interconnect Circuits Using Integrated Congruence Transform. IEEE Trans. Compon. Packag. Manufact. Technol. 2018, 8, 1956–1966. [Google Scholar] [CrossRef]
- Szypulski, D.; Fotyga, G.; Rubia, V.; Mrozowski, M. A Subspace-Splitting Moment-Matching Model-Order Reduction Technique for Fast Wideband FEM Simulations of Microwave Structures. IEEE Trans. Microw. Theory Tech. 2020, 68, 3229–3241. [Google Scholar] [CrossRef]
- Fotyga, G.; Nyka, K.; Mrozowski, M. Automatic Reduction-Order Selection for Finite-Element Macromodels. IEEE Microw. Compon. Lett. 2018, 28, 278–280. [Google Scholar] [CrossRef]
- Kuriyama, K.; Kameari, A.; Ebrahimi, H.; Fujiwara, T.; Sugahara, K.; Shindo, Y.; Matsuo, T. Cauer Ladder Network With Multiple Expansion Points for Efficient Model Order Reduction of Eddy-Current Field. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Sakamoto, H.; Okamoto, K.; Igarashi, H. Fast Analysis of Rotating Machine Using Simplified Model-Order Reduction Based on POD. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]
- Sanaie, R.; Chiprout, E.; Nakhla, M.S.; Zhang, Q. A fast method for frequency and time domain simulation of high speed VLSI interconnects. IEEE Trans. Microw. Theory Tech. 1994, 42, 2562–2571. [Google Scholar] [CrossRef]
- Feldmann, P.; Freund, R.W. Efficient linear circuit analysis by Padé approximation via the Lanczos Process. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1995, 14, 639–649. [Google Scholar] [CrossRef]
- Slone, R.D. Removing the frequency restriction on Padé via Lanczo with an error bound. In Proceedings of the 1998 IEEE International Symposium on Electromagnetic Compatibility. Part 1 (of 2), Denver, CO, USA, 24–28 August 1998; pp. 202–207. [Google Scholar]
- Bai, Z.; Slone, R.D.; Smith, W.T.; Ye, Q. Error bound for reduced system model by Padé approximation via the Lanczos process. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1999, 18, 133–141. [Google Scholar]
- Chen, J.; Hu, S.; Zhou, Q.; Yang, S.; Ren, Z. A Broadband Enhanced Nodal-Order Reduction Methodology for Large-Scale Equation Sets of 3-D Transient Field Problems. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]
- Schilders, W.H.A.; van der Vorst, H.A.; Rommes, J. Model Order Reduction: Theory, Research Aspects and Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 60–70. [Google Scholar]
- Odabasioglu, A.; Celik, M.; Pileggi, L.T. PRIMA: Passive reducedorde interconnect macromodeling algorithm. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1998, 17, 645–654. [Google Scholar] [CrossRef]
- Rubia, V.D.L.; Razafison, U.; Maday, Y. Reliable fast frequency sweep for microwave devices via the reduced-basis method. IEEE Trans. Microw. Theory Tech. 2009, 57, 2923–2937. [Google Scholar] [CrossRef][Green Version]
- Wang, W.; Paraschos, G.N.; Vouvakis, M.N. Fast frequency sweep of FEM models via the balanced truncation proper orthogonal decomposition. IEEE Trans. Antennas Propag. 2011, 59, 4142–4154. [Google Scholar] [CrossRef]
- Xu, B.; Yebi, A.; Hoffman, M.; Onori, S. A Rigorous Model Order Reduction Framework for Waste Heat Recovery Systems Based on Proper Orthogonal Decomposition and Galerkin Projection. IEEE Trans. Control Syst. Technol. 2020, 28, 635–643. [Google Scholar] [CrossRef]
- Kasolis, F.; Clemens, M. Entropy Snapshot Filtering for QR-Based Model Reduction of Transient Nonlinear Electro-Quasi-Static Simulations. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]
- Feng, L.; Korvink, J.G.; Benner, P. A Fully Adaptive Scheme for Model Order Reduction Based on Moment Matching. IEEE Trans. Compon. Packag. Manufact. Technol. 2015, 5, 1872–1884. [Google Scholar] [CrossRef]
- Rewienski, M.; Lamecki, A.; Mrozowski, M. Greedy Multipoint Model-Order Reduction Technique for Fast Computation of Scattering Parameters of Electromagnetic Systems. IEEE Trans. Microw. Theory Tech. 2016, 64, 1681–1693. [Google Scholar] [CrossRef]
- Nguyen, T.; Duc, T.L.; Tran, T.; Guichon, J.; Chadebec, O.; Meunier, G. Adaptive Multipoint Model Order Reduction Scheme for Large-Scale Inductive PEEC Circuits. IEEE Trans. Electromagn. Compat. 2017, 59, 1143–1151. [Google Scholar] [CrossRef]
- Fotyga, G.; Czarniewska, M.; Lamecki, A.; Mrozowski, M. Reliable Greedy Multipoint Model-Order Reduction Techniques for Finite-Element Analysis. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 821–824. [Google Scholar] [CrossRef]
- Chen, J.; Yang, S.; Ren, Z. A Network Topological Approach-Based Transient 3-D Electrothermal Model of Insulated-Gate Bipolar Transistor. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]

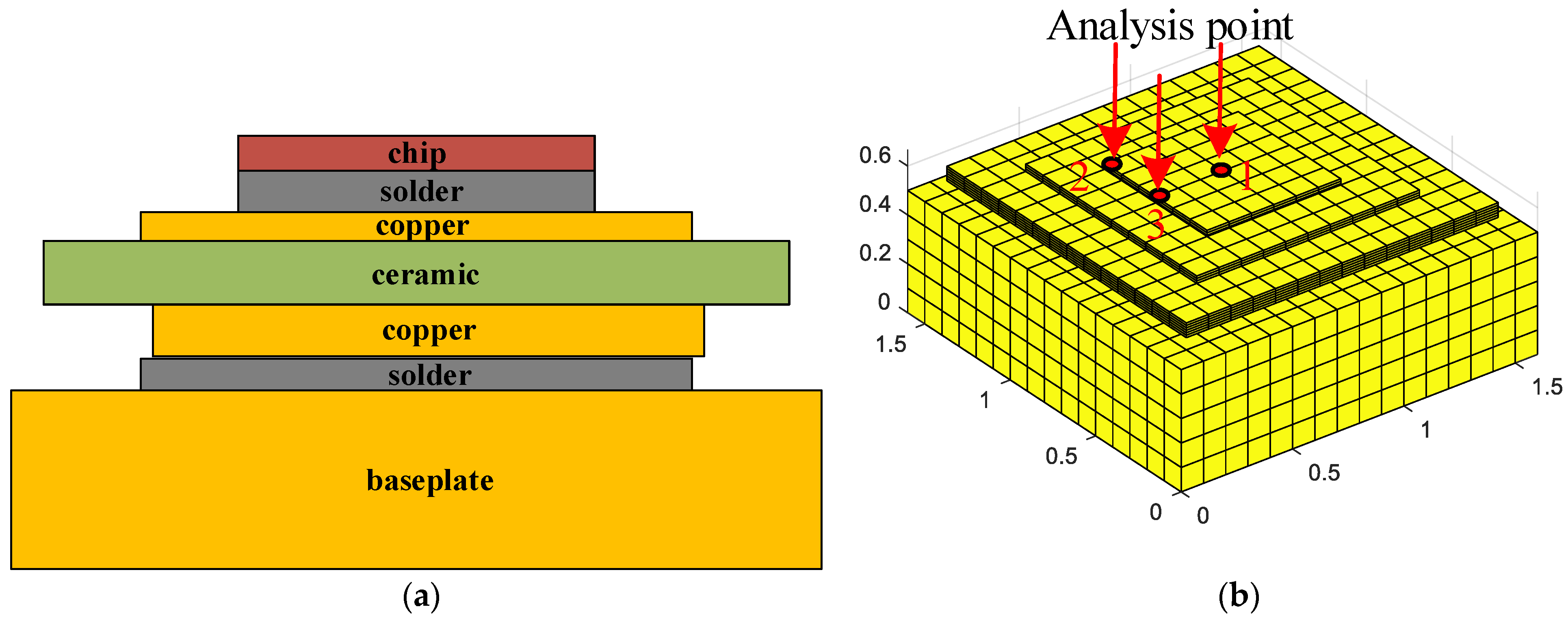





| Analysis Point | NTM Model | Proposed | ||
|---|---|---|---|---|
| max (K) | min (K) | max (K) | min (K) | |
| Point 1 | 40.9190 | −37.1739 | 40.9114 | −37.1928 |
| Point 2 | 12.3376 | −9.8100 | 12.3112 | −9.8353 |
| Point 3 | 19.9404 | −17.9279 | 19.9244 | −17.9785 |
| Analysis Point | Block Arnoldi (Order = 30) | Proposed (Order = 28) | ||||
|---|---|---|---|---|---|---|
| max (K) | min (K) | Average (K) | max (K) | min (K) | Average (K) | |
| Point 1 | 3.2275 | 0 | 0.1869 | 0.3603 | 0 | 0.0689 |
| Point 2 | 0.9803 | 0 | 0.0543 | 0.0986 | 0 | 0.0246 |
| Point 3 | 6.3752 | 0 | 0.1995 | 0.1459 | 0 | 0.0224 |
| Analysis Point | Proposed (Order = 28) | Block Arnoldi (Order = 20) | Block Arnoldi (Order = 30) |
|---|---|---|---|
| Point 1 | 0.0066 | 0.0479 | 0.0246 |
| Point 2 | 0.0065 | 0.0298 | 0.0190 |
| Point 3 | 0.0088 | 0.2659 | 0.1627 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Chen, J.; Wang, H.; Yang, S. A Block Arnoldi Algorithm Based Reduced-Order Model Applied to Large-Scale Algebraic Equations of a 3-D Field Problem. Appl. Sci. 2021, 11, 9435. https://doi.org/10.3390/app11209435
Wang N, Chen J, Wang H, Yang S. A Block Arnoldi Algorithm Based Reduced-Order Model Applied to Large-Scale Algebraic Equations of a 3-D Field Problem. Applied Sciences. 2021; 11(20):9435. https://doi.org/10.3390/app11209435
Chicago/Turabian StyleWang, Ning, Jiajia Chen, Huifang Wang, and Shiyou Yang. 2021. "A Block Arnoldi Algorithm Based Reduced-Order Model Applied to Large-Scale Algebraic Equations of a 3-D Field Problem" Applied Sciences 11, no. 20: 9435. https://doi.org/10.3390/app11209435
APA StyleWang, N., Chen, J., Wang, H., & Yang, S. (2021). A Block Arnoldi Algorithm Based Reduced-Order Model Applied to Large-Scale Algebraic Equations of a 3-D Field Problem. Applied Sciences, 11(20), 9435. https://doi.org/10.3390/app11209435






