Abstract
Community detection in a complex network is an ongoing field. While the air transport network has gradually formed as a complex system, the topological and geographical characteristics of airline networks have become crucial in understanding the network dynamics and airports’ roles. This research tackles the highly interconnected parts in weighted codeshare networks. A dataset comprising ten major international airlines is selected to conduct a comparative analysis. The result confirms that the clique percolation method can be used in conjunction with other metrics to shed light on air transport network topology, recognizing patterns of inter- and intra-community connections. Moreover, the topological detection results are interpreted and explained from a transport geographical perspective, with the physical airline network structure. As complex as it may seem, the airline network tends to be a relatively small system with only a few high-order communities, which can be characterized by geographical constraints. This research also contributes to the literature by capturing new insights regarding the topological patterns of the air transport industry. Particularly, it reveals the wide hub-shifting phenomenon and the possibility of airlines with different business models sharing an identical topology profile.
1. Introduction
Topology describes properties of space that are preserved under continuous deformations, while network topology explores the way components arrange and connect within a system [1]. With the tremendous growth of the complex networks theory and application, the air transport network has gradually formed as a complex system of flights, which considers airports and direct flights as vertices and edges [2].
Vertices or nodes with network-specific roles emphasize the determinants of the network topology and performance [3]. In a complex network, communities usually represent the multiple subgroups or clusters, which consist of groups of vertices that locally, densely interconnect, but sparsely connect to other groups [4,5]. In other words, nodes more heavily connect within the community, rather than across communities [6]. For instance, a community in the transportation industry may exist as several cities, which are frequently connected by bus, train, or flights. Further, communities may have features including motifs and cliques, where nodes are divided based on their qualities or their relationships with other nodes [7]. Subsequently, the existence of communities evidences the hierarchy among the interactions and features within the network.
While the core nodes and communities act as a pivotal part in the system, community detection facilitates the uncovering of hidden relationships, revealing the interconnections and inter-dependencies among multiple parts of the complex aviation network [8,9]. In this sense, community detection is of great value in classifying the functions of nodes and analyzing complex systems at the mesoscopic level, which cannot be easily assessed by distance measures [10,11].
This research aims to explore the way in which flights influence airline networks topologically, with a weighted clique-based community detection method. The principle aggregated frameworks that deem this research to be novel and unique are listed below in bullet point format:
- This paper examines the applicability and the robustness of the weighted clique percolation method in the commercial world, with a sample of ten major airlines with different business models.
- This paper expands the research scope by taking both codeshare agreements and the flight weights into account.
- New insights in air transport geographical and topological patterns include the following:
- The detected high-order communities can be interpreted purely based on geographical information.
- The wide-spread topological hub-shifting phenomenon is observed, resulting in inconsistency between topological gateway airports and the actual airline hubs.
- It is possible that airlines with the different business models and network sizes share an identical topology profile.
This paper is structured by first reviewing the fundamental concepts of network science and community detection methods (Section 1 and Section 2). Section 3 briefly explains the computational tool implemented and the sources of data in this research. They are followed by a network analysis of ten selected airlines, with a special focus on identifying and examining the community configuration and influential shared nodes (Section 4). The results are then interpreted and explained from a transport geographical point of view, to obtain an in-depth understanding of the network dynamics and airports’ roles. Section 5 discusses the findings and results, emphasizing the new insights, and Section 6 concludes this paper.
2. Literature Review
The study of traffic dynamics has become one of the most successful applications of the complex network theory [12]. Table 1 summarizes a brief comparison of community detection methods by the year of publication. Some of them have proven their effectiveness in the transport industry, and they will be further reviewed in this section.

Table 1.
A brief comparison of community detection methods.
2.1. Traffic Dynamics from a Low-Order Perspective
Academics have developed significant numbers of mathematical tools and computer algorithms to identify the effective approaches to detect community structures. However, most of them focused on the low-order connection patterns of individual nodes and edges. For example, the traditional technique revealed the underlying community structure by removing edges, based on the shortest path, betweenness, or successive neighborhoods [13,14,15]. Others tried to overcome the limitations of the conventional ones and proposed new methods, such as the degree-based core-vertex algorithm and local community neighborhood ratio function [7,18]. Precisely, Guimerà et al. identified the multi-community structure of the global airport network, supporting the anomalous values of centrality [3]. They insisted that the community structure cannot be explained exclusively with geographical factors. Jia et al. pointed out the spatial pattern of the airport network modular structure over time in the United States [27]. However, those structures were not characterized by geographical constraints, which is consistent with Guimerà et al. [3]. Yang et al. applied hierarchical cluster analysis to compare the community configurations between high-speed rail and airline networks [4]. Similarly, the four subgroups identified in the dendrogram for airlines cannot be explained with geographical factors like the clusters that were observed in the high-speed rail network. Additionally, no clear pattern of links between the cities’ demographic information and clusters was found in the airline networks. Wu et al. improved the Clauset–Newman–Moore modularity maximization algorithm and proposed a route-traffic-based method to detect communities in airline networks [20]. They claimed that full-service airlines had fewer communities consisted of more airports, while the low-cost carriers illustrated the opposite.
2.2. High-Order Community Detection in Aviation
A high-order connection usually refers to a sub-network, which is a graph within a larger graph, whose vertex set is a subset of the vertex set, and edge set is a subset of the edge set. A complete subgraph in the network is also called a clique. It is a common network topology class and one of the basic concepts in the mathematical area of graph theory. It requires every pair of distinct nodes to be connected by a unique edge in a simple undirected graph or a pair of unique edges in each direction [28]. For instance, a three-node clique denotes a triangle, while a four-node clique represents a quadrilateral with two diagonal lines.
Typically, the clique structures in the airline network represent a group of highly connected destinations with overall better connectivity. In general, airline hubs or bases obtain the highest connectivity within the country and to the hubs of other corresponding airlines [29]. Consequently, cliques exist more commonly among hub airports. In return, the cliques in the airline network also imply the market potential and strategic position of those distinct destinations. In this sense, proper measurements for those cliques could help an airline to facilitate its core market and adjust its strategy when necessary.
Subsequently, clique-based methods have become popular for airlines to quantify the contributions of their highly connected destinations. For instance, Cardillo et al. have displayed the characteristics of three-node cliques in a multi-layer airline network [29]. They highlighted that the merging of different airline networks generates a large density of triangles, which represent the three-node cliques in the graph. They not only noticed the opportunity brought by the self-connections between major airlines and low-cost carriers, but also believed that one airline can hardly provide round trips for all the flights in those triangles. In fact, the ever-growing codeshare partnerships allow an airline to market its partners’ products and services, and maximize the profits on more routes, without investing any additional capacity. Since the interline tickets are commonly bonded with codeshare agreements, it is not appropriate to merge airline networks randomly. Instead, the impacts of the aggregating codeshare networks need to be further examined.
Furthermore, the existing literature generally did not consider the patterns of the high-order connections, such as communities formed by cliques. Although Huang et al. tried to tackle this problem by proposing a higher-order multi-layer community detection method [25], their approach is motif-driven rather than clique-driven. Therefore, quantitatively characterizing the clique communities becomes essential to shed light on the high-order structures in the network.
2.3. The Applicability and The Robustness of The Existing Community Detection Methods
The topological positions and the properties of nodes directly affect the interactions and spreading phenomena in the network [30]. A node participating in more than one community is a common phenomenon in complex networks. In the air transport industry, the shared nodes reflect a few central gateway airports. They connect different regions with a high density of routes, propagating passengers, cargo, and even diseases to a large portion of the network. Guimerà et al. claimed that the airports connecting different communities are typically hubs within their low-order communities [3]. Rather than being classified into one community, those airports are, if not demanded equally, proportionately needed by both sides. In this sense, it is the shared nodes that also indicate the existence of community overlaps. Accordingly, methods and algorithms have been proposed to detect overlapping community structures using modularity, spectral, and matrix factorization [17]. Although scholars successfully identified the overlapping vertices, their algorithms are usually node-driven rather than clique-driven [7,16,17].
In addition, previous studies have usually constructed the aviation network as unweighted and undirected. Their network frameworks decrease the complexity of the air transport system by reducing the model to pair-wise interactions, without considering the particularities of the structure. Although it helps to stay focused on the structural properties of connections, and identify the most relevant mechanisms, additional information is naturally neglected under those circumstances, including flight schedule, aircraft type, and operator [31,32]. While the traffic en route affects the network aspect spatially, and impacts the passenger rerouting choices, it is as important as the topological characters [20]. Since flights are not equivalent, the dynamics of weights along the routes should be considered proportionally, by either flight frequency or passenger number [2]. Cui et al. investigated the fully connected subgraphs with the clustering coefficient and the belonging degrees [21,22]. However, no evidence shows the robustness of those methods in weighted networks. Li et al. accounted for unweighted and weighted networks, and they extracted the maximal cliques to find overlapping vertices or bridge vertices between communities [23]. However, they simply merged two maximal cliques into a larger subgraph for weighted graphs, which is incapable of quantitatively characterizing the effects of weights during the calculation.
To overcome the above-mentioned challenges, this paper attempts to fill the gap and tackle the highly interconnected parts in a weighted network, by introducing a clique-based community detection method to the air transport industry.
3. Methodology
3.1. Weighted Clique Percolation Method
Clique represents the complete subgraphs in the network, which requires every pair of distinct nodes to be connected. The original clique percolation method creates clique graphs by searching for communities of size . Hence, a -clique with connected pairs represents the strongest possible coupling of nodes with unweighted links. When a link is removed from a clique, it creates two -cliques sharing nodes. Those two -cliques are defined as adjacent. In other words, a -clique has connected pairs, while two adjacent -cliques share nodes.
Based on that, Farkas et al. applied an extension of the original algorithm to find modules in a weighted network [33]. They tended to include a -clique into a module only when it had an intensity () larger than a fixed threshold value (). The weight of a subgraph, defined as the subgraph intensity, is implemented by the geometric mean of the weights of its links. Consequently, a weighted clique community is defined as a maximal set of -cliques with intensities higher than . While modules can be reached via a series of -clique adjacency connections, the overlaps between the communities are allowed. The intensity of a -clique () is written as follows:
where and denote the edge number and the weight between node and , respectively.
Therefore, defining an optimal for each becomes the key for the clique percolation algorithm. If is too big, the program will exclude all -cliques, whereas a small includes all -cliques and can hardly detect any communities.
Ideally, the size distribution of the communities follows a power law. When the number of communities is small, Farkas et al. proposed to instead optimize based on the variance () of the community [33], which is defined as follows:
where represents all the communities identified in the network. More precisely, denotes a group of communities excluding the largest one, while denotes a group of communities that exclude and the largest one. As a result, the maximal variance () is associated with the optimized for each respective .
When the network or the number of communities is too small to establish a stable estimate of , the entropy based on Shannon information becomes another option [34]. The that has the maximum entropy for the respective would be desirable to optimize . The entropy can be defined as follows:
where denotes the number of communities and denotes the probability of being in community .
Lastly, a permutation test is implemented to examine if the entropy is higher than expected by chance. The test creates permutations for the network, and extracts the highest entropy for each , before calculating the confidence interval of the entropy. By comparing the entropy with the upper bound of the confidence interval, the optimized for the respective can be spotted and interpreted.
The research methodology is summarized in Figure 1.
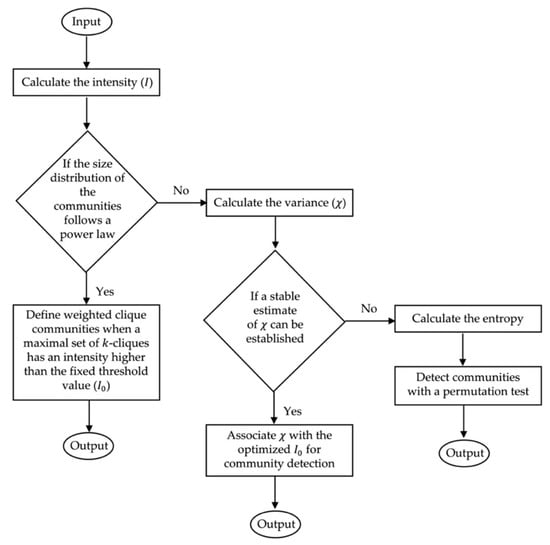
Figure 1.
Research methodology flow chart.
3.2. Dataset
To verify the effectiveness of the proposed method, this study conducts a comparative analysis with the top ten airline groups by passengers carried in 2019, including American Airlines Group, Delta Air Lines, Southwest Airlines, United Airlines, Ryanair, China Southern Airlines, Lufthansa Group, China Eastern Airlines, International Airlines Group (IAG) and Air China Group.
Intersect holdings have gained increasing attention and popularity among airlines. Instead of merging several holding airlines into one, some groups prefer to maintain airlines’ brands and liveries and operate as their subsidiaries. Therefore, the biggest airline is selected from each group to enable knowledge discovery and pattern detection. For example, the scheduled flights of British Airways will be analyzed on behalf of the complex network of IAG.
Among selected airlines, Southwest Airlines and Ryanair (including Ryanair Sun) are low-cost carriers operating point-to-point networks by themselves, whereas the rest are full-service ones operating hub-and-spoke networks with their codeshare partners. Hence, they will be investigated respectively to explore the highly interconnected parts and give particular insights in terms of the topological differences between business models.
As discussed in Section 2.2, the codeshare agreement benefits an airline considerably. It allows the airline to publish and market flights operated by partners under its flight number as part of the published timetable. Those agreements dramatically influence the airline network configuration and reshape the market dynamics worldwide [35]. Yet, most of the research considers the transportation network as an isolated system [36]. Other academics tried to tackle this issue from a multi-layer perspective. By corresponding each layer to a different airline, Hong and Liang calculated topological parameters for Chinese airlines and conducted a comparative analysis among them [26]. Similarly, Li et al. unveiled the multi-layer structure in the aviation industry with a special focus on communities bigger than ten nodes [37]. Likewise, Cardillo et al. sketched the structural properties of the air transport system in Europe [29]. They noticed that the topological properties of the airline network have resulted from multi-layer characters rather than single layers. Although they compared the networks of major airlines and low-cost ones, they only took operating carriers into account, which left the codeshare system remaining almost unexplored. Therefore, it is necessary to devote efforts to and explore the way in which codeshare partners are reshaping topological properties in the aggregate network.
A weekly scheduled non-stop flight dataset (from 1 August 2019 to 7 August 2019) is obtained from OAG (OAG is a global travel data provider with headquarters in the UK. It provides flight information data, including schedules, flight status, connection times and industry reference codes, such as airport codes), including origin, destination, operating and codeshare carriers of each flight. Because the actual passenger number is not available via multiple sources, this research weights each flight by the weekly frequency for the selected airlines accordingly. Hence, the relationships between airports are defined by both topological structures and a traffic-driven indicator. Last, but not least, this study will be primarily focused on airport level rather than city level in order to identify the key players in a multi-airport system. Hence, each airport represents a vertex, while each direct flight connecting an airport pair serves as an edge.
4. Clique Percolation Community Detection
4.1. Network Properties for Selected Airlines
Table 2 presents a summary of the transport network statistics for the chosen airlines and their codeshare networks. The number of nodes and edges measures the size of each network, where a node represents an airport, and an edge connects a pair of airports. While the edge-to-node ratio illustrates the average degree, the density investigates the ratio of the actual number of edges to the total possible number of edges. Although airline groups are selected based on the passenger number, the size of the individual airline network varies from one to another. For instance, eight legacy carriers fly to, on average, 200 destinations by themselves, whereas huge gaps are observed in the number of edges connecting those airports. More specifically, MU connects 237 airports with 1711 unique airport pairs, resulting in the highest edge-to-node ratio (7.22). On the contrary, BA connects 208 airports with 453 unique connections, achieving the lowest edge-to-node ratio (2.18). The low average degree of BA represents a loosely connected network. The limited number of edges further confirms the lack of connections, probably for most destinations in BA’s network.

Table 2.
Statistics results for selected 10 airlines (excluded subsidiaries).
A higher edge-to-node radio represents a generally better connection within the network, which can usually be confirmed by the density results. Nonetheless, those metrics are not always consistent, since the calculation of density magnifies the weight of nodes. Precisely, low-cost carriers obtain a relatively higher ratio with decentralized network structures, when compared with full-service carriers. Equipped with a higher edge-to-node ratio, FR obtains only half of the density of WN. This is because the gap in the number of their edges outweighs the one in the nodes during the processing of density.
With the wide exchange of codeshare agreements, the airline network has become more complex than ever before. Overall, the network density declines with the increase in codeshare partnerships. By that measure, all codeshare systems remain fairly sparse. Regarding the average degree, the results are quite conflicting. While the partnerships lower the edge-to-node ratio for AA, UA, CZ, and MU, other airlines witness dramatic growths in the ratio. This illustrates that the number of nodes and edges does not change proportionately for most carriers when aggregating networks with their codeshare partners. Particularly, the change rate in edges is usually smaller than the square of the rate in nodes, which leads to the drop in density. It is also noticeable that the gaps become smaller, in terms of the sizes among codeshare networks, which may indicate wide homogeneous competition in the airline industry.
4.2. Clique Percolation Community Detection Process
The traditional static network framework limits the studies to certain properties of these networks. For instance, it allows identifications for the bottlenecks or the clusters of destinations without measuring the dynamic characteristic of the aviation system [32]. In contrast, the clique percolation method proposes an algorithm to detect the interaction patterns of cliques. Although Eustace et al. worried that the number and the size of -clique may affect the quality of the detected communities [18], the nature of the airline network limits the cliques to three-/four-node communities in most cases. Subsequently, this study mainly examined the network dynamics of three-/four-clique communities in the system.
Initially, the maximum edge weight is tested as the upper limits for as was recommended by Farkas et al. [33]. For instance, the maximum edge weight of 119 is set as the upper limits for AA’s codeshare network, in steps of 0.1.
Although the airline codeshare networks seem to be sophisticated, UA’s network, for example, can be divided into a maximum of ten communities. When the optimal is identified by the emergence of the gigantic component, a small number of communities may lead to an unstable threshold. As a result, the maximal variance () is associated with the optimal for three-/four-clique community identifications for AA, BA, CZ, DL, and MU. It also helps to detect the three-clique communities for CA, LH, UA, and WN. Take AA as an example, for , the maximal variance equals 4.25, which leads to an optimal intensity (). Among 583 airports in AA’s codeshare network, 270 airports are identified and classified into three three-clique communities, while 313 nodes are isolated, including 49 nodes found in three-clique communities and 264 nodes outside cliques. LAX and SEA are identified as the shared nodes, which interconnect the coexistence of structural subgraphs in the system. Similarly, optimal (9.1) is identified at the point of maximal variance () for AA’s four-clique communities. The increase in optimal witnesses the rising number of isolated nodes (385). Three hundred and eighty-two of them are outside four-node cliques and sparsely connected to the network originally. Only 198 airports are identified in the three four-clique communities, while three airports (GRU, LAX, and MIA) are detected as shared nodes.
When detecting four-clique communities for CA, LH, UA, and WN, the number of communities tends to be too small to establish a stable estimate of . In this case, entropy becomes the primary indicator in finding the optimal for the respective . For instance, the maximum entropy for CA equals 1.002, which is higher than the upper bound of the 95% confidence interval (see Table 3). It indicates that the entropy is higher than expected by chance. Therefore, the (0.1), at this point, would be desirable to optimal . Then, the airports can be classified into two four-clique communities with two shared nodes (PEK and PVG). Similarly, four-clique communities are detected for LH, UA, and WN. Since no stable variance is calculated for FR, both its three-clique and four-clique communities are detected based on the maximum entropy. However, neither of them passes the permutation test. Therefore, no high-order community is identified in FR’s network.

Table 3.
Permutation test for CA.
4.3. Community Detection Results and Airline Network Configurations
The different airline operating patterns lead to the different network topological and community structures [20]. Unlike the structures identified in low-order communities, the clique community detection results show that most of the codeshare networks consist of three three-clique groups (see Table 4). The fewer groups identified in the four-clique community, for LH, UA, and CA, suggest an overall better connection among all the cliques. In contrast, low-cost airlines rarely have high-order communities, since their networks are combined with rolling hubs and direct origin–destination pairs. Most airlines have one big well-connected community that is covered by their own capacity and one or two small communities that are possibly guaranteed by their codeshare partners. This confirms that the partnership offers a bypass for an airline to extend its network coverage with limited capacity and traffic rights. Nevertheless, the four-clique communities detected in BA’s network limit to several key airports in each group, which is similar to the configuration of WN’s three-clique communities. Despite the business model and network size, the similarity in the communities suggests the possibility of them sharing an identical topology profile.

Table 4.
Community detection results for codeshare networks of selected 10 airlines (excluded subsidiaries).
More specifically, Figure 2 demonstrates the airports detected in high-order communities. The community groups are highlighted with different colors (yellow, orange, or red, when applicable). Regardless of the overlapping areas, the communities detected in the airline network are separated based on geographical information. This can be explained by the cliques formed in the high-order communities. An airline tends to partner with the one that provides complimentary advantages regionally. Hence, the merging of networks not only supplies existing cliques from the partners, but also generates a large density of new triangles. Basically, the geographical location of the partners’ network results in the geographical separation of clique communities. However, the separation does not necessarily mean geographical isolation by countries or continents. Take BA as an example, airports are divided into three groups for three-clique communities. Particularly, most of the airports in the biggest community located in the US and Europe, which represent BA’s home advantage across Europe and the trans-Atlantic Ocean. Another two communities are identified in Asia-Pacific (HKG, MEL, and SYD) and Africa (CPT, DUR, JNB, and PLZ). Likewise, four-clique communities are further dissociated into three groups, purely consisting of BA’s home ground, but the isolation of MAD with three shared nodes (JFK, DUB, and LHR) does not reflect a loose connection in the network. However, MAD is the headquarter of Iberia, the flag carrier of Spain, and other 100% owned subsidiaries of IAG. The separation indicates a rather dense connectivity among the four nodes. On the other hand, LH, another European carrier, demonstrates its worldwide coverage and mature network via three-clique communities, and overall better connectivity through a single four-clique community.
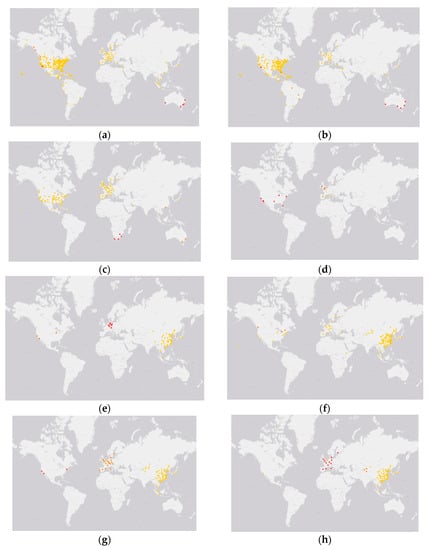
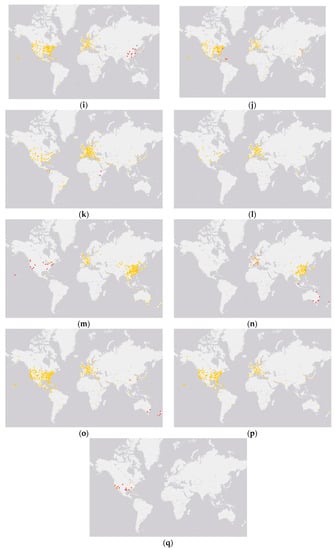
Figure 2.
Stylized network extract for community detection results. (a) Three-clique community detection results for AA; (b) four-clique community detection results for AA; (c) three-clique community detection results for BA; (d) four-clique community detection results for BA; (e) three-clique community detection results for CA; (f) four-clique community detection results for CA; (g) three-clique community detection results for CZ; (h) four-clique community detection results for CZ; (i) three-clique community detection results for DL; (j) four-clique community detection results for DL; (k) three-clique community detection results for LH; (l) four-clique community detection results for LH; (m) three-clique community detection results for MU; (n) four-clique community detection results for MU; (o) three-clique community detection results for UA; (p) four-clique community detection results for UA; (q) three-clique community detection results for WN. Notes: Figure 2 is drawn with QGIS (QGIS is a user-friendly open source geographic information system (GIS) licensed under the GNU General Public License), and the map background is Esri light grey selected from the XYZ Tiles in QGIS. Yellow, orange and red nodes denote different communities when applicable.
4.4. Airports’ Roles in Codeshare Network: Hub Shifting or Hub Concentration
In the physical airline network, the hub is usually highly connected within the country and to the hubs of other corresponding airlines [29]. This is the result of airline aggregations and alliances decisions under a series of legal, commercial, and technical considerations [38]. Further, this concept indicates the hierarchy among airports, particularly when a carrier runs a multi-hub system. Therefore, hub airports become crucial to airlines’ strategic resource optimization.
Topologically, the hub airport, connecting different parts of the network, usually refers to the shared node in the overlapped communities. Hence, at least two communities are necessary for the identification of the overlapping area. Meanwhile, if no shared node is identified, this indicates either the topological isolation of each community, or only one well-connected community detected in the network. In fact, this issue becomes especially vital in an aggregated codeshare network. Whether the hub of an airline can be identified as the shared node reflects the airline’s strategic position in the cooperation. To be more specific, if a partner’s hub is identified as the shared node, it reveals a possible hub shifting in the codeshare network. This could result from a partner with strong market power, or from the airline losing its dominant position in connecting different regions. In this sense, discovering the influential shared nodes helps airlines to not only recognize the pattern of intercommunity and intracommunity connections, but also understand its position in the network and control the network dynamics regionally.
One main function of the clique percolation method is to identify the overlapping areas. The results show that the hub-shifting phenomenon has been widely observed among six full-service airlines. For instance, although LHR and LGW are BA’s hubs in London, three airports (DUB, JFK, and LHR) are marked as influential among its four-clique communities. While JFK and DUB are the hub airports of AA and Aer Lingus (EI), the result proves the partners’ contribution in the complex codeshare network, such as enhancing the BA’s trans-Atlantic and major European market. More specifically, EI is the flag carrier and the second largest airline in Ireland, now a wholly owned subsidiary of IAG. The detection of DUB confirms the operating strategy of IAG as a group, together with the oneworld alliance partnership with AA. Similarly, only two of AA’s hubs (LAX and MIA) are marked among its ten hubs in the United States. SEA is identified as the shared node, along with LAX, among three-clique communities, while GRU, LAX, and MIA are found to be influential among four-clique communities. Since SEA and GRU are the hub airports of Alaska Air Group (AS and QX) and LATAM Brasil (JJ), it can be concluded that the codeshare inside and outside the alliance provides complementary advantages for the airline network, and leads to the hub shifting.
Similar results are found in CA’s network. Precisely, PEK and PVG are detected in the overlapped area among the four-clique communities, whereas CA originally hubs in PEK and CTU. Unlike previous examples, PVG is not a hub airport operated by CA’s partner outside China. In contrast, the outperformance of PVG establishes the international market power of Shanghai as a possibly geopolitical-based core region, connecting China to the rest of the world [39]. While constant change happens in the aviation sector, CA may encounter more hub shifting with the emerging multi-airport configurations, particularly after the operation of Beijing Daxing International Airport (PKX) and Chengdu Tianfu International Airport (TFU).
The newly identified influential airports expand the airline’s connectivity by providing additional transit opportunities and flights covering more regions. However, if only the partners’ hubs are identified as influential, it may ring the bell to the airline, indicating the loss of its position in connecting the complete subgraphs across regions. This issue has been found on the network of CZ, DL, and UA. In particular, it has been found in CZ hubs in PEK, PKX, and CAN, operating approximately 3000 domestic flights daily. However, evidence shows that AMS is the only shared node among CZ’s three-clique communities, linking Asia and Europe. Meanwhile, three airports in the United States (JFK, LAX, and SFO) tend to be isolated from the other two groups, without any overlapping area. Although CZ’s home court is well connected, there is no gateway airport located in its registration country. This gap diminishes CZ’s effort in connecting China to the rest of the world via the “Canton Route”. Additionally, only a secondary hub (URC) is marked as another shared node among four-clique communities, raising the alarm for this Guangzhou-based carrier. Likewise, CAN, ICN, and PVG are found to be influential among three-clique communities in DL’s network, none of which are DL’s hub airport located in the United States. Similarly, AKL, PEK, and SYD are found to be critical among UA’s three-clique communities.
The previous study claims that medium-sized airports are more strategic in connecting different parts of the network than larger ones, due to the architecture of the air transport system [32]. The existing research also suggested that the global hubs are not necessarily the gateway airports in low-order communities. The most connected cities are not necessarily the most central ones [3]. Those statements are also supported by the identification of URC and AKL in the high-order communities. Each serves just over 20 million passengers annually, URC and AKL seem to be much less considerable compared with other mega airports. Nonetheless, their geographical and topological positions fit the pattern of network dynamics, and connect intercommunity and intracommunity.
On the contrary, the hub airports of LH and MU prove their strategic position in the codeshare networks. FRA and PVG outrank other hubs in three-clique communities, and become the only influential node for LH and MU, respectively. This also indicates that those two airports are more substantial in their multi-hub systems. In four-clique communities, the results are controversial. The fact that no shared nodes are found in the LH’s network illustrates strong local connectivity across the single community. By contrast, the expansion of influential nodes (CDG, PVG, SIN, and SYD) in MU’s system demonstrates the partners’ contribution to improving network efficiency and connectivity worldwide. Particularly, the geographical locations of those hub airports are ideal in connecting different continents.
Lastly, it would become reasonable if no shared node is identified in low-cost carriers’ networks, since they usually operate decentralized systems. However, four influential airports are found in WN’s three-clique community, which implies the topological difference between the two major low-cost carriers. This can be explained by the geographical configurations and airline network of the United States and Europe.
5. Findings and Discussion, Contribution, Limitations and Future Work of The Study
5.1. Findings and Discussion
The research aims to assess the underlying patterns in the high-order communities, and extracts the backbone of the airline network structure with a weighted clique percolation method. Ten airlines are selected from the top ten airline groups worldwide, to exemplify a comparative analysis and verify the effectiveness of the proposed method.
Firstly, this study summarizes the patterns of major airline networks with statistical values, which illustrate the variations in the average degree and density of the selected airline networks. This paper spots the proportionate change in nodes and edges, which may result in the uncertainty of density.
Then, the weighted clique percolation method is introduced to analyze the high-order interaction and clustering properties. Typically, most of the codeshare networks are consist in three high-order communities, whereas low-cost airlines seldom have any high-order community, due to their network structure and lack of partnerships. Meanwhile, the community configuration of BA is close to what WN has, with several key airports in each group. Regardless of the business model and network size, the similarity in high-order community structures suggests the possibility of them sharing an identical topology profile, which is the opposite of what previous studies in low-order communities have found [20]. Moreover, the communities detected by this method are separated based on geographical information, which has not been achieved by other techniques. Basically, the geographical location of the partners’ network results in the geographical separation of clique communities.
The influential nodes in the overlapping area help airlines to recognize airports’ roles in the network and control the network dynamics. However, the results seem to be rather controversial. This study observes a wide hub-shifting phenomenon among six legacy airlines. The shifting can be classified into three types. The first type combines some of the airline’s hubs with their partners’, such as AA and BA. The result proves the complementary advantages brought by partners. In contrast, no partners’ hub outside China was found in CA’s network. Particularly, the outperformance of PVG establishes the international market power of Shanghai, and CA should pay attention to the emerging multi-airport configurations in China. Finally, only partners’ hubs were identified in the network of CZ, DL, and UA, which may ring the bell of airlines losing dominant positions in the codeshare network. Aside from shifting, the concentration in FRA and PVG proves their hubs’ strategic positions by outperforming other hub airports in the system. In MU’s four-clique communities, it is also noticeable that the influential nodes extend to CDG, PVG, SIN, and SYD, offering worldwide connections, contributed to by codeshare partnerships.
There has been very limited research targeting high-order communities in the airline network. Hence, it is not easy to conduct a comparative analysis among the published results from the limited available research. However, it is noticeable that some of the findings are consistent with the patterns that the previous literature has detected in the low-order structures. For instance, this paper identifies two medium-sized airports as gateway airports, which confirms the arguments of Guimerà et al. and Rocha [3,32].
5.2. Contribution
Network science has been commonly applied as a quantitative tool to contribute to a better understanding of the various layers of the aviation system. The existing literature usually considers the network of an operating carrier as a single layer, but leaves the codeshare system remaining almost unexplored. The codeshare network is definitely worthy of deeper investigative analysis, as it is the result of airline aggregations and alliances decisions, which are crucial to airlines’ strategical resource optimization. Hence, this study fills in knowledge gaps by uniquely taking the codeshare network into account, and addressing its effects on airline topology and transport geography. More importantly, the rarely discussed industry-specific issues are explored, based on the reality of the airline networks in the commercial world, rather than defining communities algorithmically.
Affecting the network aspect spatially and impacting the passenger rerouting choices, the traffic en route is as important as the topological characters for airlines and airports. However, there is very limited literature that has investigated the aviation network as a weighted system. This paper contributes to the existing literature by considering the dynamics of weights along the routes. This research increases the rationale and accuracy of the analysis by taking flight frequency into account, and expands the research scope from topological structure to the real world.
Last, but not least, this study examines the applicability and the robustness of the weighted clique percolation method with a case study, testing ten major airlines with different business models. The results argue that the clique-based analysis is quite distinct from what the existing literature found with low-order methods, which reveals new insights in air transport geographical and topological patterns. First, the result suggests that the high-order communities detected in the airline systems are separated based on geographical information, which has not been achieved by other techniques. Second, the topological hub-shifting phenomenon is observed, revealing that the topological gateway airports are not always consistent with the actual hub airports of the airlines. Third, unlike previous studies on low-order communities [20], no clear patterns in the high-order network topology and community structures are identified between legacy carriers and low-cost airlines. In contrast, this research reflects the possibility of airlines with different business models and network sizes sharing an identical topology profile. This overall ensemble of unique inputs that were applied in this study separates it from other studies.
5.3. Limitations and Future Work of The Study
This research explores the spatial distribution of the community structure. However, the analysis leaves two issues, which can be addressed in future research. First, there is no commonly accepted standard to evaluate the detection of communities [22]. Second, this study targets the dynamics of a static network. A study on the temporal network will become more meaningful in evaluating the epidemic outbreak and traffic dynamics, especially during the pandemic [40]. Therefore, further research is necessary to fill these gaps.
6. Conclusions
To yield insightful results revealing the organization of complex aviation systems, this study first summarizes the patterns of major airline networks. The statistical values support the variations in the average degree and density of the selected airline networks, including legacy carriers and low-cost ones. It is also worthy to notice that the proportionate change in nodes and edges may bring uncertainty to the calculation of density.
This study then introduces a weighted clique percolation method to the airline industry, to assess and interpret the network structures topologically. As complex as it may seem, the airline network tends to be a relatively small system with only a few high-order communities. Legacy carriers follow the hub-and-spoke structure to improve the coverage of airports and maximize efficiency, whereas low-cost airlines seem to lose interest in the centralized network. However, there are certain topological similarities between them.
A comparative analysis confirms that the proposed method can be used in conjunction with other metrics to shed light on air transport network topology, and it may become one of the most preferable ways to measure airline networks. The results quantify and interpret the high-order communities with geographical characteristics, while emphasizing the hub-shifting and hub-concentration phenomena at the level of an aggregate codeshare network. Although airlines do not usually make decisions based on topological factors, the new insights spot the connections between topological patterns and the physical and geographical perspective. Precisely, the geographical separation of the high-order communities confirms the regional complimentary advantages brought by partners. On the other hand, the hub-shifting phenomena indicates the lower hierarchy of the airline in the codeshare network. Since the hub-shifting phenomena rings the bell of one airline losing its position in the codeshare partnership, efforts are necessary for the airline to facilitate its core market, and therefore adjust its strategy and physical network accordingly.
Author Contributions
H.Y.: Writing—original draft, writing—review and editing. M.L.: writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Civil Aviation Administration of China (FDQT0006).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are available at www.oag.com (accessed on 20 January 2020).
Acknowledgments
The authors are grateful to the anonymous reviewers and the editor for their valuable suggestions, which improved the manuscript considerably.
Conflicts of Interest
The authors declare no conflict of interest regarding the publication of this paper.
Appendix A

Table A1.
Airport Abbreviation.
Table A1.
Airport Abbreviation.
| IATA Code | Airport Name | Country |
|---|---|---|
| AKL | Auckland International Airport | New Zealand |
| CAN | Guangzhou International Airport | China |
| CDG | Paris Charles de Gaulle Airport | France |
| CPT | Cape Town International Airport | South Africa |
| DEN | Denver International Airport | USA |
| DUB | Dublin (IE) International Airport | Ireland Republic of |
| DUR | Durban King Shaka International Airport | South Africa |
| FRA | Frankfurt International Airport | Germany |
| GRU | Sao Paulo Guarulhos International Airport | Brazil |
| HKG | Hong Kong International Airport | Hong Kong (sar) China |
| ICN | Seoul Incheon International Airport | Korea Republic of |
| JFK | New York J. F. Kennedy International Airport | USA |
| JNB | Johannesburg O.r. Tambo International Airport | South Africa |
| LAS | Las Vegas McCarran International Airport | USA |
| LAX | Los Angeles International Airport | USA |
| LGW | London Gatwick Airport | United Kingdom |
| LHR | London Heathrow Airport | United Kingdom |
| MAD | Madrid Adolfo Suarez-Barajas Airport | Spain |
| MDW | Chicago Midway International Airport | USA |
| MEL | Melbourne Airport | Australia |
| MIA | Miami International Airport | USA |
| PEK | Beijing Capital International Airport | China |
| PHX | Phoenix Sky Harbour International Airport | USA |
| PLZ | Port Elizabeth International Airport | South Africa |
| PVG | Shanghai Pudong International Airport | China |
| SEA | Seattle-Tacoma International Airport | USA |
| SFO | San Francisco International Airport | USA |
| SIN | Singapore Changi Airport | Singapore |
| SYD | Sydney Kingsford Smith Airport | Australia |
| URC | Urumqi International Airport | China |
References
- Bounova, G. Topological Evolution of Networks: Case Studies in the US Airlines and Language Wikipedias. Ph.D. Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Zanin, M.; Lillo, F. Modelling the air transport with complex networks: A short review. Eur. Phys. J. Spec. Top. 2013, 215, 5–21. [Google Scholar] [CrossRef] [Green Version]
- Guimerà, R.; Mossa, S.; Turtschi, A.; Amaral, L. The worldwide air transportation network: Anomalous centrality, community structure, and cities’ global. Proc. Natl. Acad. Sci. USA 2005, 102, 7794–7799. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, H.; Dobruszkes, F.; Wang, J.; Dijst, M.; Witte, P. Comparing China’s urban systems in high-speed railway and airline networks. J. Transp. Geogr. 2018, 68, 233–244. [Google Scholar] [CrossRef]
- Guo, W.; Toader, B.; Feier, R.; Mosquera, G.; Ying, F.; Oh, S.; Price-Williams, M.; Krupp, A. Global air transport complex network: Multi-scale analysis. SN Appl. Sci. 2019, 1, 680. [Google Scholar] [CrossRef] [Green Version]
- Porter, M.; Onnela, J.; Mucha, P. Communities in networks. Not. AMS 2009, 56, 1082–1097. [Google Scholar]
- Wang, X.; Li, J. Detecting communities by the core-vertex and intimate degree in complex networks. Physica A 2013, 392, 2555–2563. [Google Scholar] [CrossRef]
- Souravlas, S.; Anastasiadou, S.; Katsavounis, S. A Survey on the Recent Advances of Deep Community Detection. Appl. Sci. 2021, 11, 7179. [Google Scholar] [CrossRef]
- Wang, X.; Qin, X. Asymmetric intimacy and algorithm for detecting communities in bipartite networks. Physica A 2016, 462, 569–578. [Google Scholar] [CrossRef]
- Zanin, M.; Papo, D.; Sousa, P.A.; Menasalvas, E.; Nicchi, A.; Kubik, E.; Boccaletti, S. Combining complex networks and data mining: Why and how. Phys. Rep. 2016, 635, 1–44. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Wahlström, J.; Nehorai, A. Community Detection in Complex Networks via Clique Conductance. Sci. Rep. 2018, 8, 5982. [Google Scholar] [CrossRef]
- Huang, X.; Chen, D.; Ren, T.; Wang, D. A survey of community detection methods in multilayer networks. Data Min. Knowl. Discov. 2021, 35, 1–45. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7824. [Google Scholar] [CrossRef] [Green Version]
- Newman, M.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodrigues, F.; Travieso, G.; Costa, L.F. Fast community identification by hierarchical growth. Int. J. Mod. Phys. C 2007, 18, 937–947. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, X.; Eustace, J. Detecting overlapping communities by seed community in weighted complex networks. Physica A 2013, 392, 6125–6134. [Google Scholar] [CrossRef]
- Eustace, J.; Wang, X.; Cui, Y. Overlapping community detection using neighbourhood ratio matrix. Physica A 2014, 421, 510–521. [Google Scholar] [CrossRef]
- Eustace, J.; Wang, X.; Cui, Y. Community detection using local neighborhood in complex networks. Physica A 2015, 436, 665–677. [Google Scholar] [CrossRef]
- Behera, R.K.; Rath, S.K.; Misra, S.; Damaševicius, R.; Maskeliunas, R. Large Scale Community Detection Using a Small World Model. Appl. Sci. 2017, 7, 1173. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Zhang, H.; Zhang, S.; Witlox, F. Community Detection in Airline Networks: An Empirical Analysis of American vs. Southwest Airlines. J. Adv. Transp. 2019, 2019, 3032015. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, X.; Eustace, J. Detecting community structure via the maximal sub-graphs and belonging degrees in complex networks. Physica A 2014, 416, 198–207. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, X.; Li, J. Detecting overlapping communities in networks using the maximal sub-graph and the clustering coefficient. Physica A 2014, 405, 85–91. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; Cui, Y. Uncovering the overlapping community structure of complex networks by maximal cliques. Physica A 2014, 415, 398–406. [Google Scholar] [CrossRef]
- Edler, D.; Bohlin, L.; Rosvall, M. Mapping Higher-Order Network Flows in Memory and Multilayer Networks with Infomap. Algorithms 2017, 10, 112. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Wang, C.-D.; Chao, H.-Y. Higher-Order Multi-Layer Community Detection. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence (AAAI-19), Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 9945–9946. [Google Scholar]
- Hong, C.; Liang, B. Analysis of the weighted Chinese air transportation multilayer network. In Proceedings of the IEEE 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; pp. 2318–2321. [Google Scholar]
- Jia, T.; Qin, K.; Shan, J. An exploratory analysis on the evolution of the US airport network. Physica A 2014, 413, 266–279. [Google Scholar] [CrossRef]
- Agasse-Duval, M.; Lawford, S. Subgraphs and Motifs in a Dynamic Airline Network. 2018. Available online: https://arxiv.org/abs/1807.02585 (accessed on 31 December 2019).
- Cardillo, A.; Gomez-Gardenes, J.; Zanin, M.; Romance, M.; Papo, D.; del Pozo, F.; Boccaletti, S. Emergence of network features from multiplexity. Sci. Rep. 2013, 3, 1344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malliaros, F.; Rossi, M.; Vazirgiannis, M. Locating influential nodes in complex networks. Sci. Rep. 2016, 6, 19307. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Zhou, X.; Lordan, O.; Wang, Z.; Zhao, C.; Zhu, Y. Analysis of the Chinese Airline Network as multi-layer networks. Transp. Res. Part E Logist. Transp. Rev. 2016, 89, 108–116. [Google Scholar] [CrossRef] [Green Version]
- Rocha, L. Dynamics of Air Transport Networks: A Review from a Complex Systems Perspective. Chin. J. Aeronaut. 2017, 30, 469–478. [Google Scholar] [CrossRef]
- Farkas, I.; Abel, D.; Palla, G.; Vicsek, T. Weighted network modules. New J. Phys. 2007, 9, 180. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef] [Green Version]
- Reggiani, A.; Nijkamp, P.; Cento, A. Connectivity and Concentration in Airline Networks: A Complexity Analysis of Lufthansa’s Network; Tinbergen Institute: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Du, W.; Zhou, X.; Jusup, M.; Wang, Z. Physics of transportation: Towards optimal capacity using the multilayer network framework. Sci. Rep. 2016, 6, 19059. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Xu, G.; Jiao, L.; Zhou, Y.; Yu, W. Multi-layer network community detection model based on attributes and social interaction intensity. Comput. Electr. Eng. 2019, 77, 300–313. [Google Scholar] [CrossRef]
- Lordan, O.; Sallan, J. Core and critical cities of global region airport networks. Physica A 2019, 513, 724–733. [Google Scholar] [CrossRef]
- O’Kelly, M. Global Airline Networks: Comparative Nodal Access Measures. Spat. Econ. Anal. 2016, 11, 253–275. [Google Scholar] [CrossRef]
- Ren, G.; Wang, X. Epidemic spreading in time-varying community networks. Chaos Interdiscip. J. Nonlinear Sci. 2014, 24, 023116. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).