Abstract
For fault diagnosis and predictive maintenance of rotating machinery, the phase errors generated by the integration processing of a vibration signal are an essential investigation subject. Phase errors affect the solution of mechanical systems with multiple vibration sources and also the information transmitted through the vibration that is used for fault diagnosis. This work proposes the use of phase plane, recurrence plot (RP), and cross recurrence plot (CRP) to evaluate phase shift error effects on the solution of multiple asynchronous and simple periodic functions, and on the smoothing of a Gaussian peak with white noise. Noisy peaks were smoothed twice with the triangular method and with a different number of points. The analysis of the asynchronous periodic functions and the smoothing indicated that a small phase shift changes the phase plane and the RP pattern. These changes can affect not only the accuracy of machinery fault diagnosis but also prediction for the application of timely maintenance actions.
1. Introduction
The diagnosis of failures through the analysis of vibrations in rotating machinery is a technique that has proven to be very useful and reliable in the industry because it helps improve the performance and service life of machines. It is possible to describe the position, intensity, and force of the impact of a vibration in a mechanical system through their magnitudes of position, velocity, and acceleration, respectively. Accelerometers are the most widely used instruments to measure vibration in industrial machinery. The dynamic behavior of a body is characterized by integrating acceleration to obtain its speed and position. The main methods to integrate acceleration are based on the time domain and the frequency domain. The integration in the time domain is carried out by integrating the acceleration signal directly. During this integration, several errors are accumulated due to integration method, noise, phase shift from the signal processing, and unknown initial conditions of speed and position. Frequency domain integration converts the original signal to the frequency domain using the Fourier transform, then it performs the integral in the frequency domain, and finally it returns the signal to the time domain using the inverse Fourier transform. The Fourier transformations applied to the signal generate truncation errors, additional to those already mentioned above in the time domain. In any case, working with these errors is a challenging task for researchers in many areas of study in the fields of engineering and, specifically, predictive maintenance.
In order to simplify the analysis, most fault diagnosis and prediction techniques eliminate noise by filtering but this practice leads to baseline errors from signal processing. Several literature methods, such as that described in [1], report power prediction and noise reduction techniques in the field of underwater acoustics [2]. However, eliminating noise means losing crucial information for the fault diagnosis, especially for nonlinear faults.
This research focuses on phase shift analysis by phase plot and recurrence plot (RP) to understand the importance of signal processing. Phase shift errors can affect the accuracy of the results, especially in complex mechanical systems. This work could be applied in all engineering and research fields when transforming an acceleration signal into velocity and displacement, or when processing vibration spectra to eliminate noise.
The research demonstrated that one small phase shift error becomes more critical in mechanical systems subjected to several vibration sources. The smoothing of a Gaussian noisy peak does not eliminate noise entirely and indeed it generates additional phase shifts.
In 1890 Henri Poincaré [3] introduced the concept of RP as a graphical technique to study dynamical systems within the chaos theory. Then Eckmann, Kamphorst, and Ruelle presented the RP method formally in 1987 [4]. The RP helps the analysis of complex mechanical systems in phase space and the quantification of recurrence [5]. Another characteristic of the RP is that it can identify nonlinear vibration in nonstationary regimens. Cross recurrence plot (CRP) and recurrence quantification analysis (RQA) are RP extensions. Both CRP and RQA can analyze and quantify the time dependence behavior between two processes in a single time series [6]. The potential of the RP method has been demonstrated in many areas of science, such as medicine, physics, chemistry, biology, engineering, earth sciences, finance, and economics [7]. RP and empirical mode decomposition (EMD) were implemented to study the dynamics of traffic flow on a bridge [8]. Complex fractionated arterial electrograms were dynamically analyzed and quantified with RP and recurrence quantification analysis [9]. Recently, some researchers started to apply the RP method to identify and diagnose the condition of rotating machinery. The machine defect severity was assessed by estimating entropy from RP [10]. Bearing degradation was evaluated by RP quantification and Kalman filter [11]. Vibration analysis was used in combination with EMD to detect bearing degradation by introducing a technique called autocorrelation function [12]. RP and phase space analysis were applied to identify the parameters in cutting processes [13]. Cutting stability in the milling process of nickel-based alloy Inconel 625 was analyzed by Lajmert et al. [14]. Jauregui-Correa et al. [15] studied the effect of friction on the dynamic response of a rotor rubbing housing by wavelet, phase plane and RP, and they concluded that their models could represent the friction. However, the dynamic response model was unable to predict the behavior observed in the field. Nonlinearities in a gearbox and other mechanical components were studied with RP by Jauregui-Correa [16]. His final observations confirm that RP is a powerful technique to analyze the dynamic behavior of nonlinear mechanical systems. Nevertheless, RP has some limitations: the first one is the correlation between the topology and the characteristics of the system; the second one relates to the phase plane construction when measurement data come from an accelerometer. The basis of the RP is the phase plane that is based on the Hamilton’s principle using the relationship between kinetic energy (velocity) and potential energy (displacement). These two quantities are calculated from an accelerometer by performing a double integral of the time series obtained from the instrument. The double integral of data in the time domain in complex systems can lose valuable information if it is not solved correctly. In the fault diagnosis of rotating machinery, vibration is measured by accelerometers that can pick up high-frequency with high sensitivity. The double integration of acceleration is applied to estimate displacement or position in some practical applications. Ferrero et al. [17] demonstrated that the double integration of acceleration did not provide accurate information about the displacement due to noise and measurement errors, and they evaluated a correction method based on the Kalman filter to increase the accuracy of the results. Some authors apply several filters to make the double integration, but unfortunately, valuable information in the high-frequencies can be lost in this way. Other researchers integrated velocity and displacement from an accelerometer in the frequency domain [18] and proposed some techniques to manage errors arising during the process, which are mainly due to unknown initial conditions for velocity and displacement, and to the noise at low and high frequencies. Other researchers [19] estimated the drift by using the mean of the upper and lower envelopes of signals after integration from acceleration to velocity and displacement. Liu et al. [20] introduced a way of measuring vibration displacement using a three-axes accelerometer. At first, they worked in the frequency domain to remove the trend items and noises. Then, the resulting acceleration was converted into the acceleration spectrum by Fourier transform and, finally, the acceleration spectrum was transformed into displacement spectrum. Tezcan et al. proposed a Kernel regression approach to obtain displacement in the time domain from acceleration data [21]. Pan et al. [22] proposed to correct the integration of acceleration with the baseline of the shift or drift phenomenon. In the vibration tests of autopilot missiles, baseline drift and heavy pollution are still a problem. Zhang and He [23] suggested a morphological high filtering method to filter out the drift noise. One explicit time integration technique was developed by Kim and Lee [24] to analyze linear and nonlinear problems in structural dynamics. This method controls the amount of numerical dissipation in the high-frequency range if the matrix is diagonal, and it does not require evaluation of the initial acceleration vector. A compound fault diagnosis of bearings using improved fast spectral kurtosis with VMD was presented by Wan et al. [25] to improve the accuracy. Another method based on recursive least squares was proposed [26]. Through multi-round baseline correction, filtering, and integration, the authors developed an online and real-time acceleration integral scheme to monitor displacement of a civil structure. Xu et al. [27] introduced a recursive Simpon integral method that combines Newton–Leibniz to obtain the integral recurrence calculation of each point, and a polynomial fitting to detrend the resulting waveform. The recursive least square and least means square equalizers optimization algorithms in Rayleigh fading were improved [28] with the use of a stochastic gradient descent method in the filter related to the signal error. To solve low-resolution and diffused energy problems, time-frequency analysis of nonstationary signals using variation mode decomposition and a synchro squeezing technique was proposed by Ni et al. [29]. Arrieta et al. [30] introduced a Variational Mode Decomposition to identify electromechanical oscillatory modes in power systems. The identification process was based on the time-frequency analysis of nonlinear signals which arise after a large disturbance. Some new techniques to improve the FFT-DDI method efficiency were proposed by Ribeiro et al. [31] to remove the zero shifts from unknown initial conditions, which induce errors in structural integrity evaluations and path control. The displacement reconstruction from measured accelerations and accuracy control of integration based on an attenuation algorithm was presented by Zhu et al. [32], who controlled the integration of acceleration in the frequency domain through an accuracy control factor for low frequencies. Chen et al. [33] proposed a method to solve the difficulties of weak and time-varying fault signatures in motor stator current signal, using adaptative demodulation, Fourier transform, and Hilbert spectra. Thanks to the current availability of large amounts of data that can be modeled as signals with complex and irregular structures, graph signal processing has become an emerging field in the few last years. In this field, many engineering and research areas have used wavelet theory for data compression and signal processing. However, some works showed that when the discrete wavelet transform and its inverse were applied, the result was a combination of dilatation and translation of the scaling and wavelet functions due to the elimination of low and high frequencies [34]. Other researchers expanded the wavelet for positive definite distributions over the real line and defined a tractional derivative operator for complex functions [35]. More recently, investigations found that combining the Shannon-entropy and decomposing some low and high frequencies by filters decreased the unbalanced downsampling and achieved a better performance of the framework [36]. In recent years, entropy has been used more frequently to analyze physical and thermodynamics problems. Iterative maps can describe the chaotic motion and attractors as in the fractal geometry method. In combination with entropy, they were used to characterize fractal antennas according to the radiating structure analysis [37,38]. Moreover, recent research has been applying the link between fractal sets, attractors, and entropy to analyze the binary image for the correlation matrix [37].
According to the literature, most methodologies used to estimate displacement from double integration of acceleration are based on one vibration source. Those studies usually condition the signal and filter the noise at high and low frequencies for analysis and fault diagnosis, but this process loses important information and produces errors in the final signal. Several techniques have been implemented to solve the problems from acceleration integration in the time and frequency domain or from signal processing in other fields. In all cases, vibration spectra must be conditioned, and this process produces several phase shifts errors that affect the accuracy of fault diagnosis in rotating machinery.
2. Methods
2.1. Phase Plane
The phase plane gives the position and momentum of a particle in a reference system, and its construction represents the transformation of the particle trajectory into a two-dimensional energy field, or state variables [16]. The phase plane can be defined mechanically using Hamilton’s principle:
where p, q and are the linear momentum, the position and the potential energy of the particle, respectively. The system equilibrium is given when: and . Then, for a function , the evolution of the phase plane as a function of time is:
The dynamic stability of the system according to Liouville’s theorem is obtained when:
Equation (3) means that the volume of the phase plane is preserved in time. Assuming that the linear momentum is only a function of the velocity, the phase plane describes the relation between velocity and position of the particle (Figure 1).
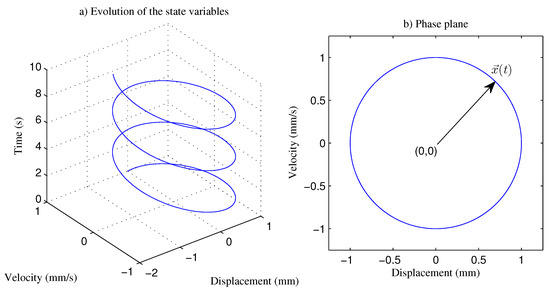
Figure 1.
(a) Evolution of the state variables; (b) phase plane of the linear harmonic for the function: .
2.2. Recurrence Plot
The RP allows the visualization of the dynamics of phase space trajectories owing to the preservation of equilibrium between the velocity and position of a particle according to the Hamilton’s principle. The trajectory along the phase plane can be represented as a discrete vector , as illustrated in Figure 1b, that represents the system state at time t:
Then, the recurrence plot [6] is defined as:
where is a predefined cut-off distance, is the norm and is the Heaviside function.
The cross recurrence plot is similarly defined as:
where and are the first and second trajectory to be analyzed.
RQA is used to quantify the similarity between phase space trajectories by calculating the following parameters [7,39]: recurrence rate , is the ratio of all recurrent states; determinism , is the ratio of recurrence points forming diagonal structures to all recurrence points; Shannon entropy of diagonal length , is a measurement of the disorder in the phase plane; laminarity , is the percentage of recurrence points that create a vertical line; averaged diagonal length , is the average time in which two segments of the trajectory are close to each other; length of the longest diagonal line , is the longest diagonal line found in the RP; trapping time , is the average length of the vertical lines; and length of the longest vertical line .
In mechanical system applications, the phase plane is determined from the differential equations or by the measurement of the dynamic response. The RP for a single time series is calculated using the time delay method by numerical integration of data taken from an accelerometer, which produces significative uncertainties [16]. Noise and vibration signal integration, conditioning, and acquisition methods cause errors [40,41]. Among these errors, there is the phase shift, which is the focus of this paper.
The proposed method to analyze phase shift effects on asynchronous functions and smoothing by phase plane, RP and CRP is presented in Figure 2.
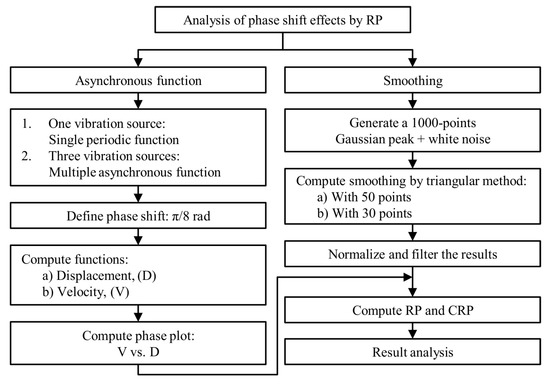
Figure 2.
Proposed flow chart to analyze the phase shift effects on functions and smoothing.
3. Results
3.1. Phase Shift Effects on Multi-Source Functions
When a mechanical object is subjected to vibration or oscillation caused by a force or moment, it tries to return to its equilibrium. Forces and moments are usually functions of displacement. The representation of a dynamic system by a second-order differential equation is expressed as:
where M, C, and K are the structural mass, the stiffness, and the damping matrix, respectively, and represents the external loads.
A simple example of a mechanical system with some vibrations sources is presented in Figure 3. The rotor assembly gives the primary vibration source, while the two bearings and the friction disk represent three more vibration sources. The most common rotating machinery is represented by an arrangement of a motor or turbine, a gear box, and one piece of equipment that transforms the dynamic torque into work.
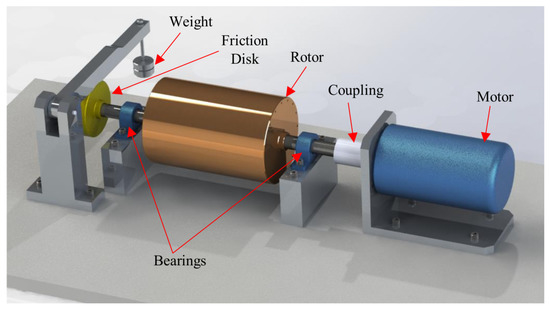
Figure 3.
Photo of one application of the proposed research.
In linear systems, the answer is proportional to the entrance function , which is composed of different periodic, synchronous and asynchronous functions.
The sine and cosine functions often appear as a solution to Equation (7). Both functions are related as . In this case, w is the frequency of oscillation of the function expressed in radians per unit time. The frequency in cycles per unit time is often denoted by f. Both frequencies are related as . In the function , A is the amplitude of oscillation. The period is the time between two adjacent peaks. Period and frequencies are related as .
In trigonometric functions, there are two types of shifts: phase shift and vertical shift. The phase shift is the movement of the function when it is displaced horizontally from the initial position. The vertical shift happens when the function moves vertically from its initial position.
The solution for the simple harmonic motion of one particle with an initial phase angle is expressed by the following sinusoidal form:
Then, velocity and acceleration are obtained by differentiating Equation (8). The displacement, velocity and acceleration are shown in Figure 4, where , , , , and . Note that there is a phase offset of between displacement–velocity and velocity–acceleration. However, can take any value, and its effects are only moving the function backward or forward.
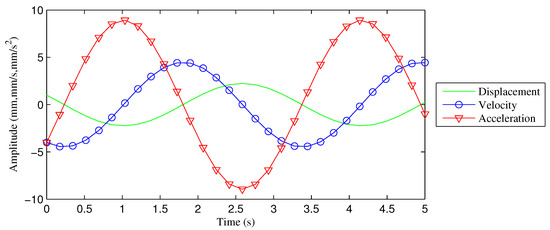
Figure 4.
Displacement, velocity and acceleration for the function: .
As commented before, the phase plane is used to describe multiple states of a system in which a single point describes a state of an arbitrary system. Assuming that a system behavior is characterized by the state , where its rate of change is , then the phase plane is given by plotting [40].
Figure 5 shows the evolution and the phase plot for a single periodic function without and with phase shift. The functions are: (a) , and (b) , , where can have any value. The evolution in Figure 5a reveals a constant displacement at both the beginning and the end of the trajectory. The phase plane in Figure 5b shows the same geometry in both cases.
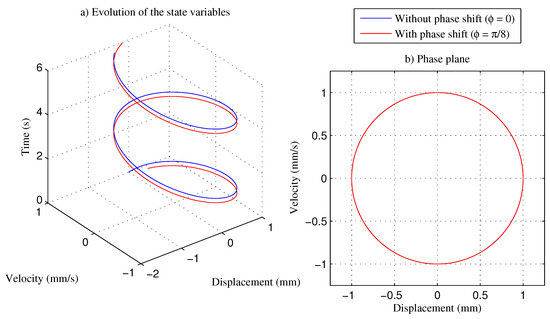
Figure 5.
Evolution of the state variables and phase plane for , and .
The RP with a threshold distance for , and is computed in Figure 6. It is a typical pattern for a simple harmonic function. The perpendicular lines moved along the main diagonal line and there are no variations in shape.
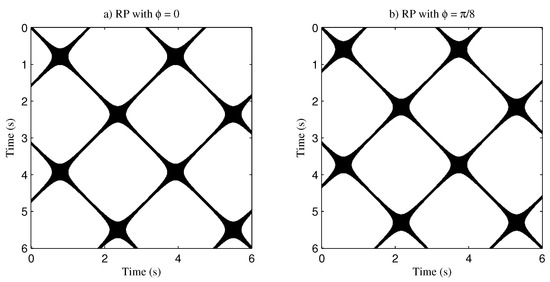
Figure 6.
Recurrence plot for : (a) without phase shift (); (b) with phase shift ().
Quantification analysis [7,39] is presented in Table 1, which reports the RQA quantifications of parameters from CRP for the single function analysis with and without phase shift. The table shows that the entropy of diagonal length and the length of the longest vertical line had a variation of and , respectively. The other parameters remained constant. According to the results, it is clear that the RP patterns were not affected by the considered phase shift.

Table 1.
Recurrence quantification analysis (RQA) quantification of the single function with different phase shifts.
In the case of signals with multiple excitations, the solution is not the same with phase shift and acceleration integration. Considering a function with three different signals sources, then:
where for synchronous functions and for asynchronous functions.
Then, if and is the shift phase error, the shift phases for each function are different:
The behavior of a function with many different vibration sources is not the same when it is affected by a phase shift because . Thus, . This means that a phase shift error changes the original signal because it produces a different displacement for each source of vibration.
The following examples are presented to illustrate this hypothesis. When considering two functions with three different vibrations sources, their displacement and velocity are described by the following equations:
The values of the variables were: amplitude mm, , , , and frequency rad/s. Each function was calculated for and rad and the normalized results were compared graphically.
The evolution of the state variable for both cases is plotted in Figure 7a. The graph shows that the trajectories do not match because of phase shift effects. Those differences can be visualized better in the phase plane in Figure 7b. According to the results, it can be observed clearly that the phase shift affects the original function.
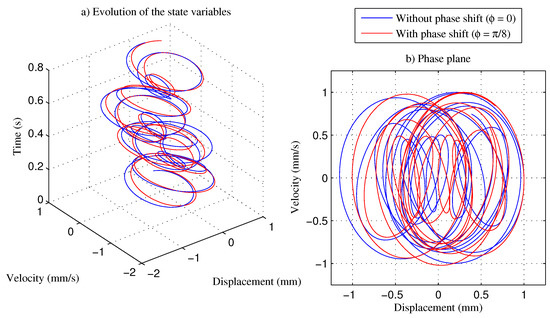
Figure 7.
Evolution of the state variables and phase plane for the multiple asynchronous function of Equation (12): (a) without phase shift (); (b) with phase shift ().
The influence of the phase shift in the RP can be clearly observed in Figure 8. The threshold distance was and there is a significant variation of the pattern due the phase shift, in addition to the displacement along the main diagonal.
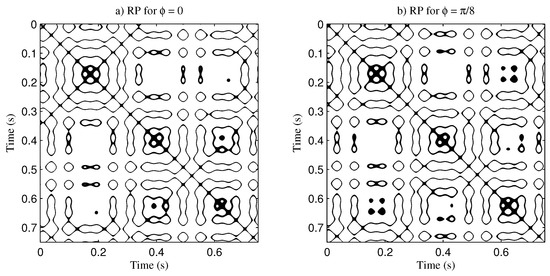
Figure 8.
Recurrence plot for the multiple asynchronous function of Equation (12): (a) without phase shift (); (b) with phase shift ().
The quantification analysis is presented in Table 2, which reports the RQA quantifications of parameters from the analysis of the multiple asynchronous function with and without phase shift. The biggest change was found for the laminarity with 17%. For the length of longest vertical line the change was −4% and for the trapping time it was 3%. The other parameters remained constant. According to the results, the RP patterns were affected by the phase shift, as seen for the laminarity.

Table 2.
RQA quantification of the multiple asynchronous function with different phase shifts.
In conclusion, the velocity with phase shift is different from the velocity without the shift for functions with many vibration sources. The small phase shifts that were considered can represent just one of the errors generated from the integration of the acceleration or from the signal conditioning process. Another conclusion is that the phase plane has a high degree of sensibility to phase shift changes. The main remark is that, when there is more than one vibration source, the double integration of the acceleration can affect the phase plot due to the phase shift errors in trigonometric solutions.
3.2. Smoothing Signal
The smoothing process of vibration spectra is a source of phase shift. Fault diagnosis in rotating machinery transfers the vibration signal from machines to computers through the measuring instruments. Then the signal is processed, analyzed, stored, and transformed. Usually, measurements have two types of errors: systematic errors due to instruments and measurement techniques, and random errors which are commonly known as noise. One common technique to reduce the noise is the smoothing method; in general, it replaces each point of the signal with an average of m adjacent points.
The most common smoothing algorithms are [42]: (a) rectangular or unweighted average smooth, that for an example with three points is for to , where is the point of the smoothed signal, is the point of the original signal, and n is the total number of points in the signal; (b) triangular smooth, which is the rectangular smooth with a weighted smoothing function. Another example of this method for five points is for to . For better results, it is necessary to apply more than one pass of any smoothing method. However, low frequencies remain after the smoothing process and they affect signal precision.
The following simulation analyzes the influence of smoothing on the shift phase of one single signal peak, although a real measurement consists of several peaks. We considered a Gaussian peak function with white noise, which is characterized by having the same power at all frequencies. Figure 9a represents a noisy Gaussian peak of 1000 signal points, with 500 points at the half-width of the peak, a peak width of 150 points and white noise. Figure 9b shows the Gaussian peak without noise.
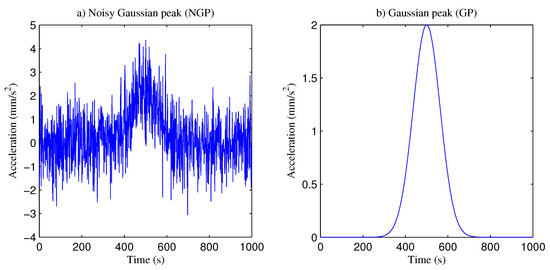
Figure 9.
The Gaussian peak for the analysis: (a) with white noise; (b) without noise.
The noisy Gaussian peak from Figure 9a was smoothed with a triangular smooth of 50-point (W–50) and 30-point (W–30) width with three passes. Results of the smoothing process for both cases are presented in Figure 10a, which shows visible deviations of the base, position, height and width of the peak, and some remaining noise, mostly low-frequency. However, the focus of this work is only the change in the position which is related to the phase shift. Figure 10b illustrates the three normalized peaks to visualize the influence on the position of the top peak. Filtering is applied to eliminate the signal at the base and to visualize more clearly the variation in the position of the peaks after the smoothing with different smooth widths.
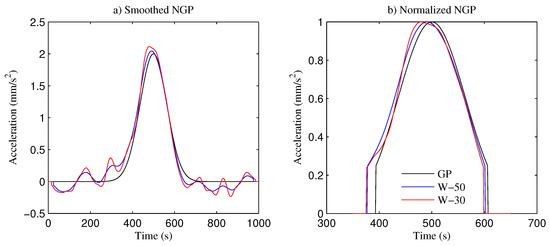
Figure 10.
The phase shifts generated by the smoothing process: (a) signals after smoothing; (b) normalized and filtered peaks.
The RP was computed for the smoothed and normalized signals in Figure 10. The RP for the Gaussian peak without noise is shown in Figure 11a. Deviations after the smoothing process affected RP for W–50 in Figure 11b and W–30 in Figure 11c. The threshold distance considered in the three figures is . According to the results, there are significant differences in the RPs. More significant variations in position were observed for the smoothing with W–30.
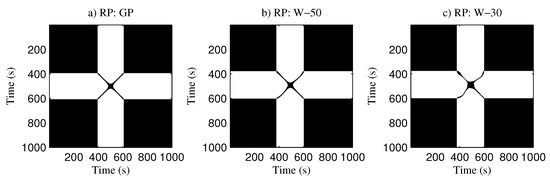
Figure 11.
Recurrence plot for each peak analyzed with a threshold distance of . (a) Gaussian peak; (b) smoothed peak for a width of 50 points; (c) smoothed peak for a width of 30 points.
The CRP quantifications parameters for the W–50 and W–30 smoothing are reported in Table 3. It was found that the displacement of the peak maximum from the initial position was six points for the W–50 smooth and four points for the W–30 smooth. This corresponds to the phase shift as a result of the smoothing. The biggest change was found for the length of the longest diagonal line, with a 10.6% difference between the two smoothing processes. The length of the longest vertical line had a difference of about 3% in the two cases. The other parameters remained practically constant. According to the results, it is evident that slight shift phase variations affect the signal precision.

Table 3.
RQA quantification for the smoothed Gaussian peaks.
Finally, another analysis was performed to evaluate the smoothing effect when the sample point number decreases and the results are reported in Figure 12. For this analysis, a noisy Gaussian peak was generated with the following characteristics: 1000, 750, 500, 250, 100, 50, and 25 signal points; 500, 375, 250, 125, 50, 25, and 13 points at the half-width of the peak; peak width of 150, 100, 63, 31, 13, 6, and 3 points; white noise in all cases. The noisy Gaussian peak showed in Figure 8a was smoothed with a triangular smooth of width 50, 40, 27, 15, 7, 5, and 3, with three passes and finally normalized. The phase shift effects were considered for each case. Changing from 1000 to 100 point samples, most parameters decreased by the following percentage: , , , , and , while and remained constant. For samples with less than 100 points, all parameters were drastically affected, and for samples from 50 to 25 points, all parameters were close or equal to zero. These results indicate that sample resolution is critical for an accurate RP quantification and at least 100 points per peak must be considered in the data analysis.
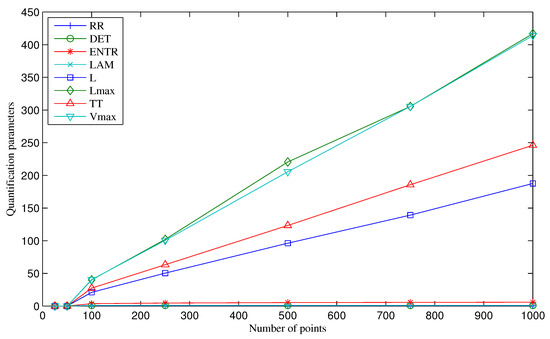
Figure 12.
RQA quantification for the smoothed Gaussian peaks with different sample points.
4. Conclusions
In this paper, the phase plane and RP are proposed to evaluate the phase shift error effect on the solution of complex asynchronous periodic functions and to quantify the smoothing of a Gaussian peak with white noise. The results show that the proposed method is useful for the analysis of the phase shift errors in both cases.
When the spectral analysis derives from the integration of the acceleration of a real-time spectrum, instead of a simulated one, many phase shift errors are due to data acquisition and signal conditioning, and most of them are generated by the integration methods. The results clearly show that the behavior of a simple harmonic function and a complex harmonic function is different due to phase shift errors.
A Gaussian peak with white noise was smoothed and analyzed for several sample points for the same proportional width and three passes each one. The results showed that after the signal smoothing process, the noise is still present and produces phase shift errors, which could be observed and quantified by RP and RQA. Another analysis demonstrated that the data acquisition resolution is a critical factor in order to have a meaningful RP quantification. At least 100 points per peak should be considered in data analysis and smoothing to quantify nonlinearities.
The present work evaluated the adverse effects of phase shifts due to the acceleration integration and the smoothing process errors, which had a clear impact on the phase plane and the recurrence plot. Thus, phase shift can have a significant influence on machinery nonlinear fault diagnosis. The simulations reported here only represent some of the numerous and varied conditions taking place in a real measurement and further work could include other adverse conditions in the calculations in order to build a more complete analysis.
Some future studies are required to quantify the effects on rotating machinery fault diagnosis due to common errors generated during the double integration process with real-time measurements, including signals with various vibration sources. Results showed that RP is affected by small changes in vibrations. Therefore, RP has a high sensitivity that could be applied to identify nonlinear mechanical systems such as friction problems in machinery applications.
Author Contributions
Conceptualization, validation, investigation, and writing original draft preparation I.T.-C.; methodology and supervision J.C.J.-C.; technical and writing editing reviewers C.S.L.-C. and S.E.-V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bokde, N.; Feijóo, A.; Villanueva, D.; Kulat, K. A Review on Hybrid Empirical Mode Decomposition Models for Wind Speed and Wind Power Prediction. Energies 2019, 12, 254. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L. A novel noise reduction technique for underwater acoustic signals based on complete ensemble empirical mode decomposition with adaptive noise, minimum mean square variance criterion and least mean square adaptive filter. Def. Technol. 2020, 16, 543–554. [Google Scholar] [CrossRef]
- Poincaré, H. On the problem of the three bodies and the equations of dynamics. Acta Math. 1890, 13, 1–270. [Google Scholar]
- Eckmann, J.; Oliffson, S.; Ruelle, D. Recurrence Plots of Dynamical Systems. World Sci. Ser. Nonlinear Sci. Ser. A 1995, 16, 441–446. [Google Scholar]
- Pham, T. Fuzzy recurrence plots. In EPL Europhysics Letters; IOP Publishing: Bristol, UK, 2016; Volume 116. [Google Scholar]
- Marwan, N.; Romano, M.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Marwan, N.; Schinke, S.; Kurths, J. Recurrence plots 25 years later—Gaining confidence in dynamical transitions. EPL (Europhys. Lett.) 2013, 101, 20007. [Google Scholar] [CrossRef]
- Zhang, E.; Shan, D.; Li, Q. Nonlinear and Non-Stationary Detection for Measured Dynamic Signal from Bridge Structure Based on Adaptive Decomposition and Multiscale Recurrence Analysis. Appl. Sci. 2019, 9, 1302. [Google Scholar] [CrossRef]
- Acharya, U.; Faust, O.; Ciaccio, E.; Wei, K.; Lih, O.; Tan, R.; Garan, H. Application of nonlinear methods to discriminate fractionated electrograms in paroxysmal versus persistent atrial fibrillation. Comput. Methods Programs Biomed. 2019, 175, 163–178. [Google Scholar] [CrossRef]
- Yan, R.; Qian, Y.; Huang, Z.; Gao, R. Recurrence plot entropy for machine defect severity assessment. Smart Struct. Syst. 2013, 11, 299–314. [Google Scholar] [CrossRef]
- Qian, Y.; Yan, R.; Hu, S. Bearing Degradation Evaluation Using Recurrence Quantification Analysis and Kalman Filter. IEEE Trans. Instrum. Meas. 2014, 6, 2599–2610. [Google Scholar] [CrossRef]
- Chegini, S.; Manjili, M.; Bagheri, A. New fault diagnosis approaches for detecting the bearing slight degradation. Meccanica 2020, 55, 261–286. [Google Scholar] [CrossRef]
- Syta, A.; Litak, G. Vibration Analysis in Cutting Materials. In Recurrence Quantification Analysis, Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 279–290. [Google Scholar]
- Lajmert, P.; Rusinek, R.; Kruszyński, B. Chatter identification in milling of Inconel 625 based on recurrence plot technique and Hilbert vibration decomposition. In Proceedings of the International Conference on Engineering Vibration (ICoEV 2017), Sofia, Bulgaria, 4–7 September 2017; EDP Sciences: Les Ulis, France, 2018. [Google Scholar]
- Jauregui-Correa, J.; Camacho, S.; Basaldua-Sanchez, J. Bearing Analysis of the effect of different friction models on the dynamic response of a rotor rubbing the housing. Adv. Mech. Mach. Sci. Mech. Mach. Sci. 2019, 73, 4227–4236. [Google Scholar]
- Jauregui-Correa, J. Identification of Nonlinearities in Mechanical Systems Using Recurrence Plots. In Nonlinear Structural Dynamics and Damping, Mechanisms and Machine Science; Springer: Cham, Switzerland, 2019; Volume 69. [Google Scholar]
- Ferrero, R.; Galindo, F.; Montrucchio, B.; Rebaudengo, M. Exploiting accelerometers to estimate displacement. In Proceedings of the 5th Mediterranean Conference on Embedded Computing (MECO), Bar, Montenegro, 12–16 June 2016; pp. 206–210. [Google Scholar]
- Han, S. Measuring displacement signal with an accelerometer. J. Mech. Sci. Technol. 2010, 24, 1329–1335. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, Y.; Kang, D. Integration on acceleration signals by adjusting with envelopes. J. Meas. Eng. 2016, 4, 117–121. [Google Scholar]
- Liu, J.; Wang, P.; Tian, X. Vibration displacement measurement based on three axes accelerometer. In Proceedings of the Chinese Automation Congress, Jinan, China, 20–22 October 2017; pp. 2374–2378. [Google Scholar]
- Tezcan, J.; Marin-Artieda, C. Least-Square-Support-Vector-Machine-based approach to obtain displacement from measured acceleration. Adv. Eng. Softw. 2017, 115, 357–362. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, R.; Luo, H.; Shen, H. Baseline correction of vibration acceleration signals with inconsistent initial velocity and displacement. Adv. Mech. Eng. 2018, 8, 1687814016675534. [Google Scholar] [CrossRef]
- Zhang, J.; He, Y. Removing baseline drift in vibration signal of autopilot based on morphology. Aeronaut. Astronaut. 2018, 44, 907–913. [Google Scholar]
- Kim, W.; Lee, H. An improved explicit time integration method for linear and nonlinear structural dynamics. Comput. Struct. 2018, 206, 42–53. [Google Scholar] [CrossRef]
- Wan, S.; Zhang, X.; Dou, L. Compound fault diagnosis of bearings using improved fast spectral kurtosis with VMD. J. Mech. Sci. Technol. 2018, 32, 5189–5199. [Google Scholar] [CrossRef]
- Zheng, W.; Dan, D.; Cheng, W.; Xia, Y. Real-time dynamic displacement monitoring with double integration of acceleration based on recursive least squares method. Measurement 2019, 141, 460–471. [Google Scholar] [CrossRef]
- Xu, J.; Xu, X.; Cui, X. A new recursive Simpson integral algorithm in vibration testings. Aust. J. Mech. Eng. 2019, 1–7. [Google Scholar] [CrossRef]
- Dela Cruz, A.; Cajayon, C.; Luna, J.; Tomboc, C. Recursive least square and least means square equalizers optimization algorithms in Rayleigh fading. Int. J. Adv. Trends Comput. Sci. Eng. 2019, 8, 689–695. [Google Scholar] [CrossRef]
- Ni, C.; Lin, T.; Xing, J.; Xue, J. A time-frequency analysis of non-stationary signals using variation mode decomposition and synchrosqueezing techniques. In Proceedings of the Prognostics and System Health Management Conference (PHM-Qingdao), Qingdao, China, 25–27 October 2019; pp. 1–6. [Google Scholar]
- Arrieta, M.; Kuar, R.; Zamora-Mendez, D. Identification of electromechanical oscillatory modes based on variational mode decomposition. Electr. Power Syst. Res. 2019, 167, 71–85. [Google Scholar] [CrossRef]
- Ribeiro, J.; de Castro, J.; Meggiolaro, M. Parameter adjustments for optimizing signal integration using the FFT-DDI method. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 104. [Google Scholar] [CrossRef]
- ZZhu, H.; Zhou, Y.; Hu, Y. Displacement reconstruction from measured accelerations and accuracy control of integration based on a low-frequency attenuation algorithm. Soil Dyn. Earthq. Eng. 2020, 133, 106122. [Google Scholar] [CrossRef]
- Chen, X.; Feng, Z. Induction motor stator current analysis for planetary gearbox fault diagnosis under time-varying speed conditions. Mech. Syst. Signal Process. 2020, 140, 106691. [Google Scholar] [CrossRef]
- Capobianco, R. A note on a practical relationship between filter coefficients and scaling and wavelet functions of Discrete Wavelet Transforms. Appl. Math. Lett. 2011, 24, 1257–1259. [Google Scholar]
- Guariglia, E.; Silvestrov, S. Fractional-Wavelet Analysis of Positive definite Distributions and Wavelets on D’(C). In Engineering Mathematics II; Silvestrov, S., Rančić, M., Eds.; Springer: Cham, Switzerland, 2016; Volume 179, pp. 337–353. [Google Scholar]
- Zheng, X.; Tang, Y.; Zhou, J. Framework of Adaptive Multiscale Wavelet Decomposition for Signals on Undirected Graphs. Graphs IEEE Trans. Signal Process. 2019, 7, 1696–1711. [Google Scholar] [CrossRef]
- Guariglia, E. Entropy and Fractal Antennas. Entropy 2016, 18, 84. [Google Scholar] [CrossRef]
- Guariglia, E. Primality, Fractality, and Image Analysis. Entropy 2019, 21, 304. [Google Scholar] [CrossRef]
- Marwan, N. CRP Toolbox. Potsdam Institute for Climate Reports. 2020. Available online: www.recurrence-plot.tk (accessed on 14 January 2021).
- Polyak, M. Phase-plane method: A practical approach. In Proceedings of the XII International forum Modern Information Society Formation—Problems, Perspectives, Innovation Approaches, Saint Petersburg, Russia, 6–11 June 2011; pp. 55–59. [Google Scholar]
- Polyak, M. Phase-plane method: A practical approach. J. Biomech. 2018, 73, 243–248. [Google Scholar]
- O’Haver, T. Pragmatic Introduction to Signal Processing 2019: Applications in Scientific Measurement; Independently Published, 2018; 459p, ISBN 10: 1792867123. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).