Multi-Model Identification of HVAC System
Abstract
:1. Introduction
2. The Proposed Simultaneous Clustering and Regression Method
| Algorithm 1 |
| Step 1—Select proper values for m, h and construct regressor and observation vector . Step 2—Initialize the probability vector for each cluster i by a random number generator. Step 3—Iterate the algorithm until converges or termination criterion is satisfied. Step 4—Update residual values for each cluster i. Step 5—Update parameters , and . Step 6—Update as Step 7—Go to step 3, and repeat until convergence. |
3. Gap Metric
- (1)
- .
- (2)
- The gap metric is an extension of common distance measures between two linear systems such as the infinity norm. For instance, the distances between two systems and in the sense of infinity norm and gap metric are infinity and 0.1, respectively.
- (3)
- One pro of the gap metric is that it measures the ‘distance’ in the closed-loop sense instead of the open-loop sense. In other words, a small distance between two systems in the gap metric sense means that there exists at least one feedback controller that stabilizes both systems and the distance between the closed loops is small in the infinity norm sense. For instance, for the distance between two systems and the gap metric is about 0.2 [13].
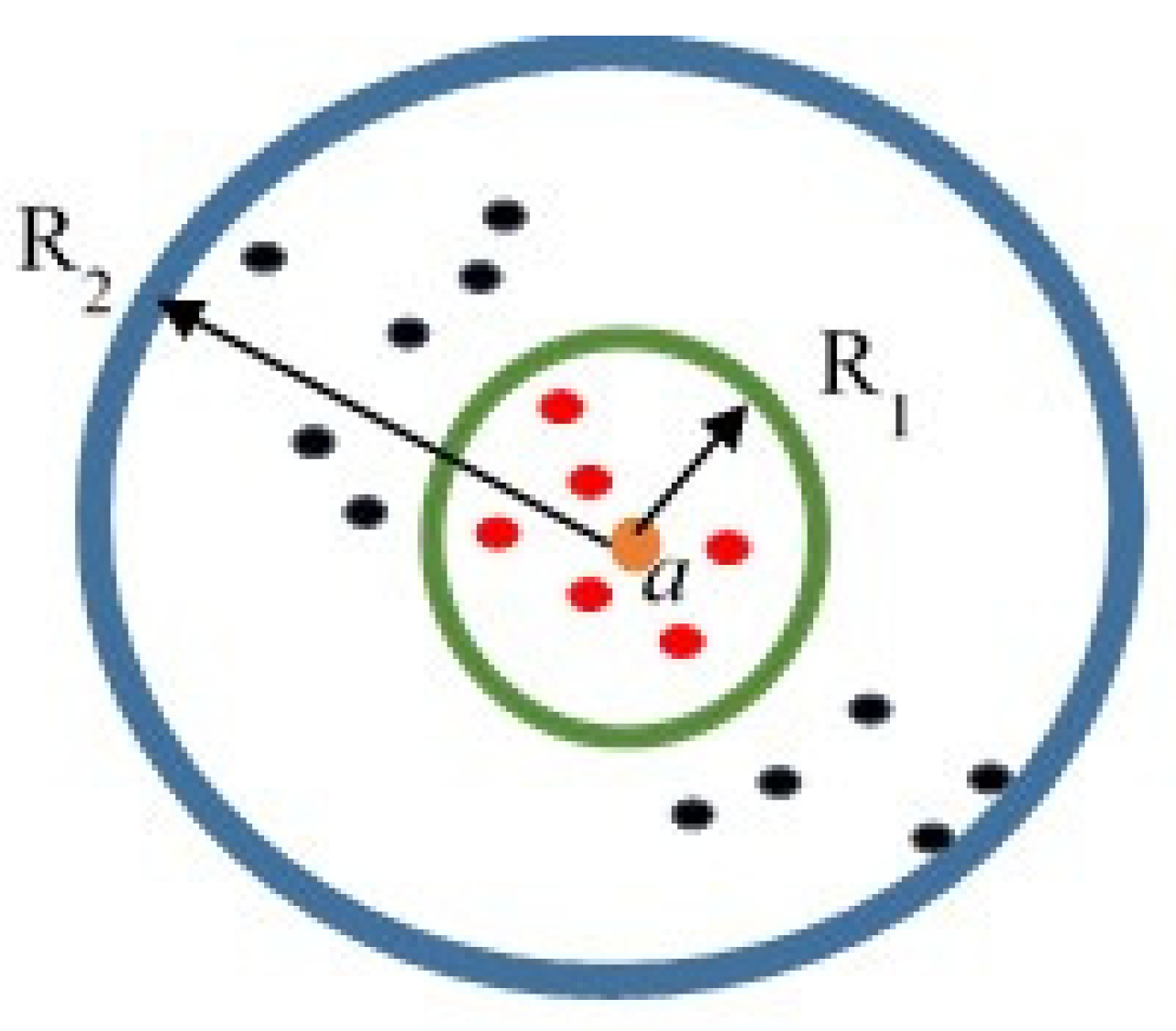
3.1. Proper Number of Mode Selection
- (1)
- Initialize the operation regions and calculate the nonlinear measure index for each operating region. Select enough operation points in each operating region.
- (2)
- Collect enough data from the system around the operating point OPi, use the proposed Algorithm 1 and get the linear models Pi.
- (3)
- Compute the gap metric between all pairs of linear models Pi and Pj (i.e., ).
- (4)
- Prescribe a threshold level τ. Cluster the local models that satisfy δj ≤ τ.
3.2. Local Model Weights
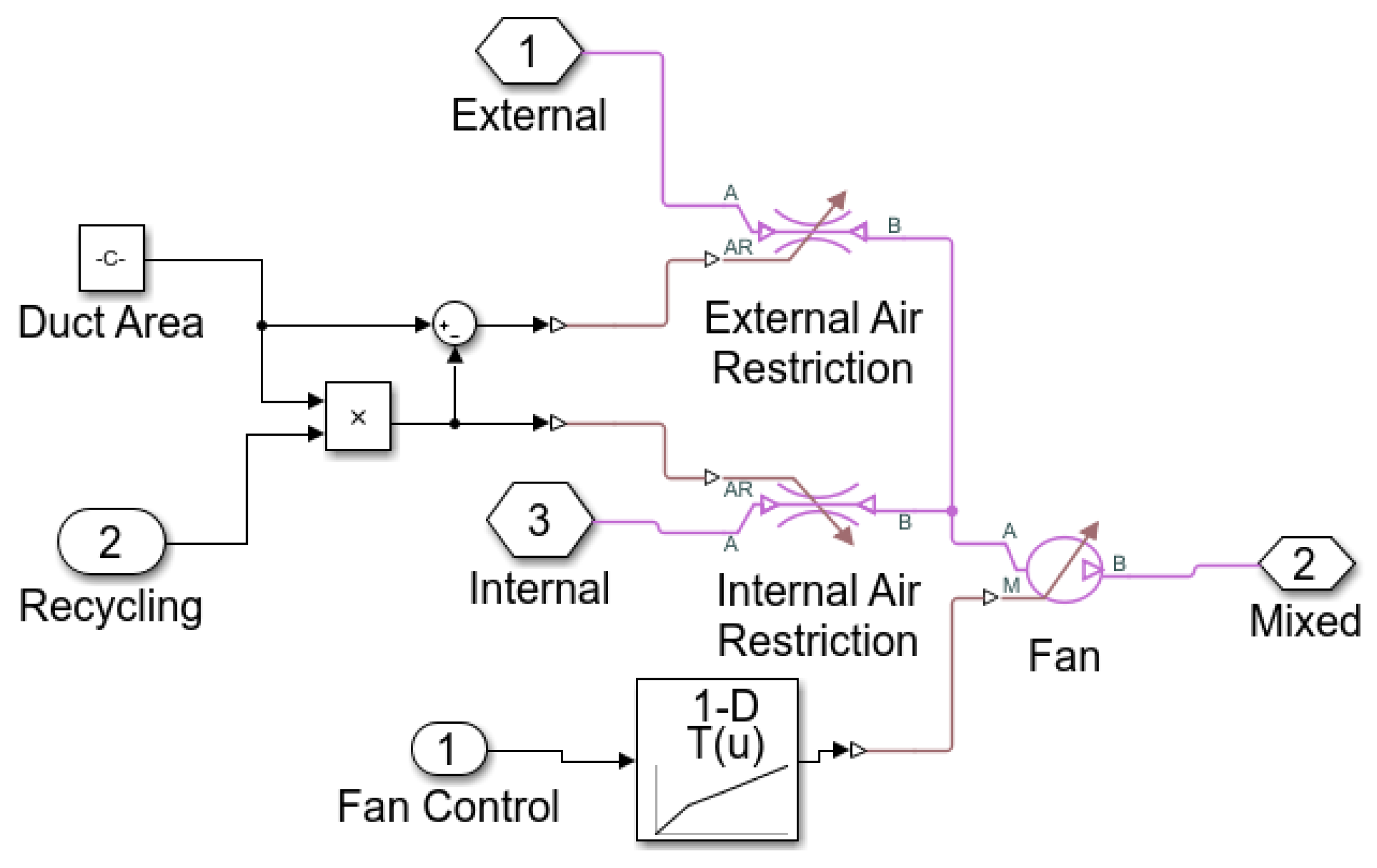
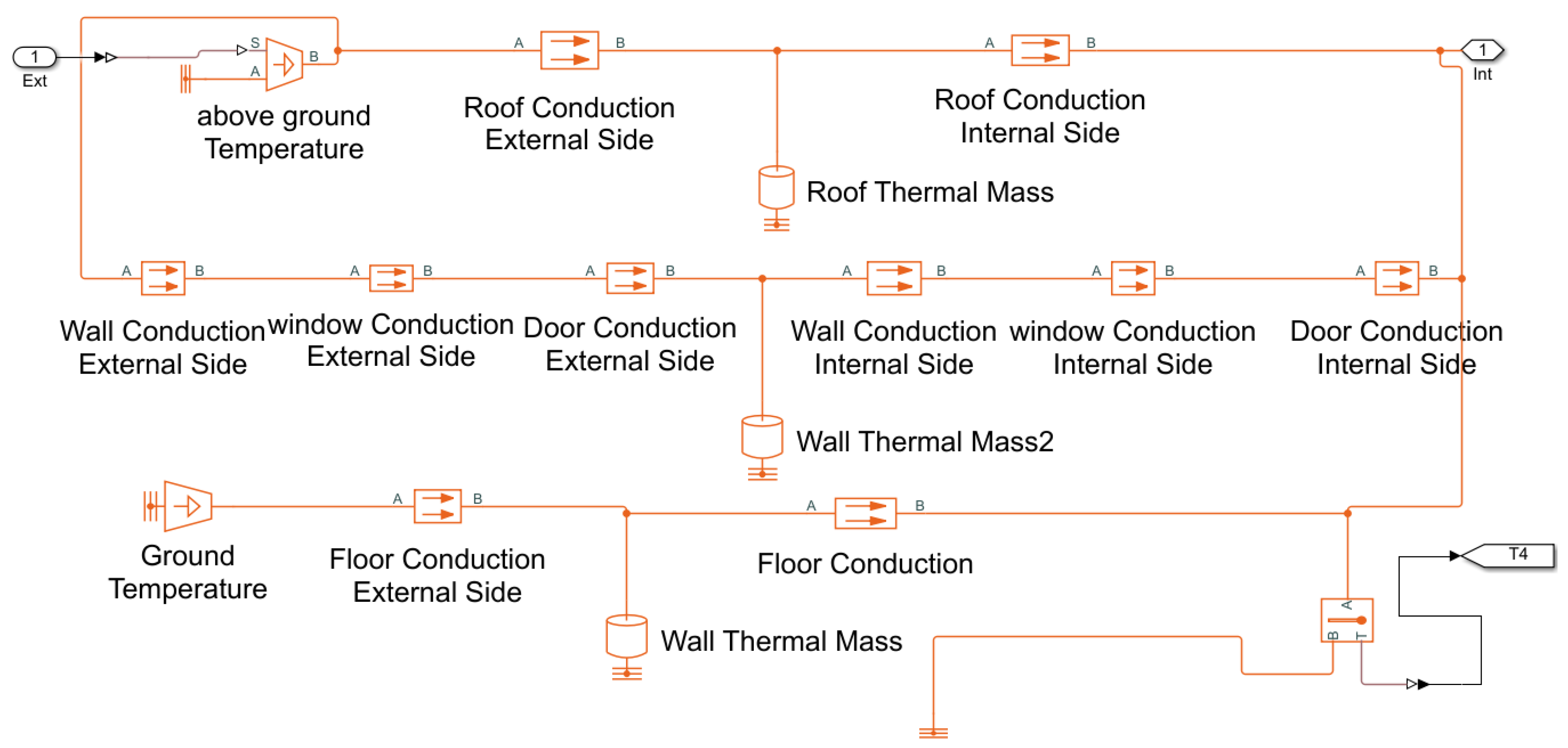
4. Simulation and Validation
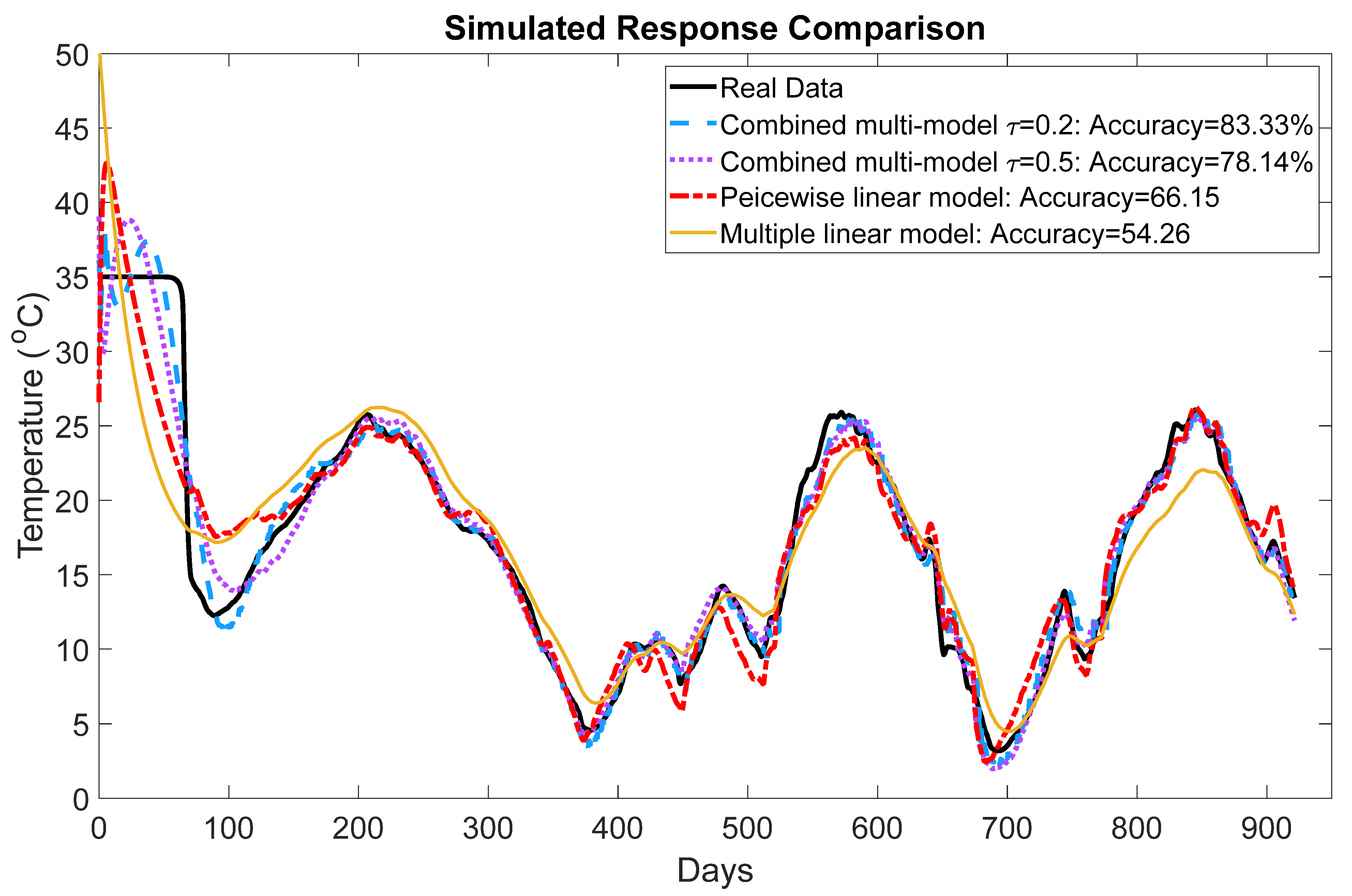
4.1. Simulation Results
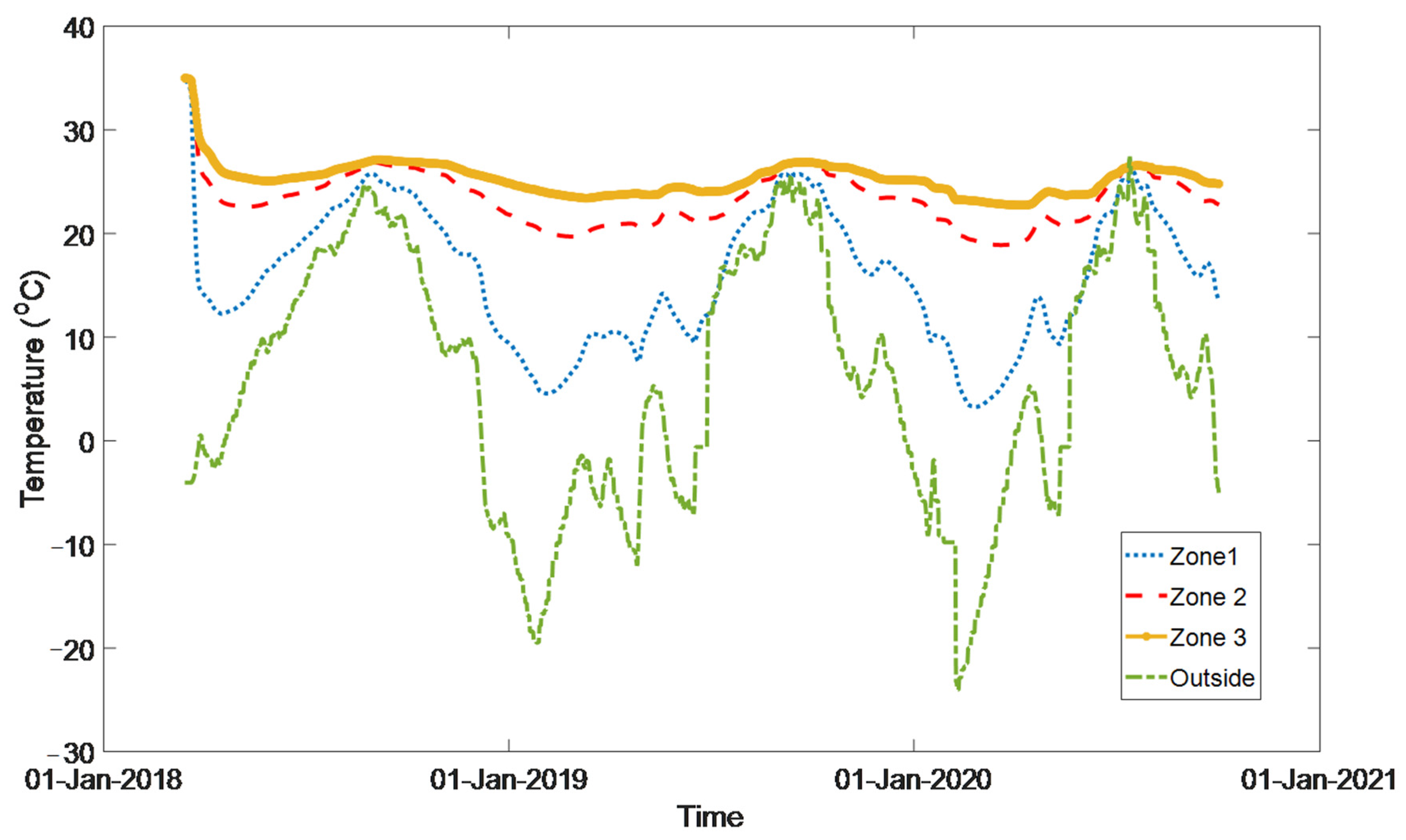
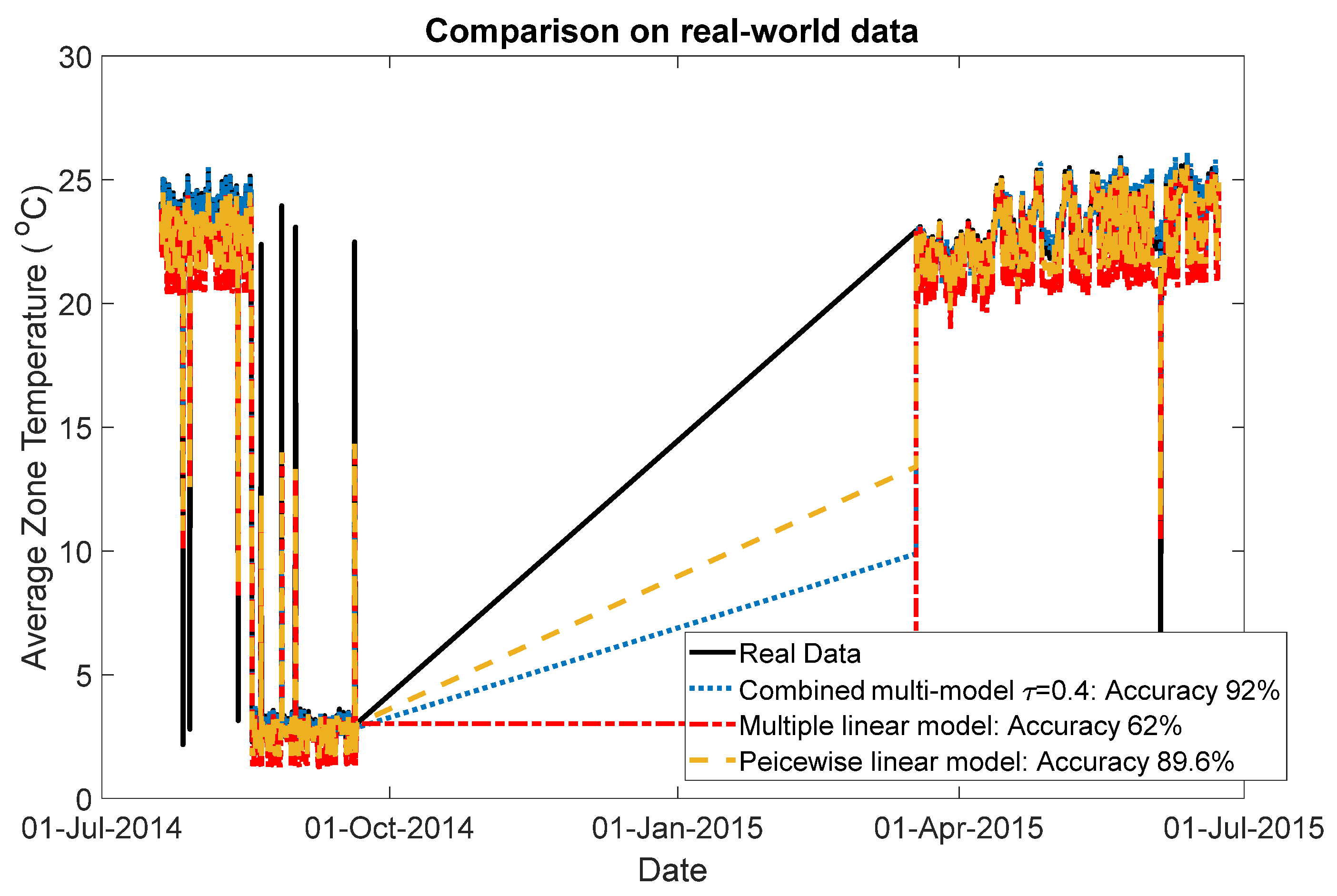
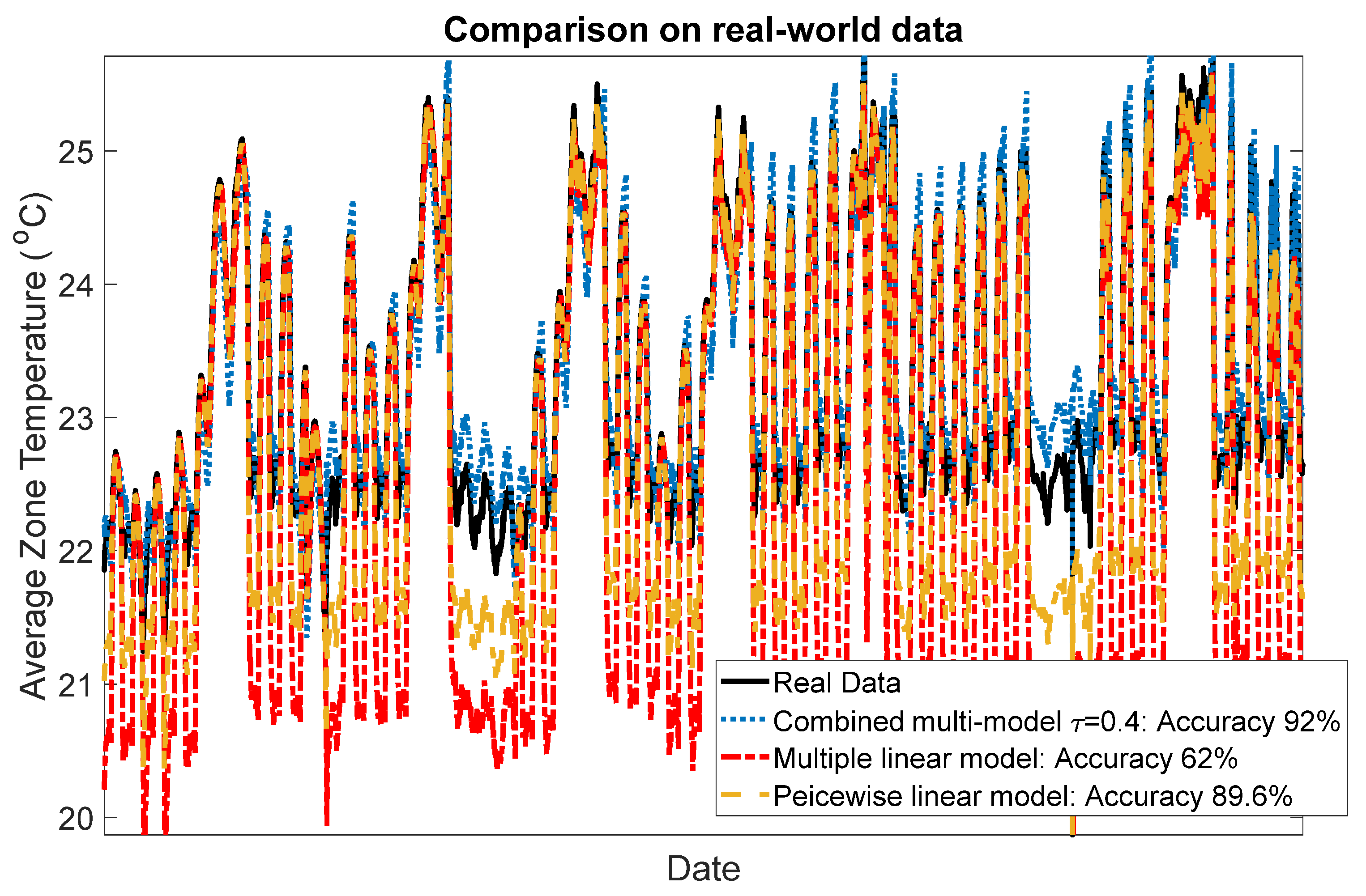
4.2. Test on Real-World Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbas, A.; Chowdhury, B. A Data-Driven Approach for Providing Frequency Regulation with Aggregated Residential HVAC Units. In Proceedings of the 2019 IEEE Conference on North American Power Symposium (NAPS), Wichita, KS, USA, 13–15 October 2019. [Google Scholar]
- Khalilnejad, A. Data-Driven Evaluation of HVAC Systems in Commercial Buildings and Identification of Savings Opportunities. Ph.D. Thesis, Case Western Reserve University, Cleveland, OH, USA, 2020. [Google Scholar]
- Yu, X.; Ergan, S.; Dedemen, G. A data-driven approach to extract operational signatures of HVAC systems and analyze impact on electricity consumption. Appl. Energy 2019, 253, 113497. [Google Scholar] [CrossRef]
- Faddel, S.; Tian, G.; Zhou, Q.; Aburub, H. Data Driven Q-Learning for Commercial HVAC Control. In Proceedings of the 2020 SoutheastCon, Raleigh, NC, USA, 28–29 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Galan, O.; Romagnoli, J.A.; Palazoglu, A.; Arkun, Y. Gap metric concept and implications for multilinear model-based controller design. Ind. Eng. Chem. Res. 2003, 42, 2189–2197. [Google Scholar] [CrossRef]
- Guay, M. Measurement of Nonlinearity in Chemical Process Control. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 1996. [Google Scholar]
- Helbig, A.; Marquardt, W.; Allgower, F. Nonlinearity measures: Definition, computation and applications. J. Process Control 2000, 10, 113–123. [Google Scholar] [CrossRef]
- Nandola, N.N.; Bhartiya, S. A multiple model approach for predictive control of nonlinear hybrid systems. J. Process Control 2008, 18, 131–148. [Google Scholar] [CrossRef]
- Hariprasad, K.; Sharad, B.; Gudi, R.D. A gap metric based multiple model approach for nonlinear switched systems. J. Process Control 2012, 22, 1743–1754. [Google Scholar] [CrossRef]
- Arslan, E.; Çamurdan, M.; Palazoglu, A.; Arkun, Y. Multimodel scheduling control of nonlinear systems using gap metric. Ind. Eng. Chem. Res. 2004, 43, 8275–8283. [Google Scholar] [CrossRef]
- Tan, W.; Marquez, H.J.; Chen, T.; Liu, J. Multimodel analysis and controller design for nonlinear processes. Comput. Chem. Eng. 2004, 28, 2667–2675. [Google Scholar] [CrossRef]
- Du, J.; Song, C.; Li, P. Application of gap metric to model bank determination in multilinear model approach. J. Process Control 2009, 19, 231–240. [Google Scholar] [CrossRef]
- Du, J.; Johansen, T.A. Integrated multimodel control of nonlinear systems based on gap metric and stability margin. Ind. Eng. Chem. Res. 2014, 53, 10206–10215. [Google Scholar] [CrossRef]
- Ben-Hur, A.; Horn, D.; Siegelmann, H.T.; Vapnik, V. Support vector clustering. J. Mach. Learn. Res. 2001, 2, 125–137. [Google Scholar] [CrossRef]
- Available online: https://www.mathworks.com/help/physmod/simscape/ug/building-ventilation.html (accessed on 7 January 2021).
- Available online: https://edmonton.weatherstats.ca/download.html (accessed on 7 January 2021).
- Chi-Man, Y.J.; Wang, S. Multiple ARMAX modeling scheme for forecasting air conditioning system performance. Energy Convers. Manag. 2007, 48, 2276–2285. [Google Scholar]
- Mustafaraj, G.; Chen, J.; Lowry, G. Development of room temperature and relative humidity linear parametric models for an open office using BMS data. Energy Build. 2010, 42, 348–356. [Google Scholar] [CrossRef]
- Benzaama, M.H.; Rajaoarisoa, L.H.; Ajib, B.; Lecoeuche, S. A data-driven methodology to predict thermal behavior of residential buildings using piecewise linear models. J. Build. Eng. 2020, 32, 101523. [Google Scholar] [CrossRef]
- Hure, N.; Vašak, M. Clustering-based identification of mimo piecewise affine systems. In Proceedings of the 2017 21st International Conference on Process Control (PC), Strbske Pleso, Slovakia, 6–9 June 2017. [Google Scholar]
- Available online: https://openei.org/datasets/dataset/long-term-data-on-3-office-air-handling-units (accessed on 7 January 2021).



| Model Parameters | ||||||
|---|---|---|---|---|---|---|
| Cluster | ||||||
| i = 1 | 2.967 | −2.935 | 0.9676 | 0.0274 | −0.05466 | 0.02726 |
| i = 2 | 1.744 | −0.7323 | −0.0119 | −0.08569 | 0.2612 | −0.1751 |
| i = 3 | 2.304 | −1.624 | 0.3201 | 0.07934 | −0.147 | 0.06769 |
| i = 4 | 1.077 | 0.8135 | 0.89 | −0.0528 | 0.126 | −0.073 |
| i = 5 | 2.927 | −2.855 | 0.9282 | 0.0168 | −0.0325 | 0.0157 |
| Model Parameters | ||||||
|---|---|---|---|---|---|---|
| Cluster | ||||||
| i = 1 | 2.967 | −2.935 | 0.9676 | 0.0274 | −0.05466 | 0.02726 |
| i = 2 | 1.744 | −0.7323 | −0.0119 | −0.08569 | 0.2612 | −0.1751 |
| i = 3 | 2.304 | −1.624 | 0.3201 | 0.07934 | −0.147 | 0.06769 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alipouri, Y.; Zhong, L. Multi-Model Identification of HVAC System. Appl. Sci. 2021, 11, 668. https://doi.org/10.3390/app11020668
Alipouri Y, Zhong L. Multi-Model Identification of HVAC System. Applied Sciences. 2021; 11(2):668. https://doi.org/10.3390/app11020668
Chicago/Turabian StyleAlipouri, Yousef, and Lexuan Zhong. 2021. "Multi-Model Identification of HVAC System" Applied Sciences 11, no. 2: 668. https://doi.org/10.3390/app11020668
APA StyleAlipouri, Y., & Zhong, L. (2021). Multi-Model Identification of HVAC System. Applied Sciences, 11(2), 668. https://doi.org/10.3390/app11020668






