Finite Elements for Higher Order Steel–Concrete Composite Beams
Abstract
Featured Application
Abstract
1. Introduction
2. Recall of the Analytical Model
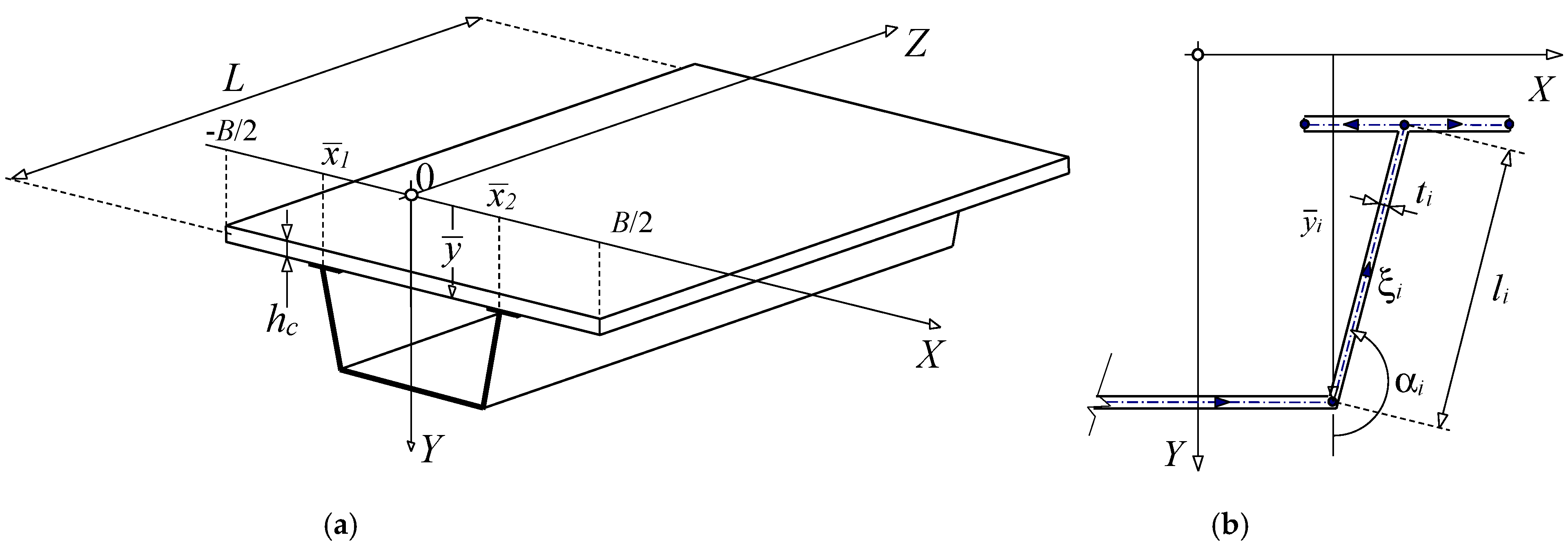
2.1. Kinematics
2.2. Active Stress Field
2.3. Balance Conditions
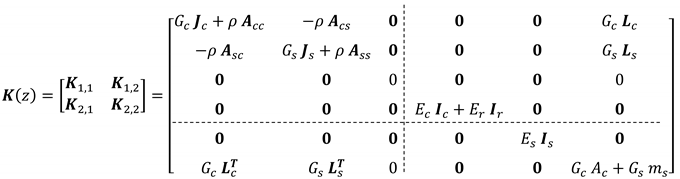
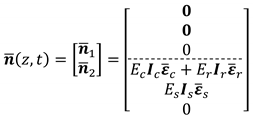
2.4. Analytical Solution
2.4.1. Beam with Imposed End Displacements
2.4.2. Beam with Distributed Loads
3. Proposed Higher Order Finite Elements
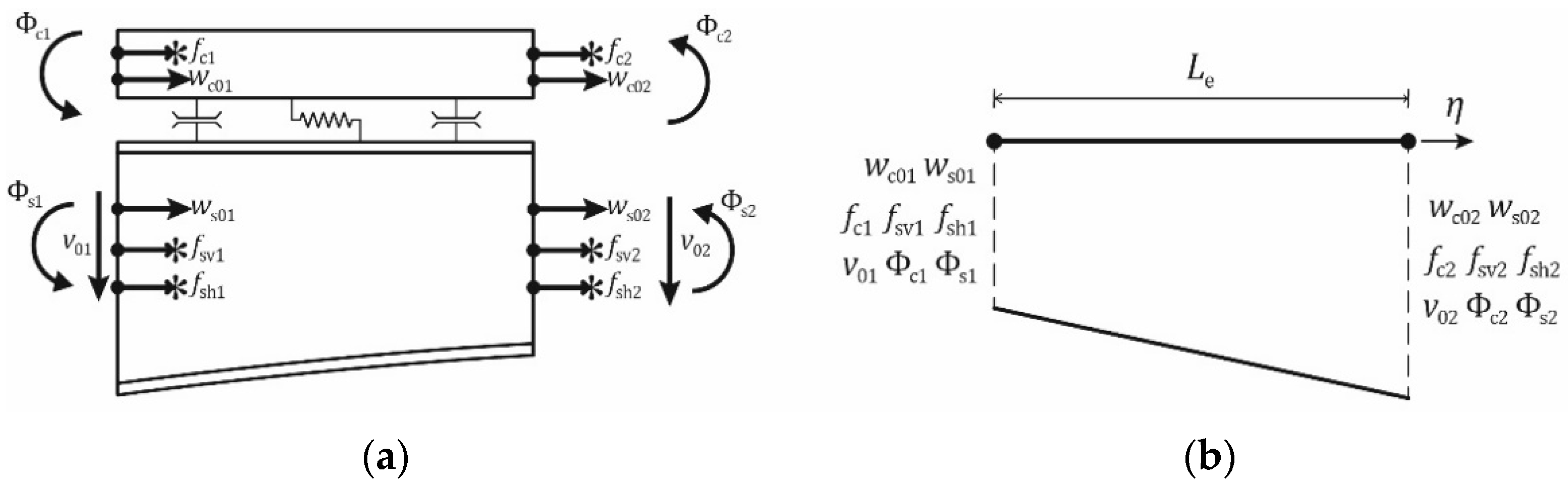
3.1. Definition of the Beam Finite Elements
3.1.1. Linear Interpolating Functions
3.1.2. Polynomial Interpolating Functions
3.1.3. Interdependent Interpolating Functions
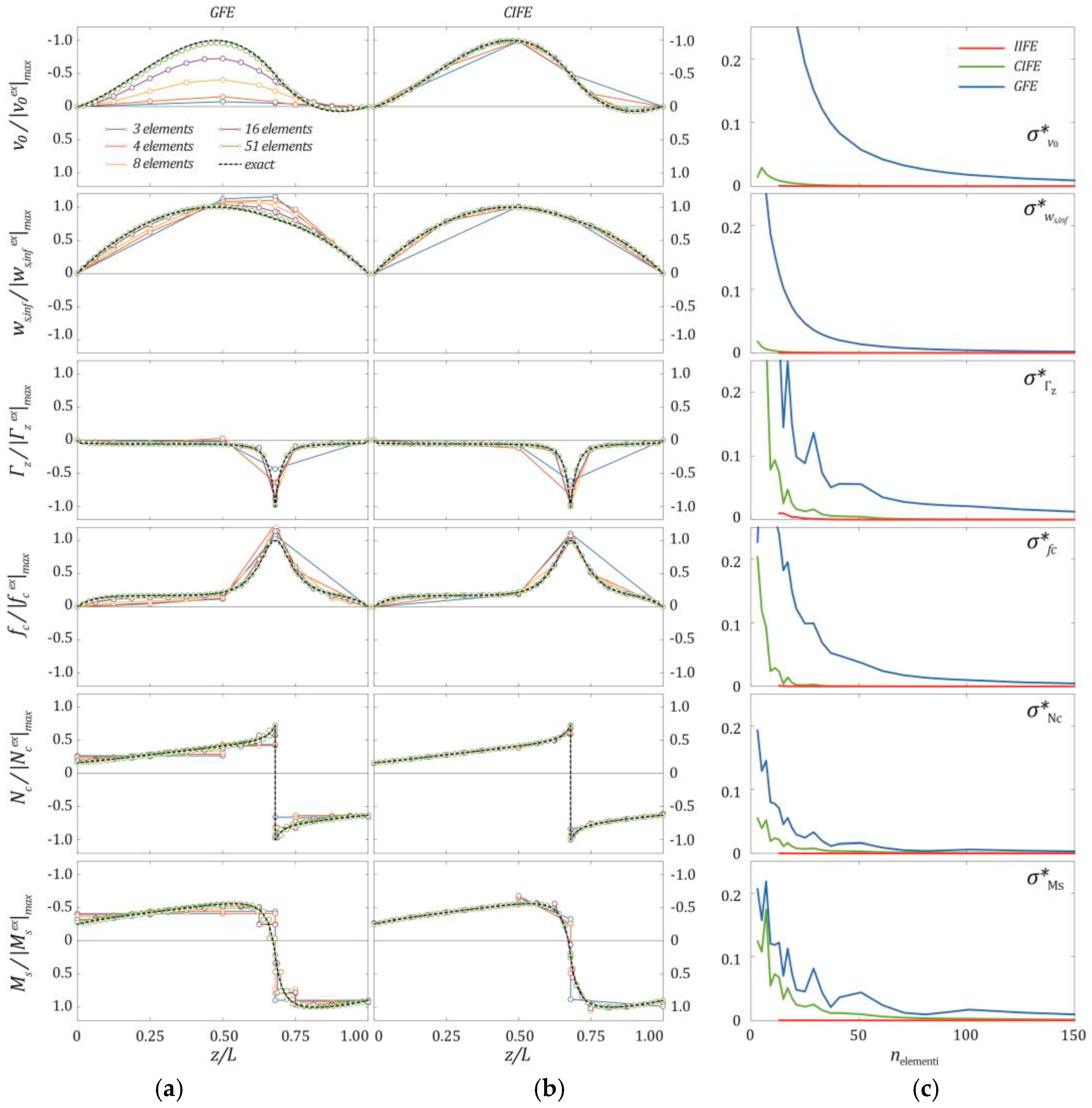
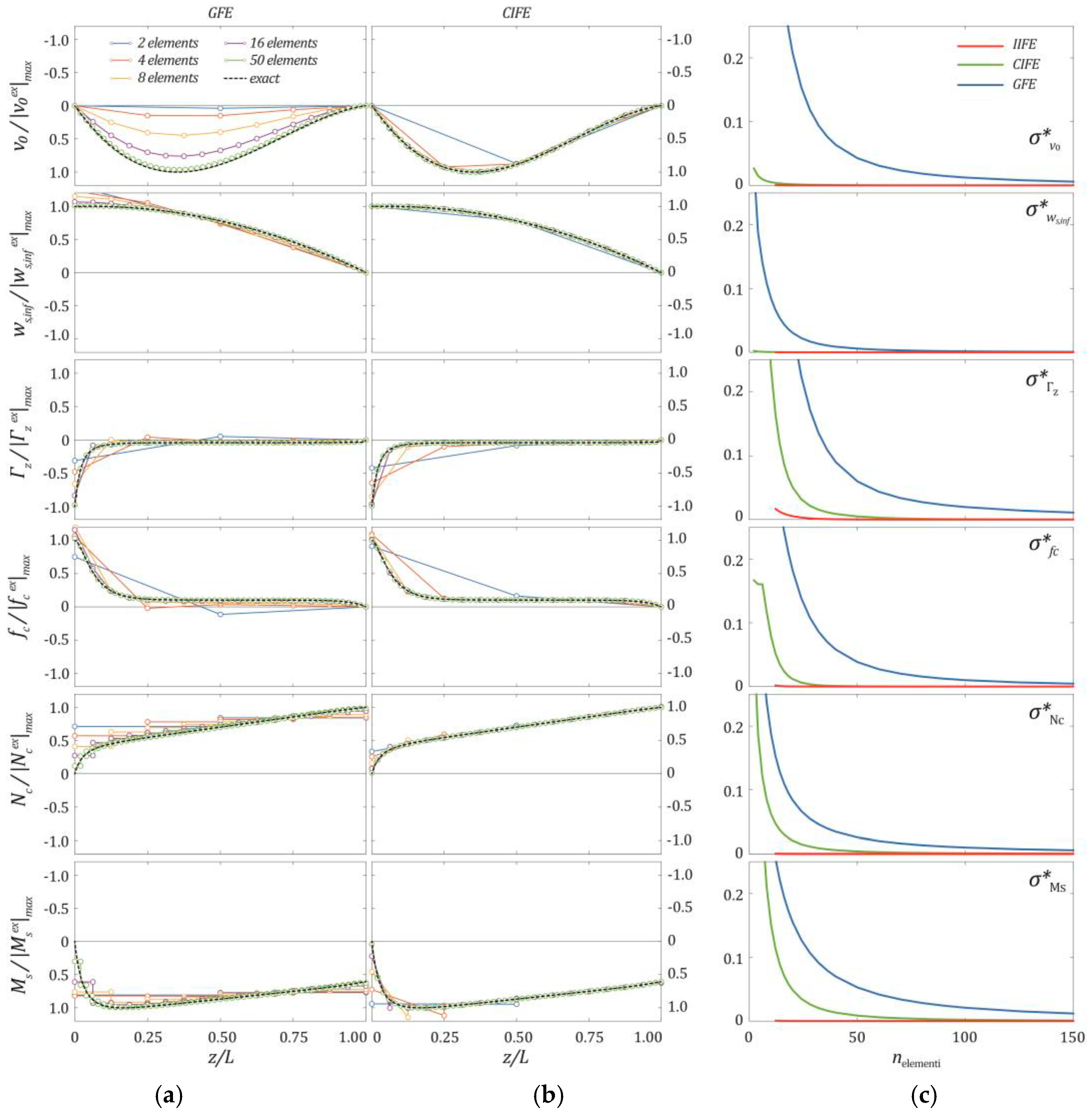
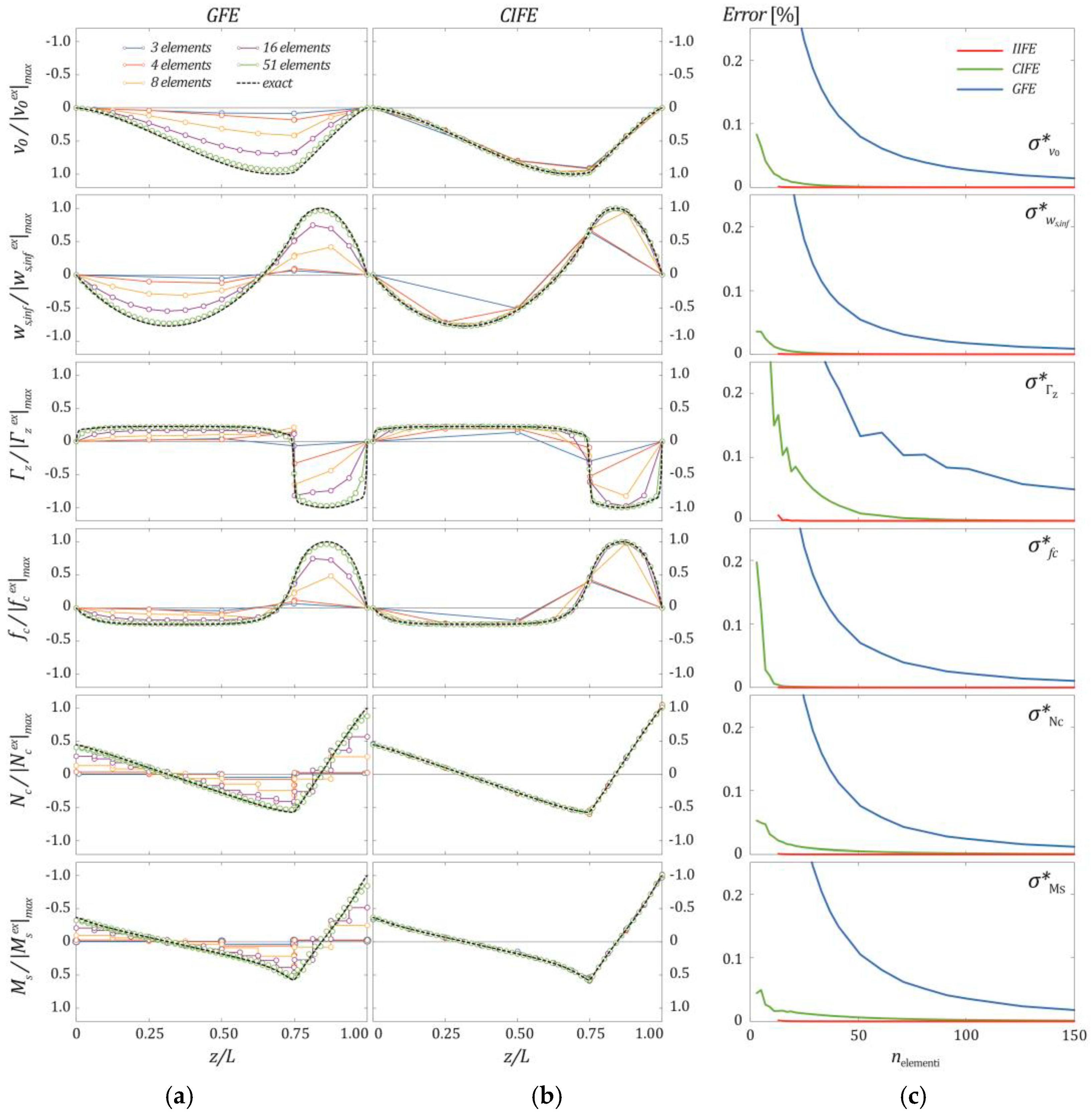
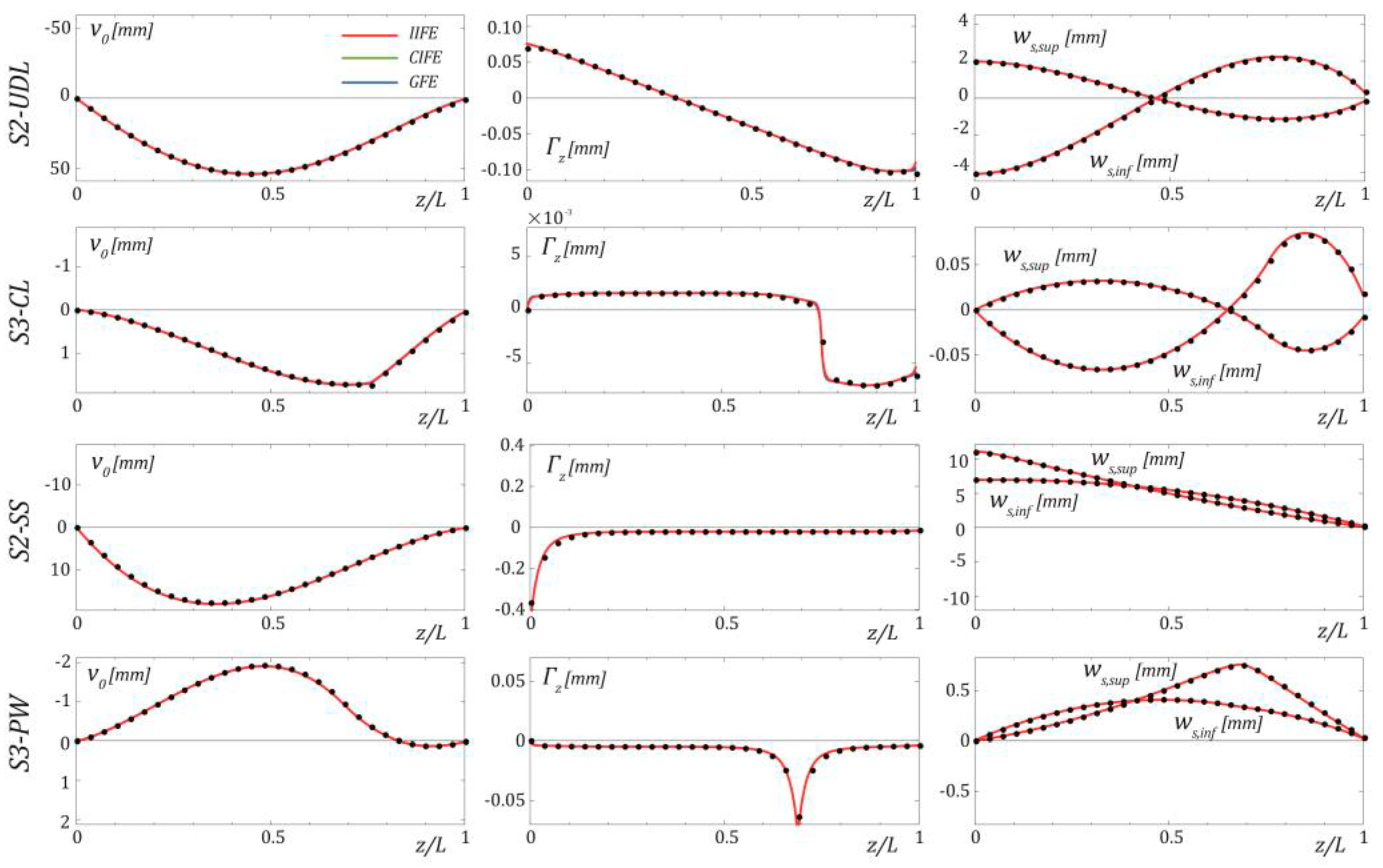
3.2. Convergence Analysis of the Proposed Finite Elements
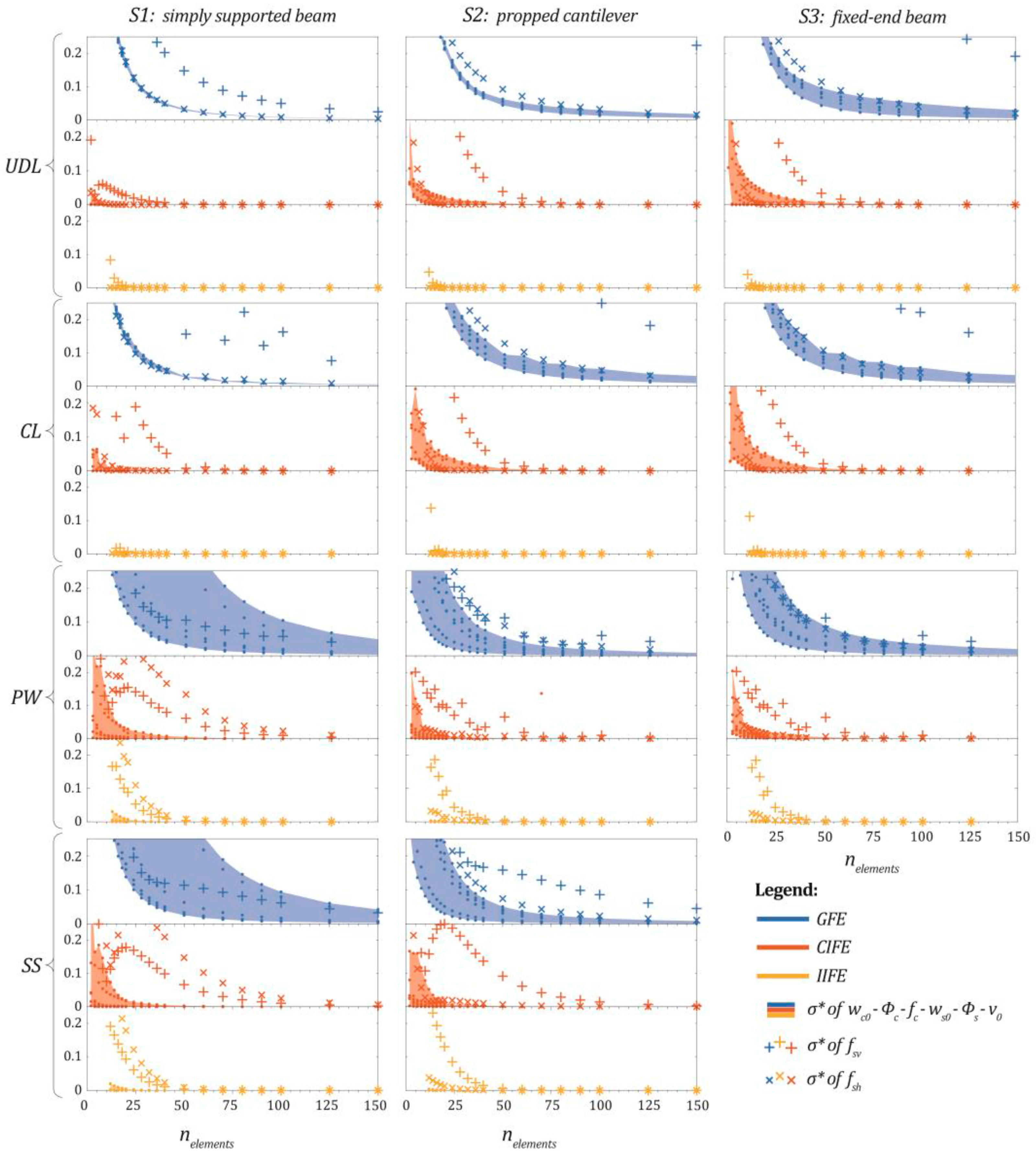
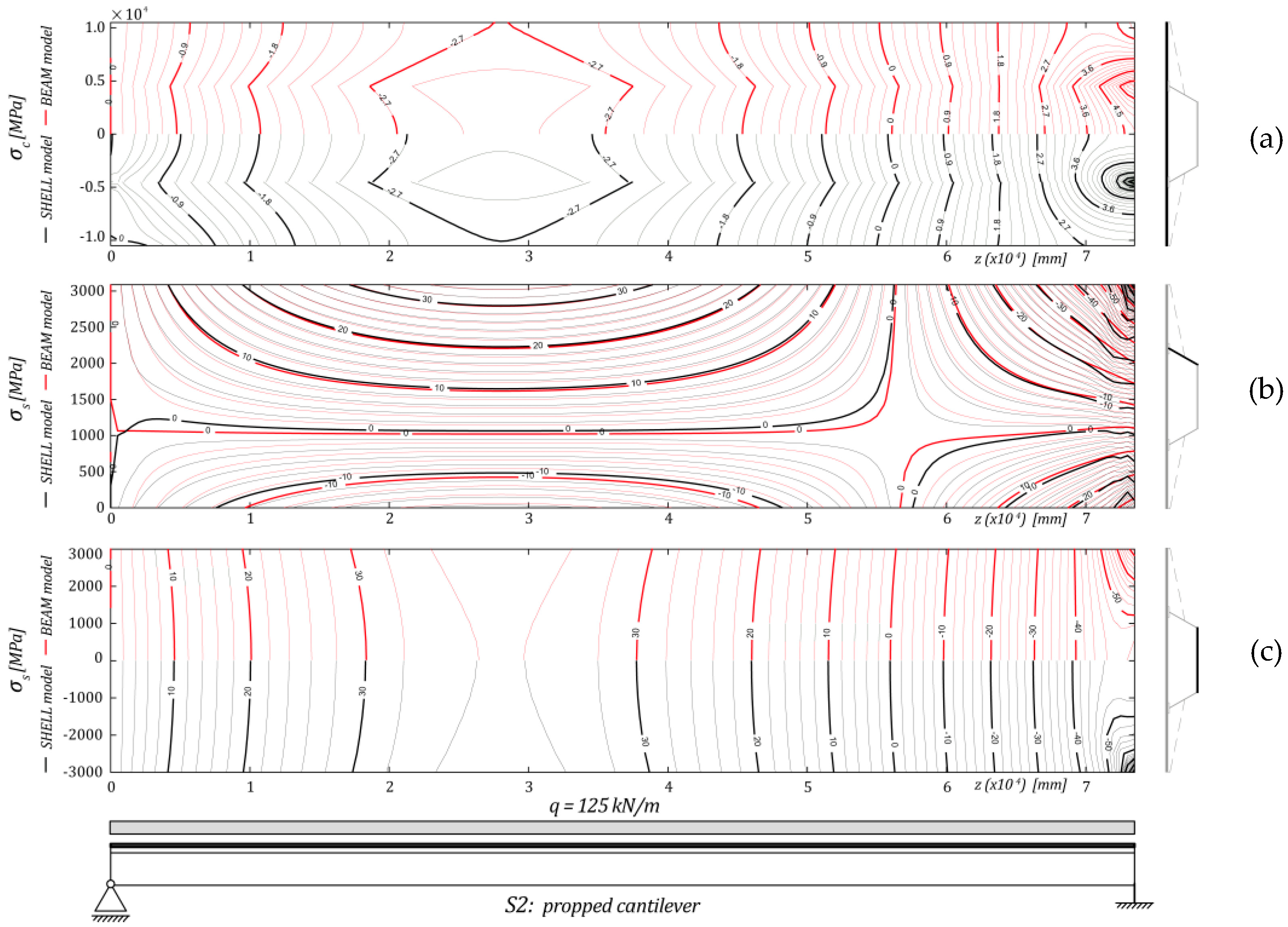
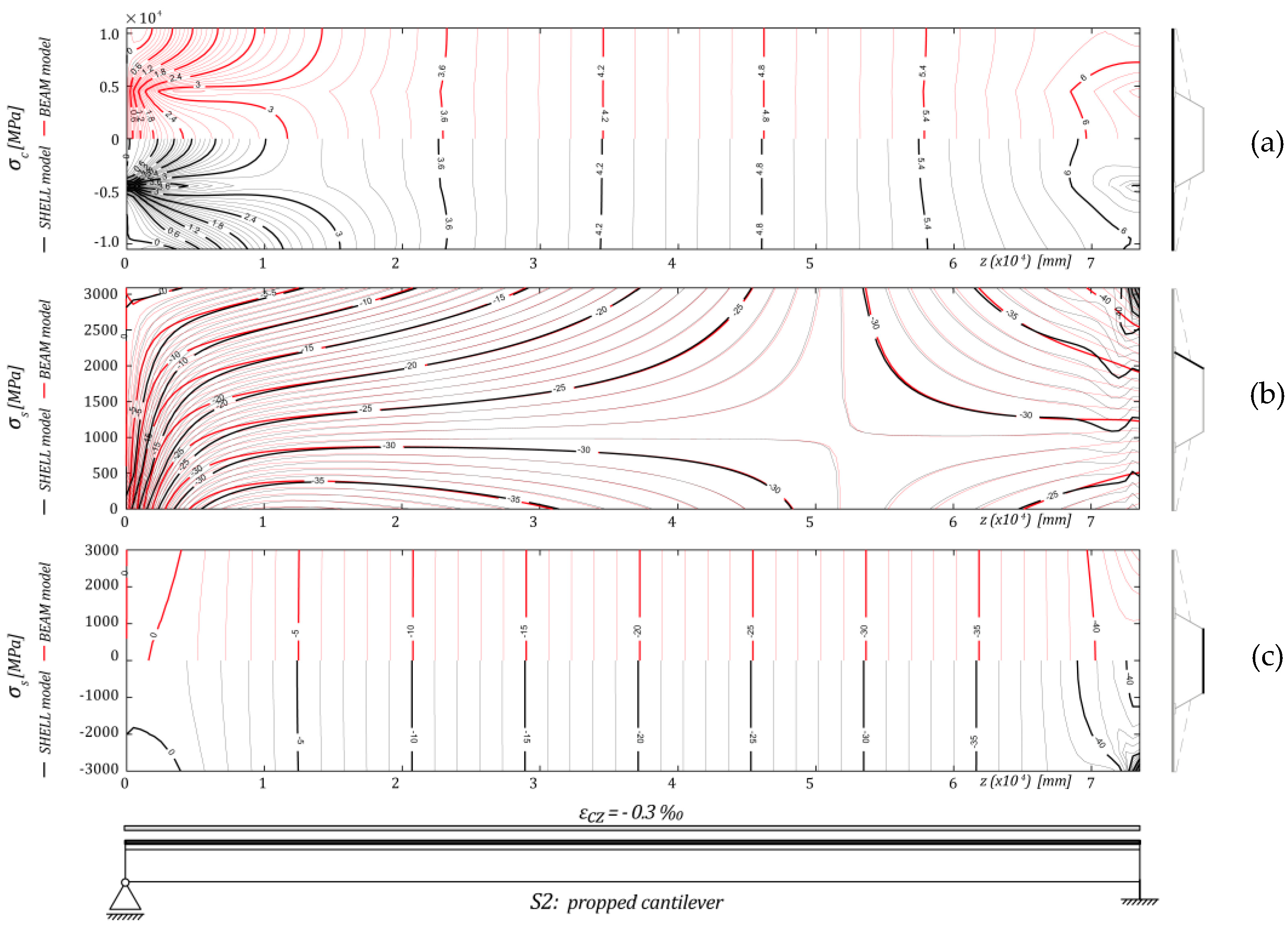
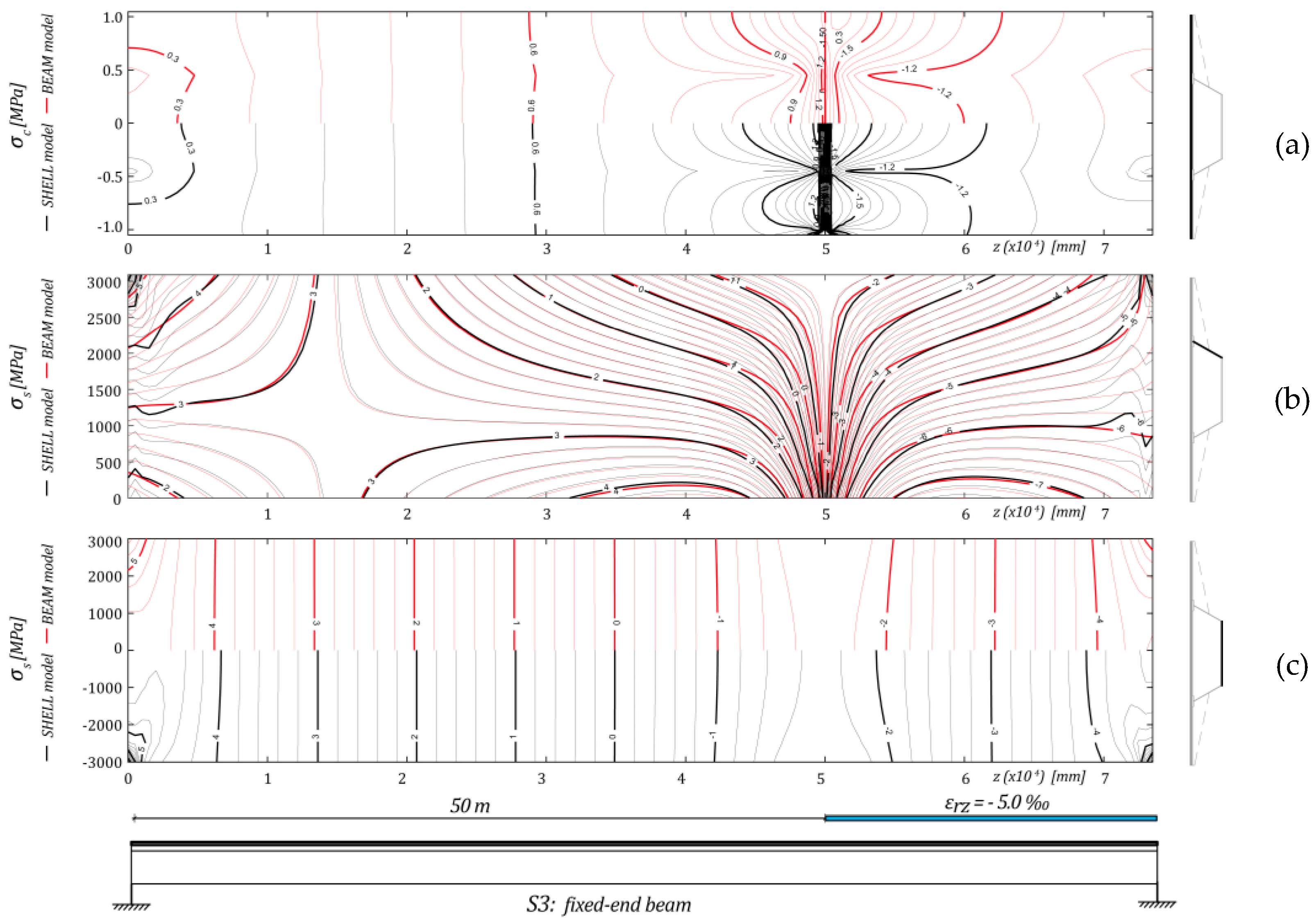
4. Numerical Comparison with More Complex Models
5. Conclusions
- The finite element based on linear shape functions (GFE) suffers from locking problems and requires a highly refined discretization to reach an accurate solution of the problem;
- The finite element implementing cubic and quadratic polynomial shape functions (CIFE) avoids locking problems and is characterised by a higher converge rate than that based on linear shape functions (GFE);
- The finite element with exponential shape functions (IIFE) is the most performant and furnishes an almost exact solution, independent of the beam discretization, provided that enough finite elements are adopted to avoid issues in the numerical evaluation of the exponential matrix;
- The CIFE is highly competitive with respect to the IIFE, especially in predicting beam displacements and rotations; in some cases, if very accurate solutions are not required, the former may provide results with a lower number of finite elements than that necessary to avoid instabilities in the computation of the exponential shape functions of the IIFE;
- In the case of distributed or concentrated loads, the convergence rate relevant to warping intensities of the steel components is much lower than that relevant to the other response parameters; differences in the convergence rate attenuate in the cases of prestressing or concrete shrinkage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Stress Resultants and Inertial Components
Appendix B
Stress State
Appendix C
Notations
| 0 | origin of Cartesian coordinate system; |
| matrix containing stiffnesses of the beam cross section; | |
| area; | |
| geometric vector; | |
| matrix containing stiffnesses of the beam cross section; | |
| vector of the integration constants; | |
| concrete slab width; | |
| matrix containing stiffnesses of the beam cross section; | |
| vector of loads and stress-independent strain along the beam; | |
| vector of all unknown displacements; | |
| differential operator; | |
| exponential matrix; | |
| Young’s modulus; | |
| vector of nodal forces; | |
| warping intensity functions; | |
| shear modulus; | |
| slab thickness; | |
| inertia matrix or identity matrix; | |
| inertia matrix; | |
| stiffness matrix of the beam element; | |
| indexes; | |
| length of the beam; | |
| length of the beam plane walls; | |
| length of the finite element; | |
| inertia matrix; | |
| bending moment at the beam end cross section; | |
| bending moment along the beam axis; | |
| longitudinal force at the beam end cross section; | |
| matrix of interpolating functions; | |
| vector of resultants of forces due to restrained stress-independent strain; | |
| number of the plane steel walls; | |
| number of finite elements | |
| resultants of external forces along the beam axis; | |
| resultants of external forces at the beam end cross section; | |
| resultant of vertical loads at the beam end cross section; | |
| longitudinal forces along the beam axis; | |
| resultant of vertical loads along the beam axis; | |
| inverse of matrix of exponential matrices evaluated at beam ends; | |
| vector grouping unknown displacements and their first derivative; | |
| thickness of the i-th plane steel wall; | |
| linear matrix operator; | |
| displacement of the two end cross sections of the beam; | |
| displacement of the end cross section of the beam; | |
| transverse displacement, along coordinate direction ; | |
| vector of the unknown nodal displacements; | |
| assembled vector of the nodal displacements of all the elements; | |
| vertical displacement of the cross section, along coordinate direction ; | |
| bi-moment at the beam end cross section; | |
| longitudinal displacement, along coordinate direction ; | |
| vector grouping the generalised displacements; | |
| coordinate axes; | |
| coordinates; | |
| coordinates of the slab–girder interface connection; | |
| direction cosine of the local abscissa; | |
| overall stress-independent strain; | |
| vector of stress-independent strains; | |
| stress-independent strain; | |
| generic nonlinear stress-independent longitudinal strain field; | |
| rotation; | |
| beam–slab interface slip; | |
| local abscissa of the finite element; | |
| normalised abscissa of the finite element | |
| interpolating function; | |
| Poisson’s ratio; interpolating function | |
| stiffness per-unit-length of the shear connection; | |
| normal stress; | |
| shear stress; | |
| interpolating function; | |
| bi-moment along the beam axis; | |
| local abscissa of the beam plane walls; | |
| slab warping function; | |
| steel warping function due to longitudinal shear flow; | |
| steel warping function due to shear force. | |
| Subscripts | |
| concrete part of the composite beam; | |
| finite element; | |
| steel reinforcement part of the composite beam; | |
| steel part of the composite beam; | |
| referred to the origin of coordinate system; | |
| partial derivatives. | |
| Symbols and Superscripts | |
| concrete part of the composite beam; | |
| derivative with respect to z variable; | |
| formal linear differential operator; | |
| variation; | |
| scalar product. | |
References
- European Committee for Standardization (CEN). Eurocode 4: Design of Composite Steel and Concrete Structures–Part 2: Rules for Bridges; EN1994-2; CEN: Brussels, Belgium, 2005. [Google Scholar]
- Newmark, N.M.; Siess, C.P.; Viest, I.M. Test and analysis of composite beams with incomplete interaction. Proc. Soc. Exp. Stress Anal. 1951, 9, 75–92. [Google Scholar]
- Nguyen, Q.H.; Hjiaj, M.; Uy, B. Time-dependent analysis of composite beams with partial interaction based on time-discrete exact stiffness matrix. Eng. Struct. 2010, 32, 2902–2911. [Google Scholar] [CrossRef]
- Ranzi, G.; Bradford, M.A. Analysis of composite beams with partial interaction using the direct stiffness approach accounting for time effects. Int. J. Numer. Methods Eng. 2009, 78, 564–586. [Google Scholar] [CrossRef]
- Gara, F.; Ranzi, G.; Leoni, G. Time analysis of composite beams with partial interaction using available modelling techniques: A comparative study. J. Constr. Steel Res. 2006, 62, 917–930. [Google Scholar] [CrossRef]
- Dezi, L.; Gara, F.; Leoni, G. Construction sequence modelling for continuous steel-concrete composite decks. Steel Compos. Struct. 2006, 6, 123–138. [Google Scholar] [CrossRef]
- Gara, F.; Leoni, G.; Dezi, L. Slab cracking control in continuous steel-concrete bridge decks. J. Bridge Engrg. ASCE 2013, 18, 1319–1327. [Google Scholar] [CrossRef]
- Ranzi, G.; Bradford, M.A. Nonlinear analysis of composite beams with partial shear interaction by means of the direct stiffness method. Steel Compos. Struct. 2009, 9, 131–158. [Google Scholar] [CrossRef]
- Virtuoso, F.; Vieira, R. Time dependent behaviour of continuous composite beams with flexible connection. J. Constr. Steel Res. 2004, 60, 451–463. [Google Scholar] [CrossRef]
- Dall’Asta, A.; Zona, A. Three-field mixed formulation for the non-linear analysis of composite beams with deformable shear connection. Finite Elem. Anal. Des. 2004, 40, 425–448. [Google Scholar] [CrossRef]
- Gara, F.; Ranzi, G.; Leoni, G. Displacement-based formulations for composite beams with longitudinal slip and vertical uplift. Int. J. Numer. Methods Eng. 2006, 65, 1197–1220. [Google Scholar] [CrossRef]
- Ranzi, G.; Gara, F.; Ansourian, P. General method of analysis for composite beams with longitudinal and transverse partial interaction. Comput. Struct. 2006, 84, 2373–2384. [Google Scholar] [CrossRef]
- Taig, G.; Ranzi, G. Generalised beam theory for composite beams with longitudinal and transverse partial interaction. Math. Mech. Solids 2017, 22, 2011–2039. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Hjiaj, M.; Guezouli, S. Exact finite element model for shear-deformable two layer beams with discrete shear connection. Finite Elem. Anal. Des. 2011, 47, 718–727. [Google Scholar] [CrossRef]
- da Silva, A.R.; Sousa, J.B.M. A family of interface elements for the analysis of composite beams with interlayer slip. Finite Elem. Anal. Des. 2009, 45, 305–314. [Google Scholar] [CrossRef]
- Gara, F.; Leoni, G.; Dezi, L. A beam finite element including shear lag effect for the time dependent analysis of steel–concrete composite decks. Eng. Struct. 2009, 31, 1888–1902. [Google Scholar] [CrossRef]
- Timoshenko, S. Theory of bending, torsion and buckling of thin walled members of open section. J. Frankl. Inst. 1945, 239, 249–268. [Google Scholar] [CrossRef]
- Xu, R.; Wang, G. Bending solutions of the Timoshenko partial-interaction composite beams using Euler-Bernoulli solutions. J. Eng. Mech. ASCE 2013, 139, 1881–1885. [Google Scholar] [CrossRef]
- Vo, T.P.; Thai, H.T. Static behaviour of composite beams using various refined shear deformation theories. Comp. Struct. 2012, 94, 2513–2522. [Google Scholar] [CrossRef]
- Zona, A.; Ranzi, G. Finite element models for nonlinear analysis of steel–concrete composite beams with partial interaction in combined bending and shear. Finite Elem. Anal. Des. 2011, 47, 98–118. [Google Scholar] [CrossRef]
- Ranzi, G.; Zona, A. A steel–concrete composite beam model with partial interaction including the shear deformability of the steel component. Eng. Struct. 2007, 29, 3026–3041. [Google Scholar] [CrossRef]
- Schnabl, S.; Saje, M.; Turk, G.; Planinc, I. Analytical solution of two-layer beam taking into account interlayer slip and shear deformation. J. Struct. Eng. 2007, 133, 886–894. [Google Scholar] [CrossRef]
- Dezi, L.; Gara, F.; Leoni, G.; Tarantino, M.A. Time dependent analysis of shear-lag effect in composite beams. J. Engrg. Mech. ASCE 2001, 127, 71–79. [Google Scholar] [CrossRef]
- Dezi, L.; Gara, F.; Leoni, G. Shear-Lag effect in twin-girder composite decks. Steel Compos. Struct. 2003, 3, 111–122. [Google Scholar] [CrossRef]
- Dezi, L.; Gara, F.; Leoni, G. Effective slab width in prestressed twin-girder composite decks. J. Struct. Engrg. ASCE 2006, 132, 1358–1370. [Google Scholar] [CrossRef]
- Macorini, L.; Fragiacomo, M.; Amadio, C.; Izzuddin, B.A. Long-term analysis of steel–concrete composite beams: FE modelling for effective width evaluation. Eng. Struct. 2006, 28, 1110–1121. [Google Scholar] [CrossRef]
- Gara, F.; Ranzi, G.; Leoni, G. Partial interaction analysis with shear-lag effects of composite bridges: A finite element implementation for design applications. Adv. Steel Constr. 2011, 7, 1–16. [Google Scholar]
- Gara, F.; Ranzi, G.; Leoni, G. Analysis of the shear lag effect in composite bridges with complex static schemes by means of a deck finite element. Int. J. Steel Struct. 2008, 8, 249–260. [Google Scholar]
- Gonçalves, R.; Camotim, D. Steel-concrete composite bridge analysis using Generalised Beam Theory. Steel Compos. Struct. 2010, 10, 223–243. [Google Scholar] [CrossRef]
- Gara, F.; Leoni, G.; Carbonari, S.; Dezi, L. A higher order steel-concrete composite beam model. Eng. Struct. 2014, 80, 260–273. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Sheikh, A.H.; Grifith, M.; Oehlers, D.J. Analysis of composite beams with longitudinal and transverse partial interactions using higher order beam theory. Int. J. Mech. Sci. 2012, 59, 115–125. [Google Scholar] [CrossRef]
- Computer and Structures, Inc. CSI Analysis Reference Manual; SAP 2000; Computer and Structures, Inc.: Berkeley, CA, USA, 2011. [Google Scholar]
- Reddy, J.N. On locking-free shear deformable beam finite elements. Comput. Methods Appl. Mech. Engrg. 1997, 149, 113–132. [Google Scholar] [CrossRef]
- Moler, C.; Van Loan, C. Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later. SIAM Rev. 2003, 45, 3–49. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gara, F.; Carbonari, S.; Leoni, G.; Dezi, L. Finite Elements for Higher Order Steel–Concrete Composite Beams. Appl. Sci. 2021, 11, 568. https://doi.org/10.3390/app11020568
Gara F, Carbonari S, Leoni G, Dezi L. Finite Elements for Higher Order Steel–Concrete Composite Beams. Applied Sciences. 2021; 11(2):568. https://doi.org/10.3390/app11020568
Chicago/Turabian StyleGara, Fabrizio, Sandro Carbonari, Graziano Leoni, and Luigino Dezi. 2021. "Finite Elements for Higher Order Steel–Concrete Composite Beams" Applied Sciences 11, no. 2: 568. https://doi.org/10.3390/app11020568
APA StyleGara, F., Carbonari, S., Leoni, G., & Dezi, L. (2021). Finite Elements for Higher Order Steel–Concrete Composite Beams. Applied Sciences, 11(2), 568. https://doi.org/10.3390/app11020568







