Partial Least Squares Improved Multivariate Adaptive Regression Splines for Visible and Near-Infrared-Based Soil Organic Matter Estimation Considering Spatial Heterogeneity
Abstract
1. Introduction
2. Study Area and Materials
2.1. Study Area
2.2. SOM Content and Spectral Measurement
3. Methods
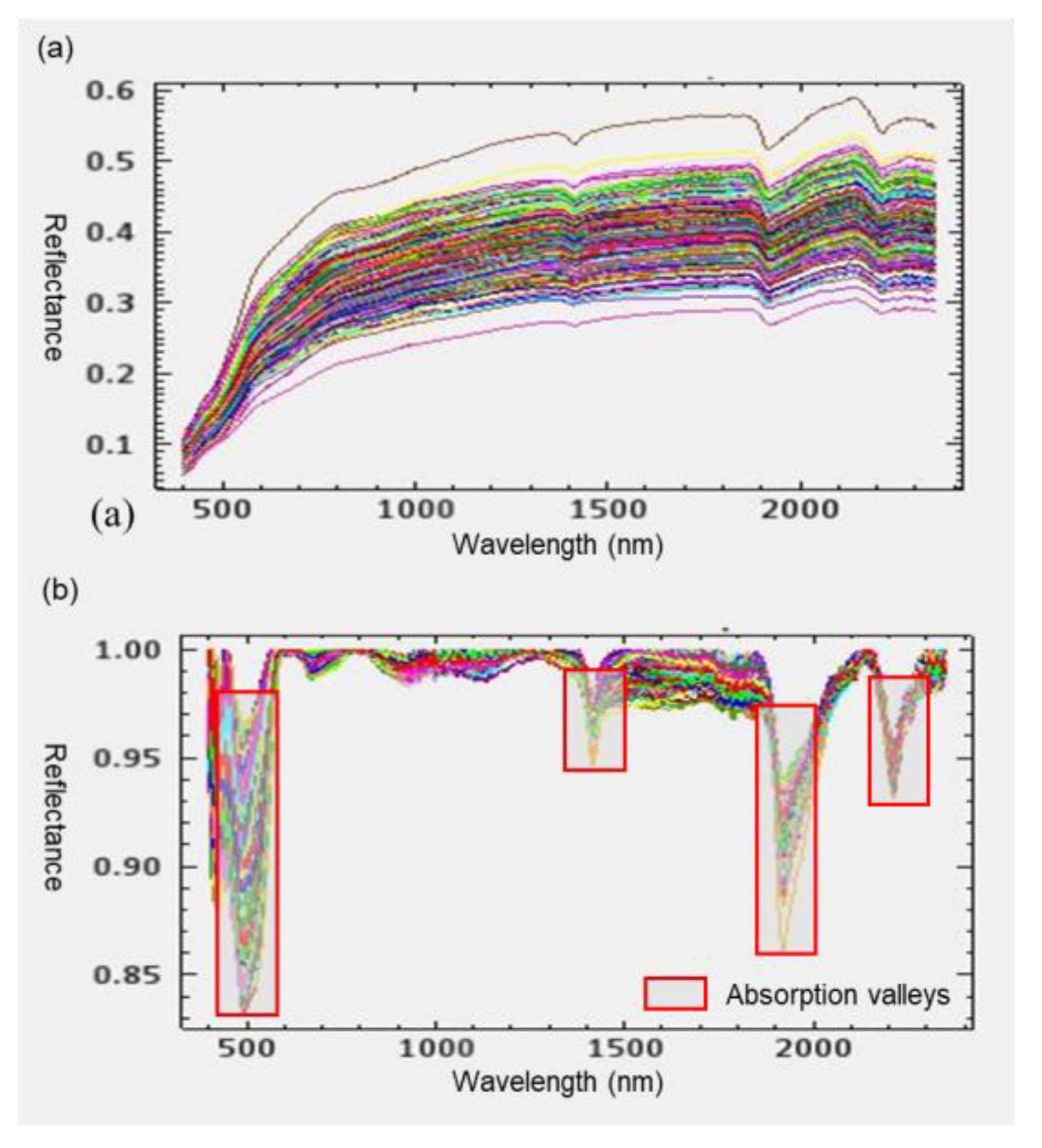
3.1. Spectral Preprocessing
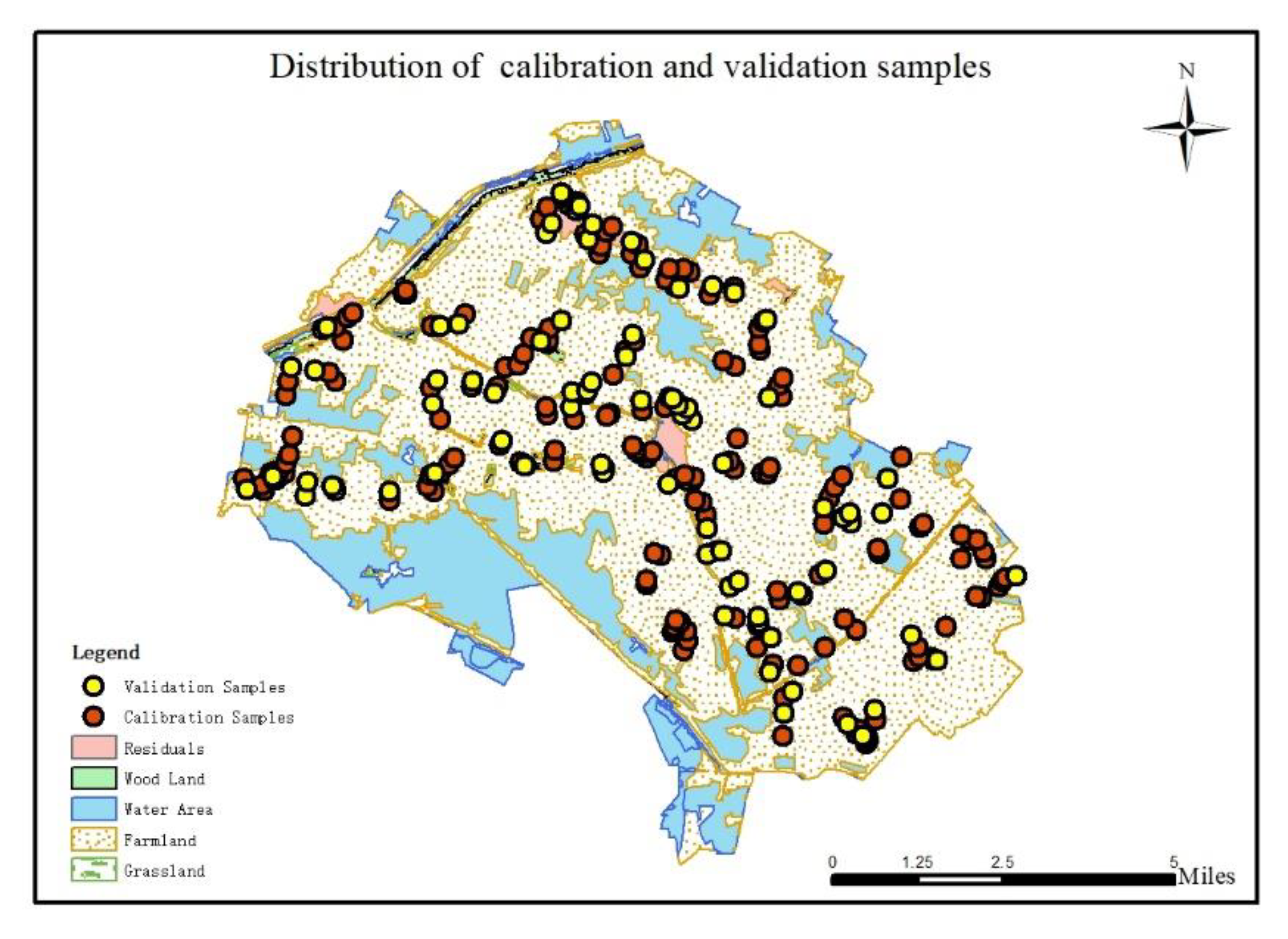
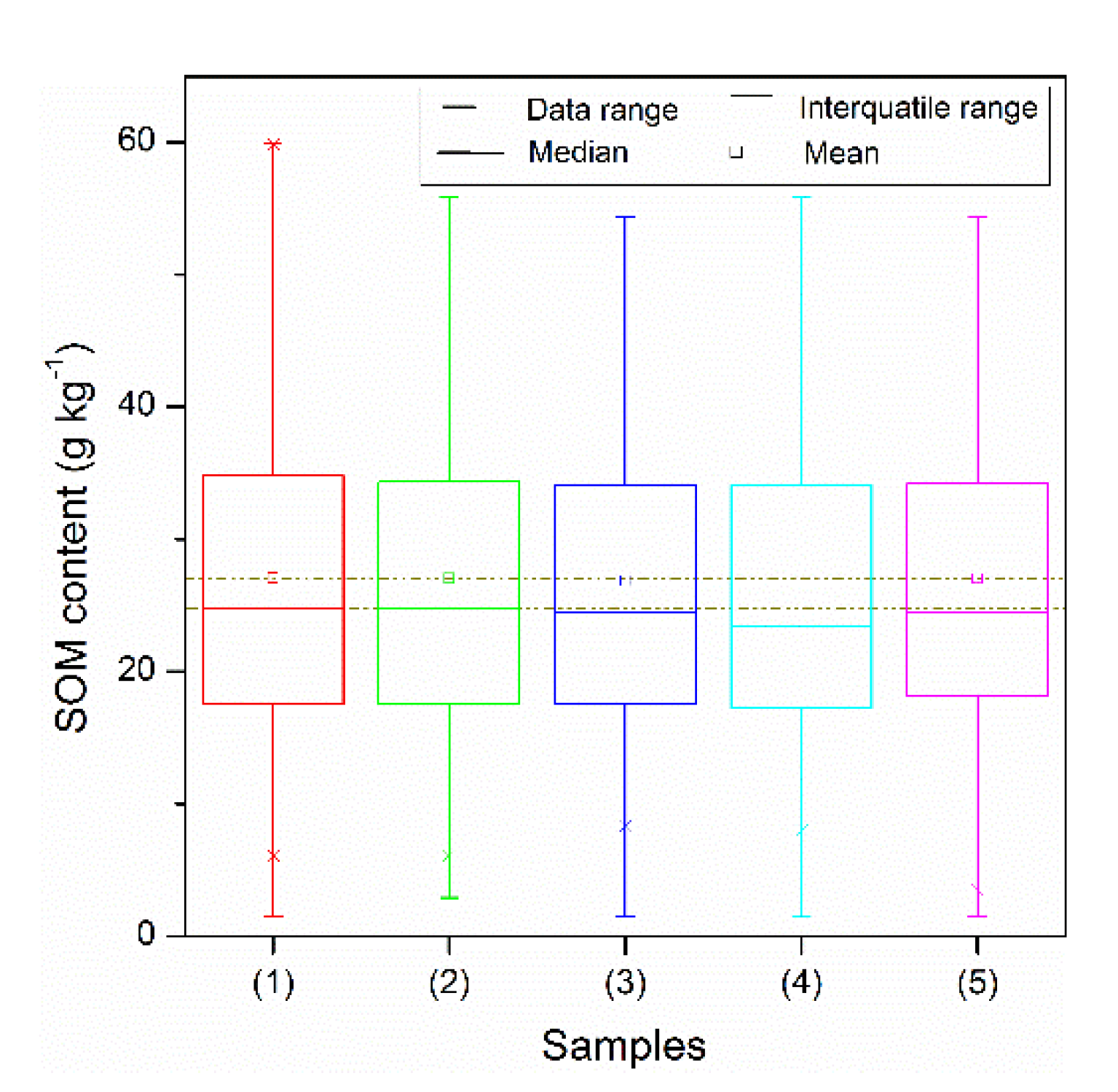
3.2. Calibration Set and Validation Set Selection Methods
3.3. VNIR-Based Prediction Methods
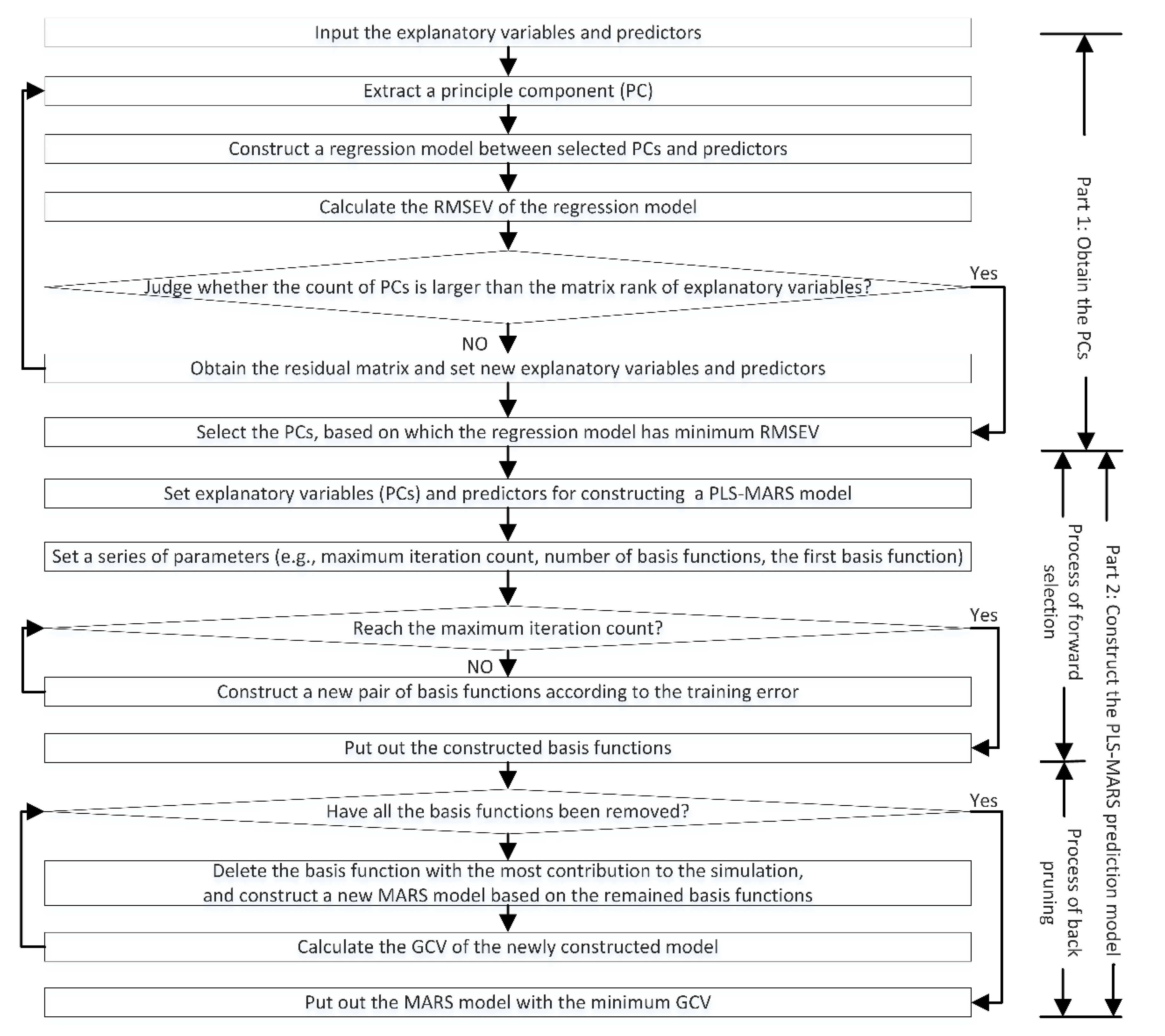
3.3.1. PLS–MARS Method
3.3.2. Fitness Assessment of the VNIR-Based Prediction Model
4. Results
4.1. Verification of PLS−MARS Method Based on a Simulated Data Set
4.2. Case Study of PLS–MARS Method
4.2.1. Calibration Set Selected Using MVARC-R-KS Method
4.2.2. Performance of the PLS–MARS Model Calibrated by the Calibration Set Selected Utilizing the MVARC-R-KS Method
4.2.3. Comparison of the PLS–MARS Model with Typical Prediction Models
5. Discussion
5.1. Influence of the Calibration Set on the Model Performance
5.2. Strategies of the PLS–MARS Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, M.; Sarkar, B.; Bolan, N.S.; Ok, Y.S.; Churchman, G.J. Decomposition of soil organic matter as affected by clay types, pedogenic oxides and plant residue addition rates. J. Hazard. Mater. 2019, 374, 11–19. [Google Scholar] [CrossRef]
- Tian, P.; Mason-Jones, K.; Liu, S.; Wang, Q.; Sun, T. Form of nitrogen deposition affects soil organic matter priming by glucose and cellulose. Biol. Fertil. Soils 2019, 55, 383–391. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y.; Guo, L.; Liu, L. Construction of the Calibration Set through Multivariate Analysis in Visible and Near-Infrared Prediction Model for Estimating Soil Organic Matter. Remote Sens. 2017, 9, 201. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, H.; Chen, Y.; Qian, J. Combining Environmental Factors and Lab VNIR Spectral Data to Predict SOM by Geospatial Techniques. Chin. Geogr. Sci. 2019, 29, 258–269. [Google Scholar] [CrossRef]
- Moura-Bueno, J.M.; Dalmolin, R.S.D.; ten Caten, A.; Dotto, A.C.; Demattê, J.A.M. Stratification of a local VIS-NIR-SWIR spectral library by homogeneity criteria yields more accurate soil organic carbon predictions. Geoderma 2019, 337, 565–581. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y. Estimation of total iron content in floodplain soils using VNIR spectroscopy—A case study in the Le’an River floodplain, China. Int. J. Remote Sens. 2012, 33, 5954–5972. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y. Feasibility of Estimating Cu Contamination in Floodplain Soils using VNIR Spectroscopy—A Case Study in the Le’an River Floodplain, China. Soil Sedim. Contam. An Int. J. 2012, 21, 951–969. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, L.; Jiang, Q.; Zhang, H.; Chen, Y. Comparing geospatial techniques to predict SOC stocks. Soil Tillage Res. 2015, 148, 46–58. [Google Scholar] [CrossRef]
- Liu, Y.; Song, Y.; Guo, L.; Chen, Y.; Lu, Y.; Liu, Y. Geostatistical models of soil organic carbon density prediction based on soil hyperspectral reflectance. Trans. Chin. Soc. Agric. Eng. 2017, 33, 183–191. [Google Scholar]
- Tekin, Y.; Tümsavas, Z.; Mouazen, A.M. Comparing the artificial neural network with parcial least squares for prediction of soil organic carbon and pH at different moisture content levels using visible and near-infrared spectroscopy. Rev. Bras. Ciência Solo 2014, 38, 1794–1804. [Google Scholar] [CrossRef]
- Liess, M.; Schmidt, J.; Glaser, B. Improving the Spatial Prediction of Soil Organic Carbon Stocks in a Complex Tropical Mountain Landscape by Methodological Specifications in Machine Learning Approaches. PLoS ONE 2016, 11, e0153673. [Google Scholar]
- Huang, N.; Wang, L.; Guo, Y.; Niu, Z. Upscaling plot-scale soil respiration in winter wheat and summer maize rotation croplands in Julu County, North China. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 169–178. [Google Scholar] [CrossRef]
- Laamrani, A.; Berg, A.A.; Voroney, P.; Feilhauer, H.; Blackburn, L.; March, M.; Dao, P.D.; He, Y.; Martin, R.C. Ensemble Identification of Spectral Bands Related to Soil Organic Carbon Levels over an Agricultural Field in Southern Ontario, Canada. Remote Sens. 2019, 11, 1298. [Google Scholar]
- Zheng, G.; Zhang, W.B.; Zhou, H.Z.; Yang, P.B. Multivariate adaptive regression splines model for prediction of the liquefaction-induced settlement of shallow foundations. Soil Dyn. Earthq. Eng. 2020, 132, 10. [Google Scholar]
- Huang, H.; Ji, X.L.; Xia, F.; Huang, S.H.; Shang, X.; Chen, H.; Zhang, M.H.; Dahlgren, R.A.; Mei, K. Multivariate adaptive regression splines for estimating riverine constituent concentrations. Hydrol. Process. 2020, 34, 15. [Google Scholar] [CrossRef]
- Liu, L.-L.; Cheng, Y.-M. Efficient system reliability analysis of soil slopes using multivariate adaptive regression splines-based Monte Carlo simulation. Comput. Geotech. 2016, 79, 41–54. [Google Scholar] [CrossRef]
- Brillante, L.; Bois, B.; Mathieu, O.; Lévêque, J. Electrical imaging of soil water availability to grapevine: A benchmark experiment of several machine-learning techniques. Precis. Agric. 2016, 17, 637–658. [Google Scholar] [CrossRef]
- Guo, L.; Zhao, C.; Zhang, H.; Chen, Y.; Linderman, M.; Zhang, Q.; Liu, Y. Comparisons of spatial and non-spatial models for predicting soil carbon content based on visible and near-infrared spectral technology. Geoderma 2017, 285, 280–292. [Google Scholar] [CrossRef]
- De Jong, E.; Schappert, H.J.V. Calculation of soil respiration and activity from CO2 profiles in the soil. Soil Sci. 1972, 113, 328–333. [Google Scholar]
- Tang, J.; Baldocchi, D.D.; Qi, Y.; Xu, L. Assessing soil CO2 efflux using continuous measurements of CO2 profiles in soils with small solid-state sensors. Agric. Forest Meteorol. 2003, 118, 207–220. [Google Scholar]
- Technometrics. Index to contents, Volume 11, 1969. Technometrics 1969, 11, 848–851. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, Z.; Yuan, H.; Song, C.; Li, X. An optimal selection method of samples of calibration set and validation set for spectral multivariate analysis. Spectrosc. Spectr. Anal. 2014, 34, 947–951. [Google Scholar]
- Liu, Y.; Lu, Y.; Guo, L.; Xiao, F.; Chen, Y. Construction of Calibration Set Based on the Land Use Types in Visible and Near-InfRared (VIS-NIR) Model for Soil Organic Matter Estimation. Acta Pedol. Sin. 2016, 53, 332–341. [Google Scholar]
- Rana, P.; Gautam, B.; Tokola, T. Optimizing the number of training areas for modeling above-ground biomass with ALS and multispectral remote sensing in subtropical Nepal. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 52–62. [Google Scholar] [CrossRef]
- Friedman, J.H.; Roosen, C.B. An introduction to multivariate adaptive regression splines. Stat. Methods Med. Res. 1995, 4, 197–217. [Google Scholar] [CrossRef] [PubMed]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically Weighted Regression. J. R. Statal Soc. Ser. D (Statian) 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Simonoff, J.S.; Tsai, C.L. Smoothing parameter selection in nonparametric regression using an improved Akaike information criterion. J. R. Statal Soc. 1998, 60, 271–293. [Google Scholar] [CrossRef]
- Shi, T.; Cui, L.; Wang, J.; Fei, T.; Chen, Y.; Wu, G. Comparison of multivariate methods for estimating soil total nitrogen with visible/near-infrared spectroscopy. Plant Soil 2012, 366, 363–375. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; McGlynn, R.N.; McBratney, A.B. Determining the composition of mineral-organic mixes using UV–vis–NIR diffuse reflectance spectroscopy. Geoderma 2006, 137, 70–82. [Google Scholar]
- Chen, Y. Spatial Autocorrelation Approaches to Testing Residuals from Least Squares Regression. PLoS ONE 2016, 11, e0146865. [Google Scholar] [CrossRef]


| Prediction Model | Selection Method | Original Data | Predicted Data | Residuals | |||
|---|---|---|---|---|---|---|---|
| I | Z-Score | I | Z-Score | I | Z-Score | ||
| Partial least squares–based geographic weighted regression (PLS–GWR) | Concentration gradient (C) method | 1.15 | 6.33 | 1.06 | 5.83 | 0.01 | 0.20 |
| Kennard-Stone (KS) method | 1.28 | 5.87 | 1.15 | 5.23 | −0.07 | −1.27 | |
| Rank–Kennard-Stone (Rank–KS) method | 1.33 | 6.30 | 1.28 | 6.03 | −0.10 | −1.35 | |
| Regional multi-variable associate rule mining and Rank–Kennard-Stone (MVARC-R-KS) method | 1.39 | 6.17 | 1.24 | 5.49 | −0.07 | −0.96 | |
| Partial least squares–based multivariate adaptive regression (PLS–MARS) | C | 1.15 | 6.33 | 1.03 | 5.69 | −0.01 | 0.06 |
| KS | 1.28 | 5.87 | 1.12 | 5.15 | 0.07 | 1.42 | |
| Rank–KS | 1.33 | 6.30 | 1.12 | 5.30 | −0.01 | 0.01 | |
| MVARC-R-KS | 1.39 | 6.17 | 1.17 | 5.23 | 0.08 | 1.33 | |
| Illustrative Functions | Explanatory Variable Size | Prediction Model | Coefficient of Determination of Simulation Analysis | Root of Mean Square Simulation Error (RMSEV (g kg−1)) | Coefficient of Determination of Prediction Analysis | Root of Mean Square Prediction Error (RMSEP (g kg−1)) | Relative Percent Deviation (RPD) |
|---|---|---|---|---|---|---|---|
| 100 | Multiple linear regression (MLR) | 0.92 | 1.08 | 0.93 | 0.99 | 3.9 | |
| partial least squares regression (PLS) | 0.92 | 1.02 | 0.93 | 0.93 | 4.2 | ||
| Support vector machine (SVM) | 0.96 | 0.71 | 0.97 | 0.61 | 6.4 | ||
| PLS–MARS | 0.94 | 0.89 | 0.96 | 0.69 | 5.7 | ||
| 500 | MLR | 0.56 | 4.29 | 0.02 | 31.2 | 0.2 | |
| PLS | 0.64 | 3.33 | 0.75 | 2.98 | 1.9 | ||
| SVM | 0.69 | 3.09 | 0.78 | 2.79 | 2.2 | ||
| PLS–MARS | 0.65 | 3.21 | 0.76 | 2.93 | 2.1 |
| Statistic Values | All Samples | Samples Selected by Typical Methods | |||
|---|---|---|---|---|---|
| C | Rank–KS | KS | MVARC-R-KS | ||
| Mean | 0.3542 | 0.3495 | 0.3563 | 0.3561 | 0.3541 |
| Variation | 0.0369 | 0.0360 | 0.0404 | 0.0401 | 0.0405 |
| Prediction Model | Selection Method | Corrected Akaike Information Criterion (AICc) | RMSEV(g kg−1) | RMSEP(g kg−1) | RPD | ||
|---|---|---|---|---|---|---|---|
| MLR | C | 1005.54 | 0.54 | 8.9 | 0.11 | 28.0 | 0.44 |
| KS | 973.4 | 0.62 | 8.19 | 0.11 | 26.0 | 0.47 | |
| Rank–KS | 948.65 | 0.50 | 9.04 | 0.22 | 23.1 | 0.52 | |
| MVARC-R-KS | 937.79 | 0.54 | 8.9 | 0.09 | 30.8 | 0.39 | |
| PLS | C | 877.64 | 0.73 | 6.39 | 0.53 | 8.21 | 1.48 |
| KS | 844.87 | 0.78 | 5.87 | 0.50 | 8.82 | 1.38 | |
| Rank–KS | 829.80 | 0.71 | 6.51 | 0.56 | 8.48 | 1.51 | |
| MVARC-R-KS | 785.50 | 0.79 | 5.83 | 0.70 | 6.98 | 1.61 | |
| SVM | C | 996.75 | 0.54 | 8.70 | 0.50 | 8.78 | 1.38 |
| KS | 972.02 | 0.58 | 8.16 | 0.39 | 9.47 | 1.29 | |
| Rank–KS | 912.02 | 0.55 | 8.17 | 0.46 | 9.34 | 1.38 | |
| MVARC-R-KS | 935.36 | 0.50 | 8.84 | 0.55 | 8.11 | 1.56 | |
| PLS–GWR | C | 1187.90 | 0.75 | 5.80 | 0.54 | 8.18 | 1.49 |
| KS | 1227.43 | 0.79 | 5.19 | 0.50 | 8.76 | 1.42 | |
| Rank–KS | 1190.26 | 0.76 | 5.55 | 0.60 | 8.02 | 1.60 | |
| MVARC-R-KS | 1213.80 | 0.74 | 6.12 | 0.66 | 6.83 | 1.78 | |
| PLS–MARS | C | 1156.61 | 0.80 | 5.45 | 0.53 | 8.20 | 1.48 |
| KS | 1213.20 | 0.83 | 5.12 | 0.55 | 8.13 | 1.50 | |
| Rank–KS | 1166.12 | 0.79 | 5.50 | 0.62 | 7.88 | 1.63 | |
| MVARC-R-KS | 1135.50 | 0.84 | 5.14 | 0.71 | 6.52 | 1.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Yang, C.; Zhou, M. Partial Least Squares Improved Multivariate Adaptive Regression Splines for Visible and Near-Infrared-Based Soil Organic Matter Estimation Considering Spatial Heterogeneity. Appl. Sci. 2021, 11, 566. https://doi.org/10.3390/app11020566
Wang X, Yang C, Zhou M. Partial Least Squares Improved Multivariate Adaptive Regression Splines for Visible and Near-Infrared-Based Soil Organic Matter Estimation Considering Spatial Heterogeneity. Applied Sciences. 2021; 11(2):566. https://doi.org/10.3390/app11020566
Chicago/Turabian StyleWang, Xiaomi, Can Yang, and Mengjie Zhou. 2021. "Partial Least Squares Improved Multivariate Adaptive Regression Splines for Visible and Near-Infrared-Based Soil Organic Matter Estimation Considering Spatial Heterogeneity" Applied Sciences 11, no. 2: 566. https://doi.org/10.3390/app11020566
APA StyleWang, X., Yang, C., & Zhou, M. (2021). Partial Least Squares Improved Multivariate Adaptive Regression Splines for Visible and Near-Infrared-Based Soil Organic Matter Estimation Considering Spatial Heterogeneity. Applied Sciences, 11(2), 566. https://doi.org/10.3390/app11020566







