Adaptive MPC Based Real-Time Energy Management Strategy of the Electric Sanitation Vehicles
Abstract
1. Introduction
1.1. Literature Review and Motivation
1.2. The Organization of the Research
2. Modeling and Energy Consumption Analysis on an Electric Sanitation Vehicle
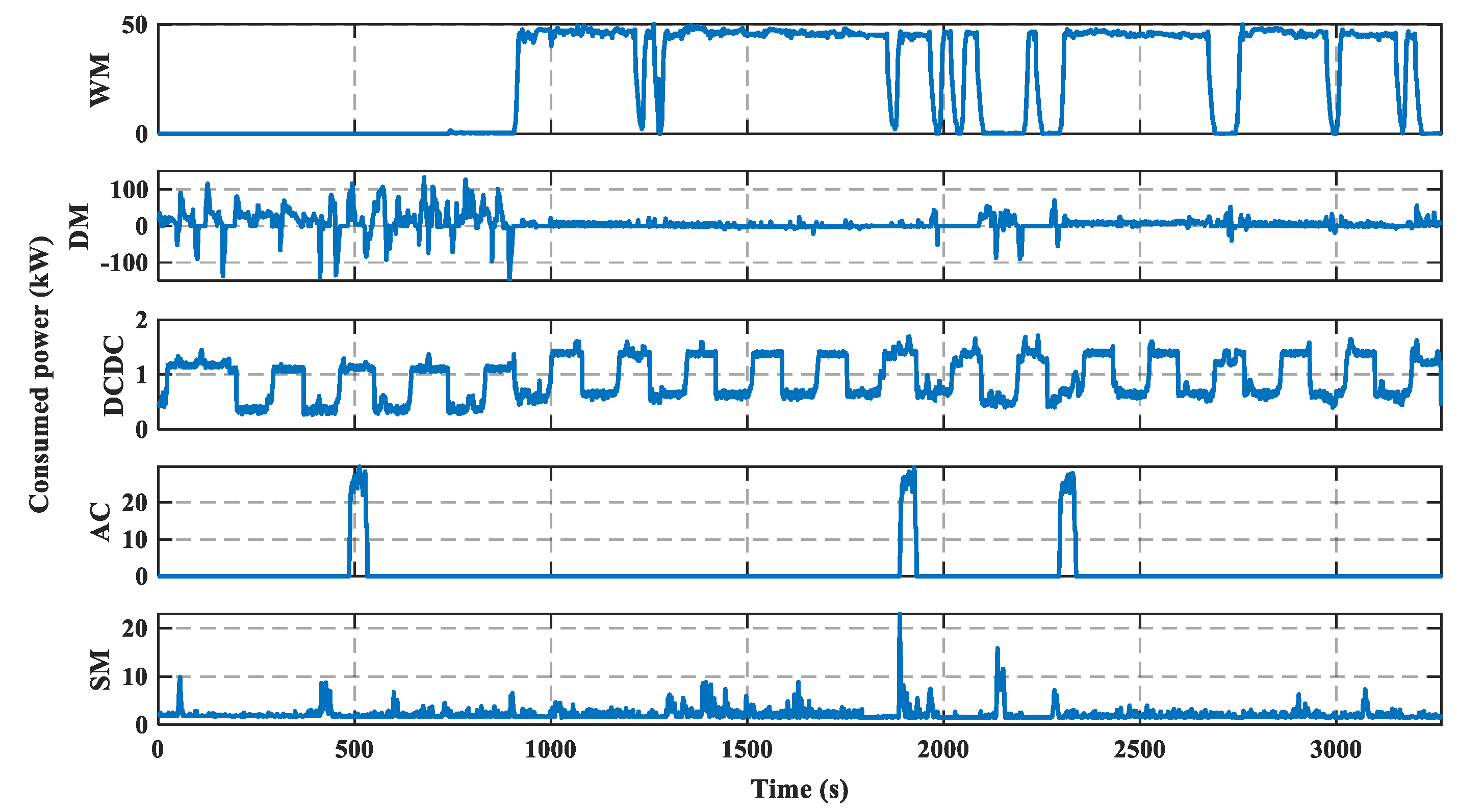
2.1. Analysis of the Energy Consumption
2.2. The Systematic Modeling
2.2.1. Modeling the Vehicle
2.2.2. Modeling the Electric Motors and Battery Pack
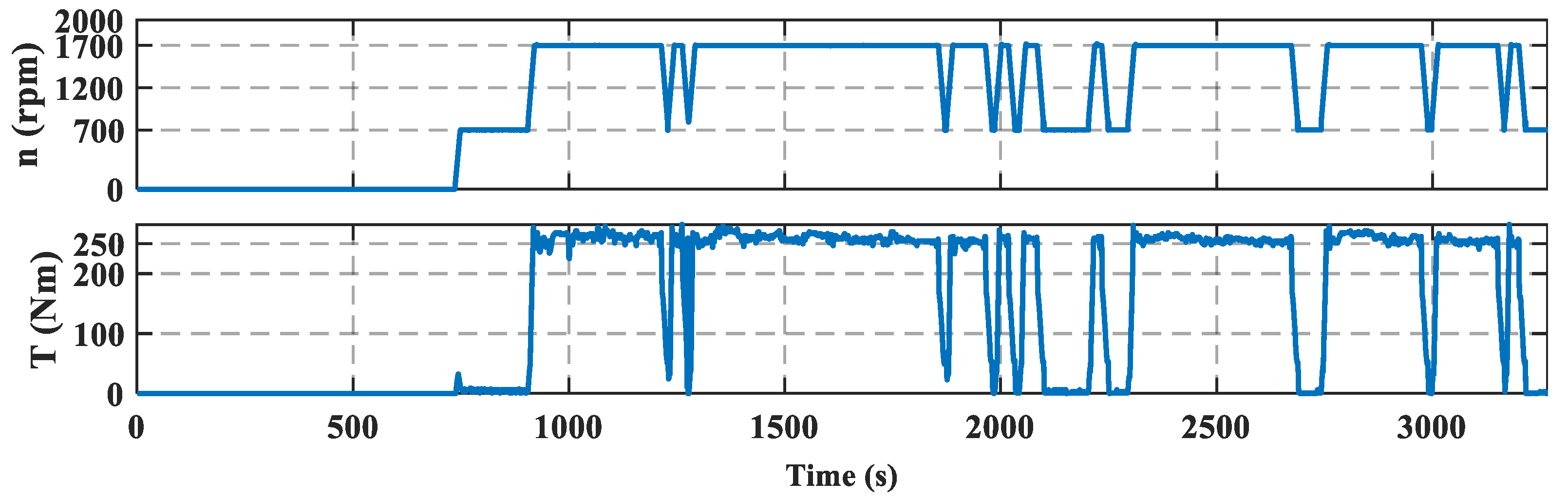
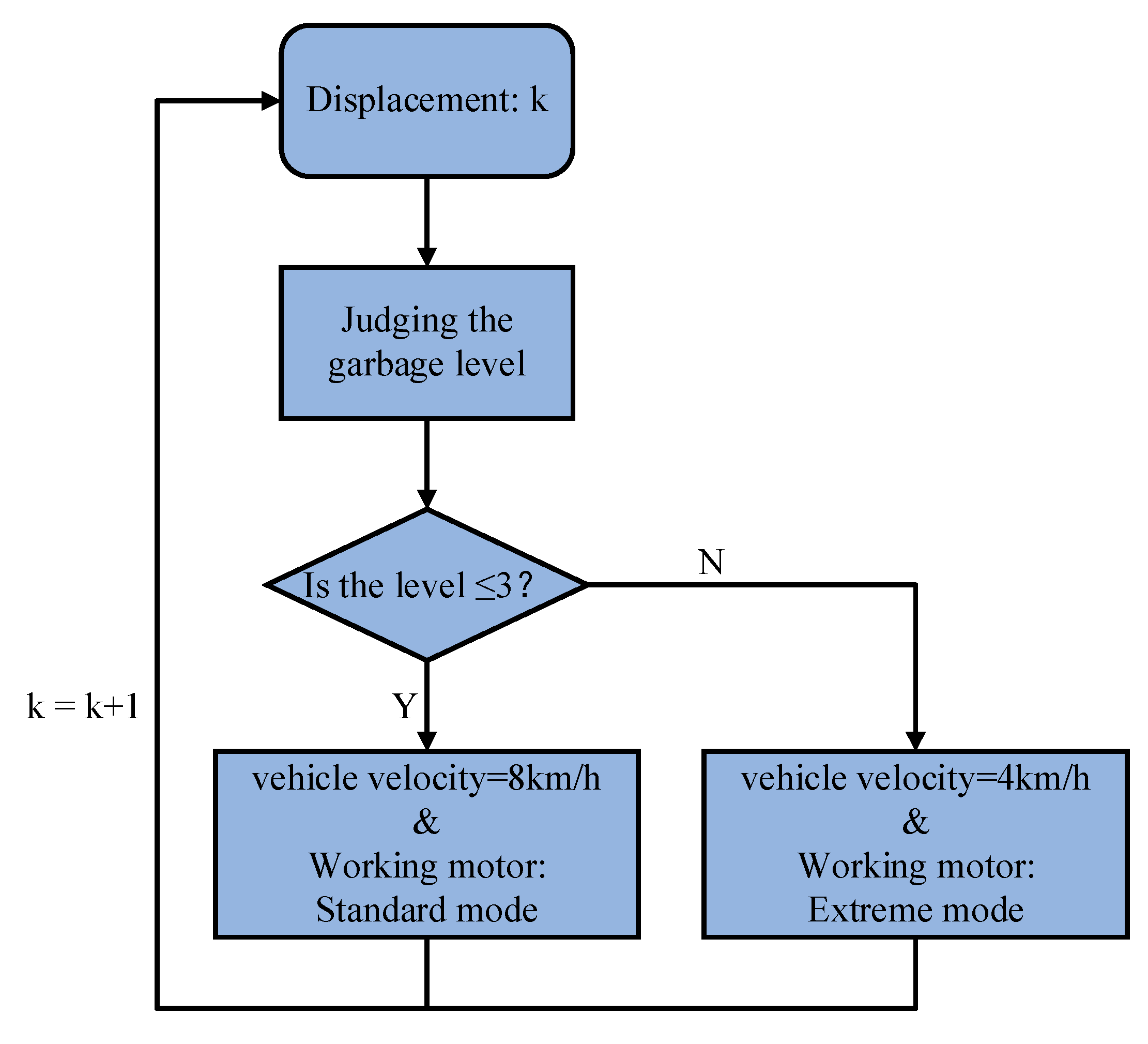
2.2.3. Modeling the Power Requirement of the Working Motor
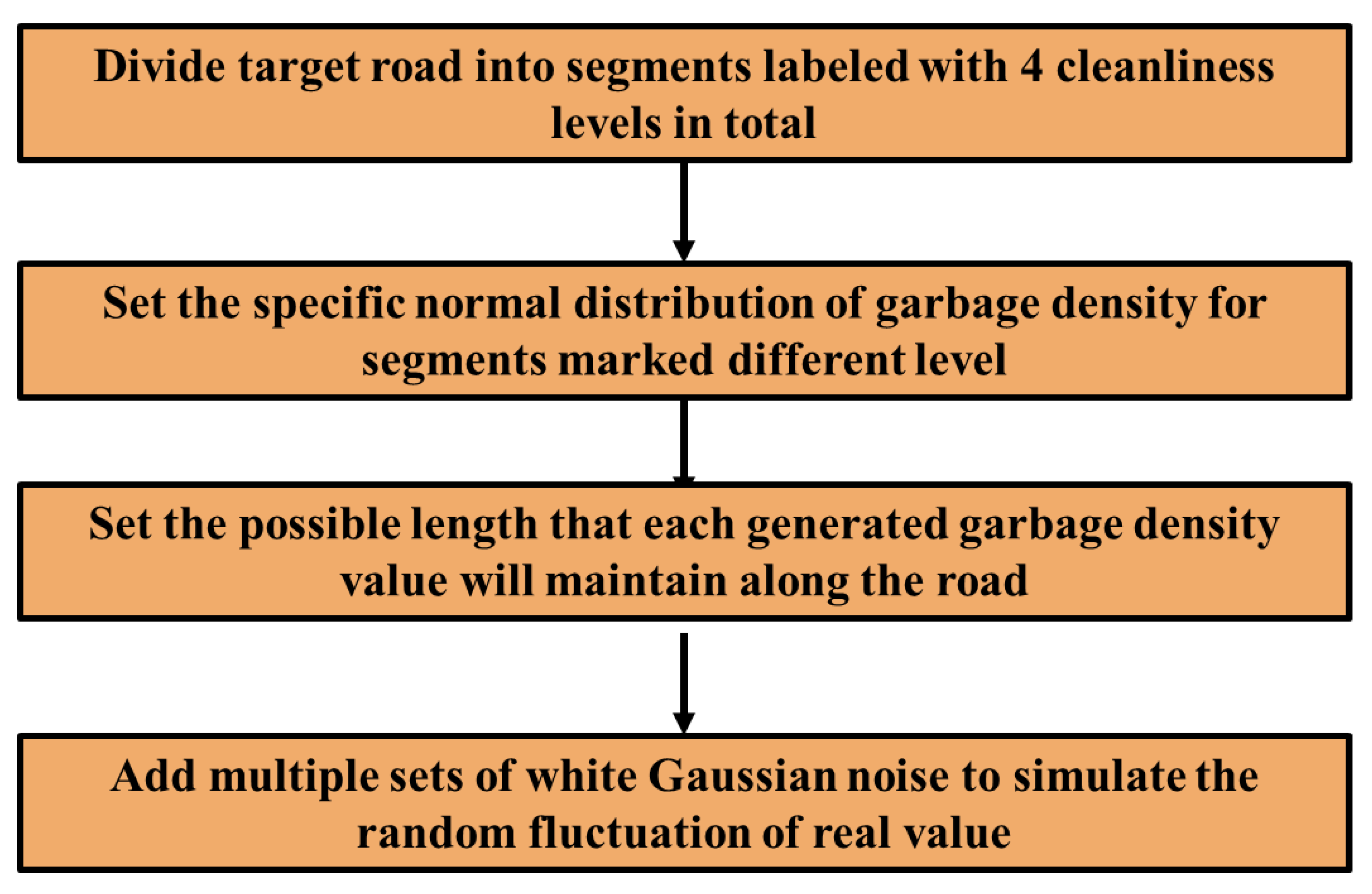
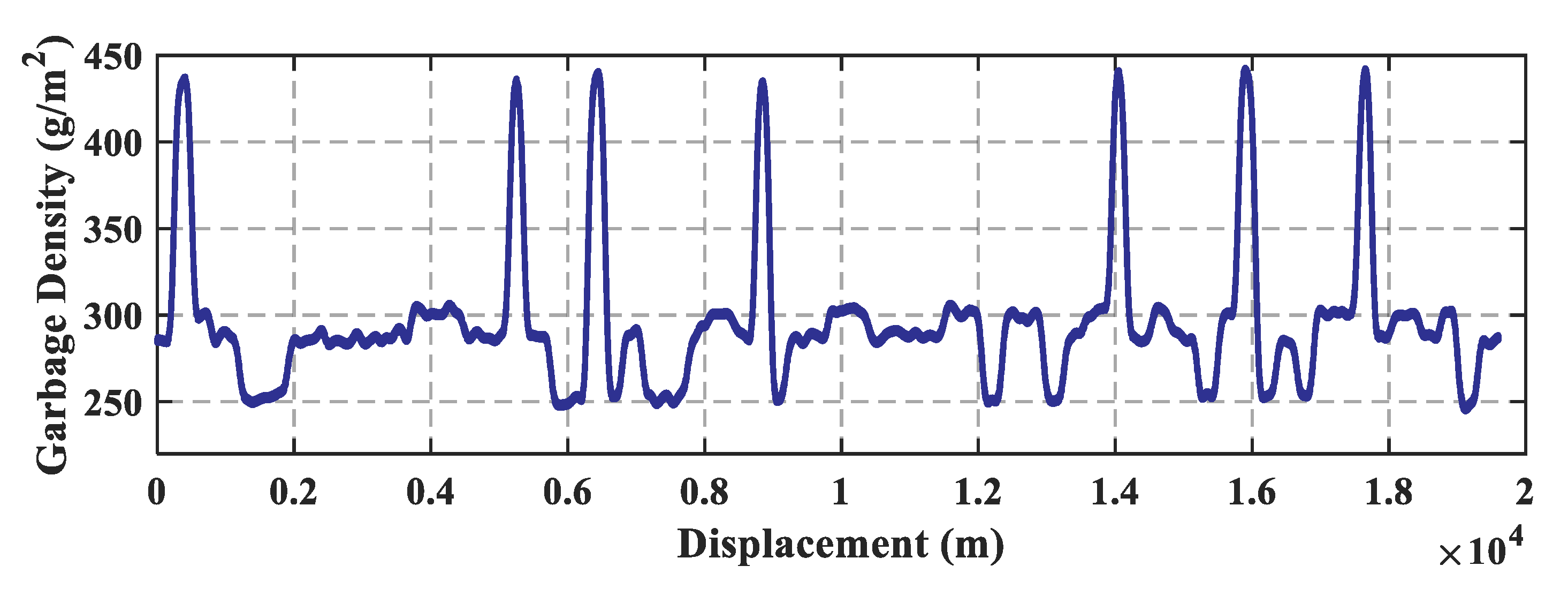
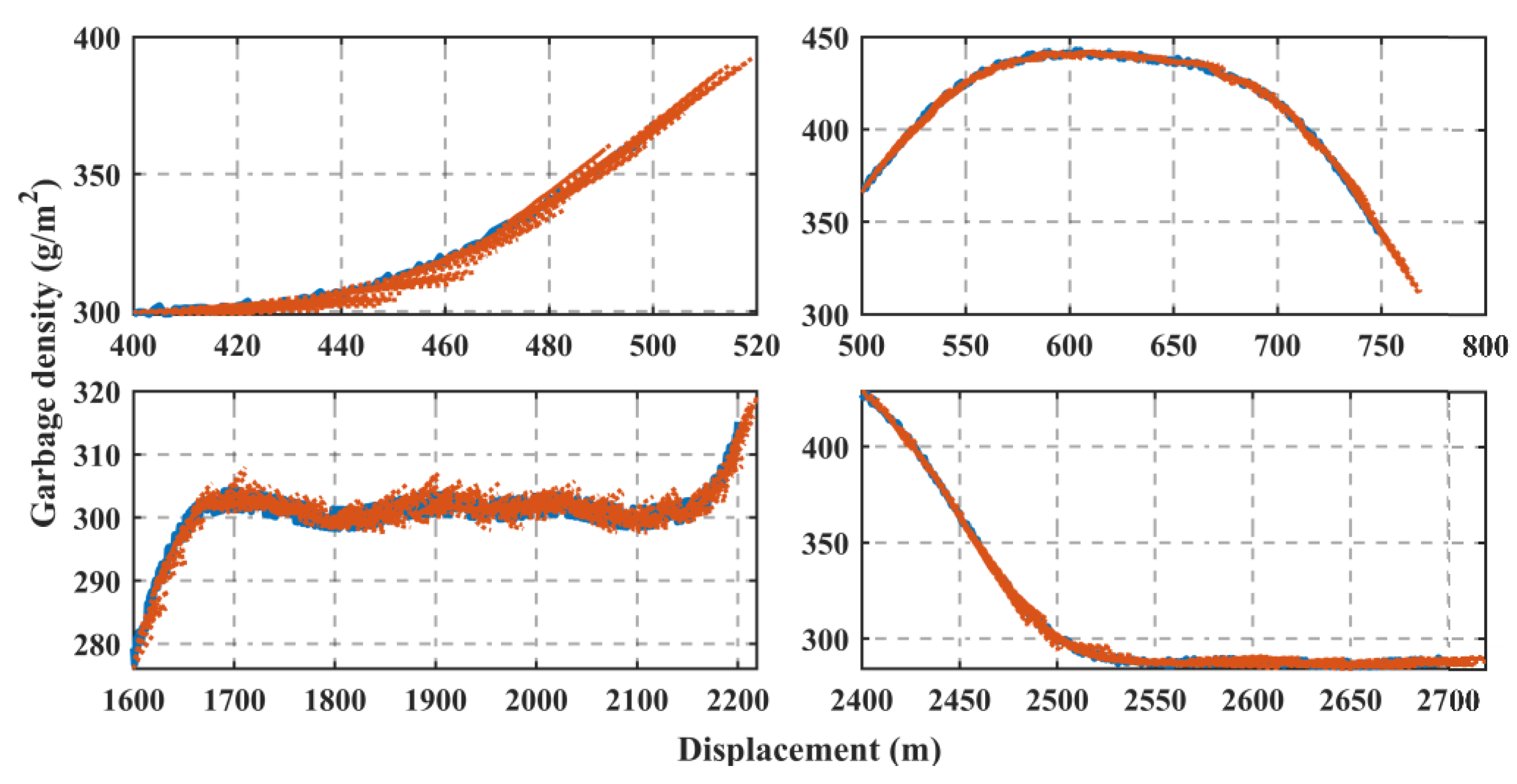
2.2.4. Modeling the Garbage Distribution on the Road Surface
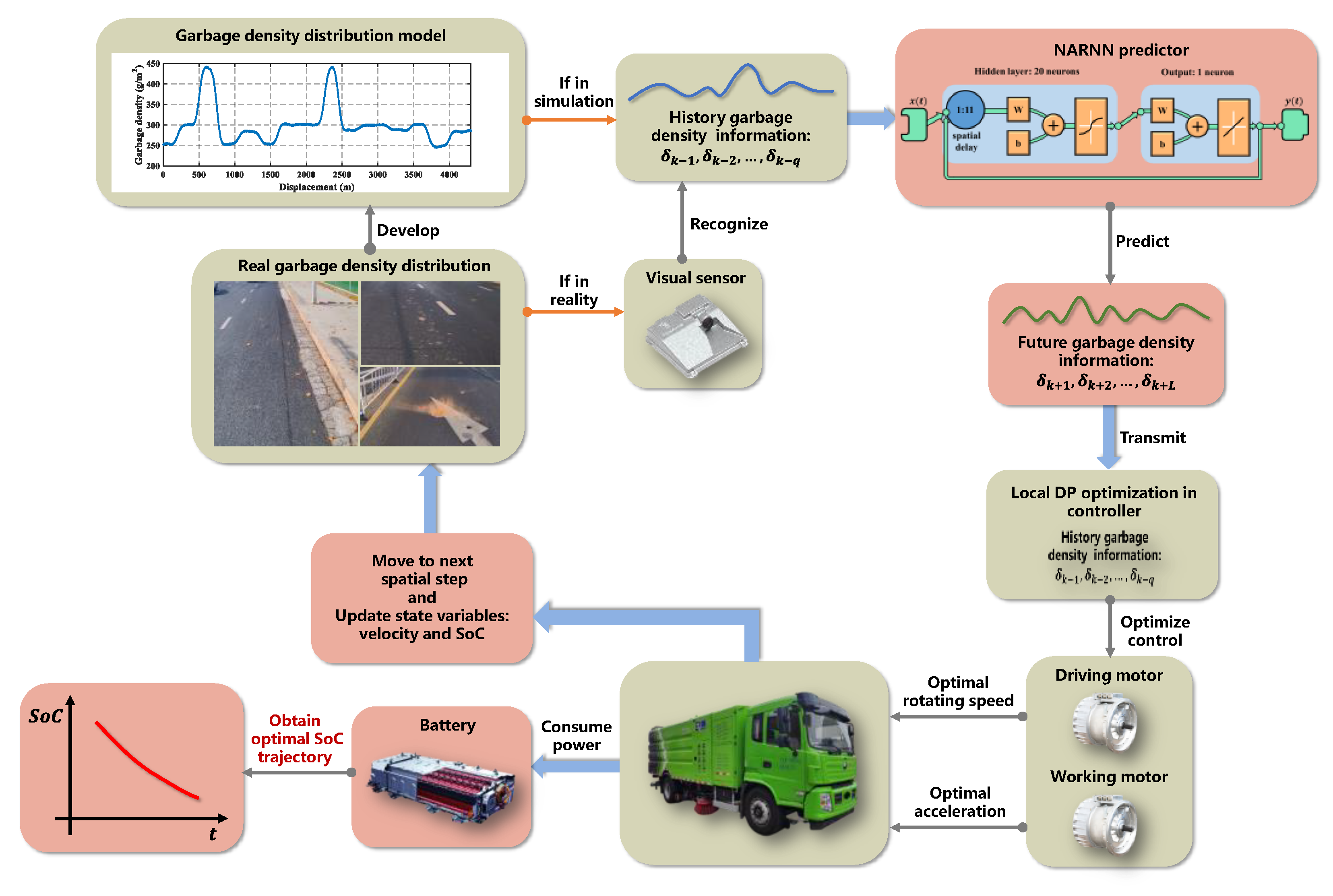
3. The Real-Time AMPC-Based EMS
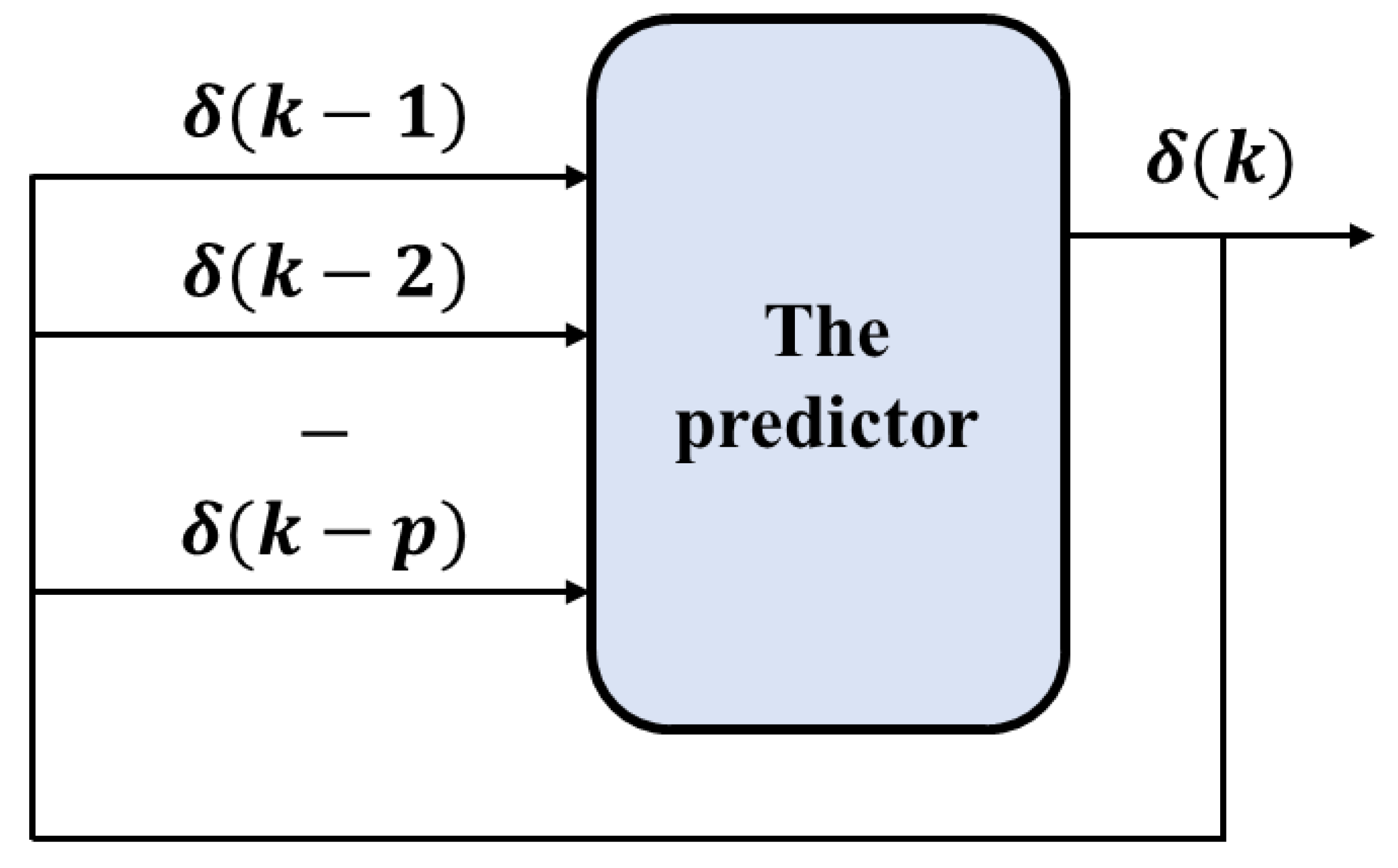
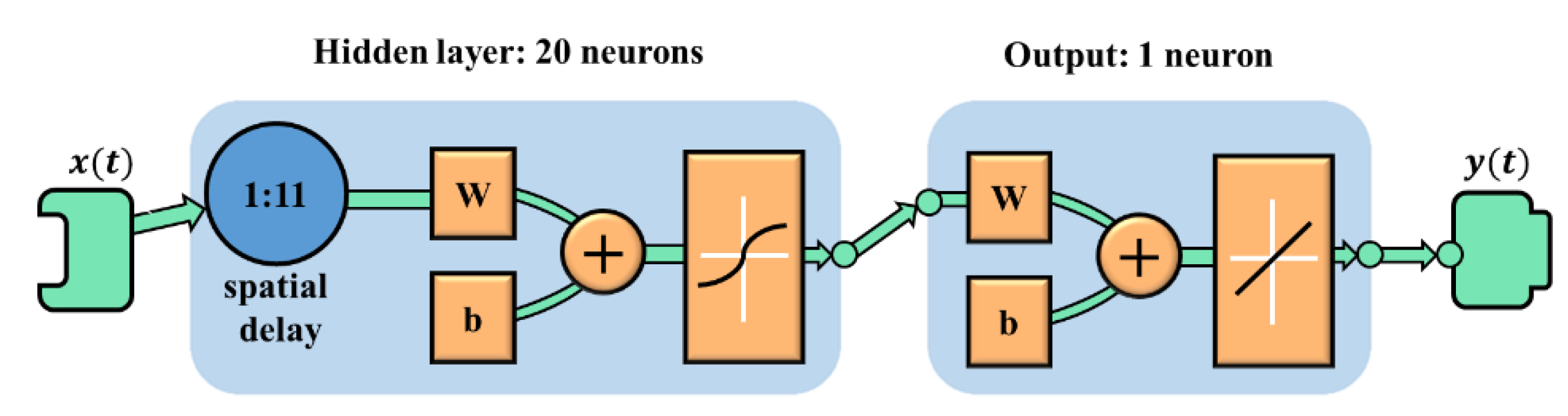
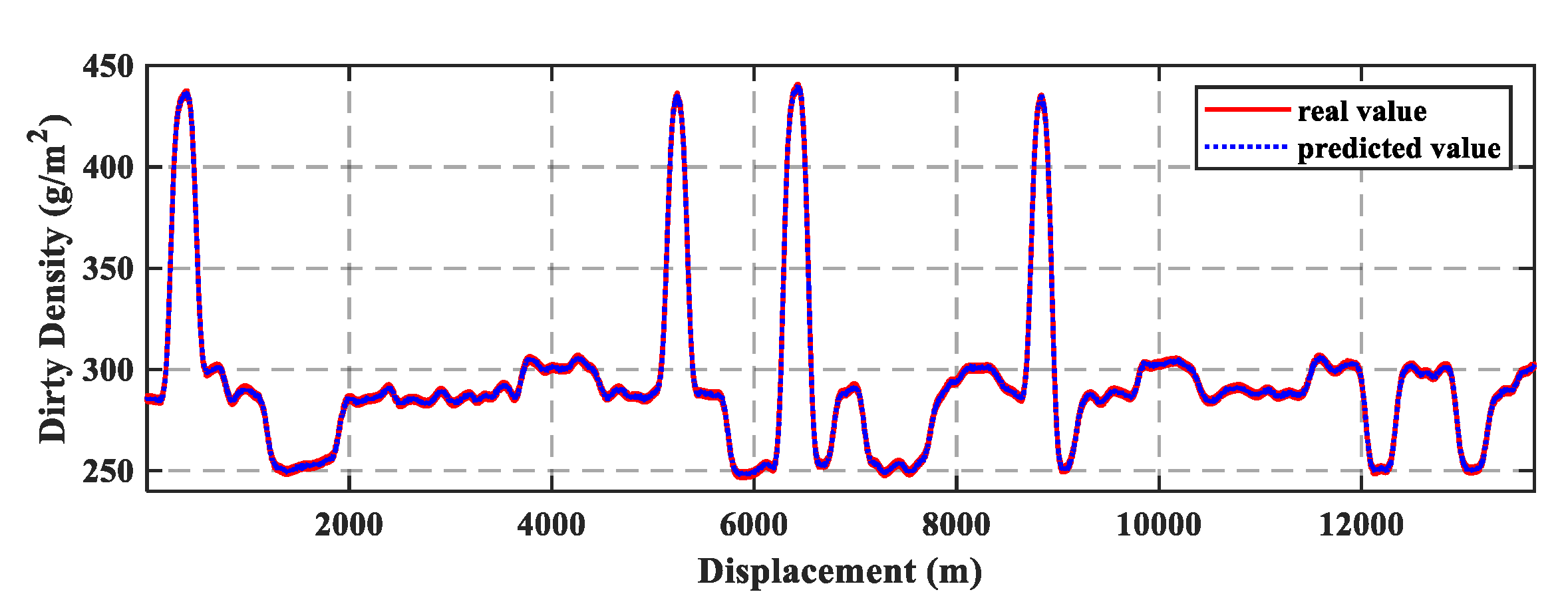
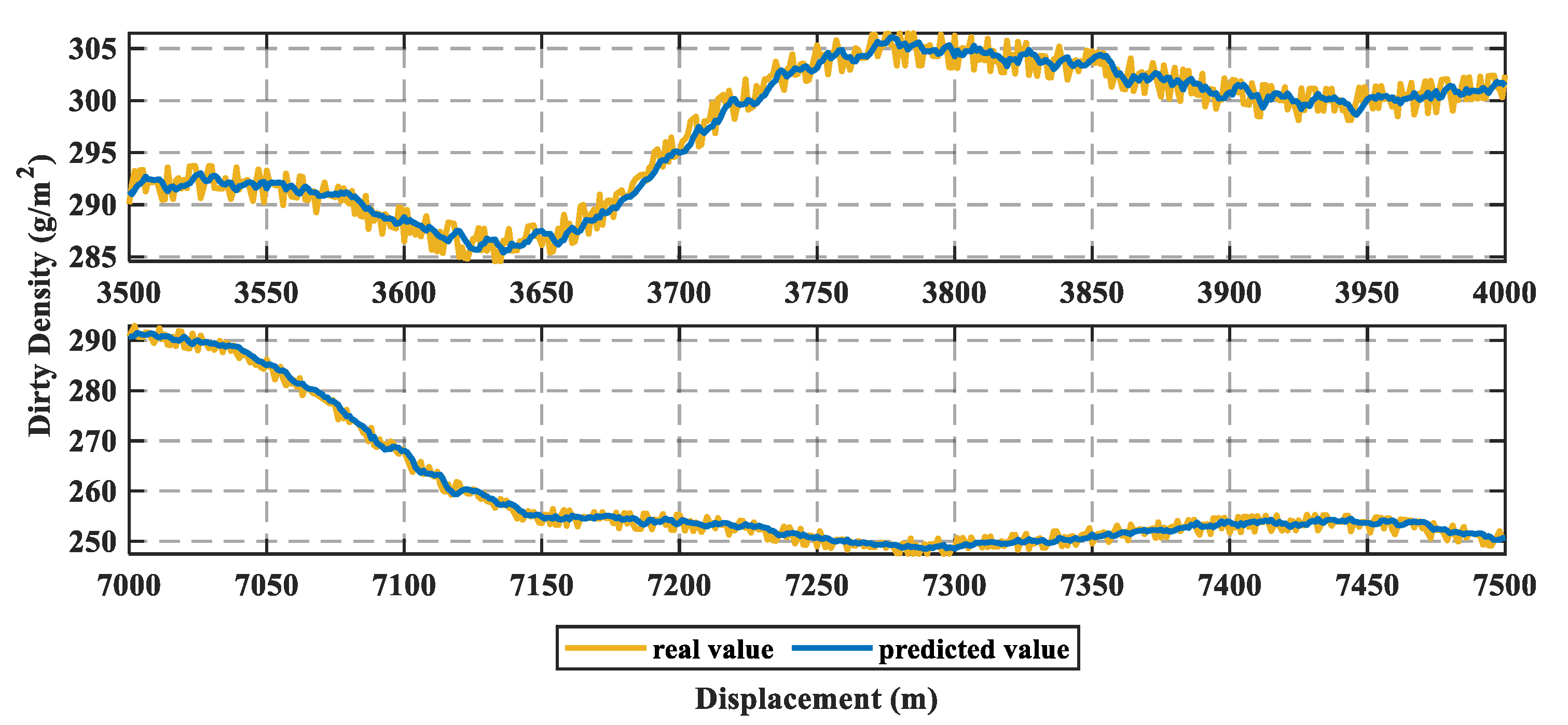
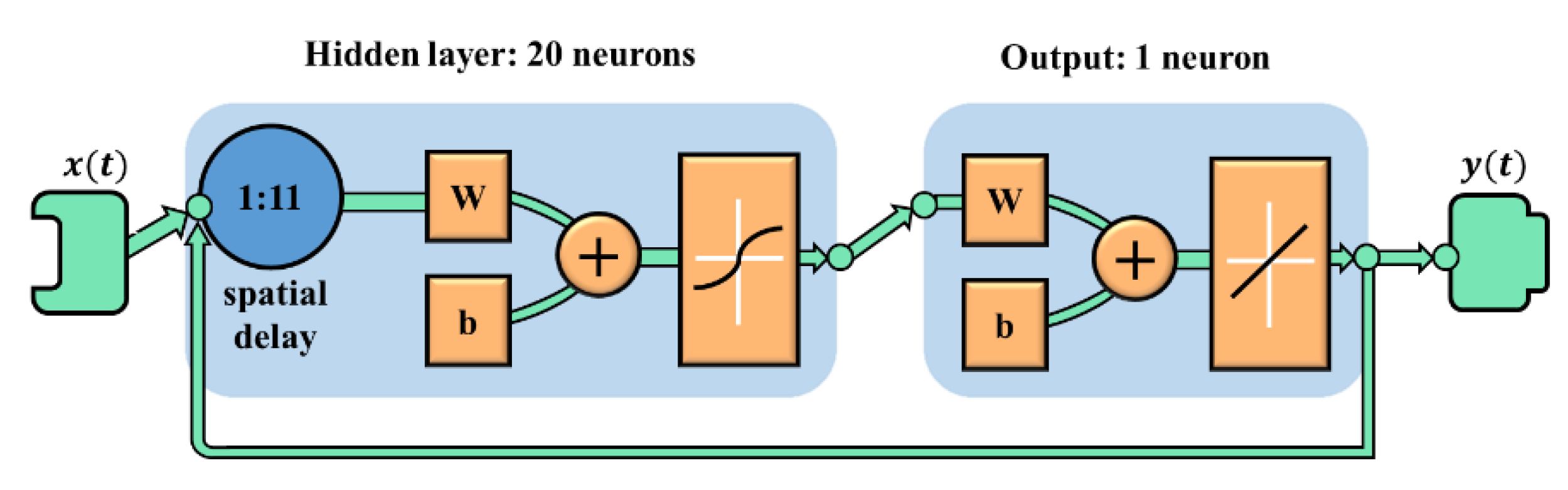
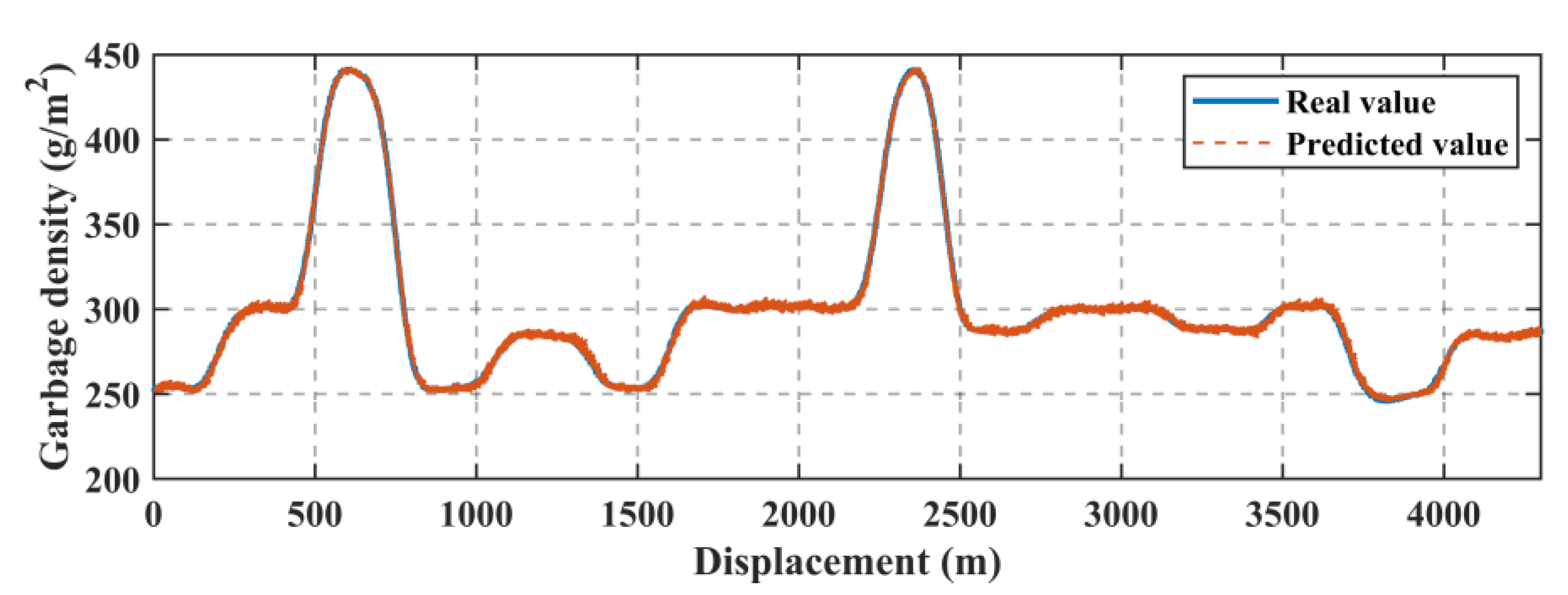
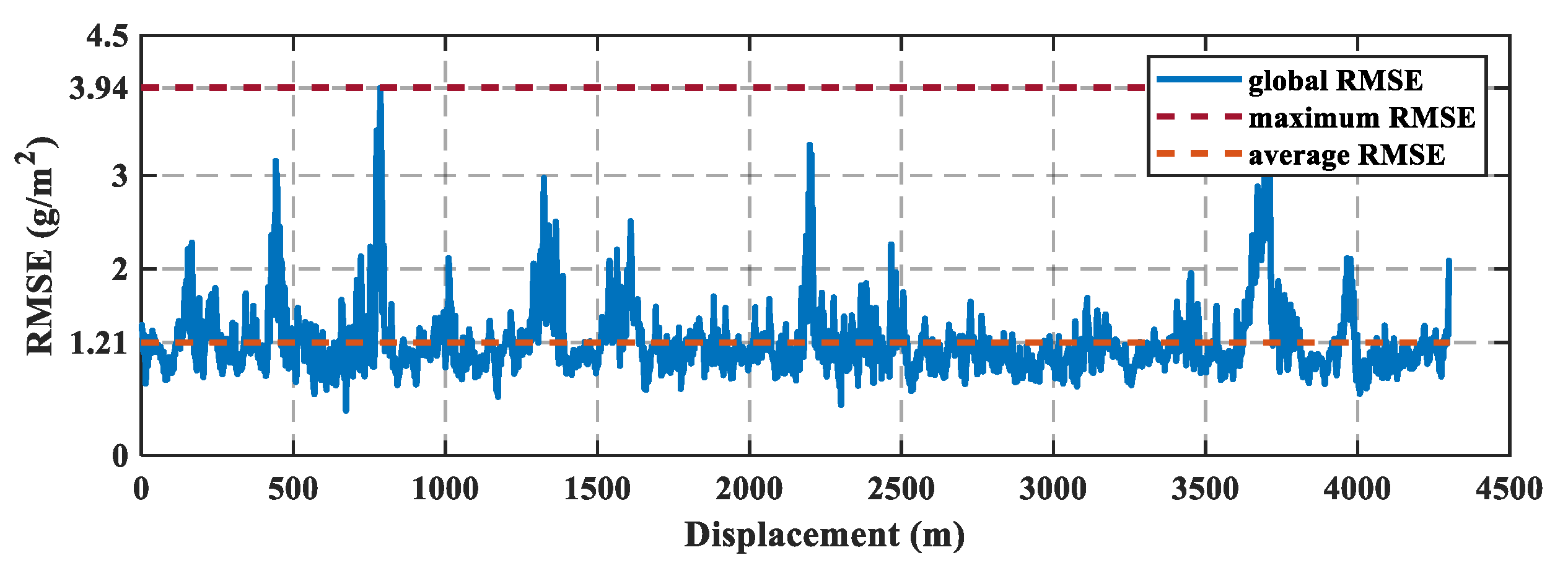
3.1. The Prediction Method
3.2. The Framework of AMPC-Based EMS
3.3. Other Existing EMSs
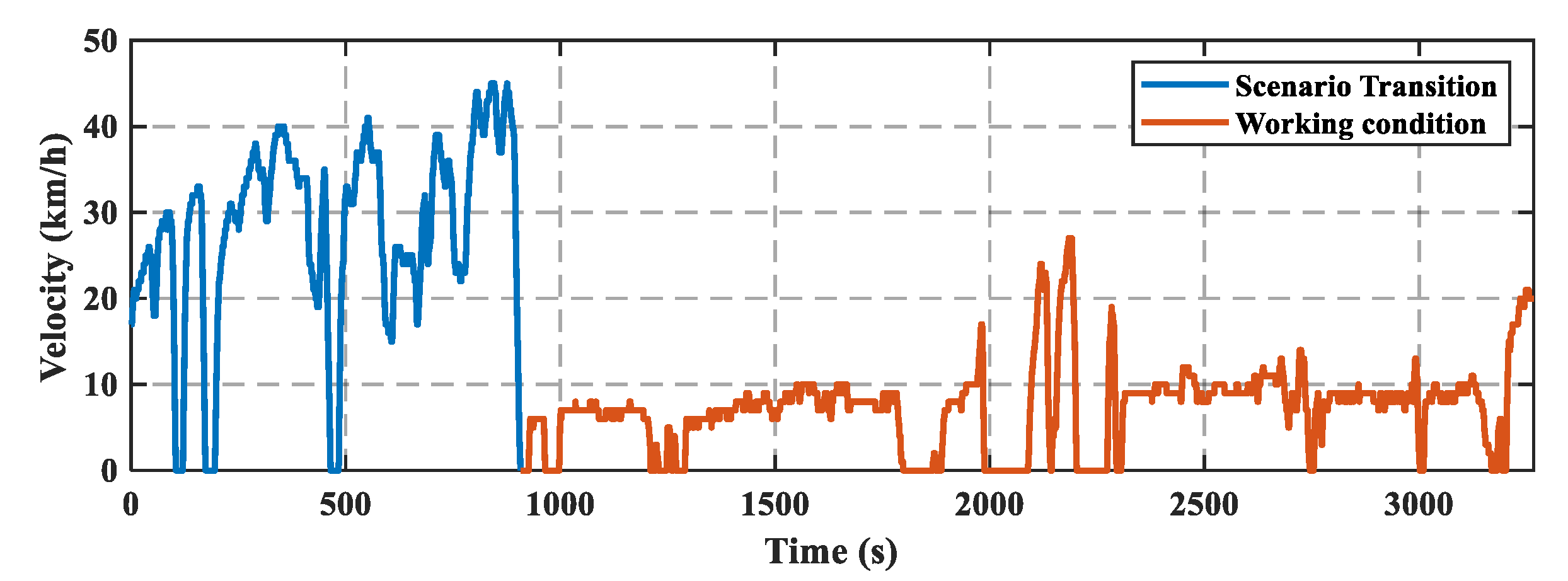
4. Results and Discussions
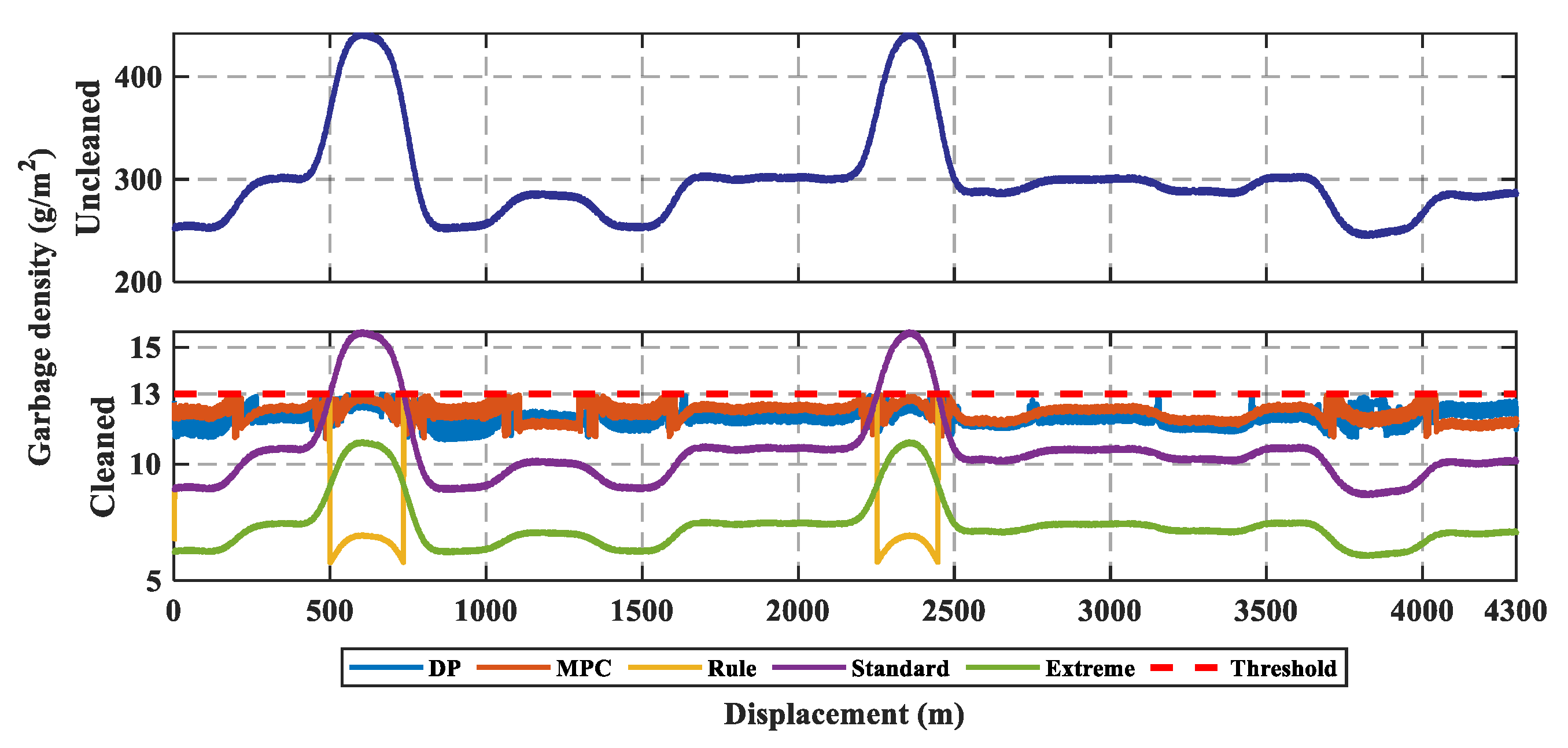
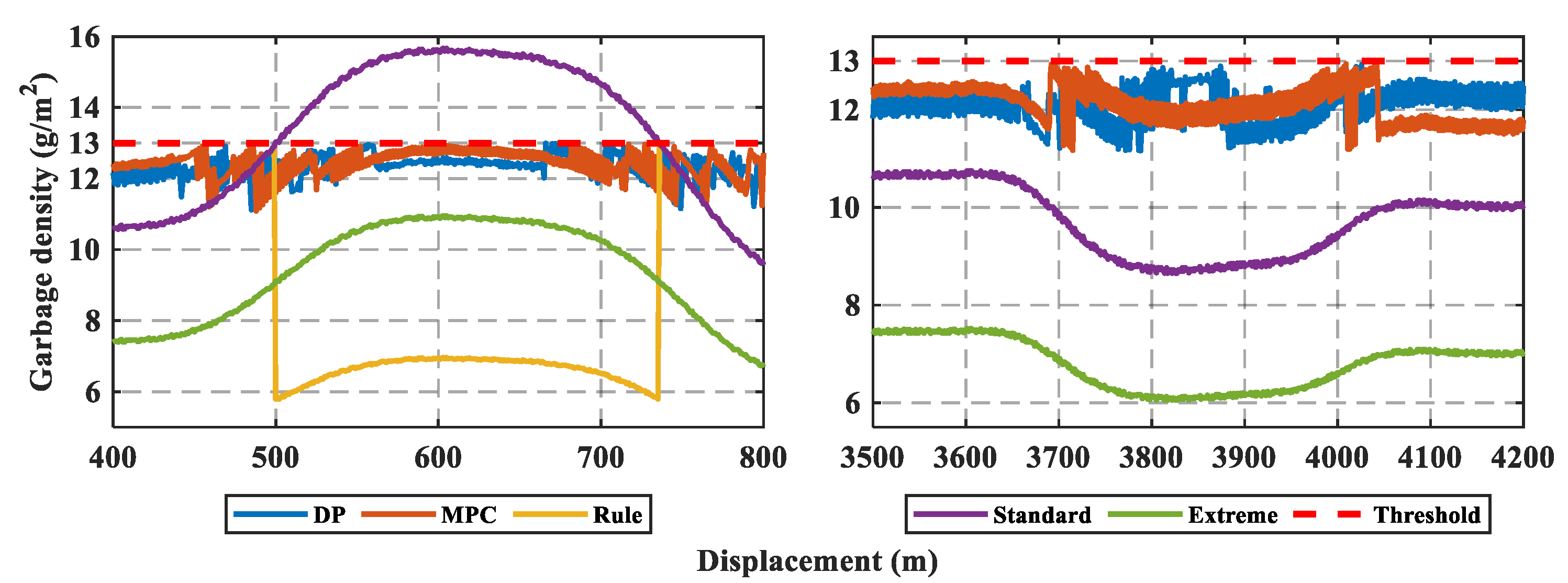
4.1. Comparison of the Garbage Residue
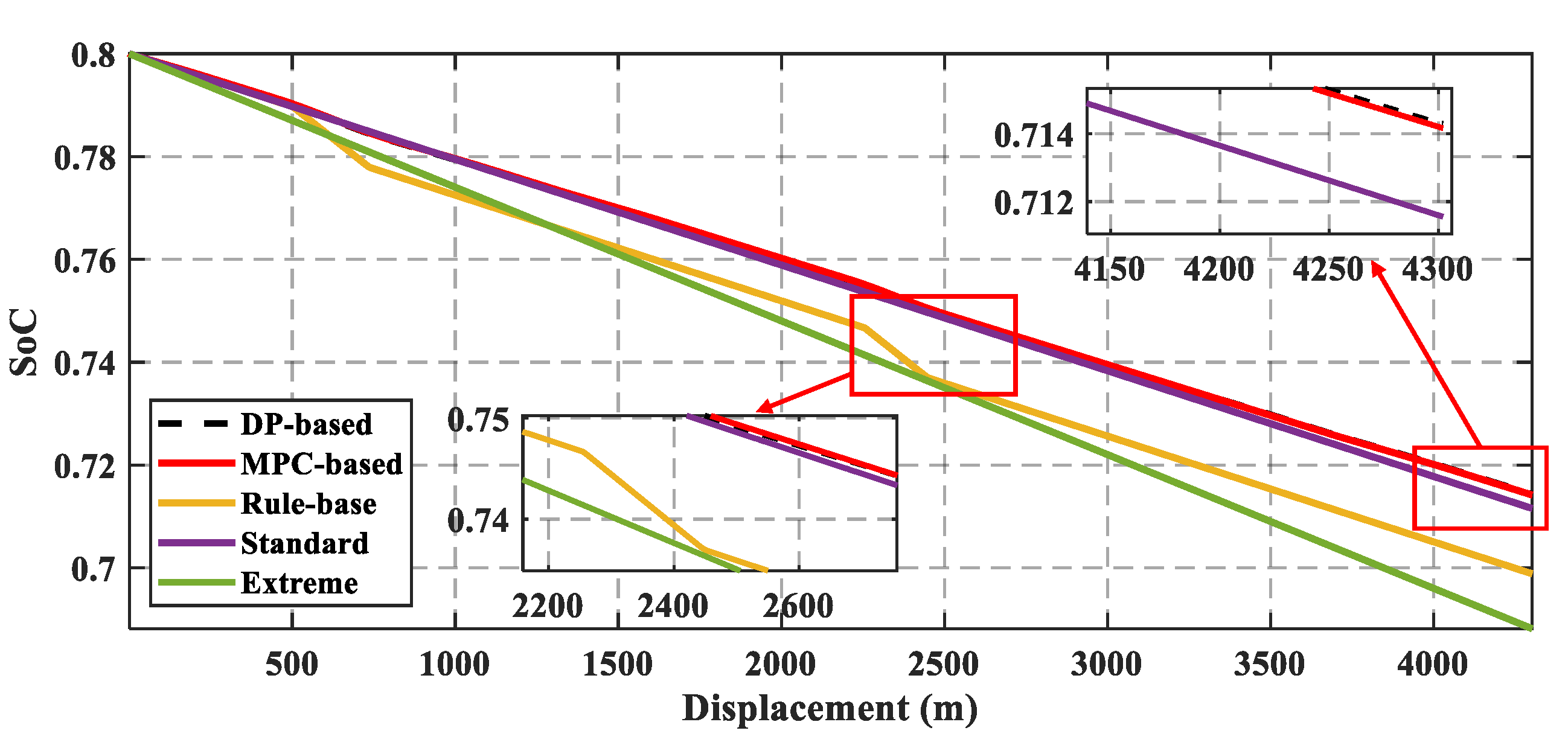
4.2. Comparison of the Electricity Consumption
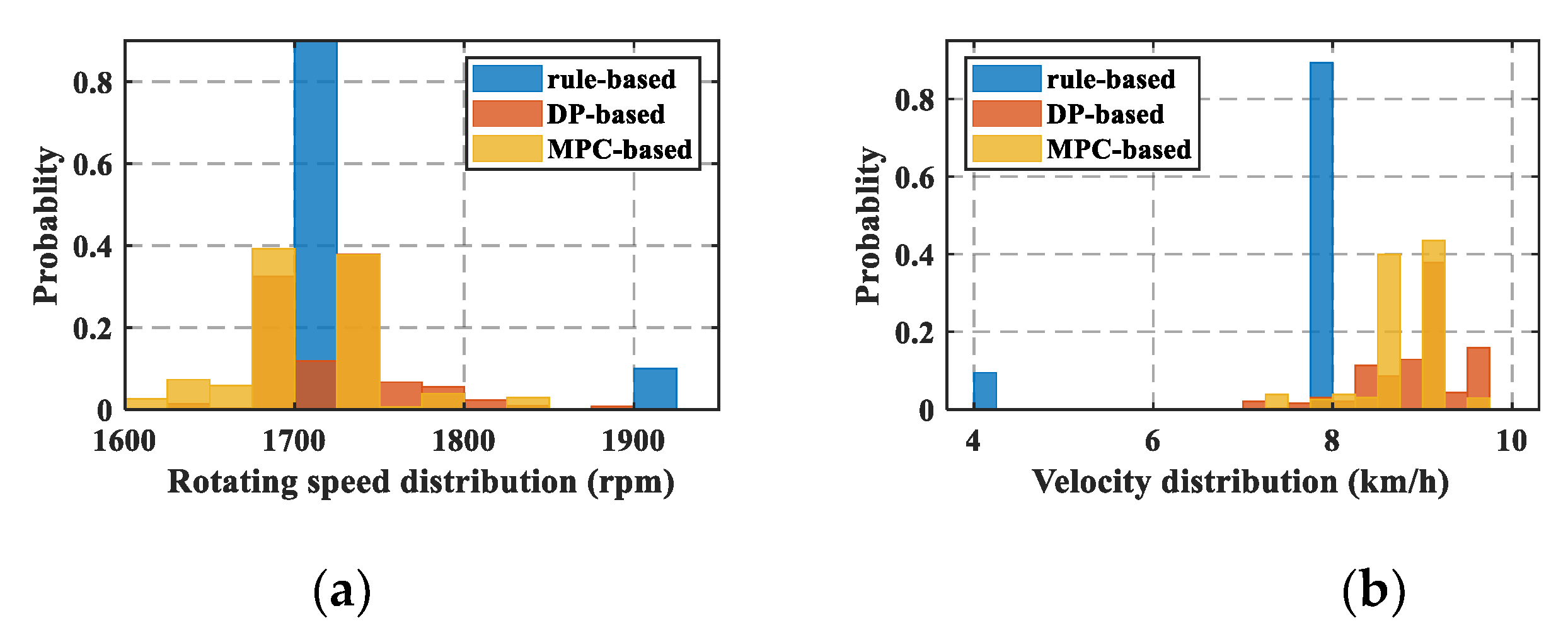
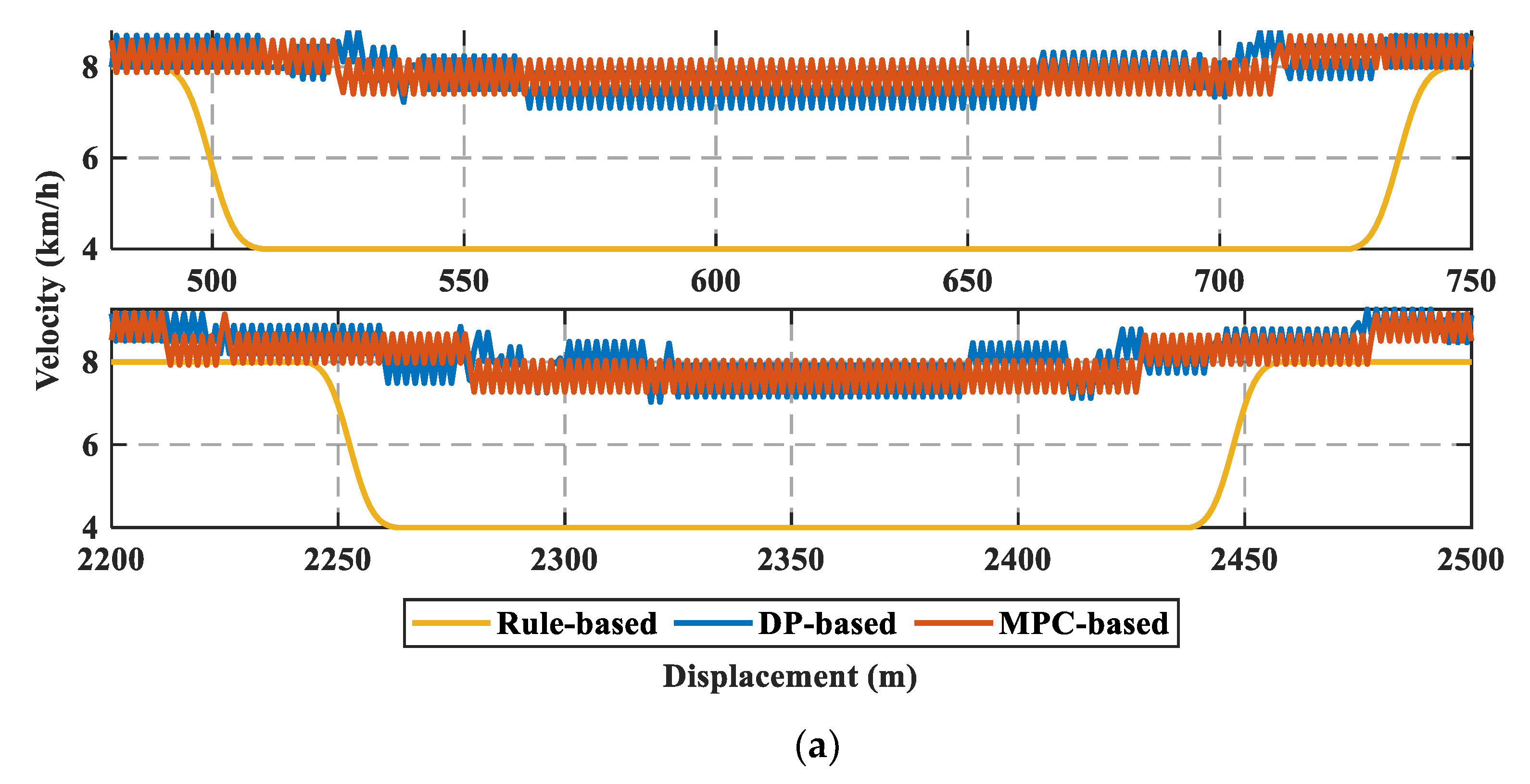
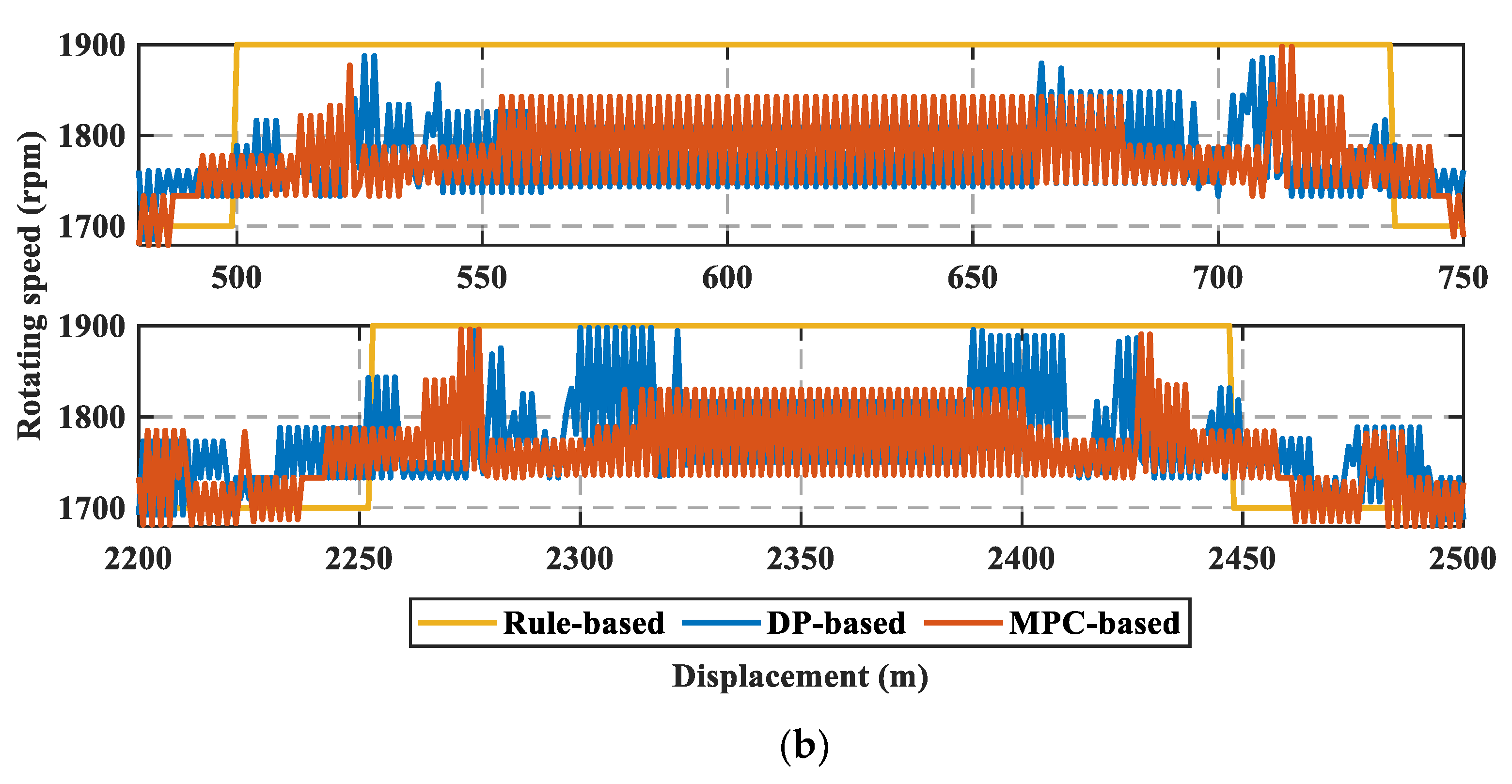
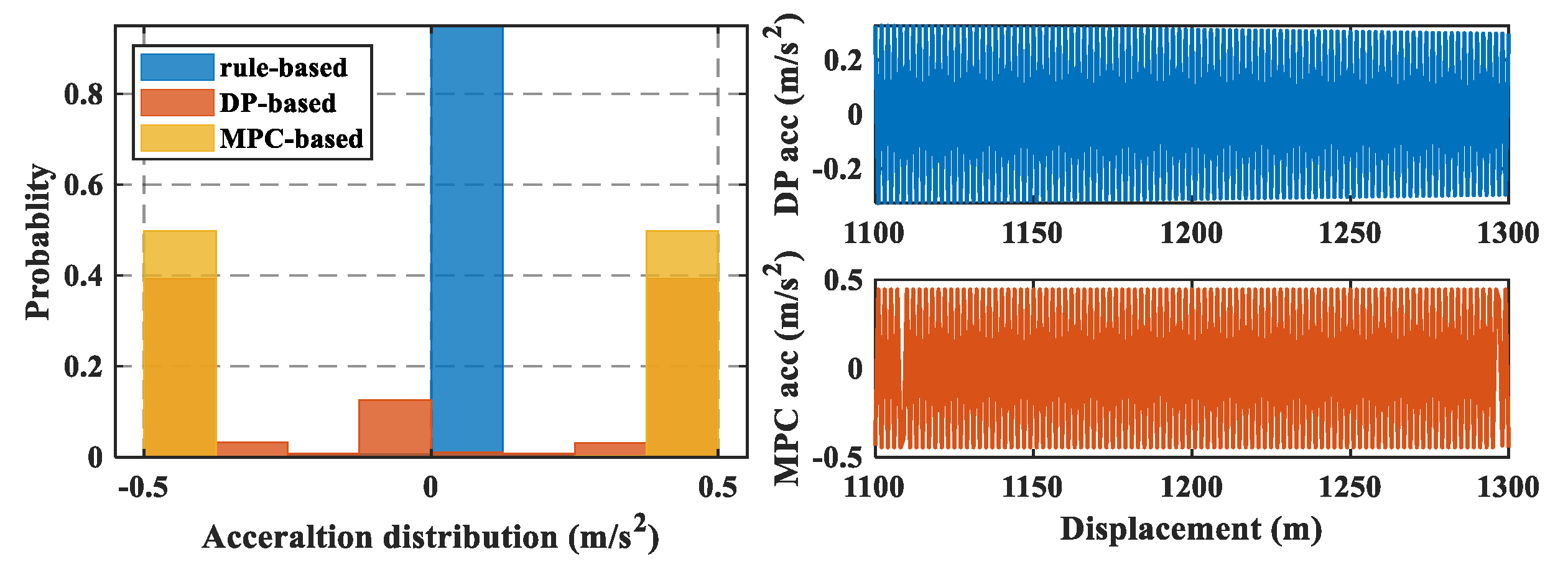
4.3. Comparison of Other Variables
5. Conclusions and Future Work
- Through the energy consumption analysis of principal devices onboard, it is concluded that the working motor and the driving motor were the main contributors, which took up to 89% of the total electricity consumption.
- Based on the practical observation of the target route, a universal garbage distribution modeling method can be concluded, which covers almost all scenarios marked level 1 to level 4.
- A clean task-oriented AMPC-based EMS using the NARNN as the predictor is proposed, and its real-time feasibility was verified. Compared with the rule-based EMS, it was substantiated that the AMPC-based EMS saved electricity by 15.53%, and well approximated the global optimization of the DP-based EMS. Additionally, the working time was lessened from 35 min to 29 min (17.14%) by the AMPC-based EMS.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yue, M.; Jemei, S.; Gouriveau, R.; Zerhouni, N. Review on health-conscious energy management strategies for fuel cell hybrid electric vehicles: Degradation models and strategies. Int. J. Hydrog. Energy 2019, 44, 6844–6861. [Google Scholar] [CrossRef]
- Geetha, A.; Subramani, C. A comprehensive review on energy management strategies of hybrid energy storage system for electric vehicles. Int. J. Energy Res. 2017, 41, 1817–1834. [Google Scholar] [CrossRef]
- Peng, J.; He, H.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2017, 185, 1633–1643. [Google Scholar] [CrossRef]
- Hofman, T.; Steinbuch, M.; van RM, D.; Serrarens, A. Rule-based energy management strategies for hybrid vehicles. Int. J. Electr. Hybrid Veh. 2007, 1, 71–94. [Google Scholar] [CrossRef]
- Banvait, H.; Anwar, S.; Chen, Y. A rule-based energy management strategy for plug-in hybrid electric vehicle (PHEV). In Proceedings of the 2009 American Control Conference, St. Louis, MI, USA, 10–12 June 2009. [Google Scholar]
- Wu, J.; Zou, Y.; Zhang, X.; Liu, T.; Kong, Z.; He, D. An online correction predictive EMS for a hybrid electric tracked vehicle based on dynamic programming and reinforcement learning. IEEE Access 2019, 7, 98252–98266. [Google Scholar] [CrossRef]
- Zhang, S.; Xiong, R. Adaptive energy management of a plug-in hybrid electric vehicle based on driving pattern recognition and dynamic programming. Appl. Energy 2015, 155, 68–78. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, T.; Sun, F.; Peng, H. Comparative study of dynamic programming and Pontryagin’s minimum principle on energy management for a parallel hybrid electric vehicle. Energies 2013, 6, 2305–2318. [Google Scholar] [CrossRef]
- Borhan, H.; Vahidi, A.; Phillips, A.M.; Kuang, M.; Kolmanovsky, I.V.; Cairano, S.D. MPC-based energy management of a power-split hybrid electric vehicle. IEEE Trans. Control Syst. Technol. 2011, 20, 593–603. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Khajepour, A.; He, H.; Ji, J. Model predictive control power management strategies for HEVs: A review. J. Power Sources 2017, 341, 91–106. [Google Scholar] [CrossRef]
- Guo, J.; He, H.; Sun, C. ARIMA-based road gradient and vehicle velocity prediction for hybrid electric vehicle energy management. IEEE Trans. Veh. Technol. 2019, 68, 5309–5320. [Google Scholar] [CrossRef]
- Zhang, Z.; He, H.; Guo, J.; Han, R. Velocity prediction and profile optimization based real-time energy management strategy for Plug-in hybrid electric buses. Appl. Energy 2020, 280, 116001. [Google Scholar] [CrossRef]
- Sun, C.; Hu, X.; Moura, S.; Sun, F. Comparison of velocity forecasting strategies for predictive control in HEVs. In Proceedings of the Dynamic Systems and Control Conference, San Antonio, TX, USA, 22–24 October 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Sun, C.; Hu, X.; Moura, S.J.; Sun, F. Velocity predictors for predictive energy management in hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2014, 23, 1197–1204. [Google Scholar]
- Xie, S.; He, H.; Peng, J. An energy management strategy based on stochastic model predictive control for plug-in hybrid electric buses. Appl. Energy 2017, 196, 279–288. [Google Scholar] [CrossRef]
- Lin, C.-C.; Peng, H.; Grizzle, J. A stochastic control strategy for hybrid electric vehicles. In Proceedings of the IEEE,2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar]
- Zhang, F.; Hu, X.; Langari, R.; Cao, D. Energy management strategies of connected HEVs and PHEVs: Recent progress and outlook. Prog. Energy Combust. Sci. 2019, 73, 235–256. [Google Scholar] [CrossRef]
- Lin, Y.; Tang, P.; Zhang, W.J. Artificial neural network modelling of driver handling behaviour in a driver-vehicle-environment system. Int. J. Veh. Des. 2005, 37, 24–45. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Golias, J.C.; Karlaftis, M.G. Short-term traffic forecasting: Overview of objectives and methods. Transp. Rev. 2004, 24, 533–557. [Google Scholar] [CrossRef]
- Park, J.; Chen, Z.; Kiliaris, L.; Kuang, M.L.; Masrur, M.A.; Phillips, A.M.; Murphey, Y.L. Intelligent vehicle power control based on machine learning of optimal control parameters and prediction of road type and traffic congestion. IEEE Trans. Veh. Technol. 2009, 58, 4741–4756. [Google Scholar] [CrossRef]
- Bodin, L.; Fagin, G.; Welebn, R.; Greenber, J. The design of a computerized sanitation vehicle routing and scheduling system for the town of Oyster Bay, New York. Comput. Oper. Res. 1989, 16, 45–54. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, R. Research on parameters matching of electric sanitation vehicle powertrain. In Proceedings of the 2013 International Conference on Mechanical and Automation Engineering, Jiujang, China, 21–23 July 2013. [Google Scholar]
- Gillespie, T.D. Fundamentals of Vehicle Dynamics; Society of Automotive Engineers: Warrendale, PA, USA, 1992; Volume 400. [Google Scholar]
- Bai, Y.; He, H.; Li, J.; Li, S.; Wang, Y.; Yang, Q. Battery anti-aging control for a plug-in hybrid electric vehicle with a hierarchical optimization energy management strategy. J. Clean. Prod. 2019, 237, 117841. [Google Scholar] [CrossRef]
- Li, L.; You, S.; Yang, C.; Yan, B.; Son, J.; Chen, Z. Driving-behavior-aware stochastic model predictive control for plug-in hybrid electric buses. Appl. Energy 2016, 162, 868–879. [Google Scholar] [CrossRef]
- Musardo, C.; Rizzoni, G.; Guezennec, Y.; Staccia, B. A-ECMS: An adaptive algorithm for hybrid electric vehicle energy management. Eur. J. Control 2005, 11, 509–524. [Google Scholar] [CrossRef]
- Benrhmach, G.; Namir, K.; Namir, A.; Bouyaghroumni, J. Nonlinear Autoregressive Neural Network and Extended Kalman Filters for Prediction of Financial Time Series. J. Appl. Math. 2020, 2020, 5057801. [Google Scholar] [CrossRef]
- Ruiz, L.G.B.; Cuéllar, M.P.; Calvo-Flores, M.D.; Jiménez, M.d.C.P. An application of non-linear autoregressive neural networks to predict energy consumption in public buildings. Energies 2016, 9, 684. [Google Scholar] [CrossRef]
- Cao, J.; Peng, J.; He, H. Research on model prediction energy management strategy with variable horizon. Energy Procedia 2017, 105, 3565–3570. [Google Scholar] [CrossRef]
- He, H.; Jia, H.; Sun, C.; Sun, F. Stochastic model predictive control of air conditioning system for electric vehicles: Sensitivity study, comparison, and improvement. IEEE Trans. Ind. Inform. 2018, 14, 4179–4189. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]

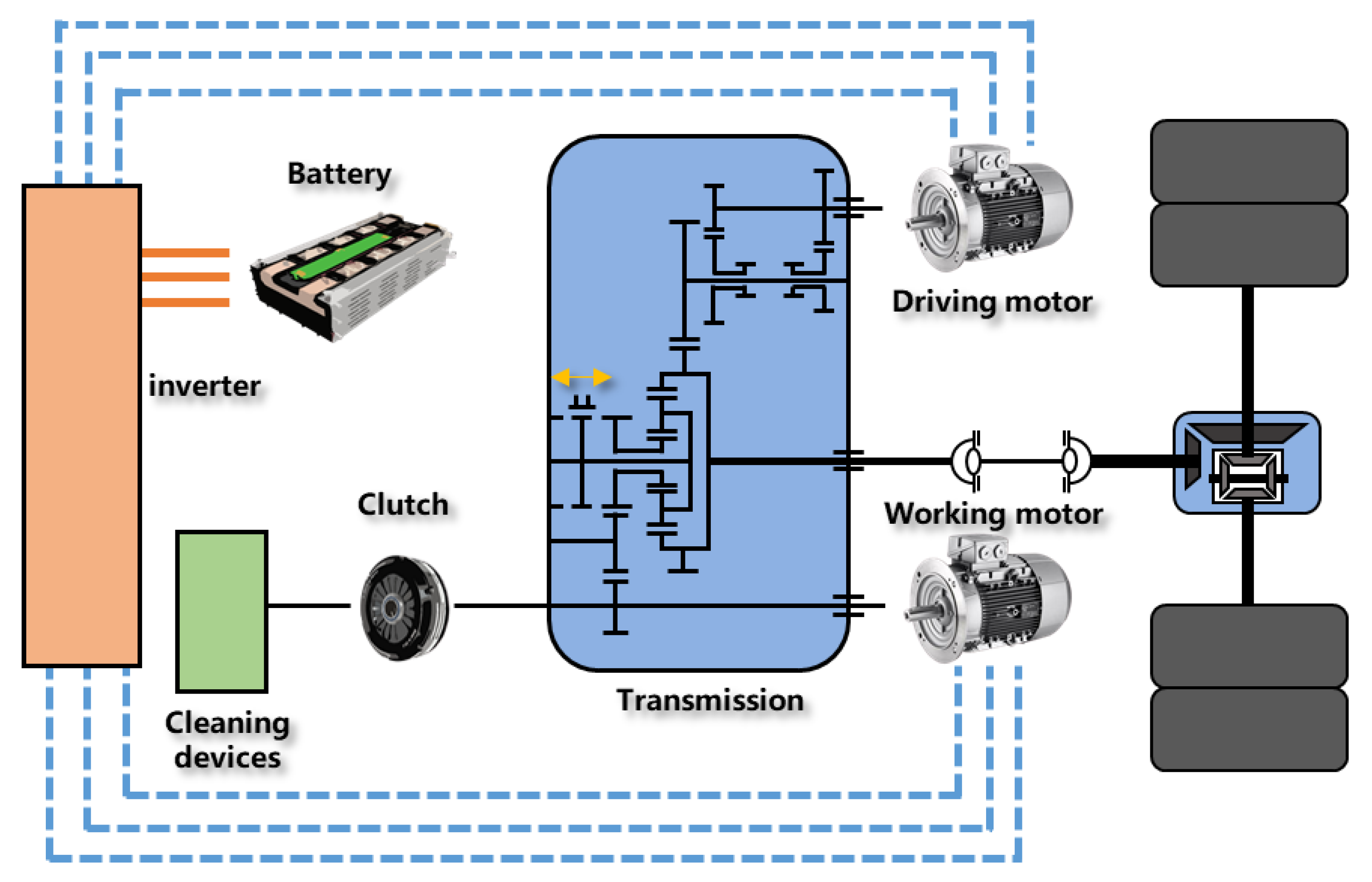
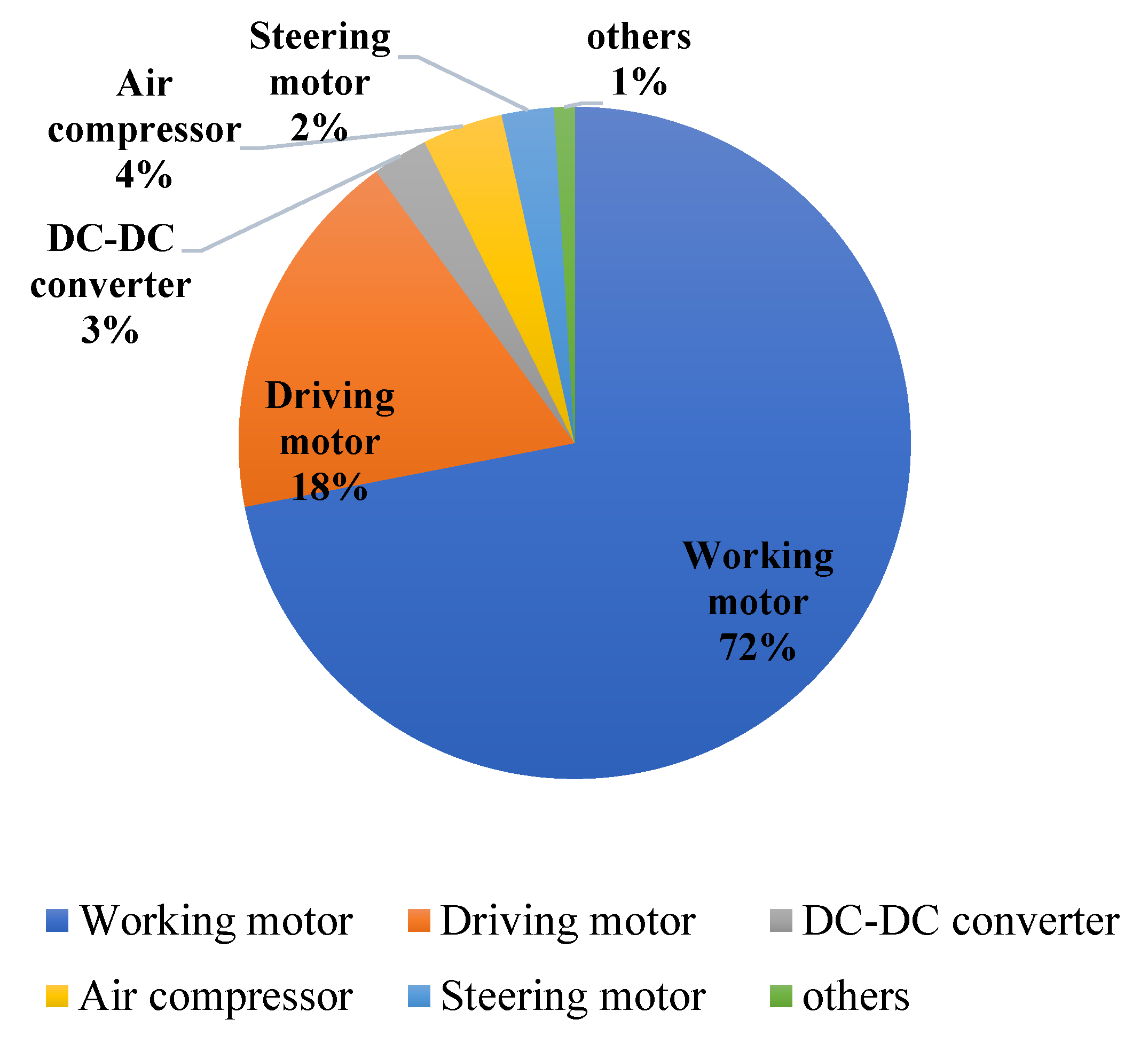
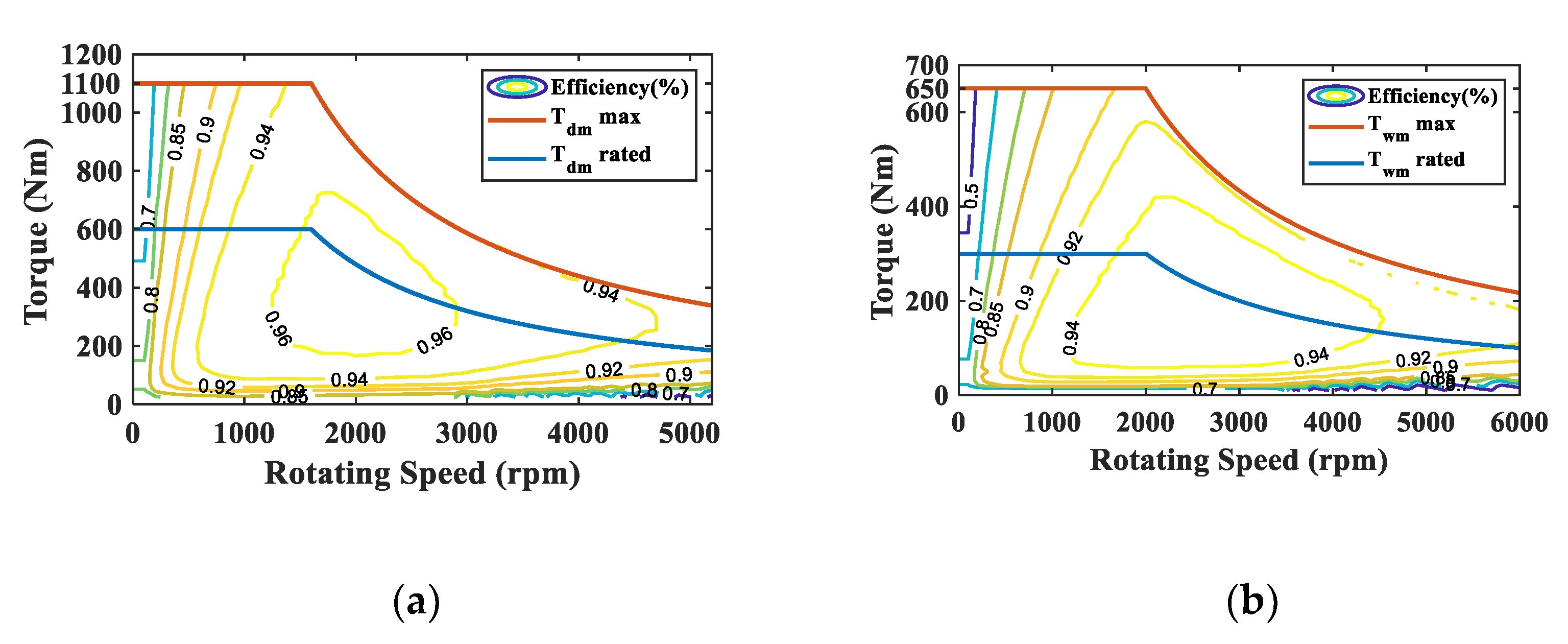
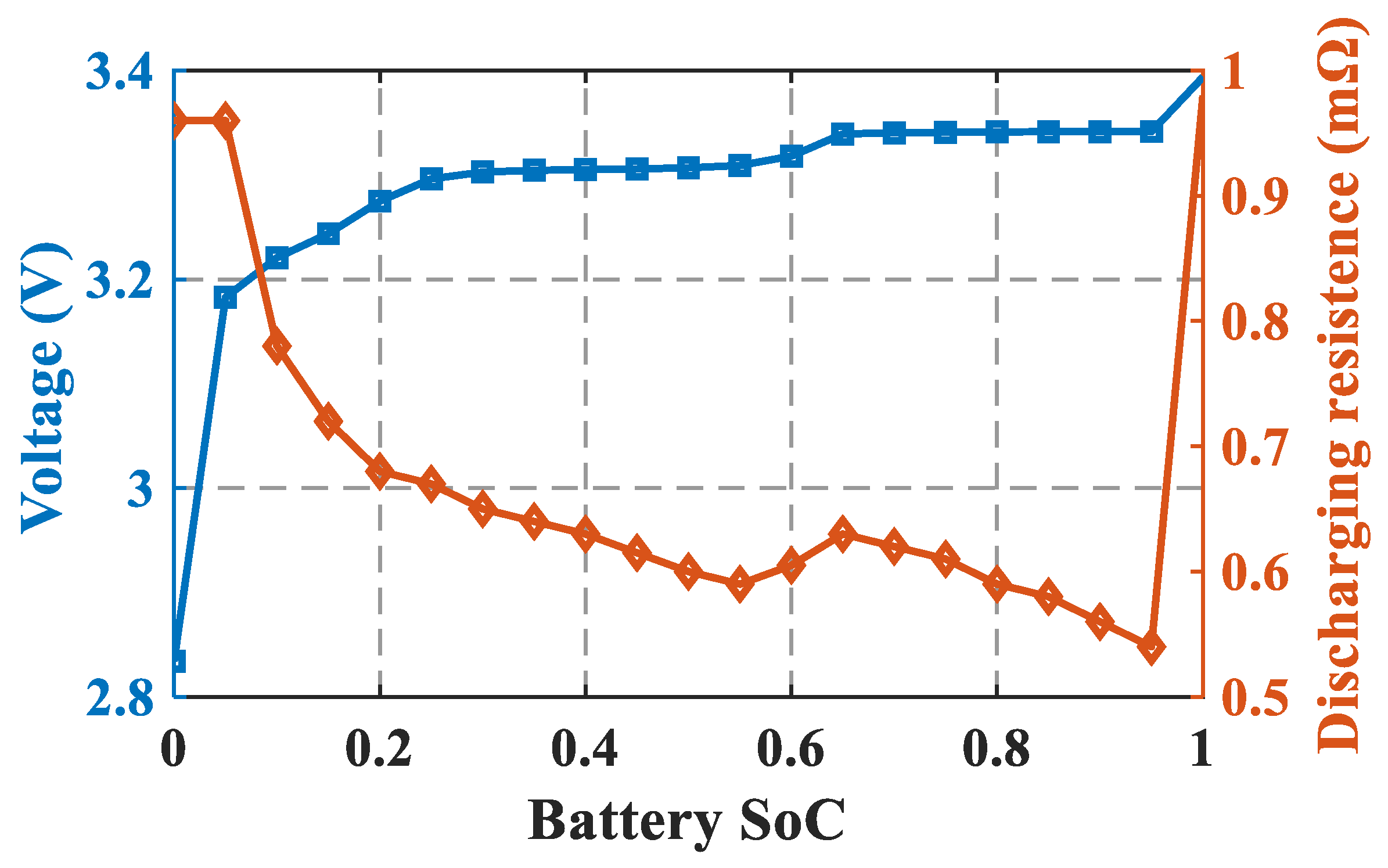

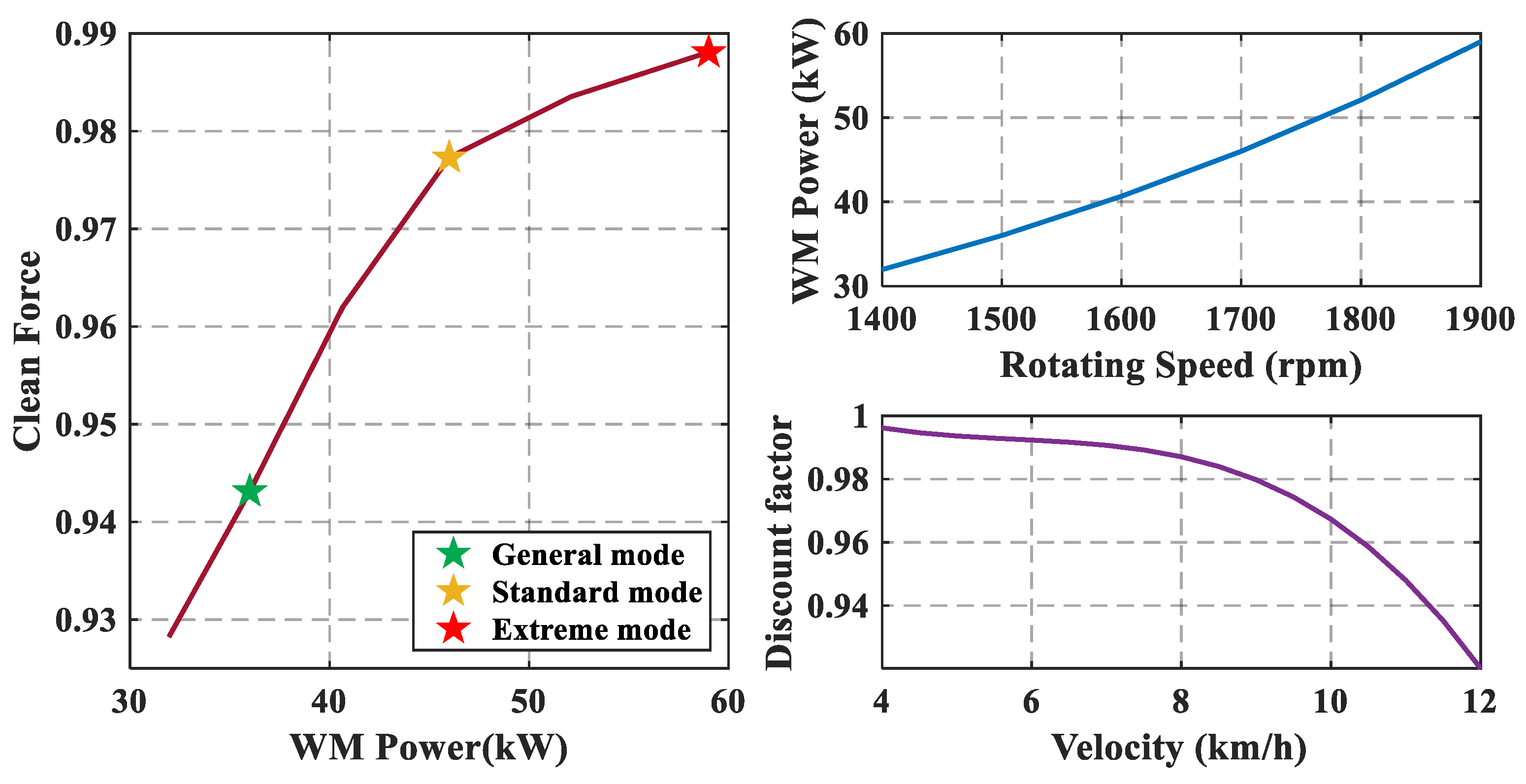


| Components | Description |
|---|---|
| Electric motor 1: Driving motor | Type: permanent magnet synchronous motor Rated/Maximum power: 100/184 kW Rated/Maximum speed: 1600/5200 rpm Rated/Peak torque: 600/1100 Nm |
| Electric motor 2: Working motor | Type: permanent magnet synchronous motor Rated/Maximum power: 63/125 kW Rated/Maximum speed: 2000/6000 rpm Rated/Peak torque: 300/650 Nm |
| Automated mechanical transmission | Gear ratio: [2.5, 1]; Average efficiency: 0.9 Final drive ratio: 4.88 × 2 (planet set ring ratio) |
| Battery | Nominal cell voltage: 3.2 V; Total cells: 384 Nominal voltage: 614.4 V; Capacity: 254 Ah |
| Vehicle | Mass: 12,000/18,000 Frontal area: 8; Air resistance coefficient: 0.55 Road resistance coefficient: 0.008; Tire radius: 0.506 m Rotational mass conversion factor: 1.1 |
| Mode Name | ||
|---|---|---|
| General mode | 1500 | 28 |
| Standard mode | 1700 | 39 |
| Extreme mode | 1900 | 54 |
| Working Mode | ||||
|---|---|---|---|---|
| General mode | 8 | 1500 | 200 g sands + 200 g rubbles | 97.3 |
| Standard mode | 8 | 1700 | 400 g sands + 200 g rubbles | 98.5 |
| Extreme mode | 8 | 1900 | 600 g sands + 200 g rubbles | 99 |
| Maximum ability test | 4 | 1900 | 1500 g sands + 200 g rubbles | 97.1 |
| Name | Value |
|---|---|
| Hidden layer | 1 |
| Neurons in the hidden layer | 20 |
| Dependent past value/Time delay | 11 |
| Length of prediction zone | 20/10 (only regional) |
| Object Name | Standard Deviation | Mean | Maximum | Minimum |
|---|---|---|---|---|
| Uncleaned garbage | 45.569 | 299.09 | 442.83 | 244.52 |
| Standard mode | 1.612 | 10.58 | 15.67 | 8.65 |
| Extreme mode | 1.127 | 7.40 | 10.96 | 6.05 |
| Rule-based strategy | 1.284 | 9.76 | 13 | 5.79 |
| DP based strategy | 0.383 | 12.01 | 12.99 | 11.05 |
| AMPC based strategy | 0.359 | 12.21 | 12.98 | 11.09 |
| Strategy | ||
|---|---|---|
| Rule-based | 32.44 | - |
| DP | 27.40 | +15.43 |
| Adaptive-AMPC | 27.43 | +15.53 |
| Fixed standard mode | 28.38 | +12.50 |
| Fixed extreme mode | 35.74 | −10.19 |
| Strategy | ||
|---|---|---|
| Rule-based | 35.4 | - |
| DP-based | 29.0 | 18.1 |
| AMPC-based | 29.5 | 16.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; He, H.; Li, J.; Bai, Y.; Chang, Y.; Yan, B. Adaptive MPC Based Real-Time Energy Management Strategy of the Electric Sanitation Vehicles. Appl. Sci. 2021, 11, 498. https://doi.org/10.3390/app11020498
Wang H, He H, Li J, Bai Y, Chang Y, Yan B. Adaptive MPC Based Real-Time Energy Management Strategy of the Electric Sanitation Vehicles. Applied Sciences. 2021; 11(2):498. https://doi.org/10.3390/app11020498
Chicago/Turabian StyleWang, Hao, Hongwen He, Jianwei Li, Yunfei Bai, Yuhua Chang, and Beizhan Yan. 2021. "Adaptive MPC Based Real-Time Energy Management Strategy of the Electric Sanitation Vehicles" Applied Sciences 11, no. 2: 498. https://doi.org/10.3390/app11020498
APA StyleWang, H., He, H., Li, J., Bai, Y., Chang, Y., & Yan, B. (2021). Adaptive MPC Based Real-Time Energy Management Strategy of the Electric Sanitation Vehicles. Applied Sciences, 11(2), 498. https://doi.org/10.3390/app11020498








