Deep Representation of a Normal Map for Screen-Space Fluid Rendering
Abstract
:1. Introduction
- We propose a cGAN-based filter to improve the results of screen-space fluid rendering effectively.
- We propose a novel loss term to encourage clear refinement of the normal map.
- Because we constructed a normal map dataset for different types of fluid simulation, the experimental results generated by the deep normal map representation demonstrated the generality of our method and its efficient applicability to arbitrary fluid scenes.
2. Related Work
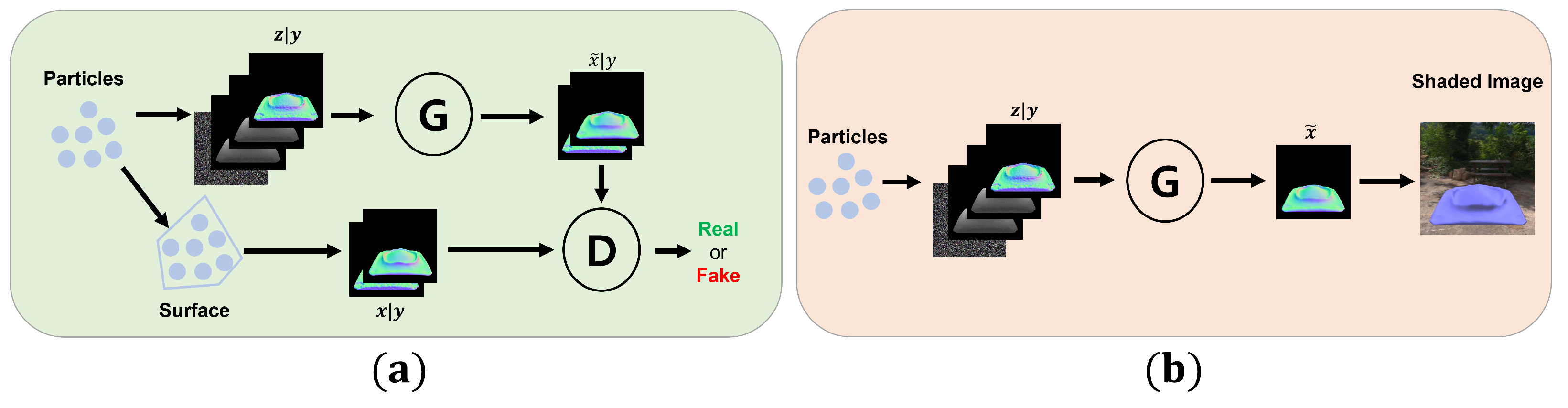
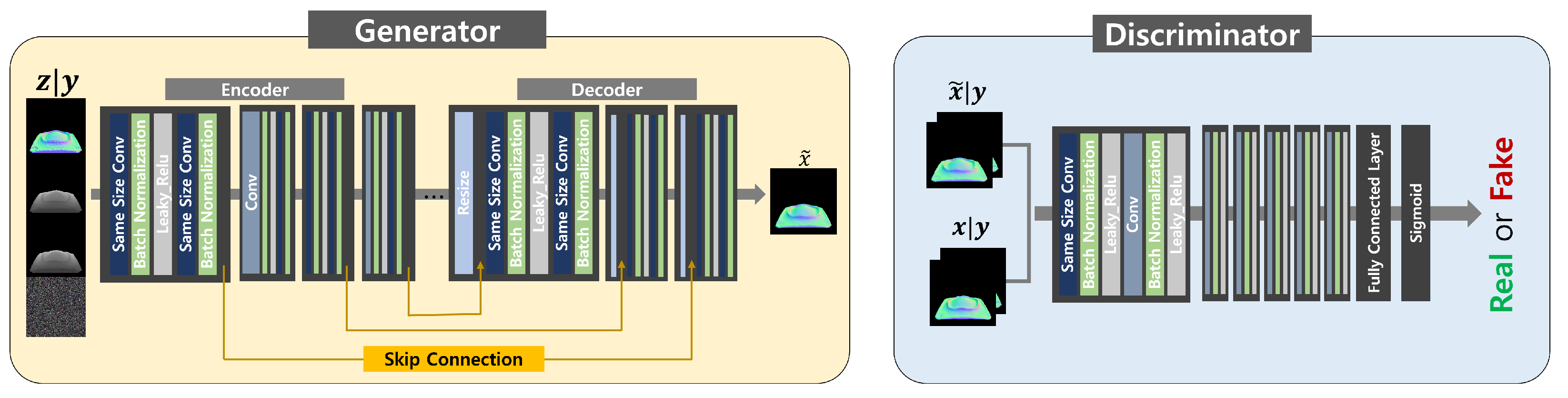
3. Deep Normal Map Representation with cGANs
3.1. Conditional Generative Adversarial Networks
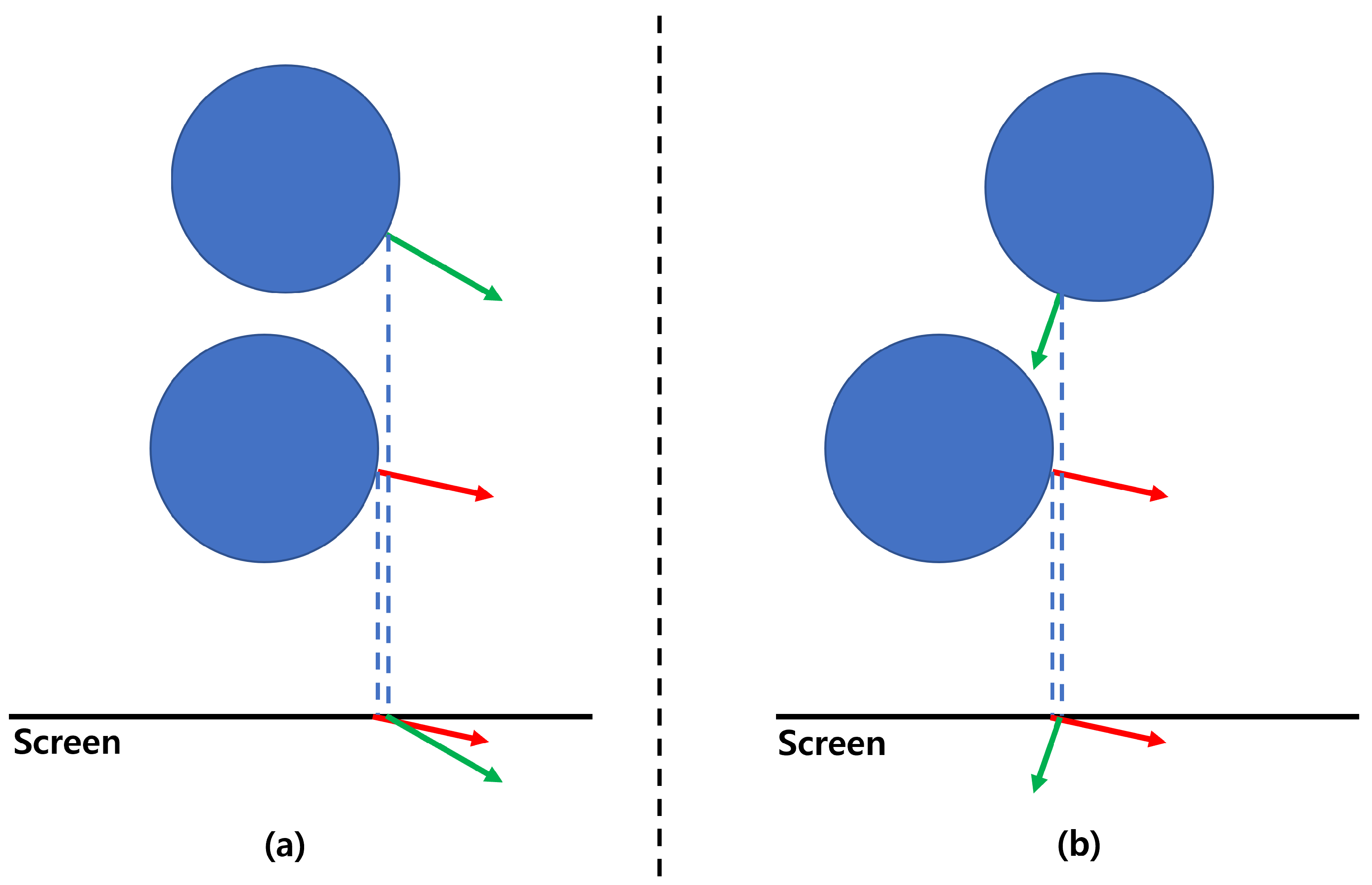
3.2. Normal Constraint Loss
3.3. Rendering
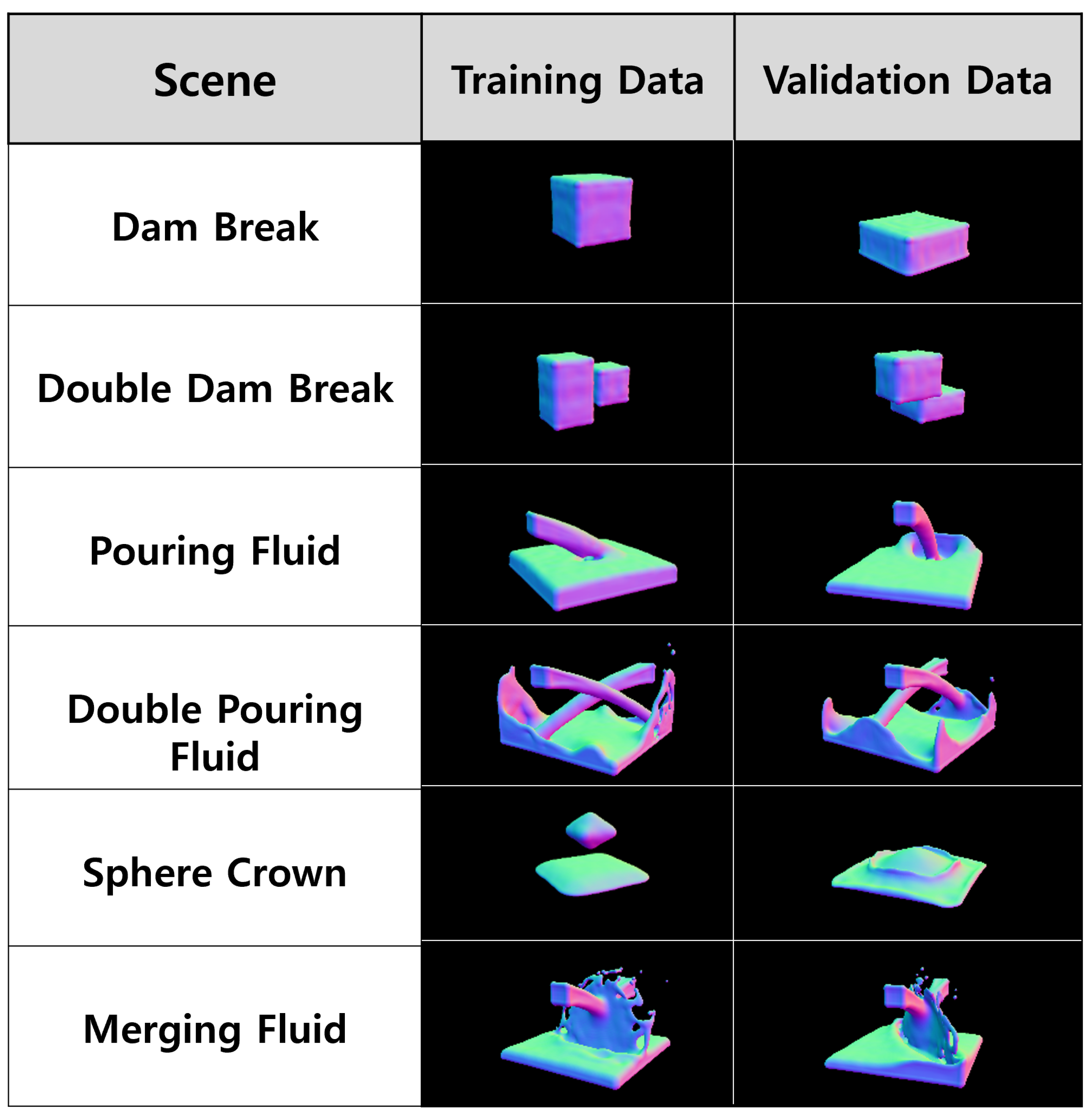
4. Training Data and Model Architecture
4.1. Datasets and Training Scenes
4.2. Model Architecture
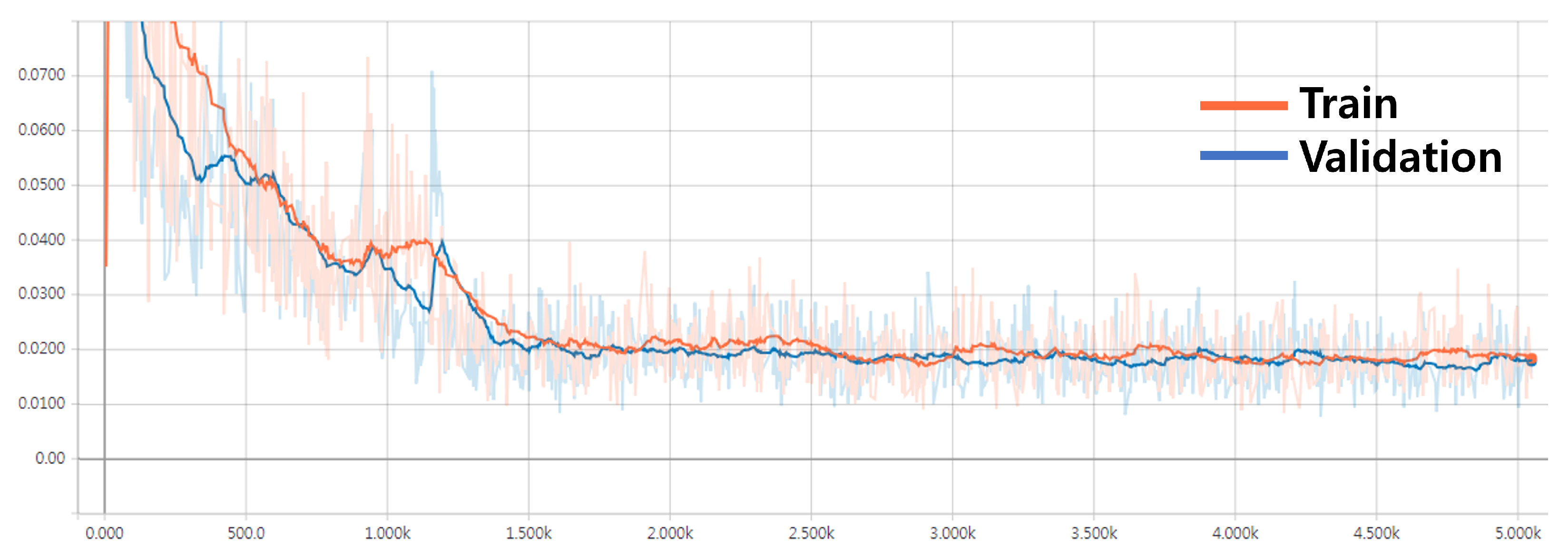
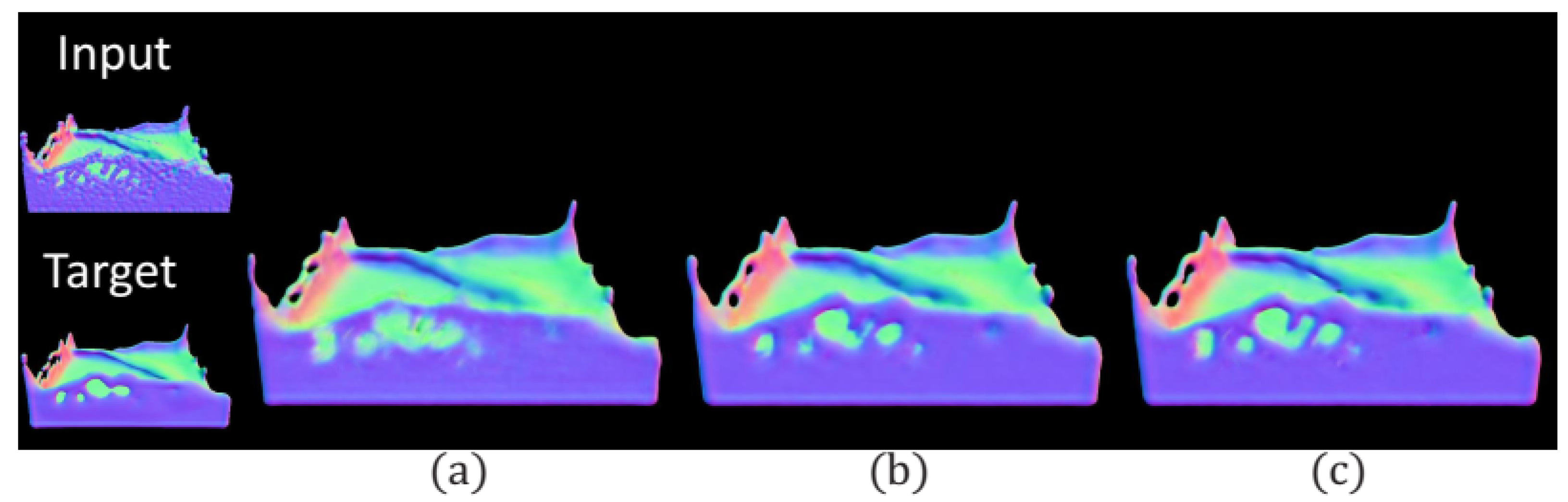
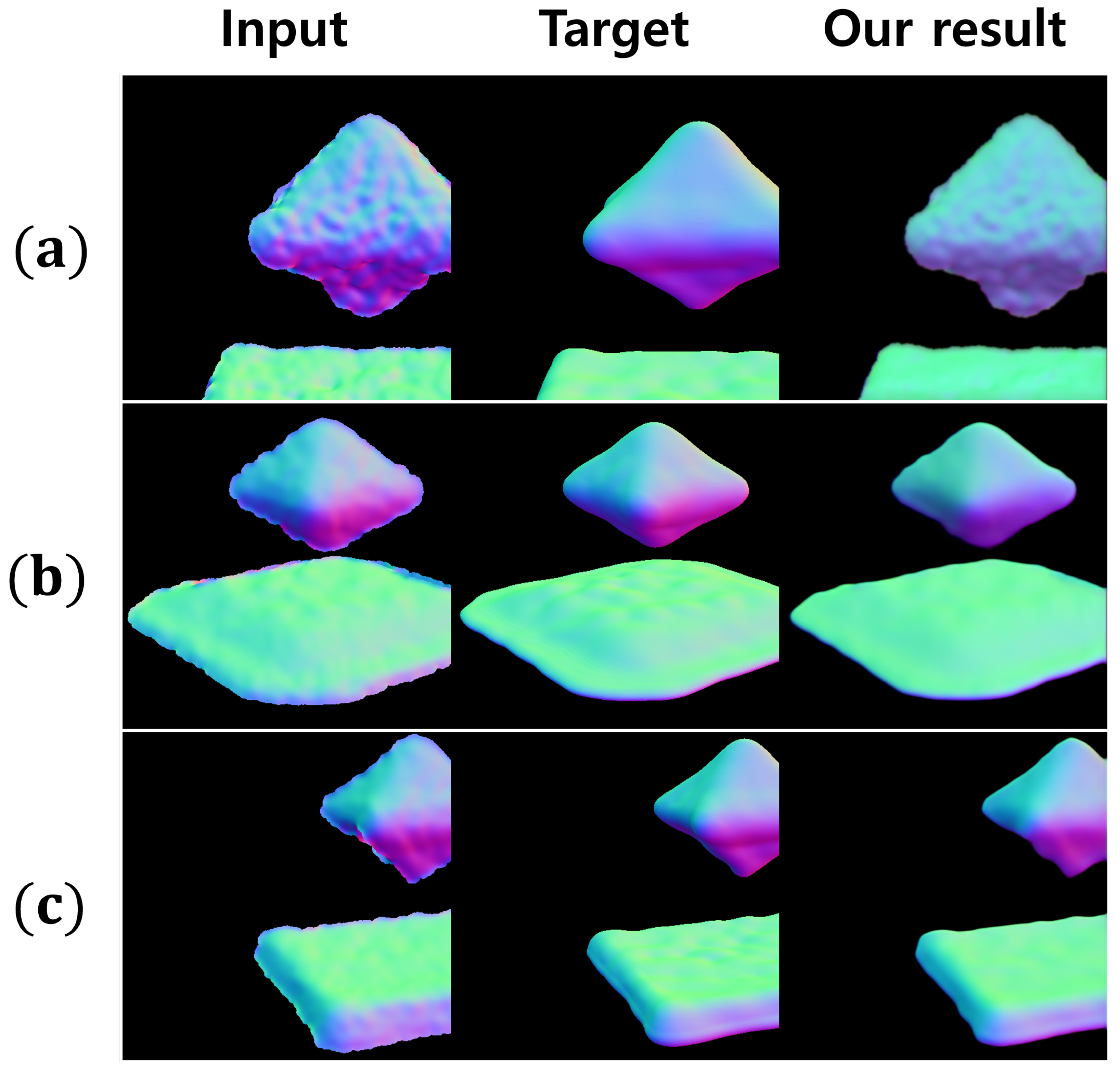
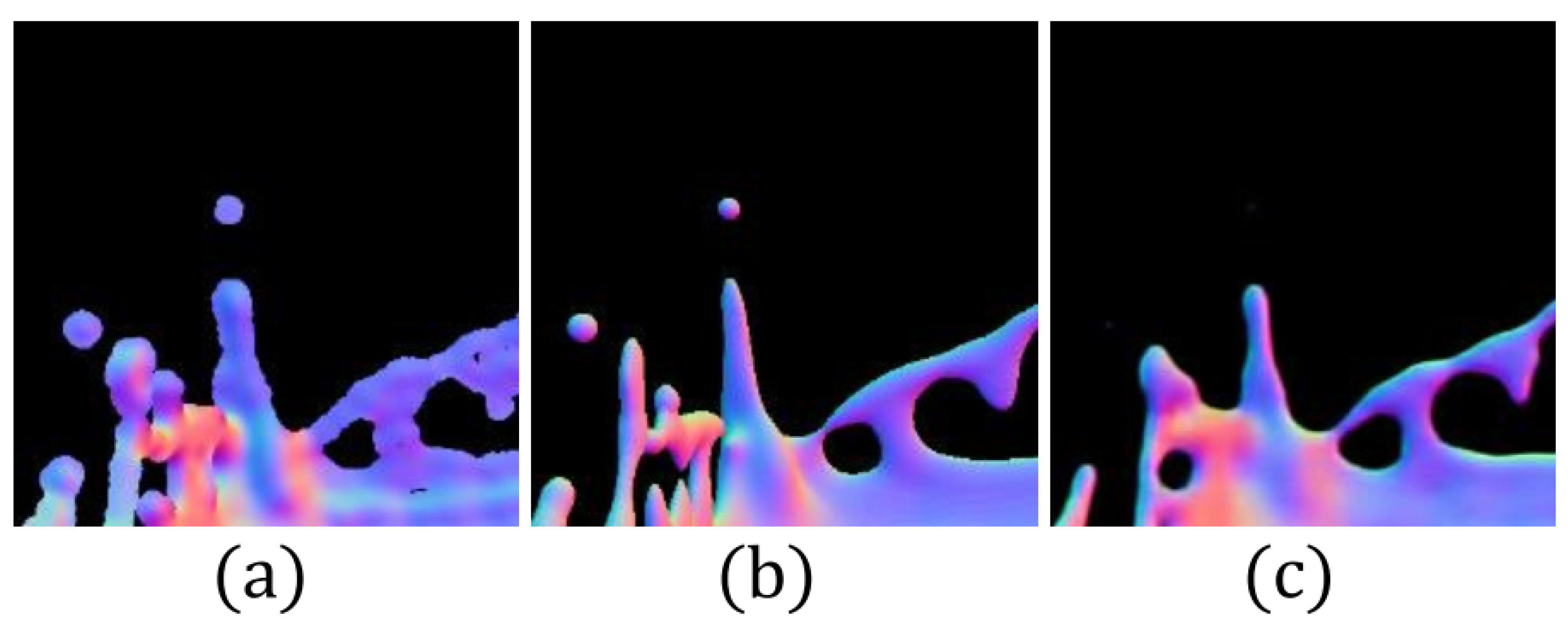
5. Experiments and Analysis
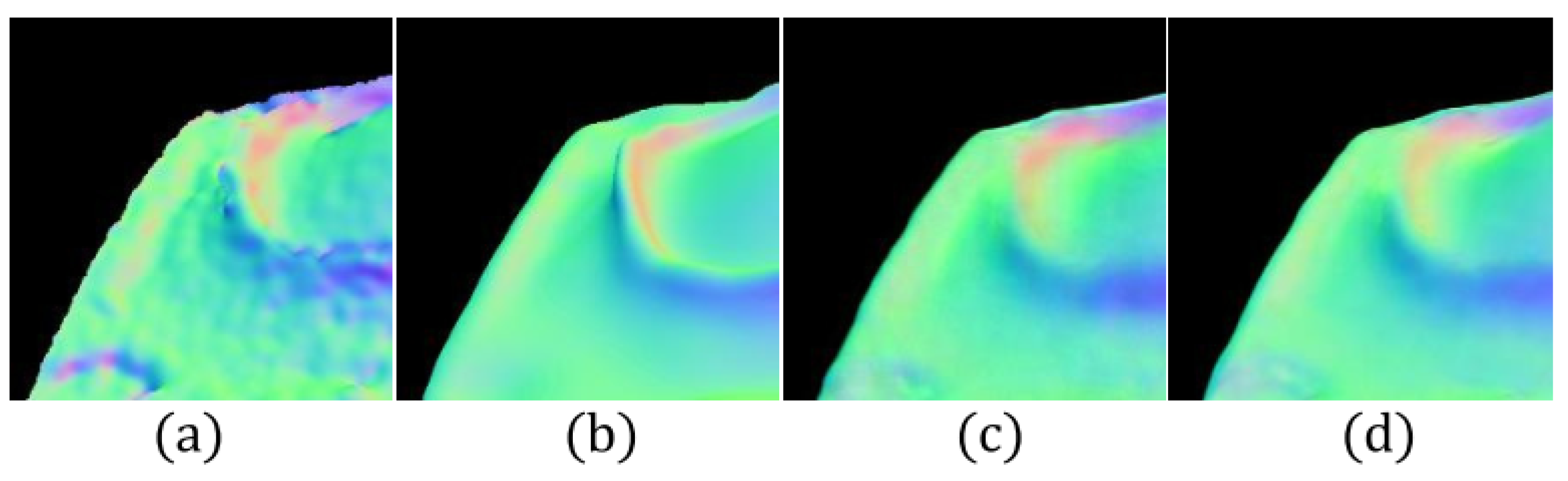
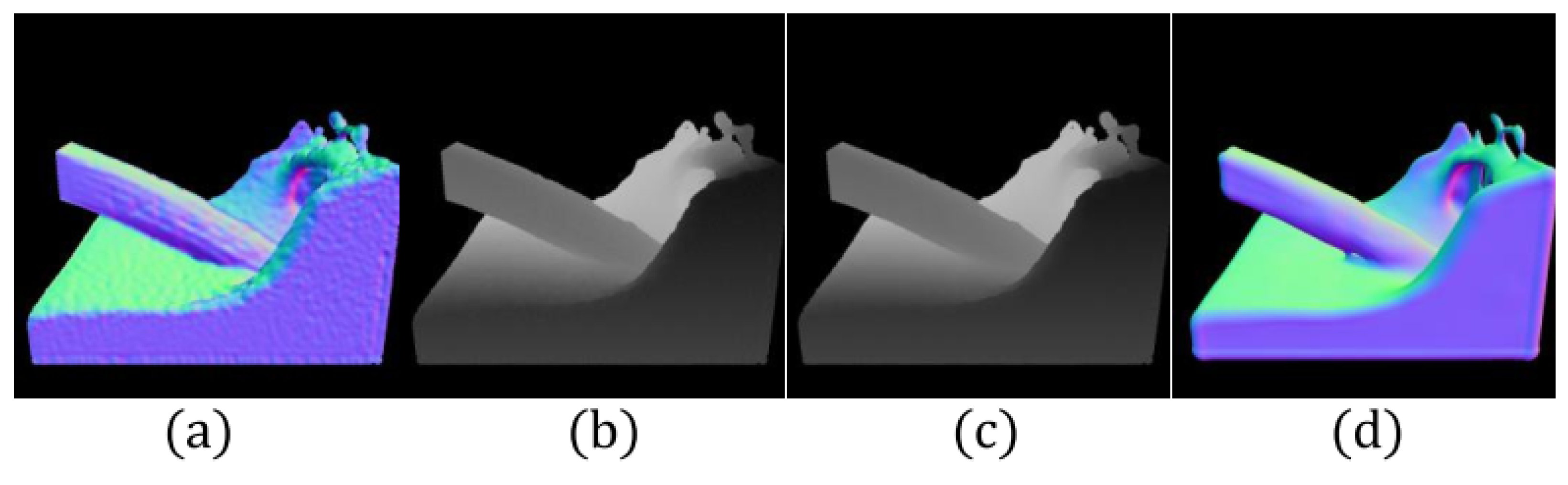
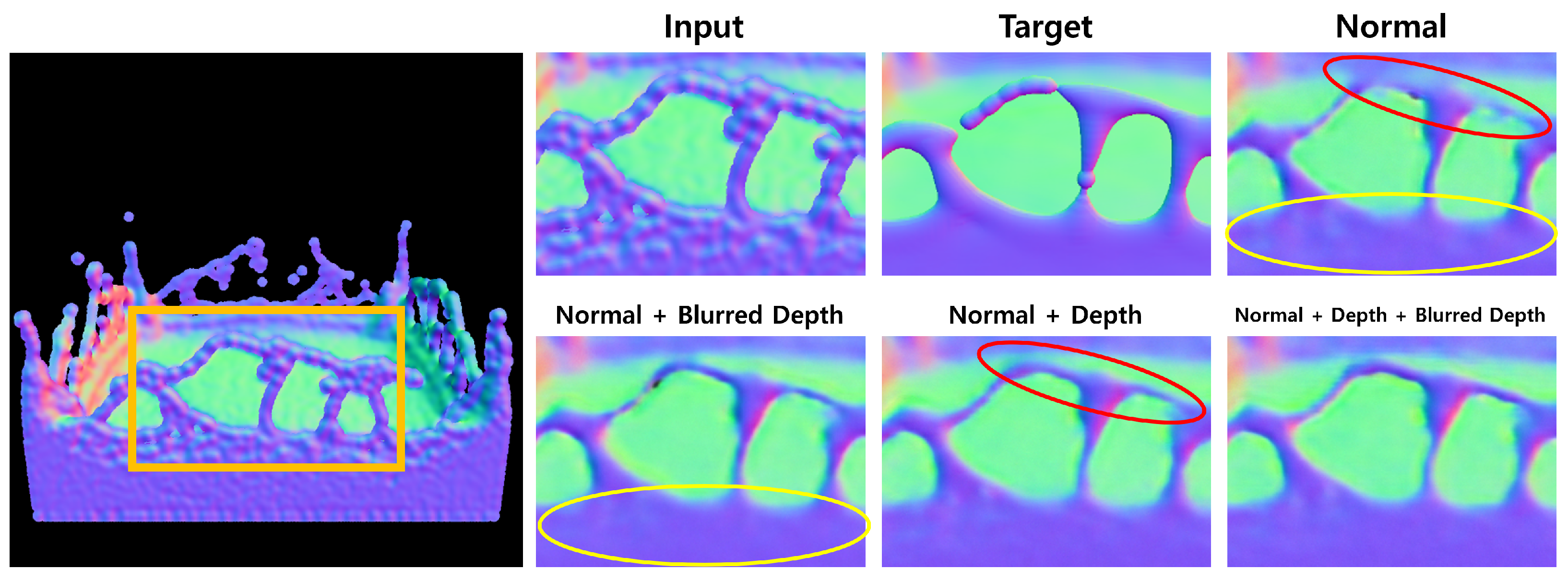
5.1. Auxiliary Features
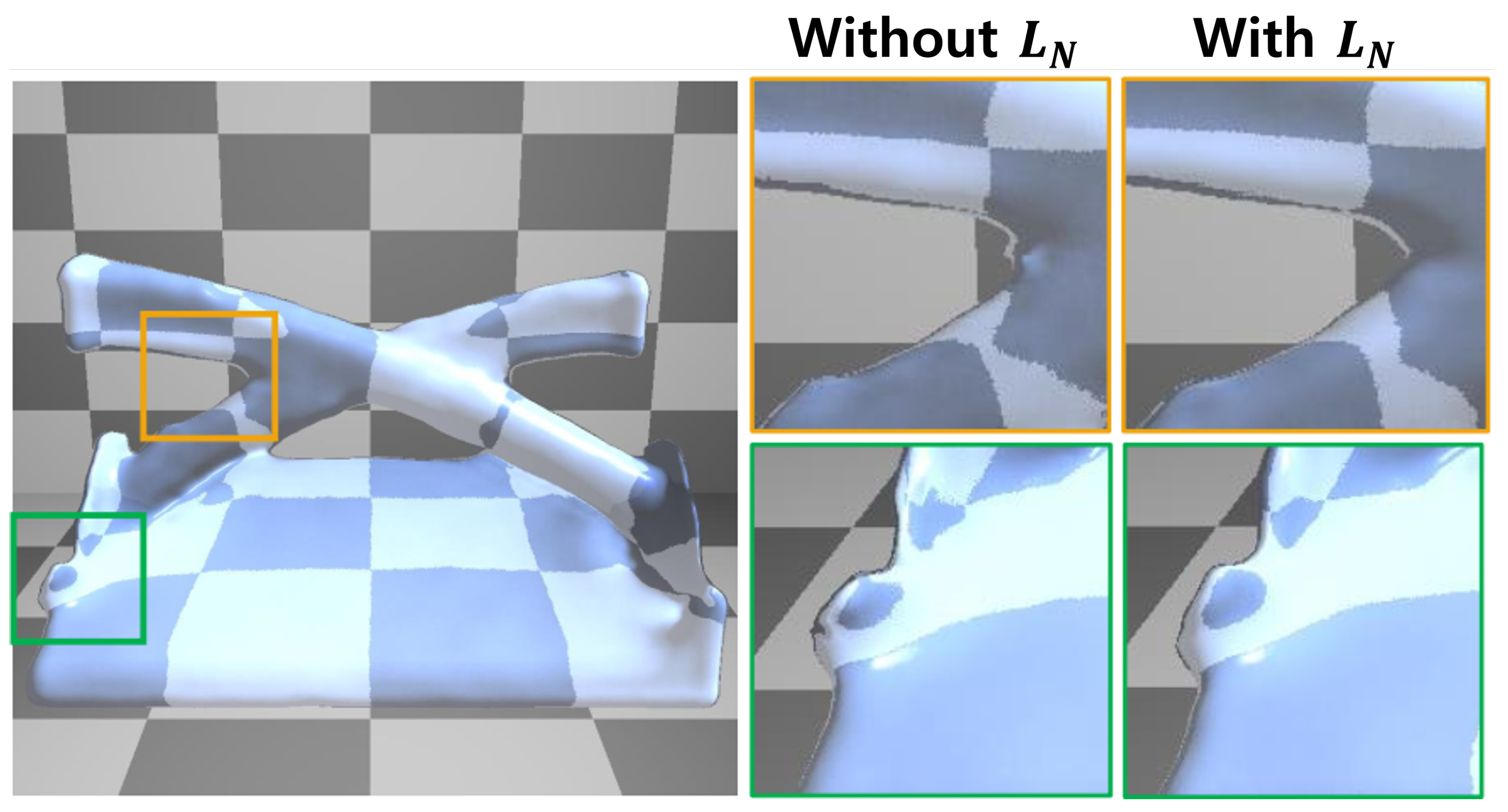
5.2. Normal Constraint Loss
5.3. Training Scene
5.4. Discussion and Limitation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Van der Laan, W.J.; Green, S.; Sainz, M. Screen space fluid rendering with curvature flow. In Proceedings of the 2009 Symposium on Interactive 3D Graphics and Games, Boston, MA, USA, 27 February–1 March 2009; ACM: New York, NY, USA, 2009; pp. 91–98. [Google Scholar]
- Truong, N.; Yuksel, C. A Narrow-Range Filter for Screen-Space Fluid Rendering. Proc. ACM Comput. Graph. Interact. Tech. 2018, 1, 17. [Google Scholar] [CrossRef]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; pp. 2672–2680. [Google Scholar]
- Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3D surface construction algorithm. ACM Siggraph Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Yu, J.; Turk, G. Reconstructing surfaces of particle-based fluids using anisotropic kernels. ACM Trans. Graph. TOG 2013, 32, 5. [Google Scholar] [CrossRef]
- Zwicker, M.; Pfister, H.; Van Baar, J.; Gross, M. Surface splatting. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques; ACM: New York, NY, USA, 2001; pp. 371–378. [Google Scholar]
- Aurich, V.; Weule, J. Non-linear Gaussian filters performing edge preserving diffusion. In Mustererkennung 1995; Springer: Berlin/Heidelberg, Germany, 1995; pp. 538–545. [Google Scholar]
- Müller, M.; Schirm, S.; Duthaler, S. Screen space meshes. In Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 2–4 August 2007; Eurographics Association: Geneva, Switzerland, 2007; pp. 9–15. [Google Scholar]
- Xiao, X.; Zhang, S.; Yang, X. Real-time high-quality surface rendering for large scale particle-based fluids. In Proceedings of the 21st ACM Siggraph Symposium on Interactive 3D Graphics and Games, San Francisco, CA, USA, 25–27 February 2017; ACM: New York, NY, USA, 2017; p. 12. [Google Scholar]
- Burkus, V.; Kárpáti, A.; Szécsi, L. Particle-Based Fluid Surface Rendering with Neural Networks; Union: Charlotte, NC, USA, 2021. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Chaitanya, C.R.A.; Kaplanyan, A.S.; Schied, C.; Salvi, M.; Lefohn, A.; Nowrouzezahrai, D.; Aila, T. Interactive reconstruction of Monte Carlo image sequences using a recurrent denoising autoencoder. ACM Trans. Graph. TOG 2017, 36, 98. [Google Scholar] [CrossRef]
- Nalbach, O.; Arabadzhiyska, E.; Mehta, D.; Seidel, H.P.; Ritschel, T. Deep shading: Convolutional neural networks for screen space shading. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2017; Volume 36, pp. 65–78. [Google Scholar]
- Sanchez-Gonzalez, A.; Godwin, J.; Pfaff, T.; Ying, R.; Leskovec, J.; Battaglia, P. Learning to simulate complex physics with graph networks. In Proceedings of the International Conference on Machine Learning, Virtual Event, 12–18 July 2020; PMLR: Long Beach, CA, USA, 2020; pp. 8459–8468. [Google Scholar]
- Shlomi, J.; Battaglia, P.; Vlimant, J.R. Graph neural networks in particle physics. Mach. Learn. Sci. Technol. 2020, 2, 021001. [Google Scholar] [CrossRef]
- Pfaff, T.; Fortunato, M.; Sanchez-Gonzalez, A.; Battaglia, P.W. Learning mesh-based simulation with graph networks. arXiv 2020, arXiv:2010.03409. [Google Scholar]
- Kochkov, D.; Smith, J.A.; Alieva, A.; Wang, Q.; Brenner, M.P.; Hoyer, S. Machine learning–accelerated computational fluid dynamics. Proc. Natl. Acad. Sci. USA 2021, 118, e2101784118. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Brox, T. Generating images with perceptual similarity metrics based on deep networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 4–9 December 2016; pp. 658–666. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Xie, Y.; Franz, E.; Chu, M.; Thuerey, N. tempogan: A temporally coherent, volumetric gan for super-resolution fluid flow. ACM Trans. Graph. TOG 2018, 37, 95. [Google Scholar] [CrossRef]
- Wang, T.C.; Liu, M.Y.; Zhu, J.Y.; Liu, G.; Tao, A.; Kautz, J.; Catanzaro, B. Video-to-Video Synthesis. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context encoders: Feature learning by inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2536–2544. [Google Scholar]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for image restoration with neural networks. IEEE Trans. Comput. Imaging 2016, 3, 47–57. [Google Scholar] [CrossRef]
- Müller, M.; Charypar, D.; Gross, M. Particle-based fluid simulation for interactive applications. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 26–27 July 2003; Eurographics Association: Geneva, Switzerland, 2003; pp. 154–159. [Google Scholar]
- Macklin, M.; Müller, M. Position based fluids. ACM Trans. Graph. TOG 2013, 32, 104. [Google Scholar] [CrossRef]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. Proc. ICML 2013, 30, 3. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Thomas, M.M.; Forbes, A.G. Deep Illumination: Approximating Dynamic Global Illumination with Generative Adversarial Network. arXiv 2017, arXiv:1710.09834. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, M.; Park, J.-H.; Zhang, Q.; Hong, B.-S.; Kim, C.-H. Deep Representation of a Normal Map for Screen-Space Fluid Rendering. Appl. Sci. 2021, 11, 9065. https://doi.org/10.3390/app11199065
Choi M, Park J-H, Zhang Q, Hong B-S, Kim C-H. Deep Representation of a Normal Map for Screen-Space Fluid Rendering. Applied Sciences. 2021; 11(19):9065. https://doi.org/10.3390/app11199065
Chicago/Turabian StyleChoi, Myungjin, Jee-Hyeok Park, Qimeng Zhang, Byeung-Sun Hong, and Chang-Hun Kim. 2021. "Deep Representation of a Normal Map for Screen-Space Fluid Rendering" Applied Sciences 11, no. 19: 9065. https://doi.org/10.3390/app11199065
APA StyleChoi, M., Park, J.-H., Zhang, Q., Hong, B.-S., & Kim, C.-H. (2021). Deep Representation of a Normal Map for Screen-Space Fluid Rendering. Applied Sciences, 11(19), 9065. https://doi.org/10.3390/app11199065






