Undrained Stability Analysis of Shallow Tunnel and Sinkhole in Soft Clay: The Cavity Contraction Method
Abstract
:1. Introduction
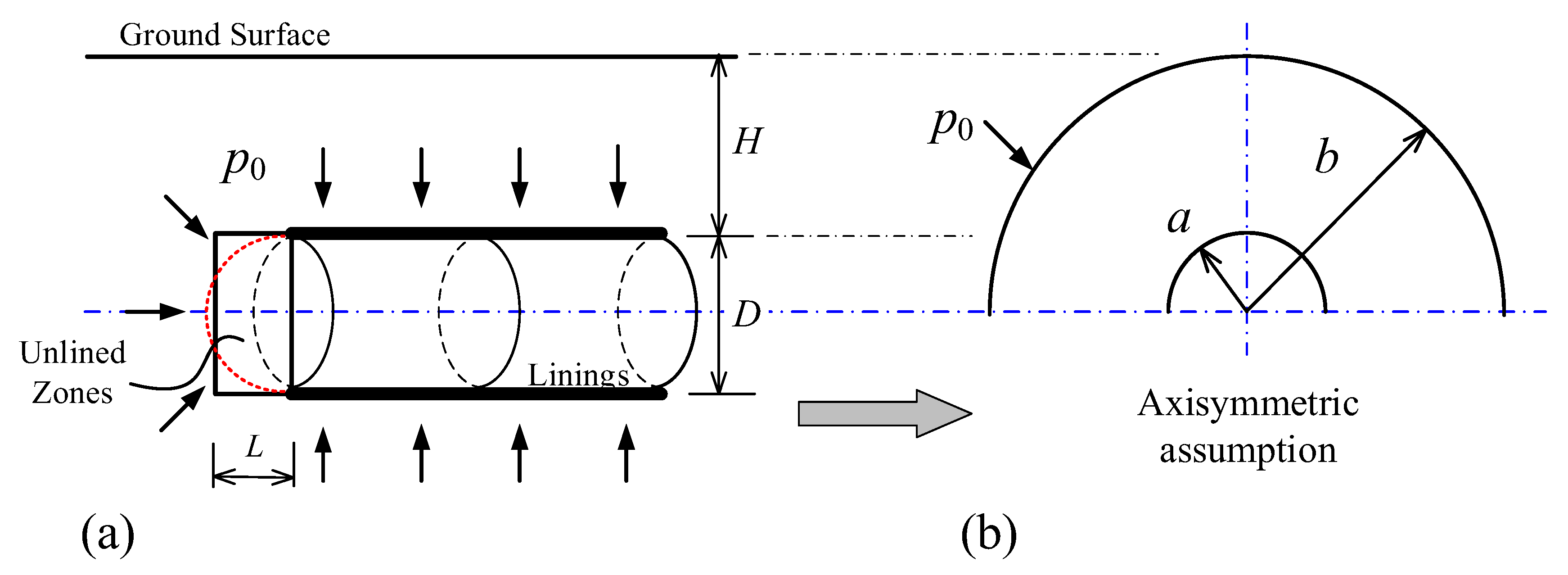
2. Problem Definition
3. Theoretical Analysis
4. Validation and Discussion
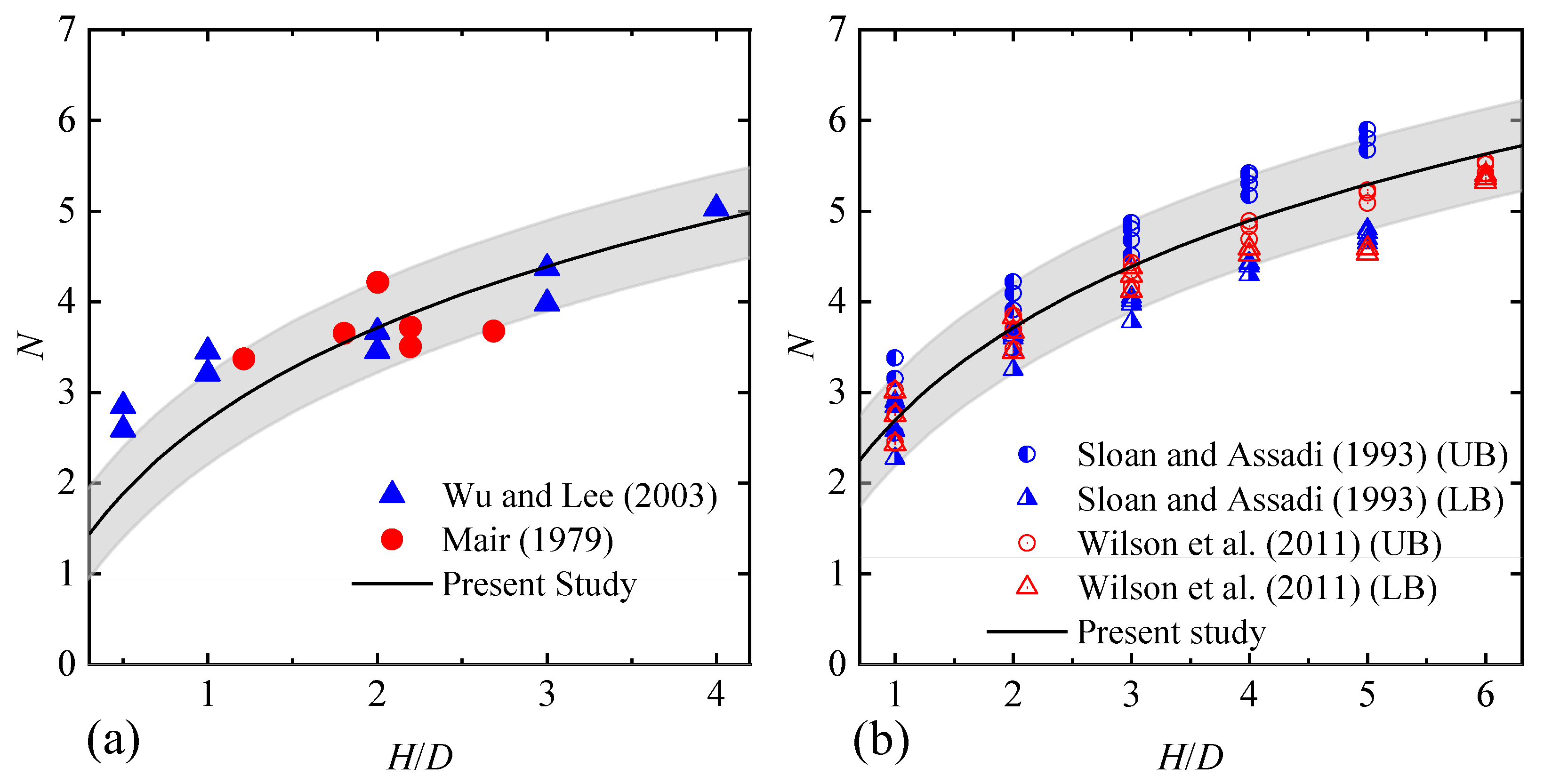
4.1. D Tunnel Stability Analysis
4.2. D Tunnel Stability Analysis: L/D ≥ 0.5
4.2.1. Assumptions and Theory
- (a)
- Equation (18) still holds in 3D conditions, but the shape factor k varies with L/D. Although the collapse mechanism for a tunnel heading is much more complicated than that for a 2D tunnel, Equation (18) is still adopted for 3D tunnel stability analysis because of its simplification, clearness and sound theoretical basis.
- (b)
- The tunnel heading stability is exactly modelled by a spherical cavity contraction (k = 2) when L/D = 0.5. With L/D increasing from 0.5 to ∞, the tunnel collapse model would change from a spherical cavity to a cylindrical cavity and the shape factor would decrease from 2 to 1.
- (c)
- The shape factor with L/D is determined following Liang [36], who investigated the ellipsoidal cavity expansion problem and presented a similar expression of k with the length-to-width ratio of a rectangular (i.e., L/D in the present paper) by the conformal mapping method. The relationship between k and L/D can be written as:
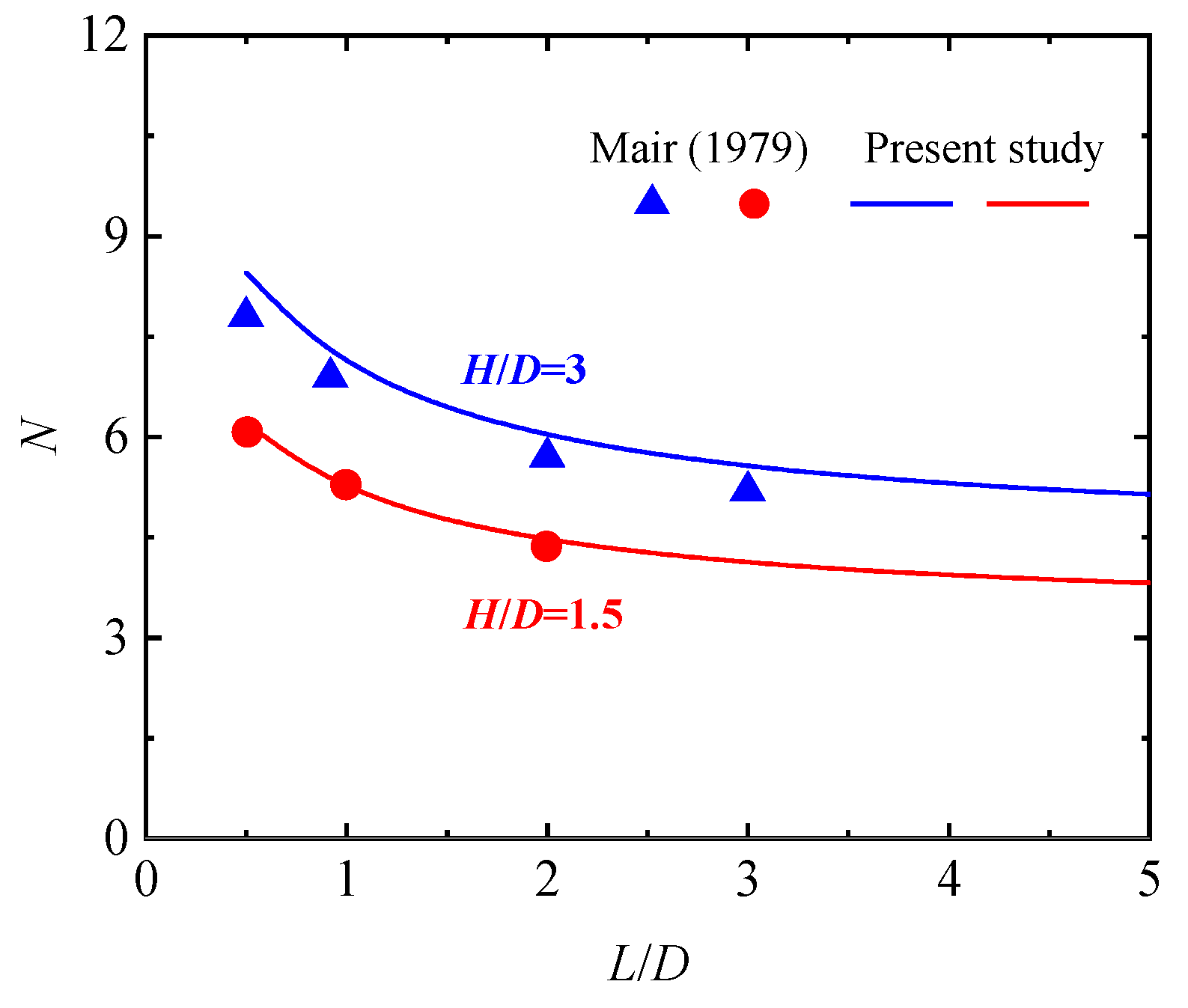
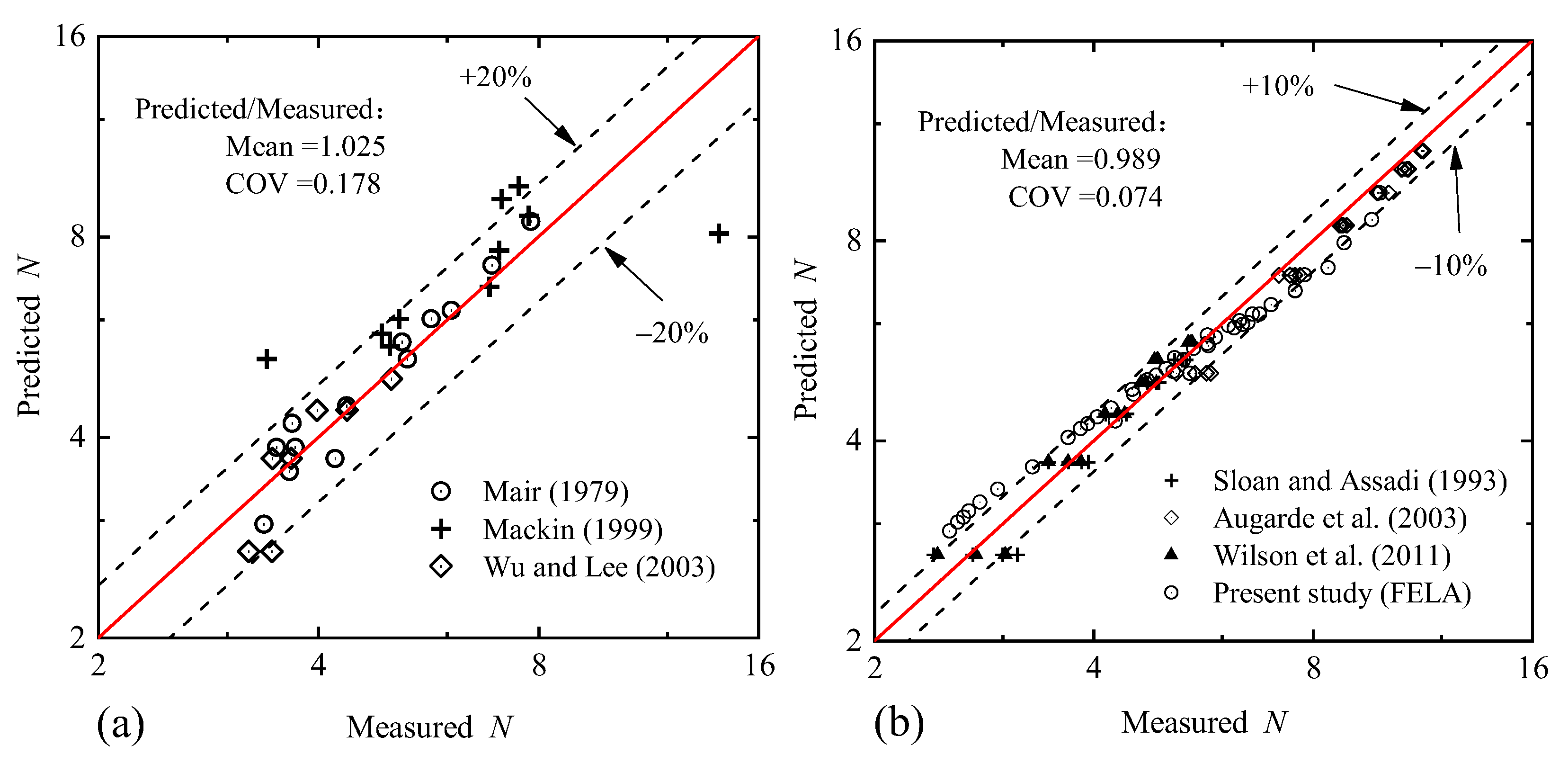
4.2.2. Comparison of Predicted Stability Numbers with Centrifuge Model Tests Results
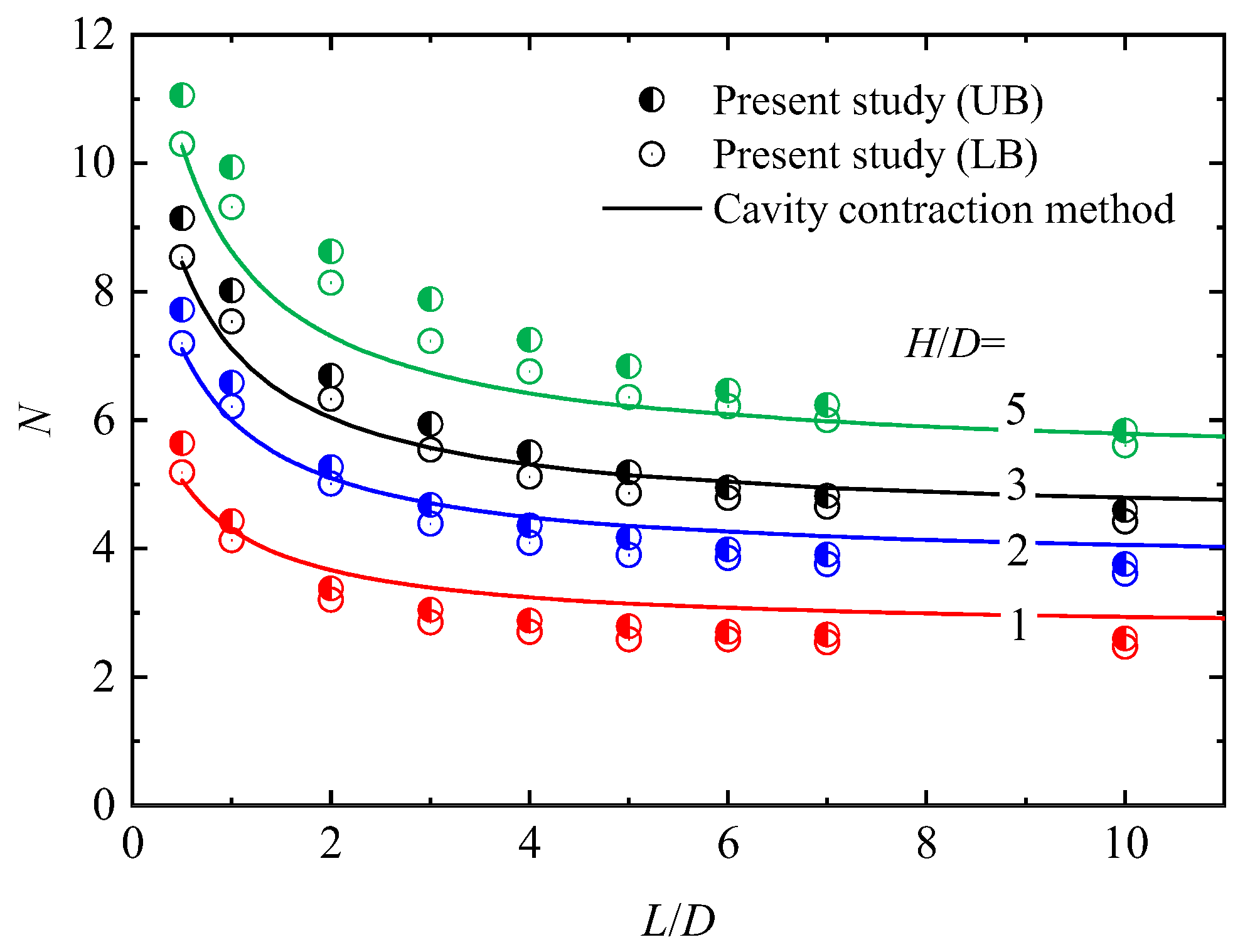
4.2.3. Comparison of Predicted Stability Numbers with FELA Results
4.3. Sinkhole Stability Analysis
4.4. Database Establishment and Error Analysis
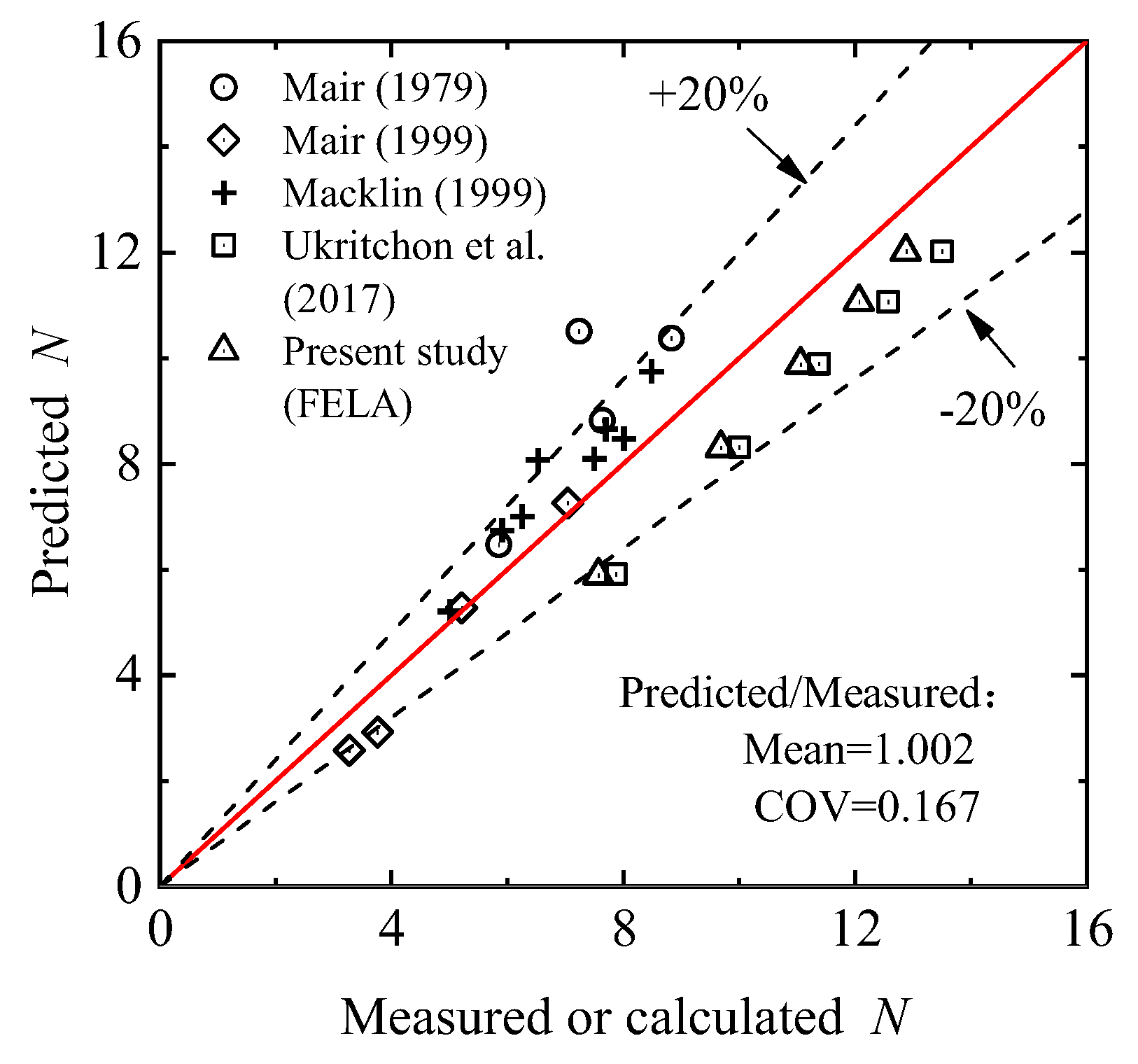
4.5. 3D Tunnel Stability Analysis: 0 ≤ L/D ≤ 0.5
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Davis, E.; Gunn, M.; Mair, R.; Seneviratine, H. The stability of shallow tunnels and underground openings in cohesive material. Géotechnique 1980, 30, 397–416. [Google Scholar] [CrossRef]
- Anagnostou, G.; Kovári, K. The face stability of slurry-shield-driven tunnels. Tunn. Undergr. Space Technol. 1994, 9, 165–174. [Google Scholar] [CrossRef]
- Mair, R.J.; Taylor, R.N. Prediction of Clay around Tunnels Uing Plasticity Solutions. In Predictive Soil Mechanics, Proceedings of the Wroth Memorial Symposium, Oxford, UK, 27–29 July 1992; Thomas Telford: Oxford, UK, 1993; pp. 449–463. [Google Scholar]
- Mair, R.J.; Taylor, R.N. Theme lecture: Bored tunnelling in the urban environment. In Proceedings of the Fourteenth International Conference on Soil Mechanics and Foundation Engineering, Hamburg, Germany, 6–12 September 1997; Balkema: Rotterdam, The Netherland, 1999; pp. 2353–2385. [Google Scholar]
- Mair, R.J. Centrifugal Modelling of Tunnel Construction in Soft Clay; University of Cambridge: London, UK, 1979. [Google Scholar]
- Wu, B.; Lee, C. Ground movements and collapse mechanisms induced by tunneling in clayey soil. Int. J. Phys. Model. Geotech. 2003, 3, 15–29. [Google Scholar] [CrossRef]
- Sloan, S.; Assadi, A. Undrained stability of a square tunnel in a soil whose strength increases linearly with depth. Comput. Geotech. 1991, 12, 321–346. [Google Scholar] [CrossRef]
- Sloan, S.W.; Assadi, A. Stability of Shallow Tunnels in Soft Ground; Predictive soil mechanics. Proceeding of the Wroth Memorial Symposium, Oxford, UK, 27–29 July 1992; Thomas Telford: London, UK, 1993; pp. 644–663. [Google Scholar]
- Augarde, C.E.; Lyamin, A.V.; Sloan, S.W. Stability of an undrained plane strain heading revisited. Comput. Geotech. 2003, 30, 419–430. [Google Scholar] [CrossRef]
- Wilson, D.W.; Abbo, A.J.; Sloan, S.W.; Lyamin, A.V. Undrained stability of a circular tunnel where the shear strength increases linearly with depth. Can. Geotech. J. 2011, 48, 1328–1342. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Continuous velocity fields for collapse and blowout of a pressurized tunnel face in purely cohesive soil. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 2061–2083. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Li, S.; Yu, J.; Tan, J.Q.W. Continuous field based upper bound analysis for three-dimensional tunnel face stability in undrained clay. Comput. Geotech. 2018, 94, 207–213. [Google Scholar] [CrossRef]
- Osman, A.; Mair, R.; Bolton, M. On the kinematics of 2D tunnel collapse in undrained clay. Géotechnique 2006, 56, 585–595. [Google Scholar] [CrossRef] [Green Version]
- Keawsawasvong, S.; Ukritchon, B. Undrained basal stability of braced circular excavations in non-homogeneous clays with linear increase of strength with depth. Comput. Geotech. 2019, 115, 103180. [Google Scholar] [CrossRef]
- Augarde, C.E.; Lyamin, A.V.; Sloan, S.W. Prediction of undrained sinkhole collapse. J. Geotech. Geoenviron. Eng. 2003, 129, 197–205. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Tang, Z.; Zhou, W.; Yuan, J. Upper bound solutions for face stability of circular tunnels in non-homogeneous and anisotropic clays. Comput. Geotech. 2018, 98, 189–196. [Google Scholar] [CrossRef]
- Ukritchon, B.; Yingchaloenkitkhajorn, K.; Keawsawasvong, S. Three-dimensional undrained tunnel face stability in clay with a linearly increasing shear strength with depth. Comput. Geotech. 2017, 88, 146–151. [Google Scholar] [CrossRef]
- Klar, A.; Osman, A.S.; Bolton, M. 2D and 3D upper bound solutions for tunnel excavation using ‘elastic’flow fields. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 1367–1374. [Google Scholar] [CrossRef]
- Zhang, F.; Gao, Y.F.; Wu, Y.X.; Zhang, N. Upper-bound solutions for face stability of circular tunnels in undrained clays. Géotechnique 2017, 68, 76–85. [Google Scholar] [CrossRef]
- Sloan, S. Lower bound limit analysis using finite elements and linear programming. Int. J. Numer. Anal. Methods Geomech. 1988, 12, 61–77. [Google Scholar] [CrossRef]
- Sloan, S. Upper bound limit analysis using finite elements and linear programming. Int. J. Numer. Anal. Methods Geomech. 1989, 13, 263–282. [Google Scholar] [CrossRef]
- Sloan, S.; Assadi, A. Undrained stability of a plane strain heading. Can. Geotech. J. 1994, 31, 443–450. [Google Scholar] [CrossRef]
- Wilson, D.W.; Abbo, A.J.; Sloan, S.W.; Lyamin, A.V. Undrained stability of a square tunnel where the shear strength increases linearly with depth. Comput. Geotech. 2013, 49, 314–325. [Google Scholar] [CrossRef]
- Mair, R.J. Tunnelling and geotechnics: New horizons. Géotechnique 2008, 58, 695–736. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.-S. Cavity Expansion Methods in Geomechanics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Mo, P.-Q.; Yu, H.-S. Undrained Cavity-Contraction Analysis for Prediction of Soil Behavior around Tunnels. Int. J. Geomech. 2017, 17, 04016121. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.-S.; Rowe, R.K. Plasticity solutions for soil behaviour around contracting cavities and tunnels. Int. J. Numer. Anal. Methods Geomech. 1999, 23, 1245–1279. [Google Scholar] [CrossRef]
- Xu, C.; Xia, C. A new large strain approach for predicting tunnel deformation in strain-softening rock mass based on the generalized Zhang-Zhu strength criterion. Int. J. Rock Mech. Min. Sci. 2021, 143, 104786. [Google Scholar] [CrossRef]
- Zhang, Q.; He, W.; Zhang, H.-Y.; Wang, H.-Y.; Jiang, B.-S. A simple numerical procedure for the elasto-plastic coupling finite strain analysis of circular tunnels in strain-softening rock masses. Comput. Geotech. 2021, 130, 103921. [Google Scholar] [CrossRef]
- Mo, P.-Q.; Marshall, A.M.; Fang, Y. Cavity Expansion–Contraction-Based Method for Tunnel–Soil–Pile Interaction in a Unified Clay and Sand Model: Drained Analysis. Int. J. Geomech. 2021, 21, 04021055. [Google Scholar] [CrossRef]
- Wroth, C.P. The interpretation of in situ soil tests. Géotechnique 1984, 34, 449–489. [Google Scholar] [CrossRef] [Green Version]
- Macklin, S. The prediction of volume loss due to tunnelling in overconsolidated clay based on heading geometry and stability number. Ground Eng. 1999, 32, 30–33. [Google Scholar]
- Broms, B.B.; Bennermark, H. Stability of clay at vertical openings. J. Soil Mech. Found. Div. 1967, 93, 71–94. [Google Scholar] [CrossRef]
- Caquot, A.; Kerisel, J. Traité de Mécanique des Sols; Gauthier-Villars: Paris, French, 1966. [Google Scholar]
- Bolton, M.D. A Guide to Soil Mechanics; Macmillan: London, UK, 2003. [Google Scholar]
- Liang, H. Advances in Ellipsoidal Cavity Expansion with Tresca Material; China University of Mining and technology: Xuzhou, China, 2010. [Google Scholar]
- Sloan, S.W. Geotechnical stability analysis. Géotechnique 2013, 63, 531–572. [Google Scholar] [CrossRef] [Green Version]


| Author(s) | Year | Number of Data | L/D | H/D | Notation |
|---|---|---|---|---|---|
| Mair [5] | 1979 | 6 | plane strain | 1~3 | centrifuge model tests |
| Mair [5] | 1979 | 7 | 0.5~3 | 1.5/3 | |
| Macklin [32] | 1999 | 10 | 0.67~5 | 1.65~5.9 | in situ tests |
| Wu and Lee [6] | 2003 | 9 | plane strain | 0.5~4 | centrifuge model tests |
| Sloan and Assadi [8] | 1993 | 20 | plane strain | 1~5 | FELA |
| Augarde, et al. [15] | 2003 | 24 | sphere | 1~6 | |
| Wilson, et al. [10] | 2011 | 18 | plane strain | 1~6 | |
| Present study | 2021 | 45 | 0.5~10 | 1~5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, H.; Cui, W.; Li, H.; Cheng, J.; Kong, L.; Wang, X.; Zhang, J.; Yang, G.; Yue, H.; Song, X. Undrained Stability Analysis of Shallow Tunnel and Sinkhole in Soft Clay: The Cavity Contraction Method. Appl. Sci. 2021, 11, 9059. https://doi.org/10.3390/app11199059
Qi H, Cui W, Li H, Cheng J, Kong L, Wang X, Zhang J, Yang G, Yue H, Song X. Undrained Stability Analysis of Shallow Tunnel and Sinkhole in Soft Clay: The Cavity Contraction Method. Applied Sciences. 2021; 11(19):9059. https://doi.org/10.3390/app11199059
Chicago/Turabian StyleQi, Hui, Wenjie Cui, Huaijian Li, Junwei Cheng, Lingdi Kong, Xiaonan Wang, Jianliang Zhang, Gongzeng Yang, Hongya Yue, and Xiuguang Song. 2021. "Undrained Stability Analysis of Shallow Tunnel and Sinkhole in Soft Clay: The Cavity Contraction Method" Applied Sciences 11, no. 19: 9059. https://doi.org/10.3390/app11199059
APA StyleQi, H., Cui, W., Li, H., Cheng, J., Kong, L., Wang, X., Zhang, J., Yang, G., Yue, H., & Song, X. (2021). Undrained Stability Analysis of Shallow Tunnel and Sinkhole in Soft Clay: The Cavity Contraction Method. Applied Sciences, 11(19), 9059. https://doi.org/10.3390/app11199059





