Real-Time Cloth Simulation Using Compute Shader in Unity3D for AR/VR Contents
Abstract
:Featured Application
Abstract
1. Introduction
- Cloth simulation is implemented based on the mass–spring system, implicit constraint enforcement, and adaptive constraint activation and deactivation (ACAD), using Unity3D compute shader.
- The parallel method of a sparse linear solving algorithm is utilized to accelerate the performance of the constraint enforcement method.
2. Related Work
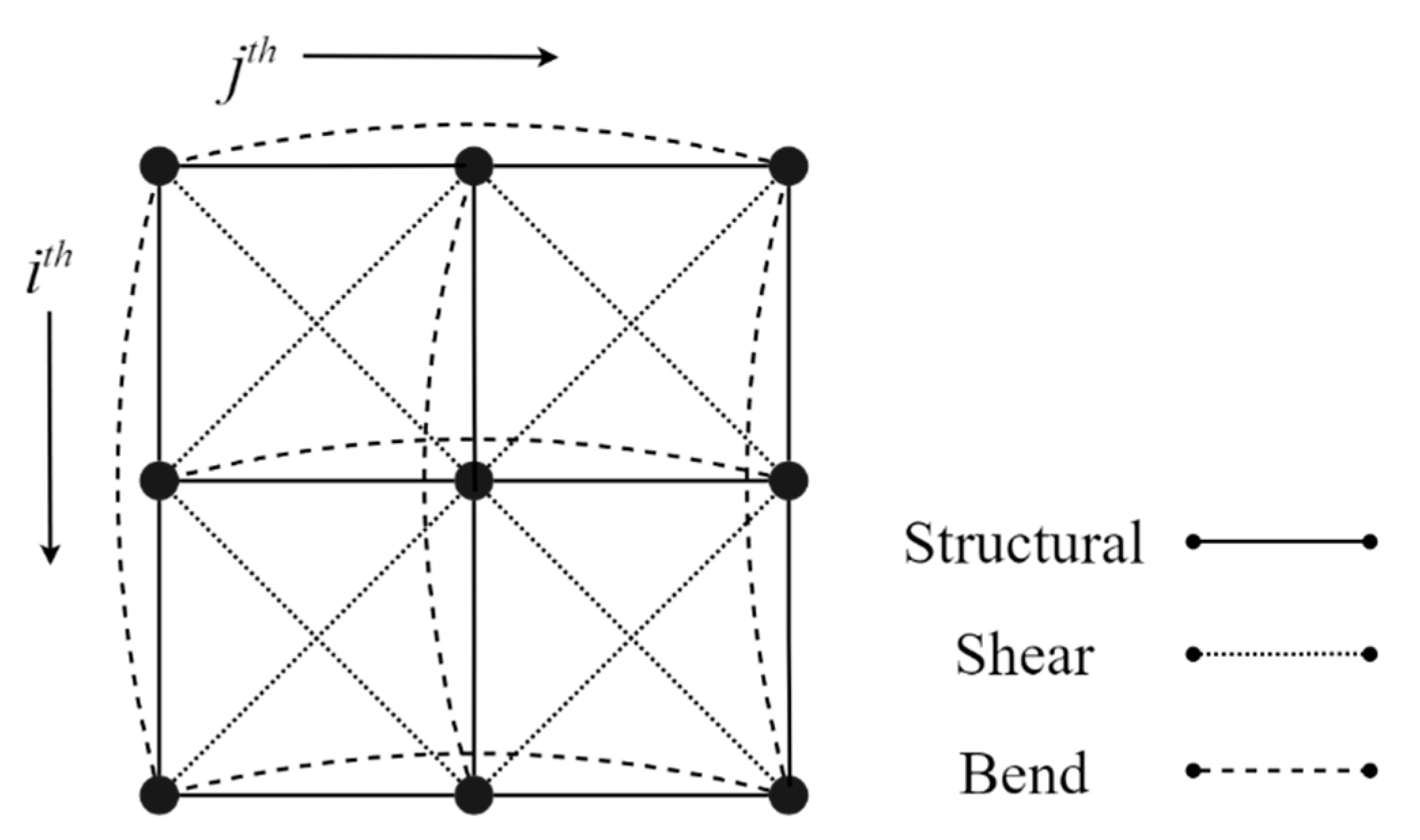
2.1. Mass–Spring System
- Structural springs: node [i, j] can be linked with node [i, j+1], [i, j-1], [i+1, j], [i-1, j].
- Shear springs: node [i, j] can be linked with node [i+1, j+1], [i+1, j-1], [i-1, j-1], [i-1, j+1].
- Bend springs: node [i, j] can be linked with to node [i, j+2], [i, j-2], [i+2, j], [i-2, j].
2.2. Implicit Constraint Enforcement
2.3. Unity3D Compute Shader
3. Implementation of Cloth Simulation in Unity3D
3.1. Mass–Spring System on the GPU
| Algorithm 1 The node’s centric algorithm to accumulate spring force. |
| Spring force accumulation kernel |
|
Input: Buffer Position, Velocity, Force Output: Buffer Force Begin i ← ThreadID.x j ← ThreadID.y index ← j×column+i Force[index] ← ComputeSpringForce(node[i, j], node[i, j+1]) Force[index] ← ComputeSpringForce(node[i, j], node[i, j-1]) Force[index] ← ComputeSpringForce(node[i, j], node[i+1, j]) Force[index] ← ComputeSpringForce(node[i, j], node[i-1, j]) Force[index] ← ComputeSpringForce(node[i, j], node[i+1, j+1]) Force[index] ← ComputeSpringForce(node[i, j], node[i+1, j-1]) Force[index] ← ComputeSpringForce(node[i, j], node[i-1, j-1]) Force[index] ← ComputeSpringForce(node[i, j], node[i-1, j+1]) Force[index] ← ComputeSpringForce(node[i, j], node[i, j+2]) Force[index] ← ComputeSpringForce(node[i, j], node[i, j-2]) Force[index] ← ComputeSpringForce(node[i, j], node[i+2, j]) Force[index] ← ComputeSpringForce(node[i, j], node[i-2, j]) End |
3.2. Constraint Enforcement on the GPU
| Algorithm 2 The SpMM algorithm kernel. |
| SpMM |
| Input: Buffer A, IA, JA, IB, JB Output: Buffer Sys Begin i ← ThreadID.x j ← ThreadID.y rowStart ← IA[i] rowEnd ← IA[i+1] colStart ← JB[j] colEnd←JB[j+1] value ← 0 for ia ← rowStart to rowEnd do: colIndex ← JA[ia] for jb ← colStart to colEnd do: rowIndex ← IB[jb] if colIndex == rowIndex do: value ← value + (A[ia] × A[jb]) end if end for end for if value != 0 do: InterlockAdd(nnzIndex,1) COO[nnzIndex] ← float3(i,j,value) end if End |
| Algorithm 3 The SpMV algorithm kernel. |
| SpMV |
| Input: Buffer Sys, nnz, P Output: Buffer Result Begin i ← ThreadID.x if i < nnz do: nnz_row ← Sys[i].x nnz_col ← Sys[i].y nnz_value ← Sys[i].z result ← nnz_value × P[nnz_col] InterlockAddFloat(Result[nnz_row],result) end if End |
3.3. Adaptive Constraint Activation and Deactivation
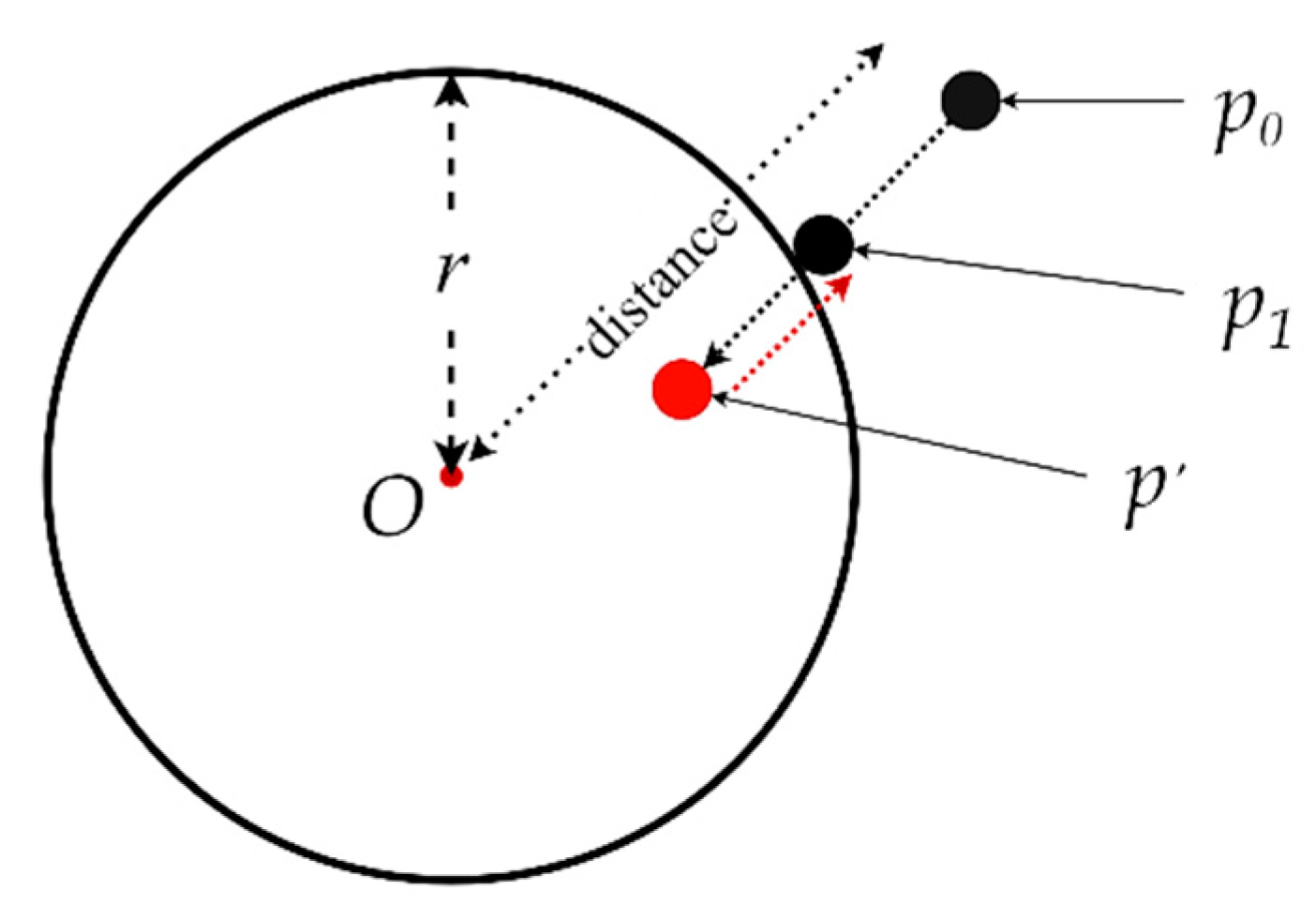
3.4. Cloth–Sphere Collision Detection and Response
| Algorithm 4 The algorithm for collision detection and response. |
| Collision detection and response |
|
Input: p0, p′, v0, O, r, offset Output: p1, v1 Begin If distance(p′-O) < r do: distance ← p0-O p1 ← O + normalize(distance) × (r + offset) v1 ← normalize(distance) + normalize(v0) End if End |
3.5. Normal Vectors Computation Based on Triangle Model on the GPU
| Algorithm 5 Pseudocode of the normal vector computation algorithm. |
| Normal vector computation |
| Input: Buffer Position Output: Buffer Normal Begin i ← ThreadID.x j ← ThreadID.y index ← j×column+i n ← vector3(0,0,0) n1 ← Compute n2 normal of 1st quadrant n3 ← Compute normal of 2nd quadrant n4 ← Compute normal of 3rd quadrant n5 ← Compute normal of 4th quadrant n ← Normal [index] ← Normalize (n) End |
4. Result
4.1. Experimental Environment
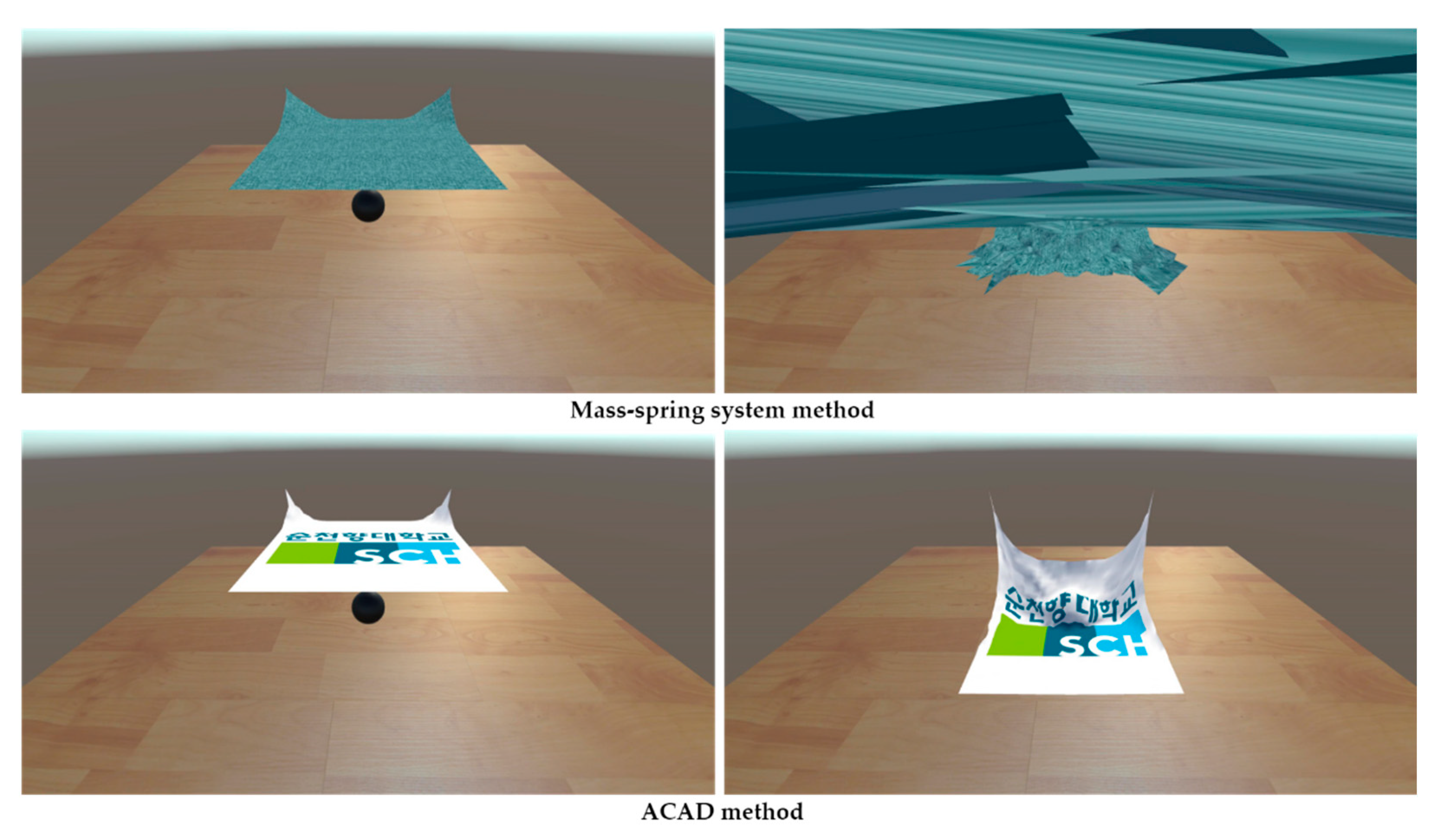
4.2. Rendering Method
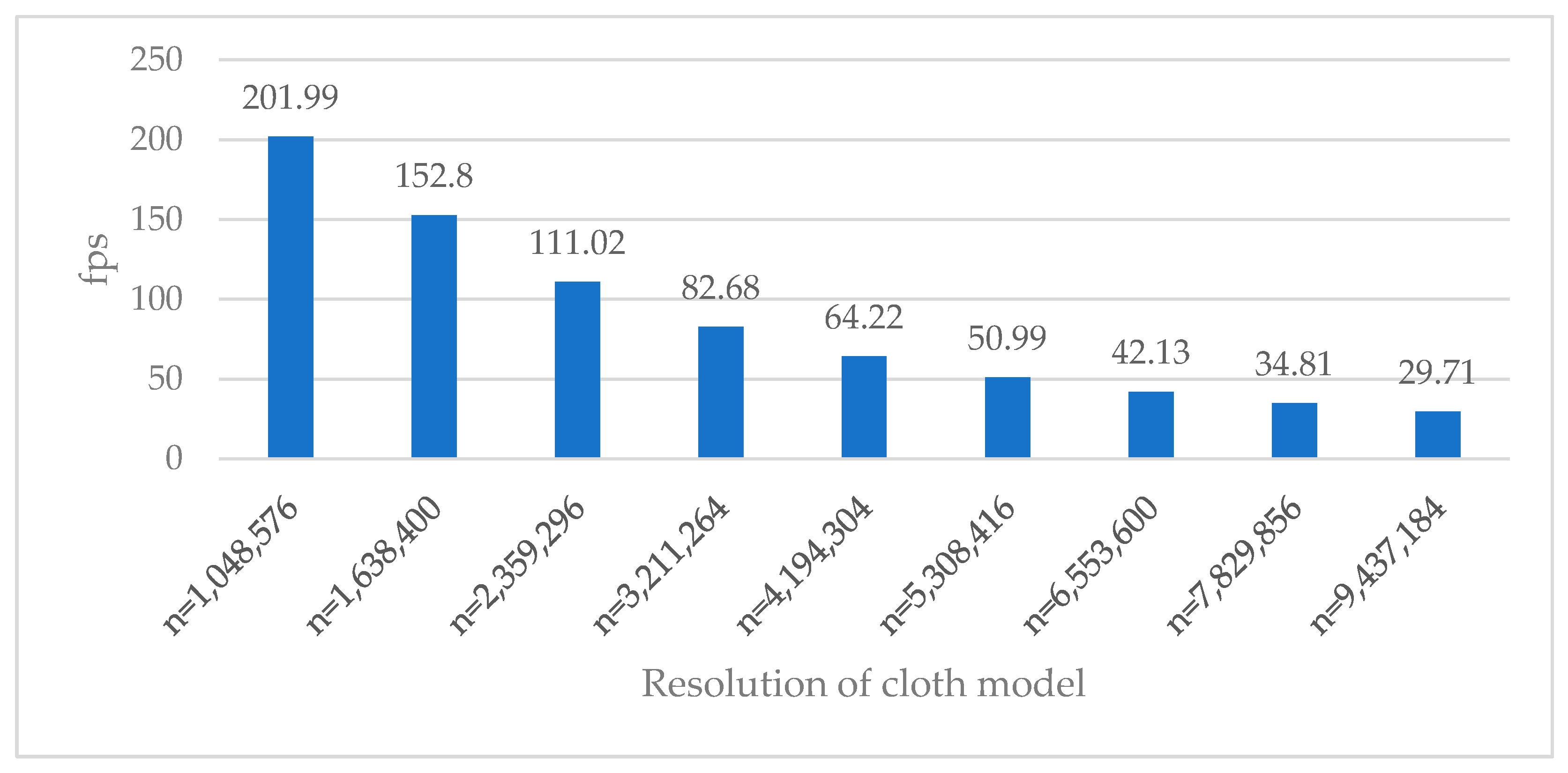
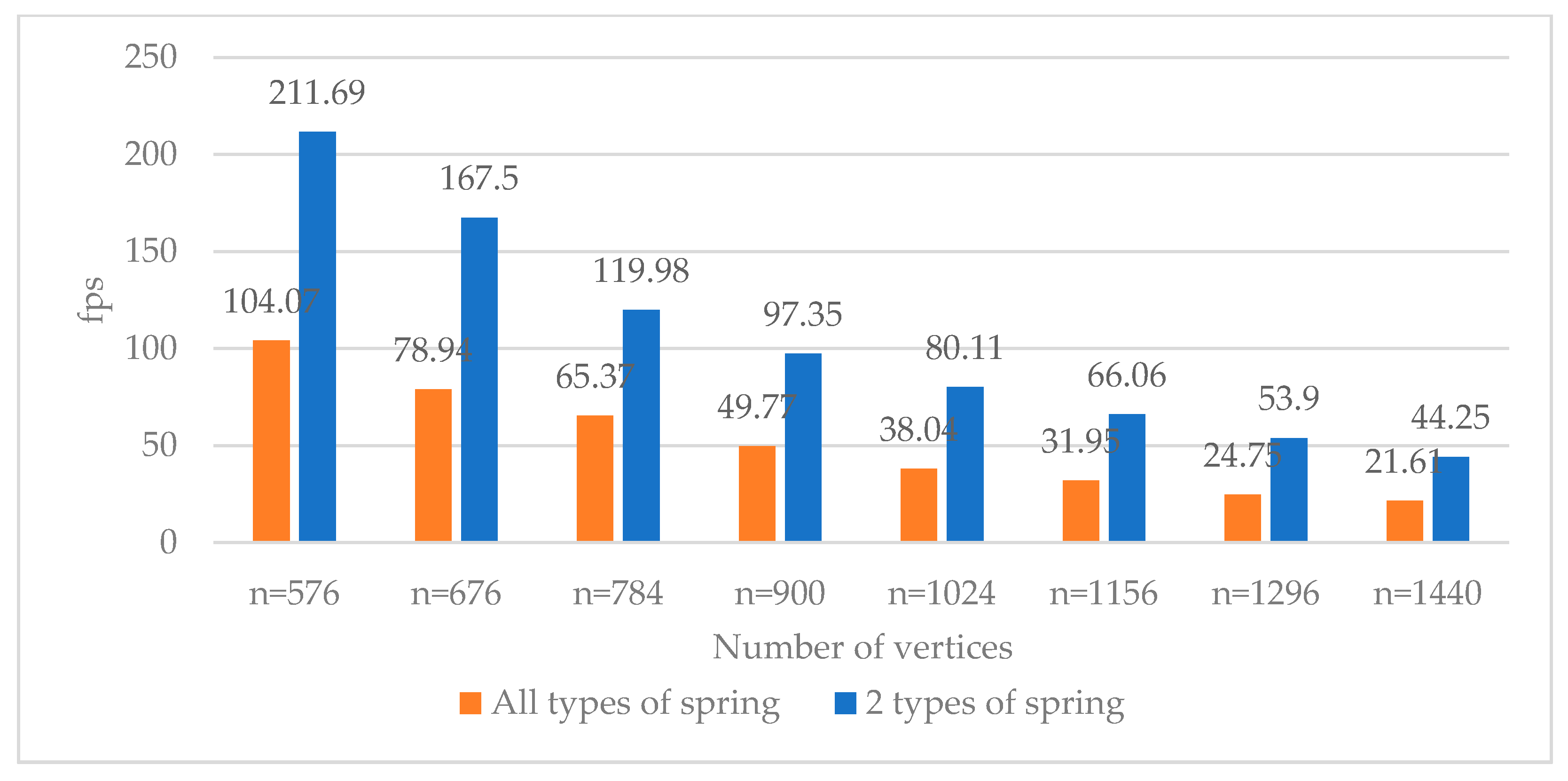
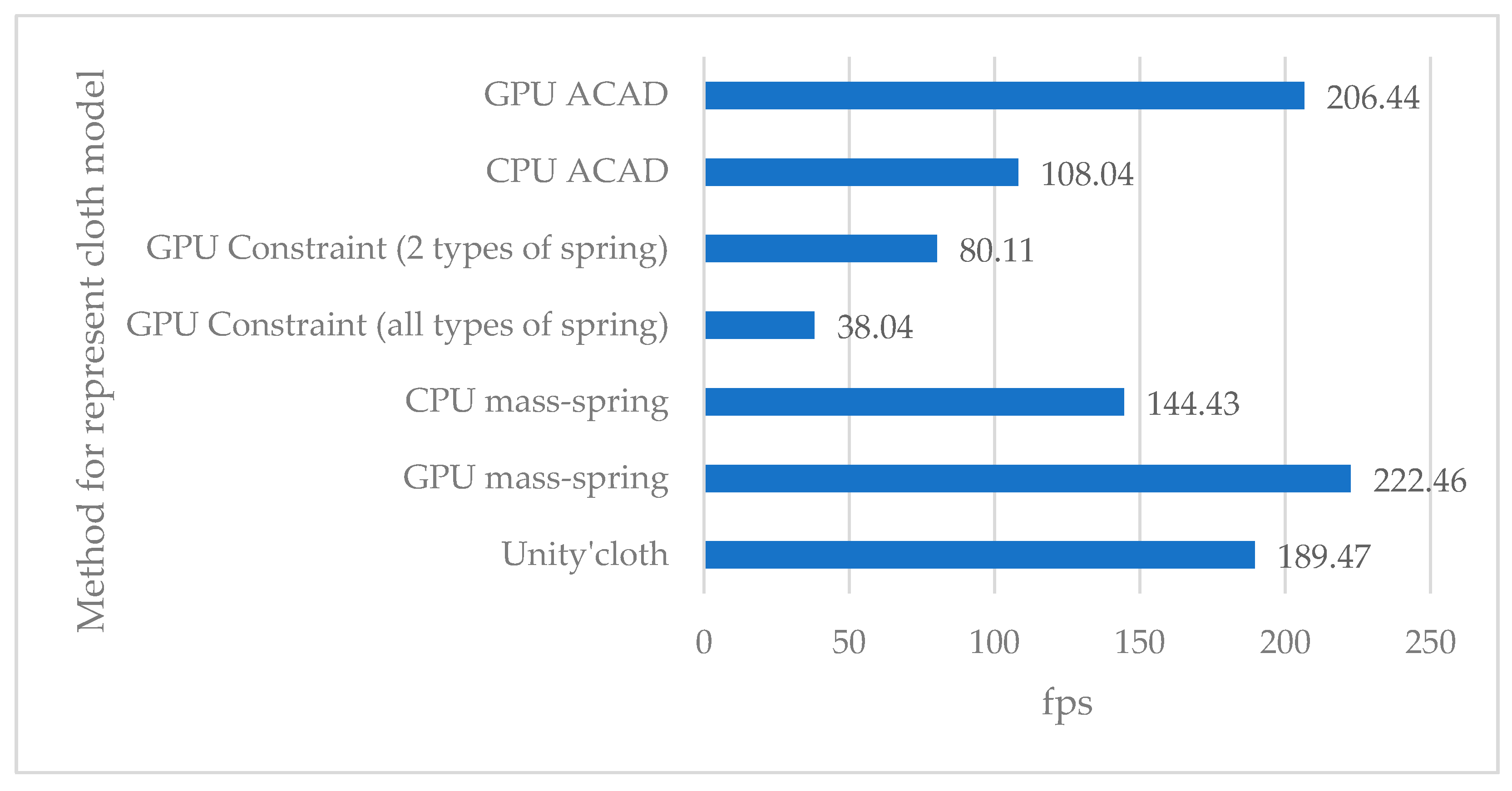
4.3. Performance Result
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Navarro-Hinojosa, O.; Ruiz-Loza, S.; Alencastre-Miranda, M. Physically-based visual simulation of the Lattice Boltzmann method on the GPU: A survey. J. Supercomput. 2018, 74, 3441–3467. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, X.; Sun, W.; Song, A. An Optimized Model for the Local Compression Deformation of Soft Tissue. KSII Trans. Internet Inf. Syst. 2020, 14, 671–686. [Google Scholar]
- Zhao, P.; Liu, J.; Li, Y.; Wu, C. A spring-damping contact force model considering normal friction for impact analysis. Nonlinear Dyn 2021, 105, 1437–1457. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, H.; Sun, W.; Yuan, C. An Optimized Mass-spring Model with Shape Restoration Ability Based on Volume Conservation. KSII Trans. Internet Inf. Syst. 2020, 14, 1738–1756. [Google Scholar]
- Tian, H.; Wana, C.; Zhana, X. A Realtime Virtual Grasping System for Manipulating Complex Objects. In Proceedings of the IEEE Conference on Virtual Reality and 3D User Interfaces (VR), Tuebingen/Reutlingen, Germany, 18–22 March 2018; pp. 1–2. [Google Scholar]
- Chen, Z.; Huang, D.; Luo, L.; Wen, M.; Zhang, C. Efficient Parallel TLD on CPU-GPU Platform for Real-Time Tracking. KSII Trans. Internet Inf. Syst. 2020, 14, 201–220. [Google Scholar]
- Li, J.; Guo, B.; Shen, Y.; Li, D. Low-power Scheduling Framework for Heterogeneous Architecture under Performance Constraint. KSII Trans. Internet Inf. Syst. 2020, 14, 2003–2021. [Google Scholar]
- Unity. Available online: https://www.unity.com (accessed on 19 July 2021).
- Obi Unified Particle Physics for Unity. Available online: http://obi.virtualmethodstudio.com (accessed on 19 July 2021).
- Marinkovic, D.; Zehn, M. Survey of Finite Element Method-Based Real-Time Simulations. Appl. Sci. 2019, 9, 2775. [Google Scholar] [CrossRef] [Green Version]
- Lamecki, A.; Dziekonski, A.; Balewski, L.; Fotyga, G.; Mrozowski, M. GPU-Accelerated 3D Mesh Deformation for Optimization Based on the Finite Element Method. Radioengineering 2017, 26, 924–929. [Google Scholar] [CrossRef]
- Volino, P.; Magnenat-Thalmann, N.; Faure, F. A simple approach to nonlinear tensile stiffness for accurate cloth simulation. ACM Trans. Graph 2009, 28, 105. [Google Scholar] [CrossRef] [Green Version]
- Weber, D.; Bender, J.; Schnoes, M.; Stork, A.; Fellner, D. Efficient GPU data structures and methods to solve sparse linear systems in dynamics applications. Comput. Graph. Forum 2013, 32, 16–26. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, X.; Guan, T. Structure-Preserving Mesh Simplification. KSII Trans. Internet Inf. Syst. 2020, 14, 4463–4482. [Google Scholar]
- Müller, M.; Heidelberger, B.; Hennix, M.; Ratcliff, J. Position based dynamics. J. Vis. Commun. Image Represent. 2007, 18, 109–118. [Google Scholar] [CrossRef] [Green Version]
- Eberhardt, B.; Etzmuß, O.; Hauth, M. Implicit-explicit schemes for fast animation with particle systems. In Computer Animation and Simulation; Springer: Vienna, Austria, 2000; pp. 137–151. [Google Scholar]
- Provot, X. Deformation constraints in a mass-spring model to describe rigid cloth behavior. In Graphics Interface; Canadian Information Processing Society: Quebec City, QC, Canada, 1995; pp. 147–154. [Google Scholar]
- Georgii, J.; Westermann, R. Mass-spring systems on the GPU. Simul. Model. Pract. Theory 2005, 13, 693–702. [Google Scholar] [CrossRef]
- Mosegaard, J.; Sorensen, T.S. GPU accelerated surgical simulators for complex morphology. In Proceedings of the IEEE VR 2005, Bonn, Germany, 12–16 March 2005; pp. 147–153. [Google Scholar]
- Hong, M.; Welch, S.; Choi, M.H. Intuitive control of dynamic simulation using improved implicit constraint enforcement. In Asian Simulation Conference; Springer: Berlin/Heidelberg, Germany, 2004; pp. 315–323. [Google Scholar]
- Goldenthal, R.; Harmon, D.; Fattal, R.; Bercovier, M.; Grinspun, E. Efficient Simulation of Inextensible Cloth. In ACM SIGGRAPH 2007 Papers; Association for Computing Machinery: New York, NY, USA, 2007; p. 49-es. [Google Scholar]
- Baraff, D.; Witkin, A. Large steps in cloth simulation. In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques 1998, Orlando, FL, USA, 19–24 July 1998; pp. 43–54. [Google Scholar]
- Hong, M.; Choi, M.H.; Jung, S.; Welch, S.; Trapp, J. Effective constrained dynamic simulation using implicit constraint enforcement. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation; IEEE: New York, NY, USA, 2005; pp. 4531–4536. [Google Scholar]
- Va, H.; Lee, D.; Hong, M. Parallel algorithm of conjugate gradient solver using OpenGL compute shader. J. Korea Soc. Comput. Inf. 2021, 26, 1–9. [Google Scholar]
- Park, H.; Baek, N. Developing an Open-Source Lightweight Game Engine with DNN Support. Electronics 2020, 9, 1421. [Google Scholar] [CrossRef]
- Compute Shader Overview. Available online: https://docs.microsoft.com/en-us/windows/win32/direct3d11/direct3d-11-advanced-stages-compute-shader (accessed on 19 July 2021).
- Steinberger, M.; Zayer, R.; Seidel, H.P. Globally homogeneous, locally adaptive sparse matrix-vector multiplication on the GPU. In Proceedings of the International Conference on Supercomputing 2017, Chicago, IL, USA, 14–16 June 2017; pp. 1–11. [Google Scholar]
- Steinberger, M.; Derlery, A.; Zayer, R.; Seidel, H.P. How naive is naive SpMV on the GPU? In Proceedings of the IEEE High-Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 13–15 September 2016; pp. 1–8. [Google Scholar]


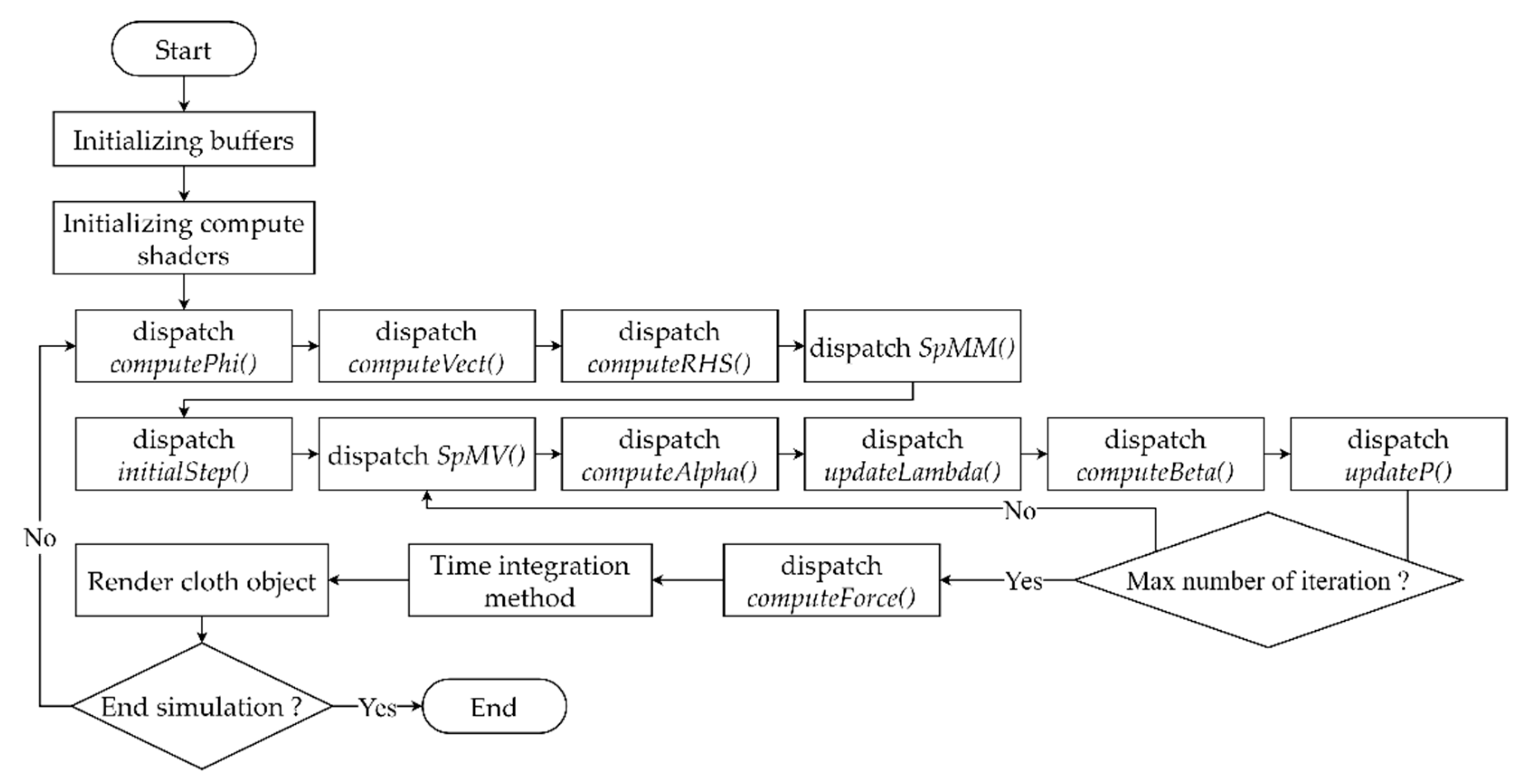






| Compute Shader | Kernel | Number of Workgroups | Thread in a Local Workgroup |
|---|---|---|---|
| ConstructingSys | computePhi() | (1024, 1, 1) | |
| computeVect() | (1024, 1, 1) | ||
| computeRHS() | (1024, 1, 1) | ||
| SpMM() | (32, 32, 1) | ||
| LinearSystemSolving (Conjugate Gradient) | initialStep() | (1024, 1, 1) | |
| SpMV() | (1024, 1, 1) | ||
| computeAlpha() | (1024, 1, 1) | ||
| updateLambda() | (1024, 1, 1) | ||
| computeBeta() | (1024, 1, 1) | ||
| updateP() | (1024, 1, 1) | ||
| ConstraintForce | computeForce() | (1024, 1, 1) |
| Buffer | Size | Data Type | Description |
|---|---|---|---|
| Phi | m | Float | Vector Φ(q, t) |
| Vect | 3n | Float | . |
| Rhs | m | Float | Right-hand side vector of Equation (11) |
| Lambda | m | Float | a vector Lagrange Multiplier (λ) |
| A | 6 × m | Float | Vector of nnz value |
| IA | m + 1 | Integer | Compressed row index for nnz value of A |
| JA | 6 × m | Integer | Column Vector of A indices |
| IB | 6 × m | Integer | Row Vector of B indices |
| JB | m + 1 | Integer | Compressed column index for nnz value |
| Sys | nnz | Vector3 | System matrix of Equation (11) |
| nnz | 1 | Integer | Number of the non-zero value of the system matrix |
| Force | 3n | Float | Vector of constraint force |
| Component | Specification |
|---|---|
| OS | Windows 10 Pro 10.0.1.19042 Build 19042 |
| CPU | Intel® Core™ i7-7700 |
| RAM | 16 GB |
| GPU | NVIDIA GeForce GTX 1070 8 GB V-RAM |
| IDE | Unity 2020.3.8f1, Microsoft Visual Studio Community 2019 version 16.10.3 |
| HLSL | Shader model 5.0 |
| MAX thread per local workgroup | 1024 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Va, H.; Choi, M.-H.; Hong, M. Real-Time Cloth Simulation Using Compute Shader in Unity3D for AR/VR Contents. Appl. Sci. 2021, 11, 8255. https://doi.org/10.3390/app11178255
Va H, Choi M-H, Hong M. Real-Time Cloth Simulation Using Compute Shader in Unity3D for AR/VR Contents. Applied Sciences. 2021; 11(17):8255. https://doi.org/10.3390/app11178255
Chicago/Turabian StyleVa, Hongly, Min-Hyung Choi, and Min Hong. 2021. "Real-Time Cloth Simulation Using Compute Shader in Unity3D for AR/VR Contents" Applied Sciences 11, no. 17: 8255. https://doi.org/10.3390/app11178255
APA StyleVa, H., Choi, M.-H., & Hong, M. (2021). Real-Time Cloth Simulation Using Compute Shader in Unity3D for AR/VR Contents. Applied Sciences, 11(17), 8255. https://doi.org/10.3390/app11178255






