SecureVision: An Open-Source User-Customizable Image Encryption Program
Abstract
:1. Introduction
2. Materials and Methods
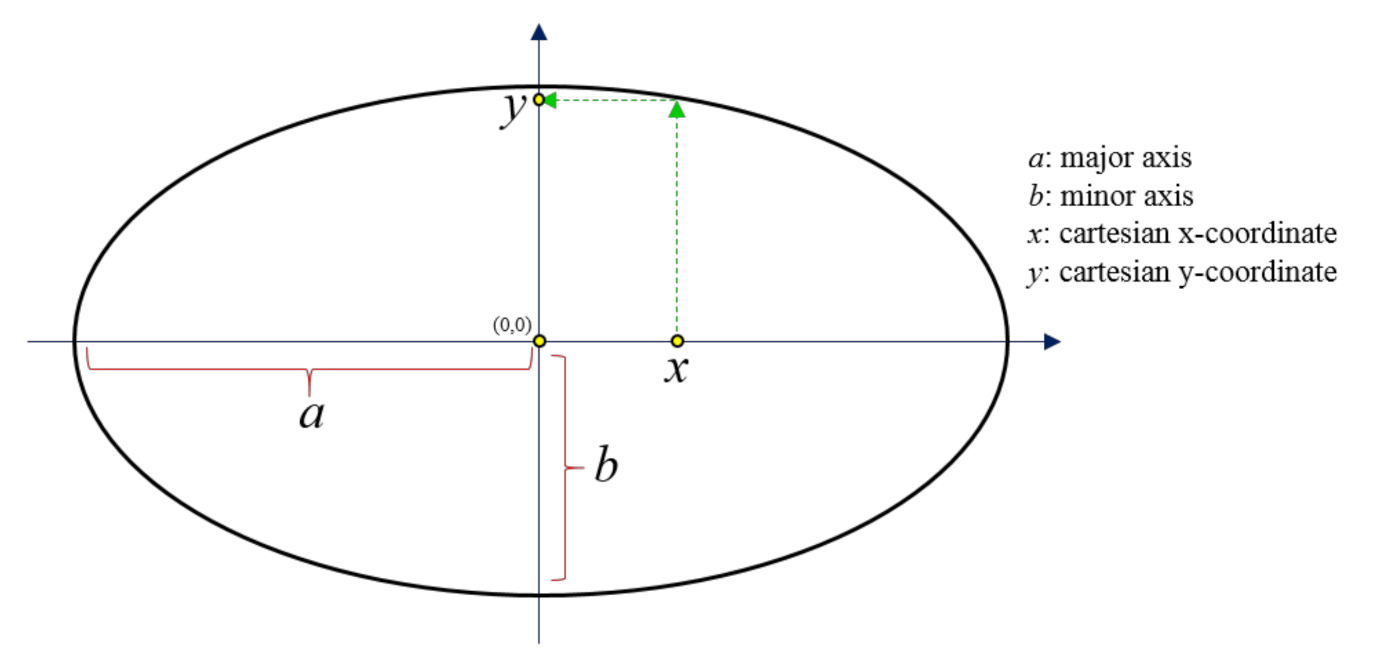
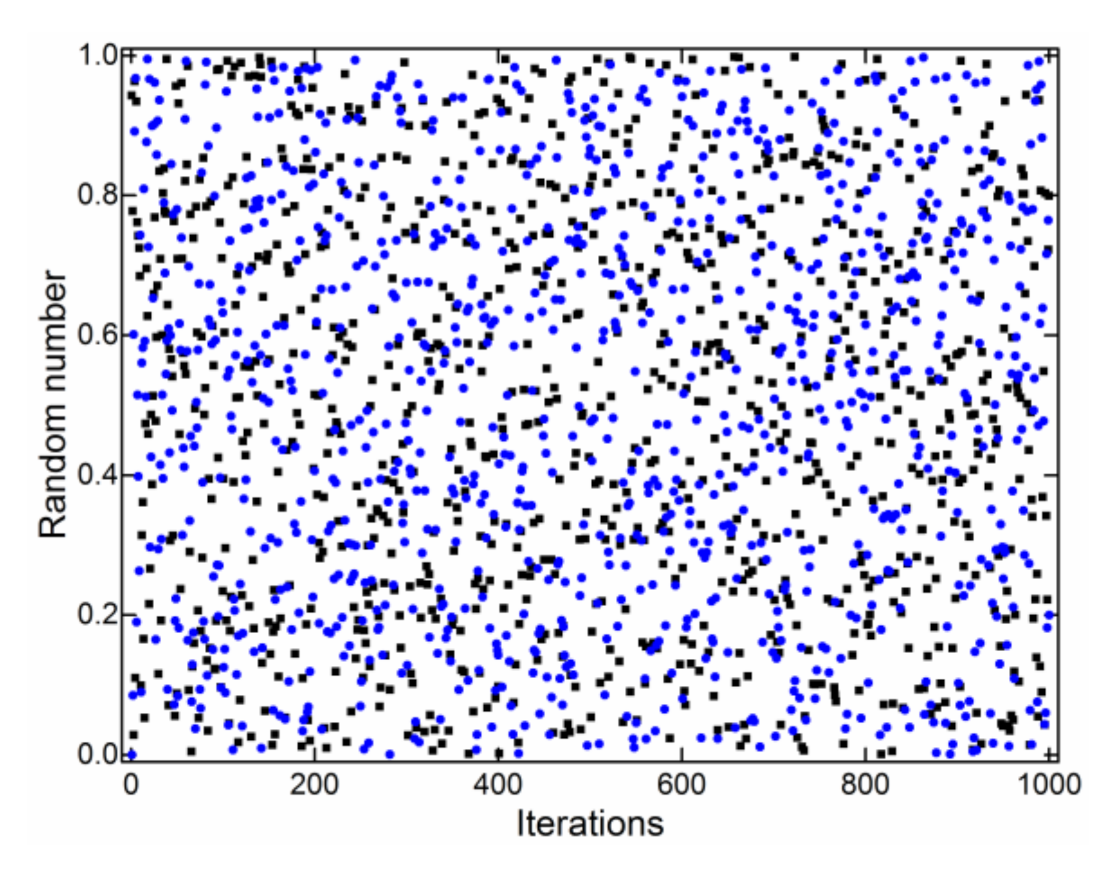
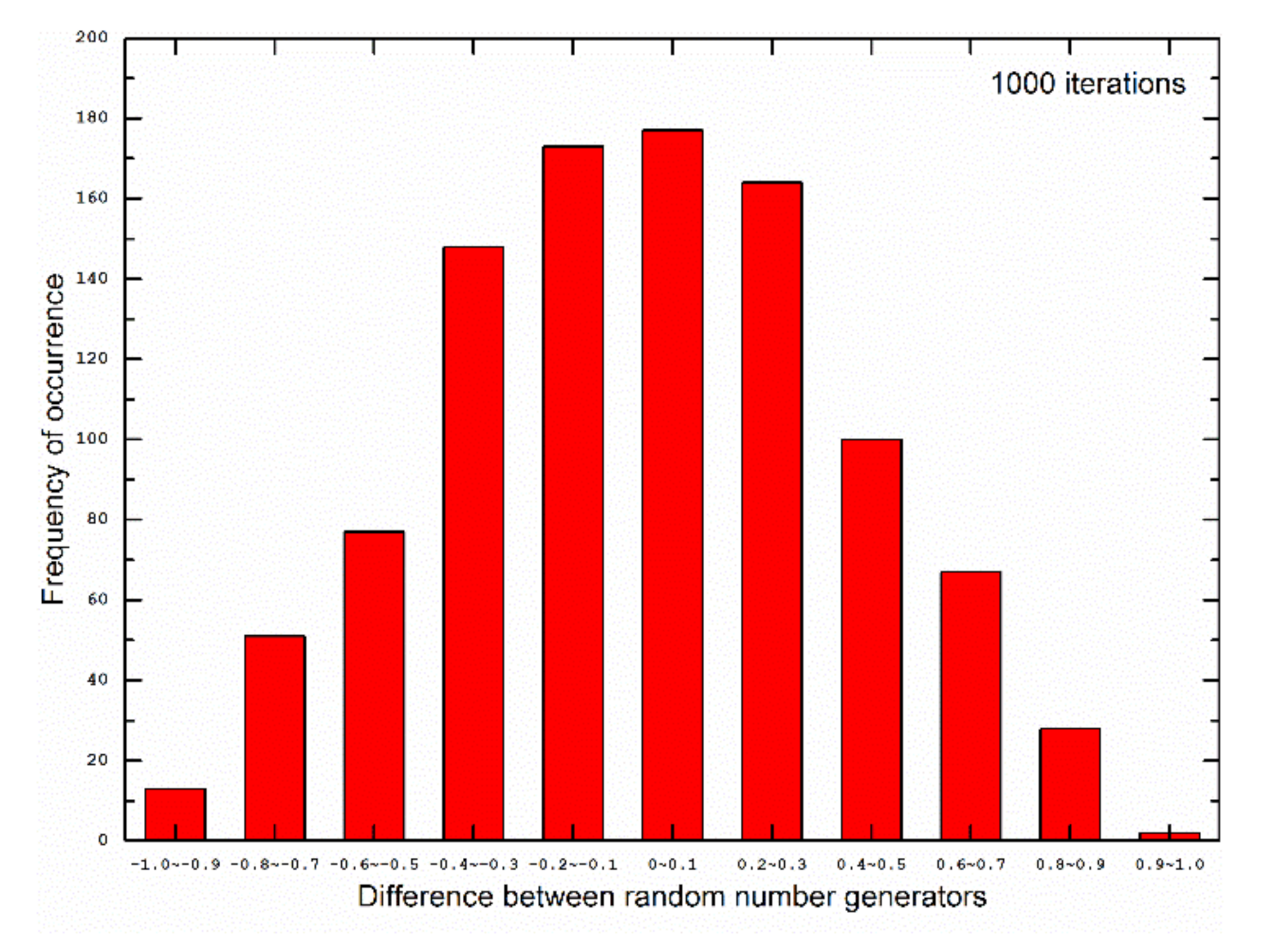
2.1. Random Number Generator
2.2. Random Shuffling of Pixel Positions
| Algorithm 1 Random Pixel Shuffling |
| 1. Initialize the variables. |
| 2. Read image size, width (w) and height (h). |
| 3. Read the private keys: x, a, b (see Equation (1)), deno, izmax, delta, A (see Equation (3)). |
| 4. Allocate 2 × 2 array, INP. |
| 5. Read image components into INP. |
| 6. Calculate the y-coordinate of ellipse based on private keys |
| 7. Calculate modulo of the y-coordinate, deno. |
| 8. Multiply the y value with the remainder of the division |
| 9. Calculate the positive decimal value from step 8, obtain random number (z). |
| 10. allocate two 2 × 2 arrays containing horizontal (pw) and vertical (ph) image coordinates |
| 11. convert z into image coordinates and read into pw and ph. |
| 12. Allocate 2 × 2 array, INPC. |
| 13. shuffle the image pixels based on pw and ph. |
| 14. store the shuffled pixel values in INPC array. |
| 15. write out INPC into an image file. |
| 16. deno + delta, then n = n + 1. |
| 17. if (n < izmax), go to step 6, if (n > izmax), then terminate, maximum iterations (izmax) reached. |
2.3. Shuffling of Pixel Values
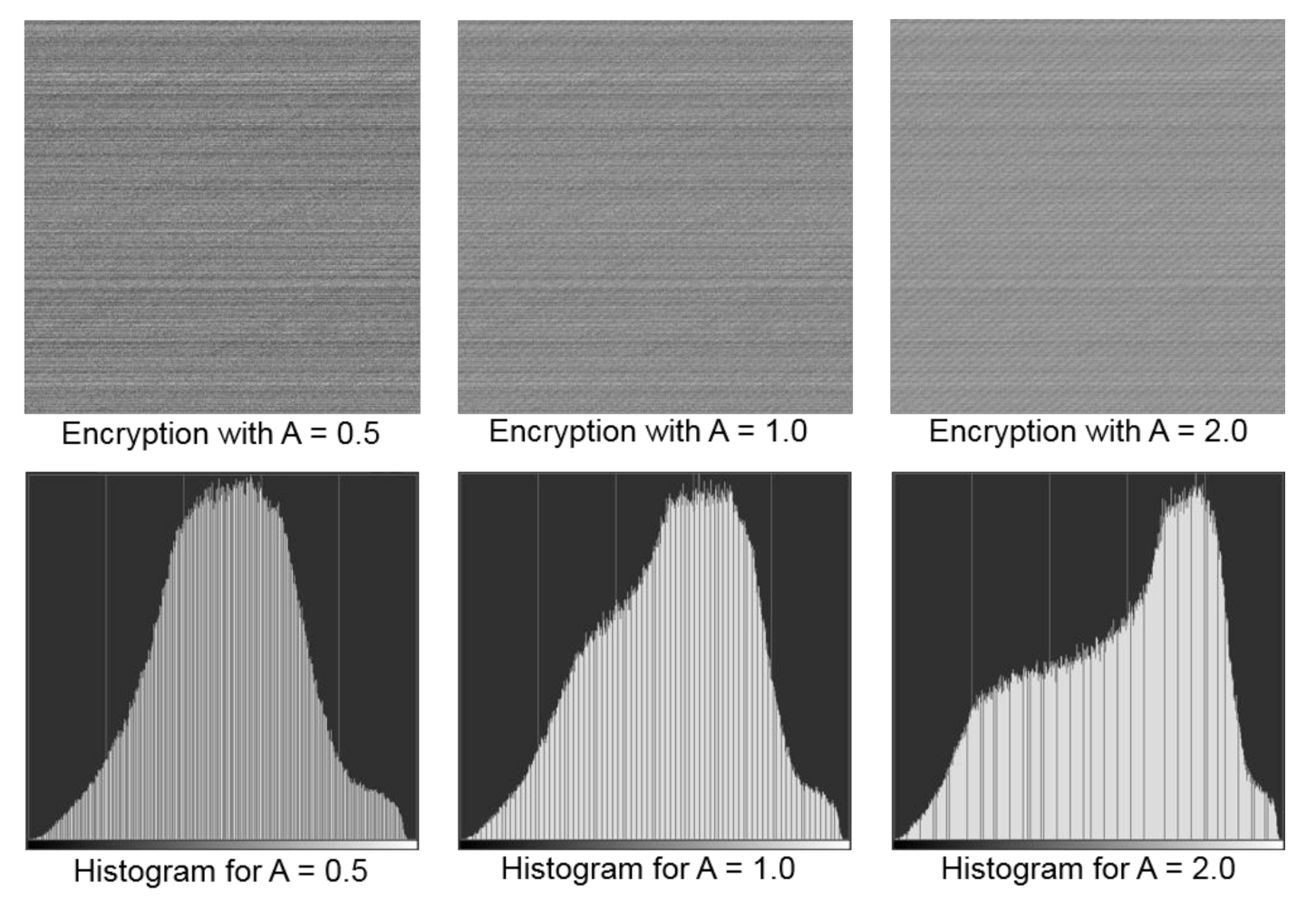
3. Results and Discussion
3.1. Decryption and Merging
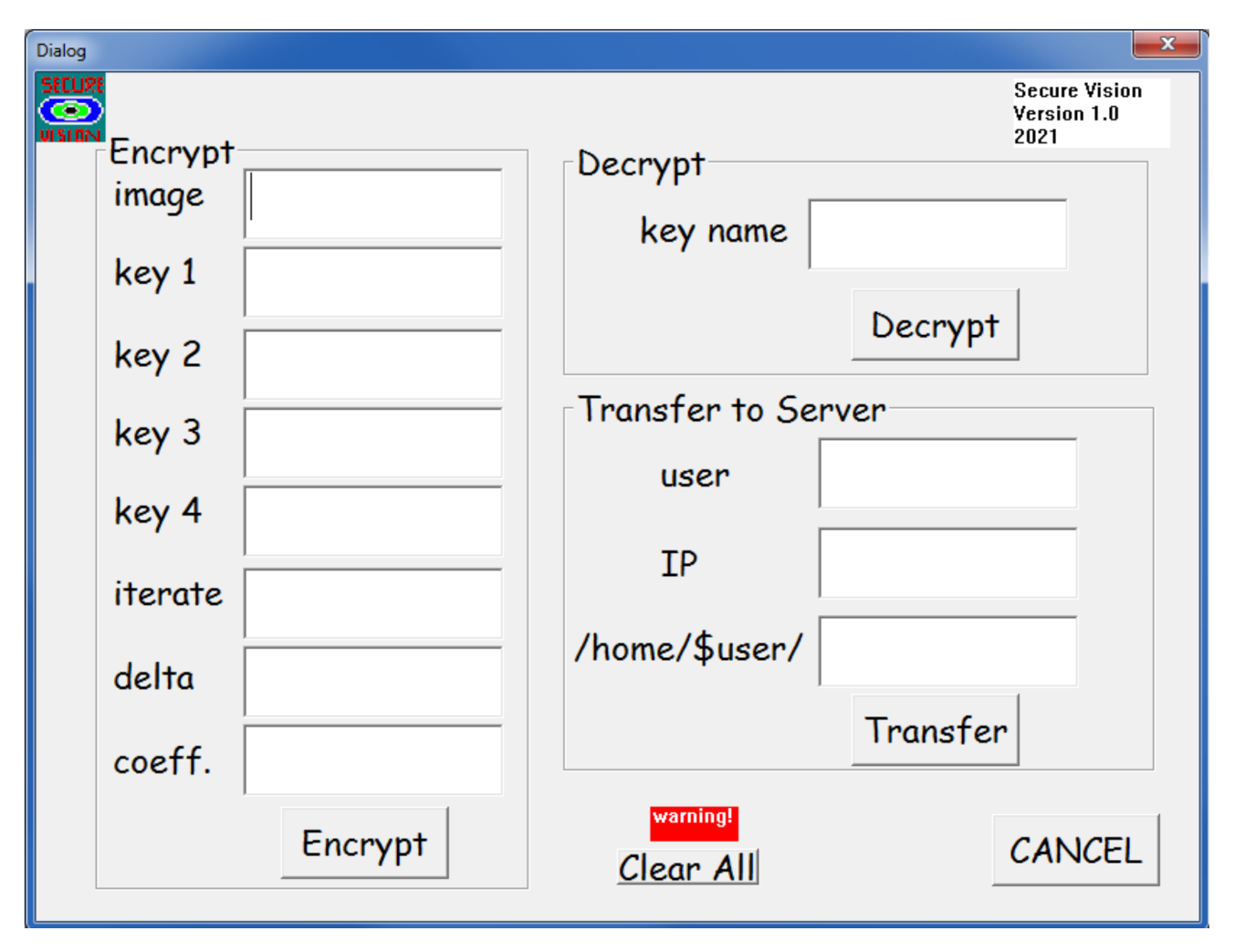
3.2. Graphical User Interface
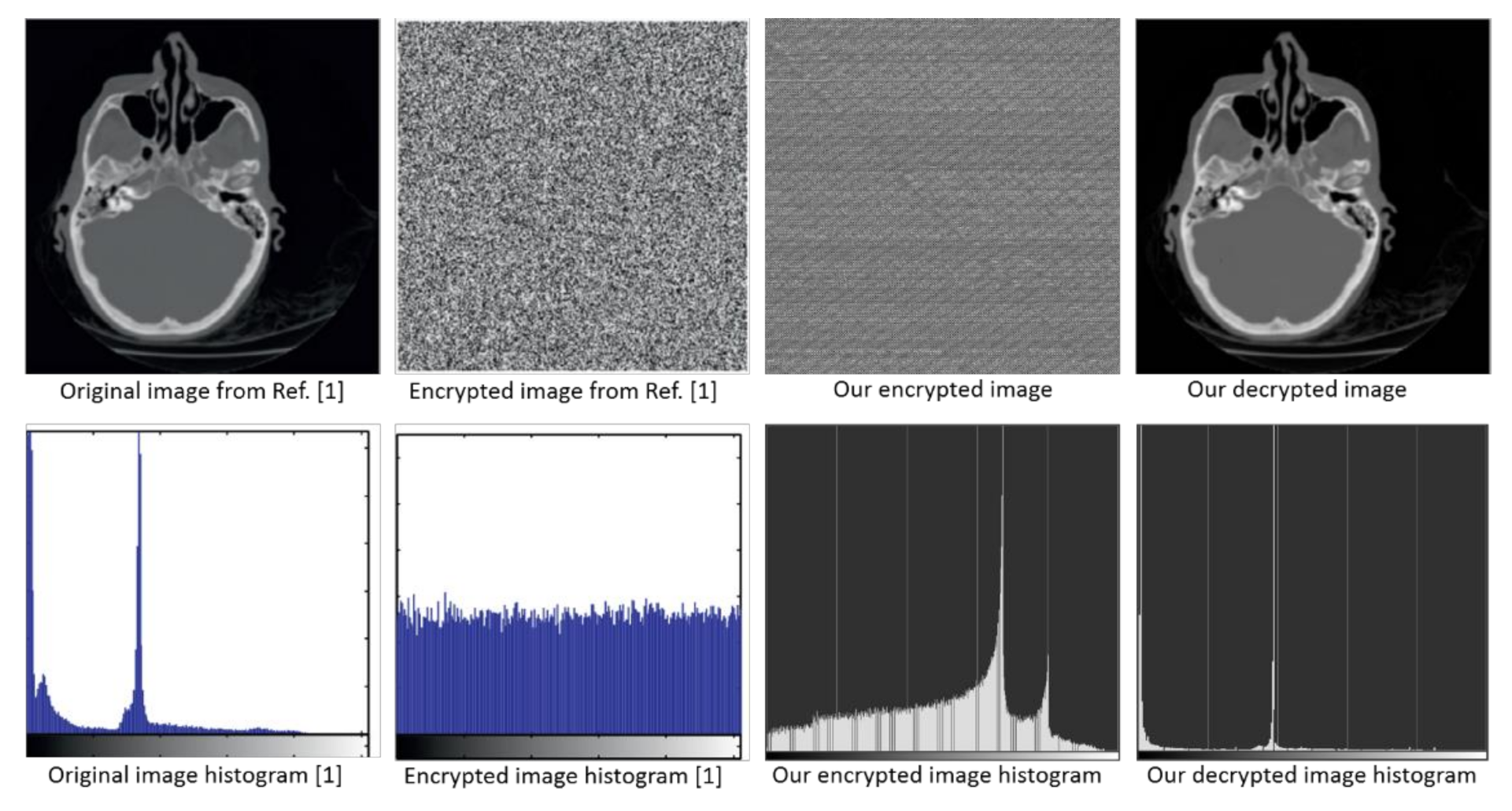
3.3. Examples and Testing
3.4. Decryption Sensitivity to Keys
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AES | Advanced Encryption Standard |
| ASCII | American Standard Code for Information Interchange |
| CUDA | Compute Unified Device Architecture |
| GPG | GNU Privacy Guard |
| GUI | Graphical User Interface |
| IP | Internet Protocol |
| MPI | Message Passing Interface |
| PSCP | PuTTY Secure Copy Client |
| QR code | Quick Response code |
| RGB | Red Green Blue |
| SSH | Secure Shell |
| a | Major axis of ellipse |
| b | Minor axis of ellipse |
| x | Cartesian x-coordinate |
| y | Cartesian y-coordinate |
| deno | Denominator for modulo operation |
| w | Image width |
| h | Image height |
| INP(i,j) | Original image element array |
| A | Cosine function amplitude controller |
References
- Hua, Z.; Yi, S.; Zhou, Y. Medical image encryption using high-speed scrambling and pixel adaptive diffusion. Signal Process. 2018, 144, 134–144. [Google Scholar] [CrossRef]
- Zinger, S.; Ruijters, D.; Do, L.; de With, P.H.N. View interpolation for medical images on autostereoscopic displays. IEEE Trans. Circuits Syst. Video Technol. 2011, 22, 128–137. [Google Scholar] [CrossRef]
- Lacoste, C.; Lim, J.H.; Chevallet, J.P.; Le, D.T. Medical-image retrieval based on knowledge-assisted text and image indexing. IEEE Trans. Circuits Syst. Video Technol. 2007, 17, 889–900. [Google Scholar] [CrossRef] [Green Version]
- Chai, X.; Chen, Y.; Broyde, L. A novel chaos-based image encryption algorithm using DNA sequence operations. Opt. Lasers Eng. 2017, 88, 197–213. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wang, X.Y. A new image encryption algorithm based on non-adjacent coupled map lattices. Appl. Soft Comput. 2015, 26, 10–20. [Google Scholar] [CrossRef]
- Ping, P.; Xu, F.; Wang, Z.J. Image encryption based on non-affine and balanced cellular automata. Signal Process. 2014, 105, 419–429. [Google Scholar] [CrossRef]
- Chai, X.; Gan, Z.; Chen, Y.; Zhang, Y. A visually secure image encryption scheme based on compressive sensing. Signal Process. 2017, 134, 35–51. [Google Scholar] [CrossRef] [Green Version]
- Li, X.W.; Lee, I.K. Modified computational integral imaging-based double image encryption using fractional Fourier transform. Opt. Lasers Eng. 2015, 66, 112–121. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X. Image encryption using DNA complementary rule and chaotic maps. Appl. Soft Comput. 2012, 12, 1457–1466. [Google Scholar] [CrossRef]
- Gong, L.; Liu, X.; Zheng, F.; Zhou, N. Flexible multiple-image encryption algorithm based on log-polar transform and double random phase encoding technique. J. Mod. Opt. 2013, 60, 1074–1082. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhang, Y.Q.; Bao, X.M. A novel chaotic image encryption scheme using DNA sequence operations. Opt. Lasers Eng. 2015, 73, 53–61. [Google Scholar] [CrossRef]
- Zhou, N.; Hu, Y.; Gong, L.; Li, G. Quantum image encryption scheme with iterative generalized Arnold transforms and quantum image cycle shift operations. Quantum Inf. Process. 2017, 16, 164. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wang, X.Y. A symmetric image encryption algorithm based on mixed linear–nonlinear coupled map lattice. Inf. Sci. 2014, 273, 329–351. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Pun, C.M.; Chen, C.P. 2D Sine Logistic modulation map for image encryption. Inf. Sci. 2015, 297, 80–94. [Google Scholar] [CrossRef]
- Tang, Z.; Yang, Y.; Xu, S.; Yu, C.; Zhang, X. Image encryption with double spiral scans and chaotic maps. Secur. Commun. Netw. 2019, 2019, 8694678. [Google Scholar] [CrossRef] [Green Version]
- Tang, Z.; Zhang, X. Secure image encryption without size limitation using Arnold transform and random strategies. J. Multimed. 2011, 6, 202. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, X.; Lan, W. Efficient image encryption with block shuffling and chaotic map. Multimed. Tools Appl. 2015, 74, 5429–5448. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, Q. A novel image encryption method based on total shuffling scheme. Opt. Commun. 2011, 284, 2775–2780. [Google Scholar] [CrossRef]
- Ye, G. Image scrambling encryption algorithm of pixel bit based on chaos map. Pattern Recognit. Lett. 2010, 31, 347–354. [Google Scholar] [CrossRef]
- Alawida, M.; Teh, J.S.; Samsudin, A. An image encryption scheme based on hybridizing digital chaos and finite state machine. Signal Process. 2019, 164, 249–266. [Google Scholar] [CrossRef]
- Prasad, M.; Sudha, K.L. Chaos image encryption using pixel shuffling. CCSEA 2011, 1, 169–179. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, G.; Hou, W.; Huang, P.; Liu, B.; Li, S. A Novel Asymmetric Hyperchaotic Image Encryption Scheme Based on Elliptic Curve Cryptography. Appl. Sci. 2021, 11, 5691. [Google Scholar] [CrossRef]
- Lin, C.H.; Hu, G.H.; Chan, C.Y.; Yan, J.J. Chaos-Based Synchronized Dynamic Keys and Their Application to Image Encryption with an Improved AES Algorithm. Appl. Sci. 2021, 11, 1329. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Tan, W.; Li, L. A novel chaos-based image encryption scheme by using randomly DNA encode and plaintext related permutation. Appl. Sci. 2020, 10, 7469. [Google Scholar] [CrossRef]
- Cao, X.; Huang, Y.; Wu, H.T.; Cheung, Y.M. Content and privacy protection in JPEG images by reversible visual transformation. Appl. Sci. 2020, 10, 6776. [Google Scholar] [CrossRef]
- Wu, H.; Wang, J.; Zhang, Z.; Chen, X.; Zhu, Z. A Multi-Image Encryption with Super-Lager-Capacity Based on Spherical Diffraction and Filtering Diffusion. Appl. Sci. 2020, 10, 5691. [Google Scholar] [CrossRef]
- Saraiva, D.A.; Leithardt, V.R.; de Paula, D.; Sales Mendes, A.; González, G.V.; Crocker, P. Prisec: Comparison of symmetric key algorithms for IoT devices. Sensors 2019, 19, 4312. [Google Scholar] [CrossRef] [Green Version]
- Reddy, K.R.; Rao, C.M. GUI implementation of image encryption and decryption using Open CV-Python script on secured TFTP protocol. In Proceedings of the AIP Conference, Secunderabad, India, 22–23 December 2017; AIP Publishing LLC: College Park, MD, USA, 2018; Volume 1952, p. 020074. [Google Scholar] [CrossRef]
- Zaman, J.K.; Ghosh, R. A review study of NIST statistical test suite: Development of an indigenous computer package. arXiv 2012, arXiv:1208.5740. [Google Scholar]
- Wang, X.Y.; Zhang, H.L. A color image encryption with heterogeneous bit-permutation and correlated chaos. Opt. Commun. 2015, 342, 51–60. [Google Scholar] [CrossRef]
- The GNU Privacy Guard. Available online: https://gnupg.org/ (accessed on 5 July 2021).
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2016, 78, 17–25. [Google Scholar] [CrossRef]
- Wang, X.Y.; Liu, L.T.; Zhang, Y.Q. A novel chaotic block image encryption algorithm based on dynamic random growth technique. Opt. Lasers Eng. 2015, 66, 10–18. [Google Scholar] [CrossRef]
- Chen, J.X.; Zhu, Z.L.; Fu, C.; Yu, H. A fast image encryption scheme with a novel pixel swapping-based confusion approach. Nonlinear Dyn. 2014, 77, 1191–1207. [Google Scholar] [CrossRef]
- Ye, G.D.; Wong, K.W. An efficient chaotic image encryption algorithm based on a generalized Arnold map. Nonlinear Dyn. 2012, 69, 2079–2087. [Google Scholar] [CrossRef]
- Sethi, N.; Sharma, D. A novel method of image encryption using logistic mapping. Int. J. Comput. Sci. Eng. 2012, 1, 115–119. [Google Scholar]












| p-Value | 0.0001–0.001 | 0.001–0.01 | 0.01–0.1 | 0.1–1.0 |
|---|---|---|---|---|
| Count | 7 | 83 | 904 | 8932 |
| Results | Non-random | Non-random | Random | Random |
| Image Size | Encryption Time (min:s:ms) | Decryption Time (min:s:ms) |
|---|---|---|
| 768 × 1024 | 00:05:53 | 00:07:39 |
| 1200 × 1600 | 00:13:42 | 00:17:95 |
| 2367 × 1957 | 00:32:56 | 00:43:06 |
| 2760 × 2184 | 00:42:67 | 00:56:92 |
| 3024 × 4032 | 01:29:20 | 02:00:32 |
| Ref. No. | Technique | Key Space | GUI | Speed | Programming Language |
|---|---|---|---|---|---|
| [32] | Bitplane decomposition and Chaotic maps | 0.25 × 1064 | No | Low | Matlab |
| [30] | Permutation and interrelated chaos | 10108 | No | Low | - |
| [33] | Dynamic random growth technique | >1096 | No | Moderate | C++ |
| [34] | Swapping-based confusion approach | 0.18 × 1060 | No | Good | C |
| [35] | Arnold map | >2100 | No | Moderate | Matlab |
| [36] | Logistic mapping | 10112 | No | Moderate | Matab |
| [19] | Scrambling encryption algorithm based on chaos map | >2100 | No | Moderate | Matab |
| [28] | AES on secured TFTP protocol | >2128 | Yes | Moderate | Python |
| Our work | Random pixel shuffling | >10100 | Yes | Good | Fortran |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahmohammadi Beni, M.; Watabe, H.; Yu, K.N. SecureVision: An Open-Source User-Customizable Image Encryption Program. Appl. Sci. 2021, 11, 7915. https://doi.org/10.3390/app11177915
Shahmohammadi Beni M, Watabe H, Yu KN. SecureVision: An Open-Source User-Customizable Image Encryption Program. Applied Sciences. 2021; 11(17):7915. https://doi.org/10.3390/app11177915
Chicago/Turabian StyleShahmohammadi Beni, Mehrdad, Hiroshi Watabe, and Kwan Ngok Yu. 2021. "SecureVision: An Open-Source User-Customizable Image Encryption Program" Applied Sciences 11, no. 17: 7915. https://doi.org/10.3390/app11177915
APA StyleShahmohammadi Beni, M., Watabe, H., & Yu, K. N. (2021). SecureVision: An Open-Source User-Customizable Image Encryption Program. Applied Sciences, 11(17), 7915. https://doi.org/10.3390/app11177915





_Kwan_Ngok_Yu.png)

