Reduction of Compression Artifacts Using a Densely Cascading Image Restoration Network

Abstract

Since high quality realistic media are widely used in various computer vision applications, image compression is one of the essential technologies to enable real-time applications. Image compression generally causes undesired compression artifacts, such as blocking artifacts and ringing effects. In this study, we propose a densely cascading image restoration network (DCRN), which consists of an input layer, a densely cascading feature extractor, a channel attention block, and an output layer. The densely cascading feature extractor has three densely cascading (DC) blocks, and each DC block contains two convolutional layers, five dense layers, and a bottleneck layer. To optimize the proposed network architectures, we investigated the trade-off between quality enhancement and network complexity. Experimental results revealed that the proposed DCRN can achieve a better peak signal-to-noise ratio and structural similarity index measure for compressed joint photographic experts group (JPEG) images compared to the previous methods.

1. Introduction

As realistic media are widespread in various image processing areas, image compression is one of the key technologies to enable real-time applications with limited network bandwidth. While image compression techniques, such as joint photographic experts group (JPEG) [1], web picture [2], and high-efficiency video coding main still picture [3], can achieve significant compression performances for efficient image transmission and storage [4], they lead to undesired compression artifacts due to lossy coding because of quantization. These artifacts generally affect the performance of image restoration methods in terms of super-resolution [5,6,7,8,9,10], contrast enhancement [11,12,13,14], and edge detection [15,16,17].

Reduction methods for compression artifacts were initially studied by developing a specific filter inside the compression process [18]. Although these approaches can efficiently remove ringing artifacts [19], the improvement in image regions is limited at high frequencies. Examples of such approaches include deblocking-oriented approaches [20,21], wavelet transforms [22,23], and shape-adaptive discrete cosine transforms [24]. Recently, artifacts reduction (AR) networks using deep learning have been developed with various deep neural networks (DNNs), such as convolutional neural networks (CNNs), recurrent neural networks (RNNs), long short-term memory (LSTM), and generative adversarial networks (GANs). Because CNN [25] can efficiently extract feature maps with deep and cascading structures, CNN-based artifact reduction (AR) methods can achieve visual enhancement in terms of peak signal-to-noise ratio (PSNR) [26], PSNR including blocking effects (PSNR-B) [27,28], and structural similarity index measures (SSIM) [29].

Despite the developments of AR, most CNN-based approaches tend to design the heavy network architecture by increasing the number of network parameters and operations. Because it is difficult to deploy such heavy models on hand-held devices operated on low complexity environments, it is necessary to design the lightweight AR networks. In this paper, we propose a lightweight CNN-based artifacts reduction model to reduce the memory capacity as well as network parameters. The main works of this study are summarized as follows:

▪

To reduce the coding artifacts of the compressed images, we propose a CNN based densely cascading image restoration network (DCRN) with two essential parts, densely cascading feature extractor and channel attention block.

▪

Through a various ablation study, the proposed network is designed to guarantee the optimal trade-off between the PSNR and the network complexity.

▪

Compared to the previous method, the proposed network is designed to obtain comparable AR performance while utilizing the small number of network parameters and memory size. In addition, it can provide the fastest inference speed, except for initial AR network [30].

▪

Compared to the latest methods to show the highest AR performances (PSNR, SSIM, and PSNR-B), the proposed method can reduce the number of parameters and total memory size maximum by 2% and 5%, respectively.

The remainder of this paper is organized as follows: in Section 2, we review previous studies related to CNN-based artifact reduction methods. In Section 3, we describe the proposed method. Finally, in Section 4 and Section 5, we present the experimental results and conclusions, respectively.

2. Related Works

Due to the advancements in deep learning technologies, research of low-level computer vision, such as super-resolution (SR) and image denoising, has been combined with a variety of CNN architectures to provide higher image restoration than that of conventional image processing. Dong et al. proposed an artifact reduction convolutional neural network (ARCNN) [30], which consists of four convolutional layers and trains an end-to-end mapping from a compressed image to a reconstructed image. After the advent of ARCNN, Mao et al. [31] proposed a residual encoder–decoder network, which conducts encoding and decoding processes with symmetric skip connections in stacking convolutional and deconvolutional layers. Chen et al. [32] proposed a trainable nonlinear reaction diffusion, which is simultaneously learned from training data through a loss-based approach with all parameters, including filters and influence functions. Zhang et al. [33] proposed a denoising convolutional neural network (DnCNN), which is composed of a combination of 17 convolutional layers with a rectified linear unit (ReLU) [34] activation function and batch normalization for removing white Gaussian noise. Cavigelli et al. [35] proposed a deep CNN for image compression artifact suppression, which consists of 12 convolutional layers with hierarchical skip connections and a multi-scale loss function.

Guo et al. [36] proposed a one-to-many network, which is composed of many stacked residual units, with each branch containing five residual units and the aggregation subnetwork comprising 10 residual units. Each residual unit uses batch normalization, ReLU activation function, and convolutional layer twice. The architecture of residual units is found to improve the recovery quality. Tau et al. [37] proposed a very deep persistent memory network with a densely recursive residual architecture-based memory block that adaptively learns the different weights of various memories. Dai et al. [38] proposed a variable-filter-size residual-learning CNN, which contains six convolutional layers and concatenates variable-filter-size convolutional layers. Zhang et al. [39] proposed a dual-domain multi-scale CNN with an auto-encoder, dilated convolution, and discrete cosine transform (DCT) unit. Liu et al. [40] designed a multi-level wavelet CNN that builds a u-net architecture with a four-layer fully convolutional network (FCN) without pooling and takes all sub-images as inputs. Each layer of a CNN block is composed of 3 × 3 kernel filters, batch normalization, and ReLU. A dual-pixel-wavelet domain deep CNN-based soft decoding network for JPEG-compressed images [41] is composed of two parallel branches, each serving as the pixel domain soft decoding branch and wavelet domain soft decoding branch. Fu et al. [42] proposed a deep convolutional sparse coding (DCSC) network that has dilated convolutions to extract multi-scale features with the same filter for three different scales. The implicit dual-domain convolutional network (IDCN) for robust color image compression AR [43] consists of a feature encoder, correction baseline and feature decoder. Zhang et al. [44] proposed a residual dense network (RDN), which consists of 16 residual dense blocks, and each dense block contains eight dense layers with local residual learning.

Although most of the aforementioned methods demonstrate better AR performance, they tend to possess more complicated network structures on account of the large number of network parameters needed and heavy memory consumption. Table 1 lists the properties of the various AR networks and compares their advantages and disadvantages.

Table 1. Properties among the artifact reduction networks.

Method	AR Performance	Complexity
ARCNN [30]	Low PSNR	Low network complexity
DnCNN [33]	Medium PSNR	Medium network complexity
DCSC [42]	Medium PSNR (High PSNR-B)	Medium network complexity
IDCN [43]	High PSNR and PSNR-B	High network complexity
RDN [44]	High PSNR and PSNR-B	High network complexity

For the network component, a residual network [45] was designed for shortcut connections to simplify identity mapping, and outputs were added to the outputs of the stacked layers. A densely connected convolutional network [46] directly connects all layers with one another based on equivalent feature map sizes. The squeeze-and-excitation (SE) network [47] is composed of global average pooling and a 1 × 1 convolutional layer. These networks use the weights of previous feature maps, and such weights are applied to previous feature maps to generate the output of the SE block, which can be provided to subsequent layers of the network. In this study, we propose an AR network to combine with those networks [45,46,47] for better image restoration performance than the previous methods.

3. Proposed Method

3.1. Overall Architecture of DCRN

Figure 1 shows the overall architecture of the proposed DCRN to remove compression artifacts caused by JPEG compression. The DCRN consists of the input layer, a densely cascading feature extractor, a channel attention block, and the output layer. In particular, the densely cascading feature extractor contains three densely cascading blocks to exploit the intermediate feature maps within sequential dense networks. In Figure 1, W × H and C are the spatial two-dimensional filter size and the number of channels, respectively. The convolution operation of the i-th layer is denoted as H_i and calculates the output feature maps (F_i) from the previous feature maps (F_i−1), as shown in Equation (1):

$$F_i=H_i(F_{i-1})=\delta (W_i\ast F_{i-1}+B_i),$$

(1)

where δ, W_i, B_i, and ∗ represent the parametric ReLU function as an activation function, filter weights, biases, and the notation of convolution operation, respectively. After extracting the feature maps of the input layer, densely cascading feature extractor generates F₅, as expressed in Equation (2). As shown in Figure 2, a densely cascading (DC) block has two convolutional layers, five dense layers, and a bottleneck layer. To train the network effectively and reduce overfitting, we designed dense layers that consist of a variable number of channels. Dense layers 1 to 4 consist of 16 channels and the final dense layer consists of 64 channels. The DC block operation $H_i^{DC}$ is presented in Equation (2):

$$F_3=H_3^{DC}(F_2)=H_3^{DC}(H_2^{DC}(H_1^{DC}(F_0)).$$

(2)

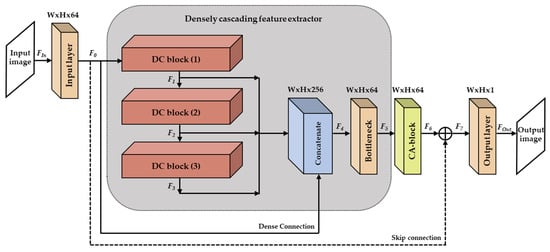
Figure 1. Overall architecture of the proposed DCRN. Symbol ‘+’ indicates the element-wise sum.

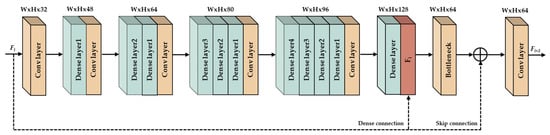
Figure 2. The architecture of a DC block.

Then, each DC block output is concatenated with the output of the input layer feature map operations. After concatenating both the output feature maps from all DC blocks and the input layer, the bottleneck layer calculates F₅ to reduce the number of channels of F₄, as in Equation (3):

$$F_5=H_5(F_4)=H_5([F_3,F_2,F_1,F_0]).$$

(3)

As shown in Figure 3, a channel attention (CA) block performs the global average pooling (GAP) followed by two convolutional layers and the sigmoid function after the output from the densely cascading feature extractor is passed to it. The CA block can discriminate the more important feature maps, and it assigns different weights to each feature map in order to adapt feature responses. After generating F₆ through the CA block, an output image is generated from the element-wise sum between the skip connection (F₀) and the feature maps (F₆).

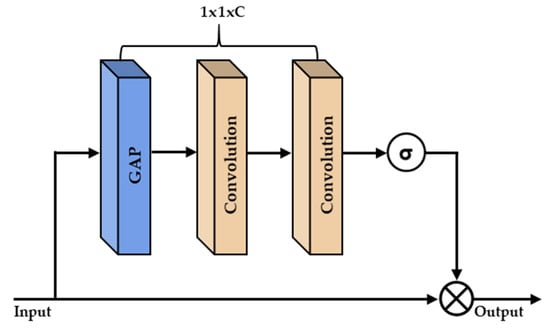
Figure 3. The architecture of a CA-block. ‘σ’ and ‘ ⊗’ indicate sigmoid function and channel-wise product, respectively.

3.2. Network Training

In the proposed DCRN, we set the filter size as 3 × 3 except for the CA block, whose kernel size is 1 × 1. Table 2 shows the selected hyper parameters in the DCRN. We used zero padding to allow all feature maps to have the same spatial resolution between the different convolutional layers. We defined L1 loss [48] as the loss function using Adam optimizer [49] with a batch size of 128. The learning rate was decreased from 10⁻³ to 10⁻⁵ for 50 epochs.

Table 2. Hyper parameters of the proposed DCRN.

Hyper Parameters	Options
Loss function	L1 loss
Optimizer	Adam
Batch size	128
Num. of epochs	50
Learning rate	10−3 to 10−5
Initial weight	Xavier
Activation function	Parametric ReLU
Padding mode	Zero padding

To design a lightweight architecture, we first studied the relationship between network complexity and performance according to the number of dense layer feature maps within the DC block. Second, we checked the performance of various activation functions. Third, we studied the performance of loss functions. Fourth, we investigated the relationship between network complexity and performance based on the number in each dense layers of DC block and the number of DC blocks. Finally, we studied the performance of the tool-off test (skip connection, channel attention block).

Table 3 lists the PSNR obtained according to the number of concatenated feature maps within the DC block. We set the optimal number of concatenated feature maps to 16 channels. Moreover, we conducted verification tests to determine the most suitable activation function for the proposed network, the results of which are shown in Figure 4. After measuring the PSNR and SSIM obtained via various activation functions, such as ReLU [34], leaky ReLU [50], and parametric ReLU [51], parametric ReLU was chosen for the proposed DCRN. Table 4 summarizes the results of the verification tests concerning loss functions, in terms of the L1 and mean square error (MSE) losses. As shown in Table 4, the L1 loss exhibits marginally improved PSNR, SSIM, and PSNR-B compared to those exhibited by the MSE loss. In addition, we verified the effectiveness the of skip connection and channel attention block mechanisms. Through the results of tool-off tests on the proposed DCRN, which are summarized in Figure 5, we confirmed that both skip connection and channel attention block affect the AR performance of the proposed method.

Table 3. Verification test on the number of concatenated feature maps within the DC block.

Category	PSNR (dB)	Num of Parameter	Total Memory Size (MB)
4 channel	29.58	316 K	33.56
8 channel	29.61	366 K	36.39
16 channel	29.64	479 K	42.10
32 channel	29.68	770 K	53.75
64 channel	29.69	1600 K	78.01

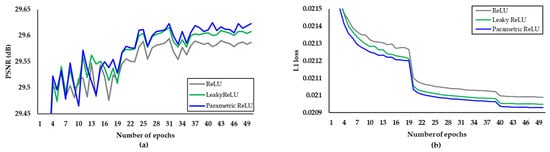
Figure 4. Verification of activation functions. (a) PSNR per epoch. (b) L1 loss per epoch.

Table 4. Verification tests for loss functions.

Category	PSNR (dB)	SSIM	PSNR-B (dB)
L1 loss	29.64	0.825	29.35
MSE loss	29.62	0.824	29.33

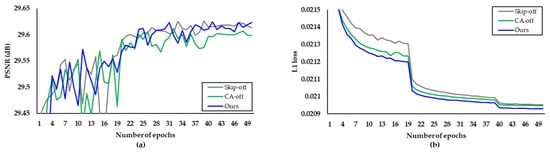
Figure 5. Verification of the skip connection off (skip-off), channel attention blocks off (CA-off) and proposed method in terms of AR performance. (a) PSNR per epoch. (b) L1 loss per epoch.

Note that the higher the number of DC blocks and dense layers, the more the memory required to store the network parameters. Finally, we performed a variety of verification tests on the validation dataset to optimize the proposed method. In this paper, we denote the number of DC blocks and the number of dense layers per DC block as DC and L, respectively. The performance comparison between the proposed and existing methods in terms of the AR performance (i.e., PSNR), model size (i.e., number of parameters), and total memory size is displayed in Figure 6 and Figure 7. We set the value of DC and L to three and five, respectively.

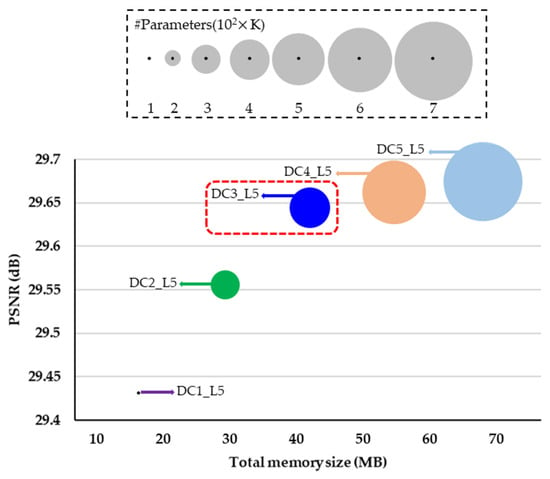
Figure 6. Verification of the number of DC blocks (DC) in terms of AR performance and complexity by using the Classic5 dataset. The circle size represents the number of parameters. The x and y-axis denote the total memory size and PSNR, respectively.

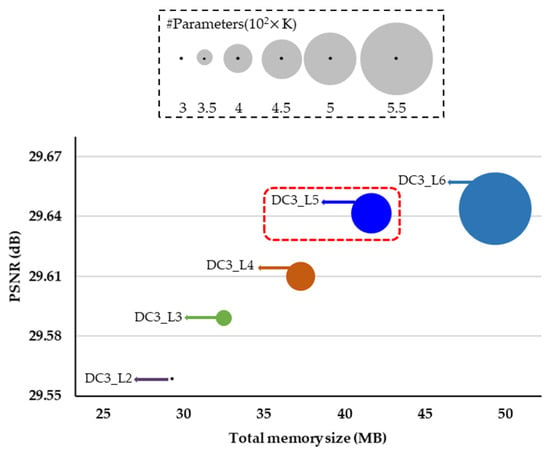
Figure 7. Verification of the number of dense layers (L) per DC block (DC) in terms of AR performance and complexity by using the Classic5 dataset. The circle size represents the number of parameters. The x and y-axis denote the total memory size and PSNR, respectively.

4. Experimental Results

We used 800 images from DIV2K [52] as the training images. After they were converted into YUV color format, only Y components were encoded and decoded by the JPEG codec under three image quality factors (10, 20, and 30). Through this process, we collected 1,364,992 patches of a 40 × 40 size from the original and reconstructed images. To evaluate the proposed method, we used Classic5 [24] (five images) and LIVE1 [53] (29 images) as the test datasets and Classic5 as the validation dataset.

All experiments were performed on an Intel Xeon Gold 5120 (14 cores @ 2.20 GHz) with 177 GB RAM and two NVIDIA Tesla V100 GPUs under the experimental environment described in Table 5.

Table 5. Experimental environments.

Experimental Environments	Options
Input size (FIn)	40 × 40 × 1
Label size (FOut)	40 × 40 × 1
CUDA version	10.1
Linux version	Ubuntu 16.04
Deep learning frameworks	Pytorch 1.4.0

In terms of the performance of image restoration, we compared the proposed DCRN with JPEG, ARCNN [30], DnCNN [33], DCSC [42], IDCN [43] and RDN [44]. In terms of the AR performance (i.e., PSNR and SSIM), the number of parameters and total memory size, the performance comparisons between the proposed and existing methods are depicted in Figure 8.

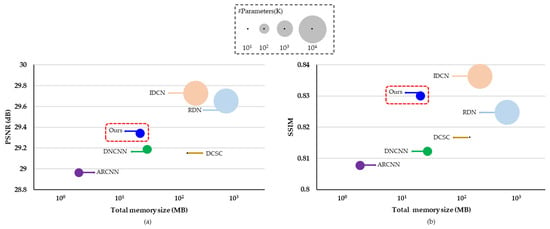
Figure 8. Comparisons of the network performance and complexity between the proposed DCRN and existing methods for the LIVE1 dataset. The circle size represents the number of parameters. (a) The x and y-axis denote the total memory size and PSNR, respectively. (b) The x and y-axis denote the total memory size and SSIM, respectively.

Table 6, Table 7 and Table 8 enumerate the results of PSNR, SSIM, and PSNR-B, respectively, for each of the methods studied. As per the results in Table 7, it is evident that the proposed method is superior to the others in terms of SSIM. However, RDN [44] demonstrate higher PSNR values. While DCRN shows a better PSNR-B compared to that of DnCNN, it has comparable performance with DCSC in terms of PSNR-B using the Classic5 dataset. While the RDN was likely to improve AR performance by increasing the number of network parameters, the proposed method was focused to design the lightweight network with the small number of network parameters.

Table 6. PSNR (dB) comparisons on the test datasets. The best results of dataset are shown in bold.

Dataset	Quality Factor	JPEG	ARCNN [30]	DnCNN [33]	DCSC [42]	RDN [44]	Ours
Classic5	10	27.82	29.03	29.40	29.25	30.00	29.64
	20	30.12	31.15	31.63	31.43	32.15	31.87
	30	31.48	32.51	32.91	32.68	33.43	33.15
LIVE1	10	27.77	28.96	29.19	29.17	29.67	29.34
	20	30.07	31.29	31.59	31.48	32.07	31.74
	30	31.41	32.67	32.98	32.83	33.51	33.16

Table 7. SSIM comparisons on the test datasets. The best results of dataset are shown in bold.

Dataset	Quality Factor	JPEG	ARCNN [30]	DnCNN [33]	DCSC [42]	RDN [44]	Ours
Classic5	10	0.780	0.793	0.803	0.803	0.819	0.825
	20	0.854	0.852	0.861	0.860	0.867	0.880
	30	0.884	0.881	0.886	0.885	0.893	0.903
LIVE1	10	0.791	0.808	0.812	0.815	0.825	0.830
	20	0.869	0.873	0.880	0.880	0.888	0.895
	30	0.900	0.904	0.909	0.909	0.915	0.922

Table 8. PSNR-B (dB) comparisons on the test datasets. The best results of dataset are shown in bold.

Dataset	Quality Factor	JPEG	ARCNN [30]	DnCNN [33]	DCSC [42]	Ours
Classic5	10	25.20	28.78	29.10	29.24	29.35
	20	27.50	30.60	31.19	31.41	31.40
	30	28.93	32.00	32.36	32.66	32.52
LIVE1	10	25.33	28.77	28.91	29.17	29.03
	20	27.56	30.79	31.08	31.47	31.21
	30	28.92	32.22	32.35	32.81	32.43

Table 9 classifies the network complexity in terms of the number of network parameters and total memory size (MB). The proposed DCRN reduced the number of parameters to as low as 72%, 5% and 2% of those needed in DnCNN, IDCN and RDN, respectively. In addition, the total memory size was as low as 91%, 41%, 17% and 5% of that required for DnCNN, DCSC, IDCN and RDN, respectively. Since the same network parameters were repeated 40 times in DCSC, the total memory size was large even though the number of network parameters was smaller than that of the other methods. As shown in Figure 9, the inference speed of the proposed method is greater than that of all networks, except for ARCNN. Although the proposed method is slower than ARCNN, it is clearly better than ARCNN in terms of PSNR, SSIM, and PSNR-B, as per the results in Table 6, Table 7 and Table 8. Figure 10 shows examples of the visual results of DCRN and the other methods on the test datasets. Based on the results, we were able to confirm that DCRN can recover more accurate textures than other methods.

Table 9. Comparisons of the network complexity between the proposed DCRN and the previous methods.

Category	Number of Parameters	Total Memory Size (MB)
ARCNN [30]	106 K	3.16
DnCNN [33]	667 K	46.31
DCSC [42]	93 K	102.34
IDCN [43]	11 M	254.13
RDN [44]	22 M	861.97
Ours	479 K	42.10

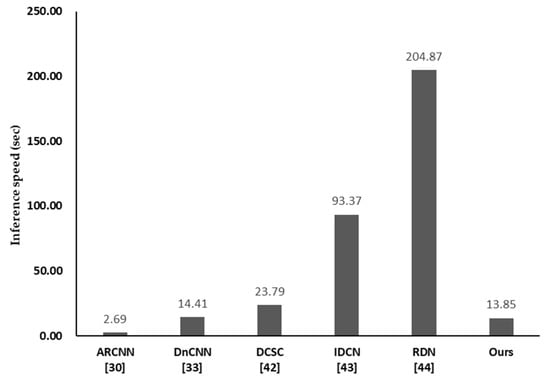
Figure 9. Inference speed on Classic5.

Figure 10. Visual comparisons on a JPEG compressed images where the figures of the second row represent the zoom-in for the area represented by the red box.

5. Conclusions

Image compression leads to undesired compression artifacts due to the lossy coding that occurs through quantization. These artifacts generally degrade the performance of image restoration techniques, such as super-resolution and object detection. In this study, we propose a DCRN, which consists of the input layer, a densely cascading feature extractor, a channel attention block, and the output layer. The DCRN aims to recover compression artifacts. To optimize the proposed network architecture, we extracted 800 training images from the DIV2K dataset and investigated the trade-off between the network complexity and quality enhancement achieved. Experimental results showed that the proposed DCRN can lead to the best SSIM for compressed JPEG images compared to that of other existing methods, except for IDCN. In terms of network complexity, the proposed DCRN reduced the number of parameters by as low as 72%, 5% and 2% compared to DnCNN, IDCN and RDN, respectively. In addition, the total memory size was as low as 91%, 41%, 17% and 5% of that required for DnCNN, DCSC, IDCN and RDN, respectively. Even though the proposed method was slower than ARCNN, it’s PSNR, SSIM, and PSNR-B are clearly better than those of ARCNN.