About the Use of Generalized Forms of Derivatives in the Study of Electromagnetic Problems
Abstract
1. Introduction
2. Lamb-Bateman Equation, Operational Methods, and Fractional Calculus
3. Generalized Exponential Operators and Fractional Electrical Circuit
Mittag–Leffler Functions and Fractional Electric Circuits
- (a)
- To state the form of the general solution of a non-homogeneous fractional equation including the initial conditions;
- (b)
- To establish the consistency between the different solutions we have obtained.
4. Fractional RLC Circuit
5. Permittivity Models and Fractional Derivatives
5.1. Summary
5.2. RC Circuit Tests Including Fractionary Dielectrics
6. Final Comments
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Mathematics in Science and Engineering; Elsevier: Amsterdam, The Netherlands, 1974; Volume 111. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Uchaikin, V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications; Gordon and Breach Science Publishers: Langhorne, PA, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus Models and Numerical Methods; World Scientific Publishing Company: New York, NY, USA, 2012. [Google Scholar]
- Dattoli, G.; Torre, A.; Quattromini, M. Miscellaneous results on the theory of evolution operators and generalized transformations. Il Nuovo Cim.-Soc. B 1999, 6, 693–708. [Google Scholar]
- Heaviside, O. Electromagnetic Induction and Its Propagation; The Electrician: 1887. Available online: https://www.gsjournal.net/Science-Journals/Historical%20Papers-Mechanics%20/%20Electrodynamics/Download/6897 (accessed on 13 August 2021).
- Bjorken, J.D.; Drell, S. Relativistic Quantum Mechanics; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar] [CrossRef]
- Baym, G. Lectures on Quantum Mechanics; Taylor & Francis Group: Boca Raton, FL, USA; CRC Press: Boca Raton, FL, USA, 1969; ISBN 9780805306675. [Google Scholar]
- Babusci, D.; Dattoli, G.; Quattromini, M. Relativistic equations with fractional and pseudodifferential operators. Phys. Rev. A 2011, 83, 062109. [Google Scholar] [CrossRef]
- Babusci, D.; Dattoli, G.; Quattromini, M.; Sabia, E. Relativistic harmonic oscillator, the associated equations of motion, and algebraic integration methods. Phys. Rev. E 2013, 87, 033202. [Google Scholar] [CrossRef]
- Dattoli, G.; Sabia, E.; Gorska, K.; Horzela, A. Relativistic wave equations: An operational approach. J. Phys. A Math. Theor. 2015, 48, 125203. [Google Scholar] [CrossRef]
- Barkai, E. Fractional Fokker-Planck equation, solution, and application. Phys. Rev. E 2001, 63, 046118. [Google Scholar] [CrossRef] [PubMed]
- Yen, C.S.; Fazarinc, Z.; Wheeler, R.L. Time-domain skin-effect model for transient analysis of lossy transmission lines. Proc. IEEE 1982, 70, 750–757. [Google Scholar]
- Cho, S.; Kim, K.R.; Park, B.-G.; Kang, I.M. Non-quasi-static modeling of silicon nanowire metal-oxide-semiconductor field-effect transistor and its model verification up to 1 THz. Jpn. J. Appl. Phys. 2010, 49, 110206. [Google Scholar] [CrossRef]
- Shang, Y.; Fei, W.; Yu, H. Fractional-order transmission line modeling. Int. J. Adv. Comput. Sci. Technol. 2013, 2, 18–24. [Google Scholar]
- Shang, Y.; Yu, H.; Fei, W. Design and Analysis of CMOS-Based Terahertz Integrated Circuits by Causal Fractional-Order RLGC Transmission Line Model. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 355–366. [Google Scholar] [CrossRef]
- Al-Daloo, M.; Soltan, A.; Yakovlev, A. Advance Interconnect Circuit Modeling Design Using Fractional-Order Elements. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2020, 39, 2722–2734. [Google Scholar] [CrossRef]
- Esser, A.T.; Smith, K.C.; Gowrishankar, T.R.; Weaver, J.C. Towards solid tumor treatment by nanosecond pulsed electric fields. Technol. Cancer Res. Treat. 2009, 8, 289–306. [Google Scholar] [CrossRef]
- Rekanos, I.T. FDTD Schemes for Wave Propagation in Davidson-Cole Dispersive Media Using Auxiliary Differential Equations. IEEE Trans. Antennas Propag. 2012, 60, 1467–1478. [Google Scholar] [CrossRef]
- Rekanos, I.T. FDTD Modeling of Havriliak-Negami Media. IEEE Microw. Wirel. Compon. Lett. 2012, 22, 49–51. [Google Scholar] [CrossRef]
- Tofighi, M. FDTD Modeling of Biological Tissues Cole–Cole Dispersion for 0.5–30 GHz Using Relaxation Time Distribution Samples—Novel and Improved Implementations. IEEE Trans. Microw. Theory Tech. 2009, 57, 2588–2596. [Google Scholar] [CrossRef]
- Abdullah, H.H.; Elsadek, H.A.; ElDeeb, H.E.; Bagherzadeh, N. Fractional Derivatives Based Scheme for FDTD Modeling of nth-Order Cole–Cole Dispersive Media. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 281–284. [Google Scholar] [CrossRef]
- Mescia, L.; Bia, P.; Caratelli, D. Fractional Derivative Based FDTD Modeling of Transient Wave Propagation in Havriliak–Negami Media. IEEE Trans. Microw. Theory Tech. 2014, 62, 1920–1929. [Google Scholar] [CrossRef]
- Lamb, H. On the diffraction of a solitary wave. Proc. Lond. Math. Soc. 1910, 28, 422–437. [Google Scholar] [CrossRef]
- Martin, P.A. Harry Bateman: From Manchester to Manuscript Project. Available online: https://studylib.net/doc/13384560/harry-bateman-from-manchester-to-manuscript-project (accessed on 13 August 2021).
- Babusci, D.; Dattoli, G.; Sacchetti, D. The Lamb-Bateman integral equation and the fractional derivatives. Fract. Calc. Appl. Anal. 2011, 14, 317–320. [Google Scholar] [CrossRef][Green Version]
- Babusci, D.; Dattoli, G.; Licciardi, S.; Sabia, E. Mathematical Methods for Physics; World Scientific: Singapore, 2019. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. Geophys. J. R. Astr. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Caputo, M. Elasticitá e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Caputo, M.; Fabrizio, M. Applications of new time and spatial fractional derivatives with exponential kernels. Progr. Fract. Differ. Appl. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional calculus. Integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: Wien, NY, USA, 1997; pp. 223–276. [Google Scholar]
- Licciardi, S. Umbral Calculus, a Different Mathematical Language. Ph.D. Thesis, Department of Mathematics and Computer Sciences, XXIX Cycle, University of Catania, Catania, Italy, 2018. [Google Scholar]
- Dattoli, G.; Górska, K.; Horzela, A.; Penson, K.A.; Sabia, E. Theory of relativistic heat polynomials and one-sided Lévy distributions. J. Math. Phys. 2017, 58, 063510. [Google Scholar] [CrossRef]
- Górska, K.; Horzela, A. The higher-order heat-type equations via signed Lévy stable and generalized Airy functions. J. Phys. A Math. Theor. 2013, 46, 425001. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Torre, A.; Vazquez, L. Evolution operator equations: Integration with algebraic and finite difference methods. Applications to physical problems in classical and quantum mechanics and quantum field theory. Riv. Nuovo Cim. 1997, 20, 3. [Google Scholar] [CrossRef]
- Anderssen, R.S.; Husain, S.A.; Loy, R.J. The Kohlrausch function: Properties and applications. Anziam J. 2004, 45, C800–C816. [Google Scholar] [CrossRef]
- Górska, K.; Horzela, A. Lévy stable distributions via associated integral transform. J. Math. Phys. 2012, 53, 053302. [Google Scholar] [CrossRef]
- Penson, K.A.; Górska, K. Exact and Explicit Probability Densities for One-Sided Lévy Stable Distributions. Phys. Rev. Lett. 2010, 105, 210604. [Google Scholar] [CrossRef] [PubMed]
- Feynman, R. The Feynman Lectures on Physics; California Institute of Technology, Michael A. Gottlieb and Rudolf Pfeiffer: Pasadena, CA, USA, 1964; Volume II, Chapter 22. [Google Scholar]
- Mittag-Leffler, M.G. Une généralisation de l’intégrale de Laplace-Abel. Comptes Rendus Hebd. Séances l’Académie Sci. 1903, 136, 537–539. [Google Scholar]
- Weisstein, E.W. Mittag-Leffler Function, from MathWorld—A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/Mittag-LefflerFunction.html (accessed on 13 August 2021).
- Dattoli, G.; Gorska, K.; Horzela, A.; Licciardi, S.; Pidatella, R.M. Comments on the Properties of Mittag-Leffler Function. Eur. Phys. J. Spec. Top. 2017, 226, 3427–3443. [Google Scholar] [CrossRef]
- Gorenflo, R.; Loutschko, J.; Luchko, Y. Computation of the Mittag–Leffler function and its derivatives. Fract. Calc. Appl. Anal. 2002, 5, 491–518. [Google Scholar]
- Gomez, F.; Rosales, J.; Guia, M. RLC electrical circuit of non-integer order. Cent. Eur. J. Phys. 2013, 11, 1361–1365. [Google Scholar] [CrossRef]
- Guia, M.; Gomez, F.; Rosales, J. Analysis of the time and frequency domain for the RC electric circuit of fractional order. Cent. Eur. J. Phys. 2013, 11, 1366–1371. [Google Scholar]
- Atangana, A.; Nieto, J.J. Numerical solution for the model of RLC circuit via the fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Atangana, A.; Badr, S.T.A. Extension of the RLC electrical circuit to fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7, 1–6. [Google Scholar]
- Alsaedi, A.; Nieto, J.J.; Vencatesh, V. Fractional electric circuits. Mech. Eng. Adv. 2015. [Google Scholar] [CrossRef]
- Shah, P.V.; Patel, A.D.; Salehbhai, I.A.; Shukla, A.K. Analytic solution for the RLC electric circuit model in fractional order. Abstr. Appl. Anal. 2014, 24, 343814. [Google Scholar]
- Artioli, M.; Dattoli, G.; Licciardi, S.; Pagnutti, S. Fractional Derivatives, Memory kernels and solution of Free Electron Laser Volterra type equation. Mathematics 2017, 5, 73. [Google Scholar] [CrossRef]
- Ruehli, A.; Antonini, G.; Jiang, L. PEEC Models for Dielectrics. In Circuit Oriented Electromagnetic Modeling Using the PEEC Techniques; John Wiley & Sons: New York, NY, USA, 2017; pp. 249–283. [Google Scholar] [CrossRef]
- Jahanshahi, S.; Babolian, E.; Torres, D.F.M.; Vahidi, A. Solving Abel integral equations of first kind via fractional calculus. J. King Saud Univ. Sci. 2015, 27, 161–167. [Google Scholar] [CrossRef]
- Dattoli, G.; Giannessi, L.; Quattromini, M.; Torre, A. Exponential operators, operational rules and evolution problems. Il Nuovo C. B 1998, 113, 699. [Google Scholar]
- Laskin, N. Fractional Schroedinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef] [PubMed]
- Dattoli, G.; Torre, A.; Mignani, R. Non Hermitian Evolution of Two-Level Quantum Systems. Phys. Rev. A 1990, 42, 1467. [Google Scholar] [CrossRef]
- Hermann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Hackensack, NJ, USA, 2011; ISBN 978-981-4340-24-3. [Google Scholar]
- Dattoli, G.; Ricci, P.E.; Khomasuridze, I. Operational methods, special polynomial and functions and solution of partial differential equations. Int. Transf. Spec. Funct. 2004, 15, 309–321. [Google Scholar] [CrossRef]
- Baskakov, V.A.; Popov, A.V. Implementation of transparent boundaries for numerical solution of the Schroedinger equation. Wave Motion 1991, 14, 123–128. [Google Scholar] [CrossRef]
- Popov, A.V. Accurate modeling of transparent boundaries in quasi-optics. Radio Sci. 1996, 31, 1781–1790. [Google Scholar] [CrossRef]
- Antoine, X.; Arnold, A.; Besse, C.; Ehrhardt, M.; Schadle, A. A review of transparent and artificial boundary conditions techniques for linear and nonlinear Schroedinger equations. Commun. Comput. Phys. 2008, 4, 729–796. [Google Scholar]
- Feshchenko, R.M.; Popov, A.V. Exact transparent boundary condition for the three-dimensional Schroedinger equation in a rectangular cuboid computational domain. Phys. Rev. E 2013, 88, 053308. [Google Scholar] [CrossRef]
- Hristov, J. Electrical Circuits of Non-integer Order: Introduction to an Emerging Interdisciplinary Area with Examples. In Analysis and Simulation of Electrical and Computer Systems; Mazur, D., Golębiowski, M., Korkosz, M., Eds.; Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2017; Volume 452. [Google Scholar] [CrossRef]
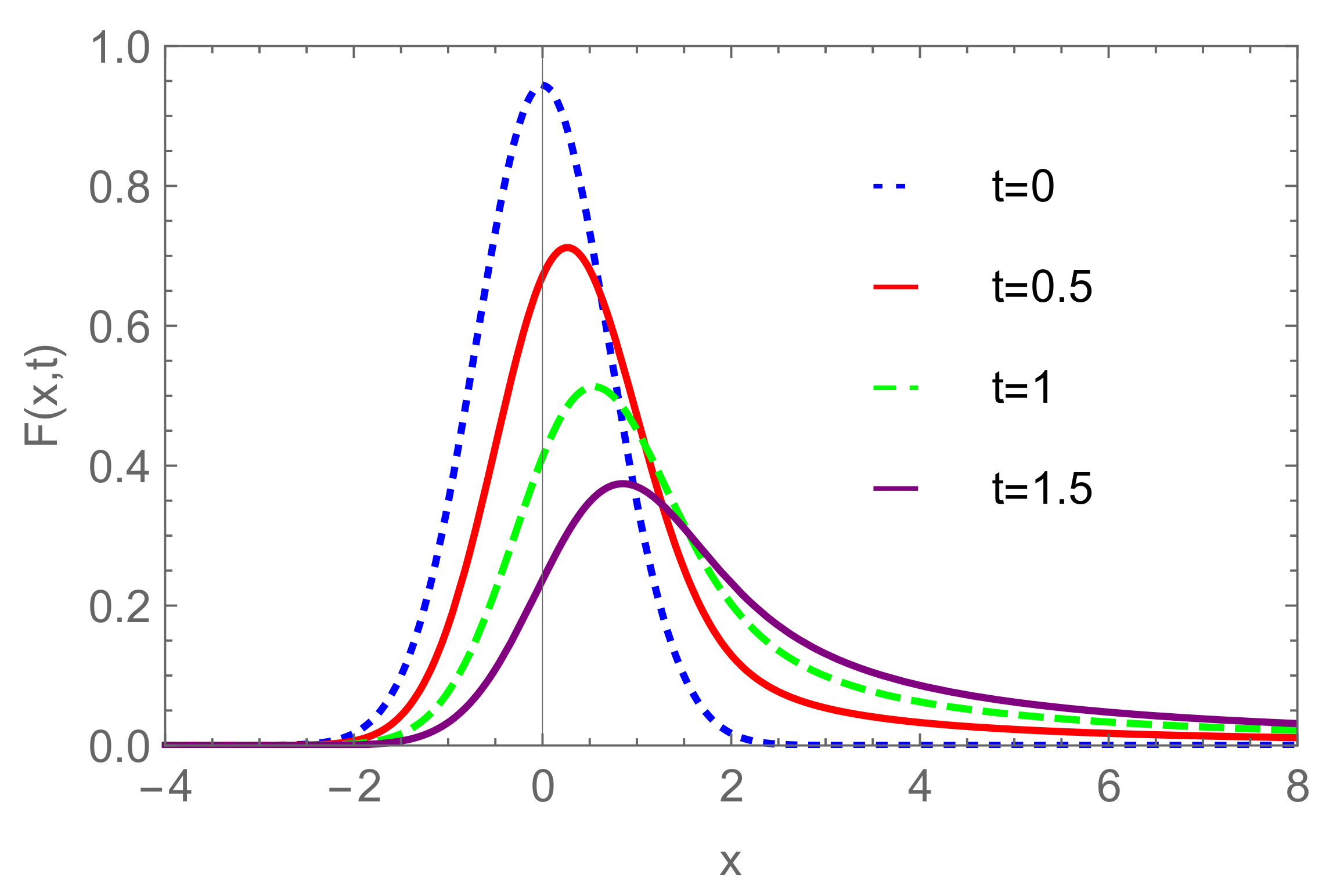
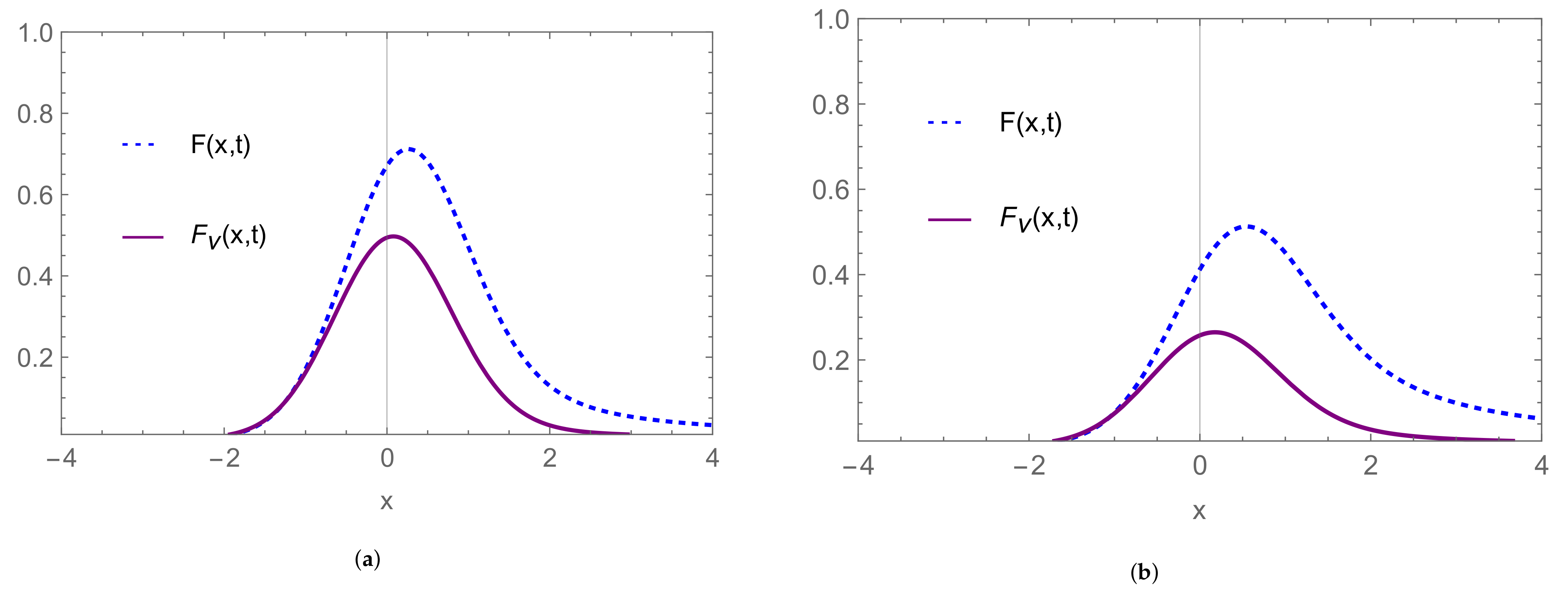

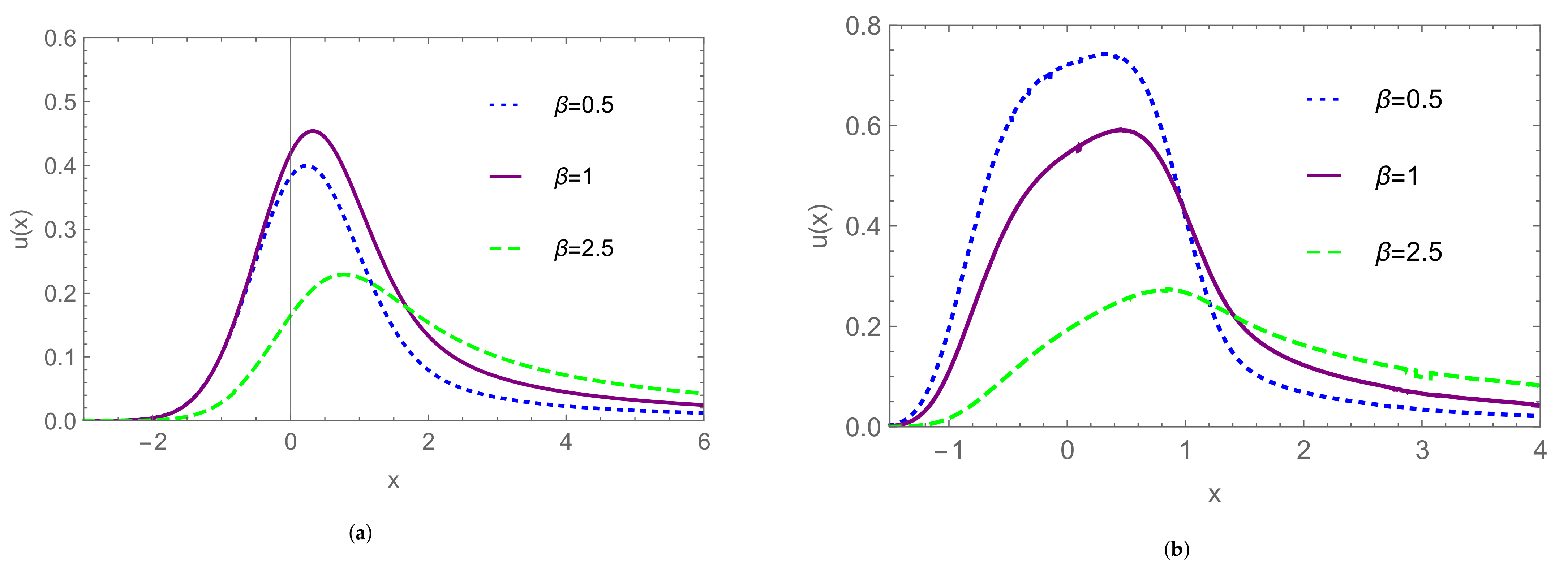
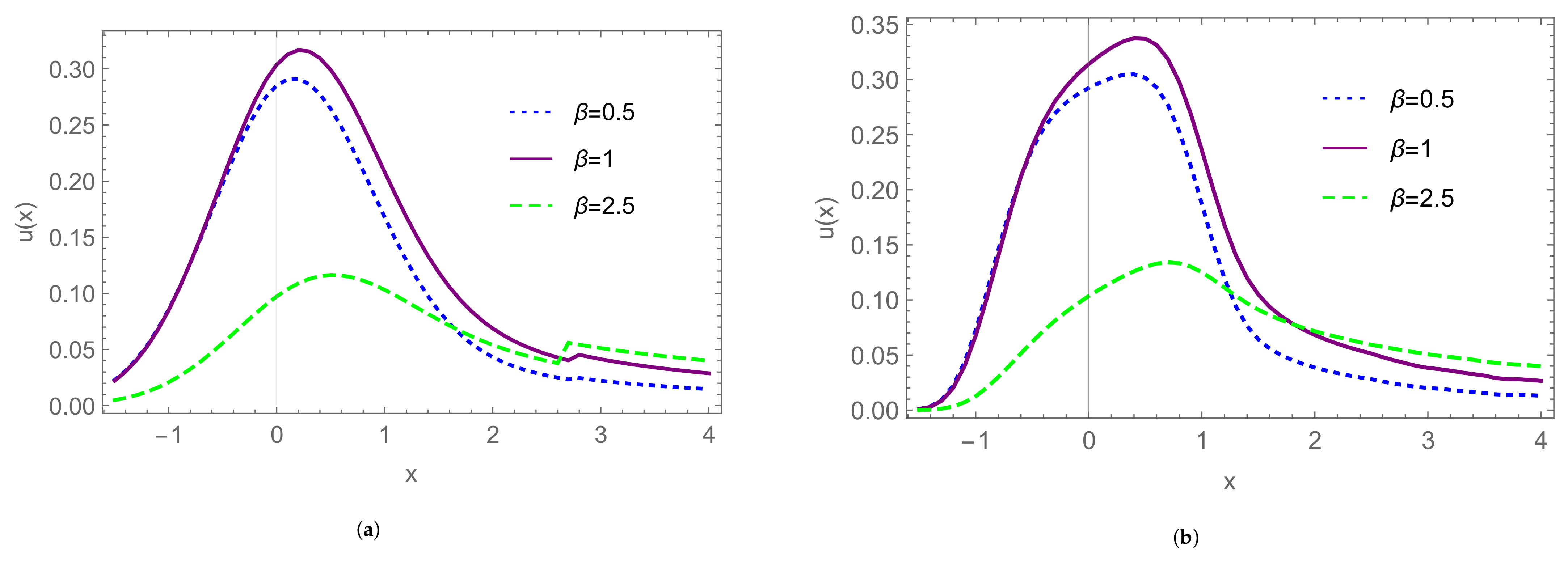
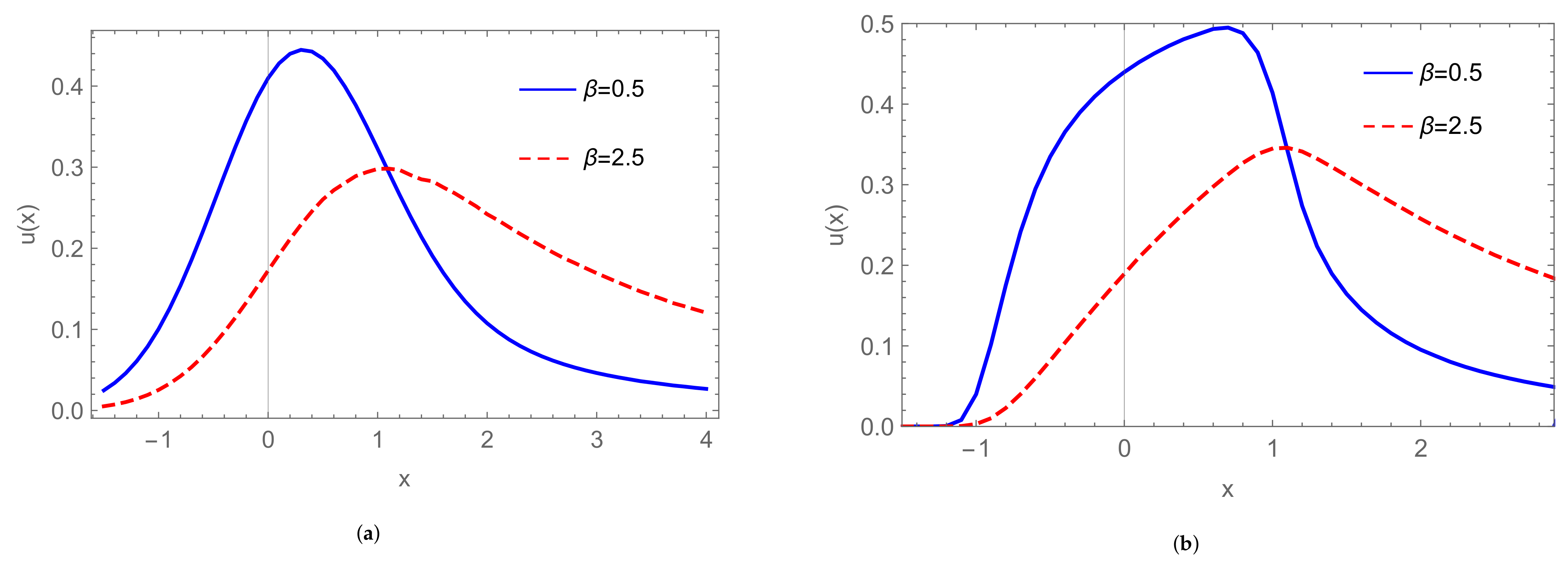

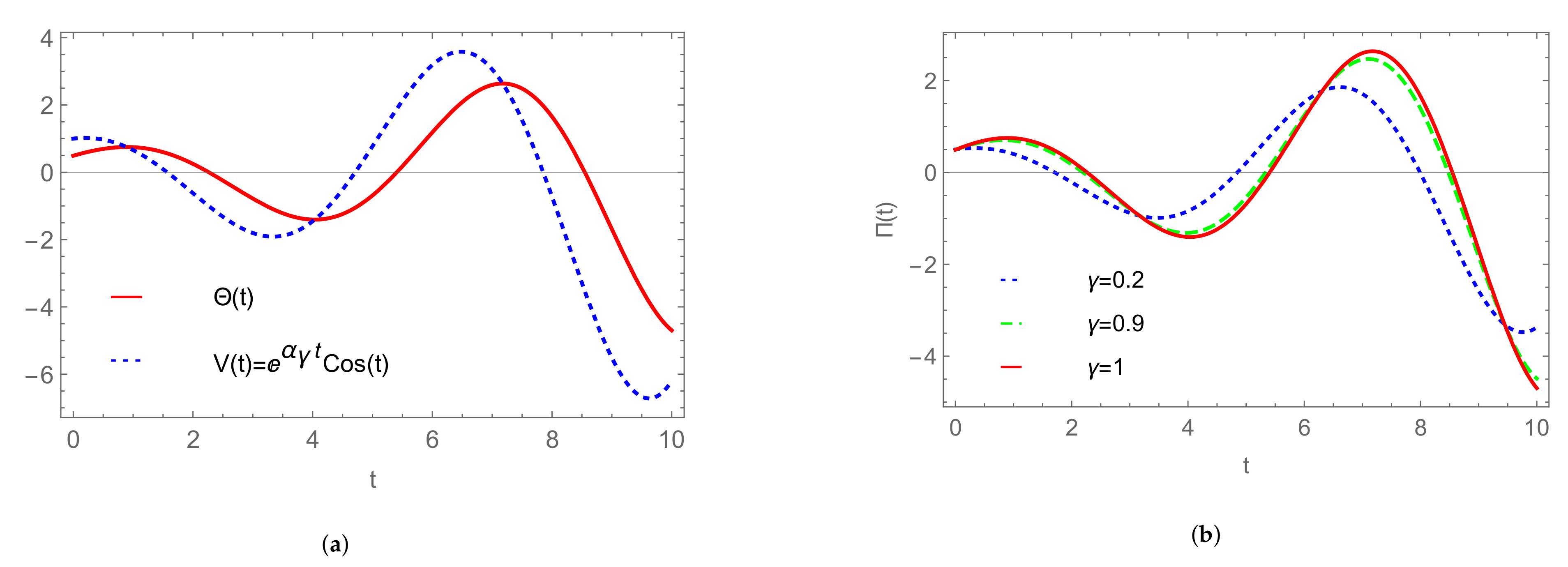
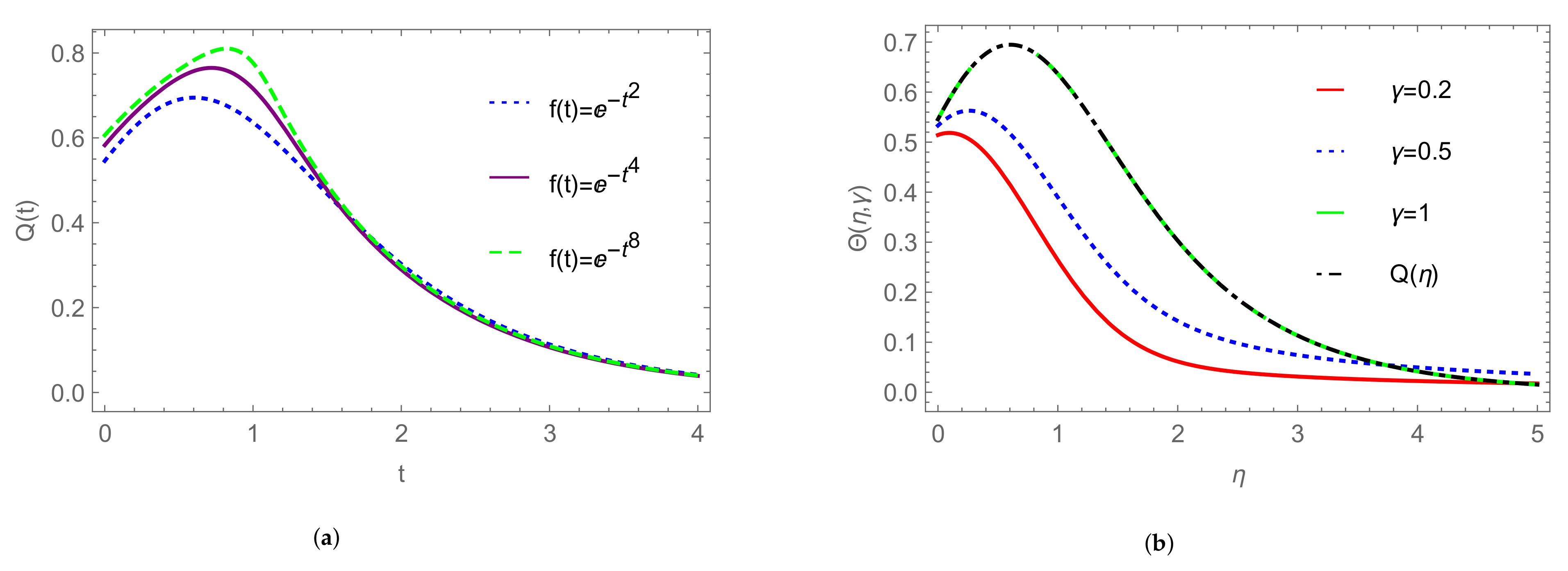
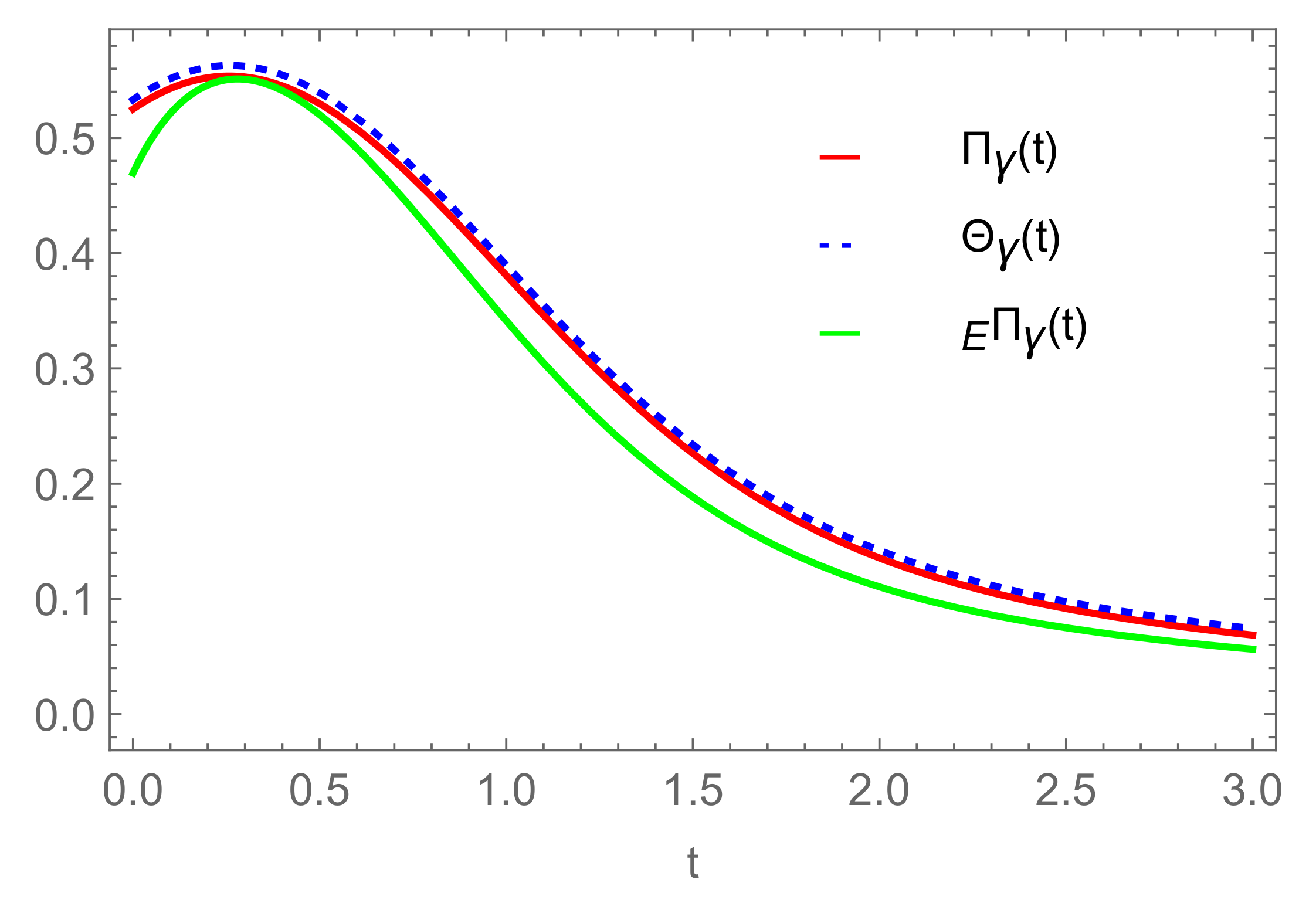
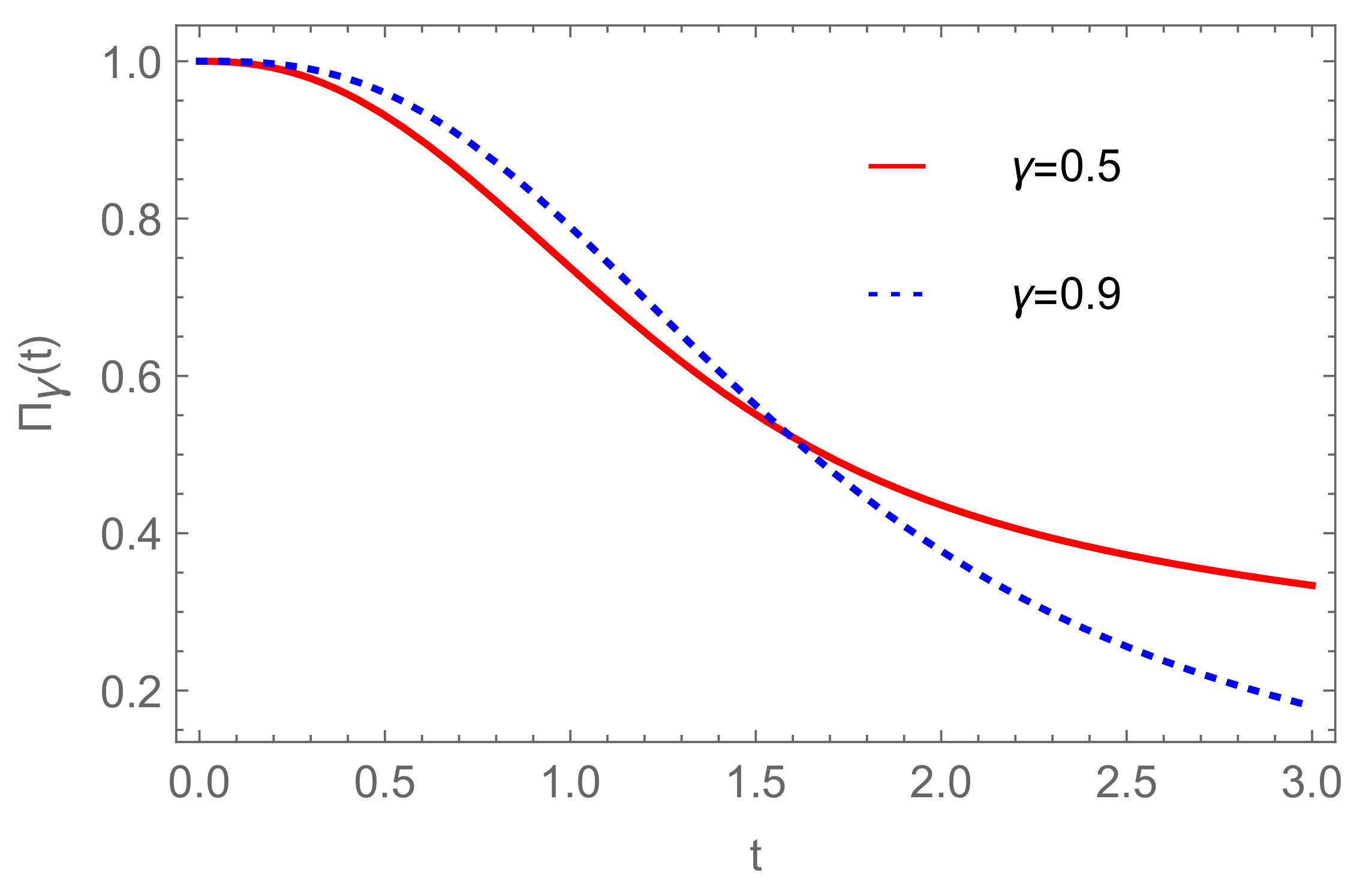
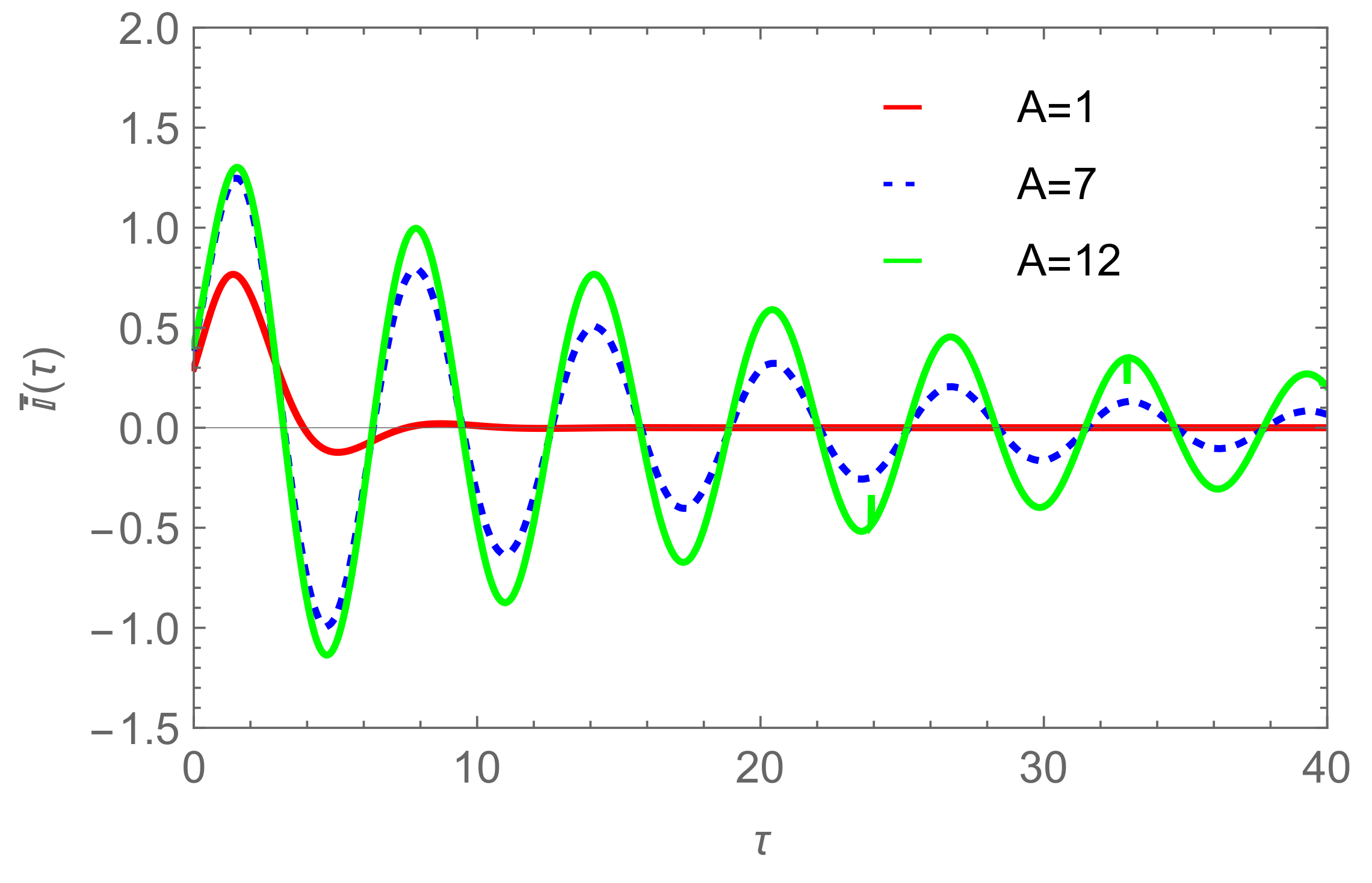
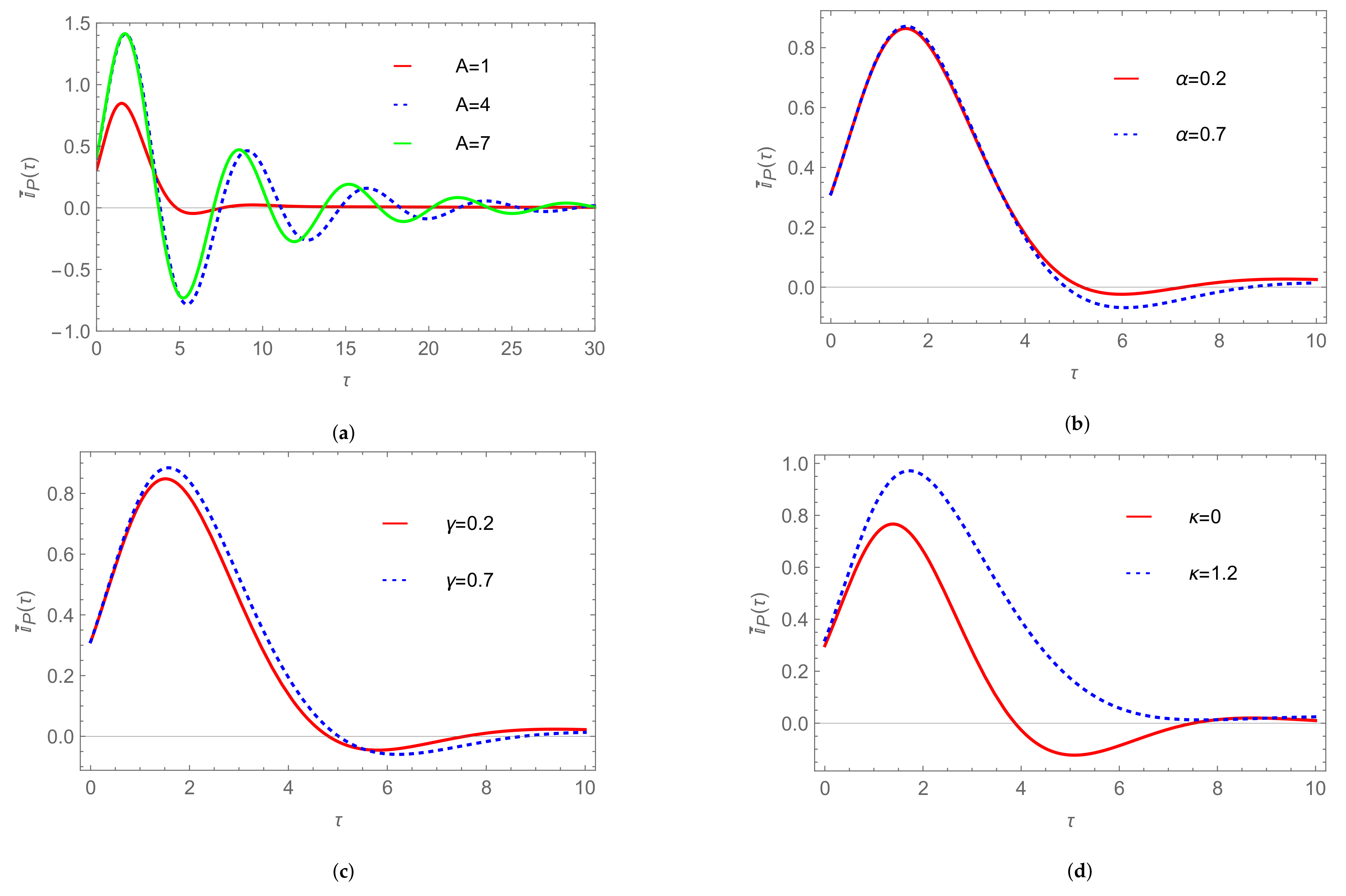
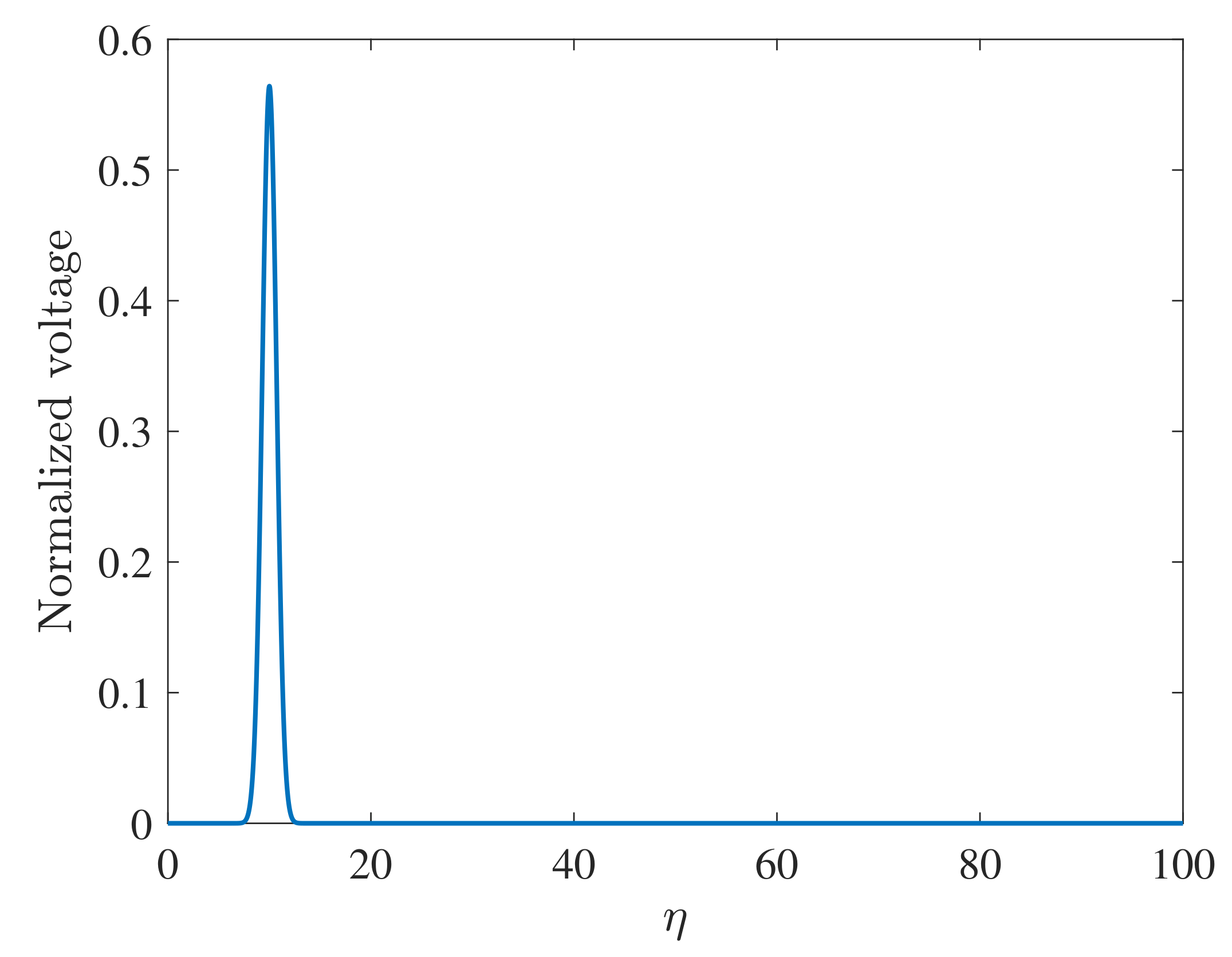

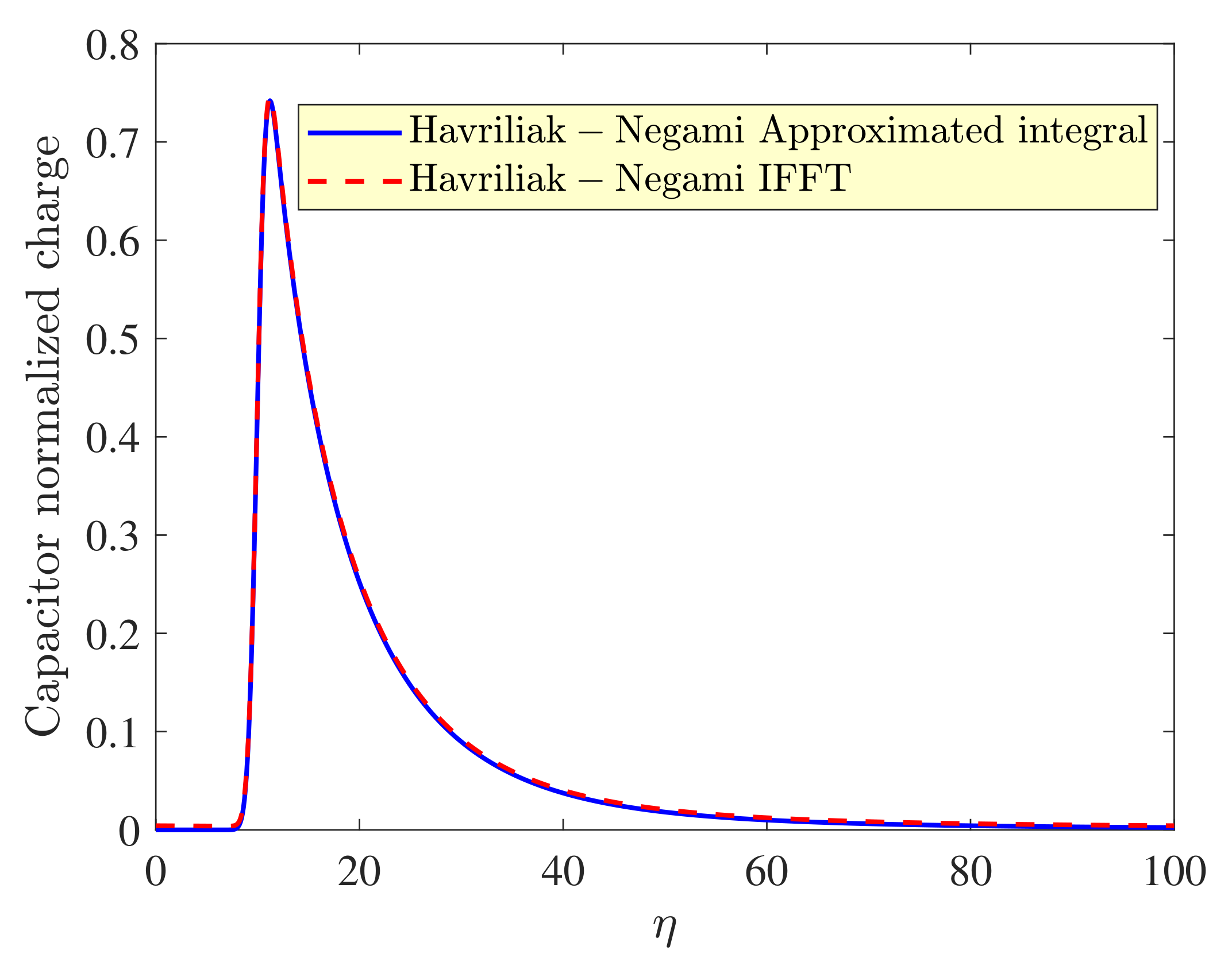
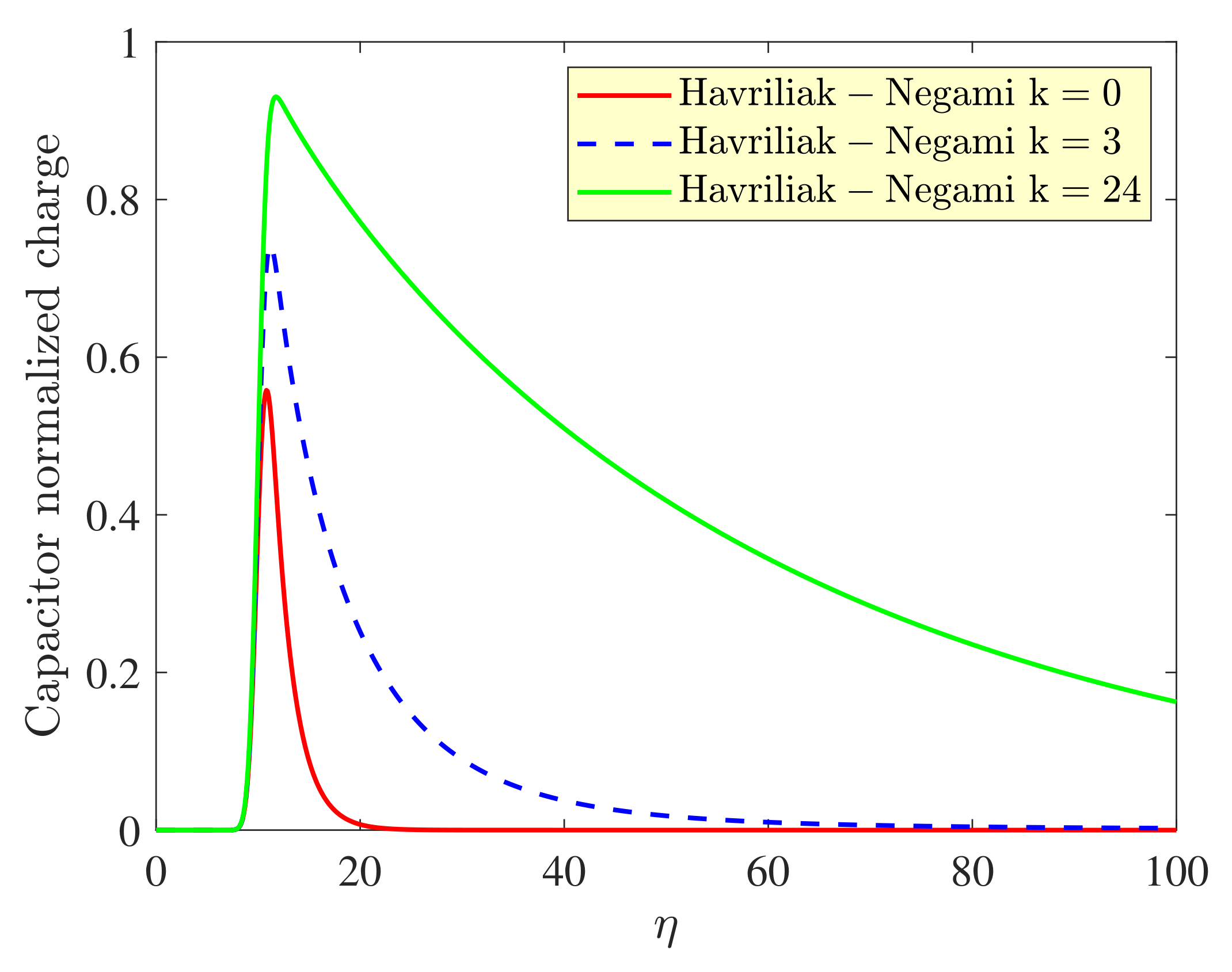
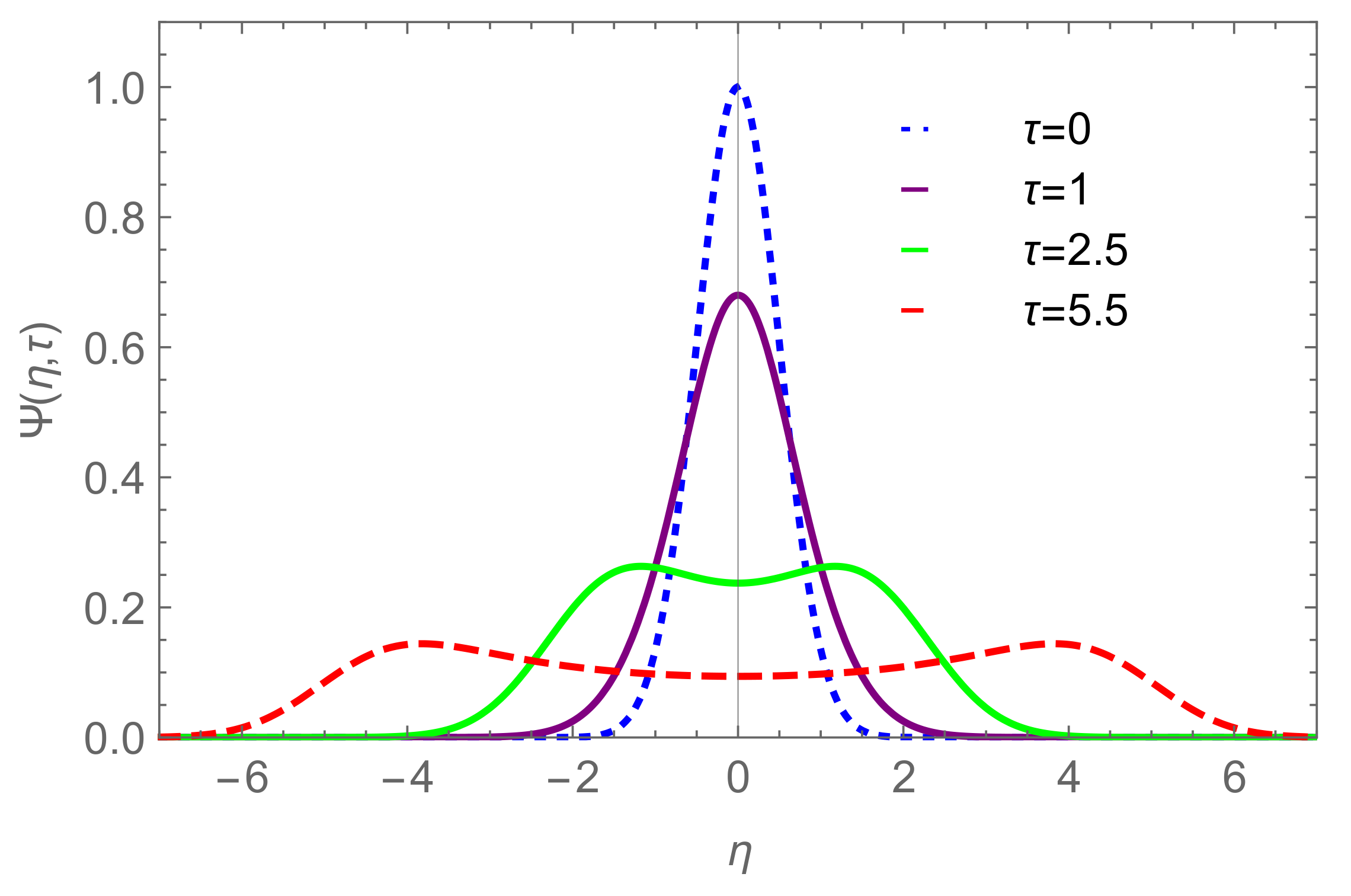

| Model | α | β |
| Debye | 0 | 0 |
| Cole—Cole | 0.4 | 0 |
| Cole—Davidson | 0 | 0.1 |
| Havriliak—Negami | 0.4 | 0.1 |
| τ | 153 ps |
| ps | |
| 3 | |
| 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antonini, G.; Dattoli, G.; Frezza, F.; Licciardi, S.; Loreto, F. About the Use of Generalized Forms of Derivatives in the Study of Electromagnetic Problems. Appl. Sci. 2021, 11, 7505. https://doi.org/10.3390/app11167505
Antonini G, Dattoli G, Frezza F, Licciardi S, Loreto F. About the Use of Generalized Forms of Derivatives in the Study of Electromagnetic Problems. Applied Sciences. 2021; 11(16):7505. https://doi.org/10.3390/app11167505
Chicago/Turabian StyleAntonini, Giulio, Giuseppe Dattoli, Fabrizio Frezza, Silvia Licciardi, and Fabrizio Loreto. 2021. "About the Use of Generalized Forms of Derivatives in the Study of Electromagnetic Problems" Applied Sciences 11, no. 16: 7505. https://doi.org/10.3390/app11167505
APA StyleAntonini, G., Dattoli, G., Frezza, F., Licciardi, S., & Loreto, F. (2021). About the Use of Generalized Forms of Derivatives in the Study of Electromagnetic Problems. Applied Sciences, 11(16), 7505. https://doi.org/10.3390/app11167505








