HORSIC+: An Efficient Post-Quantum Few-Time Signature Scheme

Abstract

It is well known that conventional digital signature algorithms such as RSA and ECDSA are vulnerable to quantum computing attacks. Hash-based signature schemes are attractive as post-quantum signature schemes in that it is possible to calculate the quantitative security level and the security is proven. SPHINCS is a stateless hash-based signature scheme and introduces HORST few-time signature scheme which is an improvement of HORS. However, HORST as well as HORS suffers from pretty large signature sizes. HORSIC is proposed to reduce the signature size, yet does not provide in-depth security analysis. In this paper, we propose HORSIC+, which is an improvement of HORSIC. HORSIC+ differs from HORSIC in that HORSIC+ does not apply f as a plain function to the signature key, but uses a member of a function family. In addition, HORSIC+ uses the chaining function similar to W-OTS${}^{+}$. These enable the strict security proof without the need for the used function family to be a permutation or collision resistant. HORSIC+ is existentially unforgeable under chosen message attacks, assuming a second-preimage resistant family of undetectable one-way functions and cryptographic hash functions in the random oracle model. HORSIC+ reduces the signature size by as much as 37.5% or 18.75% compared to HORS and by as much as 61.5% or 45.8% compared to HORST for the same security level.

1. Introduction

Nowadays, digital signatures are widely used in various security applications to provide authentication, integrity, and non-repudiation. RSA [1] and ECDSA [2] are two of the most widely used digital signature schemes. The security of RSA and ECDSA is based on the difficulty of factoring and computing discrete logarithms, respectively. However, in 1994, Shor proposed a polynomial-time quantum algorithm for integer factorization and discrete logarithm problems [3]. If a large-scale quantum computer is built, RSA and ECDSA cannot be used anymore. Thus, alternative digital signature schemes which are resilient to attacks by quantum computers are needed. They are called post-quantum cryptography [4,5].

Various post-quantum signature schemes such as lattice-based [6], multivariate [7], code-based [8], and hash-based have been studied. Lattice-based signature schemes are relatively fast with a reasonably small signature size. However, it is difficult to calculate the quantitative security level and the security is not proven against quantum adversaries. Multivariate signature schemes are relatively fast with an extremely small signature size. However, it is also difficult to estimate the security of multivariate signature schemes against quantum attacks. Code-based signature schemes have a reasonably small signature size and it is possible to calculate the quantitative security level to some extent. However, code-based signature schemes need too large keys to be secure against quantum attacks. Hash-based signature schemes receive a lot of attention in that it is possible to calculate the quantitative security level and the security is also proven [9]. Moreover, hash-based signature schemes are considered to be a good candidate for the security of IoT devices due to their simplicity of implementation and customization [10,11].

The hash-based signature schemes XMSS (eXtended Merkle Signature Scheme) [12] and SPHINCS [13] were introduced in 2011 and 2015, respectively. XMSS is stateful, meaning that the signer and the verifier have to maintain their own state information, while SPHINCS is stateless. SPHINCS introduces a few-time signature scheme named HORST (HORS with Trees). HORST is an improvement of a few-time signature scheme HORS (Hash to Obtain Random Subset) [14]. In the context of SPHINCS, each full signature should contain not only a HORST signature but also a HORST public key. HORST uses a Merkle tree to reduce the public key size to a single hash value. However, HORST as well as HORS suffers from pretty large signature sizes.

HORSIC (Hash to Obtain Random Subset and Integer Composition) [15] is a few-time signature scheme for broadcast authentication in wireless sensor networks. HORSIC reduces the signature size compared to HORS and HORST. Whereas HORS and HORST use only a cryptographic hash function H, making it infeasible to find two different messages that will produce the same k-element subset, HORSIC decreases the probability of forgery by using another cryptographic hash function G and a bijective function $C_{k,z}$ as well as H to make it infeasible to find two different messages that will produce the same k-part integer composition as well as the same k-element subset. The security analysis of HORSIC is performed on the unrealistic assumption that it is impossible for an adversary to invert the one-way permutation f. In fact, the probability of inverting f is not zero, but negligible. The security analysis should consider the probability of inverting f.

This paper proposes HORSIC+, an improvement of HORSIC. HORSIC+ differs from HORSIC in that HORSIC+ does not apply f as a plain function to the signature key, but uses a member of a function family which is second-preimage resistant, undetectable, and one-way. In addition, HORSIC+ uses the chaining function $c^s(x,\overrightarrow{r})$ similar to W-OTS${}^{+}$ [16]. These enable the strict security proof without the need for the used function family to be a permutation or collision resistant. We prove HORSIC+ is existentially unforgeable under chosen message attacks, if the used function family is a second-preimage resistant family of undetectable one-way functions and H and G are cryptographic hash functions in the random oracle model. HORSIC+ reduces the signature size by as much as 37.5% or 18.75% compared to HORS and by as much as 61.5% or 45.8% compared to HORST for the same security level.

The rest of the paper is organized as follows. Section 2 introduces some preliminaries and presents two signature schemes that HORSIC+ is based on. Section 3 describes the details of the proposed scheme HORSIC+. Section 4 discusses the security of HORSIC+ including a comparison with HORS and HORST. Section 5 presents the conclusions.

2. Preliminaries and Related Works

In this section, we discuss two signature schemes that HORSIC+ is based on. One is the Winternitz one-time signature scheme (W-OTS) [17], and the other is HORSIC [15]. We begin by introducing some preliminaries and then describe W-OTS and HORSIC.

2.1. Preliminaries

We start this subsection with several definitions and notions related to digital signature schemes and function families [16,18,19]. From now on, we write $x\stackrel{\$}{\leftarrow }S$ if x is chosen randomly from the finite set S using a uniform distribution.

Definition 1.

Let $\mathcal{M}$ be a message space. A digital signature scheme $\mathit{Dss}=(\mathit{Kg},\mathit{Sign},\mathit{Vf})$ is a triple of probabilistic polynomial time algorithms:

• $\mathit{Kg}\left(1^n\right)$ takes as input a security parameter $1^n$ and outputs a signature key X and a verification key Y;
• $\mathit{Sign}(X,M)$ outputs a signature σ under the signature key X for message $M\in \mathcal{M}$;
• $\mathit{Vf}(Y,M,\sigma )$ outputs 1 iff σ is a valid signature on M under the verification key Y;

such that $\forall (X,Y)\leftarrow \mathit{Kg}\left(1^n\right),\forall (M\in \mathcal{M})$ : $\mathit{Vf}(Y,M,\mathit{Sign}(X,M\left)\right)=1$.

Let $\mathit{Dss}\left(1^n\right)$ be a digital signature scheme with security parameter n. The standard definition of security for digital signature schemes is existential unforgeability under adaptive chosen message attack (EU-CMA). EU-CMA is defined using the following experiment.

Experiment${\mathrm{Exp}}_{\mathit{Dss}\left(1^n\right)}^{\mathrm{EU}-\mathrm{CMA}}\left(\mathcal{A}\right)$

$(X,Y)\leftarrow \mathit{Kg}\left(1^n\right)$

$(M^{\prime },{\sigma }^{\prime })\leftarrow {\mathcal{A}}^{\mathit{Sign}(X,·)}\left(Y\right)$

Let ${\left\{(M_i,{\sigma }_i)\right\}}_1^q$ be the query-answer pairs of $\mathit{Sign}(X,·)$.

Return 1 iff $\mathit{Vf}(Y,M^{\prime },{\sigma }^{\prime })=1$ and $M^{\prime }\notin {\left\{M_i\right\}}_1^q$.

The success probability of an adversary $\mathcal{A}$ in the above experiment can be written by:

$${\mathrm{Succ}}_{\mathit{Dss}\left(1^n\right)}^{\mathrm{EU}-\mathrm{CMA}}\left(\mathcal{A}\right)=\mathrm{Pr}[{\mathrm{Exp}}_{\mathit{Dss}\left(1^n\right)}^{\mathrm{EU}-\mathrm{CMA}}\left(\mathcal{A}\right)=1].$$

(1)

Definition 2.

Let $n,T,q\in \mathbb{N}$ and $T,q=poly\left(n\right)$. A digital signature scheme $\mathit{Dss}\left(1^n\right)$ is EU-CMA secure if the success probability of any adversary $\mathcal{A}$ running in time $\le T$ and making at most q queries to the oracle $\mathit{Sign}$ in the above experiment is negligible in n:

$${\mathrm{InSec}}^{\mathrm{EU}-\mathrm{CMA}}(\mathrm{Dss}\left(1^n\right);T,q)\stackrel{def}{=}\underset{\mathcal{A}}{max}\left\{{\mathrm{Succ}}_{\mathit{Dss}\left(1^n\right)}^{\mathrm{EU}-\mathrm{CMA}}\left(\mathcal{A}\right)\right\}=negl\left(n\right).$$

(2)

We then discuss several security properties for function families: preimage resistance (one-wayness, OW), second preimage resistance (SPR), collision resistance (CR), and undetectability (UD). Let $n\in \mathbb{N}$ be the security parameter and

$${\mathcal{F}}_n=\{f_{\kappa }:{\{0,1\}}^n\to {\{0,1\}}^n\mid \kappa \in \mathcal{K}\}$$

(3)

be a family of functions. The elements of $\mathcal{K}$ are called keys and each key $\kappa$ specifies a particular function $f_{\kappa }$ in the family ${\mathcal{F}}_n$.

A function is preimage resistant (or one-way) if it is easy to compute but difficult to invert. The success probability of an adversary against the preimage resistance of ${\mathcal{F}}_n$ is

$${\mathrm{Succ}}_{{\mathcal{F}}_n}^{OW}\left(\mathcal{A}\right)=Pr[\kappa \stackrel{\$}{\leftarrow }\mathcal{K};x\stackrel{\$}{\leftarrow }{\{0,1\}}^n,y\leftarrow f_{\kappa }\left(x\right);x^{\prime }\stackrel{\$}{\leftarrow }\mathcal{A}(\kappa ,y):y=f_{\kappa }\left(x^{\prime }\right)].$$

(4)

Definition 3.

We call ${\mathcal{F}}_n$ preimage resistant (or one-way), if the success probability of any adversary $\mathcal{A}$ running in time $\le T$ against the preimage resistance of ${\mathcal{F}}_n$ is negligible in n:

$${\mathrm{InSec}}^{\mathrm{OW}}({\mathcal{F}}_n;T)\stackrel{def}{=}\underset{\mathcal{A}}{max}\left\{{\mathrm{Succ}}_{{\mathcal{F}}_n}^{\mathrm{OW}}\left(\mathcal{A}\right)\right\}=negl\left(n\right).$$

(5)

A function is second preimage resistant if, given some x in the domain, it is difficult to find some $x^{\prime }$ unequal to x that maps the same value. The success probability of an adversary against the second preimage resistance of ${\mathcal{F}}_n$ is

$${\mathrm{Succ}}_{{\mathcal{F}}_n}^{SPR}\left(\mathcal{A}\right)=Pr[\kappa \stackrel{\$}{\leftarrow }\mathcal{K};x\stackrel{\$}{\leftarrow }{\{0,1\}}^n;x^{\prime }\stackrel{\$}{\leftarrow }\mathcal{A}(\kappa ,x):x\ne x^{\prime }\wedge f_{\kappa }\left(x\right)=f_{\kappa }\left(x^{\prime }\right)].$$

(6)

Definition 4.

We call ${\mathcal{F}}_n$ second preimage resistant, if the success probability of any adversary $\mathcal{A}$ running in time $\le T$ against the second preimage resistance of ${\mathcal{F}}_n$ is negligible in n:

$${\mathrm{InSec}}^{\mathrm{SPR}}({\mathcal{F}}_n;T)\stackrel{def}{=}\underset{\mathcal{A}}{max}\left\{{\mathrm{Succ}}_{{\mathcal{F}}_n}^{\mathrm{SPR}}\left(\mathcal{A}\right)\right\}=negl\left(n\right).$$

(7)

A function is collision resistant if it is hard to find any pair $(x,x^{\prime })$ in the domain that maps to the same value. The success probability of an adversary against the collision resistance of ${\mathcal{F}}_n$ is

$${\mathrm{Succ}}_{{\mathcal{F}}_n}^{CR}\left(\mathcal{A}\right)=Pr[\kappa \stackrel{\$}{\leftarrow }\mathcal{K};(x,x^{\prime })\stackrel{\$}{\leftarrow }\mathcal{A}\left(\kappa \right):x\ne x^{\prime }\wedge f_{\kappa }\left(x\right)=f_{\kappa }\left(x^{\prime }\right)].$$

(8)

Definition 5.

We call ${\mathcal{F}}_n$ collision resistant, if the success probability of any adversary $\mathcal{A}$ running in time $\le T$ against the collision resistance of ${\mathcal{F}}_n$ is negligible in n:

$${\mathrm{InSec}}^{\mathrm{CR}}({\mathcal{F}}_n;T)\stackrel{def}{=}\underset{\mathcal{A}}{max}\left\{{\mathrm{Succ}}_{{\mathcal{F}}_n}^{\mathrm{CR}}\left(\mathcal{A}\right)\right\}=negl\left(n\right).$$

(9)

To define the undetectability property, we need to define the (distinguishing) advantage of an adversary.

Definition 6.

Let $\mathcal{X}$ and $\mathcal{Y}$ be two distributions. The advantage ${\mathrm{Adv}}_{\mathcal{X},\mathcal{Y}}\left(\mathcal{A}\right)$ of an adversary $\mathcal{A}$ in distinguishing between these two distributions is defined as

$${\mathrm{Adv}}_{\mathcal{X},\mathcal{Y}}\left(\mathcal{A}\right)=\mid \mathrm{Pr}[1\leftarrow \mathcal{A}\left(\mathcal{X}\right)]-\mathrm{Pr}[1\leftarrow \mathcal{A}\left(\mathcal{Y}\right)]\mid .$$

(10)

A function family is undetectable if no adversary can distinguish its outputs from uniformly random values. Consider two distributions ${\mathcal{D}}_{\mathrm{UD},\mathcal{U}}$ and ${\mathcal{D}}_{\mathrm{UD},{\mathcal{F}}_n}$ over ${\{0,1\}}^n\times \mathcal{K}$. A sample $(u,\kappa )$ from the first distribution ${\mathcal{D}}_{\mathrm{UD},\mathcal{U}}$ is obtained in the following way: $u\stackrel{\$}{\leftarrow }{\{0,1\}}^n$, $\kappa \stackrel{\$}{\leftarrow }\mathcal{K}$. A sample $(u,\kappa )$ from the second distribution ${\mathcal{D}}_{\mathrm{UD},{\mathcal{F}}_n}$ is obtained in the following way: $x\stackrel{\$}{\leftarrow }{\{0,1\}}^n$, $\kappa \stackrel{\$}{\leftarrow }\mathcal{K}$, and then calculating $u=f_{\kappa }\left(x\right)$. The advantage of an adversary against the undetectability of ${\mathcal{F}}_n$ is defined as the distinguishing advantage for these two distributions:

$${\mathrm{Adv}}_{{\mathcal{F}}_n}^{\mathrm{UD}}\left(\mathcal{A}\right)={\mathrm{Adv}}_{{\mathcal{D}}_{\mathrm{UD},\mathcal{U}},{\mathcal{D}}_{\mathrm{UD},{\mathcal{F}}_n}}\left(\mathcal{A}\right).$$

(11)

Definition 7.

We call ${\mathcal{F}}_n$ undetectable, if the advantage of any adversary $\mathcal{A}$ running in time $\le T$ against the undetectability of ${\mathcal{F}}_n$ is negligible in n:

$${\mathrm{InSec}}^{\mathrm{UD}}({\mathcal{F}}_n;T)\stackrel{def}{=}\underset{\mathcal{A}}{max}\left\{{\mathrm{Adv}}_{{\mathcal{F}}_n}^{\mathrm{UD}}\left(\mathcal{A}\right)\right\}=negl\left(n\right).$$

(12)

Table 1 summarizes the best known generic attacks against different functions given different environments [20]. Using generic(brute-force) classical attacks, one requires $\mathrm{\Theta }\left(2^n\right)$ evaluations of the function to compute preimages or second preimages. Because of the birthday paradox, one requires $\mathrm{\Theta }\left(2^{n/2}\right)$ evaluations of the function to find a collision with probability greater than $\frac{1}{2}$ [21]. Using generic quantum attacks such as Grover’s algorithm [9], one requires $\mathrm{\Theta }\left(2^{n/2}\right)$ evaluations of the function to compute preimages or second preimages and $\mathrm{\Theta }\left(2^{n/3}\right)$ evaluations of the function to find a collision [22].

Table 1. Generic Security.

	OW	SPR	CR
Classical	$\mathrm{\Theta }\left(2^n\right)$	$\mathrm{\Theta }\left(2^n\right)$	$\mathrm{\Theta }\left(2^{n/2}\right)$
Quantum	$\mathrm{\Theta }\left(2^{n/2}\right)$	$\mathrm{\Theta }\left(2^{n/2}\right)$	$\mathrm{\Theta }\left(2^{n/3}\right)$

2.2. Winternitz One-Time Signature Scheme (W-OTS)

In this subsection, we discuss W-OTS and its two variants, W-OTS${}^{\$}$ and W-OTS${}^{+}$.

2.2.1. W-OTS

W-OTS produces much shorter signatures than Lamport-Diffie one-time signature scheme [23] by iteratively applying a function on a secret key, whereas the number of iterations depends on the signed message [17]. W-OTS uses a one-way function

$$f:{\{0,1\}}^n\to {\{0,1\}}^n.$$

(13)

Key generation: A Winternitz parameter w, which is the number of bits to be signed simultaneously is chosen. In the following, we restrict the length of the message to be signed to m bits. It is straightforward to generalize to arbitrary sized messages by using a collision resistant hash function.

The signature key X consists of l bit strings of length n chosen uniformly at random,

$$X=(x_1,x_2,\dots ,x_l)\stackrel{\$}{\leftarrow }{\{0,1\}}^{ln},$$

(14)

where l is computed as follows.

$$l_1=\lceil \frac{m}{w}\rceil ,l_2=\lceil \frac{\lfloor {log}_2{l}_1\rfloor +1+w}{w}\rceil ,l=l_1+l_2.$$

(15)

The chaining function $c^s\left(x\right)$ for W-OTS is defined as follows.

$$c^s\left(x\right)=\left\{\begin{array}{cc}x,\hfill & \mathrm{if}s=0\hfill \\ f\left(c^{s-1}\left(x\right)\right)\hfill & \mathrm{if}1\le s\le 2^w-1\hfill \end{array}\right.$$

(16)

The verification key Y is calculated by applying the chaining function to each $x_i$ in the signature key $2^w-1$ times. Thus we have

$$Y=(y_1,y_2,\dots ,y_l)=(c^{2^w-1}\left(x_1\right),c^{2^w-1}\left(x_2\right),\dots ,c^{2^w-1}\left(x_l\right)).$$

(17)

Signature generation: A message M is split into $l_1$ bit strings of length w and each bit string is converted to an integer in base-w. So we have

$$M=(m_1,m_2,\dots ,m_{l_1})$$

(18)

where

$$m_i\in \{0,1,\dots ,2^w-1\},1\le i\le l_1.$$

(19)

Then the checksum C is calculated as follows.

$$C=\sum _{i=1}^{l_1}(2^w-m_i)$$

(20)

The checksum C is converted to base w. The base w representation of the checksum C is $C^{\prime }=(c_1,c_2,\dots ,c_{l_2})$. The signature of M is computed as

$$\begin{array}{cc}\hfill \sigma & =({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_{l_1},{\sigma }_{l_1+1},{\sigma }_{l_1+2},\dots ,{\sigma }_l)\hfill \\ \hfill & =(c^{m_1}\left(x_1\right),c^{m_2}\left(x_2\right),\dots ,c^{m_{l_1}}\left(x_{l_1}\right),c^{c_1}\left(x_{l_1+1}\right),c^{c_2}\left(x_{l_1+2}\right),\dots ,c^{c_{l_2}}\left(x_l\right))\hfill \end{array}$$

(21)

Signature verification: For the verification of the signature $\sigma =({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_l)$, the base-w strings $M=(m_1,m_2,\dots ,m_{l_1})$ and $C^{\prime }=(c_1,c_2,\dots ,c_{l_2})$ are calculated as described above. Then we check if

$$\begin{array}{c}\hfill (c^{2^w-1-m_1}\left({\sigma }_1\right),\dots ,c^{2^w-1-m_{l_1}}\left({\sigma }_{l_1}\right),c^{2^w-1-c_1}\left({\sigma }_{l_1+1}\right),\dots ,c^{2^w-1-c_{l_2}}\left({\sigma }_l\right))\\ \hfill =(y_1,\dots ,y_{l_1},y_{l_1+1},\dots ,y_l)\end{array}$$

(22)

It is proved that W-OTS is strongly unforgeable under chosen message attacks if ${\mathcal{F}}_n$ is a collision resistant family of undetectable one-way functions [20].

2.2.2. W-OTS${}^{\$}$

W-OTS${}^{\$}$ differs from W-OTS in that W-OTS${}^{\$}$ uses a family of pseudo random functions instead of a one-way function [24]. The chaining function $c^s\left(x\right)$ for W-OTS${}^{\$}$ is defined as follows.

$$c^s\left(x\right)=\left\{\begin{array}{cc}x,\hfill & \mathrm{if}s=0\hfill \\ f_{c^{s-1}\left(x\right)}\left(r\right)\hfill & \mathrm{if}1\le s\le 2^w-1\hfill \end{array}\right.$$

(23)

It is proved that W-OTS${}^{\$}$ is existentially unforgeable under chosen message attacks if ${\mathcal{F}}_n$ is a pseudorandom function family [24].

2.2.3. W-OTS${}^{+}$

W-OTS${}^{+}$ uses a second preimage resistant family of undetectable one-way functions [16]. It uses bitmasks to replace the collision resistant one-way function families. The idea of using bitmasks comes from the “XOR tree” [25]. The chaining function $c^s(x,\overrightarrow{r})$ for W-OTS${}^{+}$ is defined as follows.

$$c^s(x,\overrightarrow{r})=\left\{\begin{array}{cc}x,\hfill & ifs=0\hfill \\ f_{\kappa }(c^{s-1}(x,\overrightarrow{r})\oplus r_s)\hfill & if1\le s\le 2^w-1\hfill \end{array}\right.$$

(24)

where the bitmasks $\overrightarrow{r}$ consist of $2^w-1$ bit strings of length n chosen uniformly at random,

$$\overrightarrow{r}=(r_1,r_2,\dots ,r_{2^w-1})\stackrel{\$}{\leftarrow }{\{0,1\}}^{(2^w-1,n)}.$$

(25)

It is proved that W-OTS${}^{+}$ is strongly unforgeable under chosen message attacks if ${\mathcal{F}}_n$ is a second preimage resistant family of undetectable one-way functions [16].

2.3. HORSIC

HORSIC [15] is basically an extension of HORS [14]. Whereas HORS uses only a cryptographic hash function H, making it infeasible to find two different messages that will produce the same k-element subset, HORSIC decreases the probability of forgery by using another cryptographic hash function G and a bijective function $C_{k,z}$ as well as H to make it infeasible to find two different messages that will produce the same k-part integer composition as well as the same k-element subset.

Let $f:{\{0,1\}}^n\to {\{0,1\}}^n$ be a one-way permutation operating on n-bit strings. Let $H:{\{0,1\}}^{*}\to {\{0,1\}}^{k{log}_{2}t}$ and $G:{\{0,1\}}^{*}\to \left[0,\left(\genfrac{}{}{0pt}{}{z-1}{k-1}\right)\right)$ be cryptographic hash functions in the random oracle model [26]. t, k, and z are security parameters. The public key size is linear in t, and the signature size is linear in k.

HORSIC uses a bijective function $C_{k,z}$ that, on input g, where $0\le g<\left(\genfrac{}{}{0pt}{}{z-1}{k-1}\right)$, outputs the g-th solution of the following equation:

$$z=\sum _{i=1}^k{a}_i,a_i\mathrm{is}\mathrm{an}\mathrm{integer}\mathrm{such}\mathrm{that}{a}_i\ge 1.$$

(26)

Note that the number of solutions to the above equation, which is the number of compositions of z into exactly k parts, is denoted by the binomial coefficient $\left(\genfrac{}{}{0pt}{}{z-1}{k-1}\right)$ [27]. For example, suppose $k=3$ and $z=5$. The equation $a_1+a_2+a_3=5$ has 6 solutions ($\left(\genfrac{}{}{0pt}{}{z-1}{k-1}\right)=\left(\genfrac{}{}{0pt}{}{5-1}{3-1}\right)=\left(\genfrac{}{}{0pt}{}{4}{2}\right)=6$) : $C_{3,5}\left(0\right)=(1,1,3)$, $C_{3,5}\left(1\right)=(1,2,2)$, $C_{3,5}\left(2\right)=(1,3,1)$, $C_{3,5}\left(3\right)=(2,1,2)$, $C_{3,5}\left(4\right)=(2,2,1)$, and $C_{3,5}\left(5\right)=(3,1,1)$.

Algorithm 1 represents the key generation of HORSIC. If first generates t random n-bit numbers and then creates a one-way chain of length w for each n-bit number.

Algorithm 1: Key generation of HORSIC ($K{g}_{HORSIC}\left(\right)$)

System Parameters: Parameters n, t, k, z, and w Output: Signature key X and verification key Y 1: Choose $X=(x_1,x_2,\dots ,x_t)\stackrel{\$}{\leftarrow }{\{0,1\}}^{(t,n)}$ 2: Compute $Y=(y_1,y_2,\dots ,y_t)=(f^w\left(x_1\right),f^w\left(x_2\right),\dots ,f^w\left(x_t\right))$ 3: return$(X,Y)$

Algorithm 2 represents the signing of HORSIC. HORSIC uses a bijective function $C_{k,z}$ and two cryptographic hash functions H and G. A cryptographic hash function H is used to map each message M to a k-element ordered subset $(i_1,i_2,\dots ,i_k)$ of a t-element set $\{1,2,\dots ,t\}$. A counter $ctr$ is used to ensure that all $i_j$ are distinct. A cryptographic hash function G and a bijective function $C_{k,z}$ are used to map each message M to a k-part integer composition $(a_1,a_2,\dots ,a_k)$ of z.

Algorithm 2: Signing of HORSIC ($Sig{n}_{HORSIC}(X,M)$)

System Parameters: Parameters n, t, k, z, and w Input: Signature key X and message M Output: Signature $\sigma$ 1: Compute $g=G\left(M\right)$ 2: Compute $(a_1,a_2,\dots ,a_k)=C_{k,z}\left(g\right)$ 3: Set $ctr=0$ 4: Compute $h=H(M\mid ctr)$ 5: Split h into k pieces $(h_1,h_2,\dots ,h_k)$ of length ${log}_{2}t$ bits each 6: Interpret each $h_j$ as an integer $i_j$ for all $j\in \{1,2,\dots ,k\}$ 7: if there exist p and q with $p,q\in \{1,2,\dots ,k\}$ such that $i_p=i_q$ and $p\ne q$ then 8: $ctr=ctr+1$ and go to Step 4 9: Compute $si{g}_j=f^{w-a_j}\left(x_{i_j}\right)$ for all $j\in \{1,2,\dots ,k\}$ 10: return $\sigma =(ctr,si{g}_1,si{g}_2,\dots ,si{g}_k)$

Algorithm 3 represents the verification of HORSIC. Each $si{g}_j$ is verified by applying the one-way permutation $a_j$ times and comparing it with the verification key.

Algorithm 3: Verification of HORSIC ($V{f}_{HORSIC}(Y,M,\sigma )$)

System Parameters: Parameters n, t, k, z, and w Input: Verification key Y, message M, and signature $\sigma$ Output: “accept” or “reject” 1: Compute $g=G\left(M\right)$ 2: Compute $(a_1,a_2,\dots ,a_k)=C_{k,z}\left(g\right)$ 3: Compute $h=H(M\mid ctr)$ 4: Split h into k pieces $(h_1,h_2,\dots ,h_k)$ of length ${log}_{2}t$ bits each 5: Interpret each $h_j$ as an integer $i_j$ for all $j\in \{1,2,\dots ,k\}$ 6: if there exist p and q with $p,q\in \{1,2,\dots ,k\}$ such that $i_p=i_q$ and $p\ne q$ then 7:     return “reject” 8: if there exist $j\in \{1,2,\dots ,k\}$ such that $f^{a_j}\left(si{g}_j\right)\ne y_{i_j}$ then 9:     return “reject” 10: return “accept”

The probability of a forgery for HORSIC is $\frac{k!(k-1)!(z-k)!}{t^k(z-1)!}$ [15]. Note that it does not depend on the security parameter n. The security analysis of HORSIC is performed on the unrealistic assumption that it is impossible for an adversary to invert the one-way permutation f. In fact, the probability of inverting f is not zero, but negligible. The security analysis should consider the probability of inverting f. Moreover, HORSIC requires f to be a one-way permutation. Whereas one-way functions can be based on various assumptions, candidate one-way permutation families are remarkably rare [28].

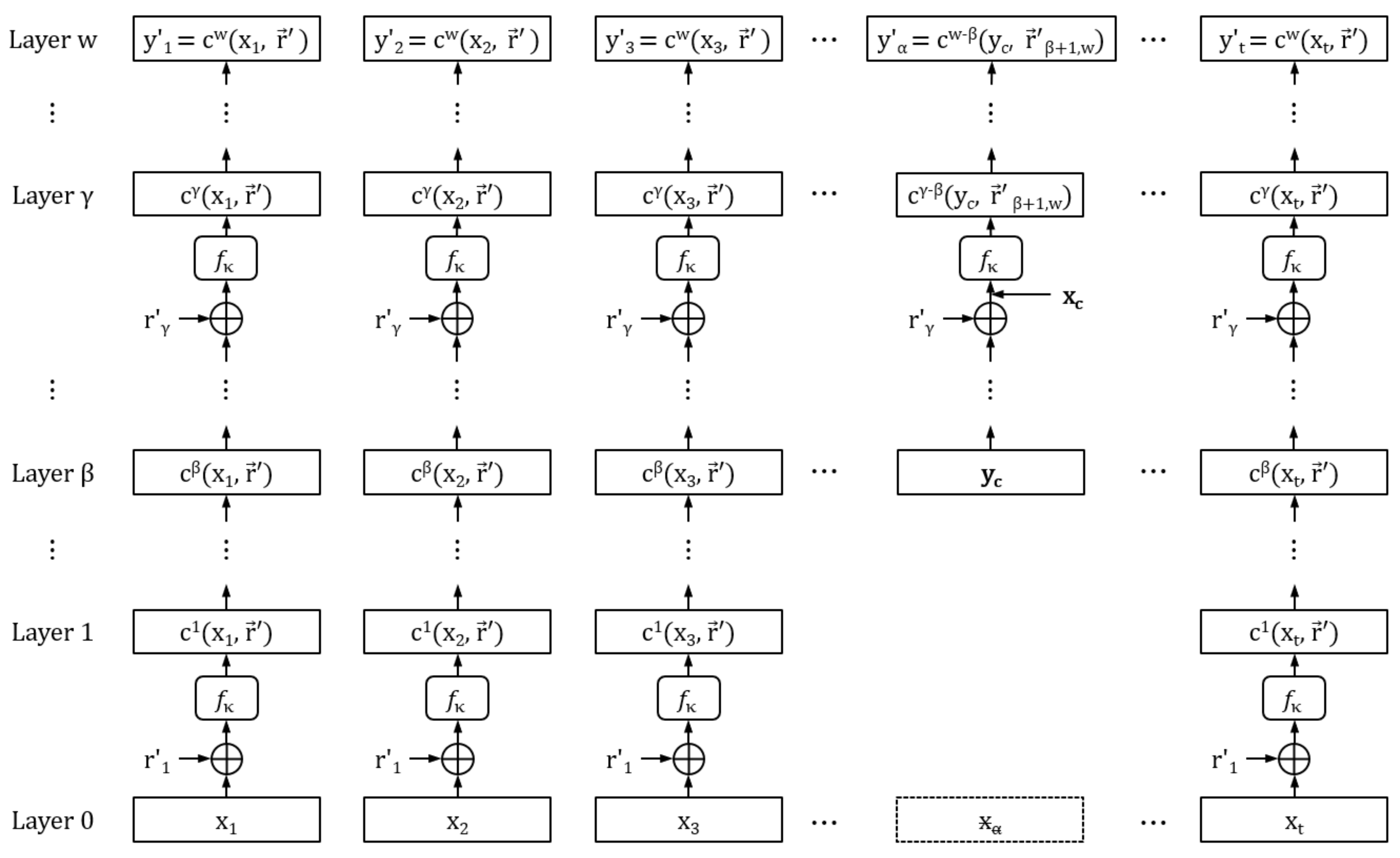
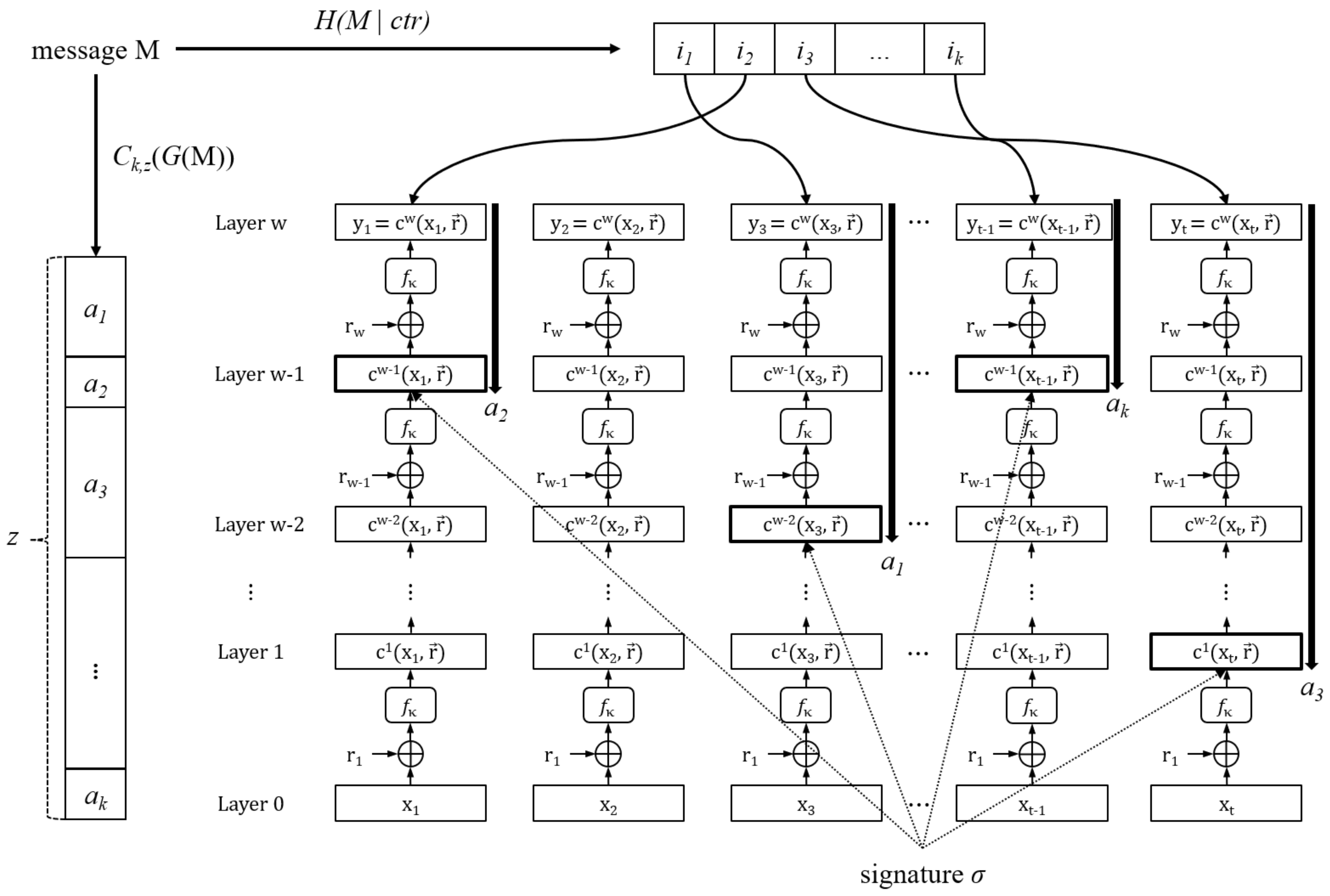
3. The HORSIC+ Signature Scheme

In this section, we describe HORSIC+ focusing on the differences with HORSIC. Firstly, HORSIC+ does not apply f as a plain function to the signature key, but uses a member of a function family. Let ${\mathcal{F}}_n=\{f_{\kappa }:{\{0,1\}}^n\to {\{0,1\}}^n\mid \kappa \in \mathcal{K}\}$ be a family of functions which is second-preimage resistant, undetectable and one-way. The function key $\kappa \stackrel{\$}{\leftarrow }\mathcal{K}$ specifies a particular function $f_{\kappa }$ in the family ${\mathcal{F}}_n$. The function key $\kappa$ is chosen at random at key generation time and is the same for all function calls. In addition, HORSIC+ uses the chaining function $c^s(x,\overrightarrow{r})$ similar to W-OTS${}^{+}$ [16]. It enables the strict security proof without the need for the used function family to be collision resistant.

$$c^s(x,\overrightarrow{r})=\left\{\begin{array}{cc}x,\hfill & \mathrm{if}s=0\hfill \\ f_{\kappa }(c^{s-1}(x,\overrightarrow{r})\oplus r_s)\hfill & \mathrm{if}1\le s\le w\hfill \end{array}\right.$$

(27)

where bitmasks $\overrightarrow{r}$ is defined as

$$\overrightarrow{r}=(r_1,r_2,\dots ,r_w)\in {\{0,1\}}^{(w,n)}$$

(28)

We denote ${\overrightarrow{r}}_{a,b}$ as the substring $(r_a,\dots ,r_b)$ of $\overrightarrow{r}$. We also define ${\overrightarrow{r}}_{a,b}$ to be the empty string when $a>b$.

Let $H:{\{0,1\}}^{*}\to {\{0,1\}}^{k{log}_{2}t}$ and $G:{\{0,1\}}^{*}\to \left[0,\left(\genfrac{}{}{0pt}{}{z-1}{k-1}\right)\right)$ be cryptographic hash functions in the random oracle model. HORSIC+ uses a bijective function $C_{k,z}$ same as HORSIC. Algorithm 4 describes the implementation of the function $C_{k,z}\left(g\right)$. It is based on the following equation:

$$\left(\genfrac{}{}{0pt}{}{z-1}{k-1}\right)=\left(\genfrac{}{}{0pt}{}{z-2}{k-2}\right)+\left(\genfrac{}{}{0pt}{}{z-3}{k-2}\right)+\dots +\left(\genfrac{}{}{0pt}{}{k-2}{k-2}\right)=\sum _{j=1}^{z-k+1}\left(\genfrac{}{}{0pt}{}{z-1-j}{k-2}\right)$$

(29)

In Equation (29), $\left(\genfrac{}{}{0pt}{}{z-2}{k-2}\right)$, $\left(\genfrac{}{}{0pt}{}{z-3}{k-2}\right)$ and $\left(\genfrac{}{}{0pt}{}{k-2}{k-2}\right)$ are the number of solutions when $a_1$ is 1, 2 and $z-k+1$, respectively. First, Algorithm 4 checks whether $g<\left(\genfrac{}{}{0pt}{}{z-2}{k-2}\right)$. If so, $a_1=1$ and $z-1={\sum }_{i=2}^k{a}_i$. If not, Algorithm 4 checks whether $g<\left(\genfrac{}{}{0pt}{}{z-2}{k-2}\right)+\left(\genfrac{}{}{0pt}{}{z-3}{k-2}\right)$. If so, $a_1=2$ and $z-2={\sum }_{i=2}^k{a}_i$, and so on.

Algorithm 4: Implementation of the function $C_{k,z}\left(g\right)$

System Parameters: Parameters k and z where $k\le z$ Input: g where $0\le g<\left(\genfrac{}{}{0pt}{}{z-1}{k-1}\right)$ Output: $(a_1,a_2,\dots ,a_k)$ 1: $s=0$, $r=k$ 2: for $i=1$ to $k-2$ do 3:     for $j=1$ to $z-r+1$ do 4:         if$g<s+\left(\genfrac{}{}{0pt}{}{z-1-j}{r-2}\right)$then 5:             $a_i=j$, $r=r-1$, $z=z-j$ 6:             break 7:         $s=s+\left(\genfrac{}{}{0pt}{}{z-1-j}{r-2}\right)$ 8: $a_{k-1}=g-s+1$, $a_k=z-a_{k-1}$

Algorithm 5 represents the key generation of HORSIC+. It first chooses t and wn-bit strings uniformly at random. The first t bit strings are used as the signature key and the remaining w bit strings are used as the bitmasks $\overrightarrow{r}=(r_1,r_2,\dots ,r_w)$. Then it also chooses a function key $\kappa \stackrel{\$}{\leftarrow }\mathcal{K}$. The function key $\kappa$ specifies a particular function $f_{\kappa }$ in the family ${\mathcal{F}}_n$. It is important to note that the verification key Y includes $(\kappa ,\overrightarrow{r})$ and thus known to everybody.

Algorithm 5: Key generation of HORSIC+ ($K{g}_{HORSIC+}\left(\right)$)

System Parameters: Parameters n, t, k, z, and w Output: Signature key X and verification key Y 1: Choose $X=(x_1,x_2,\dots ,x_t)\stackrel{\$}{\leftarrow }{\{0,1\}}^{(t,n)}$ 2: Choose $\overrightarrow{r}=(r_1,r_2,\dots ,r_w)\stackrel{\$}{\leftarrow }{\{0,1\}}^{(w,n)}$ 3: Choose $\kappa \stackrel{\$}{\leftarrow }\mathcal{K}$ 4: Compute $Y=(y_0,y_1,y_2,\dots ,y_t)=((\kappa ,\overrightarrow{r}),c^w(x_1,\overrightarrow{r}),c^w(x_2,\overrightarrow{r}),\dots ,c^w(x_t,\overrightarrow{r}))$ 5: return$(X,Y)$

Figure 1 and Algorithm 6 represent the signing of HORSIC+. HORSIC+ uses a bijective function $C_{k,z}$ and two cryptographic hash functions H and G. A cryptographic hash function H is used to map each message M to a k-element ordered subset $(i_1,i_2,\dots ,i_k)$ of a t-element set $\{1,2,\dots ,t\}$. A counter $ctr$ is used to ensure that all $i_j$ are distinct. A cryptographic hash function G and a bijective function $C_{k,z}$ are used to map each message M to a k-part integer composition $(a_1,a_2,\dots ,a_k)$ of z. Each $si{g}_j$ is generated by applying the chaining function $w-a_j$ times on $x_{i_j}$.

Algorithm 6: Signing of HORSIC+ ($Sig{n}_{HORSIC+}(X,M,\kappa ,\overrightarrow{r})$)

System Parameters: Parameters n, t, k, z, and w Input: Signature key X, message M, function key $\kappa$, and bitmasks $\overrightarrow{r}$ Output: Signature $\sigma$ 1: Compute $g=G\left(M\right)$ 2: Compute $(a_1,a_2,\dots ,a_k)=C_{k,z}\left(g\right)$ 3: Set $ctr=0$ 4: Compute $h=H(M\mid ctr)$ 5: Split h into k pieces $(h_1,h_2,\dots ,h_k)$ of length ${log}_{2}t$ bits each 6: Interpret each $h_j$ as an integer $i_j$ for all $j\in \{1,2,\dots ,k\}$ 7: if there exist p and q with $p,q\in \{1,2,\dots ,k\}$ such that $i_p=i_q$ and $p\ne q$ then 8:    $ctr=ctr+1$ and go to Step 4 9: Compute $si{g}_j=c^{w-a_j}(x_{i_j},\overrightarrow{r})$ for all $j\in \{1,2,\dots ,k\}$ 10: return$\sigma =(ctr,si{g}_1,si{g}_2,\dots ,si{g}_k)$

Figure 1. Signing of HORSIC+.

Algorithm 7 represents the verification of HORSIC+. Each $si{g}_j$ is verified by applying the chaining function $a_j$ times and comparing it with the verification key.

Algorithm 7: Verification of HORSIC+ ($V{f}_{HORSIC+}(Y,M,\sigma )$)

System Parameters: Parameters n, t, k, z, and w Input: Verification key Y, message M, and signature $\sigma$ Output: “accept” or “reject” 1: Compute $g=G\left(M\right)$ 2: Compute $(a_1,a_2,\dots ,a_k)=C_{k,z}\left(g\right)$ 3: Compute $h=H(M\mid ctr)$ 4: Split h into k pieces $(h_1,h_2,\dots ,h_k)$ of length ${log}_{2}t$ bits each 5: Interpret each $h_j$ as an integer $i_j$ for all $j\in \{1,2,\dots ,k\}$ 6: if there exist p and q with $p,q\in \{1,2,\dots ,k\}$ such that $i_p=i_q$ and $p\ne q$ then 7:     return “reject” 8: if there exist $j\in \{1,2,\dots ,k\}$ such that $c^{a_j}(si{g}_j,{\overrightarrow{r}}_{w-a_j+1,w})\ne y_{i_j}$ then 9:    return “reject” 10: return “accept”

4. Analysis

In this section, we analyze the security of HORSIC+ and calculate its security level. We also compare HORSIC+ with HORS and HORST for the same security levels.

4.1. Security Analysis

In this subsection, we analyze the security of HORSIC+. We prove HORSIC+ is existentially unforgeable under chosen message attacks, if the used function family ${\mathcal{F}}_n$ is a second-preimage resistant family of undetectable one-way functions and H and G are cryptographic hash functions in the random oracle model.

Theorem 1.

Suppose ${\mathcal{F}}_n=\{f_{\kappa }:{\{0,1\}}^n\to {\{0,1\}}^n\mid \kappa \in \mathcal{K}\}$ is a second-preimage resistant, undetectable one-way function family and H and G are cryptographic hash functions in the random oracle model. Then the insecurity of HORSIC+ against an EU-CMA attack is bounded by

$$\begin{array}{cc}\hfill & {\mathrm{InSec}}^{\mathrm{EU}-\mathrm{CMA}}(\mathrm{HORSIC}+(1^n,t,k,z,w);T,1)\hfill \\ \hfill & \le max\{T·\frac{k!(k-1)!(z-k)!}{t^k(z-1)!},\hfill \\ \hfill & w·{\mathrm{InSec}}^{\mathrm{UD}}({\mathcal{F}}_n;T^{\star })+wt·max\{{\mathrm{InSec}}^{\mathrm{OW}}({\mathcal{F}}_n;T^{\prime }),w·{\mathrm{InSec}}^{\mathrm{SPR}}({\mathcal{F}}_n;T^{\prime })\}\}\hfill \end{array}$$

(30)

with the time $T^{\prime }=T+(t+2k)w$ and $T^{\star }=T+(t+2k+1)w-1$.

Proof of Theorem 1. 

The proof is provided in Appendix A.    □

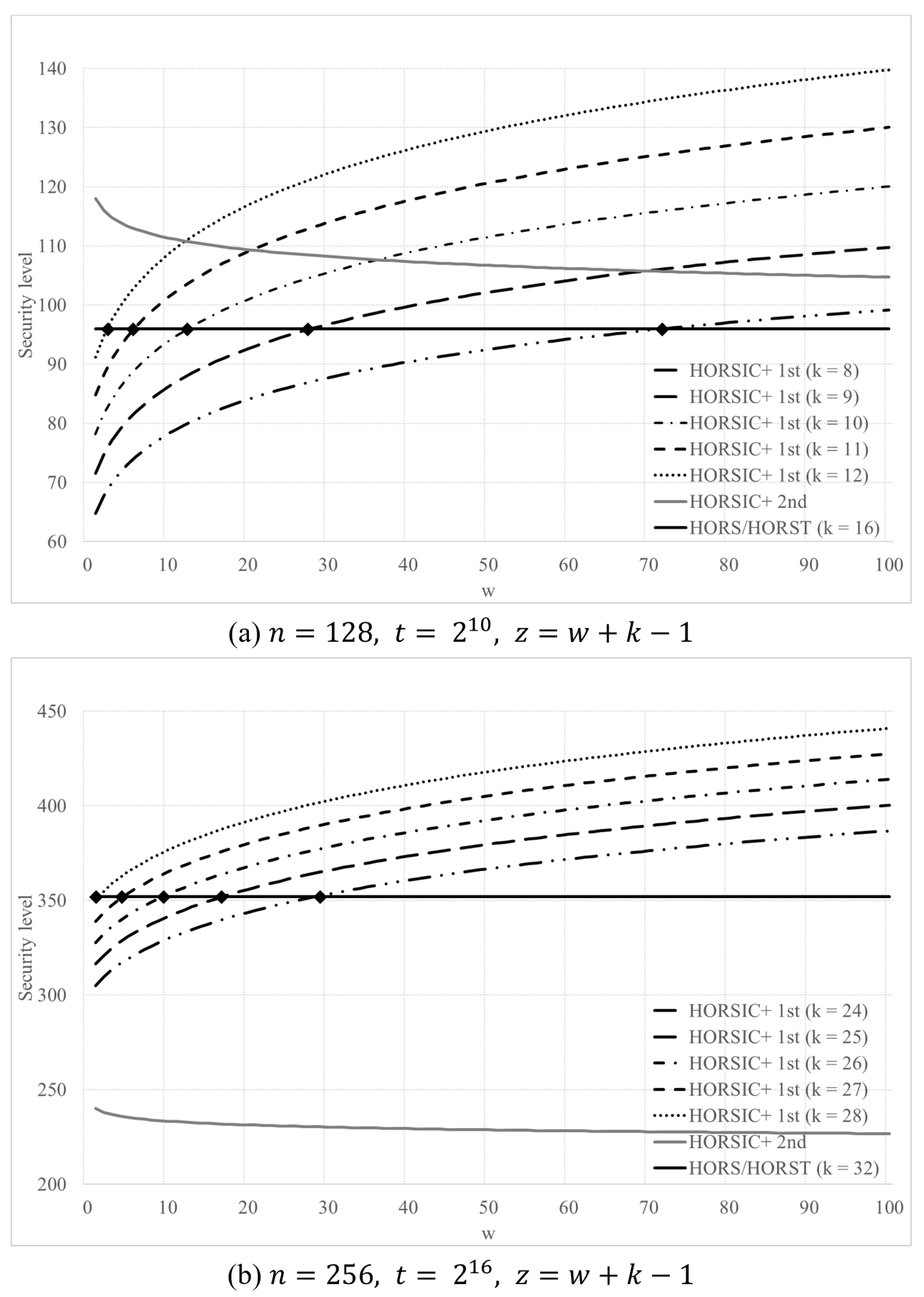
4.2. Security Level

In this subsection, we calculate the security level of HORSIC+ using Theorem 1. According to [29], HORSIC+ has security level b if a successful attack on HORSIC+ is expected to require $2^{b-1}$ evaluations of functions from ${\mathcal{F}}_n$ on average. The security level of HORSIC+ can be calculated by finding a lower bound for T such that $\frac{1}{2}\le {\mathrm{InSec}}^{\mathrm{EU}-\mathrm{CMA}}(\mathrm{HORSIC}+(1^n,t,k,z,w);T,1)$.

Table 1 in Section 2.1 and [20] can be used to compute the insecurity of ${\mathcal{F}}_n$ under generic attacks:

$${\mathrm{InSec}}^{\mathrm{OW}}({\mathcal{F}}_n;T)={\mathrm{InSec}}^{\mathrm{SPR}}({\mathcal{F}}_n;T)={\mathrm{InSec}}^{\mathrm{UD}}({\mathcal{F}}_n;T)=\frac{T}{2^n}.$$

(31)

From now on, we assume $T=T^{\prime }=T^{\star }$, since $(t+2k)w$ and $(t+2k+1)w-1$ are negligible when compared to the value T. We calculate the lower bound on T.

$$\begin{array}{cc}\hfill \frac{1}{2}& \le {\mathrm{InSec}}^{\mathrm{EU}-\mathrm{CMA}}(\mathrm{HORSIC}+(1^n,t,k,z,w);T,1)\hfill \\ \hfill & \le max\{T·\frac{k!(k-1)!(z-k)!}{t^k(z-1)!},w·\frac{T}{2^n}+wt·max\{\frac{T}{2^n},w·\frac{T}{2^n}\}\}\hfill \\ \hfill & =max\{T·\frac{k!(k-1)!(z-k)!}{t^k(z-1)!},\frac{wT}{2^n}+\frac{w^{2}tT}{2^n}\}\hfill \\ \hfill & =T·max\{\frac{k!(k-1)!(z-k)!}{t^k(z-1)!},\frac{w^{2}t+w}{2^n}\}.\hfill \end{array}$$

(32)

Solving this for T gives us

$$\begin{array}{cc}\hfill T& \ge \frac{1}{2}·min\{\frac{t^k(z-1)!}{k!(k-1)!(z-k)!},\frac{2^n}{w^{2}t+w}\}\hfill \\ \hfill & =2^{min\{{log}_2\left(\frac{t^k(z-1)!}{k!(k-1)!(z-k)!}\right),n-{log}_2(w^{2}t+w)\}-1}\hfill \end{array}$$

(33)

So, we can obtain the security level b for HORSIC+:

$$b\ge min\{{log}_2\left(\frac{t^k(z-1)!}{k!(k-1)!(z-k)!}\right),n-{log}_2(w^{2}t+w)\}.$$

(34)

4.3. Comparison with HORS and HORST

In this subsection, we compare HORSIC+ with HORS and HORST for the same security levels. Since the security level of HORS is the same as that of HORST with the same parameters, we refer to HORS and HORST together as HORS/HORST.

4.3.1. Security Parameters for HORSIC+

In this sub-subsection, we choose security parameters for HORSIC+ having the same security levels as HORS/HORST. Figure 2 shows the security level of HORSIC+ for various choices of k and HORS/HORST for signing a single message. In this case, we set $z=w+k-1$ for HORSIC+. The X-axis represents the parameter w, which affects the computational cost. The Y-axis corresponds to the security level.

Figure 2. Security level of HORSIC+ for various choices of k and HORS/HORST for signing a single message. The parameters are chosen from (a) HORS and (b) HORST as used in SPHINCS.

The parameters for HORS/HORST in Figure 2 are chosen from (a) HORS [14] and (b) HORST as used in SPHINCS [13]. The original HORS scheme recommends to use SHA-1 [30] or RIPEMD-160 [31] as a cryptographic hash function H which has an output length of 160 bits [14]. Thus, the original HORS scheme uses $t=2^{10}$ and $k=16$ ($10\times 16=160$). The parameters for SPHINCS-256 ($t=2^{16}$, $k=32$) are selected to provide long-term $2^{128}$ security against attackers with access to quantum computers.

The security level of HORS/HORST can be obtained from the following equation [14,32]:

$$k({log}_{2}t-{log}_{2}k).$$

(35)

When using the parameters in Figure 2a,b, the security levels of HORS/HORST are 96 and 352, respectively.

$$\begin{array}{cc}\hfill & 16({log}_2{2}^{10}-{log}_{2}16)=16(10-4)=96.\hfill \\ \hfill & 32({log}_2{2}^{16}-{log}_{2}32)=32(16-5)=352.\hfill \end{array}$$

(36)

In Figure 2, ‘HORSIC+ 1st’ refers to the first argument of the min function in Equation (34) (i.e., ${log}_2\left(\frac{t^k(z-1)!}{k!(k-1)!(z-k)!}\right)$). ‘HORSIC+ 2nd’ refers to the second argument of the min function in Equation (34) (i.e., $n-{log}_2(w^{2}t+w)$). ‘HORSIC+ 1st’ corresponds to the case where the adversary succeeds in forging only with already revealed secret values. As the number of signatures using the same HORSIC+ key increases, the number of revealed secret values also increases. Thus, the security level of ‘HORSIC+ 1st’ decreases more rapidly than that of ‘HORSIC+ 2nd’. So it is more appropriate to compare the security level of ‘HORSIC+ 1st’ with that of HORS/HORST.

To get a security level of 96 bits for HORSIC+, w should be 3, 6, 13, 28, and 72, when k is 12, 11, 10, 9, and 8, respectively. See the diamond marker in Figure 2a. To get a security level of 352 bits for HORSIC+, w should be 2, 5, 10, 17, and 29, when k is 28, 27, 26, 25, and 24, respectively. See the diamond marker in Figure 2b.

In HORSIC+, as the parameter k decreases, the signature size also decreases, but the parameter w should increase to offer the same security level. Figure 2 shows that increased w results in increased security level of ‘HORSIC+ 1st’. However, it also results in increased overhead in key generation, signing, and verification. We choose two sets of parameters taking into account the relative importance of speed and signature size. The first is $n=128$, $t=2^{10}$, $k=10$, and $w=13$, implying $z=22$ which offers 96-bit security level. The second is $n=256$, $t=2^{16}$, $k=26$, and $w=10$, implying $z=35$ which offers 352-bit security level. Based on these two sets of parameters, a comparison of HORSIC+ with HORS/HORST will be presented in Section 4.3.3.

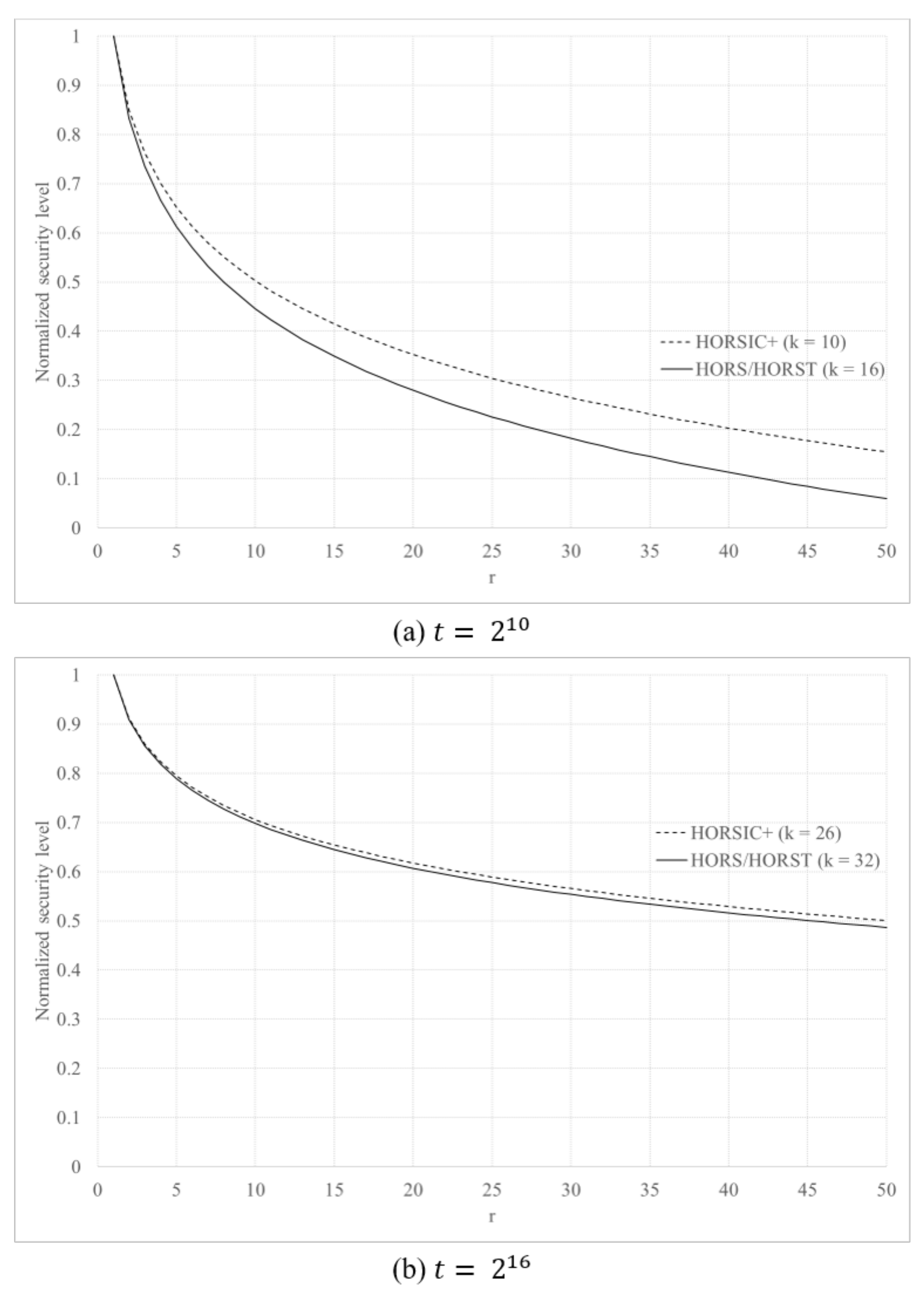
4.3.2. Security for Multiple Messages

HORSIC+ can be used as a few-time signature scheme in two ways. The first is for the signer and the verifier to maintain their own state information as in [15,33]. It is a good strategy when HORSIC+ is used in broadcast authentication in wireless sensor networks. However, it is not appropriate when used as a general signature scheme because maintaining the state information means it is stateful. If the state information update fails, then HORSIC+ cannot be used anymore. The second is to use HORSIC+ many times without state information as HORST in [13]. In this case, the security level decreases as the number of signatures using the same key increases.

To investigate how rapidly the security level decreases as the number of signatures using the same key (r) increases, we normalize the security level for $r=1$ to 1 and compare the normalized security level of HORSIC+ and HORS/HORST. For simplicity, we compute the normalized security level of HORSIC+ by solving the subset-resilience problem.

Figure 3 shows the normalized security level of HORSIC+ and HORS/HORST for multiple messages. The x-axis shows the number of signatures using the same key (r). We can see that the normalized security level of HORSIC+ decreases more slowly than that of HORS/HORST. It is because HORSIC+ uses smaller k than HORS/HORST for the same security level.

Figure 3. Normalized security level of HORSIC+ and HORS/HORST for multiple messages.

4.3.3. Comparison

Table 2 compares HORSIC+ with HORS and HORST for the same security levels (96 bit, 352 bit). For simplicity, we assume that HORST does not apply any optimizations in [13]. The table shows that a HORSIC+ signature size is smaller than a HORS and HORST signature size with a comparable security level. With parameters $n=128, t=2^{10}, k=10,z=22, w=13$, HORSIC+ signatures are 37.5% shorter than HORS signatures and 61.5% shorter than HORST signatures to offer a 96-bit security level. With parameters $n=256, t=2^{16}, k=26, z=35, w=10$, HORSIC+ signatures are 18.75% shorter than HORS signatures and 45.8% shorter than HORST signatures to offer a 352-bit security level. HORSIC+ reduces the signature size at the cost of increased overhead in key generation, signing, and verification. The key generation overhead and the signing overhead of HORSIC+ are larger than those of HORS and HORST. However, it does not affect the usability of HORSIC+, since the key generation has to be performed only once and the signing overhead is still tolerable. Since asymmetric key algorithms are typically hundreds to thousands of times slower than symmetric key algorithms and hash algorithms [34], the costs of signing HORSIC+ (130 with 96-bit security level and 260 with 352-bit security level) are relatively low.

Table 2. Comparison of HORS, HORST, and HORSIC+.

Scheme	Key Gen.	Signing	Verification	Sig. Size	V. K. Size	Security Level
HORS($1^n,t,k$)	t	1	$k+1$	$kn$	$tn$	$k\left({log}_2(t/k)\right)$
HORST($1^n,t,k$)	$2t-1$	1	$k({log}_{2}t+1)$	$(k+{log}_{2}t)n$	n	$k\left({log}_2(t/k)\right)$
HORSIC+($1^n,t,k,z,w$)	$wt$	$kw$	$kw$	$kn$	$(1+w+t)n$	Equation (34)
HORS($1^{128},2^{10},16$)	1024	1	17	$16\times 128$	$1024\times 128$	96
HORST($1^{128},2^{10},16$)	2047	1	$16\times 11$	$26\times 128$	128	96
HORSIC+($1^{128},2^{10},10,22,13$)	13,312	$10\times 13$	$10\times 13$	$10\times 128$	$1038\times 128$	$min\{96,111\}$
HORS($1^{256},2^{16},32$)	65,536	1	33	$32\times 256$	$65,536\times 256$	352
HORST($1^{256},2^{16},32$)	131,071	1	$32\times 17$	$48\times 256$	256	352
HORSIC+($1^{256},2^{16},26,35,10$)	655,360	$26\times 10$	$26\times 10$	$26\times 256$	$65,547\times 256$	$min\{353,233\}$

5. Conclusions

In this paper, we proposed HORSIC+, an efficient post-quantum few-time signature scheme. HORSIC+ differs from HORSIC in that HORSIC+ does not apply f as a plain function to the signature key, but uses a member of a function family which is second-preimage resistant, undetectable, and one-way. Moreover, HORSIC+ uses the chaining function $c^s(x,\overrightarrow{r})$ similar to W-OTS${}^{+}$. These enable the strict security proof without the need for the used function family to be a permutation or collision resistant. We proved HORSIC+ is existentially unforgeable under chosen message attacks, if the used function family is a second-preimage resistant family of undetectable one-way functions and H and G are cryptographic hash functions in the random oracle model. HORSIC+ reduces the signature size by as much as 37.5% or 18.75% compared to HORS and by as much as 61.5% or 45.8% compared to HORST for the same security level. Future work includes further analysis of HORSIC+ and integration of HORSIC+ in SPHINCS.