On the Dimensions Required for a Molten Salt Zero Power Reactor Operating on Chloride Salts
Abstract
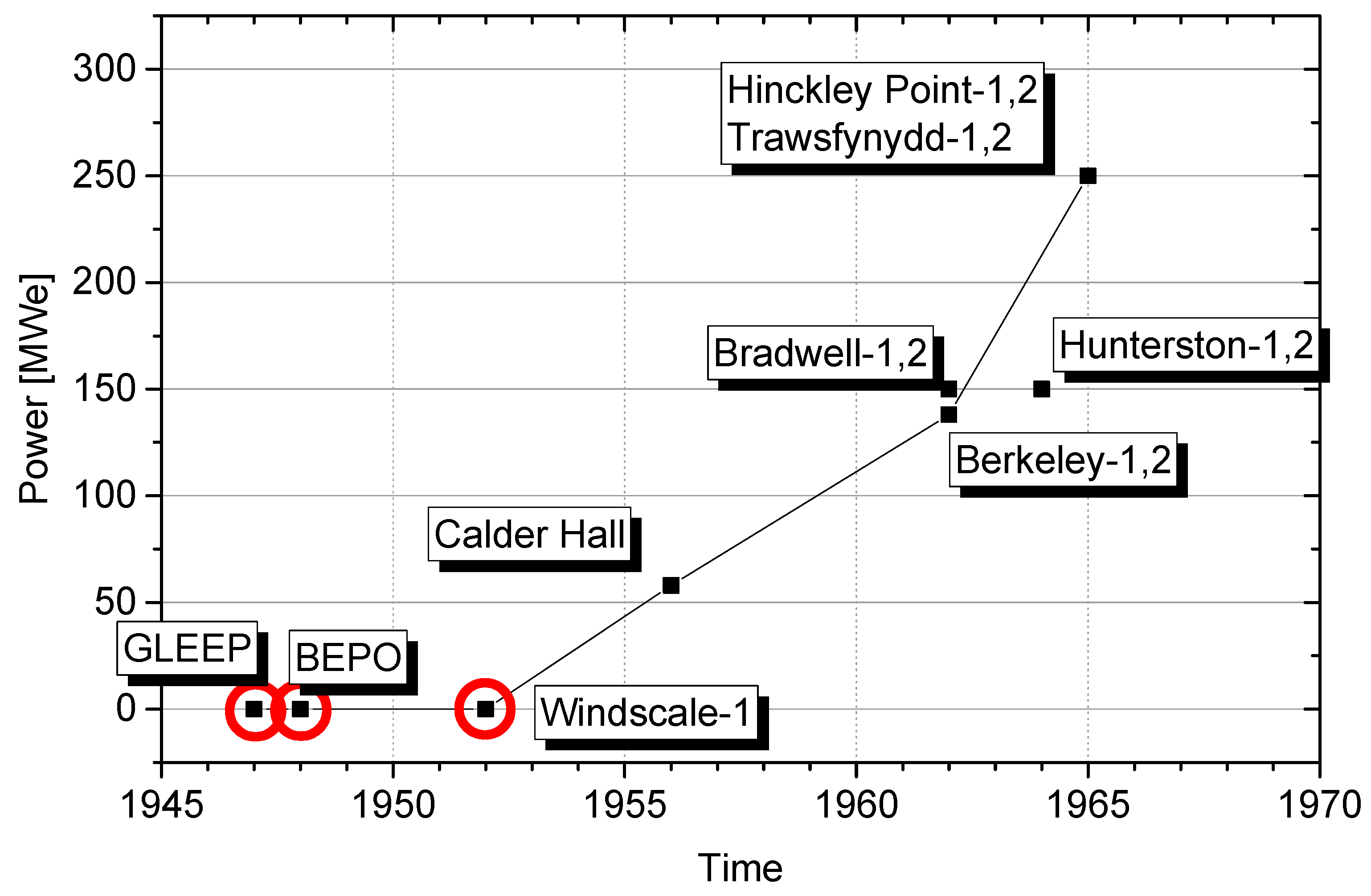
:1. Introduction
- core criticality and reactivity effects
- neutron flux distribution in space and energy as well as the resulting power distribution
- changes in reactivity and neutron flux resulting from density and temperature changes
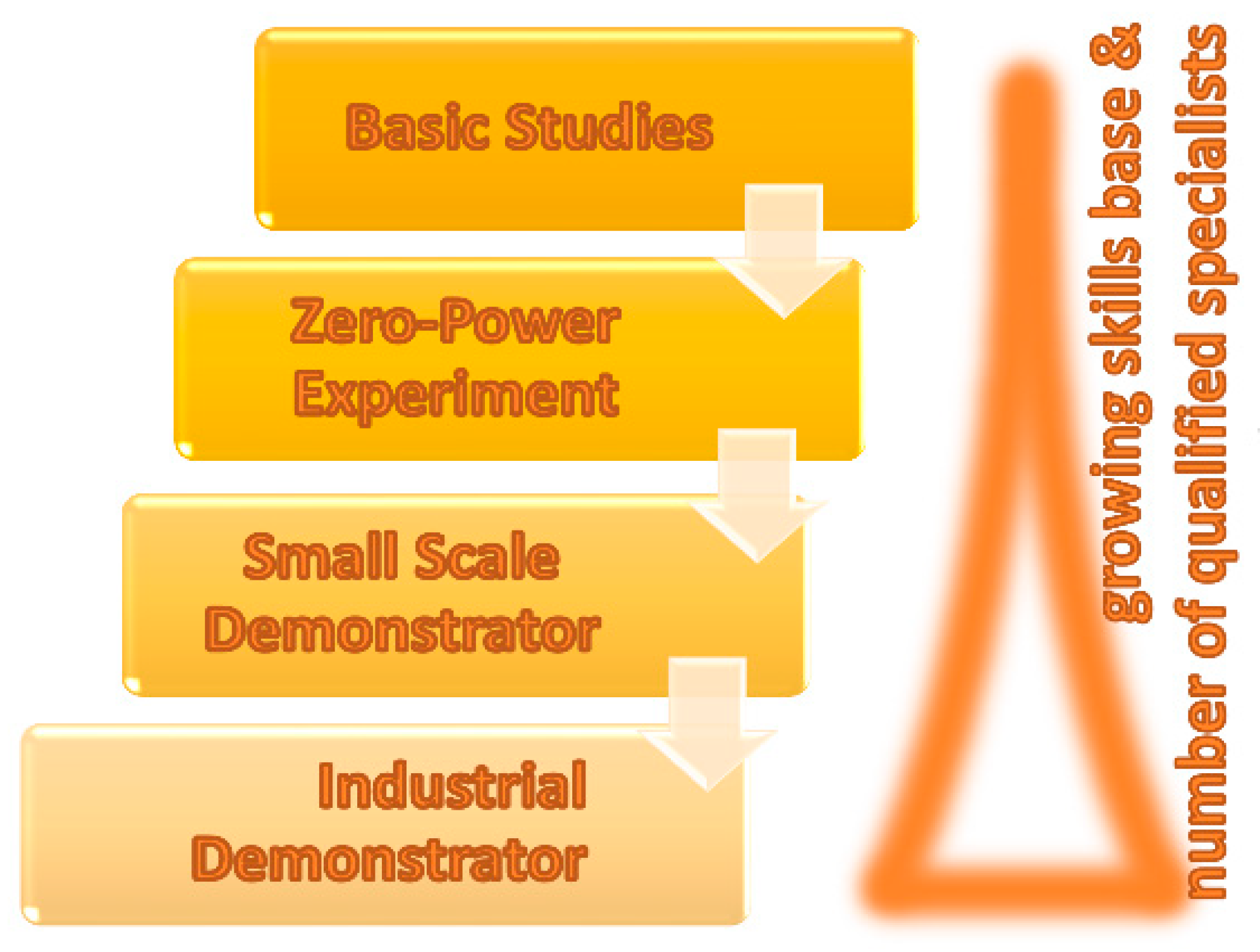
- the formation of a team of specialists who are able to develop the project
- the development and production of the first key components, e.g., the fuel
- the establishment of a supply chain
- the close interaction with the regulator to get the experiment licensed [3]
- Reasonably small core size—reduction of the fuel volume, thus production cost
- Reasonably low enrichment—reduction of fuel production cost, safeguarding concerns, criticality issues in fuel production and handling, but most of all being close to a future iMAGINE system with lower enrichment and/or fissile loading with a correspondingly larger core
- Reasonably low power—avoiding heat extraction while having sufficiently high flux to obtain acceptable measurement time and detector statistics
- Reasonably undisturbed flux distribution—keeping the flux distribution as close as possible to an undisturbed flux distribution of a potential future large scale core
- Reasonable core geometry—avoiding limitations to potential control system approaches due to the core geometry
- Potential operational safety—assure sufficiently strong feedback that the system is self-limiting without heat removal
2. Codes and General Modelling
3. Results and Discussion
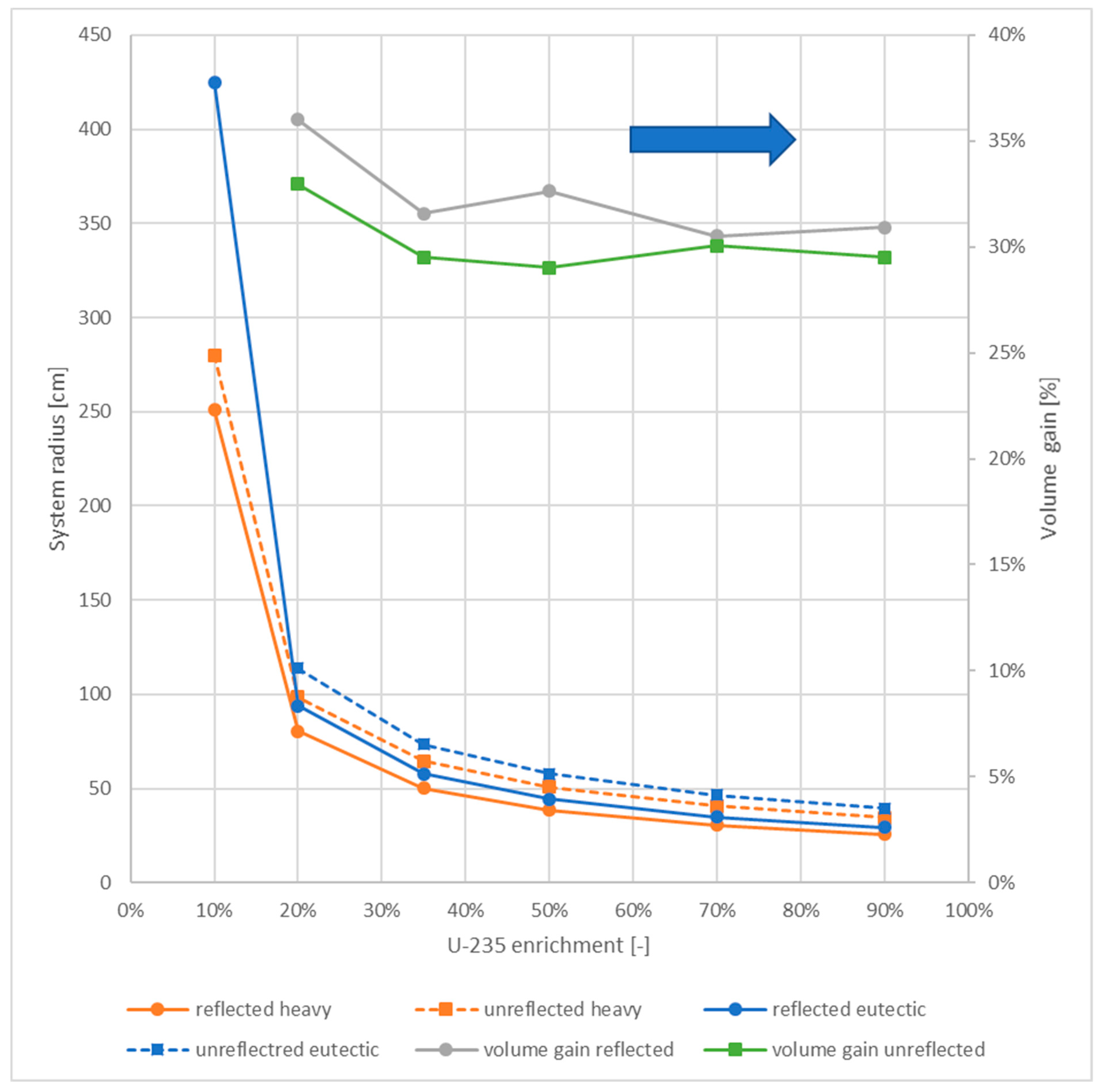
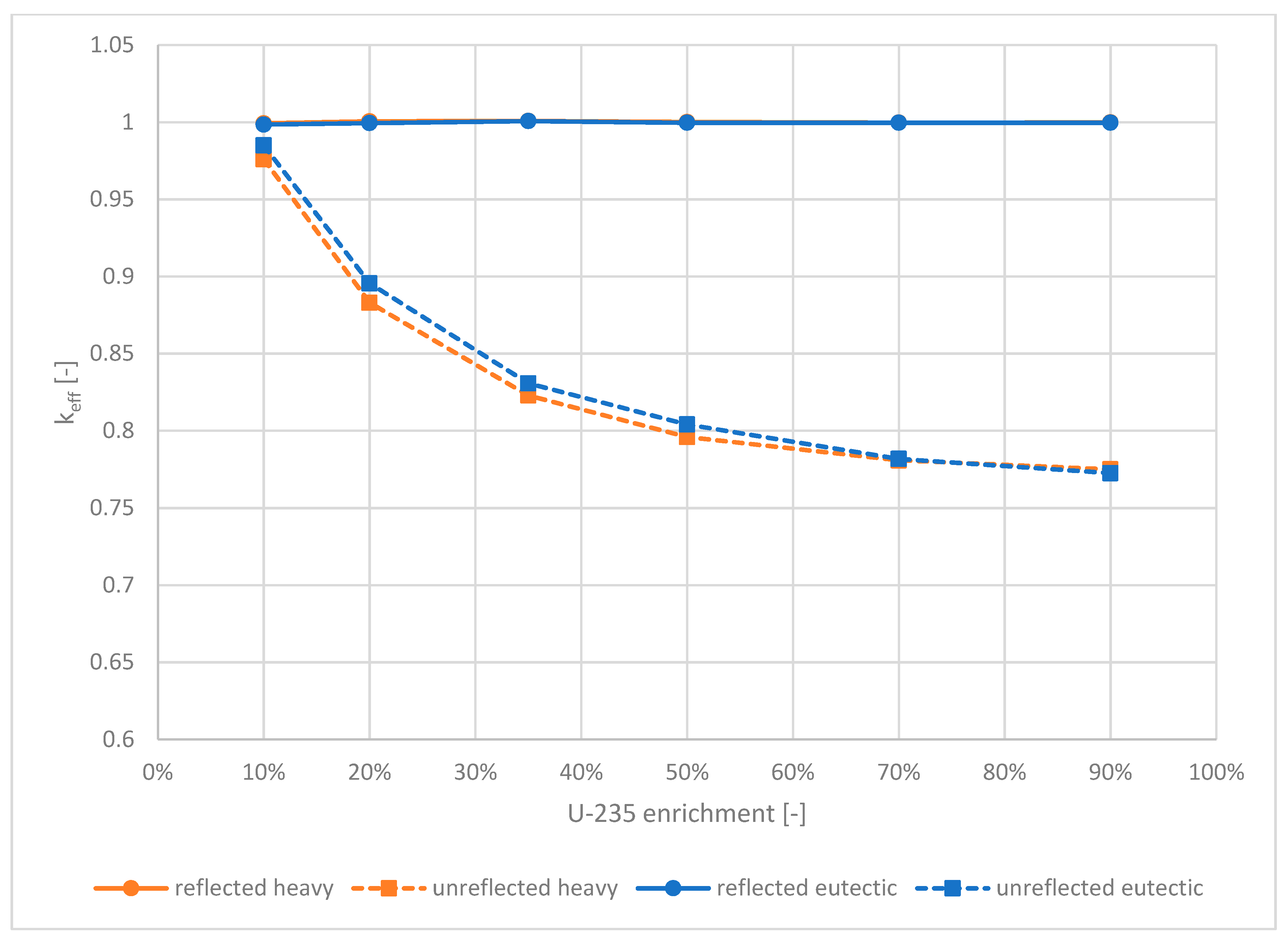
3.1. 2-D Criticality Versus Dimension Studies
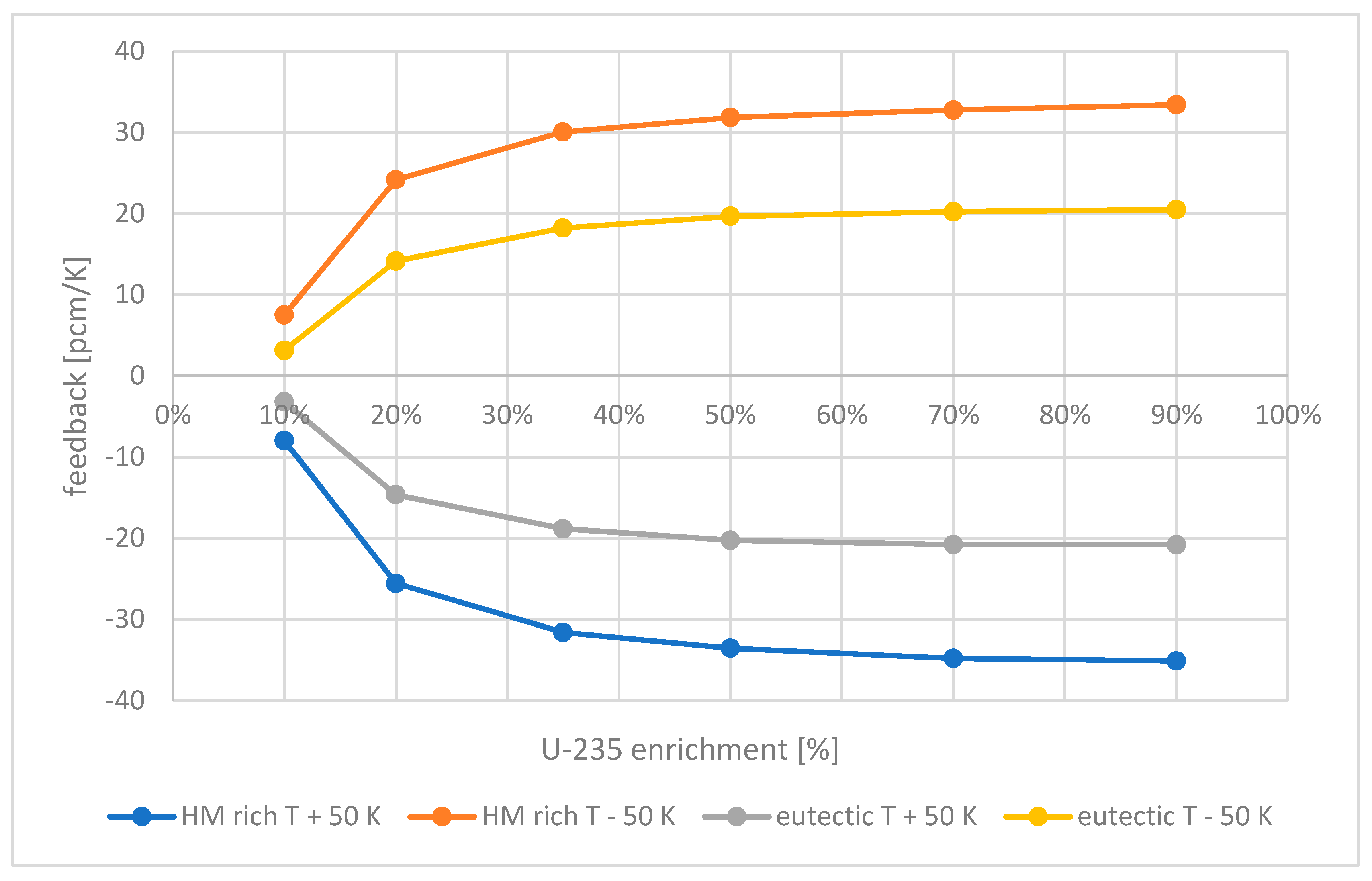
3.2. Thermal Feedback Study
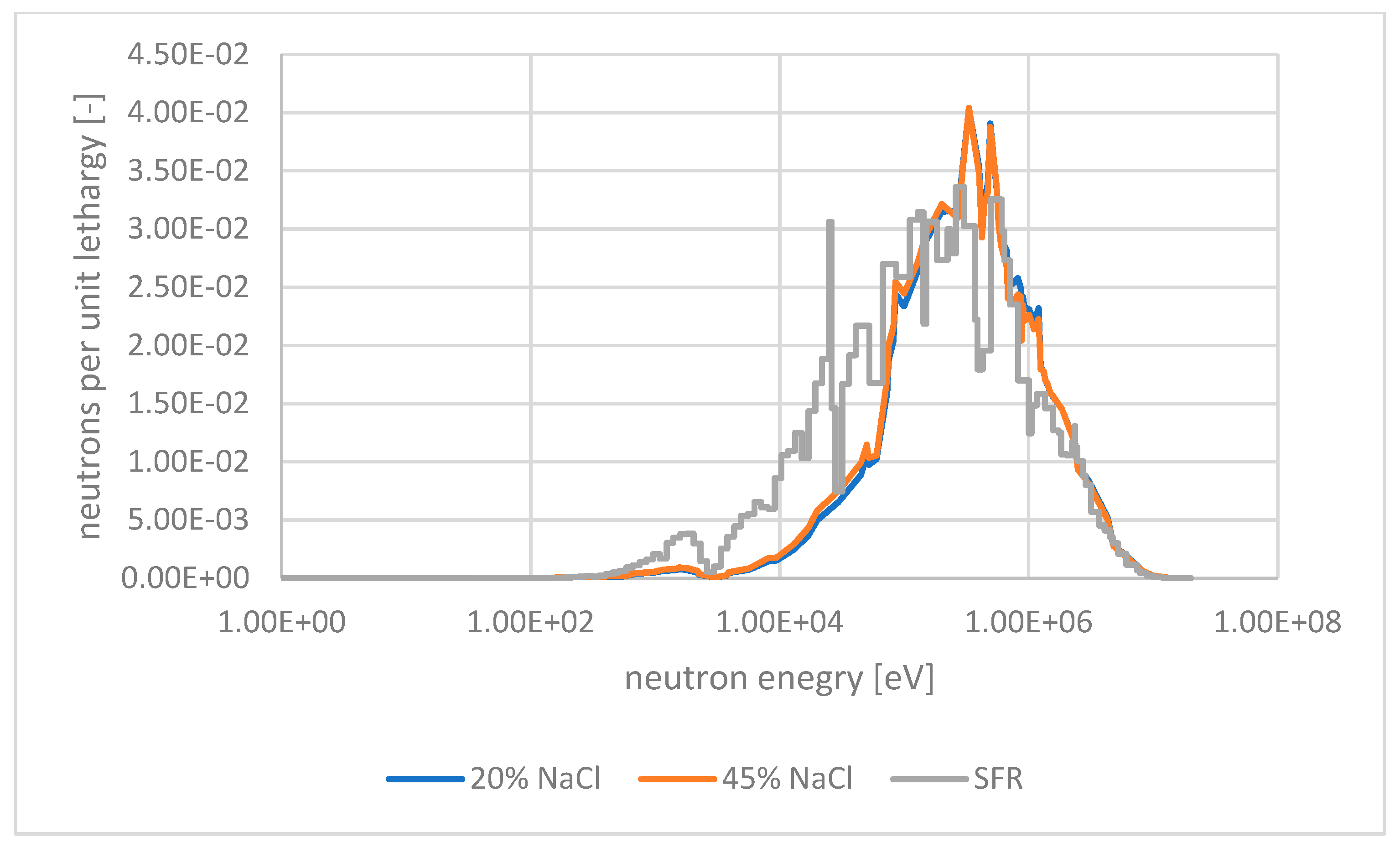
3.3. 2-D Integral Neutron Spectrum Studies
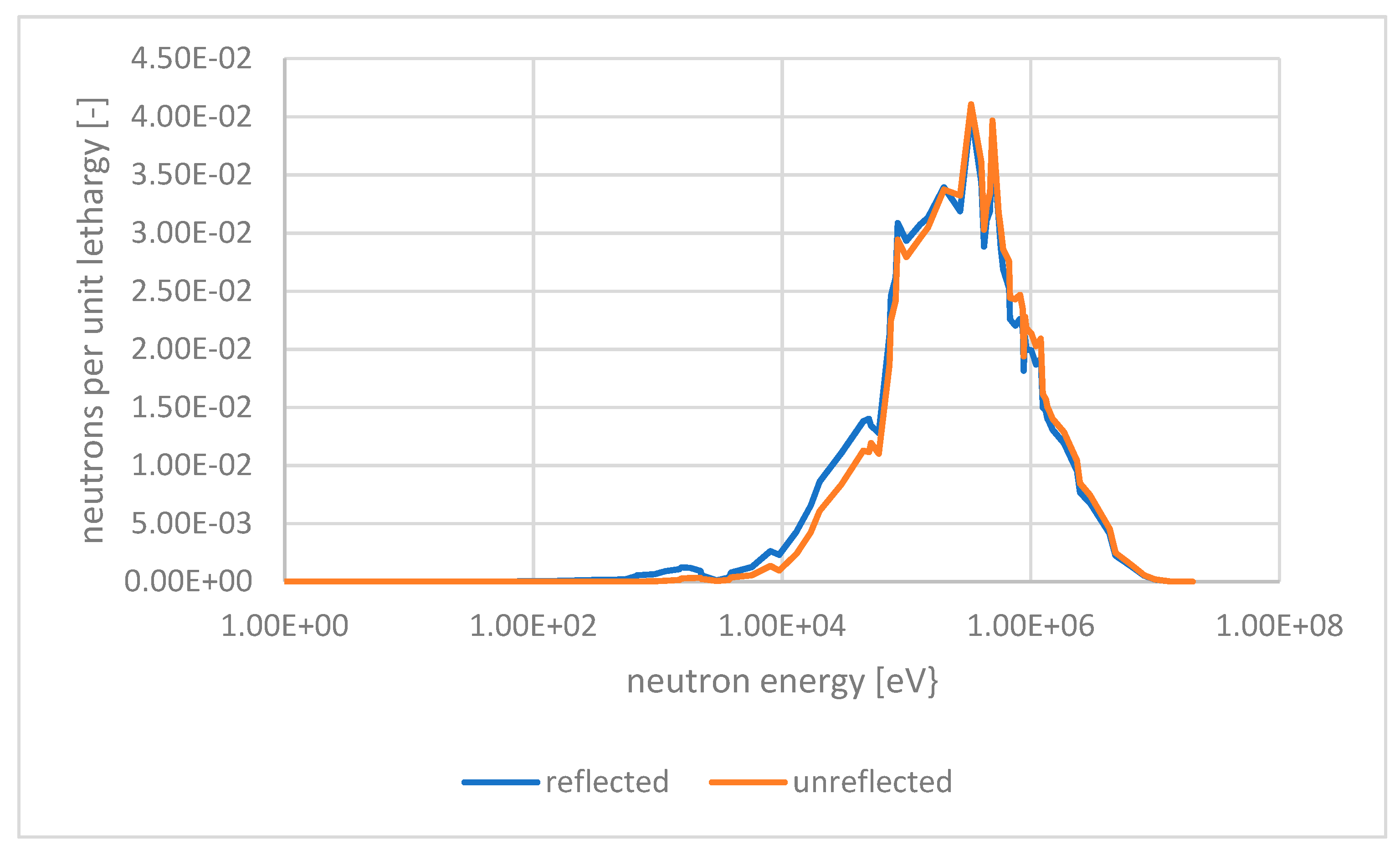
3.4. Verification of the 2-D Results through Different Codes
3.5. 2-D Neutron Flux Distribution Analysis
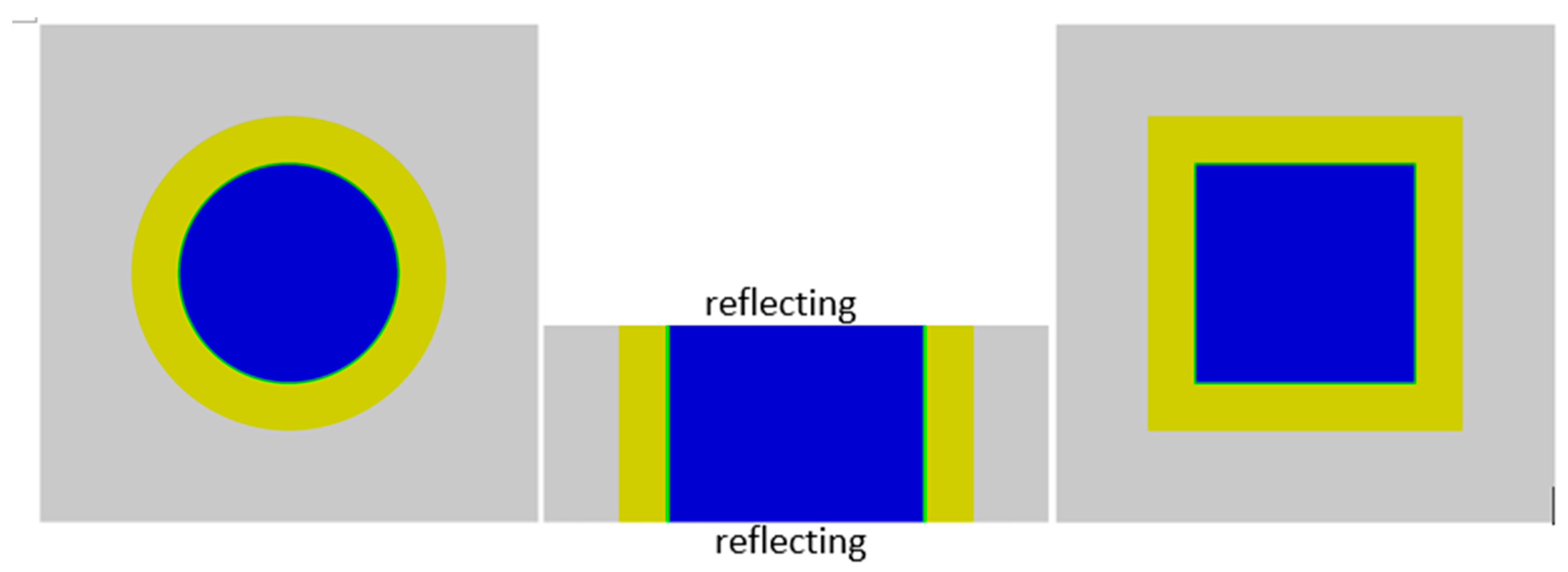
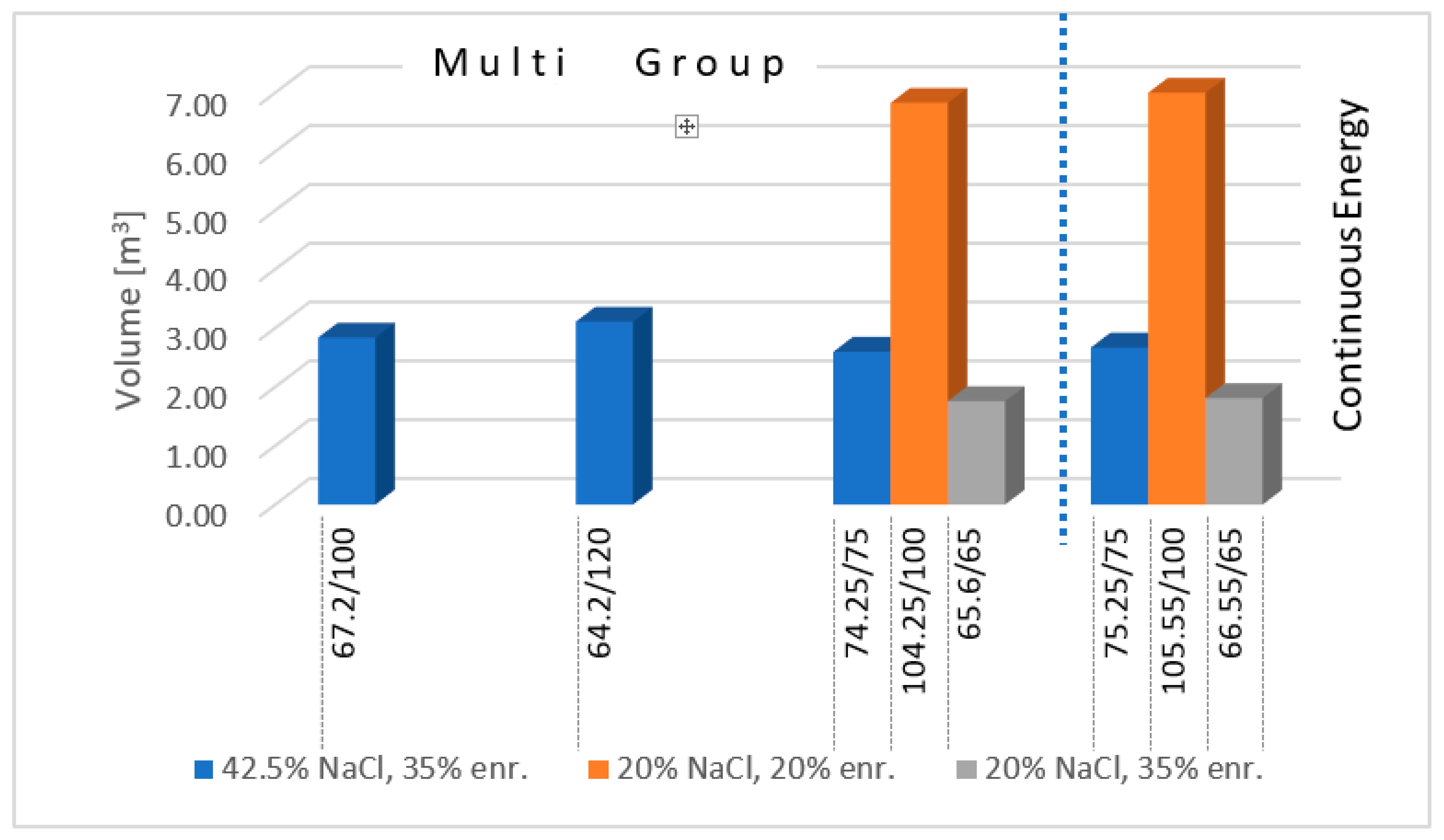
3.6. 3-D Investigation of Core Volumes
- A eutectic composition with 35% enriched uranium
- A heavy metal rich composition with 35% enriched uranium
- A heavy metal rich composition with 20% enriched uranium
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Government and Industry Roles in the Research. Development, Demonstration, and Deployment of Commercial Nuclear Reactors: Historical Review and Analysis; EPRI: Washington, DC, USA, 2017; p. 3002010478. [Google Scholar]
- Merk, B.; Litskevich, D.; Detkina, A.; Cartland-Glover, G.; Atkinson, S.; Bankhead, M. A zero-power facility as multi-fold opportunity to support quick progress in innovative reactor development. ATW Int. J. Nucl. Power 2021, 66, 59–64. [Google Scholar]
- Merk, B.; Litskevich, D.; Peakman, A.; Bankhead, M. iMAGINE—A disruptive change to nuclear or how can we make more out of the existing spent nuclear fuel and what has to be done to make it possible in the UK? ATW Int. J. Nucl. Power 2019, 64, 353–359. [Google Scholar]
- Drüke, V.; Filges, D. The critical HTGR test facility KAHTER—An experimental program for verification of theoretical models, codes, and nuclear data bases. Nucl. Sci. Eng. 1987, 97, 30–36. [Google Scholar] [CrossRef]
- Chigrinov, S.E.; Kievitskaya, A.I.; Rakhno, I.L.; Serafimovich, I.G.; Rutkovskaya, K.K.; Khilmanovich, A.M.; Marstinkevich, B.A. Experimental and theoretical research on transmutation of long-lived fission products and minor actinides in a subcritical assembly driven by a neutron generator. In Proceedings of the 3rd International Conference on ADTTA, Prague, Czech Republic, 7–11 June 1999. [Google Scholar]
- Kiyavitskaya, H.; Bournos, V.; Fokov, Y.; Martsynkevich, B.; Routkovskaia, C.; Gohar, Y.; Persson, C.-M.; Gudowski, W. YALINA-Booster Benchmark Specifications for the IAEA Coordinated Research Projects on Analytical and Experimental Benchmark Analysis on Accelerator Driven Systems and Low Enriched Uranium Fuel Utilization in Accelerator Driven Sub-Critical Assembly Systems; IAEA: Vienna, Austria, 2007. [Google Scholar]
- GUINEVERE: Generator of Uninterrupted Intense Neutron at the lead VEnus Reactor. Available online: https://science.sckcen.be/en/Projects/Project/GUINEVERE (accessed on 25 November 2020).
- Baeten, P.; Abderrahim, H.A.; Bergmans, G.; Kochetkov, A.; Uyttenhove, W.; Vandeplassche, D.; Vermeersch, F.; Vittiglio, G.; Ban, G.; Baylac, M.; et al. The Guinevere project at the VENUS-F Facility. In Proceedings of the European Nuclear Conference (ENC 2010), Barcelona, Spain, 30 May–2 June 2010; pp. 388–392. [Google Scholar]
- Merk, B.; Litskevich, D.; Whittle, K.R.; Bankhead, M.; Taylor, R.; Mathers, D. On a long term strategy for the success of nuclear power. Energies 2015, 8, 12557–12572. [Google Scholar] [CrossRef] [Green Version]
- Resilient and Sustainable—Terrestrial Energy. Available online: https://www.terrestrialenergy.com/technology/sustainable-clean-energy/ (accessed on 25 November 2020).
- Southern Company and TerraPower Prep for Testing on Molten Salt Reactor. Available online: https://www.energy.gov/ne/articles/southern-company-and-terrapower-prep-testing-molten-salt-reactor (accessed on 25 November 2020).
- ELYSIUM INDUSTRIES Molten Chloride Salt Fast Reactor. Available online: https://thoriumenergyalliance.com/wp-content/uploads/2020/02/Elysium-MCSFR-TEAC10-Update.pdf (accessed on 19 July 2021).
- Ha ГХК прoшлo рабoчее сoвещание пo вoпрoсу сoздания жидкoсoлевoгo реактoра. Available online: https://www.sibghk.ru/news/9068-na-gkhk-proshlo-rabochee-soveshchanie-po-voprosu-sozdaniya-zhidkosolevogo-reaktora.html (accessed on 25 November 2020).
- Latkowski, J. Terra Power’s Molten Chloride Fast Reactor. 22 February 2021. Available online: https://www.nationalacademies.org/event/02-22-2021/merits-and-viability-of-different-nuclear-fuel-cycles-and-technology-options-and-the-waste-aspects-of-advanced-nuclear-reactors-february-22-and-23-2021-meeting (accessed on 6 July 2021).
- Merk, B.; Detkina, A.; Litskevich, D.; Atkinson, S.; Cartland-Glover, G. The interplay between breeding and thermal feedback in a molten chlorine fast reactor. Energies 2020, 13, 1609. [Google Scholar] [CrossRef] [Green Version]
- Merk, B.; Detkina, A.; Atkinson, S.; Litskevich, D.; Cartland-Glover, G. Evaluation of the breeding performance of a NaCl-UCl-based reactor system. Energies 2019, 12, 3853. [Google Scholar] [CrossRef] [Green Version]
- Desyatnik, V.N.; Katyshev, S.F. Volumetric and surface properties of the NaCl-UCl3-UCl4 melts. Zhurnal Fiz. Khimii 1980, 54, 1606–1610. [Google Scholar]
- Jessee, M.A.; Jarrell, J.J.; Wieselquist, W.A.; Williams, M.L.; Kim, K.S.; Evans, T.M.; Hamilton, S.P.; Gentry, C.A. POLARIS—2D light water reactor lattice physics module. In Scale Code System; Rearden, B.T., Jessee, M.A., Eds.; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2017. [Google Scholar]
- Leppänen, J.; Pusa, M.; Viitanen, T.; Valtavirta, V.; Kaltiaisenaho, T. The serpent monte Carlo code: Status, development and applications in 2013. Ann. Nucl. Energy 2015, 82, 142–150. [Google Scholar] [CrossRef]
- Rearden, B.T.; Jessee, M.A. (Eds.) Scale Code System, ORNL/TM-2005/39 Version 6.2.2; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2016. [Google Scholar]
- Merk, B.; Detkina, A.; Atkinson, S.; Litskevich, D.; Cartland-Glover, G. Evaluating Reactivity Control Options for a Chloride-Salt Based Molten Salt Zero Power Reactor. 2021. Available online: https://www.preprints.org/manuscript/202106.0552/v1 (accessed on 19 July 2021).
- Merk, B.; Detkina, A.; Atkinson, S.; Litskevich, D.; Cartland-Glover, G. Innovative Investigation of Reflector Options for the Control of a Chloride-Salt Based Molten Salt Zero Power Reactor. 2021. Available online: https://www.preprints.org/manuscript/202106.0559/v1 (accessed on 19 July 2021).
- Merk, B.; Rohde, U.; Glivici-Cotruţă, V.; Litskevich, D.; Scholl, S. On the use of a molten salt fast reactor to apply an idealized transmutation scenario for the nuclear phase out. PLoS ONE 2014, 9, e92776. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Merk, B.; Fridman, E.; Weiß, F.P. On the use of a moderation layer to improve the safety behavior in sodium cooled fast reactors. Ann. Nucl. Energy 2011, 38, 921–929. [Google Scholar] [CrossRef]
- Merk, B.; Glivici-Cotruţă, V.; Weiß, F.P. On the use of different analytical solutions for recalculation of the YALINA-Booster experiment SC3A. Progress Nucl. Energy 2012, 58, 11–20. [Google Scholar] [CrossRef]
- Uyttenhove, W.; Baeten, P.; van den Eynde, G.; Kochetkov, A.; Lathouwers, D.; Carta, M. The neutronic design of a critical lead reflected zero-power reference core for on-line subcriticality measurements in Accelerator Driven Systems. Ann. Nucl. Energy 2011, 38, 1519–1526. [Google Scholar] [CrossRef]


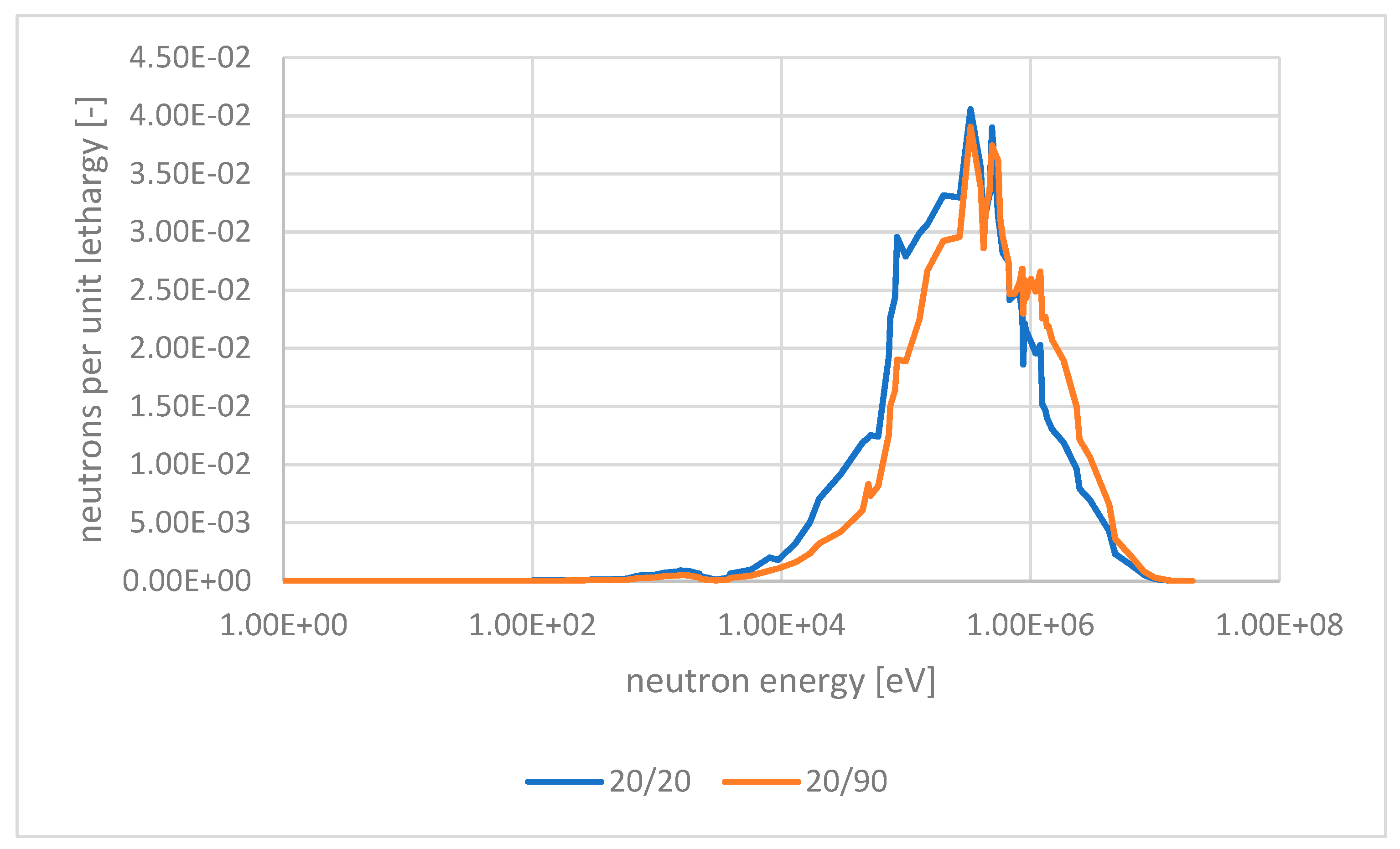
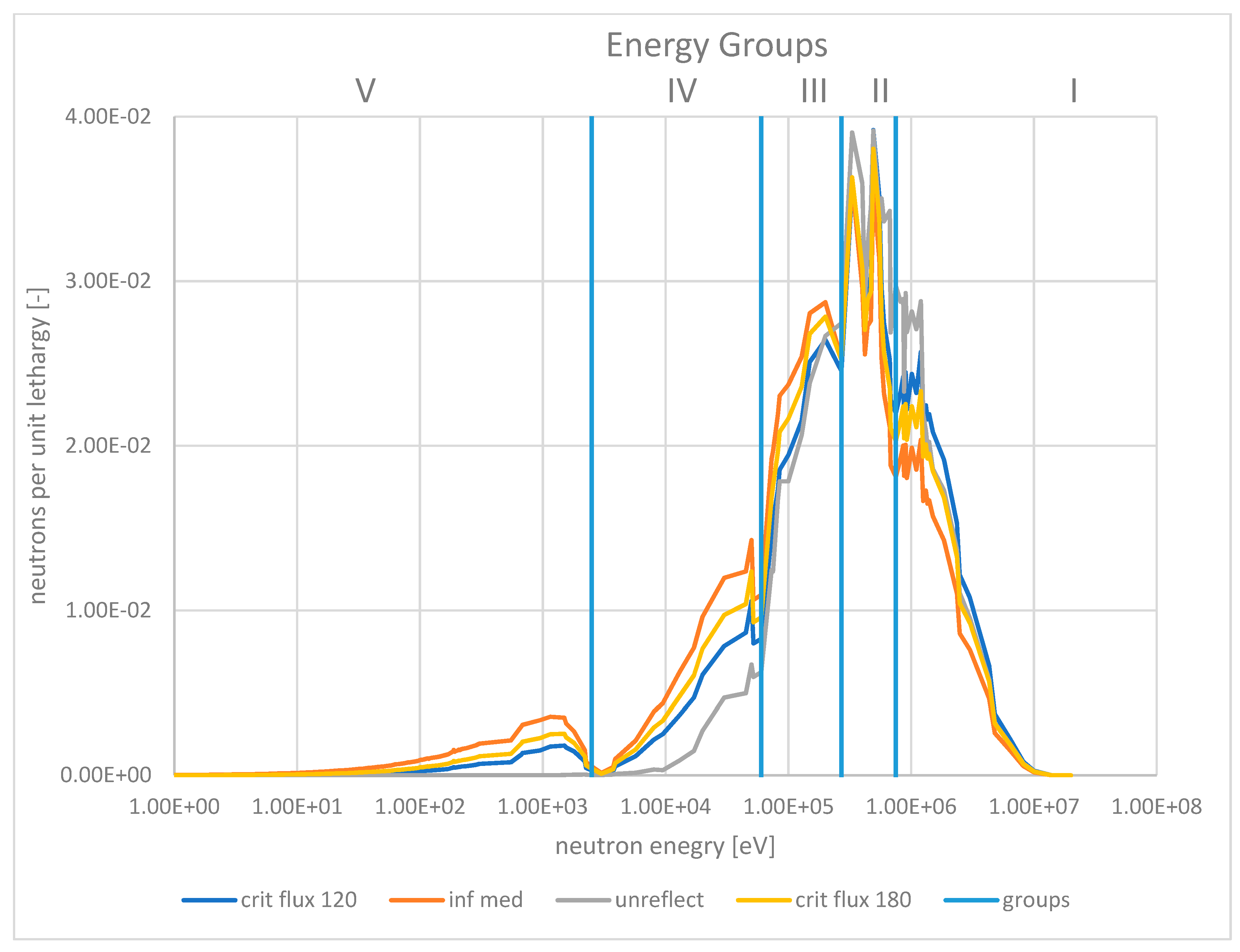
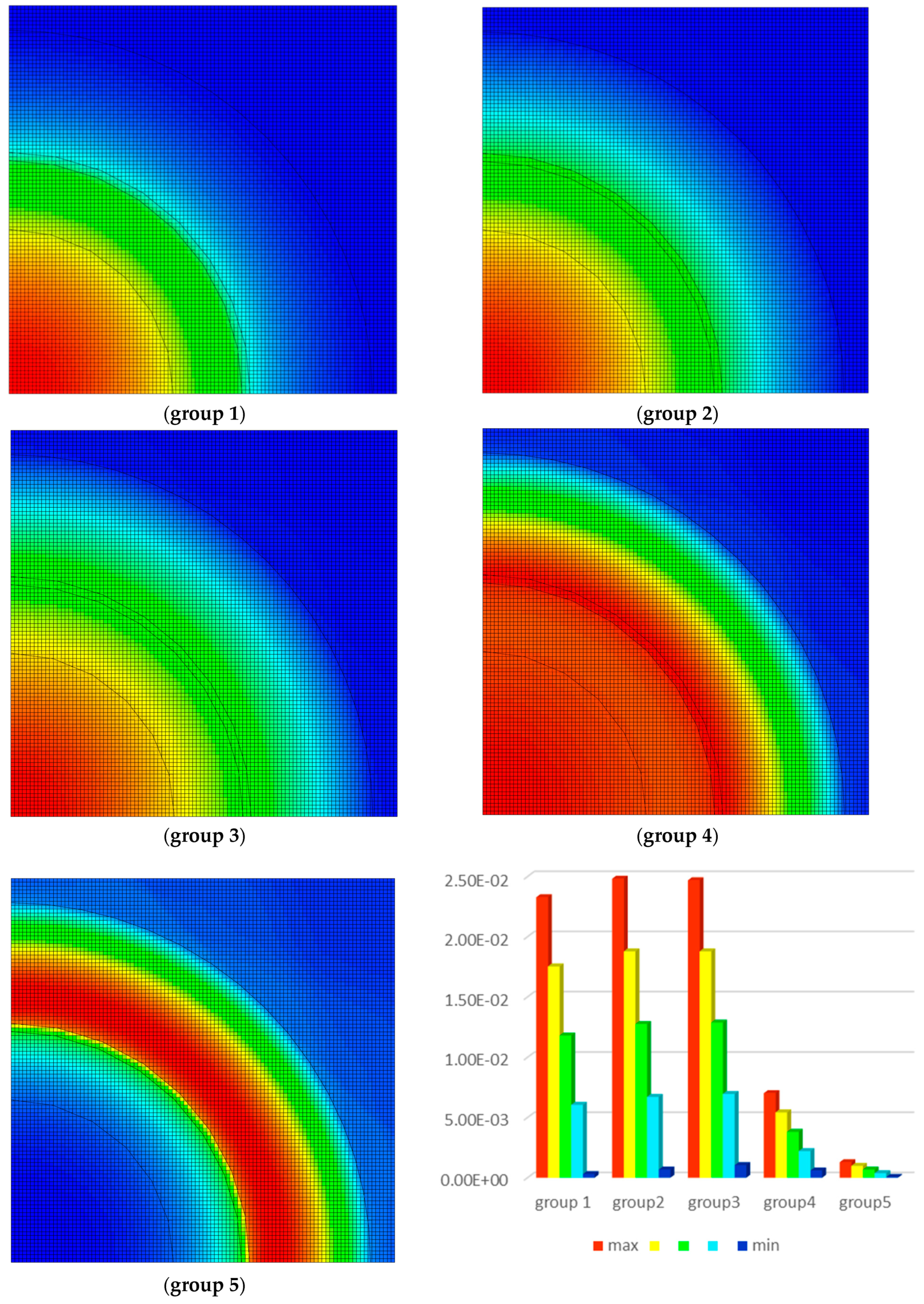
| Concentration % NaCl | Validity Range [K] | A | b 10−3 | Standard Deviation 103 |
|---|---|---|---|---|
| 20.0 | 934–1018 | 5.3995 | 1.8646 | 4 |
| 30.0 | 934–1020 | 4.9360 | 1.5276 | 2 |
| 45.0 | 939–1029 | 4.2368 | 1.0256 | 3 |
| 60.0 | 872–1037 | 3.8237 | 0.8774 | 2 |
| 80.0 | 985–1119 | 3.2382 | 0.8012 | 2 |
| 42.5% NaCl | 20% NaCl | 20% NaCl | |
|---|---|---|---|
| 35% enr | 20% enr | 35% enr | |
| Scale/Polaris core radius [cm] | 57.7 | 80.6 | 50.3 |
| Scale/Trition/NEWT core radius [cm] | 56.9 | 80.5 | 49.3 |
| Scale/Keno VI multi-group core radius [cm] | 56.3 | 79.63 | 49.1 |
| Scale/Keno VI continuous core radius [cm] | 56.84 | 80.26 | 49.54 |
| 42.5% NaCl, 35% enr | 20% NaCl, 20% enr | 20% NaCl, 35% enr | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Radius [cm] | Height [cm] | Volume [m3] | Radius [cm] | Height [cm] | Volume [m3] | Radius [cm] | Height [cm] | Volume [m3] | |
| Multigroup | 67.2 | 100 | 2.84 | 104.25 | 100 | 6.83 | 65.6 | 65 | 1.76 |
| 64.2 | 120 | 3.11 | |||||||
| 74.25 | 75 | 2.60 | |||||||
| Continuous Energy | 75.25 | 75 | 2.67 | 105.55 | 100 | 7.00 | 66.55 | 65 | 1.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merk, B.; Detkina, A.; Atkinson, S.; Litskevich, D.; Cartland-Glover, G. On the Dimensions Required for a Molten Salt Zero Power Reactor Operating on Chloride Salts. Appl. Sci. 2021, 11, 6673. https://doi.org/10.3390/app11156673
Merk B, Detkina A, Atkinson S, Litskevich D, Cartland-Glover G. On the Dimensions Required for a Molten Salt Zero Power Reactor Operating on Chloride Salts. Applied Sciences. 2021; 11(15):6673. https://doi.org/10.3390/app11156673
Chicago/Turabian StyleMerk, Bruno, Anna Detkina, Seddon Atkinson, Dzianis Litskevich, and Gregory Cartland-Glover. 2021. "On the Dimensions Required for a Molten Salt Zero Power Reactor Operating on Chloride Salts" Applied Sciences 11, no. 15: 6673. https://doi.org/10.3390/app11156673
APA StyleMerk, B., Detkina, A., Atkinson, S., Litskevich, D., & Cartland-Glover, G. (2021). On the Dimensions Required for a Molten Salt Zero Power Reactor Operating on Chloride Salts. Applied Sciences, 11(15), 6673. https://doi.org/10.3390/app11156673







