Assessment of Tire Features for Modeling Vehicle Stability in Case of Vertical Road Excitation
Abstract
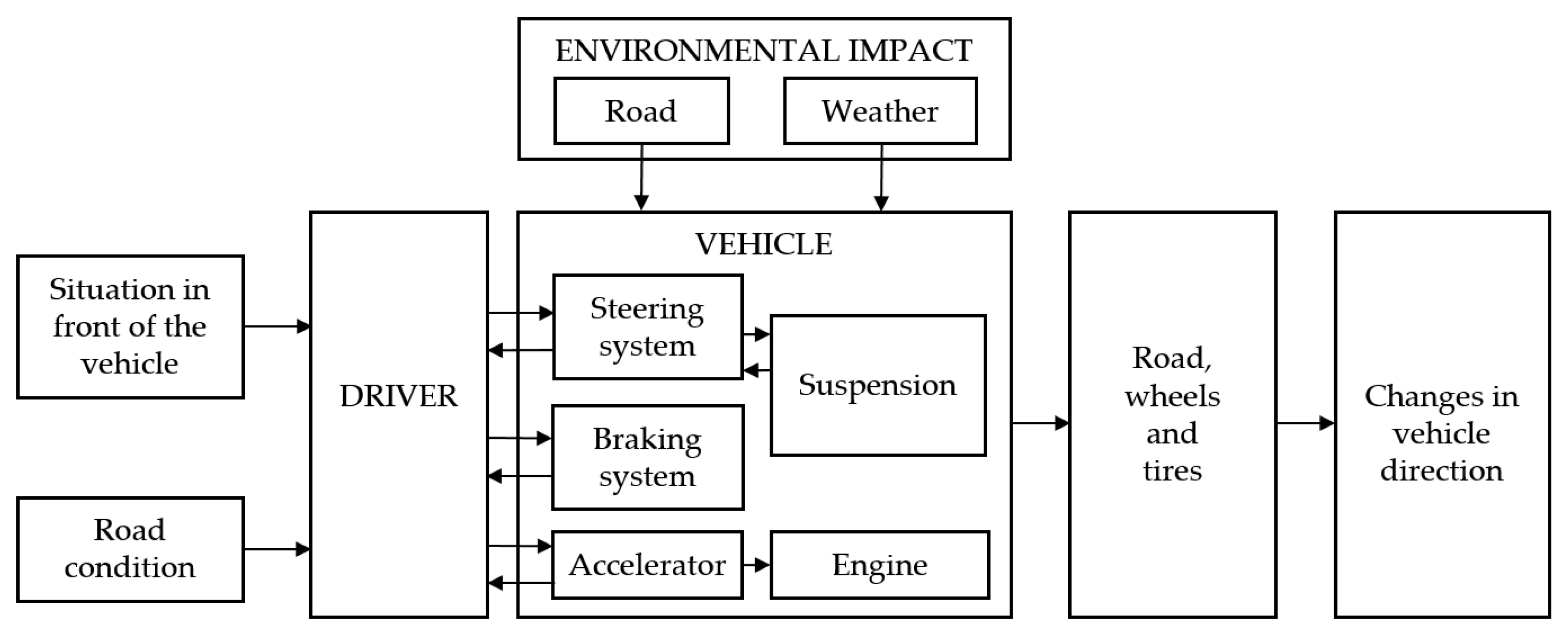
1. Introduction
2. Investigation the Tire-Road Interaction
2.1. Investigation of the Tire Properties
- the contact with the road has an elliptical shape and is limited by the tire width and length of the contact with the road;
- the layers under the tread are sufficiently stiff, and their length does not change during deformation of the tire (ld ≈ l0) (Figure 3a);
- there is the linear dependency between the radial load of the tire and radial deformation Δh;
- the pressure is distributed evenly across the contact surface.
- model deflection hz assuming that the band does not deform in the radial direction:
- contact zone length—2x0;
- contact pressure distribution—qz(x);
- load Fz:
2.2. Deformation Properties of the Ring
2.3. Investigation of Tread Deformation
- the contact with the road has an elliptical shape and is limited by the tire width and length of the contact with the road;
- the layers under the tread are sufficiently stiff, and their length does not change during deformation of the tire;
- there is the linear dependency between the radial deformation and radial load;
- the pressure is distributed evenly across the contact surface.
3. Vehicle Excitation by Road Unevenness
3.1. Suspension Models
3.2. Excitation during Movement on the Asphalt Pavement
3.3. Experimental Investigation
3.4. Comparison of Excitation from Road Unevenness and Experimental Study
4. Discussion
Further Investigations
- development of a dynamic model of a comprehensive integrated assessment of the suspension characteristics, suspension kinematics, steering mechanism, and pavement condition. The model would provide the development of a methodology for determination of the vehicles handling characteristics on roads of known quality using the numerical models.
- investigation of the sensitivity of the individual suspension types to vertical excitation in terms of directional stability criteria and to evaluate the technical condition of the vehicle if the tendency of changes in suspension parameters during known operation. To evaluate the technical condition of the vehicle by modifying the stiffness of the suspension components.
- analysis of vehicle stability in cornering, taking into account the changing position of the wheels as the vehicle is steered, which may have an effect on the vehicle stability. The stability of a vehicle in a turning situation requires the consideration of two criteria: the loss of stability of the vehicle when skidding, and the loss of stability of the vehicle when overturning. In addition, it is necessary to specify the effect of changes in the vehicle’s trajectory in a corner due to the deformation of the suspension and the changes in the position of the wheels as the vehicle is steered.
- integrating driver reactions into the vehicle stability model. Without a driver model, such a simulation is not effective, as the vehicle model changes direction due to random effects and requires frequent correction to simulate steering course corrections.
5. Conclusions
- The revised model of the tire equalizing function was developed. The coordinates of relative measures were found to cause no essential difference in assessment of tire deformations of different vehicle tires. This means that the number of tire groups may be reduced for assessment of their impact on stability.
- The tread deformation characteristics of the tire were investigated by numerical modeling and experiment and showed that the tread deformations could be assessed by simplified models instead of the modulus of elasticity of the tread material, Er = 6 MPa using the calculated modulus of elasticity E1z = 27 MPa.
- Studies on different types of cars (passenger cars, light-duty trucks and SUVs) have shown that the 3D suspension models more accurately provide reflection of the real situation in terms of stability assessment, while simpler quarter-car models can be used for comfort assessment. Comparison of the quarter-car model with the 3D model has shown that, in case of the latter, the resulting wheel travel is higher by up to 20%.
- The results of the experiment on the asphalt pavement were compared with the model. Certain issues were observed in the analysis of experimental results due to additional oscillations and vibrations occurring in the body and suspension elements, which could be avoided by modeling the movement after recording the road microprofile with a profilograph. The parameters that have the greatest impact on the stability of the direction—the difference between the displacement of the sprung and unsprung masses in the model versus the field experiment—did not exceed 15%.
- Changes in the car behavior at changing speed are related not only to the slip effect but also to changes in the wheel spatial position due to the suspension kinematics and suspension incompatibility with the steering mechanism. This effect can be particularly pronounced when road defects (pits, ruts) lead to an increase in the suspension travel.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Misaghi, S.; Tirado, C.; Nazarian, S.; Carrasco, C. Impact of pavement roughness and suspension systems on vehicle dynamic loads on flexible pavements. Transp. Eng. 2021, 3, 100045. [Google Scholar] [CrossRef]
- Mahajan, G.R.; Radhika, B.; Biligiri, K.P. A critical review of vehicle-pavement interaction mechanism in evaluating flexible pavement performance characteristics. Road Mater. Pavement Des. 2020. [Google Scholar] [CrossRef]
- Zoccali, P.; Loprencipe, G.; Lupascu, R.C. Acceleration measurements inside vehicles: Passengers’ comfort mapping on railways. Measurement 2018, 129, 489–498. [Google Scholar] [CrossRef]
- Rill, G.; Castro, A. Road Vehicle Dynamics: Fundamentals and Modeling with MATLAB, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Yechen, Q.; Hong, W.; Huang, Y.; Xiaolin, T. Real-Time Road Profile Identification and Monitoring: Theory and Application; Morgan & cLaypool Publishers: San Rafael, CA, USA, 2019. [Google Scholar] [CrossRef]
- Yang, S.; Chen, L.; Li, S. Dynamics of Vehicle-Road Coupled System; Springer: Beijing, China, 2015. [Google Scholar]
- Leitner, B.; Decký, M.; Kováč, M. Road pavement longitudinal evenness quantification as stationary stochastic process. Transport 2019, 34, 195–203. [Google Scholar] [CrossRef]
- Loprencipe, G.; Zoccali, P.; Cantisani, G. Effects of Vehicular Speed on the Assessment of Pavement Road Roughness. Appl. Sci. 2019, 9, 1783. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, H.; Hui, B. Driving Safety Analysis Using Grid-Based Water-Filled Rut Depth Distribution. Adv. Mater. Sci. Eng. 2021, 5568949. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, H.; Hui, B. Analysis of the lateral slope’s impact on the calculation of water-filled rut depth. PLoS ONE 2020, 15, e0243952. [Google Scholar] [CrossRef]
- Ružinskas, A.; Giessler, M.; Gauterin, F.; Wiese, K.; Bogdevičius, M. Experimental investigation of tire performance on slush. Eksploat. I Niezawodn. Maint. Reliab. 2021, 23, 103–109. [Google Scholar] [CrossRef]
- Gogoi, R.; Das, A.; Chakroborty, P. Rut depth measurement of an asphalt pavement from its original profile. Aust. J. Civ. Eng. 2020, 18, 119–125. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, C.; Sun, M.; Bridgelall, R. Application of a Machine Learning Method to Evaluate Road Roughness from Connected Vehicles. J. Transp. Eng. Part B Pavements 2018, 144, 04018043. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, C.; Bridgelall, R.; Sun, M. Road profile reconstruction using connected vehicle responses and wavelet analysis. J. Terramech. 2018, 80, 21–30. [Google Scholar] [CrossRef]
- Hussan, S.; Kamal, M.A.; Hafeez, I.; Ahmad, N.; Khanzada, S.; Ahmed, S. Modelling asphalt pavement analyzer rut depth using different statistical techniques. Road Mater. Pavement Des. 2020, 21, 117–142. [Google Scholar] [CrossRef]
- Prażnowski, K.; Mamala, J.; Śmieja, M.; Kupina, M. Assessment of the Road Surface Condition with Longitudinal Acceleration Signal of the Car Body. Sensors 2020, 20, 5987. [Google Scholar] [CrossRef] [PubMed]
- Lenkutis, T.; Čerškus, A.; Šešok, N.; Dzedzickis, A.; Bučinskas, V. Road Surface Profile Synthesis: Assessment of Suitability for Simulation. Symmetry 2021, 13, 68. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Besselink, I. Tire and Vehicle Dynamics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2012; Available online: http://scholar.google.com/scholar_lookup?hl=en&publication_year=2012&author=HB+Pacejka&author=I.+Besselink&title=Tire+and+vehicle+dynamics (accessed on 5 January 2021).
- Shaohua, L. Dynamics of Vehicle-Road Coupled System; Science Press: Beijing, China; Springer: Heidelberg/Berlin, Germany, 2015; Available online: https://scholar.google.lt/scholar?hl=lt&as_sdt=0%2C5&q=Dynamics+of+Vehicle%E2%80%93Road+Coupled+System&btnG (accessed on 10 March 2021).
- Mavromatis, S.; Laiou, A.; Yannis, G. Safety assessment of control design parameters through vehicle dynamics model. Accid. Anal. Prev. 2019, 125, 330–335. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Wen, H.; Sun, L.; Hou, W. Study on the Influence of Road Geometry on Vehicle Lateral Instability. J. Adv. Transp. 2020, 7943739. [Google Scholar] [CrossRef]
- Saeedi, M.A. Simultaneous improvement of handling and lateral stability via a new robust control system. Mech. Based Des. Struct. Mach. 2021. [Google Scholar] [CrossRef]
- Vijaykumar, V.; Anand, P. Design Optimization of Suspension and Steering Systems for Commercial Vehicles. In Proceedings of the ICDMC 2019, Chenai, India, 28–29 March 2019; Lecture Notes in Mechanical Engineering. Yang, L.J., Haq, A., Nagarajan, L., Eds.; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Yan, B.; Liu, C.; Wang, X.; Fang, J. Simultaneous estimation of tire side-slip angle and lateral tire force for vehicle lateral stability control. Mech. Syst. Signal Process. 2019, 132, 168–182. [Google Scholar] [CrossRef]
- Joa, E.; Yi, K.; Hyun, Y. Estimation of the tire slip angle under various road conditions without tire–road information for vehicle stability control. Control. Eng. Pract. 2019, 86, 129–143. [Google Scholar] [CrossRef]
- Huang, Y.; Liang, W.; Chen, Y. Estimation and analysis of vehicle lateral stability region. In Proceedings of the American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 4303–4308. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, P.; Li, Z.; Wang, F.; Chen, H. Estimation and Analysis of Vehicle Stability Region under Complex Road Conditions. In Proceedings of the Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 3036–3041. [Google Scholar] [CrossRef]
- Xu, N.; Huang, Y.; Askari, H.; Tang, Z. Tire Slip Angle Estimation Based on the Intelligent Tire Technology. IEEE Trans. Veh. Technol. 2021, 70, 2239–2249. [Google Scholar] [CrossRef]
- Cheli, F.; Sabbioni, E.; Pesce, M.; Melzi, S. A methodology for vehicle side slip angle identification: Comparison with experimental data. Veh. Syst. Dyn. 2007, 45, 549–563. [Google Scholar] [CrossRef]
- Shekh, M.; Umrao, O.P.; Singh, D. Kinematic Analysis of Steering Mechanism: A Review. In Proceedings of the International Conference in Mechanical and Energy Technology. Smart Innovation, Systems and Technologies, Greater Noida, India, 7–8 November 2019; Yadav, S., Singh, D., Arora, P., Kumar, H., Eds.; Springer: Singapore, 2019; Volume 174. [Google Scholar] [CrossRef]
- Pradhan, D.; Ganguly, K.; Swain, B.; Roy, H. Optimal kinematic synthesis of 6 bar rack and pinion Ackerman steering linkage. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 1660–1669. [Google Scholar] [CrossRef]
- Lv, T.; Zhang, Y.; Duan, Y.; Yang, J. Kinematics & compliance analysis of double wishbone air suspension with frictions and joint clearances. Mech. Mach. Theory 2021, 156, 104127. [Google Scholar] [CrossRef]
- von Wysocki, T.; Chahkar, J.; Gauterin, F. Small Changes in Vehicle Suspension Layouts Could Reduce Interior Road Noise. Vehicles 2020, 2, 18–34. [Google Scholar] [CrossRef]
- Ciampaglia, A.; Santini, A.; Belingardi, G. Design and analysis of automotive lightweight materials suspension based on finite element analysis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 1501–1511. [Google Scholar] [CrossRef]
- Böhm, F. Dynamic rolling process of tires as layered structures. Mech. Compos. Mater. 1996, 32, 568–576. [Google Scholar] [CrossRef]
- Sapragonas, J.; Dargužis, A. Model of radial deformations of protector of vehicle tire. Mechanics 2011, 17, 21–29. [Google Scholar] [CrossRef][Green Version]
- Sapragonas, J.; Keršys, A.; Makaras, R.; Lukoševičius, V.; Juodvalkis, D. Research of the influence of tire hydroplaning on directional stability of vehicle. Transport 2013, 28, 374–380. [Google Scholar] [CrossRef]
- Levin, M.A.; Fufaev, N.A. Theory of Deformable Wheel Rolling; Nauka: Moscow, Russia, 1989. (In Russian) [Google Scholar]
- Berthelot, J.M. Matėriaux Composites, 5th ed.; Masson: France, Paris, 2012; (In French). Available online: https://scholar.google.com/scholar_lookup?author=M.+Berthelot&journal=Mat%C3%A9riaux+Composites.+Comportement+m%C3%A9canique+et+analyse+des+structures&publication_year=1999 (accessed on 15 July 2020).
- Sharma, S. Composite Materials, 1st ed.; CRC Press: New York, NY, USA, 2021. [Google Scholar]
- Cristensen, R.M. Mechanics of Composite Materials; Dover Publications, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Gay, D. Matériaux Composites; Hermes: Paris, France, 1997; Available online: https://scholar.google.com/scholar_lookup?author=D.+Gay&journal=Mat%C3%A9riaux+Composites&publication_year=1997 (accessed on 15 July 2020).
- Pakalnis, A. Investigation of elasticity characteristics in a tyre ring model. Mechanics 2000, 3, 59–62. [Google Scholar]
- Hilyard, N.C. Mechanics of Cellular Plastics; Macmillan: New York, NY, USA, 1982. [Google Scholar]
- Matlin, M.; Kazankina, E.; Kazankin, V. Mechanics of initial dot contact. Mechanics 2009, 76, 20–23. Available online: https://web.a.ebscohost.com/ehost/pdfviewer/pdfviewer?vid=0&sid=412aad69-e974-47ff-ab94-820fa51cb935%40sdc-v-sessmgr01 (accessed on 15 March 2021).
- Haddar, M.; Chaari, R.; Baslamisli, S.C.; Chaari, F.; Haddar, M. Intelligent optimal controller design applied to quarter car model based on non-asymptotic observer for improved vehicle dynamics. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2021, 235, 929–942. [Google Scholar] [CrossRef]
- Negash, B.A.; You, W.; Lee, J.; Lee, C.; Lee, K. Semi-active control of a nonlinear quarter-car model of hyperloop capsule vehicle with Skyhook and Mixed Skyhook-Acceleration Driven Damper controller. Adv. Mech. Eng. 2021. [Google Scholar] [CrossRef]
- Jain, S.; Saboo, S.; Pruncu, C.I.; Unune, D.R. Performance Investigation of Integrated Model of Quarter Car Semi-Active Seat Suspension with Human Model. Appl. Sci. 2020, 10, 3185. [Google Scholar] [CrossRef]
- Filipozzi, L.; Assadian, F.; Kuang, M.; Johri, R.; Velazquez Alcantar, J. Estimation of Tire Normal Forces including Suspension Dynamics. Energies 2021, 14, 2378. [Google Scholar] [CrossRef]
- Aljarbouh, A.; Fayaz, M. Hybrid Modelling and Sliding Mode Control of Semi-Active Suspension Systems for Both Ride Comfort and Road-Holding. Symmetry 2020, 12, 1286. [Google Scholar] [CrossRef]
- Shahid, Y.; Wei, M. Comparative Analysis of Different Model-Based Controllers Using Active Vehicle Suspension System. Algorithms 2020, 13, 10. [Google Scholar] [CrossRef]
- Khan, M.A.; Abid, M.; Ahmed, N.; Wadood, A.; Park, H. Nonlinear Control Design of a Half-Car Model Using Feedback Linearization and an LQR Controller. Appl. Sci. 2020, 10, 3075. [Google Scholar] [CrossRef]
- Ahmad, E.; Iqbal, J.; Arshad Khan, M.; Liang, W.; Youn, I. Predictive Control Using Active Aerodynamic Surfaces to Improve Ride Quality of a Vehicle. Electronics 2020, 9, 1463. [Google Scholar] [CrossRef]
- Zhang, Q.; Hou, J.; Duan, Z.; Jankowski, Ł.; Hu, X. Road Roughness Estimation Based on the Vehicle Frequency Response Function. Actuators 2021, 10, 89. [Google Scholar] [CrossRef]
- Perrelli, M.; Farroni, F.; Timpone, F.; Mundo, D. Analysis of Tire Temperature Influence on Vehicle Dynamic Behaviour Using a 15 DOF Lumped-Parameter Full-Car Model. In Advances in Service and Industrial Robotics; Mechanisms and Machine Science; Zeghloul, S., Laribi, M., Sandoval Arevalo, J., Eds.; Springer: Cham, Switzerland, 2020; Volume 84. [Google Scholar] [CrossRef]
- Mei, T.; Vanliem, N. Control performance of suspension system of cars with PID control based on 3D dynamic model. J. Mech. Eng. Autom. Control. Syst. 2020, 1, 1–10. [Google Scholar] [CrossRef]
- Blekhman, I.; Kremer, E. Vertical-longitudinal dynamics of vehicle on road with unevenness. Procedia Eng. 2019, 199, 3278–3283. [Google Scholar] [CrossRef]
- Dimaitis, M. Modern Technologies for Evaluating the Condition of Road Surfaces; Ex Arte: Vilnius, Lithuania, 2008; pp. 32–35. (In Lithuanian) [Google Scholar]
- Vibration Processing Collection and Analysis System VAS–21. User Guide; UAB Elintos Prietaisai: Kaunas, Lithuania, 2003. (In Lithuanian)
- PicoScope 3000 Series High–Performance Oscilloscopes. Available online: http://www.picotech.com/picoscope3000.html (accessed on 15 July 2020).
- Wilcoxon Low Frequency Accelerometers. Available online: http://www.wilcoxon.com (accessed on 15 July 2020).






























| Tire | Tire Element | ||
|---|---|---|---|
| Thickness, mm | Fiber Angle | ||
| A | 175/70R13 Breaker, 3 layers Cord, 1 layer | δ1a = 8.0 δ1b = 7.0 δ2 = 4.1 δ3 = 1.2 δ4 = 1.0 | – – θ2 = 20° θ3 = 90° – |
| B | 195/50R15 Breaker, 2 layers Cord, 2 layers | δ1a = 8.1 δ1b = 7.8 δ2 = 3.9 δ3 = 1.7 δ4 = 1.3 | – – θ2 = 20° θ3 = 90° – |
| C | 185/75R14C Breaker, 2 layers Cord, 2 layers | δ1a = 12.0 δ1b = 11.0 δ2 = 3.2 δ3 = 1.8 δ4 = 1.0 | – – θ2 = 20° θ3 = 90° – |
| D | 12.00R20 Breaker, 4 layers Cord, 6 layers | δ1a = 17.0 δ1b = 15.0 δ2 = 6.4 δ3 = 7.2 δ4 = 1.0 | θ2 = 20° θ3 = 90° – |
| Characteristics | Tire | ||||
|---|---|---|---|---|---|
| A | B | C | D | ||
| El | 1667·103 | 1667·103 | ––– | 1367·103 | |
| Breaker (with nylon) | Et | 26,736 | 26.736 | ––– | 24,568 |
| Er | 26,736 | 26.736 | ––– | 24,568 | |
| El | 73,119 | 73,119 | 73,119 | 73,119 | |
| Breaker (with steel) | Et | 21,737 | 21,737 | 21,737 | 21,737 |
| Er | 23,684 | 23,684 | 23,684 | 23,684 | |
| El | 24,625 | 24,625 | 26,819 | ––– | |
| Cord (with viscose) | Et | 3553·103 | 3553·103 | 4339·103 | ––– |
| Er | 24,625 | 24,625 | 26,819 | ––– | |
| Inner sealing layer E | 18 | 18 | 18 | 18 | |
| Part of the ring up to the cord E | 16,601 | 16,630 | 17,118 | 16,511 | |
| Whole ring E | 16,890 | 16,906 | 17,311 | 16,541 | |
| Sidewall elasticity modulus during radial tension E, | 507.5 | 531.15 | 788.1 | 551.7 | |
| Equivalent sidewall elasticity modulus during radial bending E | |||||
| flat band, | 23.32 | 24.37 | 29.77 | 67.89 | |
| ring. | 42.69 | 43.04 | 61.51 | 113.4 | |
| Equivalent modulus of elasticity of the band bending Ec | |||||
| flat band in the circular direction, | 15.89 | 17.74 | 19.63 | 15.92 | |
| perpendicular to the circular direction ring, | 15.35 | 17.37 | 16.34 | 15.90 | |
| in the circular direction. | 23.73 | 24.21 | 22.50 | 18.50 | |
| Relative position of the neutral layer at bending | |||||
| flat band in the circular direction, | 0.288 | 0.281 | 0.383 | 0.377 | |
| perpendicular to the circular direction ring, | 0.108 | 0.11 | 0.088 | 0.124 | |
| in the circular direction. | 0.286 | 0.277 | 0.376 | 0.372 | |
| Tire Type | Part with a Pattern E1a, | Continuous Part E1b, | Tread E1, |
|---|---|---|---|
| A | 5.72 | 7.84 | 6.16 |
| B | 5.88 | 7.84 | 6.22 |
| C | 7.08 | 7.84 | 6.51 |
| D | 5.33 | 7.84 | 5.37 |
| Tire Type | Band Number | Length a, mm | Width b, mm | β Band |
|---|---|---|---|---|
| A | 1 | 39 | 29 | 3.83 |
| 2 | 32 | 29.6 | 3.67 | |
| B | 1 | 37 | 29 | 3.75 |
| 2 | 31 | 29 | 3.67 | |
| 3 | 239 | 24 | 4.58 | |
| C | 1 | 33 | 20 | 2.62 |
| 2 | 36 | 18 | 2.08 | |
| D | 1 | 116 | 42 | 3.33 |
| 2 | 90 | 41 | 3.17 |
| Layer No. | Layer Designation | Thickness, mm |
|---|---|---|
| 1 | Tread with a pattern | 2.9 |
| 2 | Tread without a pattern | 2.1 |
| 3 | Nylon-rubber | 0.8 |
| 4 | Steel-rubber | 0.9 |
| 5 | Rubber | 0.9 |
| 6 | Steel-rubber | 0.9 |
| 7 | Viscose-rubber | 0.9 |
| 8 | Sealing layer | 0.9 |
| Parameter | Quarter-Car Model | 3D Model | |
|---|---|---|---|
| Front | Rear | ||
| Sprung mass m3, kg | 246 | 246 | 205 |
| Unsprung mass m2, kg | 27.5 | 27.5 | 32 |
| Mass of the tire element m1, kg | 0.3 | 0.3 | 0.3 |
| Suspension spring stiffness c3, kN/m | 18 | 18 | 24 |
| Tire stiffness c2, kN/m | 157 | 157 | 157 |
| Tread stiffness c1, kN/m | 15,000 | 15,000 | 15,000 |
| Shock absorber damping k3, Ns/m | 1835 | 1835 | 1835 |
| Tire damping k2, Ns/m | 475 | 475 | 475 |
| Tread damping k1, Ns/m | 0 | 0 | 0 |
| Incoming signal values | ±20 mV to ±20 V |
| Measured frequencies, max | 10 MHz |
| Error | 1% |
| Overload protection | ±100 V |
| Incoming signal values | 1 MΩ in parallel to 20 pF |
| Input | BNC |
| Characteristics | Sensor | |
|---|---|---|
| WILCOXON Model 793L | WILCOXON Model 784A | |
| Sensitivity, ±20%, 25 °C | 500 mV/g | 100 mV/g |
| Measurement limits | ±10 g | ±50 g |
| Measured frequencies | 0.6–700 Hz | 4–7000 Hz |
| Supply voltage | 18–30 V | 18–30 V |
| Sensor mass | 142 g | 45 g |
| Overall Dimensions, mm | Base, mm | Mass, kg | Tire Dimensions | Static Radius, mm | Tire Diameter, mm | |||
|---|---|---|---|---|---|---|---|---|
| Length | Width | Height | Tare | Payload | ||||
| 3985 | 1665 | 1415 | 2475 | 870 | 1400 | 175/70R13 | 261 | 293 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lukoševičius, V.; Makaras, R.; Dargužis, A. Assessment of Tire Features for Modeling Vehicle Stability in Case of Vertical Road Excitation. Appl. Sci. 2021, 11, 6608. https://doi.org/10.3390/app11146608
Lukoševičius V, Makaras R, Dargužis A. Assessment of Tire Features for Modeling Vehicle Stability in Case of Vertical Road Excitation. Applied Sciences. 2021; 11(14):6608. https://doi.org/10.3390/app11146608
Chicago/Turabian StyleLukoševičius, Vaidas, Rolandas Makaras, and Andrius Dargužis. 2021. "Assessment of Tire Features for Modeling Vehicle Stability in Case of Vertical Road Excitation" Applied Sciences 11, no. 14: 6608. https://doi.org/10.3390/app11146608
APA StyleLukoševičius, V., Makaras, R., & Dargužis, A. (2021). Assessment of Tire Features for Modeling Vehicle Stability in Case of Vertical Road Excitation. Applied Sciences, 11(14), 6608. https://doi.org/10.3390/app11146608







