A Link Prediction Method Based on Neural Networks
Abstract
:1. Introduction
- We try to combine artificial intelligence method with complex network theory, and propose a link prediction method based on neural networks.
- A link pruning strategy based on the greedy algorithm is applied to solve the problem of neural network generalization on experiments.
- According to the traditional reliability, the quantitative formula of global network structure reliability is given to measure the performance of extended networks.
- By conducting two kinds of experiments on several networks with N = 30, 50, 80 and 100, we prove that the neural network method is the best in improving network efficiency and global network structure reliability compared with different link prediction models.
2. Literature Review
3. Problem Description and Formula
3.1. Link Prediction Models
3.2. Reliability Indexes
3.2.1. Network Efficiency (E)
3.2.2. Global Network Structure Reliability (P)
4. Method
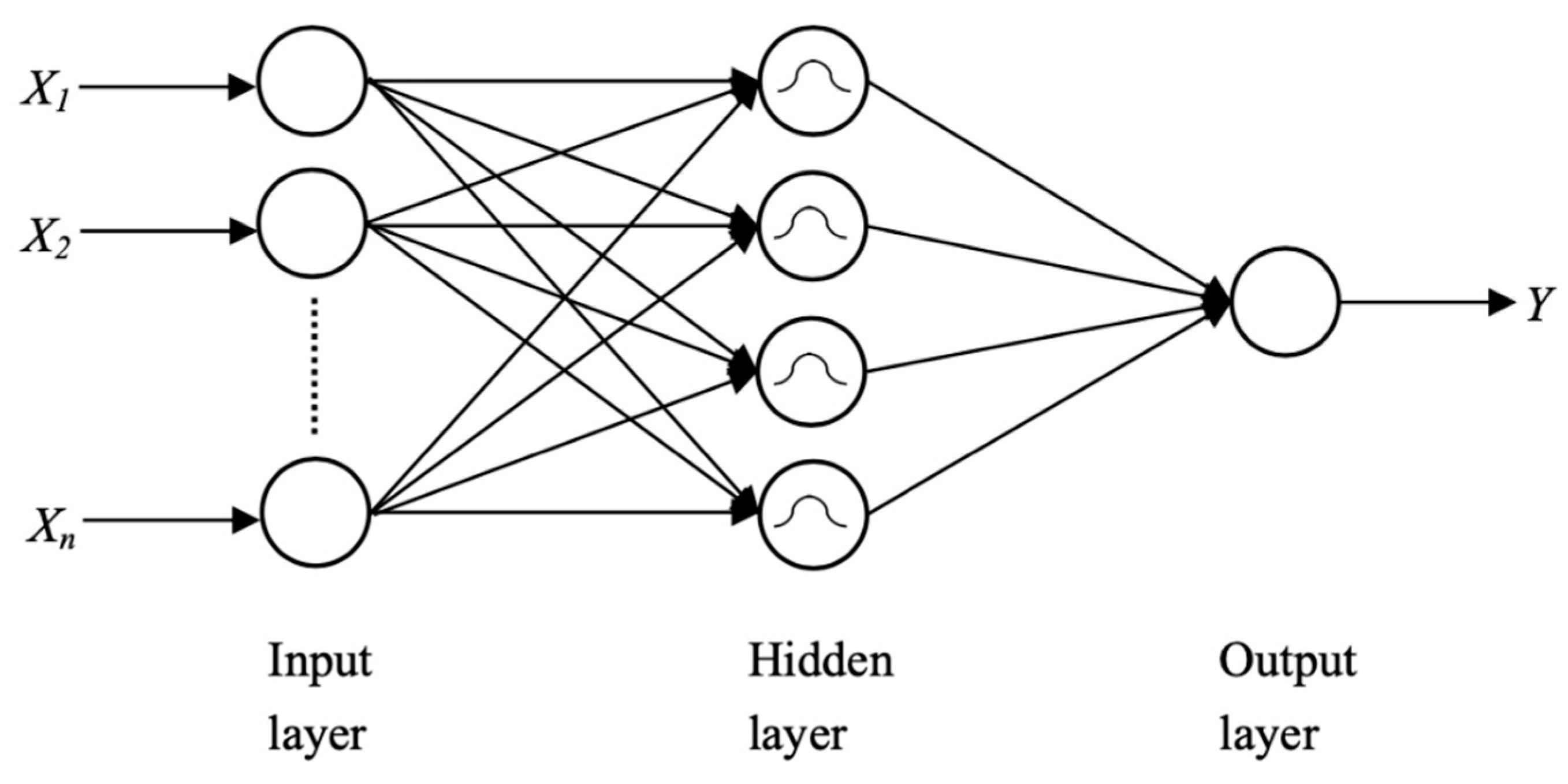
4.1. Neural Networks (NN)
4.2. Link Pruning
4.3. General Scheme
5. Experiment Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sohn, I. Small-world and scale-free network models for IoT systems. Mob. Inf. Syst. 2017, 61, 1–9. [Google Scholar] [CrossRef]
- Li, G.; Deng, L.; Xiao, G.; Tang, P.; Wen, C.Y.; Hu, W.H.; Pei, J.; Shi, L.P.; Stanley, H.E. Enabling controlling complex networks with local topological information. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef]
- Guimerà, R.; Sales-Pardo, M. Missing and spurious interactions and the reconstruction of complex networks. Proc. Natl. Acad. Sci. USA 2009, 106. [Google Scholar] [CrossRef] [Green Version]
- Sherkat, E.; Rahgozar, M.; Asadpour, M. Structural link prediction based on ant colony approach in social networks. Physica A Stat. Mech. Appl. 2015, 41, 80–94. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newman, M.E.J. Clustering and preferential attachment in growing networks. Phys. Rev. E 2001, 64, 025102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, C.H.; Zhou, T.; Zhang, H.F. Playing the role of weak clique property in link prediction: A friend recommendation model. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [Green Version]
- Fan, C.; Liu, Z.; Lu, X.; Xiu, B.; Chen, Q. An efficient link prediction index for complex military organization. Physica A Stat. Mech. Appl. 2017, 469, 572–587. [Google Scholar] [CrossRef]
- Gao, M.; Chen, L.; Li, B.; Li, Y.; Liu, W.; Xu, Y. Projection-based link prediction in a bipartite network. Inform. Sci. 2017, 376, 158–171. [Google Scholar] [CrossRef]
- Aghabozorgi, F.; Khayyambashi, M.R. A new similarity measure for link prediction based on local structures in social networks. Physica A Stat. Mech. Appl. 2018, 501, 12–23. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Zhu, X.; Tian, L. Link prediction via significant influence. Physica A Stat. Mech. Appl. 2018, 492, 1523–1530. [Google Scholar] [CrossRef]
- Pech, R.; Hao, D.; Lee, Y.L.; Yuan, Y.; Zhou, T. Link prediction via linear optimization. Physica A Stat. Mech. Appl. 2019, 528. [Google Scholar] [CrossRef] [Green Version]
- Balls-Barker, B.; Webb, B. Link prediction in networks using effective transitions. Linear Algebra Appl. 2020, 599, 79–104. [Google Scholar] [CrossRef]
- Li, K.Y.; Tu, L.L.; Chai, L. Ensemble-model-based link prediction of complex networks. Comput. Netw. 2020, 166. [Google Scholar] [CrossRef]
- Bai, S.S.; Zhang, Y.K.; Li, L.J.; Shan, N.; Chen, X.Y. Effective link prediction in multiplex networks: A TOPSIS method. Expert Syst. Appl. 2021, 177. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Q.M.; Lü, L.Y.; Zhou, T. Link prediction in complex networks: A local naive Bayes model. Europhys. Lett. 2011, 96. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.H. A generalized tree augmented naive Bayes link prediction model. J. Comput. Sci. 2018, 27, 206–217. [Google Scholar] [CrossRef]
- Wang, Y.S.; Liu, F.B.; Xia, S.T.; Wu, J. Link sign prediction by variational Bayesian probabilistic matrix factorization with student-t prior. Inform. Sci. 2017, 405, 175–189. [Google Scholar] [CrossRef]
- Xiao, Y.P.; Li, X.X.; Wang, H.H.; Xu, M. 3-HBP: A three-level hidden Bayesian link prediction model in social networks. IEEE Trans. Comput. Soc. Syst. 2018, 5, 430–443. [Google Scholar] [CrossRef]
- Yuan, W.W.; He, K.Y.; Guan, D.H.; Zhou, L.; Li, C.L. Graph kernel based link prediction for signed social networks. Inform. Fusion 2019, 46, 1–10. [Google Scholar] [CrossRef]
- Shan, N.; Li, L.J.; Zhang, Y.K.; Bai, S.S.; Chen, X.Y. Supervised link prediction in multiplex networks. Knowl. Based Syst. 2020, 203. [Google Scholar] [CrossRef]
- Wang, G.H.; Wang, Y.F.; Li, J.M.; Liu, K.D. A multidimensional network link prediction algorithm and its application for predicting social relationships. J. Comput. Sci. 2021, 53. [Google Scholar] [CrossRef]
- Sanchez, E.N.; Rodriguez-Castellanos, D.I.; Chen, G.R.; Ruiz-Cruz, R. Pinning control of complex network synchronization: A recurrent neural network approach. Int. J. Control Autom. 2017, 15, 1405–1414. [Google Scholar] [CrossRef]
- Li, J.C.; Zhao, D.L.; Ge, B.F.; Yang, K.W. A link prediction method for heterogeneous networks based on BP neural network. Physica A Stat. Mech. Appl. 2018, 495, 1–17. [Google Scholar] [CrossRef]
- Ozcan, A.; Oguducu, S.G. Link prediction in evolving heterogeneous networks using the NARX neural networks. Knowl. Inf. Syst. 2018, 55, 333–360. [Google Scholar] [CrossRef]
- Cai, X.L.; Shu, J.; Al-Kall, M. Link prediction approach for opportunistic networks based on recurrent neural network. IEEE Access 2019, 7, 2017–2025. [Google Scholar] [CrossRef]
- Lee, Y.H.; Sohn, I. Reconstructing damaged complex networks based on neural networks. Symmetry 2017, 9, 310. [Google Scholar] [CrossRef] [Green Version]
- Al-Kuwaiti, M.; Kyriakopoulos, N.; Hussein, S. A comparative analysis of network dependability, fault-tolerance, reliability, security, and survivability. IEEE Commun. Surv. Tut. 2009, 11, 106–124. [Google Scholar] [CrossRef]
- Shi, C.; Peng, Y.; Zhuo, Y.; Tang, J.Y.; Long, K.P. A new way to improve the robustness of complex communication networks by allocating redundancy links. Phys. Scripta 2012, 85. [Google Scholar] [CrossRef]
- Shargel, B.; Sayama, H.; Epstein, I.R.; Bar-Yam, Y. Optimization of robustness and connectivity in complex networks. Phys. Rev. Lett. 2003, 90. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, Y.; Matsukubo, J. Improvement the robustness on geographical networks by adding shortcuts. Physica A Stat. Mech. Appl. 2007, 380, 552–562. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Y.D.; Lao, S.Y.; Hou, L.L.; Small, M.; Bai, L. Effects of edge directions on the structural controllability of complex networks. PLoS ONE 2015, 10, e0135282. [Google Scholar] [CrossRef]
- Yan, H.Y.; Hou, L.L.; Ling, Y.X.; Wu, G.H. Optimizing complex networks controllability by local structure information. Int. J. Mod. Phys. C 2016, 27. [Google Scholar] [CrossRef]
- Sohn, I. A robust complex network generation method based on neural networks. Physica A Stat. Mech. Appl. 2019, 523, 593–601. [Google Scholar] [CrossRef]
- Kwon, H.; Yoon, H.; Choi, D. Restricted evasion attack: Generation of restricted-area adversarial example. IEEE Access 2019, 7, 60908–60919. [Google Scholar] [CrossRef]
- Kwon, H.; Yoon, H.; Park, K.W. Acoustic-decoy: Detection of adversarial examples through audio modification on speech recognition system. Neurocomputing 2020, 417, 357–370. [Google Scholar] [CrossRef]
- Lü, L.Y.; Jin, C.H.; Zhou, T. Similarity index based on local paths for link prediction of complex networks. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.Y.; Li, Y.L.; Yin, H.; Le, H.; Rui, M. The algorithm of link prediction on social network. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Yao, L.; Wang, L.N.; Pan, L.; Yao, K. Link prediction based on common-neighbors for dynamic social network. Procedia Comput. Sci. 2016, 83, 82–89. [Google Scholar] [CrossRef] [Green Version]
- Adamic, L.A.; Adar, E. Friends and neighbors on the web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef] [Green Version]
- Zhou, T.; Lü, L.; Zhang, Y.C. Predicting missing links via local information. Eur. Phys. J. B 2009, 71, 623–630. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Xu, B.W.; Wu, Y.R.; Zhou, X.Y. Link prediction in social networks: The state-of-the-art. Sci. China Inform. Sci. 2015, 58. [Google Scholar] [CrossRef] [Green Version]
- Ravasz, E.; Somera, A.L.; Mongru, D.A.; Oltvai, Z.N.; Barabási, A.L. Hierarchical organization of modularity in metabolic networks. Science 2002, 297, 1551–1555. [Google Scholar] [CrossRef] [Green Version]
- Fouss, F.; Pirotte, A.; Renders, J.M.; Saerens, M. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation. IEEE T. Knowl. Data En. 2007, 19, 355–369. [Google Scholar] [CrossRef]
- Lü, L.Y.; Zhou, T. Link prediction in complex networks: A survey. Physica A Stat. Mech. Appl. 2011, 390, 1150–1170. [Google Scholar] [CrossRef] [Green Version]
- Chebotarev, P.; Shamis, E.V. The matrix-forest theorem and measuring relations in small social groups. Automat. Rem. Contr. 1997, 58, 1505–1514. [Google Scholar]
- Zanin, M.; Sun, X.Q.; Wandelt, S. Studying the topology of transportation systems through complex networks: Handle with care. J. Adv. Transport. 2018, 3156137. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Generalized exponential distribution: Existing results and some recent developments. J. Stat. Plan. Infer. 2007, 137, 3525–3536. [Google Scholar] [CrossRef]
- Xu, T.Q.; Chen, Y.P. Two-sided M-Bayesian credible limits of reliability parameters in the case of zero-failure data for exponential distribution. Appl. Math. Model. 2014, 38, 2586–2600. [Google Scholar] [CrossRef]
- Liu, N.; Zhang, J.; Zhang, H.; Liu, W.X. Security assessment for communication networks of power control systems using attack graph and MCDM. IEEE Trans. Power Deliver. 2010, 25, 1492–1500. [Google Scholar] [CrossRef]
- Xiao, Y.H.; Wu, W.T.; Wang, H.; Xiong, M.M.; Wang, W. Symmetry-based structure entropy of complex networks. Physica A Stat. Mech. Appl. 2008, 387, 2611–2619. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.Y.; Li, X.; Liu, T.; Liu, B. Approximating betweenness centrality to identify key nodes in a weighted urban complex transportation network. J. Adv. Transport. 2019, 9024745. [Google Scholar] [CrossRef]
- Krishnaveni, S.; Pethalakshmi, A. Toward automatic quality detection of Jasmenum flower. ICT Express 2017, 3, 148–153. [Google Scholar] [CrossRef]
- Wang, R.B.; Xu, H.Y.; Li, B.; Feng, Y. Research on method of determining hidden layer nodes in BP neural network. Comput. Technol. Dev. 2018, 28, 31–35. [Google Scholar]


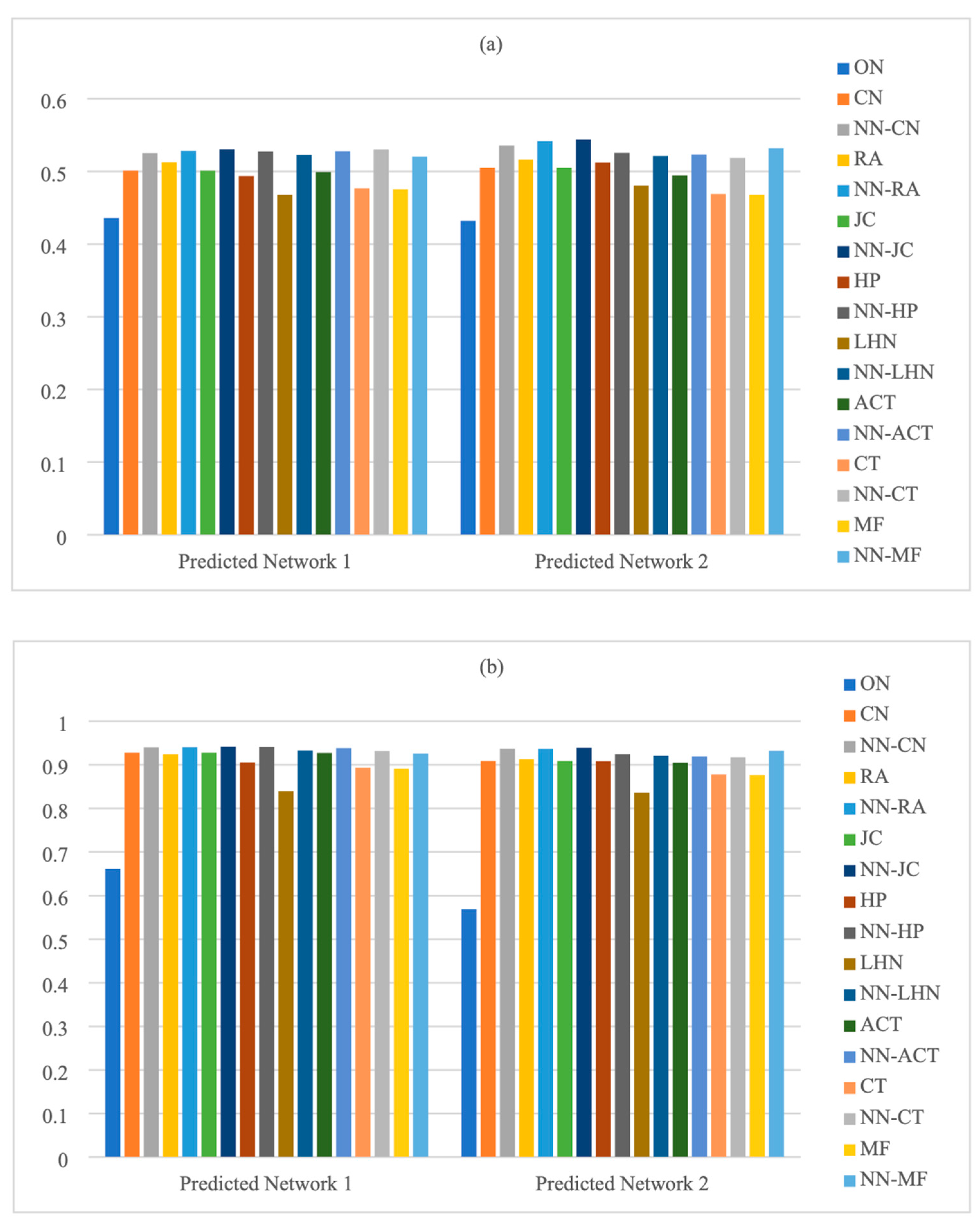


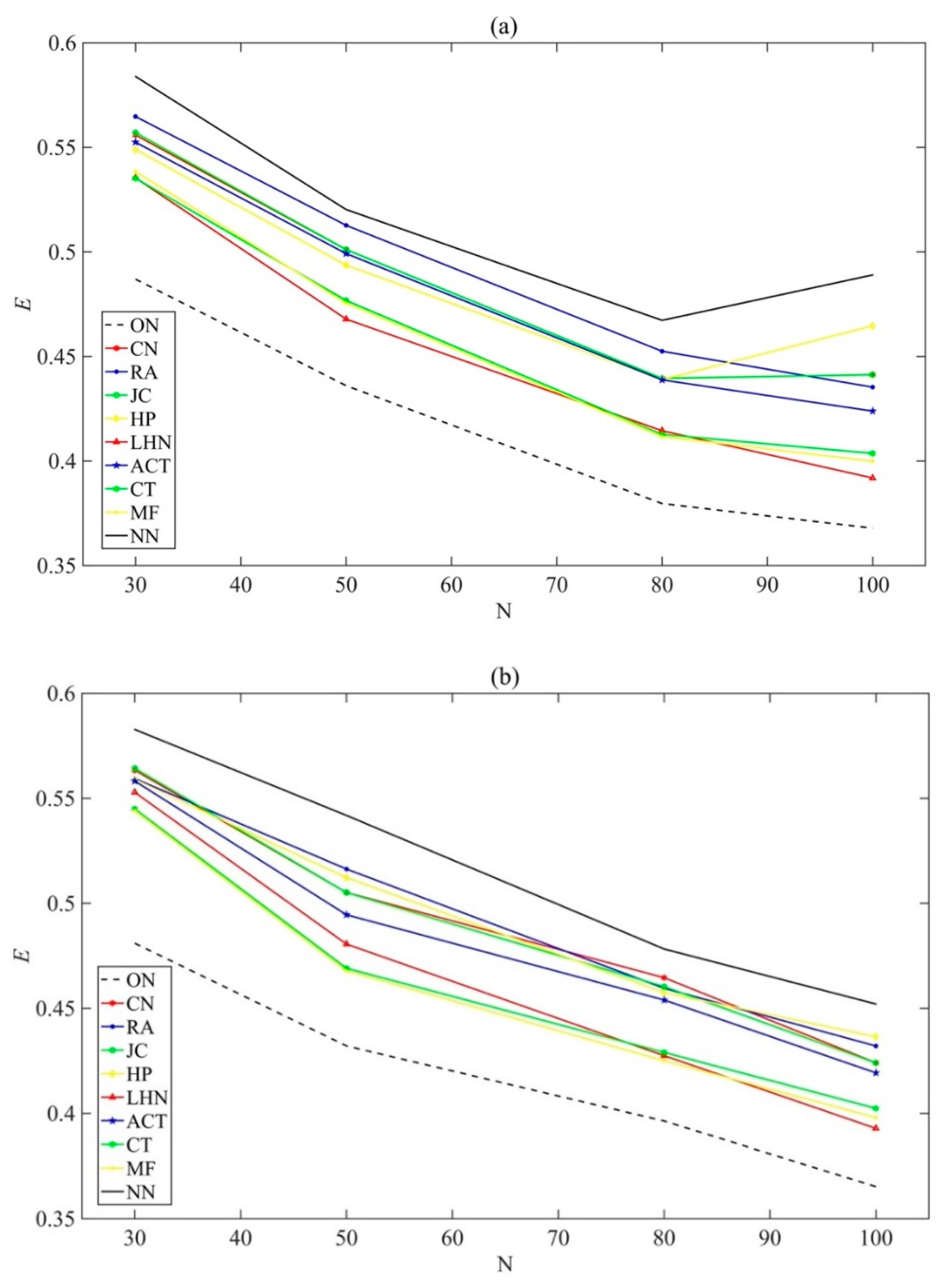

| Index | N | Predicted Network | ON | CN | RA | JC | HP | LHN | ACT | CT | MF | NN |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | 30 | 1 | 0.4869732 | 0.5559387 | 0.5647510 | 0.5570881 | 0.5490422 | 0.5354406 | 0.5524904 | 0.5352490 | 0.5385058 | 0.5839081 |
| 2 | 0.4809962 | 0.5634100 | 0.5593870 | 0.5643678 | 0.5590038 | 0.5528736 | 0.5582376 | 0.5450192 | 0.5442529 | 0.5827586 | ||
| 50 | 1 | 0.4360408 | 0.5011565 | 0.5127211 | 0.5011565 | 0.4937415 | 0.4678776 | 0.4991837 | 0.4768027 | 0.4756463 | 0.5202721 | |
| 2 | 0.4320952 | 0.5051701 | 0.5163265 | 0.5051701 | 0.5123401 | 0.4806122 | 0.4945578 | 0.4691157 | 0.4679592 | 0.5418367 | ||
| 80 | 1 | 0.3796730 | 0.4395359 | 0.4525053 | 0.4395886 | 0.4390243 | 0.4144937 | 0.4388133 | 0.4128006 | 0.4117880 | 0.4672996 | |
| 2 | 0.3963555 | 0.4646097 | 0.4595464 | 0.4603376 | 0.4575791 | 0.4274895 | 0.4539821 | 0.4290348 | 0.4251319 | 0.4782437 | ||
| 100 | 1 | 0.3678956 | 0.4413333 | 0.4353300 | 0.4413333 | 0.4646667 | 0.3918721 | 0.4238990 | 0.4037037 | 0.3999360 | 0.4889899 | |
| 2 | 0.3652727 | 0.4240774 | 0.4320842 | 0.4240774 | 0.4365152 | 0.3928552 | 0.4192862 | 0.4024478 | 0.3980572 | 0.4520875 | ||
| P | 30 | 1 | 0.6823815 | 0.9154475 | 0.9168245 | 0.9104210 | 0.9042422 | 0.8596296 | 0.9315846 | 0.9055676 | 0.8974670 | 0.9388779 |
| 2 | 0.6763270 | 0.9278472 | 0.9103899 | 0.9289363 | 0.9165503 | 0.8806171 | 0.9315667 | 0.9089169 | 0.9048870 | 0.9387938 | ||
| 50 | 1 | 0.6612709 | 0.9276401 | 0.9239963 | 0.9276401 | 0.9053636 | 0.8396845 | 0.9272298 | 0.8934019 | 0.8909736 | 0.9277433 | |
| 2 | 0.5693640 | 0.9087218 | 0.9129838 | 0.9087218 | 0.9083342 | 0.8359719 | 0.9047767 | 0.8777054 | 0.8767607 | 0.9439408 | ||
| 80 | 1 | 0.4570695 | 0.8651847 | 0.8807530 | 0.8633415 | 0.8425382 | 0.7697039 | 0.8694548 | 0.8234131 | 0.8140307 | 0.8994345 | |
| 2 | 0.5195350 | 0.9115835 | 0.9004921 | 0.9037903 | 0.8911566 | 0.8022490 | 0.9034039 | 0.8425871 | 0.8441484 | 0.9272361 | ||
| 100 | 1 | 0.4596644 | 0.8791856 | 0.8640235 | 0.8791856 | 0.8941482 | 0.7420475 | 0.8421491 | 0.8128243 | 0.8105283 | 0.9234288 | |
| 2 | 0.3797415 | 0.8563602 | 0.8617217 | 0.8563602 | 0.8548664 | 0.7152076 | 0.8246843 | 0.8174176 | 0.8009378 | 0.9001898 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Gu, S.; Yan, D. A Link Prediction Method Based on Neural Networks. Appl. Sci. 2021, 11, 5186. https://doi.org/10.3390/app11115186
Li K, Gu S, Yan D. A Link Prediction Method Based on Neural Networks. Applied Sciences. 2021; 11(11):5186. https://doi.org/10.3390/app11115186
Chicago/Turabian StyleLi, Keping, Shuang Gu, and Dongyang Yan. 2021. "A Link Prediction Method Based on Neural Networks" Applied Sciences 11, no. 11: 5186. https://doi.org/10.3390/app11115186
APA StyleLi, K., Gu, S., & Yan, D. (2021). A Link Prediction Method Based on Neural Networks. Applied Sciences, 11(11), 5186. https://doi.org/10.3390/app11115186






