Theoretical Modelling of Ion Exchange Processes in Glass: Advances and Challenges
Abstract
:1. Introduction
2. Basic Model
2.1. Nernst–Planck and Poisson Equations
2.2. Charge Neutrality Approximation in Field-Assisted Ion Exchange
2.3. Boundary Conditions
2.4. Some Particular Solutions
3. The Mixed Ion Effect
3.1. Brief Review of Theories
3.2. The Cation Flux Density
3.3. Generalized Equations and Boundary Conditions
3.4. Changes in the Solutions with Respect to the Basic Model
4. Future Challenges
4.1. Glass Poling
4.2. Electro-Diffusion of Multivalent Metals
4.3. Formation/Dissolution of Silver Nanoparticles
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DC | Direct current |
| IE | Ion exchange |
| MIE | Mixed ion effect |
References
- Mazzoldi, P.; Sada, C. A trip in the history and evolution of ion exchange process. Mater. Sci. Eng. B 2008, 149, 112–117. [Google Scholar] [CrossRef]
- Kistler, S.S. Stresses in Glass Produced by Nonuniform Exchange of Monovalent Ions. J. Am. Ceram. Soc. 1962, 45, 59–68. [Google Scholar] [CrossRef]
- Nordberg, M.E.; Mochel, E.L.; Garfinkel, H.M.; Olcott, J.S. Strengthening by Ion Exchange. J. Am. Ceram. Soc. 1964, 47, 215–219. [Google Scholar] [CrossRef]
- Miller, S.E. Integrated Optics: An Introduction. Bell Syst. Tech. J. 1969, 48, 2059–2069. [Google Scholar] [CrossRef]
- Izawa, T.; Nakagone, H. Optical Waveguides Formed by Electrically Induced Migration of Ions in Glass Plates. Appl. Phys. Lett. 1972, 21, 584–586. [Google Scholar] [CrossRef]
- Almeida, R.M.; Marques, A.C. The potential of ion exchange in sol-gel derived photonic materials and structures. Mater. Sci. Eng. B 2008, 149, 118–122. [Google Scholar] [CrossRef]
- Gy, R. Ion exchange for glass strengthening. Mater. Sci. Eng. B 2008, 149, 159–165. [Google Scholar] [CrossRef]
- Karlsson, S.; Jonson, B.; Stålhandske, C. The technology of chemical glass strengthening—A review. Glass Technol. 2010, 51, 41–54. [Google Scholar]
- Varshneya, A.K. Chemical Strengthening of Glass: Lessons Learned and Yet To Be Learned. Int. J. Appl. Glass Sci. 2010, 1, 131–142. [Google Scholar] [CrossRef]
- Guldiren, D.; Erdem, I.; Aydin, S. Influence of silver and potassium ion exchange on physical and mechanical properties of soda lime glass. J. Non-Cryst. Solids 2016, 441, 1–9. [Google Scholar] [CrossRef]
- Macrelli, G.; Varshneya, A.K.; Mauro, J.C. Ion Exchange in Silicate Glasses: Physics of Ion Concentration, Residual Stress, and Refractive Index Profiles. arXiv 2020, arXiv:2002.08016. [Google Scholar]
- Najafi, S.I. (Ed.) Introduction to Glass Integrated Optics; Artech House: Boston, MA, USA; London, UK, 1992. [Google Scholar]
- Opilski, A.; Rogoziński, R.; Gut, K.; Błahut, M.; Opilski, Z. Present state and perspectives involving application of ion exchange in glass. Opto-Electron. Rev. 2000, 8, 117–127. [Google Scholar]
- Honkanen, S.; West, B.R.; Yliniemi, S.; Madasamy, P.; Morrell, M.; Auxier, J.; Schülzgen, A.; Peyghambarian, N.; Carriere, J.; Frantz, J.; et al. Recent advances in ion exchanged glass waveguides and devices. Phys. Chem. Glas. Eur. J. Glass Sci. Andtechnol. Part B 2006, 47, 110–120. [Google Scholar]
- Quaranta, A.; Cattaruzza, E.; Gonella, F. Modelling the ion exchange process in glass: Phenomenological approaches and perspectives. Mater. Sci. Eng. B 2008, 149, 133–139. [Google Scholar] [CrossRef]
- Tervonen, A.; West, B.R.; Honkanen, S. Ion exchanged glass waveguide technology: A review. Opt. Eng. 2011, 50. [Google Scholar] [CrossRef] [Green Version]
- Brusberg, L.; Schröder, H.; Herbst, C.; Frey, C.; Fiebig, C.; Zakharian, A.; Kuchinsky, S.; Liu, X.; Fortusini, D.; Evans, A. High performance ion exchanged integrated waveguides in thin glass for board-level multimode optical interconnects. In Proceedings of the 2015 European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Pun, E.Y.B.; Lin, H. Alkaline aluminum phosphate glasses for thermal ion exchanged optical waveguide. Opt. Mater. 2015, 42, 484–490. [Google Scholar] [CrossRef]
- Salmio, R.P.; Saarinen, J. Graded-Index Diffractive Elements by Thermal Ion Exchange in Glass. Appl. Phys. Lett. 1995, 66, 917–919. [Google Scholar] [CrossRef]
- Singer, W.; Dobler, B.; Schreiber, H.; Brenner, K.H.; Messerschmidt, B. Refractive-index measurement of gradient-index microlenses by diffraction tomography. Appl. Opt. 1996, 35, 2167–2171. [Google Scholar] [CrossRef] [PubMed]
- Montero-Orille, C.; Moreno, V.; Prieto-Blanco, X.; Mateo, E.F.; Ip, E.; Crespo, J.; Liñares, J. Ion exchanged glass binary phase plates for mode-division multiplexing. Appl. Opt. 2013, 52, 2332–2339. [Google Scholar] [CrossRef] [PubMed]
- Rogoziński, R. Ion Exchange in Glass—The Changes of Glass Refraction. Ion Exch. Technol. 2012, 155–190. [Google Scholar] [CrossRef] [Green Version]
- Helfferich, F.; Plesset, M.S. Ion Exchange Kinetics. A Non Linear Diffusion Problem. J. Chem. Phys. 1958, 28, 418–424. [Google Scholar] [CrossRef] [Green Version]
- Abou-el-Leil, M.; Cooper, A.R. Analysis of Field-Assisted Binary Ion Exchange. J. Am. Ceram. Soc. 1979, 62, 390–395. [Google Scholar] [CrossRef]
- Tervonen, A. A General Model for Fabrication Processes of Channel Waveguides by Ion Exchange. J. Appl. Phys. 1990, 67, 2746–2752. [Google Scholar] [CrossRef]
- Cheng, D.; Saarinen, J.; Saarikoski, H.; Tervonen, A. Simulation of Field-assisted Ion exchange for Glass Channel Waveguide Fabrication: Effect of Nonhomogeneous Time-dependent Electric Conductivity. Opt. Commun. 1997, 134, 233–238. [Google Scholar] [CrossRef]
- Fleming, J.W., Jr.; Day, D.E. Relation of Alkali Mobility and Mechanical Relaxation in Mixed-Alkali Silicate Glasses. J. Am. Ceram. Soc. 1972, 55, 186–192. [Google Scholar] [CrossRef]
- Inman, J.M.; Houde-Walter, S.; McIntyre, B.L.; Liao, Z.M.; Parker, R.S.; Simmons, V. Chemical Structure and the Mixed Mobile Ion Effect in Silver-for-Sodium Ion Exchange in Silicate Glass. J. Non-Cryst. Solids 1996, 194, 85–92. [Google Scholar] [CrossRef]
- Lupascu, A.; Kevorkian, A.; Bondet, T.; Saint-André, F.; Persegol, D.; Levy, M. Modeling Ion Exchange in Glass with Concentration Dependent Diffusion Coefficients and Mobilities. Opt. Eng. 1996, 35, 1603–1610. [Google Scholar] [CrossRef]
- Prieto-Blanco, X. Electro-diffusion equations of monovalent cations in glass under charge neutrality approximation for optical waveguide fabrication. Opt. Mater. 2008, 31, 418–428. [Google Scholar] [CrossRef]
- Petrov, M.I.; Lepen’kin, Y.A.; Lipovskii, A.A. Polarization of glass containing fast and slow ions. J. Appl. Phys. 2012, 112, 043101. [Google Scholar] [CrossRef]
- Okorn, B.; Sancho-Parramon, J.; Oljaca, M.; Janicki, V. Metal doping of dielectric thin layers by electric field assisted film dissolution. J. Non-Cryst. Solids 2021, 554, 120584. [Google Scholar] [CrossRef]
- Gonella, F. Silver doping of glasses. Ceram. Int. 2015, 41, 6693–6701. [Google Scholar] [CrossRef]
- Doremus, R.H. Exchange and Diffusion of Ions in Glass. J. Phys. Chem. 1964, 68, 2212–2218. [Google Scholar] [CrossRef]
- Mrozek, P. Numerical modeling of field-assisted Ag+–Na+ ion exchanged channel waveguides using varied explicit space charge density approach. Opt. Appl. 2019, 49. [Google Scholar] [CrossRef]
- Prieto, X.; Srivastava, R.; Liñares, J.; Montero, C. Prediction of Space-Charge Density and Space-Charge Field in Thermally Ion Exchanged Planar Surface Waveguides. Opt. Mater. 1996, 5, 145–151. [Google Scholar] [CrossRef]
- Day, D.E. Mixed Alkali Glasses—Their Properties and Uses. J. Non-Cryst. Solids 1976, 21, 343–372. [Google Scholar] [CrossRef]
- Batchelor, S.; Oven, R.; Ashworth, D.G. Characterization of Electric Field Assisted Diffused Potasium Ion Planar Optical Waveguides. Electron. Lett. 1996, 32, 2082–2083. [Google Scholar] [CrossRef]
- Zheng, W.; Yang, B.; Hao, Y.; Wang, M.; Jiang, X.; Yang, J. Charge-density flux model for electric-field-assisted ion exchange in glass. Opt. Eng. 2011, 50, 1–9. [Google Scholar] [CrossRef]
- Rothmund, V.; Kornfeld, G. Der Basenanstausch im Permutit, I. Z. Anorg. Allg. Chem. 1918, 103, 129. [Google Scholar] [CrossRef]
- Eisenman, G. Cation selective glass electrodes and their mode of operation. Biophys. J. 1962, 2, 259–323. [Google Scholar] [CrossRef] [Green Version]
- Garfinkel, H.M. Ion Exchange Equilibria between Glass and Molten Salts. J. Phys. Chem. 1968, 72, 4175–4181. [Google Scholar] [CrossRef]
- Chludzinski, P.; Ramaswamy, R.V.; Anderson, T.J. Ion Exchange Between Soda-Lime-Silica Glass and Sodium Nitrate-Silver Nitrate Moten Salts. Phys. Chem. Glas. 1987, 28, 169–173. [Google Scholar]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford Clarenton Press: Oxford, UK, 1979. [Google Scholar]
- Stewart, G.; Laybourn, P.J. Fabrication of Ion Exchanged Optical Waveguides from Dilute Silver Nitrate Melts. IEEE J. Quantum Electron. 1978, QE-14, 930–934. [Google Scholar] [CrossRef]
- Liñares, J.; Prieto, X.; Montero, C. A Novel Refractive Index Profile for Optical Characterization of Nonlinear Diffusion Processes and Planar Waveguides in Glass. Opt. Mater. 1994, 3, 229–236. [Google Scholar] [CrossRef]
- Prieto, X.; Linares, J.; Montero, C. Perturbative method to modelize ion exchange processes: Application to surface waveguides. In Fiber and Integrated Optics; International Society for Optics and Photonics: Bellingham, WA, USA, 1996; Volume 2954, pp. 62–66. [Google Scholar]
- Prieto, X.; Liñares, J. Increasing Resistivity Effects in Field-Assisted Ion Exchange for Planar Optical Waveguide Fabrication. Opt. Lett. 1996, 21, 1–3. [Google Scholar] [CrossRef]
- Anderson, O.L.; Stuart, D.A. Calculation of Activation Energy of Ionic Conductivity in Silica Glasses by Classical Methods. J. Am. Ceram. Soc. 1954, 37, 573–580. [Google Scholar] [CrossRef]
- McVay, G.L.; Day, D.E. Diffusion and Internal Friction in Na-Rb Silicate Glasses. J. Am. Ceram. Soc. 1970, 53, 508–513. [Google Scholar] [CrossRef]
- Hayami, R.; Terai, R. Diffusion of Alkali Ions in Na2O-Cs2O-SiO2 Glasses. Phys. Chem. Glas. 1972, 13, 102–106. [Google Scholar]
- Isard, J. The mixed alkali effect in glass. J. Non-Cryst. Solids 1969, 1, 235–261. [Google Scholar] [CrossRef]
- Terai, R.; Hayami, R. Ionic Diffusion in Glasses. J. Non-Cryst. Solids 1975, 18, 217–264. [Google Scholar] [CrossRef]
- Ingram, M.D. Ionic conductivity in glass. Phys. Chem. Glas. 1987, 28, 215–234. [Google Scholar]
- Araujo, R.J. Interdiffusion in a One-Dimensional Interacting System. J. Non-Cryst. Solids 1993, 152, 70–74. [Google Scholar] [CrossRef]
- Inman, J.M.; Bentley, J.L.; Houde-Walter, S. Modeling Ion Exchanged Glass Photonics: The Modified Quasi-Chemical Diffusion Coefficient. J. Non-Cryst. Solids 1995, 191, 209–215. [Google Scholar] [CrossRef]
- Tomozawa, M. Structure of mixed alkali glasses. J. Non-Cryst. Solids 1996, 196, 280–284. [Google Scholar] [CrossRef]
- Kahnt, H. Ionic transport in glasses. J. Non-Cryst. Solids 1996, 203, 225–231. [Google Scholar] [CrossRef]
- Ngai, K. The dynamics of ions in glasses: Importance of ion–ion interactions. J. Non-Cryst. Solids 2003, 323, 120–126. [Google Scholar] [CrossRef]
- Terai, R. The Mixed Alkali Effect in the Na2O-Cs2O-SiO2 Glasses. J. Non-Cryst. Solids 1971, 6, 121–135. [Google Scholar] [CrossRef]
- Terai, R.; Wakabayashi, H.; Yamanaka, H. Haven ratio in mixed alkali glass. J. Non-Cryst. Solids 1988, 103, 137–142. [Google Scholar] [CrossRef]
- Messerschmidt, B.; Hsieh, C.H.; McIntyre, B.L.; Houde-Walker, S. Ionic Mobility in an Ion Exchanged Silver-Sodium Boroaluminosilicate Glass for Micro-Optics Applications. J. Non-Cryst. Solids 1997, 217, 264–271. [Google Scholar] [CrossRef]
- Lezzi, P.; Tomozawa, M. Enthalpy of mixing of mixed alkali glasses. J. Non-Cryst. Solids 2010, 356, 1439–1446. [Google Scholar] [CrossRef]
- Lezzi, P.; Tomozawa, M. Effect of alumina on enthalpy of mixing of mixed alkali silicate glasses. J. Non-Cryst. Solids 2011, 357, 2086–2092. [Google Scholar] [CrossRef]
- Kouyate, A.; Ahoussou, A.; Yapi, A.; Diabate, D.; Rogez, J.; Trokourey, A. Influence of alkali mixed effect on the mixing enthalpy in 0.75 B2O3 – 0.25 [xNa2O–(1-x)K2O] glass system. Chin. Chem. Lett. 2008, 19, 1252–1255. [Google Scholar] [CrossRef]
- Florian, P.; Vermillion, K.; Grandinetti, P.; Farnan, I.; Stebbins, J. Cation distribution in mixed alkali disilicate glasses. J. Am. Chem. Soc. 1996, 118, 3493–3497. [Google Scholar] [CrossRef]
- Gee, B.; Eckert, H. Cation Distribution in Mixed-Alkali Silicate Glasses. NMR Studies by 23Na-{7Li} and 23Na-{6Li} Spin Echo Double Resonance. J. Phys. Chem. 1996, 100, 3705–3712. [Google Scholar] [CrossRef]
- Ratai, E.; Chan, J.C.; Eckert, H. Local coordination and spatial distribution of cations in mixed-alkali borate glasses. Phys. Chem. Chem. Phys. 2002, 4, 3198–3208. [Google Scholar] [CrossRef]
- Swenson, J.; Matic, A.; Karlsson, C.; Börjesson, L.; Meneghini, C.; Howells, W. Random ion distribution model: A structural approach to the mixed-alkali effect in glasses. Phys. Rev. B 2001, 63, 132202. [Google Scholar] [CrossRef]
- Maass, P.; Bunde, A.; Ingram, M.D. Ion transport anomalies in glasses. Phys. Rev. Lett. 1992, 68, 3064–3067. [Google Scholar] [CrossRef]
- Bunde, A.; Ingram, M.D.; Maass, P. The Dynamic Structure Model for Ion Transport in Glasses. J. Non-Cryst. Solids 1994, 172–174, 1222–1236. [Google Scholar] [CrossRef]
- Bunde, A.; Funke, K.; Ingram, M.D. A unified site relaxation model for ion mobility in glassy materials. Solid State Ionics 1996, 86, 1311–1317. [Google Scholar] [CrossRef]
- Davidson, J.E.; Ingram, M.D.; Bunde, A.; Funke, K. Ion hopping processes and structural relaxation in glassy materials. J. Non-Cryst. Solids 1996, 203, 246–251. [Google Scholar] [CrossRef]
- Murch, G.E. The Nernst-Einstein equation in high-defect-content solids. Philos. Mag. A 1982, 45, 685–692. [Google Scholar] [CrossRef]
- Prieto-Blanco, X.; Montero, C.; Crespo, J.; Barral, D.; Mouriz, D.; Nistal, M.C.; Mateo, E.F.; Moreno, V.; Liñares, J. Hyperbolic interdiffusion for the double alkali effect on index profiles of ion exchanged glass slab optical elements. In Proceedings of the 3rd Congress of the International Commission for Optics, Santiago de Compostela, Spain, 26–29 August 2014. [Google Scholar]
- Prieto Blanco, X. Interferometric characterization and analysis of silver-exchanged glass waveguides buried by electromigration: Slab, channel and slab-sided channel configurations. J. Opt. A Pure Appl. Opt. 2006, 8, 123. [Google Scholar] [CrossRef]
- Sviridov, S.I. Influence of the composition of a molten salt on the field-assisted diffusion of potassium ions in the 20Na2O·80SiO2 glass. Glass Phys. Chem. 2007, 33, 550–555. [Google Scholar] [CrossRef]
- Nogami, M.; Tomozawa, M. Effect of Stress on Water Diffusion in Silica Glass. J. Am. Ceram. Soc. 1984, 67, 151–154. [Google Scholar] [CrossRef]
- Varshneya, A.K.; Dumais, G.A. Influence of Externally Applied Stresses on Kinetics of Ion Exchange in Glass. J. Am. Ceram. Soc. 1985, 68, C-165–C-166. [Google Scholar] [CrossRef]
- Varshneya, A.K. The physics of chemical strengthening of glass: Room for a new view. J. Non-Cryst. Solids 2010, 356, 2289–2294. [Google Scholar] [CrossRef]
- Cooper, A.R. Method for Fabricating Buried Waveguides. EP 0 380 468 A2. Available online: https://data.epo.org/publication-server/document?iDocId=660504&iFormat=0 (accessed on 24 April 2008).
- Tervonen, A.; Honkanen, S. Model for Waveguide Fabrication in Glass by Two-Step Ion Exchange with Ionic Masking. Opt. Lett. 1988, 13, 71–73. [Google Scholar] [CrossRef] [PubMed]
- Lipovskii, A.A.; Rusan, V.V.; Tagantsev, D.K. Imprinting phase/amplitude patterns in glasses with thermal poling. Solid State Ionics 2010, 181, 849–855. [Google Scholar] [CrossRef]
- Garcia, F.C.; Carvalho, I.C.S.; Hering, E.; Margulis, W.; Lesche, B. Inducing a large second-order optical nonlinearity in soft glasses by poling. Appl. Phys. Lett. 1998, 72, 3252–3254. [Google Scholar] [CrossRef]
- Zhurikhina, V.; Sadrieva, Z.; Lipovskii, A. Single-mode channel optical waveguides formed by the glass poling. Optik 2017, 137, 203–208. [Google Scholar] [CrossRef]
- Myers, R.A.; Mukherjee, N.; Brueck, S.R.J. Large second-order nonlinearity in poled fused silica. Opt. Lett. 1991, 16, 1732–1734. [Google Scholar] [CrossRef]
- Fleming, S.C.; An, H. Poled glasses and poled fibre devices. J. Ceram. Soc. Jpn. 2008, 116, 1007–1023. [Google Scholar] [CrossRef] [Green Version]
- An, H.; Fleming, S. Near-anode phase separation in thermally poled soda lime glass. Appl. Phys. Lett. 2006, 88, 181106. [Google Scholar] [CrossRef]
- Kudlinski, A.; Quiquempois, Y.; Martinelli, G. Modeling of the χ(2) susceptibility time-evolution in thermally poled fused silica. Opt. Express 2005, 13, 8015–8024. [Google Scholar] [CrossRef]
- Petrov, M.I.; Omelchenko, A.V.; Lipovskii, A.A. Electric field and spatial charge formation in glasses and glassy nanocomposites. J. Appl. Phys. 2011, 109, 094108. [Google Scholar] [CrossRef]
- Lipovskii, A.; Omelchenko, A.; Petrov, M. Modeling charge transfer dynamics and electric field distribution in glasses during poling and electrostimulated diffusion. Tech. Phys. Lett. 2010, 36, 1028–1031. [Google Scholar] [CrossRef]
- Brennand, A.L.R.; Wilkinson, J.S. Planar waveguides in multicomponent glasses fabricated by field-driven differential drift of cations. Opt. Lett. 2002, 27, 906–908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oven, R. Analytical model of electric field assisted ion diffusion into glass containing two indigenous mobile species, with application to poling. J. Non-Cryst. Solids 2021, 553, 120476. [Google Scholar] [CrossRef]
- Gonella, F.; Cattaruzza, E.; Quaranta, A.; Ali, S.; Argiolas, N.; Sada, C. Diffusion behavior of transition metals in field-assisted ion exchanged glasses. Solid State Ionics 2006, 177, 3151–3155. [Google Scholar] [CrossRef] [Green Version]
- Cattaruzza, E.; Battaglin, G.; Gonella, F.; Quaranta, A.; Mariotto, G.; Sada, C.; Ali, S. Chromium doping of silicate glasses by field-assisted solid-state ion exchange. J. Non-Cryst. Solids 2011, 357, 1846–1850. [Google Scholar] [CrossRef]
- Cattaruzza, E.; Gonella, F.; Peruzzo, G.; Quaranta, A.; Sada, C.; Trave, E. Field-assisted ion diffusion in dielectric matrices: Er3+ in silicate glass. Mater. Sci. Eng. B 2008, 146, 163–166. [Google Scholar] [CrossRef]
- Kenyon, A. Recent developments in rare-earth doped materials for optoelectronics. Prog. Quantum Electron. 2002, 26, 225–284. [Google Scholar] [CrossRef]
- Kalisky, Y. Cr4+-doped crystals: Their use as lasers and passive Q-switches. Prog. Quantum Electron. 2004, 28, 249–303. [Google Scholar] [CrossRef]
- Thévenin-Annequin, C.; Levy, M.; Pagnier, T. Electrochemical study of the silver-sodium substitution in a borosilicate glass. Solid State Ionics 1995, 80, 175–179. [Google Scholar] [CrossRef]
- Marchi, G.D.; Caccavale, F.; Gonella, F.; Mattei, G.; Mazzoldi, P.; Battaglin, G.; Quaranta, A. Silver nanoclusters formation in ion exchanged waveguides by annealing in hydrogen atmosphere. Appl. Phys. A 1996, 63, 403–407. [Google Scholar] [CrossRef]
- Mohr, C.; Dubiel, M.; Hofmeister, H. Formation of silver particles and periodic precipitate layers in silicate glass induced by thermally assisted hydrogen permeation. J. Phys. Condens. Matter 2000, 13, 525–536. [Google Scholar] [CrossRef] [Green Version]
- Cattaruzza, E.; Mardegan, M.; Trave, E.; Battaglin, G.; Calvelli, P.; Enrichi, F.; Gonella, F. Modifications in silver-doped silicate glasses induced by ns laser beams. Appl. Surf. Sci. 2011, 257, 5434–5438. [Google Scholar] [CrossRef]
- Chen, Y.; Karvonen, L.; Säynätjoki, A.; Ye, C.; Tervonen, A.; Honkanen, S. Ag nanoparticles embedded in glass by two-step ion exchange and their SERS application. Opt. Mater. Express 2011, 1, 164–172. [Google Scholar] [CrossRef]
- Kaganovsky, Y.S.; Antonov, I.; Rosenbluh, M.; Ihlemann, J.; Lipovskii, A. Two- and Three-Dimensional Photonic Crystals Produced by Pulsed Laser Irradiation in Silver-Doped Glass. Functional Nanomaterials for Optoelectronics and other Applications. In Solid State Phenomena; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2004; Volume 99, pp. 65–72. [Google Scholar] [CrossRef]
- Kumar, P.; Mathpal, M.C.; Tripathi, A.K.; Prakash, J.; Agarwal, A.; Ahmad, M.M.; Swart, H.C. Plasmonic resonance of Ag nanoclusters diffused in soda-lime glasses. Phys. Chem. Chem. Phys. 2015, 17, 8596–8603. [Google Scholar] [CrossRef]
- Warren, S.; Thimsen, E. Plasmonic solar water splitting. Energy Environ. Sci. 2012, 5, 5133–5146. [Google Scholar] [CrossRef]
- Berger, A. Concentration and size depth profile of colloidal silver particles in glass surfaces produced by sodium-silver ion exchange. J. Non-Cryst. Solids 1992, 151, 88–94. [Google Scholar] [CrossRef]
- Redkov, A.; Zhurikhina, V.; Lipovskii, A. Formation and self-arrangement of silver nanoparticles in glass via annealing in hydrogen: The model. J. Non-Cryst. Solids 2013, 376, 152–157. [Google Scholar] [CrossRef]
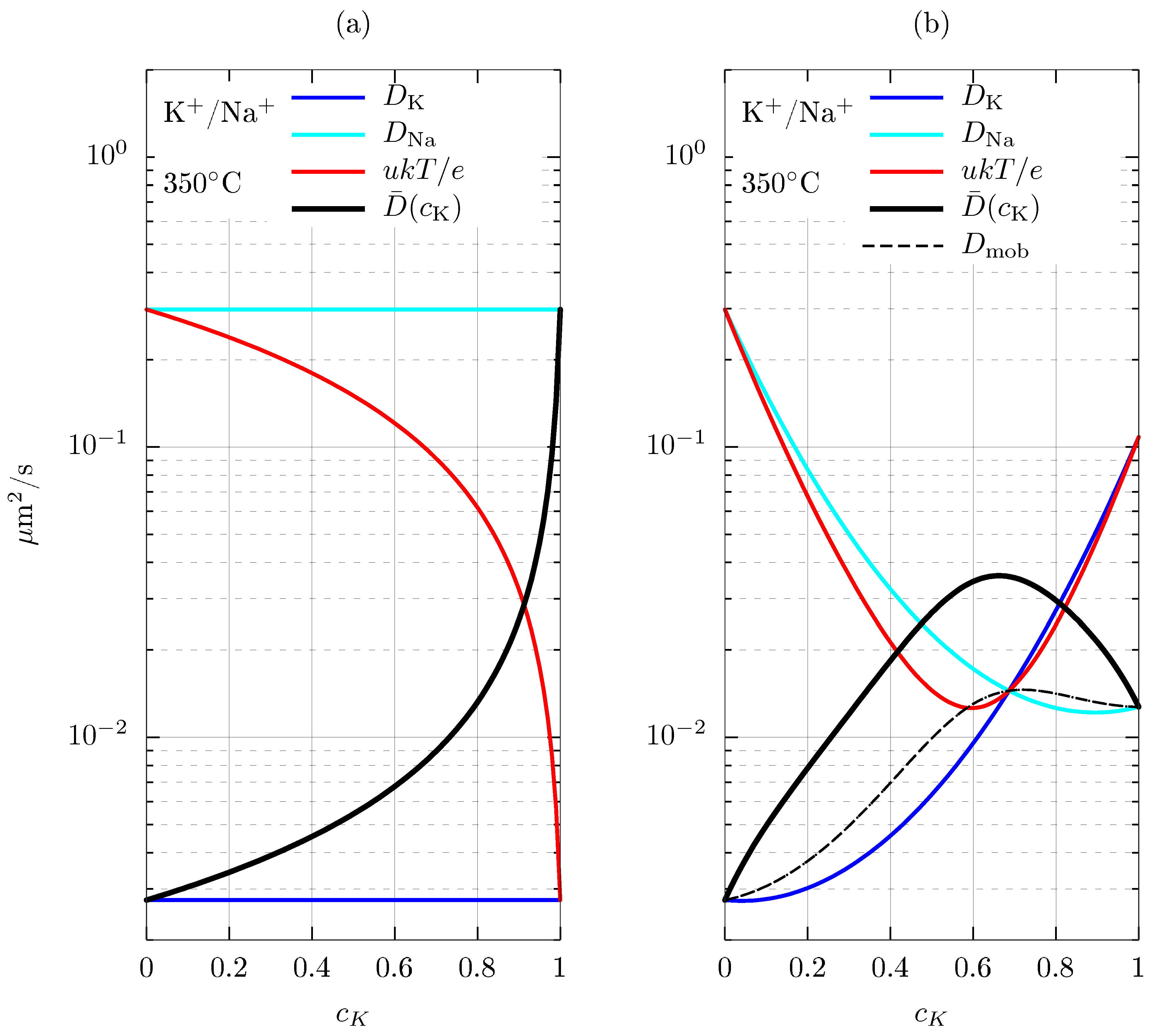
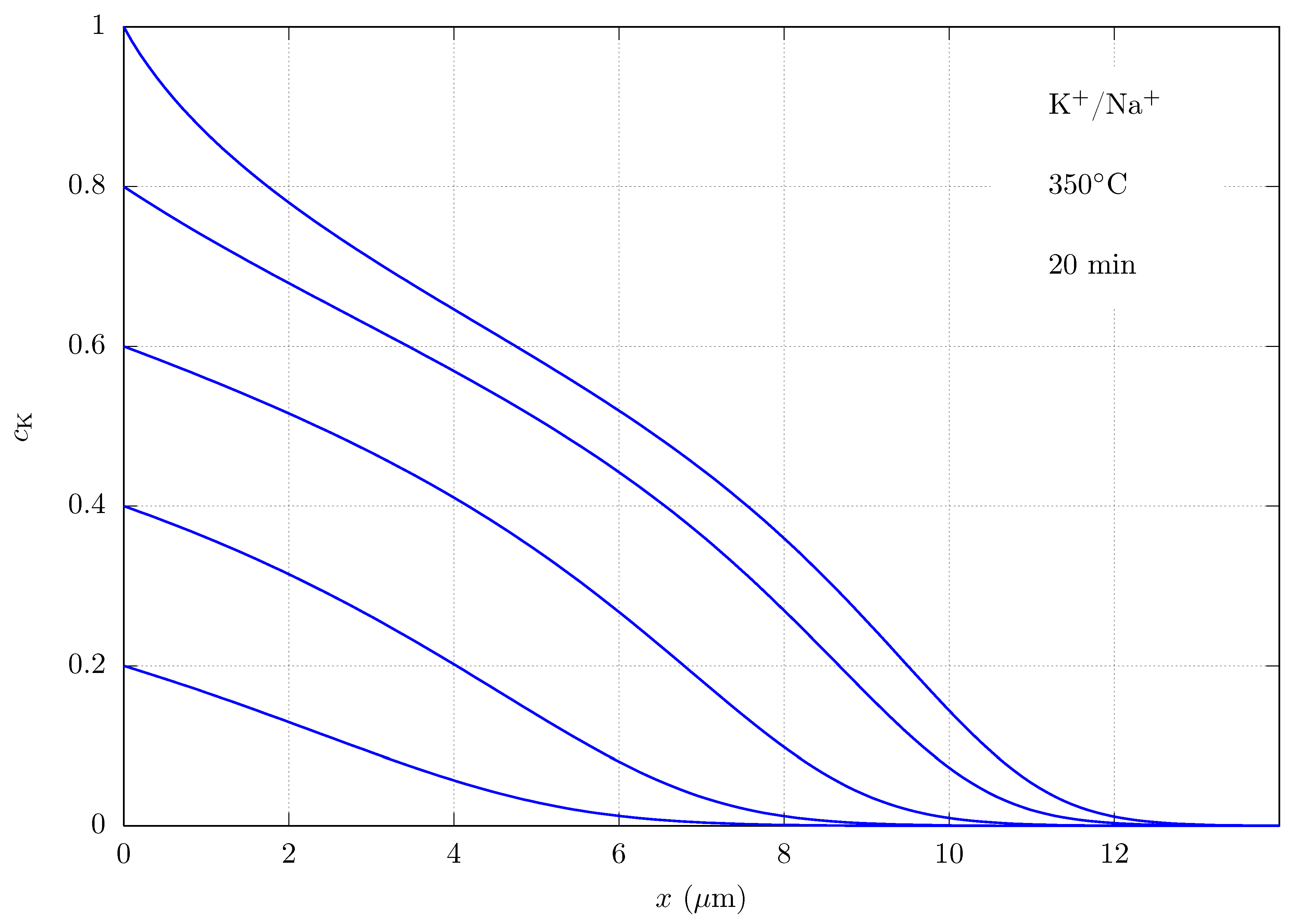
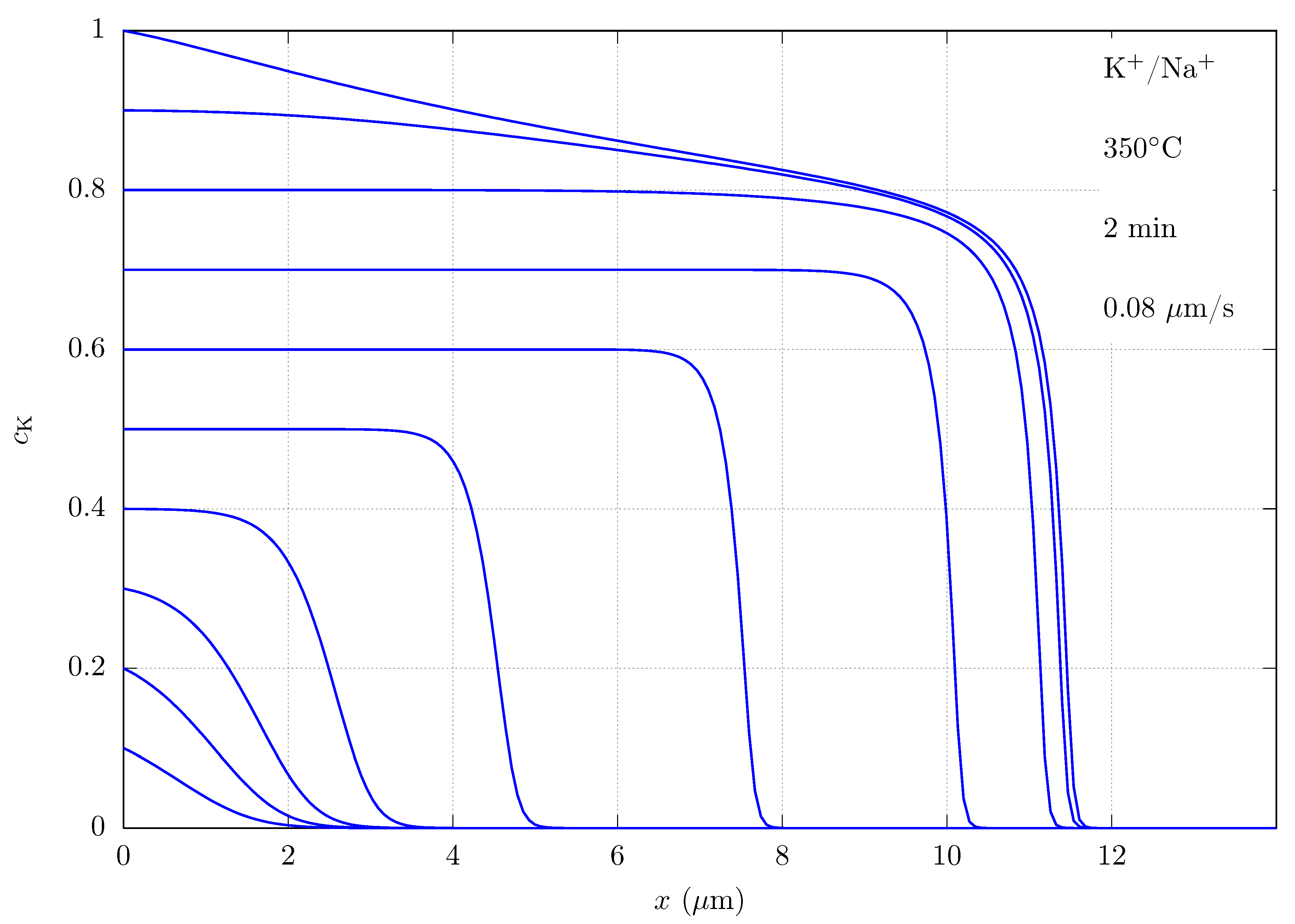
| Equations | ||
| Salt | ||
| Film | ||
| Mask/Air | ||
| with | ||
| Equations | ||
| Salt | ||
| Film | ||
| Mask/Air | ||
| with | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prieto-Blanco, X.; Montero-Orille, C. Theoretical Modelling of Ion Exchange Processes in Glass: Advances and Challenges. Appl. Sci. 2021, 11, 5070. https://doi.org/10.3390/app11115070
Prieto-Blanco X, Montero-Orille C. Theoretical Modelling of Ion Exchange Processes in Glass: Advances and Challenges. Applied Sciences. 2021; 11(11):5070. https://doi.org/10.3390/app11115070
Chicago/Turabian StylePrieto-Blanco, Xesús, and Carlos Montero-Orille. 2021. "Theoretical Modelling of Ion Exchange Processes in Glass: Advances and Challenges" Applied Sciences 11, no. 11: 5070. https://doi.org/10.3390/app11115070






