Search-Space Reduction for S-Boxes Resilient to Power Attacks

Abstract

The search of bijective $n\times n$ S-boxes resilient to power attacks in the space of dimension $\left(2^n\right)!$ is a controversial topic in the cryptology community nowadays. This paper proposes partitioning the space of $\left(2^n\right)!$ S-boxes into equivalence classes using the hypothetical power leakage according to the Hamming weights model, which ensures a homogeneous theoretical resistance within the class against power attacks. We developed a fast algorithm to generate these S-boxes by class. It was mathematically demonstrated that the theoretical metric confusion coefficient variance takes constant values within each class. A new search strategy—jumping over the class space—is justified to find S-boxes with high confusion coefficient variance in the space partitioned by Hamming weight classes. In addition, a decision criterion is proposed to move quickly between or within classes. The number of classes and the number of S-boxes within each class are calculated, showing that, as n increases, the class space dimension is an ever-smaller fraction of the space of S-boxes, which significantly reduces the space of search of S-boxes resilient to power attacks, when the search is performed from class to class.

1. Introduction

Technology has taken an important role in modern society, increasing the amount of transmitted information. The methods for data encryption protect the access to such information and ensure its confidentiality. In particular, in symmetric cryptography, in block cipher design, particularly, S-boxes are essential components that provide the confusion on encryption and decryption processes [1].

Traditional S-box design criteria focus on the resistance to differential and linear attacks [2,3]. Some S-box transformations, equivalences and classes have been proposed to address this goal. In [4], Biryukov et al. presented algorithms to detect linear and affine equivalences between two S-boxes. They solved the affine equivalence problem by finding unique representatives for the linear equivalence classes. Leander et al. [5] classified all optimal 4-bit S-boxes into 16 different affine equivalence classes, given a representative for each class. The classification criteria were the optimal values for S-boxes concerning linear and differential cryptanalysis, known as values for dimension four. Such a result is remarkable and relevant because exhaustively checking all permutations to find good S-boxes is not a feasible option; the number of mappings from n-bit to n-bit is large; and the classification into optimal classes reduces the work and helps find the most area-efficient S-box.

Despite the encouraging results in traditional S-box design [6], some other interesting approaches from combinatorial optimization have arisen [7,8]. The rising number of cyberattacks based on physical information leaks, known as side-channel analysis, gives way to a new design context [9]. In particular, power attacks are a real threat to cryptographic algorithm implementations [10,11], and it is necessary to find a balance between the intrinsic resistance of S-boxes to to those attacks and the resistance against linear and differential cryptanalysis [12]. To measure the theoretical resistance of S-boxes to differential power attacks, different metrics have been proposed, such as the order of transparency redefined and revisited under the Hamming distance leakage model [13,14], and  the confusion coefficient of the variance under the Hamming weight leakage model [15]. In this context, different methods have been used to search for S-boxes with high nonlinearity and high resistance to power attacks [8,16,17]. In these attacks, different models are used to simulate the hypothetical power leakage, the most common being the Hamming weight model, Hamming distance and its adaptations to different scenarios [18].

Motivated by the benefits provided by the definition of equivalence classes in [5] and the non-existence of equivalence classes in the new design context, we propose in this investigation a new equivalence relationship between bijective S-boxes using the Hamming weight leakage model. This relationship provides us with a way to define equivalence classes represented by the Hamming weight vector of the S-boxes’ outputs. According to the Hamming weight leakage model, all S-boxes in the same class have the same hypothetical power leakage. We also present a new algorithm, which receives an initial S-box as an input and randomly generates a new S-box equivalent to the initial one; both S-boxes belong to the same Hamming weight class. The algorithm is simple but not trivial, since it depends on the representation of the class in sets of inputs for each weight, which is also a novel result of this work. We used the algorithm to confirm our hypotheses. We generated random S-boxes belonging to the same Hamming weight class and selected some elementary classes, such as the Advanced Encryption Standard S-box class. When we performed correlation power attacks on these S-boxes using their hypothetical leaks but the same real leaks generated by the Advanced Encryption Standard cipher, we obtained the same results for all of them and probed that the theoretical confusion coefficient variance metric returns the same value for all generated S-boxes belonging to the same class. Our equivalence relationship does not attempt to reflect resistance against linear and differential attacks. We follow the goal, not to obtain good S-boxes in the sense of trade-off classical resistance and the resistance against power attacks, but to provide a novel formal framework for the actual S-box design context. This result can be applied to search over the Hamming weight class space instead of searching over the entire S-box space, which entails reducing the space and improving the performance of the search process.

Taking into account that all S-boxes belonging to the same Hamming weight class have, by the way the classes are defined, the same hypothetical leakage according to the Hamming weight leakage model, it is intuitively expected that all of them have the same resistance to power attacks, when quantified using the confusion coefficient variance metric, since this metric is based on that leakage model. Based on this idea, it was experimentally verified that the value of the variance of the confusion coefficient is constant within each Hamming weight class, and, to explain these experimental results, this property was theoretically demonstrated. However, to present the content in a more logical sequence, the document presents first the theoretical proof and then its experimental and statistical confirmations: (1) effective attack on 1000 S-boxes that belongs to the Advanced Encryption Standard S-box class; and (2) constant confusion coefficient variance value on S-boxes in the same class. In both cases, we generated the S-boxes using our new randomized algorithm.

The paper is structured as follows. Section 2 includes the necessary basics concepts. Section 3 presents the contributions about the new equivalence relationship; the Hamming weight equivalence classes and their representatives; the algorithm to generate the S-boxes into each class; and the theoretical demonstration and experimental verification that random S-boxes of a class have the same resistance to power attacks. The number of classes and the number of S-boxes within each class are calculated, showing that, as n increases, the class space dimension is an ever-smaller fraction of the space of S-boxes, which significantly reduces the space of search of S-boxes resilient to power attacks, when the search is performed from class to class. Finally, Section 4 provides concluding remarks.

2. Basic Concepts

We begin by stating some basic definitions. Bijective S-boxes are vector functions used in most block ciphers, represented as a mapping $F:{\{0,1\}}_{}^n\to {\{0,1\}}_{}^n,n\in \mathbb{N}$. For each binary vector $x\in {\{0,1\}}_{}^n$, $HW\left(x\right)$ represents the Hamming weight of x [10]. Its objective is to cause the greatest possible confusion by masking the relationship between the plain text and the ciphertext [2,19].

The correlation power attack (CPA) [20] uses the linear correlation coefficient as a distinction to quantify the statistical dependence between the real power leak $Y_{k,p}$ generated from the K key and the hypothetical leak $X_{j,p}$ calculated with the model from the assumed key J. In the Hamming weight model [2], the hypothetical leakage $X_{j,p}$ of the power consumption evaluating an S-box is represented by the value $X_{j,p}=HW\left(F(j\oplus p)\right)$, where F is the S-box, p represents the clear text and j is the assumed subkey to encrypt the plain text.

S-boxes have a set of properties that allow for the evaluation of their cryptographic quality, such as the high degree of nonlinearity (NL) that protects against linear attacks. The coefficient of confusion (CC) and the confusion coefficient variance (CCV) are two of the used metrics to measure resistance to differential power attacks (DPA). The coefficient of confusion (CC) theoretical metric was introduced by Y. Fei et al. in 2012 [21], who defined the confusion coefficient $\kappa$ over two keys $(k_i,k_j)$ as:

$$\kappa =\kappa (k_i,k_j)=Pr[(L\mid k_i)\ne (L\mid k_j)]=\frac{N_{(L\mid k_i)\ne (L\mid k_j)}}{N_t},$$

(1)

where $N_t$ is the total number of values for the relevant cipher-text bits and $N_{(L\mid k_i)\ne (L\mid k_j)}$ is the number of occurrences for which different key hypotheses $k_i$ and $k_j$ result in different L values. In the DPA model, L has only two possible outcomes 0 and 1, but, in other power attack models, L can take more than two values. Then, in [22], the authors defined a general confusion coefficient as:

$$\kappa (k_i,k_j)=E[{(L\mid k_i-L\mid k_j)}^2].$$

(2)

Particularly, under the DPA model, $E[{(L\mid k_i-L\mid k_j)}^2]$ becomes $Pr[(L\mid k_i)\ne (L\mid k_j)]$.

In [15], Picek et al. considered $\kappa (k_i,k_j)$ equal to the expected value $E_P$ (among all the possible p plain texts) of the distance between the power leaks $L\left(F(k_i\oplus p)\right)$ and $L\left(F(k_j\oplus p)\right)$, using the pair of keys $k_i$ and $k_j$, i.e.,

$$\kappa (k_i,k_j)=E_P\left[L(F(k_i\oplus p)-L{\left(F(k_j\oplus p)\right)}^2\right],$$

(3)

and proposed to take a new theoretical metric as the variance $\left({\sigma }^2\right)$ of the CC vector over all possible pairs of keys:

$$CCV\left(F\right)={\sigma }^2\left[\overline{\overline{k}}\right]={\sigma }^2\left[\kappa (k_i,k_j)|\forall i<j\right].$$

(4)

When using the Hamming weight leakage model as the L function, the CCV is:

$$CCV\left(F\right)={\sigma }^2\left[E_P\left[(HW\left(F(k_i\oplus p)\right)-HW{\left(F(k_j\oplus p)\right)}^2\right]|\forall i<j\right]$$

(5)

We expect that arbitrary keys, different from a real key, will look the same for the DPA attack at a higher value of variance. It increases the DPA resistance of the S-box [22,23].

Next, we recall the Stirling formula for factorial calculation. The value of $n!$ grows extremely quickly, but, for large values of n, it can be estimated using the well-known Stirling formula (see Table 1), the full proof of which appears in [24],

$$n!\approx \sqrt{2\pi n}{n}^n{e}^{-n},$$

(6)

which, using base 10 logarithm, can be expressed equivalently as:

$$n!={10}^{\frac{1}{2}log\left(2\pi \right)+\frac{1}{2}log\left(n\right)+nlog\left(n\right)-nlog\left(e\right)}.$$

(7)

A refinement of the Stirling formula, in terms of lower and upper bounds is given by

$$(\sqrt{2\pi }·n^{n+\frac{1}{2}}·e^{-n})\left(e^{{(12n+1)}^{-1}}\right)<n!<(\sqrt{2\pi }·n^{n+\frac{1}{2}}·e^{-n})\left(e^{{\left(12n\right)}^{-1}}\right).$$

(8)

Table 1. Examples of estimating $n!$ by the Stirling formula, for $n=8,28,56,70$.

Factorial	Stirling’s Formula	Upper Bound	Lower Bound
70!	${10}^{100}$	${10}^{100.0779669}$	${10}^{100.0779665}$
56!	${10}^{75}$	${10}^{75.846396}$	${10}^{75.846395}$
28!	${10}^{29}$	${10}^{29.48214}$	${10}^{29.48213}$
8!	${10}^4$	${10}^{4.60537}$	${10}^{4.60532}$

Table 1. Examples of estimating $n!$ by the Stirling formula, for $n=8,28,56,70$.

Factorial	Stirling’s Formula	Upper Bound	Lower Bound
70!	${10}^{100}$	${10}^{100.0779669}$	${10}^{100.0779665}$
56!	${10}^{75}$	${10}^{75.846396}$	${10}^{75.846395}$
28!	${10}^{29}$	${10}^{29.48214}$	${10}^{29.48213}$
8!	${10}^4$	${10}^{4.60537}$	${10}^{4.60532}$

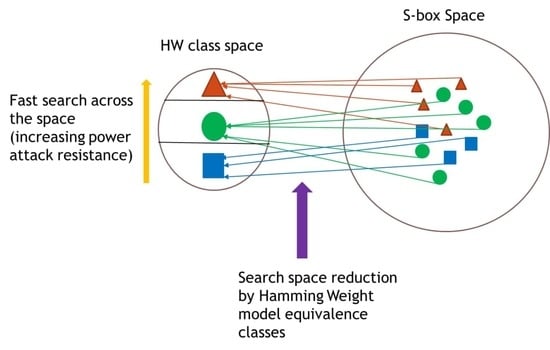
3. Our Contributions: Reduction of the S-Boxes Search-Space into a Hamming Weight Class SEARCH-Space

In this work, we only work with bijective S-boxes.

3.1. S-Boxes HW Equivalent

Definition 1.

Two bijective S-boxes $F_1,F_2$ of order $n\times n$ are called HW equivalent if they have the same leakage of power according to the Hamming weight model, i.e., $F_1,F_2$ are HW equivalent if and only if $HW\left(F_1\left(x\right)\right)=HW\left(F_2\left(x\right)\right)$, for all $x\in \{0,\dots ,2^n-1\}$.

Proposition 1.

The HW equivalence relationship defined in the space of all S-boxes F of order $n\times n$, is an equivalence relationship.

Proof. 

It is immediate from the definition that the S-boxes meet the properties of reflexivity, symmetry and transitivity. It proves the HW equivalent relation between the S-boxes. The HW equivalence class $<F_a>$ associated with any S-box, $F_a$ can be expressed as:

$$<F_a>=\left\{F_b\right|HW\left(F_b\left(x\right)\right)=HW\left(F_a\left(x\right)\right),\forall x\in \{0,\dots ,2^n-1\}\}.$$

(9)

   □

This equivalence relation is used to partition the space of bijective S-boxes into Hamming weight classes. The cardinality of the class space is much smaller than the cardinality of the S-box space. According to the confusion coefficient variance, the theoretical resistance to power attacks is constant within each class and can be different between classes. It is proposed to replace the search in the space of S-boxes by the search in the class space Hamming weight (when trying to search for S-boxes resistant to Power attacks).

Now, we discuss the representation of the HW classes using the vector of weights of the S-boxes outputs that compose it. Considering that the vector of weights of outputs of the S-boxes that belong to a class is the same for all S-class boxes. This vector of weights is used to represent any class: $<F_a>=(HW\left(F_a\left(0\right)\right),\dots ,HW\left(F_a(2^n-1)\right))$.

Example 1

(PRINT cipher). The following example represents the PRINT S-box $F_{Print}\left(x\right)$ and its HW class $<F_{Print}>=(0,1,2,2,3,1,2,1)$ using its vector of output weights. This S-box has a variance of the CCV confusion coefficient of 0.275510 (see

Table 2. PRINT S-box $F_{Print}\left(x\right)$ and its HW class $<F_{Print}>$.

x	0	1	2	3	4	5	6	7
${\mathbf{F}}_{\mathbf{Print}}\left(\mathbf{x}\right)$	0	1	3	6	7	4	5	2
$<{\mathbf{F}}_{\mathbf{Print}}>$	0	1	2	2	3	1	2	1

).

Example 2

(PRESENT). The representation of the PRESENT S-box class $<F_{PRESENT}>$, through its weight vector, is given in the Appendix A (see

Table A1. PRESENT S-box Hamming weight class.

	0	1	2	3
0	2	2	2	3
1	2	0	2	3
2	2	3	4	1
3	1	3	1	1

and

Table A2. S-box $4\times 4$ equivalent to the PRESENT cipher S-box from its HW class.

	0	1	2	3
0	C	5	6	B
1	9	0	A	D
2	3	E	F	8
3	2	7	1	4

).

Example 3

(AES). The representation of the AES S-box class $<F_{AES}>$, through its weight vector, is given in the Appendix B (see

Table A3. Class HW $<F_{AES}>$ of the S-box of the AES algorithm.

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	4	5	6	6	5	5	6	4	2	1	5	4	7	6	5	5
1	4	2	4	6	6	4	4	4	5	4	3	6	4	3	4	2
2	6	7	4	3	4	6	7	4	3	4	5	5	4	4	3	3
3	1	5	3	4	2	4	2	4	3	2	1	4	6	4	4	5
4	2	3	3	3	4	5	4	2	3	5	5	5	3	5	5	2
5	4	4	0	6	1	6	4	5	4	5	6	4	3	3	3	6
6	3	7	4	7	3	4	4	3	3	6	1	7	2	4	6	3
7	3	4	1	5	3	5	3	6	5	5	5	2	1	8	6	4
8	5	2	3	5	6	5	2	4	3	5	6	5	3	5	3	5
9	2	2	5	5	2	3	2	2	3	6	4	2	6	5	3	6
A	3	3	4	2	3	2	2	4	3	5	4	3	3	4	4	5
B	6	3	5	5	4	5	4	4	4	4	5	5	4	5	5	1
C	5	4	3	4	3	4	4	4	4	6	4	5	4	6	4	3
D	3	5	5	4	2	2	6	3	3	4	5	5	3	3	4	5
E	4	5	3	2	4	5	4	3	5	4	4	5	5	4	2	7
F	3	3	3	3	7	5	2	3	2	4	4	4	3	3	6	3

and

Table A4. S-box $F_b\in <F_{AES}>$ equivalent to the AES S-box.

x0

xl

x2

x3

x4

x5

x6

x7

x8

x9

xa

xb

xc

xd

xe

xf

0x

63

f2

77

7b

7c

67

6f

c5

30

01

6b

2b

fe

d7

76

ab

lx

ca

82

c9

7d

fa

59

47

fO

ad

d4

a2

af

9c

a4

72

c0

2x

b7

fd

93

26

36

3f

f7

ce

34

a5

e5

fl

71

d8

31

15

3x

04

c7

23

c3

lb

96

05

9a

07

12

80

e2

eb

27

b2

75

4x

09

83

2c

la

lb

6e

5a

a0

52

3b

d6

b3

29

e3

2f

84

5x

53

dl

00

ed

20

fe

bl

5b

6a

cb

be

39

la

4c

59

cf

6x

dO

ef

aa

fb

43

4d

33

85

45

f9

02

7f

50

3c

9f

aa

7x

51

a3

40

8f

92

9d

38

fS

be

b6

da

21

10

ff

f3

d2

8x

cd

0c

13

ec

5f

97

44

17

c4

a7

7e

3d

64

5d

19

73

9x

60

81

4f

de

22

2a

90

89

46

ee

b8

14

de

5e

0b

db

ax

e0

32

3a

0a

49

06

24

5e

c2

d3

ac

62

91

95

e4

79

bx

e7

c9

37

6d

8d

d5

4e

a9

6c

56

f4

ea

65

7a

ae

08

ex

ba

78

25

2e

le

a6

b4

c6

e8

dd

74

lf

4b

bd

8b

9a

dx

70

3e

b5

66

4b

03

f6

0e

61

35

57

b9

86

el

ld

9e

ex

el

f8

9b

11

69

d9

be

94

9b

le

87

e9

ce

55

2b

df

fx

be

al

89

0d

b f

e6

42

69

41

99

2d

0f

b0

54

bb

16

).

Considering that all S-boxes in a class have the same hypothetical power leakage according to the Hamming weight model, it is theoretically expected that all S-boxes in a class have the same resistance to power attacks. We also look forward in the direction of having some invariant theoretical metric.

Proposition 2

(CCV is constant within each class). Let $F_a$ and $F_b$ be two S-boxes defined in the same domain and image {0,1${\}}^n$. If $F_a$ and $F_b$ are HW equivalents, then $CCV\left(F_a\right)=CCV\left(F_b\right)$.

Proof. 

In the CCV expression under the Hamming weight leakage model,

$$CCV\left(F\right)={\sigma }^2\left[E_P\left[(HW\left(F(k_i\oplus p)\right)-HW{\left(F(k_j\oplus p)\right)}^2\right]|\forall i<j\right].$$

(10)

It can be seen that two HW equivalent S-boxes have the same CCV value because, for all x, $HW\left(F_a\left(x\right)\right)=HW\left(F_b\left(x\right)\right)$, the Hamming weights of the outputs of each S-box are equal to each other for all possible inputs, and  therefore the expected value and the variance that define the CCV are equal.    □

The proposition ensures that two S-boxes of the same class have the same CCV value, but the CCV values of different HW classes could be the same or different. This is a problem that will be investigated in future works.

3.2. Redefining the Equivalence Relation and the HW Classes

For the generation of the elements of each class $<F_a>$, it is convenient to redefine it, representing it from the following $(n+1)$ subsets:

$$C{\left(F\right)}_k=\left\{x\right|HW\left(F\left(x\right)\right)=k,\forall x\in \{0,\dots ,2^n-1\}\}.$$

(11)

Thus, $C{\left(F\right)}_k$ is the set of inputs of the S-box F whose outputs have weight k.

Proposition 3

(Necessary and sufficient condition of HW equivalence). $F_1,F_2$ are HW equivalents if and only if $C{\left(F_1\right)}_k=C{\left(F_2\right)}_k,\forall k\in \{0,\dots ,n\}$.

Proof. 

Starting from the hypothesis, $HW\left(F_1\left(x\right)\right)=HW\left(F_2\left(x\right)\right),\forall x\in \{0,\dots ,2^n-1\}$. If it is assumed that x exists such that $x\in C{\left(F_1\right)}_k$ and $x\notin C{\left(F_2\right)}_k$, then the hypothesis contradicts. On the other hand, assuming that $C{\left(F_1\right)}_k=C{\left(F_2\right)}_k,\forall k\in \{0,1,2,\dots ,n\}$, if there exists an $x\in C{\left(F_1\right)}_k$, then $x\in C{\left(F_2\right)}_k$, and  therefore $HW\left(F_1\left(x\right)\right)=HW\left(F_2\left(x\right)\right)=k$. By redefining the equivalence relationship, the class associated with the S-box $F_a$ can be expressed as: $<F_a>=\left\{F_b\right|C{\left(F_b\right)}_k=C{\left(F_a\right)}_k,\forall k\in \{0,\dots ,n\}\}$. From the redefinition of the class, it is easy to see that it is determined by the $(n+1)$ sets $C{\left(F_a\right)}_k,\forall k\in \{0,\dots ,n\}$.    □

Example 4

(Redefinition of class $<F_{Print}>$.). Let $<F_{Print}>=(HW\left(F_{Print}\left(0\right)\right),\dots ,$ $HW\left(F_{Print}\left(7\right)\right))=(0,1,2,2,3,1,2,1)$. The $C{\left(F_a\right)}_k$ sets that determine the class $<F_{Print}>$ associated with the S-box of PRINT are:

• $C{\left(F_{Print}\right)}_0=\left\{0\right\}$: $F_{Print}\left(x\right)$ inputs x such that $HW\left(F_{Print}\left(x\right)\right)=0$.
• $C{\left(F_{Print}\right)}_1=\{1,5,7\}$: $F_{Print}\left(x\right)$ inputs x such that $HW\left(F_{Print}\left(x\right)\right)=1$.
• $C{\left(F_{Print}\right)}_2=\{2,3,6\}$: $F_{Print}\left(x\right)$ inputs x such that $HW\left(F_{Print}\left(x\right)\right)=2$.
• $C{\left(F_{Print}\right)}_3=\left\{4\right\}$: $F_{Print}\left(x\right)$ inputs x such that $HW\left(F_{Print}\left(x\right)\right)=3$.

Example 5

(Redefinition of class $<F_{AES}>$). The sets $C{\left(F_a\right)}_k$ that determine the class $<F_{AES}>=(HW\left(F_{AES}\left(0\right)\right),\dots ,HW\left(F_{AES}\left(255\right)\right))$ associated with the S-box $F_{AES}$ of the AES, are:

• $C{\left(F_{AES}\right)}_0=\left\{75\right\}$.
• $C{\left(F_{AES}\right)}_1=\{53,57,76,9a,c8,cc,e9,ea\}$.
• C(F_AES)₂ = {5,6,9,24,50,54,5c,5f,71,72,7a,7d,7e,7f,91,9d,b3,b8,c0,c3,c4,cb,cf,e2,e6,ed,f3,ff}.
• $$\begin{gathered} C{\left(F_{AES}\right)}_3=\{1,2,a,b,e,20,23,27,2b,2c,2f,45,51,52,58,5b,5e, \\ 64,68,6b,6f,70,73,77,79,7b,7c,90,92,96,99,9b, \\ 9c,9e,b0,b7,bb,bc,be,bf,c2,c5,c7,c9,ce,d1,da,de, \\ e0,e1,e4,e5,ee,f0,f8,fc\} \end{gathered}$$.
• $$\begin{gathered} C{\left(F_{AES}\right)}_4=\{0,3,4,7,8,c,d,f,1b,1c,1f,21,22,28,29,2d,2e,31, \\ 36,3d,41,42,46,4a,4d,55,56,59,5a,5d,60,63,67,6c, \\ 74,78,80,84,88,8b,8c,93,94,95,97,98,a6,a7,a9,aa, \\ b1,b2,b4,b6,b9,bd,c6,ca,d0,d6,dd,e3,e7,e8,eb,ec, \\ ef,f4,f7,fb\} \end{gathered}$$.
• $$\begin{gathered} C{\left(F_{AES}\right)}_5=\{10,13,14,17,18,19,1e,25,26,2a,32,35,37,3a,3b, \\ 3e,43,47,48,49,4b,4c,4e,61,62,65,66,69,6a,6e,83, \\ 87,8f,9f,a0,a1,a2,a5,ad,ae,b5,ba,c1,cd,d2,d3,d4, \\ d5,d7,d8,d9,f5,f9,fa,fd,fe\} \end{gathered}$$.
• $$\begin{gathered} C{\left(F_{AES}\right)}_6=\{12,15,16,1d,30,33,38,39,3c,3f,40,44,4f,6d,82, \\ 85,89,8a,8e,a3,a4,ab,ac,dc,df,f1,f2,f6\} \end{gathered}$$.
• $C{\left(F_{AES}\right)}_7=\{11,1a,34,81,86,a8,af,db\}$.
• $C{\left(F_{AES}\right)}_8=\left\{8d\right\}$.

The determination of the class by the $(n+1)$ sets allows deducing an algorithm to easily generate the elements of a class: Let $F_a$ be an arbitrary initial S-box. Any permutation of two or more elements within a $C{\left(F_a\right)}_k$ set (or within several $C{\left(F_a\right)}_k$ sets simultaneously), generates a new S-box $F_b$, which belongs to the same HW class $<F_a>$ as the initial S-box $F_a,(F_b\in <F_a>$) since within each subset the weights of their outputs are the same.

3.3. Generation of HW Equivalent S-Boxes. ESboxG Algorithm

We present an equivalent S-box Generator (ESboxG) (Algorithm 1) to generate S-boxes belonging to a class by permuting elements of $C{\left(F_a\right)}_k$ sets.

Algorithm 1 ESboxG

Input: S-box s   Integer $nss$ //Number of sets to be swapped   Integer $mnos$ // Max number of outputs that can be swapped Output: S-box r // HW equivalent with s 1: Select $nss$ weights 2: for each k weight do 3:  create two lists $Inputs\left[k\right]$ and $Outputs\left[k\right]$ // where each input holds in    $Inputs\left[k\right],HW\left(s\right[input\left]\right)=k$ 4: end for 5: for each of the selected $nss$ k weights do 6: $shuffle\left(Outputs\right[k],mnos)$ 7: for $p=0$ to $|C_k|-1$ do 8:   $r\left[Inputs\right[k\left]\right[p\left]\right]=Outputs\left[k\right]\left[p\right]$ 9:  end for 10: end for 11: return r

The complexity of this algorithm is determined by the permutations it performs within the subsets $C{\left(F_a\right)}_k$ (Lines 5–10), in particular by the values of the two parameters $(nss,mnos)$. Three possible cases of different complexity are highlighted:

• The maximum complexity is reached when all elements of all sub-assemblies are exchanged (maximum values of $nss$ and $mnos$).
• The complexity can be reduced by exchanging only elements of a single subset $C{\left(F_a\right)}_k,(nss=1)$.
• The minimum complexity is reached when only two elements are permuted within a single subset ($nss=1,mnos=2$).

Proposition 4

(Necessary condition of belonging to the same class). If two S-boxes $F_a\left(x\right)$ and $F_b\left(x\right)$ belong to the same class, then $C{\left(F_a\right)}_0=C{\left(F_b\right)}_0$ and $C{\left(F_a\right)}_n=C{\left(F_b\right)}_n$, or equivalently: $F_a^{-1}\left(0\right)=F_b^{-1}\left(0\right)$ and $F_a^{-1}(2^n-1)=F_b^{-1}(2^n-1),\forall F_b\in <F_a>$.

Proof. 

The proof is straightforward and is essentially based on two conditions:

1.

The S-boxes of a class are generated by permuting the elements inside the sets

$C{\left(F_a\right)}_k,k=1,\dots n-1$

2.

The sets $C{\left(F_a\right)}_0$ and $C{\left(F_a\right)}_n$ have a single element.

By Condition 2, for each of the sets $C{\left(F_a\right)}_0$ and $C{\left(F_a\right)}_n$, it is not possible to permute elements of equal weight within the same class.

If an element of one of these sets is permuted, it will necessarily be permuted with an element of a different weight, which immediately leads to another HW class through Condition 1. □

3.4. Experimental Verification That all S-Boxes of a Class Have the Same Resistance to Power Attacks

SILK is a high level of abstraction simulator that builds a leakage trace based on a source code of an algorithm and several user-defined parameters. As source code, we used the AES cipher, which is executed using a plain text and a key. We also used the default SILK consumption power noise.

The objective of this experiment was to verify that all the S-boxes of a Hamming weight class have the same resistance to power attacks since they all have the same hypothetical power leakage, according to the Hamming weight leakage model. In particular, it was verified that, with the power leakage traces of an arbitrary S-box $F_a\left(x\right)$, the power attack can be performed on all the S-boxes of its class $<F_a>$. The S-box of the AES cryptographic algorithm was selected as S-box $F_a\left(x\right)$, taking into account that this S-box is vulnerable to this type of attack. The SILK simulator was used only once to generate the power drain traces of the AES S-box. The proposed HW equivalent relationship theoretically ensure homogeneous DPA resistance within each class. To verify it practically, the following experiment was carried out in two steps:

Step 1. With the ESboxG algorithm, 1000 S-boxes belonging to the $<F_{AES}>$ class were generated. The SILK simulator [25] was used to generate the energy leak traces of the AES S-box, using 200 plain texts and the key 00112233445566778899aabbccddeeff. We also used the default SILK consumption power noise. Subsequently, the power attack (CPA) was carried out on the 1000 S-boxes, but, in all cases, the energy leakage generated with the SILK Simulator was used for the first S-box.

It was found that, for each of the 1000 S-boxes generated, the same results were obtained (the correct 16 bytes of the key) as for the first S-box. It is important to note that, in all cases (the 1000 S-boxes), the traces of the first S-box were used. This experimental result confirms that, in practice, HW classes fulfill the theoretically expected property of Section 3.1.

Step 2. The objective of this second step was to illustrate in practice that Step 1 is not obtained with S-boxes that do not belong to the $<F_{AES}>$ class. First, 1000 S-boxes not belonging to the $<F_{AES}>$ class were randomly generated, and the attack was carried out again with the same energy leak traces from step one. Unsurprisingly, no byte was obtained correctly from the key, and the results were different for each S-box.

3.5. Experimental Verification of the Constant Value of Confusion Coefficient Variance CCV within HW Classes

To experimentally confirm that the CCV metric has a constant value within each HW class, a sample of 4 HW classes were taken: $<F_{AESCC}>$, $<F_{SCREAM}>$, $<F_{AES}>$ and $<F_{STRIBOG}>$. In each class, 10,000 S-boxes were generated by the ESboxG algorithm, and its CCV value was calculated. The results after experimenting were as expected. For the 10,000 S-boxes, the same constant value of CCV was obtained within the class in each class.

There are differences between the CCV values of the four analyzed classes.

• $CCV(<F_{AESCC}>)=0.149357$;
• $CCV(<F_{SCREAM}>)=0.121967$;
• $CCV(<F_{AES}>)=0.111304$; and
• $CCV(<F_{STRIBOG}>)=0.097765$.

By decreasing these CCV values, the S-boxes are decreased by their theoretical resistance to power attacks as follows: AESCC, SCREAM, AES and STRIBOG (as in [26]).

3.6. New Search Strategy for S-Boxes Resistant to Power Attacks Based on HW Classes

This section proposes a new search strategy for S-boxes resistant to power attacks based on the HW classes. It reduces the search space avoiding unnecessary operations. We suggest moving between HW classes and avoiding analyzing all S-boxes in the same class because they have the same DPA resistance. This new partition in classes allows us to define a new approach to search S-boxes with high CCV, and that also satisfies other desirable properties such as high nonlinearity. The proposed new strategy consists of two steps:

Step 1. As long as the S-box evaluated has a CCV value less than the desired one, the HW class must be changed.

Step 2. When a high CCV value is reached, it is necessary to search within that class the S-boxes that meet the other cryptographic properties, such as high nonlinearity.

The practical application of this strategy supports two aspects. First, changing classes is enough to swap at least two elements of the input whose outputs have different weights, and, second, the generation algorithm of S-boxes within the class (ESboxG algorithm) is easy to use and not complicated to implement. It is enough to permute two elements within one of the subsets $C{\left(F\right)}_k$ defined in Section 3.2.

Different meta-heuristics can be used to perform movement between classes and within classes. The objective function used for the search within the classes will depend on the remaining cryptographic properties of the S-box to be optimized.

3.7. Comparison between the Partition of the Space of S-Boxes in Related Classes and Hamming Weight Classes

Properties of the Partition of the space of S-boxes in Affine Classes.

1.

Constant cryptographic properties within classes.

–

The nonlinearity is constant within each class: the classes, by way of construction, fulfill the property that all the S-boxes of a class have the same nonlinearity value. This ensures that all S-boxes in a class have the same resistance against linear attacks.

–

Other cryptographic properties are not constant within each class since they were not taken into account for the definition of these classes. For example, the resistance to power attacks is not constant within the class; if measured with the theoretical metric of the confusion coefficient variance (CCV), this metric can take different values for S-boxes that belong to the same class.

2.

Movement between classes and within classes.

–

Movement within each class: Given an S-box $F_a$, to obtain another S-box $F_b$ of the same class, transformations related to $F_a$ are performed.

–

Movement between different classes: Given an S-box $F_a$, to obtain another S-box $F_b$ belonging to a different class, it is enough that affine transformations do not relate the two S-boxes.

3.

Number of classes.

–

The number of affine classes is approximately $\left(2^n\right)!/{\left|G\right|}^2$, where $\left|G\right|$ is the linear or affine group size, as estimated in [27].

Properties of the S-box Space Partition in Hamming Weight Classes (HW) Based on the Theoretical Resistance to Power Attacks According to the Metric of the Confusion Coefficient Variance (CCV).

1.

Constant cryptographic properties within classes.

–

The variance of the confusion coefficient variance (CCV) is constant within each class: the “theoretical” resistance to power attacks is constant within the class. The HW classes, by the way of construction, fulfill the property that all the S-boxes of a class have the same value of the confusion coefficient variance (CCV). This ensures that all S-boxes in a class have the same “theoretical” resistance against power attacks, based on this metric.

–

None of the known theoretical metrics of resistance against Power Attacks is exact, nor is the confusion coefficient variance (CCV), therefore, the actual resistance against these attacks is “approximately” constant within the class.

–

Other cryptographic properties are not constant within each class, since they were not taken into account for the definition of these classes. For example, nonlinearity can take different values for S-boxes that belong to the same Hamming weight class.

2.

Movement between classes and within classes.

–

Movement within each class: Given an S-box $F_a$, to obtain another S-box $F_b$ of the same class, it is necessary and sufficient to swap between two elements of the output of $F_a$ that have the same Hamming weight. The swap can be generalized between several pairs of elements, as long as the two elements of each pair have the same weight, which can be different between the pairs.

–

Movement between different classes: Given an S-box $F_a$, to obtain another S-box $F_b$ belonging to a different class, it is necessary and sufficient to perform the swap between two elements of the output that have different Hamming weights.

3.

Number of classes.

–

The number of classes and the number of S-boxes in each class are estimated in this work (by two different ways) for any n, by means of Propositions 5 and 6.

–

The number of classes is exponentially less than the number of S-boxes.

–

For $n=3$, in Partition of the 3 × 3S-box space into equivalence classes, the list of the 1120 HW classes is given.

3.8. Quantifying the Search-Space Reduction Achieved Using the Partition into HW Classes Instead of Searching by S-Boxes

In previous sections, a new partition in equivalence classes is proposed for the S-boxes of $n\times n$, denoted as a partition in Hamming weight (HW) classes. According to the Hamming weight model, all S-boxes in an HW class have the same hypothetical power leakage. According to the CCV metric, we experimentally verified that all S-boxes of a class have the same theoretical resistance to power attacks. Based on this result, we propose a new strategy consisting of going through the class space and not the S-box space, and we argue that this reduces the search space, when the search is performed from class to class.

In this section, for the S-boxes of $n\times n$, we obtain the expression of the exact number of Hamming weight classes and the number of S-boxes within each class. Using this expression, we quantify the reduction in the search space associated with this new strategy. In particular, it is shown that, as n increases, the number of classes represents an increasingly smaller proportion of the number of S-boxes. For $n=3,4,5,6,7,8$, we calculate the total number of classes, the number of S-boxes per class and the reduction achieved in the search space when going through the class space HW and not the space of S-boxes.

3.8.1. Estimate of the Number of HW Classes and the Number of S-Boxes in Each Class as Permutation with Repetition

Proposition 5

(Calculating the number of HW classes). When the space of $\left(2^n\right)!$ S-boxes of dimension $n\times n$ is partitioned into Hamming weight (HW) classes:

(a) 

The total number of HW equivalence classes is: $P{R}_{2^n}^{C(n,0),\dots ,C(n,n)}=\frac{\left(2^n\right)!}{{\prod }_{r=0}^{n}C(n,r)!}$.

(b) 

The total number of S-boxes in each HW equivalence class is: ${\prod }_{r=0}^{n}C(n,r)!$.

Proof. 

The demonstration is direct because the HW classes definition meets that each class is equivalent to a permutation with repetition of $2^n$ elements grouped into $(n+1)$ groups, where group r has exactly $C(n,r)$ equal elements. Keep in mind that, if the $2^n$ outputs of the S-boxes $\{S\left(X\right):X=0,\dots ,2^n-1\}$ are grouped by their weights, then the $2^n$ weights of these outputs $\{\parallel S\left(X\right)\parallel :S\left(X\right)=0,\dots ,2^n-1\}$ are divided into $(n+1)$ groups corresponding to the $(n+1)$ different values $r=0,\dots ,n$, which can take their weights $\{\parallel S(X)\parallel =r:r=0,\dots ,n\}$. The essential observation is that classes are defined by the permutations of the positions occupied by the $(n+1)$ groups. In turn, within a class, the S-boxes are determined by the permutation of the groups’ elements.

In group r, there are $C(n,r)$ elements (the ways of locating r ones in a binary vector of length n), corresponding to outputs of the S-box whose weights are equal to r. It is important to note that the order is not crucial in each group because all the weights are equal to r (indistinguishable elements). However, the order is essential between groups because they correspond to different weights (distinguishable elements). Therefore, to find the number of HW classes of the S-boxes of $n\times n$, we directly applied the formula $P{R}_{2^n}^{C(n,0),\dots ,C(n,n)}$ which calculates the number of permutations with repetition. From here (a) follows.

Given that in group r, there are precise $C(n,r)$ elements equal to r; then, they can be permuted in $\left(C\right(n,r\left)\right)!$ ways. In general, we can permute the elements within the groups in ${\prod }_{r=0}^{n}C(n,r)!$, which corresponds to the number of S-boxes within a class, demonstrating the statement in (b). □

We now dwell in an interpretation of Proposition 5. Notice that the numerator $\left(2^n\right)!$ corresponds to the total number of S-boxes of $n\times n$, while the denominator ${\prod }_{r=0}^{n}C(n,r)!$ is the number of S-boxes within a class and its quotient is exactly the number of classes. Although this is an exact expression very appropriate for theoretical analysis, it should be noted that, in practice, for large values of $\left(2^n\right)$ and $C(n,r)$, the calculation of their factorials will be approximate, using the Stirling formula. The following Corollary will be very useful to quantify the reduction of the search space.

Corollary 1.

The number of HW classes among the number of S-boxes of $n\times n$ is equal to:

$$\frac{NumberofHWclasses}{NumberofS\text{-}boxesofn\times n}=\frac{P{R}_{2^n}^{C(n,0),\dots ,C(n,n)}}{\left(2^n\right)!}=\frac{1}{{\prod }_{r=0}^{n}C(n,r)!}.$$

(12)

Proof. 

Using Proposition 5, $P{R}_{2^n}^{C(n,0),\dots ,C(n,n)}=\frac{\left(2^n\right)!}{{\prod }_{r=0}^{n}C(n,r)!}$

$$\frac{NumberofHWclasses}{Numberof\mathrm{S}\text{-}\mathrm{boxes}ofn\times n}=\frac{P{R}_{2^n}^{C(n,0),\dots ,C(n,n)}}{\left(2^n\right)!}=\frac{\frac{\left(2^n\right)!}{{\prod }_{r=0}^{n}C(n,r)!}}{\left(2^n\right)!}=\frac{1}{{\prod }_{r=0}^{n}C(n,r)!}.$$

(13)

□

3.8.2. Reduced Search-Space

The corollary above provides an inverse measure of the reduction in search space achieved by replacing the S-boxes path with the path over the HW classes. It tells us what fraction of the initial space of S-boxes is reduced by HW’s classes space. The lower the value of $\frac{1}{{\prod }_{r=0}^{n}C(n,r)}$ = $\frac{1}{{\prod }_{r=1}^{n-1}C(n,r)}$, the more significant the reduction achieved when going through the classes and not the S-boxes.

Now, we discuss the reduction speed as a function of n. Note that as n increases, the value ${\prod }_{r=0}^{n}C(n,r)!$ grows very quickly and $\frac{1}{{\prod }_{r=0}^{n}C(n,r)!}$ decreases very rapidly. Note that

$$\underset{n\to \infty }{lim}\frac{NumberofHWclasses}{NumberofS-boxesofn\times n}=\underset{n\to \infty }{lim}(\frac{1}{{\prod }_{r=0}^{n}C(n,r)!})=0.$$

(14)

The above expression shows that as n increases, the class space’s dimension becomes an ever-smaller fraction of the S-box space. This fraction decreases very rapidly as n grows.

3.8.3. Examples of the Number of HW Classes, the Number of S-Boxes per Class and the Reduction in Search-Space Achieved with the New Proposed Strategy

In this subsection, we illustrate the previous proposition’s application to estimate the search space reduction using some examples (see

Table 3. Example for $n=3,4,5,6,7,8$ estimate of the number of S-boxes, number of HW classes, the number of S-boxes per class and the reduction in search space.

n	Number $\left(2^{\mathit{n}}\right)!$ of S-Boxes $\mathit{n}\times \mathit{n}$	Number ${\mathit{PR}}_{2^{\mathit{n}}}^{\mathit{C}(\mathit{n},0),\mathit{\dots },\mathit{C}(\mathit{n},\mathit{n})}$ of HW Classes	${\prod }_{\mathit{r}=0}^{\mathit{n}}\mathit{C}(\mathit{n},\mathit{r})!$ of S-Boxes in Each Class	$\frac{1}{{\prod }_{\mathit{r}=0}^{\mathit{n}}\mathit{C}(\mathit{n},\mathit{r})}$
3	$8!=40320$∼${10}^4$	1120∼${10}^3$	36∼${10}^1$	∼${10}^{-1}$
4	$16!$∼${10}^{13}$	∼${10}^7$	∼${10}^6$	∼${10}^{-6}$
5	$32!$∼${10}^{35}$	∼${10}^{18}$	∼${10}^{17}$	∼${10}^{-17}$
6	$64!$∼${10}^{89}$	∼${10}^{46}$	∼${10}^{43}$	∼${10}^{-43}$
7	$128!$∼${10}^{215}$	∼${10}^{163}$	∼${10}^{52}$	∼${10}^{-52}$
8	256∼${10}^{506}$	∼${10}^{190}$	∼${10}^{316}$	∼${10}^{-316}$

).

We next discuss some observations on the data shown in Table 3. With respect to the dimension of the class space, notice how for $n=3,4,5,6,7,8$ the dimension of the class space is, respectively, equal to ${10}^{-1}$, ${10}^{-6}$, ${10}^{-17},{10}^{-43}$, ${10}^{-52}$ and ${10}^{-316}$, i.e., for each part of the initial space of S-boxes, there is a smaller and smaller fraction of the initial space. Note that, for $n=3,4,5,6,7$, the number of classes is greater than the class’s cardinal, while, for $n=8$, the number of classes is less than the class’s cardinal.

On the exponential reduction of space, for $n=8$, the dimension of the class space is approximately ${10}^{316}$ times less than the initial space of S-boxes. Therefore, when applying the proposed strategy of moving from class to class and not from S-box to S-box, the reduction of the search space is of the order ${10}^{316}$. Importantly, by rejecting a class for having a low CCV value, one is simultaneously rejecting approximately ∼${10}^{316}$ S-boxes. On the other hand, accepting a class, due to having a high value of CCV, there are approximately ${10}^{316}$ S-boxes among which to look for some that meet the remaining cryptographic properties.

Now, relating the comparison of S-box space partitions, consider the case $n=4$. In [5], for $n=4$, the bijective S-box space is partitioned into classes considering the resistance to differential and linear cryptanalysis. In this work, the space of S-boxes is divided into HW classes according to their theoretical resistance to power attacks, according to the CV metric. It would be very interesting to compare both partitions, which is left for future work.

With respect to all S-boxes in a $3\times 3$ class, consider the following. For the $3\times 3$ S-box of the PRINT cryptographic algorithm [28], the 36 equivalent S-boxes were generated. They are shown in the Appendix. It is observed how the necessary condition given in Proposition 4 is fulfilled. The preimages of 0 and $7=2^3-1$ are constant within the class: $F_a^{-1}\left(0\right)=F_b^{-1}\left(0\right)=0$ and $F_a^{-1}\left(7\right)=F_b^{-1}\left(7\right)=4$, $\forall F_b\in <F_a>$. The 1120 HW equivalence classes were constructed.

3.8.4. Estimation of the Number of HW classes and the Number of S-boxes in Each Class as an Occupation Problem

The following proposition provides another alternative way of calculating the number of classes and the number of S-boxes per class.

Proposition 6

(Calculating the S-box number within each HW class). When we partition the space of $\left(2^n\right)!$ S-boxes of dimension $n\times n$, into Hamming weight (HW) classes, then the following hold:

(a) 

The number of “$HammingWeight$” equivalence classes is equal to:

$$N_{HW}=2^n\prod _{r=1}^{n}C\left(\left[2^n-\sum _{i=0}^{r-1}C(n,i)\right],C(n,r)\right)$$

(15)

(b) 

The number of S-boxes within each HW equivalence class is exactly equal to:

$$N_S=\frac{\left(2^n\right)!}{2^n{\prod }_{r=1}^{n}C\left(2^n-{\sum }_{i=0}^{r-1}C(n,i),C(n,r)\right)}$$

(16)

Proof. 

The demonstration of Statement (a) is based on modeling the construction of the classes using an occupation problem, with successive dependent launches. It is taken into account that the $2^n$ weights $\{\parallel S\left(X\right)\parallel :S\left(X\right)=0,\dots ,2^n-1\}$ of the outputs of the S-boxes can be divided into $(n+1)$ groups corresponding to the $(n+1)$ different values $\{r:r=0,\dots ,n\}$ that can take their weights $\{\parallel S(X)\parallel =r:r=0,\dots ,n\},$ where the group r contains exactly $C(n,r)$ equal elements. The essential observation is that each class corresponds to a different location of the $(n+1)$ weight groups in the $2^n$ places. Without loss of generality, it can be assumed that the groups are located in increasing order of the value of r.

The first group corresponds to the weight $r=0$, containing $C(n,0)=1$, only one element and can be located in any of the $C(2^n,1)=2^n$ possible places. For the remaining groups $r=1,\dots ,(n-1)$, the reduction in the number of available places caused by the location of the previous groups must be taken into account, as discussed below.

In general, to locate the $C(n,r)$ elements of the rth group, for $r=1,\dots ,(n-1)$, there are exactly $\left[2^n-{\sum }_{i=0}^{r-1}C(n,i)\right]$ available places, since the $\left[{\sum }_{i=0}^{r-1}C(n,i)\right]$ places occupied by the previous groups are subtracted from the $2^n$ starting places. The selection of those $C(n,r)$ positions among the available $\left[2^n-{\sum }_{i=0}^{r-1}C(n,i)\right]$ can be done in $C\left(\left[2^n-{\sum }_{i=0}^{r-1}C(n,i)\right],C(n,r)\right)$ forms. Therefore, the total number of ways to locate the $(n+1)$ weight groups in the $2^n$ places is equal to $2^n{\prod }_{r=1}^{n}C(2^n-{\sum }_{i=0}^{r-1}C(n,i),C(n,r))$, which is exactly the number of HW classes.

Now, we turn to Statement (b). By dividing the total number $\left(2^n\right)!$ of S-boxes of $n\times n$ between the number of classes, $\left(2^n\right){\prod }_{r=1}^{n}C(\left[2^n-{\sum }_{i=0}^{r-1}C(n,i)\right],C(n,r))$ calculated for Statement (a), it is obtained that the number of S-boxes inside each class is

$$N_S=\frac{\left(2^n\right)!}{2^n{\prod }_{r=1}^{n}C(2^n-{\sum }_{i=0}^{r-1}C(n,i),C(n,r))}.$$

(17)

□

3.9. Examples Using Proposition 6

In this subsection, we present some examples derived from Proposition 6.

Example 6.

Let $n=3$. The number of classes is equal to

$2^n{\prod }_{r=1}^{n}C(\left[2^n-{\sum }_{i=0}^{r-1}C(n,i)\right],C(n,r))=2^3{\prod }_{r=1}^{3}C(\left[2^3-{\sum }_{i=0}^{r-1}C(3,i)\right],C(3,r))$

$$\begin{gathered} =8\left[C(8-1,3)\right]\left[C(7-3,3)\right]\left[C(4-3,1)\right] \\ =8\left[C(7,3)\right]\left[C(4,3)\right]\left[C(1,1)\right] \\ =8(35)(4)(1)=1120HWclassesof3\times 3. \end{gathered}$$

This example illustrates the calculation of the number of HW classes by Proposition 6, according to which there are 1120 classes. This statement was tested experimentally and the 1120 classes obtained are shown in the Appendix C (see

Table A5. The 36 S-boxes equivalent to $F_{Print}$ and the 1120 HW classes of $3\times 3$.

Row/Column	1	2	3	4	5	6	7	8
Input x to the S-box	0	1	2	3	4	5	6	7
$F1=F_{Print}-$S-box	0	1	3	6	7	4	5	2
S-box equiv. F2	0	1	3	5	7	4	6	2
S-box equiv.F3	0	1	5	3	7	4	6	2
S-box equiv.F4	0	1	5	6	7	4	3	2
S-box equiv.F5	0	1	6	3	7	4	5	2
S-box equiv.F6	0	1	6	5	7	4	3	2
S-box equiv.F7	0	1	3	6	7	2	5	4
S-box equiv.F8	0	1	3	5	7	2	6	4
S-box equiv.F9	0	1	5	3	7	2	6	4
S-box equiv.F10	0	1	5	6	7	2	3	4
S-box equiv.F11	0	1	6	3	7	2	5	4
S-box equiv.F12	0	1	6	5	7	2	3	4
S-box equiv.F13	0	4	3	6	7	1	5	2
S-box equiv.F14	0	4	3	5	7	1	6	2
S-box equiv.F15	0	4	5	3	7	1	6	2
S-box equiv.F16	0	4	5	6	7	1	3	2
S-box equiv.F17	0	4	6	3	7	1	5	2
S-box equiv.F18	0	4	6	5	7	1	3	2
S-box equiv.F19	0	4	3	6	7	2	5	1
S-box equiv.F20	0	4	3	5	7	2	6	1
S-box equiv.F21	0	4	5	3	7	2	6	1
S-box equiv.F22	0	4	5	6	7	2	3	1
S-box equiv.F23	0	4	6	3	7	2	5	1
S-box equiv.F24	0	4	6	5	7	2	3	1
S-box equiv.F25	0	2	3	6	7	1	5	4
S-box equiv.F26	0	2	3	5	7	1	6	4
S-box equiv.F27	0	2	5	3	7	1	6	4
S-box equiv.F28	0	2	5	6	7	1	3	4
S-box equiv.F29	0	2	6	3	7	1	5	4
S-box equiv.F30	0	2	6	5	7	1	3	4
S-box equiv.F31	0	2	3	6	7	4	5	1
S-box equiv.F32	0	2	3	5	7	4	6	1
S-box equiv.F33	0	2	5	3	7	4	6	1
S-box equiv.F34	0	2	5	6	7	4	3	1
S-box equiv.F35	0	2	6	3	7	4	5	1
S-box equiv.F36	0	2	6	5	7	4	3	1

).

Example 7.

For $n=8$, $\left(2^n\right)!$ = $\left(256\right)!\sim {10}^{506}$ by F. Stirling (see

Table 4. Number of classes for $n=8$, by Proposition 5.

r	$\mathit{C}\left(\left[2^{\mathit{n}}-{\sum }_{\mathit{i}=0}^{\mathit{r}-1}\mathit{C}\left(\mathit{n},\mathit{i}\right)\right],\mathit{C}\left(\mathit{n},\mathit{r}\right)\right)$	Estimated Value	Accumulated Product
0	C(256, 1) = 256	∼${10}^2$	∼${10}^2$
1	C(256-1, 8) = C(255, 8)	∼${10}^{15}$	∼${10}^{17}$
2	C(255-8, 28) = C(247, 28)	∼${10}^{37}$	∼${10}^{54}$
3	C(255-8, 28) = C(219, 56)	∼${10}^{54}$	∼${10}^{108}$
4	C(219-56, 70) = C(163, 70)	∼${10}^{47}$	∼${10}^{155}$
5	C(163-70, 56) = C(93, 56)	∼${10}^{27}$	∼${10}^{182}$
6	C(93-56, 28) = C(37, 28)	∼${10}^9$	∼${10}^{191}$
7	C(37-28, 8) = C(9, 8) = 9	∼${10}^1$	∼${10}^{192}$
8	C(9-8, 1) = C(1, 1) = 1	∼${10}^0$	∼${10}^{192}$
# of classes	Exactly $[256\times C(255,8)\times C(247,28)\times$ $C(219,56)\times C(163,70)\times$ $C(93,56)\times C(37,28)\times 9]$		Approximately ∼${10}^{192}$

). This example illustrates the difficulty in calculating the number of S-boxes even for small values of $n(n=8)$ if it is necessary and convenient to use the Stirling formula.

Finally, we establish a comparison of the number of classes estimated by Propositions 5 and 6. For $n=3$, it is observed that both values coincide $(1120HWclassesof3\times 3)$, as expected since they are exact calculations. For $n=8$, the Stirling formula was used in both cases to approximate different factorials, so there may be differences between the two estimates (see

Table 5. $n=8$, number of classes estimated by Propositions 5 and 6.

	Estimated Number of HW Classes of $8\times 8$
Proposition 5	∼${10}^{190}$
Proposition 6	∼${10}^{192}$

). The difference between both estimates is of the order ${10}^2$. It can be considered acceptable, given the dimensions of the spaces being estimated. This comparison can be improved using the refinement of the Stirling formula.

4. Conclusions

The main results of the present work are the proposal of a new equivalence relationship between S-boxes and their application to exponentially reduce the search space for nonlinear S-boxes and resistance to power attacks, when the search is performed from class to class.

This result provides new theoretical knowledge about the internal structure of the bijective S-box space and its partition into equivalence classes according to its resistance to power attacks. As far as we know, there are no previous reports of results of this type

New equivalence classes: This paper proposes a new definition of equivalence classes to relate S-boxes according to their power leak following the Hamming weight model (HW equivalence). A new algorithm is presented, which randomly generates an S-box HW equivalent to the initial one, given an initial S-box of input. Three variants of different complexity are proposed to apply this algorithm. It was demonstrated that the metric “variance of the confusion coefficient (CCV)” that theoretically measures the resistance of an S-box against power attacks takes constant values within the HW classes. This result was confirmed experimentally (using the previous algorithm) for four S-boxes classes, corresponding to the S-boxes of the AESCC, SCREAM, AES and STRIBOG algorithms.

Exponential reduction of the search space: Based on these new HW equivalence classes, a new strategy was proposed to search for S-boxes resistant to power attacks, essentially consisting of moving in the class space and not in the S-box space, changing of classes as long as the CCV value is low. When a high CCV class is found, the S-boxes inside the class are scanned to evaluate the remaining cryptographic properties of the S-boxes, such as nonlinearity. An advantage of this strategy is that it is easily applied because, to change classes, it is enough to swap at least two elements of different hamming weights, while, to change S-boxes within the class, it is enough to swap at least two elements of equal weight. The main advantage of this strategy is that it allows an exponential reduction of the search space. The cardinal of the class space was calculated using two different methods. Its comparison with the cardinal of the space of S-boxes shows that, as n increases, the class space represents a smaller and smaller fraction of the space of S-boxes. For $n=8$, this reduction reaches the order of ${10}^{316}$. This result was confirmed experimentally for $n=3$.

In future work, we will investigate the probability distribution of other S-box cryptographic properties within these new HW classes and how to use these distributions to improve the effectiveness or efficiency of searching for S-boxes that are not linear with a high value of CCV. On the other hand, although all S-boxes in a class have the same CCV value, we will investigate different HW classes with the same CCV value and the conditions that these classes must meet. Future studies will investigate whether the increase in the number of permuted elements influences the search’s effectiveness. If positive, the optimal number of elements to be exchanged must be determined, considering the compromise between effectiveness and efficiency. In this work, the space of S-boxes was divided into HW classes according to their theoretical resistance to power attacks, according to the CCV metric. For $n=4$, it would be interesting to compare with the partition of G. Leander and A. Poschmann [5], which is left proposed.